An Ultrashort Wavelength Multi/Demultiplexer via Rectangular Liquid-Infiltrated Dual-Core Polymer Optical Fiber
Abstract
1. Introduction
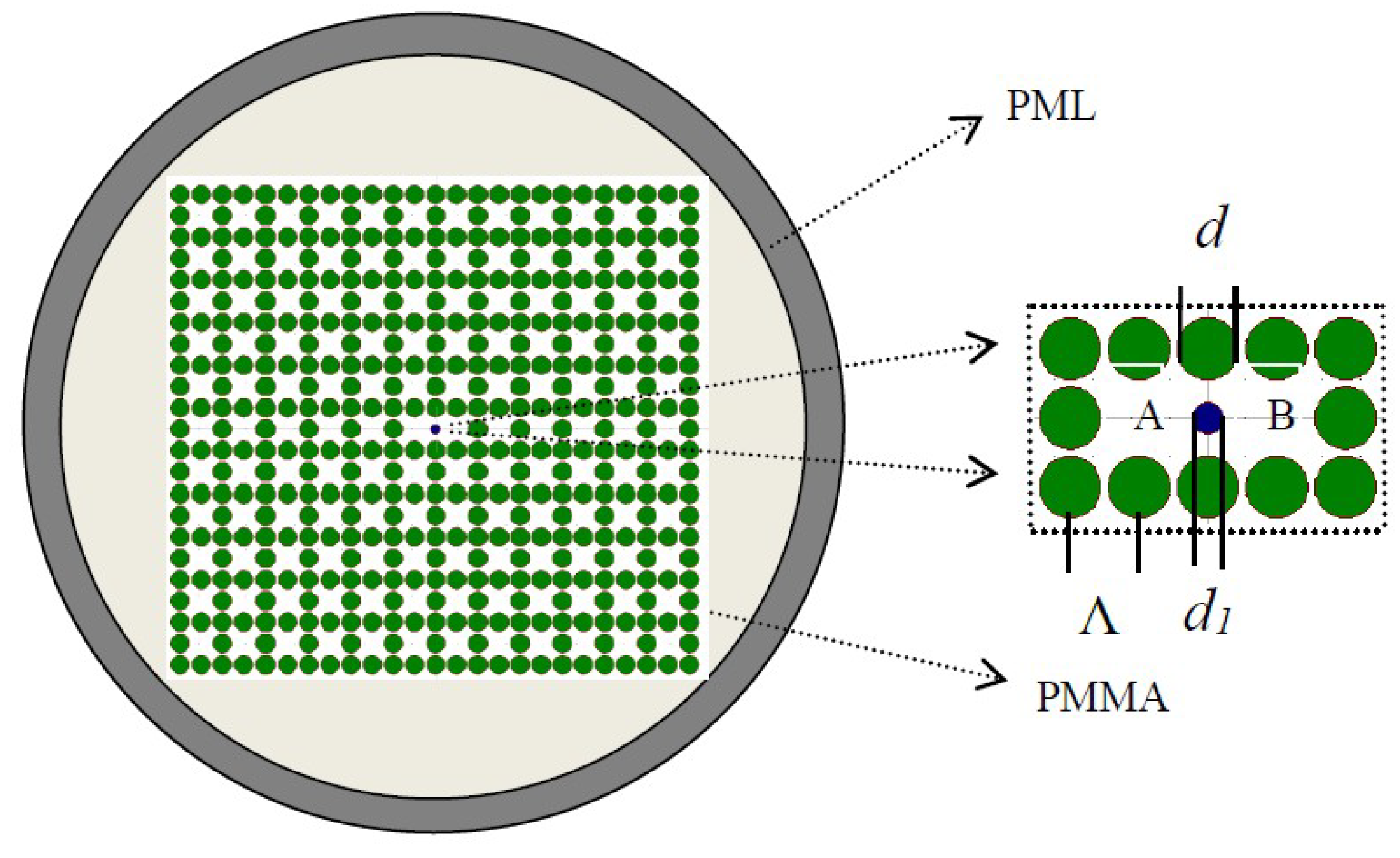
2. Design Principle and Theoretical Modeling
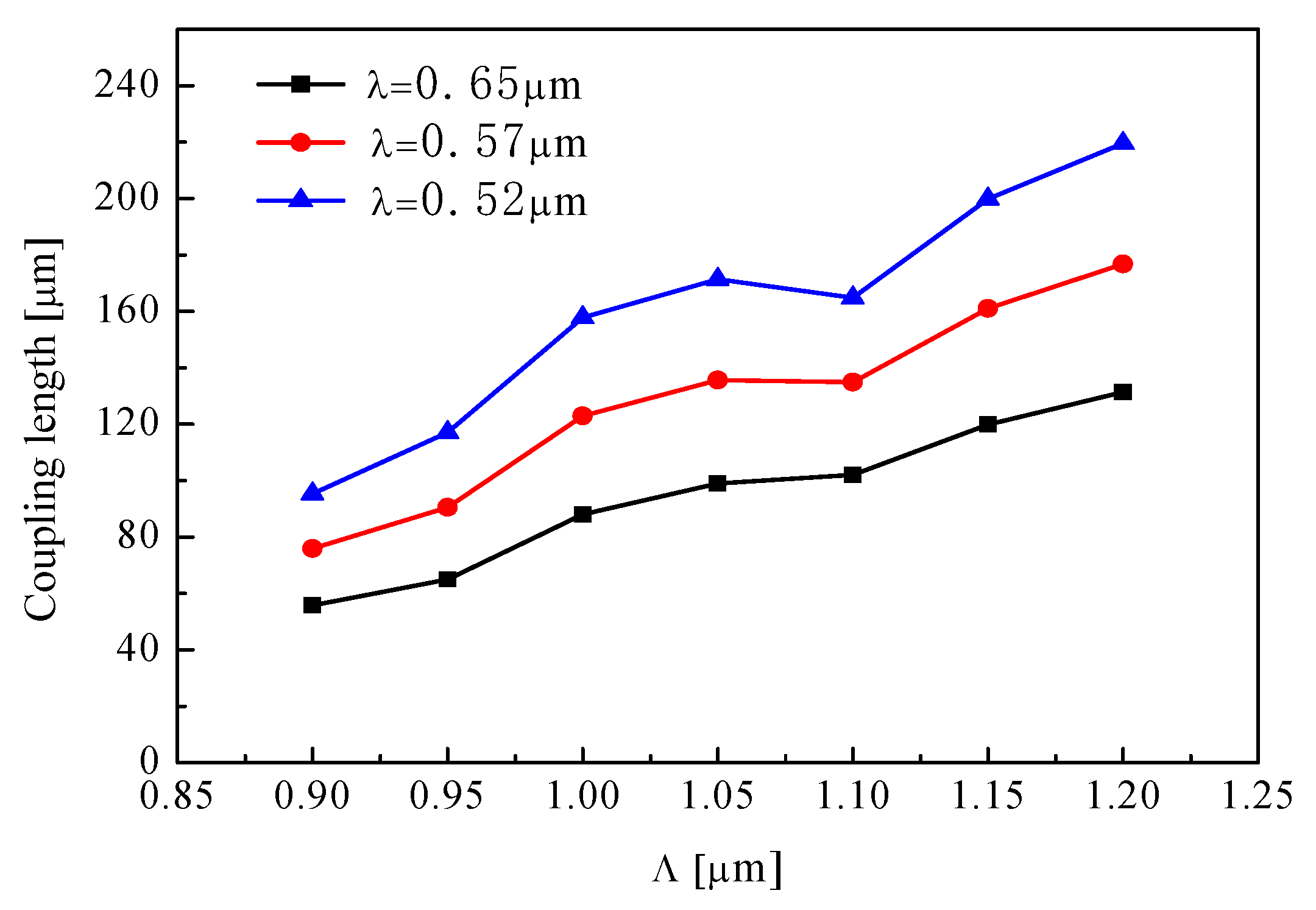
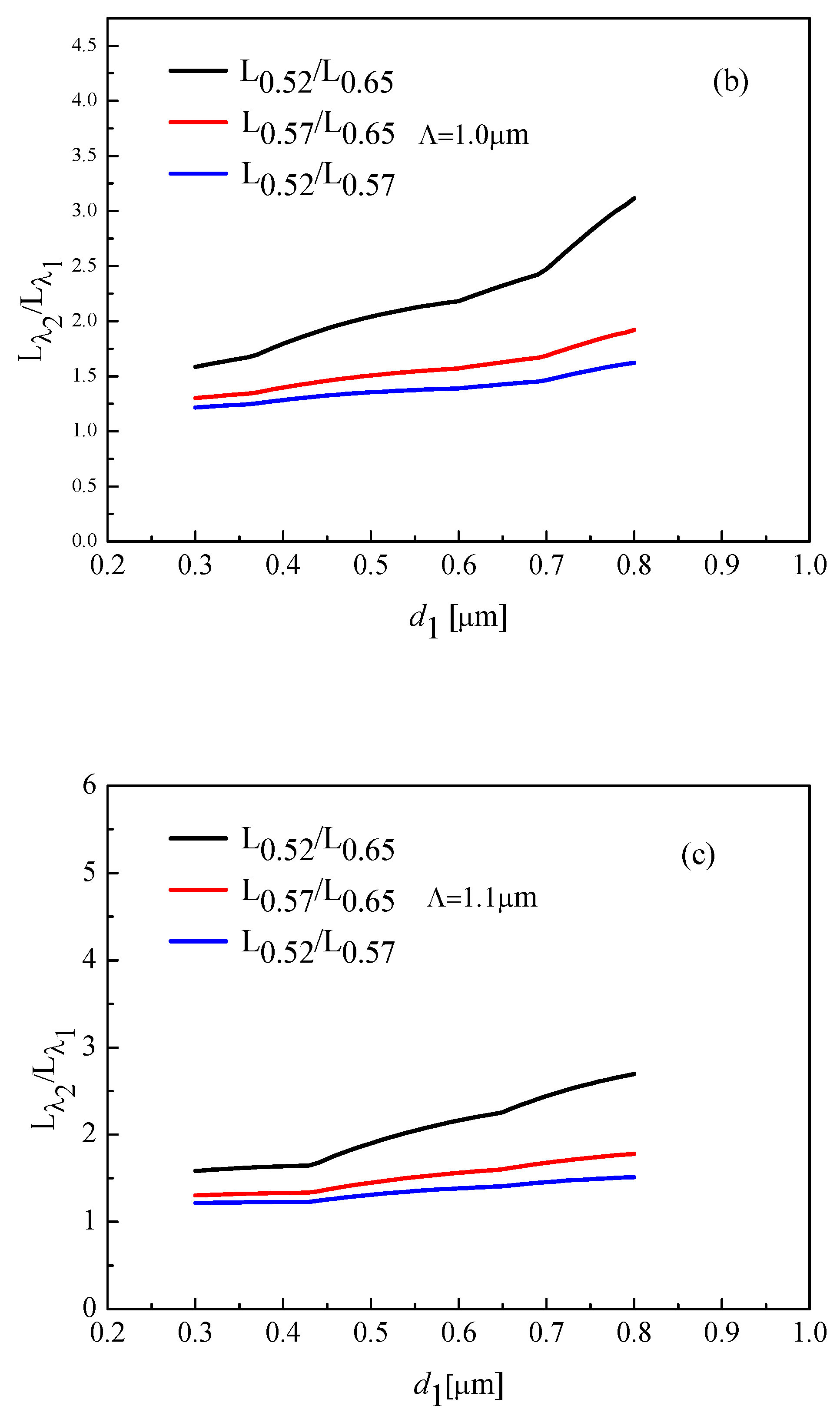
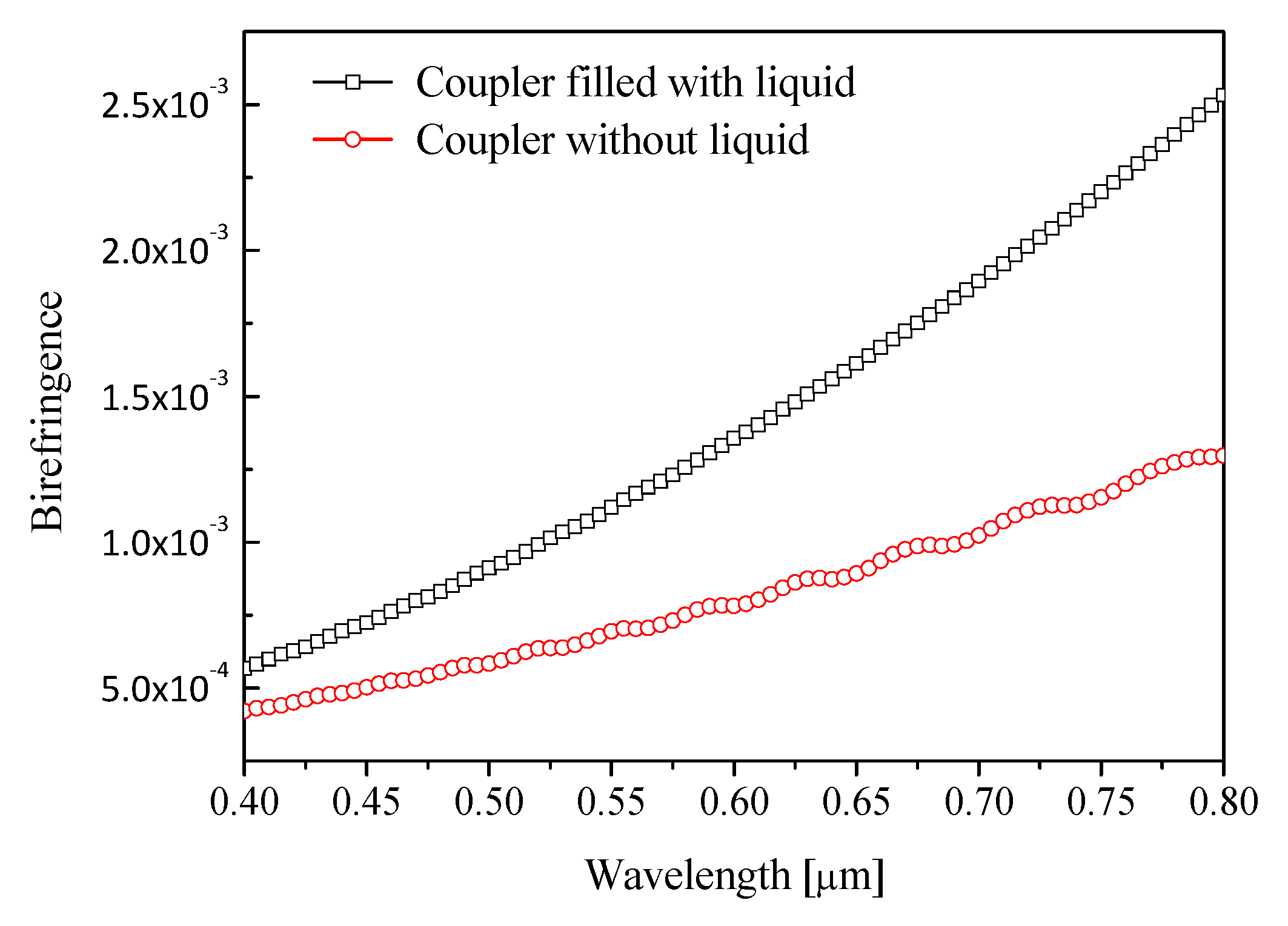
3. Simulated Results and Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Han, Y.; Hu, G. A novel MUX/DEMUX based on few-mode FBG for mode division multiplexing system. Opt. Commun. 2016, 367, 161–166. [Google Scholar] [CrossRef]
- Kudo, M.; Ohta, S.; Taguchi, E.; Fujisawa, T.; Sakamoto, T.; Matsui, T.; Tsujikawa, K.; Nakajima, K.; Saitoh, K. A proposal of Mach–Zehnder mode/wavelength multi/demultiplexer based on Si/silica hybrid PLC platform. Opt. Commun. 2019, 433, 168–172. [Google Scholar] [CrossRef]
- Tomlinson, W.; Lin, C. Optical wavelength-division multiplexer for the 1–1.4 μm spectral region. Electron. Lett. 1978, 14, 345. [Google Scholar] [CrossRef]
- Saitoh, K.; Sato, Y.; Koshiba, M. Coupling characteristics of dual-core photonic crystal fiber couplers. Opt. Express 2003, 11, 3188. [Google Scholar] [CrossRef]
- Saitoh, K.; Hanzawa, N.; Sakamoto, T.; Fujisawa, T.; Yamashita, Y.; Matsui, T.; Tsujikawa, K.; Nakajima, K. PLC-based mode multi/demultiplexers for mode division multiplexing. Opt. Fiber Technol. 2017, 35, 80–92. [Google Scholar] [CrossRef]
- Ren, F.; Yu, J.; Wang, J. Spatial-mode switchable ring fiber laser based on low mode-crosstalk all-fiber mode MUX/DEMUX. Opt. Fiber Technol. 2018, 101, 21–24. [Google Scholar] [CrossRef]
- Nozhat, N.; Granpayeh, N. Analysis of the plasmonic power splitter and MUX/DEMUX suitable for photonic integrated circuits. Opt. Commun. 2011, 284, 3449–3455. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L.; Yang, X. Computationally efficient coherent detection and parameter estimation algorithm for maneuvering target. Signal Process. 2019, 155, 130–142. [Google Scholar]
- Dutta, A.K.; Dutta, N.K.; Fujiwara, M. WDM Technologies: Passive Optical Components; Academic Press: Cambridge, UK, 2003. [Google Scholar]
- Louro, P.; Vieira, M.; Vieira, M.; Fernandes, M.; Fantoni, A.; Francisco, C.; Barata, M. Optical multiplexer for short range communications. Physica E Low Dimens. Syst. Nanostruct. 2009, 41, 1082–1085. [Google Scholar]
- Lee, M.H.; Ha, C.; Jeong, H.-S.; Kim, D.W.; Lee, S.H.; Lee, M.H.; Kim, K.H. Wavelength-division-multiplexed InGaAs/InP avalanched photodiodes for quantum key distributions. Opt. Commun. 2016, 361, 162–167. [Google Scholar] [CrossRef]
- Romero, R.; Frazăo, O.; Floreanic, F.; Zhang, L.; Marquesa, P.V.S.; Salgado, H.M. Chirped fiber Bragg grating based multiplexer and demultiplexer for DWDM applications. Opt. Lasers Eng. 2005, 43, 987–994. [Google Scholar] [CrossRef]
- Palai, G.; Beura, S.; Gupta, N.; Sinha, R. Optical MUX/DEMUX using 3D photonic crystal structure: A future application of silicon photonics. Optik 2017, 128, 224–227. [Google Scholar] [CrossRef]
- Palai, G. Optimization of optical waveguide for optical DEMUX at optical windows. Optik 2016, 127, 2590–2593. [Google Scholar] [CrossRef]
- Palai, G. Band analysis of polymer photonic structure for MUX/DEMUX application. Optik 2017, 140, 1086–1090. [Google Scholar] [CrossRef]
- Knight, J.C. Photonic crystal fiber. Nature 2003, 424, 847–851. [Google Scholar] [CrossRef] [PubMed]
- Russell, P. Photonic crystal fiber. Science 2003, 299, 358–362. [Google Scholar] [CrossRef]
- Buczynski, R. Photonic crystal fibers. Acta Phys. Polonica A 2004, 106, 147–167. [Google Scholar] [CrossRef]
- Barkou, S.E.; Broeng, J.; Bjarklev, A. Silica-air photonic crystal fiber design that permits waveguiding by a true photonic bandgap effect. Opt. Lett. 1999, 24, 46. [Google Scholar] [CrossRef]
- Ferrando, A.; Silvestre, E.; Miret, J.J.; Andras, P.; Andrãs, M.V. Donor and acceptor guided modes in photonic crystal fibers. Opt. Lett. 2000, 25, 1328. [Google Scholar] [CrossRef]
- Ferrando, A.; Miret, J.J. Sing-polarization sing-mode intraband guidance in supersquare photonic crystals fibers. Appl. Phys. Lett. 2001, 78, 3184–3186. [Google Scholar] [CrossRef]
- Chen, M.; Yu, R.; Zhao, A. Highly birefringence rectangular lattice photonic crystal fiber. J. Opt. A Pure Appl. Opt. 2004, 6, 997–1000. [Google Scholar] [CrossRef]
- Kim, S.; Kee, C.-S.; Lee, C.G. Modified rectangular lattice photonic crystal fibers with high birefringence and negative dispersion. Opt. Express 2009, 17, 7952. [Google Scholar] [CrossRef]
- Yang, T.; Wang, E.; Jiang, H.; Hu, Z.; Xie, K. High birefringence photonic crystal fiber with high nonlinearity and low confinement loss. Opt. Express 2009, 23, 8329–8337. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Li, S.; An, G.; Li, J.; Fan, Z.; Han, Y. Polarization splitter based on D-shaped dual-core photonic crystal fibers with gold film. Plasmonics 2015, 10, 57–61. [Google Scholar] [CrossRef]
- Wang, Y. Surface plasmon resonance biosensor based on gold-coated side-polished hexagonal structure photonic crystal fiber. Opt. Express 2017, 25, 20313. [Google Scholar]
- Klantsataya, E.; François, A.; Ebendorff-Heidepriem, H.; Hoffmann, P.; Monro, T.M.; Passaro, V.M. Surface Plasmon Scattering in Exposed Core Optical Fiber for Enhanced Resolution Refractive Index Sensing. Sensors 2015, 15, 25090–25102. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.J.J.; Pui, H. Recent advances in plasmonic photonic crystal fiber: design, fabrication and applications. Adv. Opt. Photonics 2017, 9, 259–314. [Google Scholar] [CrossRef]
- Chiang, J.-S. Analysis of Leaky Modes in Photonic Crystal Fibers Using the Surface Integral Equation Method. Crystals 2018, 8, 177. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, C. A Novel Polarization Splitter Based on the Photonic Crystal Fiber With Nonidentical Dual Cores. IEEE Photonics Technol. Lett. 2004, 16, 1670–1672. [Google Scholar] [CrossRef]
- Yu, Y.; Sun, B. Ultra-Wide-Bandwidth Tunable Magnetic Fluid-Filled Hybrid Connected Dual-Core Photonic Crystal Fiber Mode Converter. Crystals 2018, 8, 95. [Google Scholar]
- Zhang, H.; Zhang, X.; Li, H.; Deng, Y.; Xi, L.; Tang, X.; Zhang, W. The Orbital Angular Momentum Modes Supporting Fibers Based on the Photonic Crystal Fiber Structure. Crystals 2017, 7, 286. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Dinovitser, A.; Faisal, M.; Islam, M.R.; Ng, B.W.-H.; Abbott, D. Zeonex-based asymmetrical terahertz photonic crystal fiber for multichannel communication and polarization maintaining applications. Appl. Opt. 2018, 57, 666–672. [Google Scholar] [CrossRef] [PubMed]
- Vincent Tse, M.; Liu, Z.; Cho, L.; Lu, C.; Wai, P.A.; Tam, H. Super lattice microstructured optical fiber. Materials 2014, 7, 4567–4573. [Google Scholar]
- Jens, K.; Jörg, B.; Katrin, W.; Claudia, A.; Zhiwen, P.; Sonja, U.; Kay, S.; Hartmut, B. Diffusion and Interface Effects during Preparation of All-Solid Microstructured Fibers. Materials 2014, 7, 6879–6892. [Google Scholar] [CrossRef]
- Dumitrache, C.; Rath, J.; Yalin, A.P. High Power Spark Delivery System Using Hollow Core Kagome Lattice Fibers. Materials 2014, 7, 5700–5710. [Google Scholar] [CrossRef]
- Peng, L.; Shi, F.; Zhou, G.; Ge, S.; Hou, Z.; Xia, C. A surface plasmon biosensor based in a D-shaped microstructured optical fiber with rectangular lattice. Opt. Express 2015, 7, 4801309. [Google Scholar]
- Xu, Q.; Miao, R.; Zhang, Y. Highly nonlinear low-dispersion photonic crystal fiber with high birefringence. Opt. Mater. 2012, 35, 217–221. [Google Scholar] [CrossRef]
- Xu, Q. Highly Nonlinear Dispersion-Flattened Photonic Crystal Fiber with High Birefringence. J. Nanoelectron. Optoelectron. 2013, 8, 306–310. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.-G.; Shi, M. Fiber Sagnac interferometer based on a liquid-filled photonic crystal fiber for temperature sensing. Opt. Commun. 2016, 381, 1–6. [Google Scholar] [CrossRef]
- Sun, B.; Chen, M.; Zhang, Y.; Zhou, J. Polarization-dependent coupling characteristics of metal-wire filled dual-core photonic crystal fiber. Opt. Quantum Electron. 2015, 47, 441–451. [Google Scholar] [CrossRef]
- Fan, Z.; Li, S.; Liu, Q.; Chen, H.; Wang, X. Plasmonic Broadband Polarization Splitter Based on Dual-Core Photonic Crystal Fiber with Elliptical Metallic Nanowires. Plasmonics 2016, 11, 1565–1572. [Google Scholar] [CrossRef]
- Benabid, F.; Knight, J.; Antonopoulos, G.; Russell, P.S.J. Stimulated Raman Scattering in Hydrogen-Filled Hollow-Core Photonic Crystal Fiber. Science 2002, 298, 399–402. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.K.C.; Kuhlmey, B.T.; Eggleton, B.J. Ultrasensitive photonic crystal fiber refractive index sensor. Opt. Lett. 2009, 34, 322. [Google Scholar] [CrossRef]
- Wang, D.; Chen, G.; Wang, L. Thermal tunability of photonic bandgaps in liquid crystal filled polymer photonic crystal fiber. Opt. Fiber Technol. 2016, 29, 95–99. [Google Scholar] [CrossRef]
- Miluski, P.; Kochanowicz, M.; Zmojda, J.; Dorosz, D. 1,4-Bis(2-methylstyryl)benzene doped PMMA fibre for blue range fluorescent applications. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2018, 192, 88–92. [Google Scholar] [CrossRef]
- Xu, Z.; Lim, J.; Hu, D.J.J.; Sun, Q.; Wong, R.Y.-N.; Li, K.; Jiang, M.; Shum, P.P. Investigation of temperature sensing characteristics in selectively infiltrated photonic crystal fiber. Opt. Express 2016, 24, 1699. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Xu, Y.; Yariv, A. Fabrication of functional microstructured optical fibers through a selective-filling technique. Appl. Phys. Lett. 2004, 85, 5182. [Google Scholar] [CrossRef]
- Sultana, J.; Islam, M.S.; Ahmed, K.; Dinovitser, A.; Ng, B.W.-H.; Abbott, D. Terahertz detection of alcohol using a photonic crystal fiber sensor. Appl. Opt. 2018, 57, 2426–2433. [Google Scholar] [CrossRef] [PubMed]
- Haakestad, M.; Alkeskjold, T.; Nielsen, M.; Scolari, L.; Riishede, J.; Engan, H.; Bjarklev, A. Electrically tunable photonic bandgap guidance in a liquid-crystal-filled photonic crystal fiber. IEEE Photonics Technol. Lett. 2005, 17, 819–821. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, C. Polarization splitter based on photonic crystal fibers. Opt. Express 2003, 11, 1015. [Google Scholar] [CrossRef]
- Kim, S.; Kee, C.-S.; Lee, J.; Jung, Y.; Choi, H.-G.; Oh, K. Ultrahigh birefringence of elliptic core fibers with irregular air holes. J. Appl. Phys. 2007, 102, 16101. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, C. Photonic crystal fibers with squeezed hexagonal lattice. Opt. Express 2004, 12, 2371. [Google Scholar] [CrossRef]
- Eijkelenborg, M.A.V.; Large, M.C.J.; Argyros, A.; Zagari, J.; Manos, S.; Issa, N.A.; Bassett, I.; Fleming, S.; McPhedran, R.C.; Sterke, C.M.D.; Nicorovici, N.A.P. Microstructured polymer optical fibre. Opt. Express 2001, 9, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Bunge, C.A.; Beckers, M.; Gries, T. Polymer Optical Fibres; Woodhead Publishing: Cambridge, UK, 2017. [Google Scholar]
- Webb, D.J. Polymer photonic crystal fibre for sensor applications. Opt. Sens. Detection 2010, 7726, 77260Q. [Google Scholar]
- Pakarzadeh, H.; Rezaei, S.; Namroodi, L. Hollow-core photonic crystal fibers for efficient terahertz transmission. Opt. Commun. 2019, 433, 81–88. [Google Scholar] [CrossRef]
- Dash, N.J.; Jha, R. SPR biosensor based on polymer PCF coated with conducting metal oxide. IEEE Photonics Technol. Lett. 2014, 26, 595–598. [Google Scholar] [CrossRef]
- Charas, A.; Menonca, A.L.; Clark, J.; Cabanillas-gonzalez, J.; Bazzana, L.; Nocivelli, A.; Lanzani, G.; Morgado, J. Gain and ultrafast optical switching in PMMA optical fibers and films doped with luminescent conjugated polymers and oligomers. Front. Optoelectron. China 2010, 3, 45–53. [Google Scholar] [CrossRef]
- Fujimoto, S. Recent advances in plastic optical fiber in Japan. SPIE-New Mater. Opt. Waveguides 1987, 799, 139–145. [Google Scholar]
- Loyez, C.; Lethien, C.; Deparis, N.; Vilcot, J.-P.; Kassi, R.; Rolland, N.; Goffin, A.; Rolland, P.A. An Impulse System for 60-GHz Wireless Networks Based on Polymer Optical Fiber. IEEE Photonics Technol. Lett. 2007, 19, 1964–1966. [Google Scholar] [CrossRef]
- Large, M.C.J.; Ponrathnam, S.; Argyros, A.; Pujari, N.S.; Cox, F. Solution doping of microstructured polymer optical fibers. Opt. Express 2004, 12, 1966–1971. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.; Wang, L. Fabrication and experimental observation of monolithic multi-air-core fiber array for image transmission. Opt. Express 2008, 16, 7703. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Wang, L.; Ren, L.; Zhao, W.; Miao, R.; Large, M.C.J.; Van Eijkelenborg, M.A. Casting preforms for microstructured polymer optical fibre fabrication. Opt. Express 2006, 14, 5541. [Google Scholar] [CrossRef] [PubMed]
- Van Eijkelenborg, M.A.; Argyros, A.; Barton, G.; Bassett, I.M.; Fellew, M.; Henry, G.; Issa, N.A.; Large, M.C.; Manos, S.; Padden, W.; et al. Recent progress in microstructured polymer optical fibre fabrication and characterisation. Opt. Fiber Technol. 2003, 9, 199–209. [Google Scholar] [CrossRef]
- Feit, M.D.; Fleck Jr, J.A. Light propagation in graded-index optical fiber. Appl. Opt. 1978, 24, 3990–3998. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Sun, X. A Modified full-vectorial finite-difference beam propagation method based on H-fields for optical waveguides with step-index profiles. Opt. Commun. 2006, 266, 505–511. [Google Scholar] [CrossRef]
- Xie, K.; Boardman, A.D.; Xie, M.; Yang, Y.J.; Jiang, H.M.; Yang, H.J.; Wen, G.J.; Li, J.; Chen, K.; Chen, F.S. A Simulation of longitudinally magnetized three-dimensional magneto-optical devices by a full-vectorial beam propagation method. Opt. Commun. 2008, 281, 3275–3285. [Google Scholar] [CrossRef]
- Bard, D.; Kihal, W.; Schillinger, C.; Fermanian, C.; Segala, C.; Glorion, S.; Arveiler, D.; Weber, C. Traffic-related air pollution and the onset of myocardial infarction: disclosing benzene as a trigger? A small-area case-crossover study. PLoS ONE 2014, 9, e100307. [Google Scholar] [CrossRef]
- Xu, Q.; Miao, R.; Zhang, Y. High birefringence low-dispersion of nonlinear photonic crystal fiber. Optik 2013, 124, 2269–2272. [Google Scholar]
- Eisenmann, M.; Weidel, E. Single-mode fused biconical coupler optimized for polarization beam splitting. J. Lightwave Technol. 1991, 9, 853–858. [Google Scholar] [CrossRef]
- Li, X.-Y.; Sun, B.; Yu, Y.-Y.; He, K.-P. Bending dual-core photonic crystal fiber coupler. Optik 2014, 125, 6478–6482. [Google Scholar] [CrossRef]
- Wang, E.; Cheng, Q.; Li, J.; Zhang, C. Tunable wavelength division multiplexer based on thermal liquid-filled photonic crystal fiber. Optik 2018, 160, 13–16. [Google Scholar] [CrossRef]
- Zi, J.; Li, S.; An, G.; Fan, Z. Short-length polarization splitter based on dual-core photonic crystal fiber with hexagonal lattice. Opt. Commun. 2016, 363, 80–84. [Google Scholar] [CrossRef]
- Kruglov, R.; Vinogradov, J.; Ziemann, O.; Loquai, S.; Bunge, C.-A. 10.7-Gb/s Discrete Multitone Transmission Over 50-m SI-POF Based on WDM Technology. IEEE Photonics Technol. Lett. 2012, 24, 1632–1634. [Google Scholar] [CrossRef]
- Joncic, M.; Kruglov, R.; Haupt, M.; Caspary, R.; Vinogradov, J.; Fischer, U.H.P. Four-channel WDM transmission over 50-m SI-POF at 14.77 Gb/s using DMT modulation. IEEE Photonics Technol. Lett. 2014, 26, 1328–1331. [Google Scholar] [CrossRef]




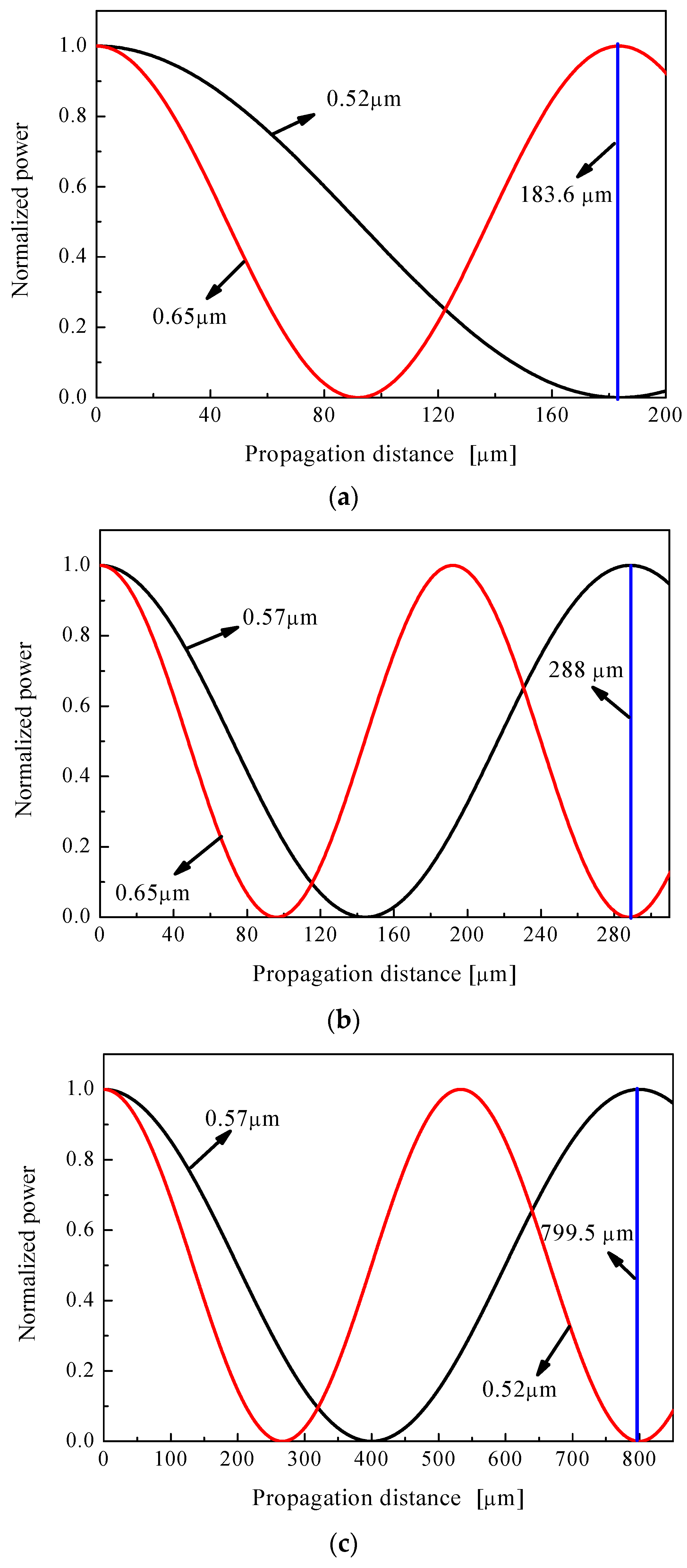

| Parameters | Couplers | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 (Reference [72]) | 5 (Reference [73]) | 6 (Reference [4]) | |
| λ1 [μm] | 0.65 | 0.65 | 0.57 | 1.55 | 1.55 | 1.55 |
| λ2 [μm] | 0.52 | 0.57 | 0.52 | 0.85/0.98/1.3/1.48 | 0.98/1.31 | 0.85/0.98/1.3/1.48 |
| Λ [μm] | 0.9 | 0.9 | 0.9 | - | - | - |
| d/Λ | 0.9 | 0.9 | 0.9 | - | - | - |
| d1 [μm] | 0.48/0.4 | 0.49 | 0.62 | - | - | - |
| Length [μm] | 183.6/452.3 | 288 | 799.5 | 4168 | 2475 | 1178/418/712/2284 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Li, K.; Copner, N.; Lin, S. An Ultrashort Wavelength Multi/Demultiplexer via Rectangular Liquid-Infiltrated Dual-Core Polymer Optical Fiber. Materials 2019, 12, 1709. https://doi.org/10.3390/ma12101709
Xu Q, Li K, Copner N, Lin S. An Ultrashort Wavelength Multi/Demultiplexer via Rectangular Liquid-Infiltrated Dual-Core Polymer Optical Fiber. Materials. 2019; 12(10):1709. https://doi.org/10.3390/ma12101709
Chicago/Turabian StyleXu, Qiang, Kang Li, Nigel Copner, and Shebao Lin. 2019. "An Ultrashort Wavelength Multi/Demultiplexer via Rectangular Liquid-Infiltrated Dual-Core Polymer Optical Fiber" Materials 12, no. 10: 1709. https://doi.org/10.3390/ma12101709
APA StyleXu, Q., Li, K., Copner, N., & Lin, S. (2019). An Ultrashort Wavelength Multi/Demultiplexer via Rectangular Liquid-Infiltrated Dual-Core Polymer Optical Fiber. Materials, 12(10), 1709. https://doi.org/10.3390/ma12101709





