Effectiveness of Dowels in Concrete Pavement
Abstract
:1. Introduction
2. Materials and Methods
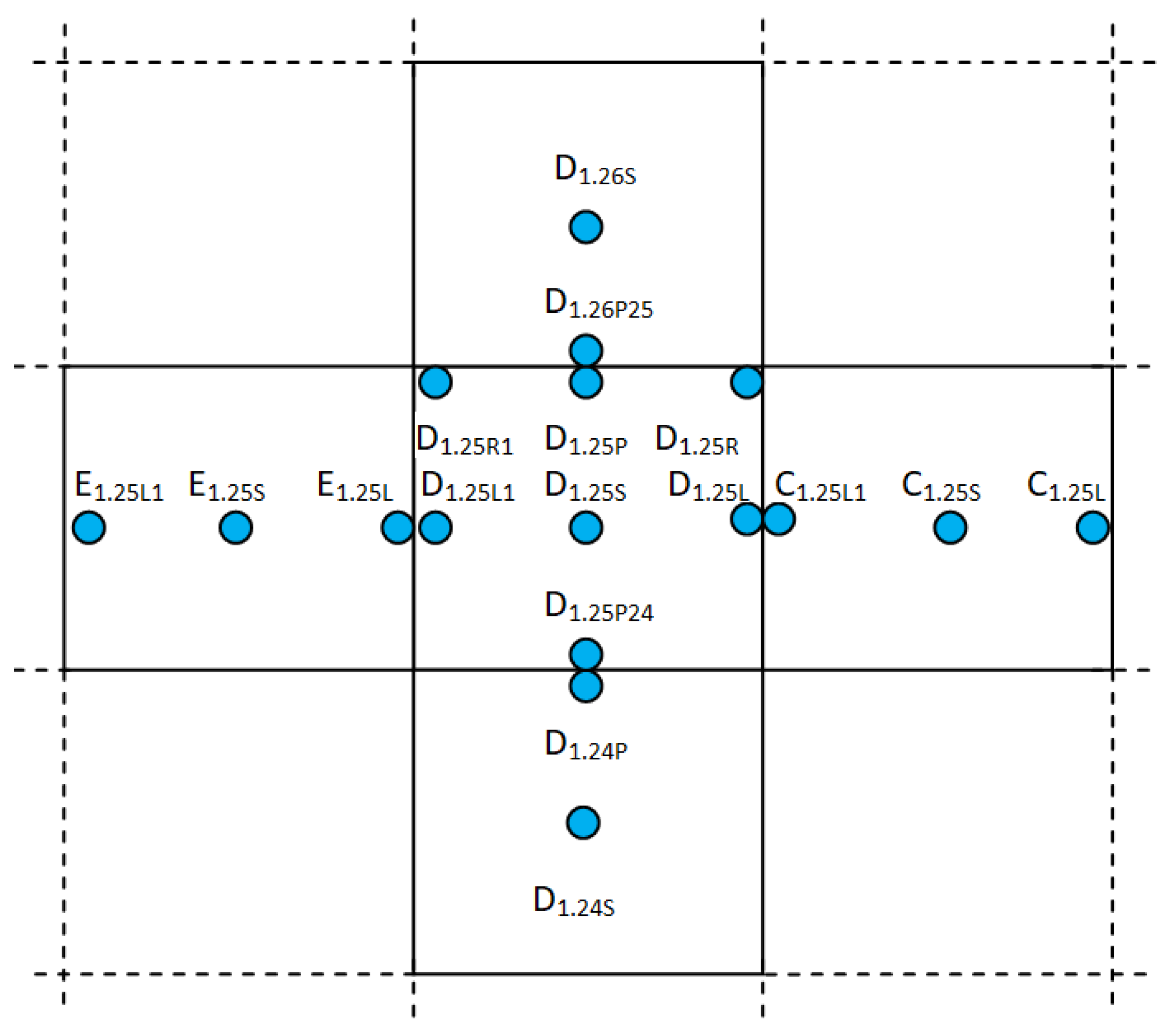
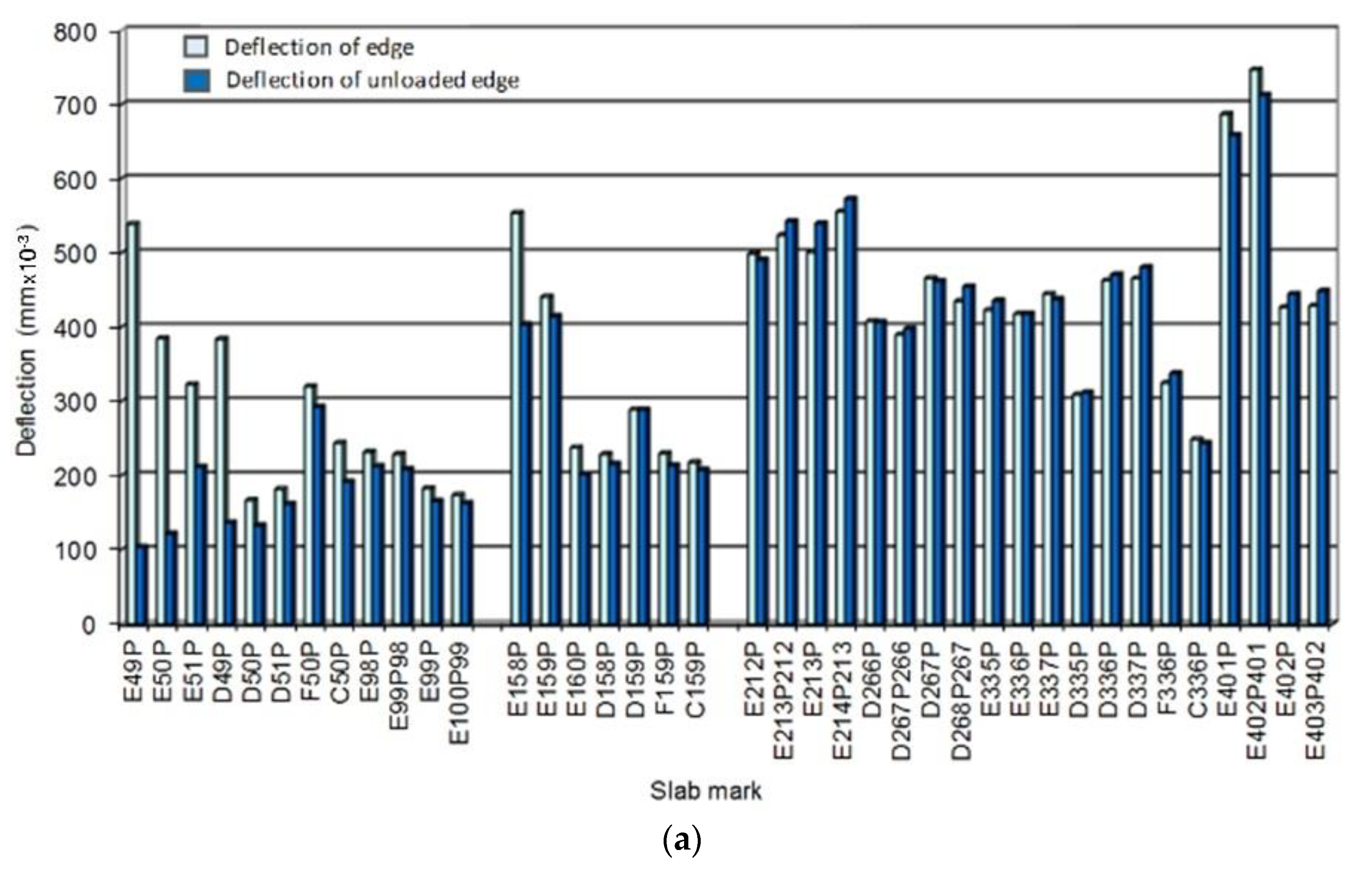
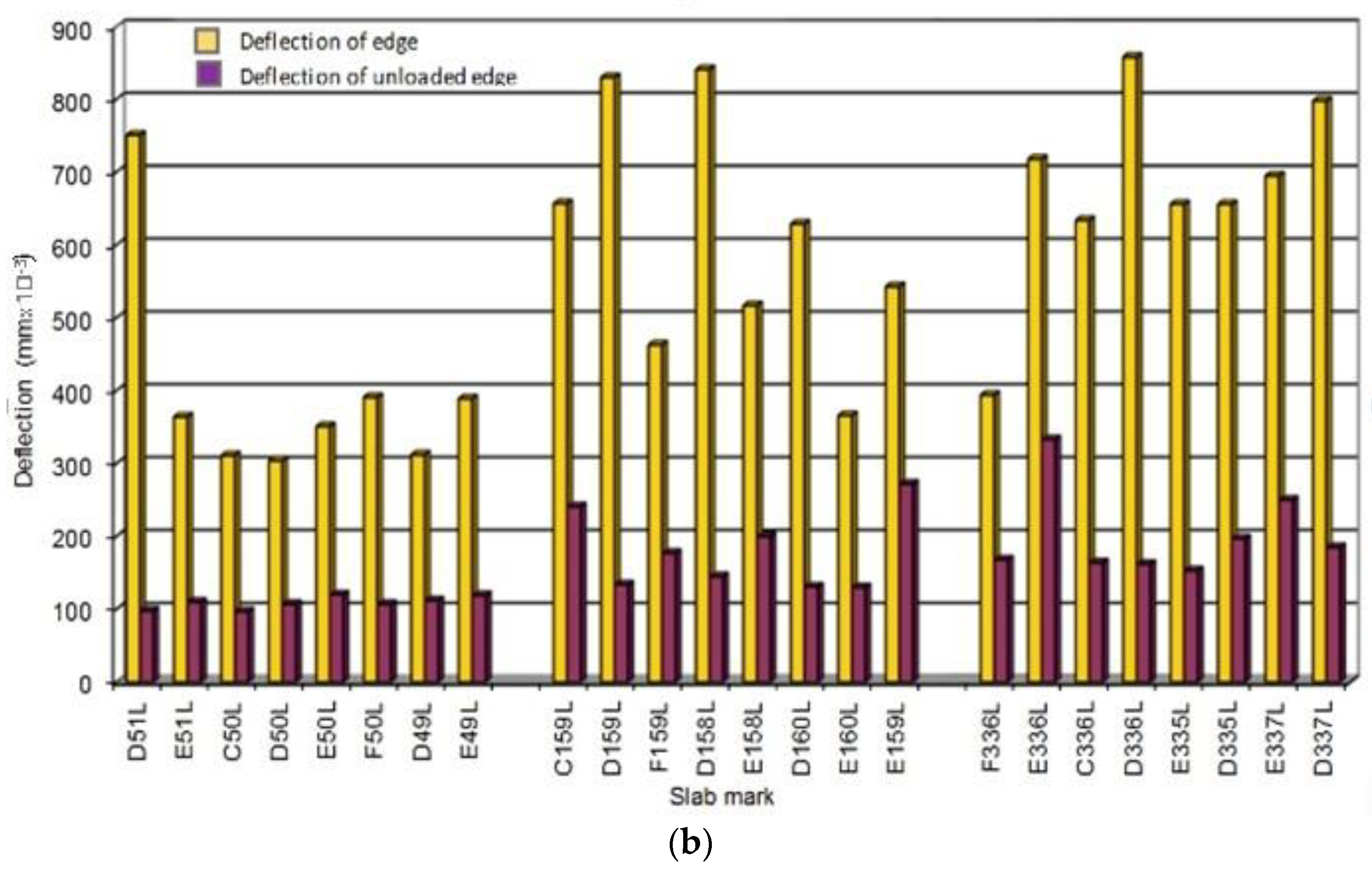
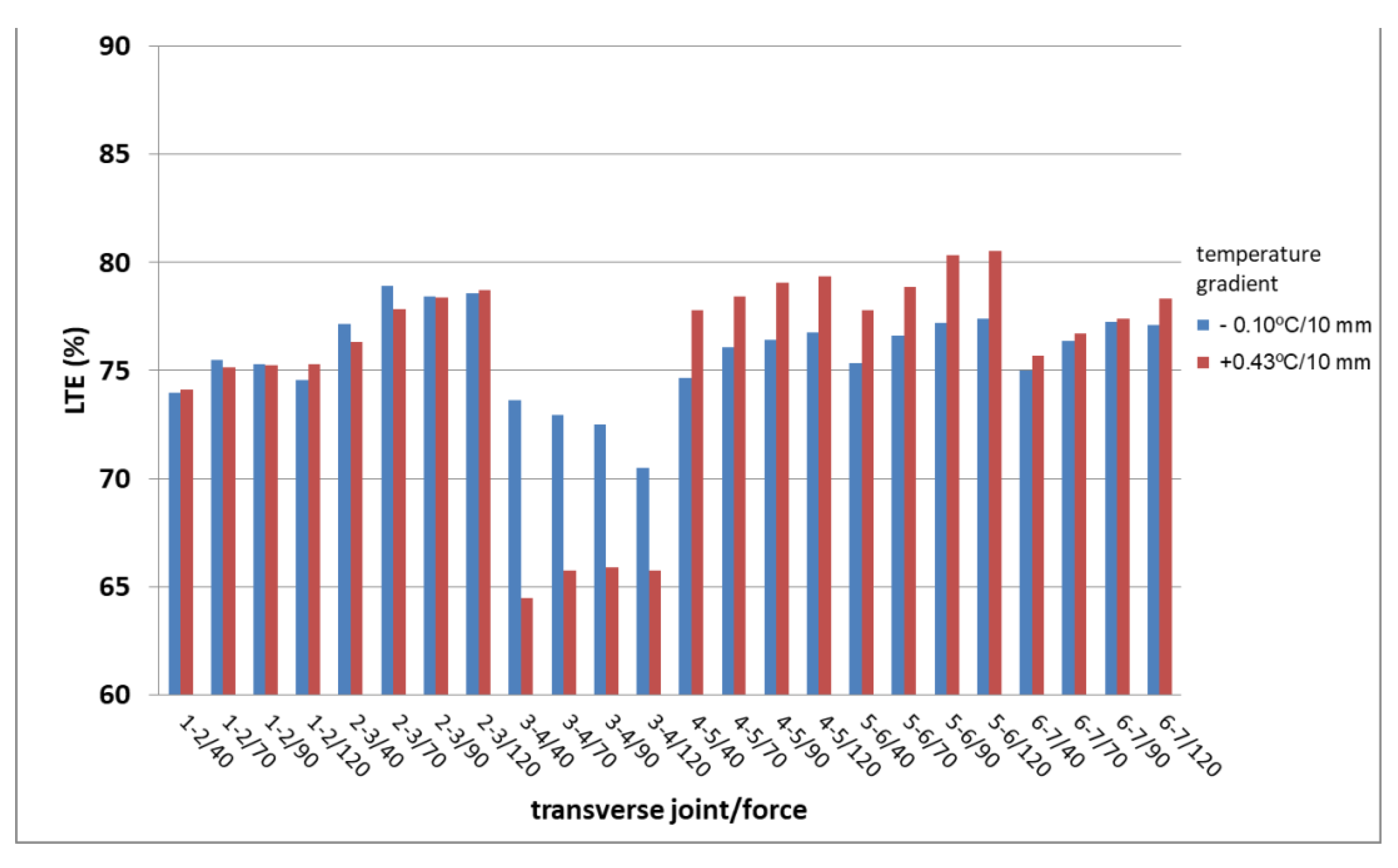
2.1. LTE Measurement on Existing Pavements Methodology
2.1.1. Bratislava Airport
2.1.2. Highway D1 and R1
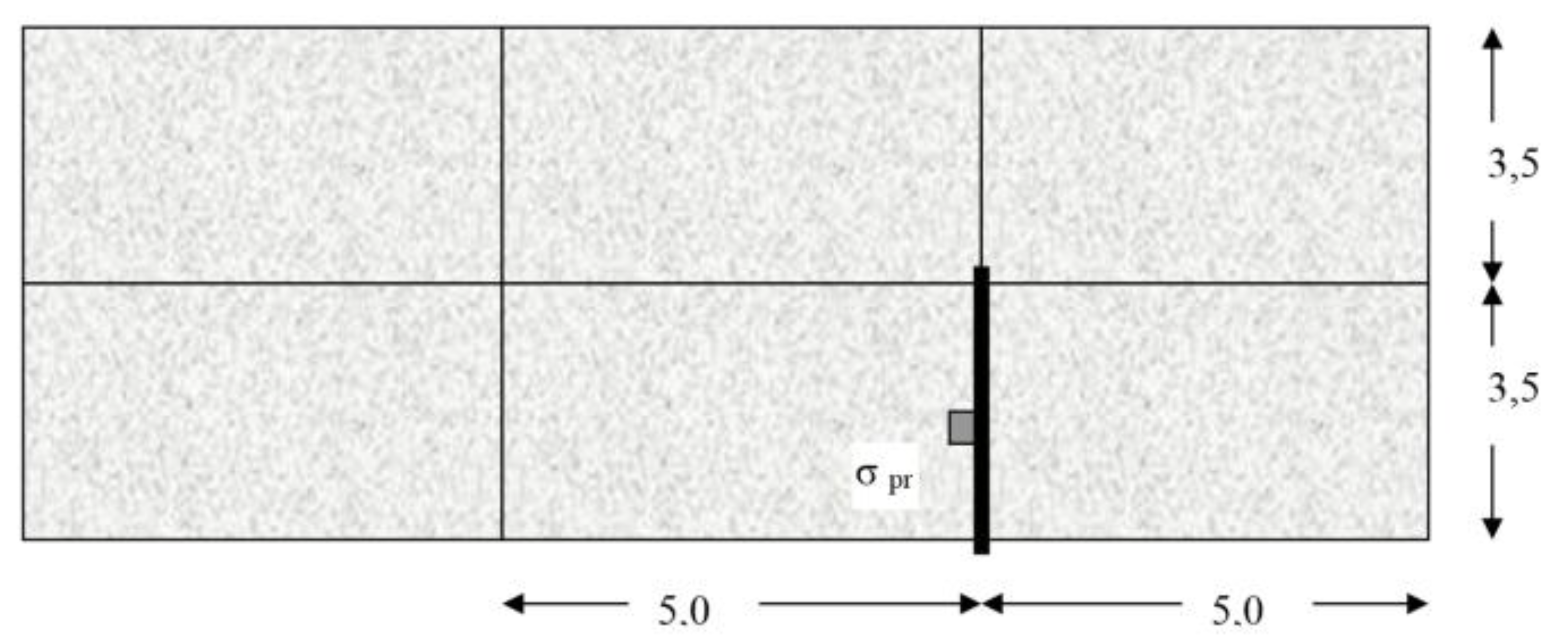
2.2. Modeling of Stress on Slab Edges by FEM Methodology
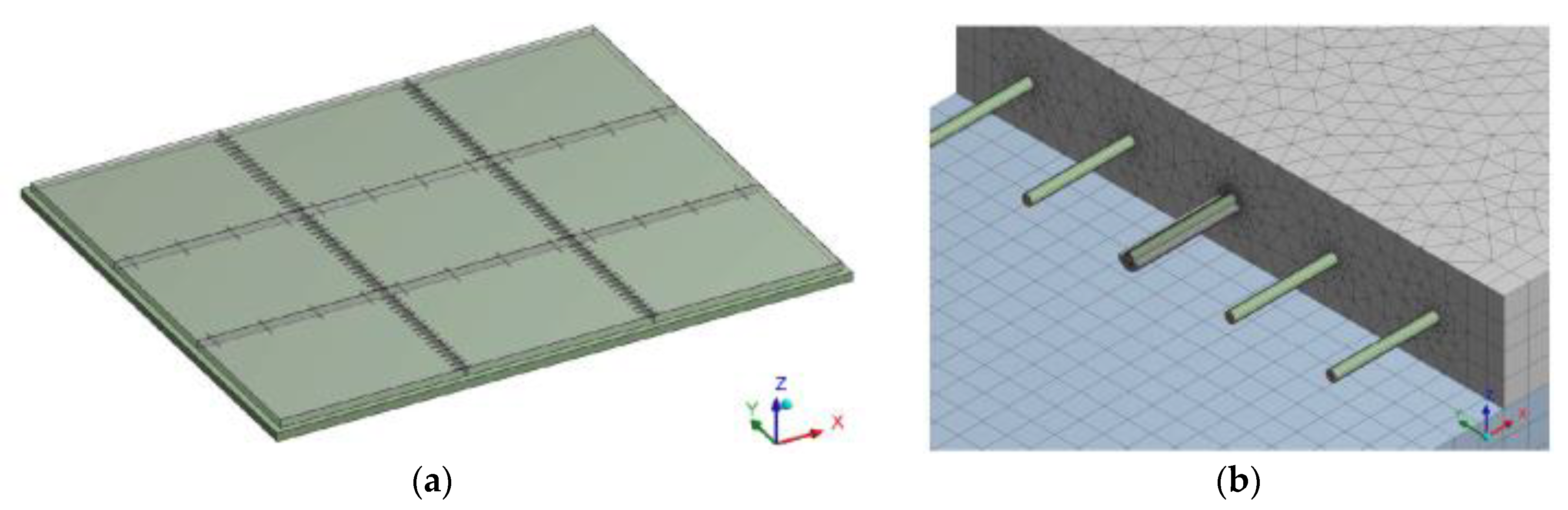
2.2.1. Software SCIA Nexis
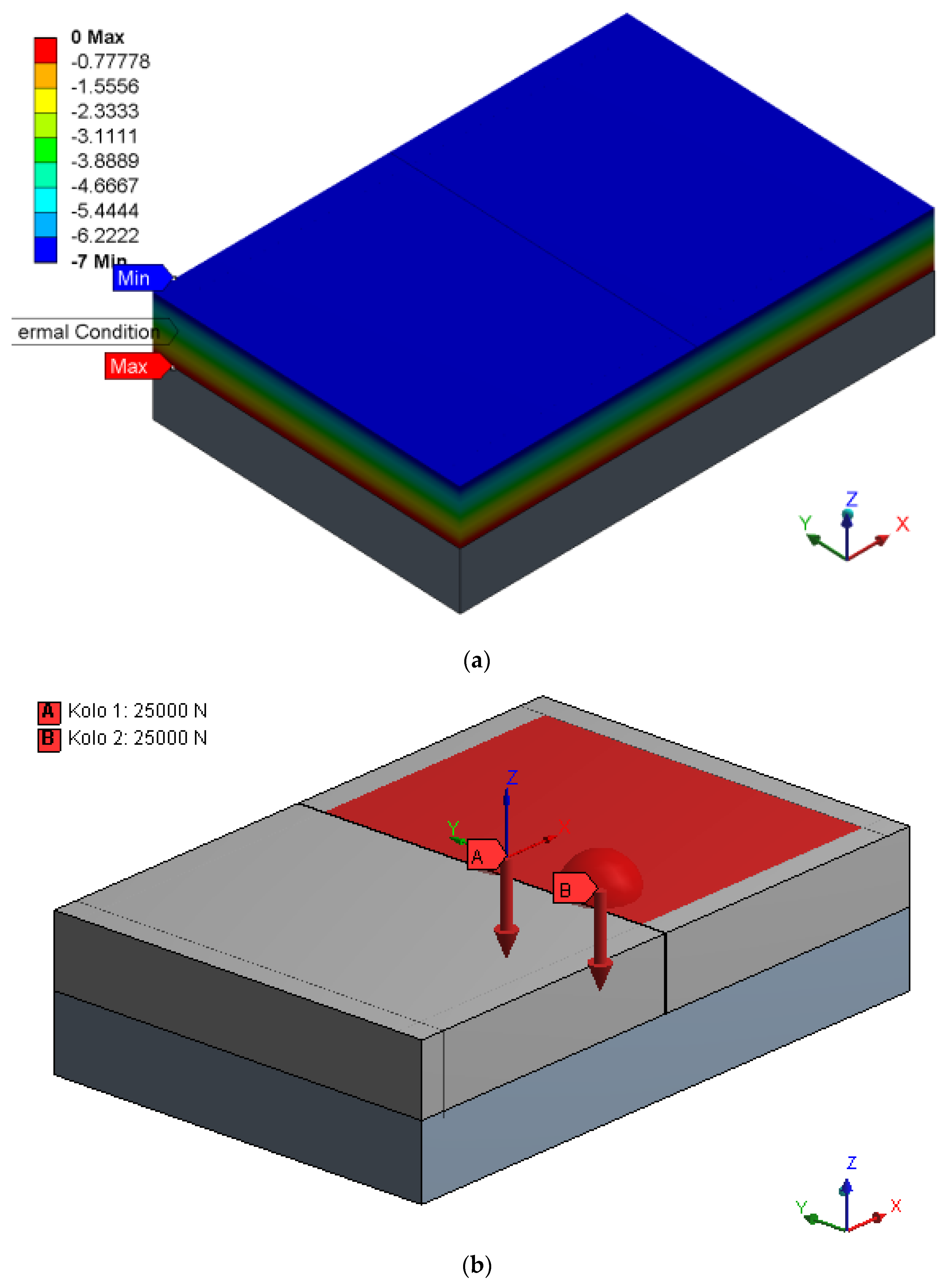
2.2.2. Software ANSYS
- Global numeric model ZS1 (pavement weight, temperature field);
- Global numeric model ZS2 (load by axle);
- Local numeric model ZS1 (pavement weight, temperature field); and
- Local numeric model ZS2 (load by axle).
3. Results and Discussion
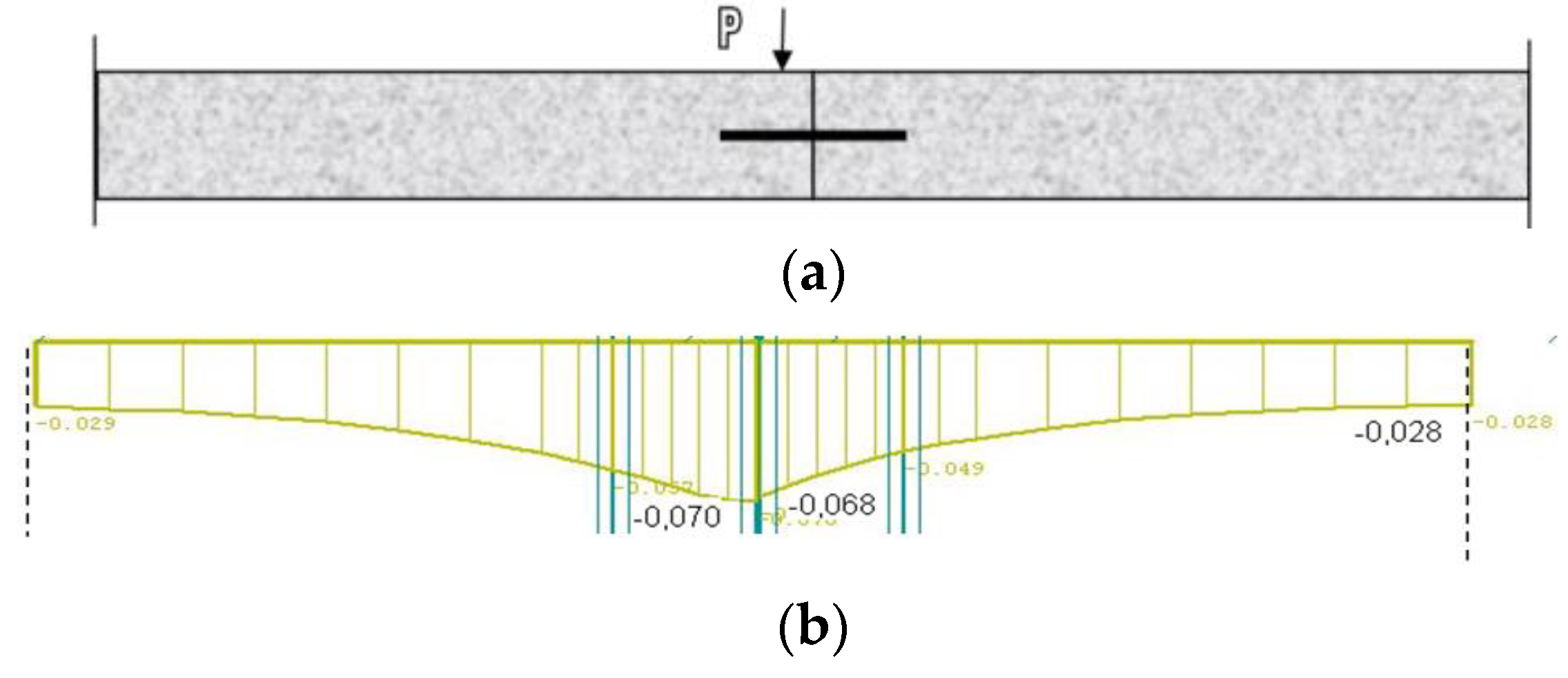
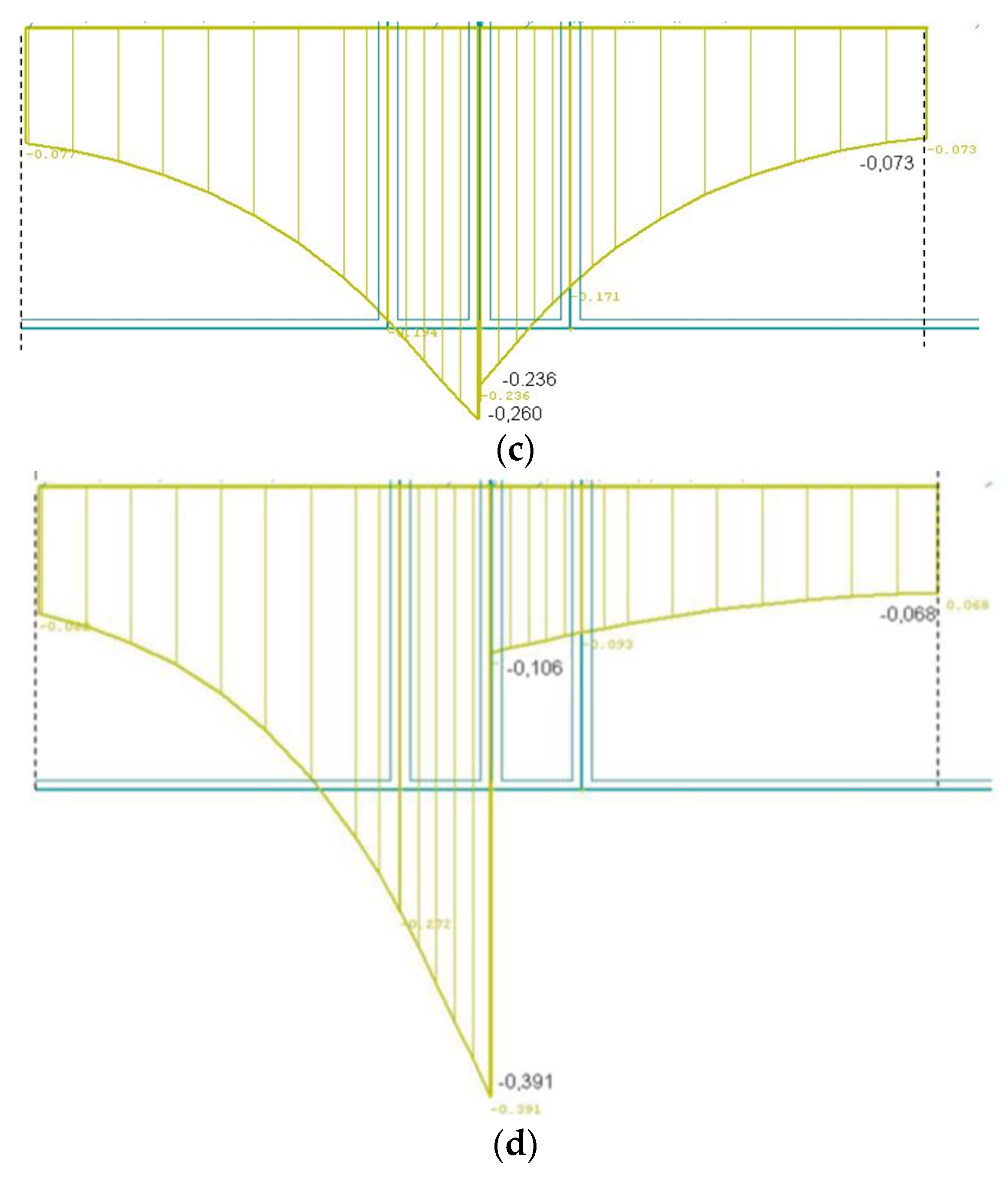
3.1. SCIA Nexis Results
3.2. ANSYS Results
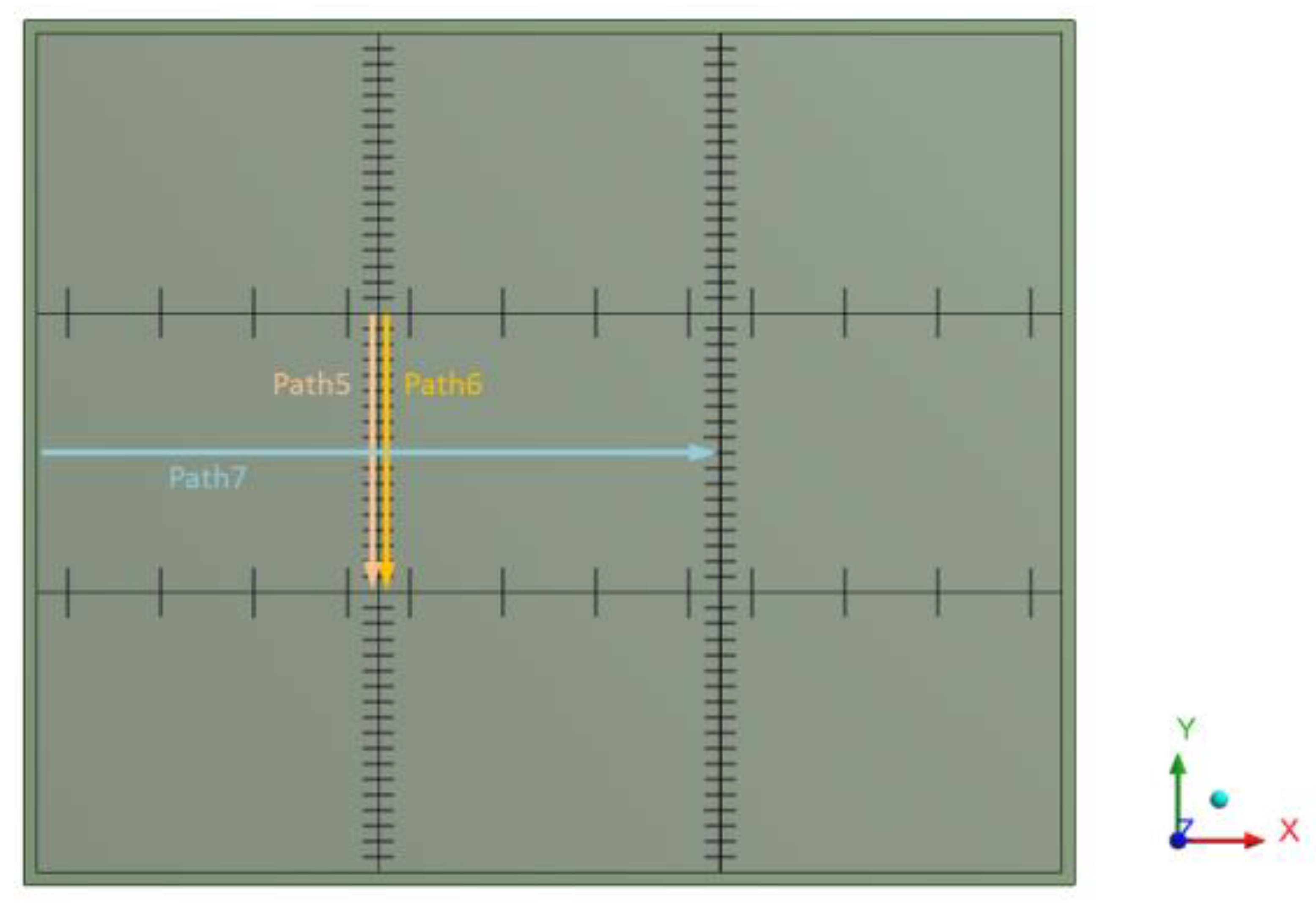
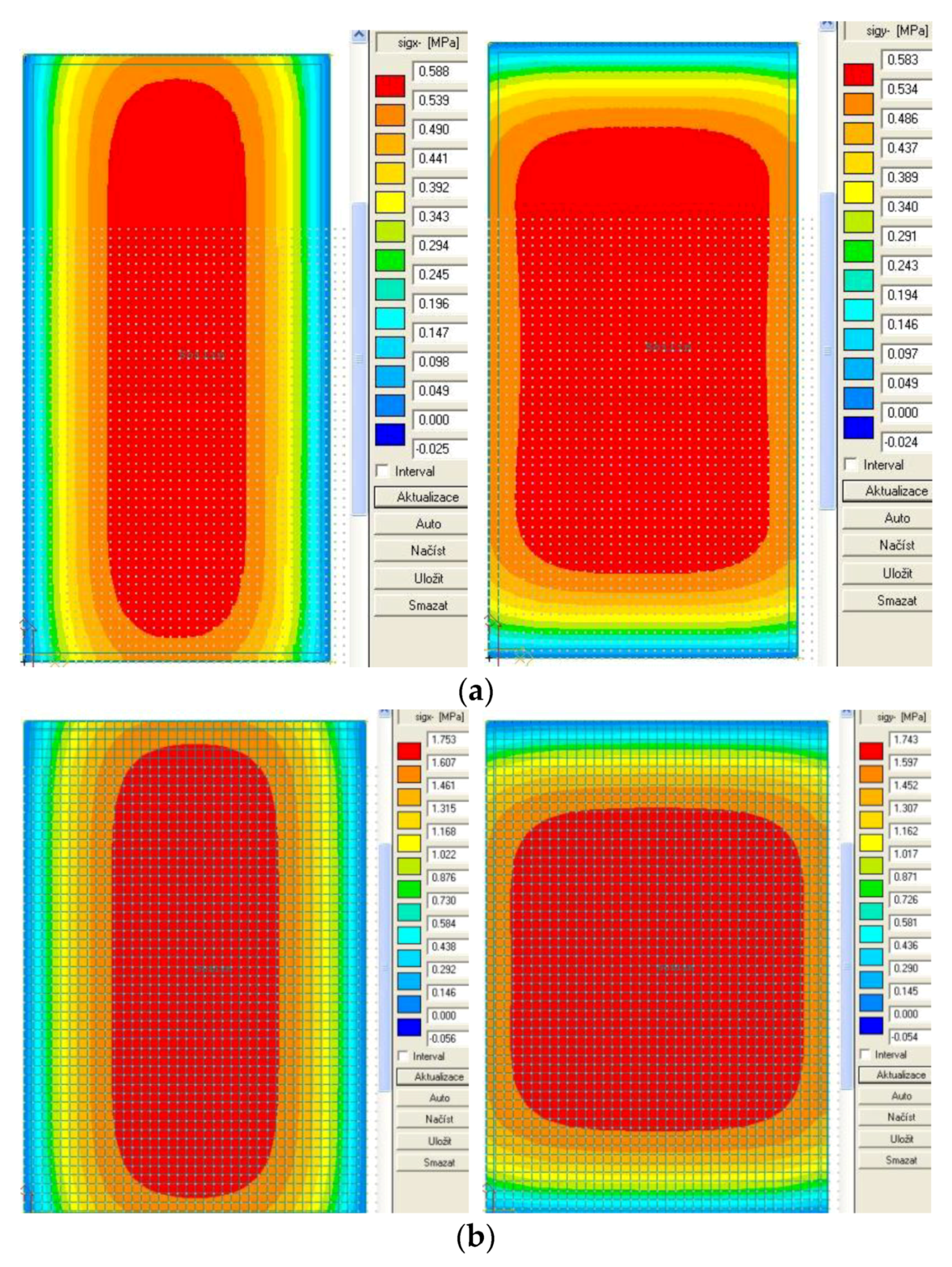
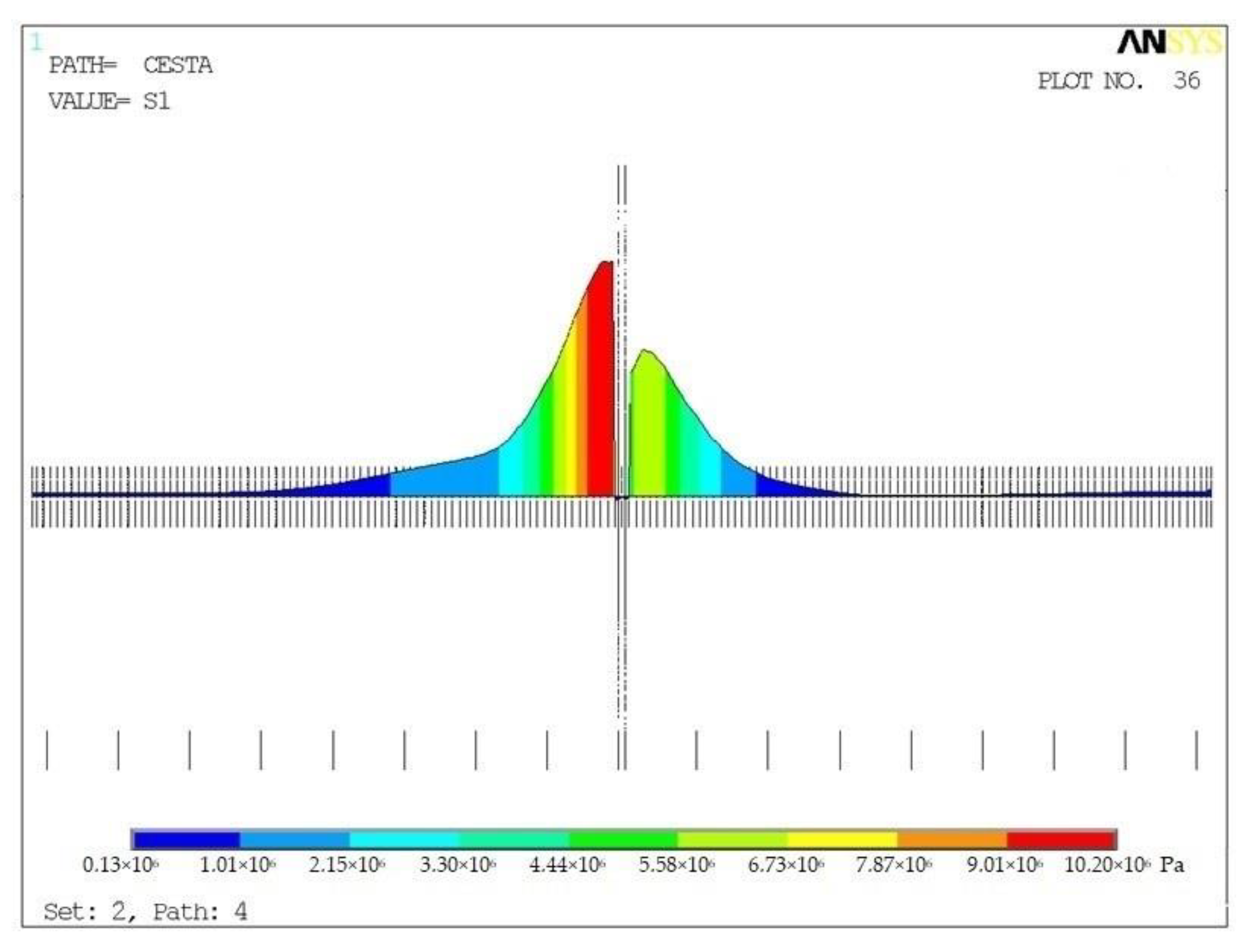
3.2.1. Stress at Bottom Part of Concrete Slab
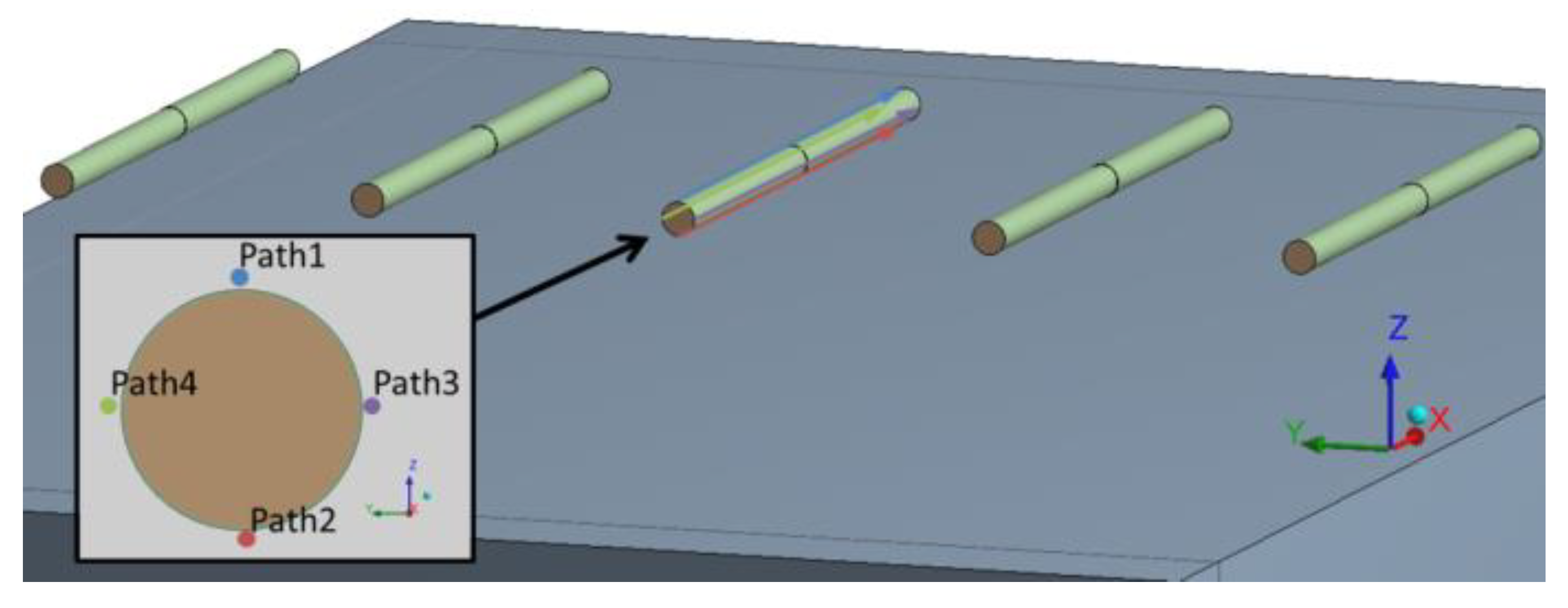
3.2.2. Stress around Dowel of Concrete Slab
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- AASHTO. Guide for Design of Pavement Structures; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1993. [Google Scholar]
- ACPA. Stitching Concrete pavement cracks and joints, Special Report SR903P; American Concrete Pavement Association: Skokie, IL, USA, 2001. [Google Scholar]
- ACPA. Guide Specification: Dowel Bar Alignment and Location for Placement by Mechanical Dowel Bar Insertion; American Concrete Pavement Association: Skokie, IL, USA, 2013. [Google Scholar]
- TP 92. Design maintenance and repair of concrete pavement; Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2010. [Google Scholar]
- COST 336. Use of Falling Weight Deflectometer in Pavement Evaluation (final report), 2nd ed.; COST: Brussels, Belgium, 2005. [Google Scholar]
- BAST HEFT S65: Untersuchungen von Dübel lagen zur Optimierung des Betondeckenbaus, Berichte der Bundesanstalt für Straßenwesen; Federal Highway Research Institute: Bergisch Gladbach, Germany, 2010.
- Larson, R.; Smith, K. Evaluation of alternative dowel bar materials and coatings; Applied Pavement Technology Inc.: Columbus, OH, USA, 2011. [Google Scholar]
- Khazanovich, L.; Neeraj, B.; Alex, G. Evaluation of Alignment Tolerances for Dowels and their Effects on Joint Performance; Michigan State University: Ann Arbor, MI, USA, 2001. [Google Scholar]
- Shoukry, S.N.; William, G.W.; Riad, M. Evaluation of Load Transfer Efficiency Measurement; West Virginia University College of Engineering and Mineral Resources: Morgantown, WV, USA, 2005. [Google Scholar]
- NCC. Recommendations for Standardization of Dowel Load Transfer Systems for Jointed Concrete Roadway Pavements; Iowa State University: Ames, IA, USA, 2011. [Google Scholar]
- NCHRP. Report 637: Guidelines for Dowel Alignment in Concrete Pavements; National Cooperative Highway Research Program: Washington, DC, USA, 2009. [Google Scholar]
- Villaret, S. Imperfektionen der Dübellage—Einfluss auf die Dauerhaftigkeit der Betondecke. In Proceedings of the 5th International Conference of Concrete Pavements, Prague, Czech Republic, 17 May 2012; pp. 79–83. [Google Scholar]
- Zuzulova, A. Efficiency of Dowels in Concrete Pavement. In Research and technical development in road construction, XIXth Seminar of Ivan Poliacek with International Participation; Kongres STUDIO: Bratislava, Slovakia, 2014; pp. 179–184. [Google Scholar]
- EN 13877-1. Concrete pavements—Part 1: Materials; Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2006. [Google Scholar]
- EN 13877-2. Concrete pavements—Part 2: Functional requirements for concrete pavement; Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2006. [Google Scholar]
- EN 13877-3. Concrete pavements—Part 3: Specification for dowels to be used in concrete pavements; Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2006. [Google Scholar]
- ČSN 736123-1. Road building—Concrete pavements—Part 1: Construction and conformity assessment; Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2014. [Google Scholar]
- Stryk, J.; Herrmann, P.; Chupik, V. Certified methodology: Technical regulation for measurement and evaluation of bearing capacity of pavements using FWD equipment; Transport Research Centre: Brno, Czech Republic, 2013. [Google Scholar]
- FHWA 2007. Best Practices for Dowel Placement Tolerances, Federal Highway Administration, FHWA-HIF-07-021. Available online: http://www.fhwa.dot.gov/pavement/concrete/pubs/07021/ (accessed on 1 June 2007).
- Li, L.; Tan, Y.; Gong, X.; Li, Y. Characterization of Contact Stresses Between Dowels and Surrounding Concrete in Jointed Concrete Pavement. In Proceedings of the 10th International Conference on Concrete Pavements, Québec, Canada, 8–12 June 2012. [Google Scholar]
- Nishizawa, T.; Ozeki, T.; Kawano, H. Surface Stresses of Thick Concrete Pavement Slabs Due To Traffic Loads and Non-Linear Temperature Distributions. In Proceedings of the 10th International Conference on Concrete Pavements, Québec, Canada, 8–12 June 2012. [Google Scholar]
- Shoukry, S.N.; William, G.W.; Riad, M. Application of LS-DYNA in Identifying Critical Stresses Around Dowels. In Proceedings of the 8th International LS-DYNA Users Conference, Detroit, MI, USA, 2–4 May 2004. [Google Scholar]
- Mackiewicz, P. Analysis of stresses in concrete pavement under a dowel according to its diameter and load transfer efficiency. Can. J. Transp. Eng. 2015, 141, 845–853. [Google Scholar] [CrossRef]
- Mackiewicz, P. Thermal stress analysis of jointed plane in concrete pavements. Appl. Therm. Eng. 2014, 73, 1167–1174. [Google Scholar] [CrossRef]
- Channakeshava, C.; Barzegar, F.; Voyiadjis, G.Z. Non-linear FE analysis of plain concrete pavements with doweled joints. J. Transp. Eng. 1993, 119, 763–781. [Google Scholar] [CrossRef]
- Sii, H.B.; Chai, G.W.; van Staden, R.; Guan, H. Effect of dowel looseness on response of jointed concrete pavements using three-dimensional finite element analysis. Adv. Mater. Res. 2014, 900, 435–444. [Google Scholar] [CrossRef]
- Davids, W.G. 3D finite element study on load transfer at doweled joints in flat and curled rigid pavements. Inter. J. Geomech. 2001, 1, 309–323. [Google Scholar] [CrossRef]
- Salajka, V.; Čada, Z. Final Report: Variant calculation of the influence dowel position on the concrete slabs stress, first series; FCE VUT Brno: Brno-střed, Czech Republic, 2013. [Google Scholar]
- TP 098. Design of concrete pavements on motorways; Slovak Road Administration: Bratislava, Slovakia, 2015. [Google Scholar]
| No. | Layer | Thickness (m) | Modulus E (MPa) | Poisson Ratio (-) |
|---|---|---|---|---|
| 1 | Concrete slab | 0.24 | 37 500 | 0.20 |
| 2 | Subbase (crushed aggregate) | 0.30 | 600 | 0.25 |
| 3 | Subgrade | 2.50 | 120 | 0.33 |
| - | Dowel | - | 210 000 | 0.27 |
| - | Dowel coating | - | 200 | 0.40 |
| Structure | Position of the Load | Stress (MPa) Load 100 kN | Stress (MPa) Load 115 kN | Stress (MPa) Temperature 1 |
|---|---|---|---|---|
| K EX | center | 0.781 | 0.881 | 1.753 |
| longitudinal edge | 1.237 | 1.409 | 1.468 | |
| transverse edge | 1.272 | 1.446 | 1.404 |
| Structure | Position of the Load | Stress (MPa) Load 100 kN | Stress (MPa) Load 115 kN | Stress (MPa) Temperature 1 |
|---|---|---|---|---|
| K INT | center | 0.757 | 0.854 | 0.588 |
| longitudinal edge | 1.232 | 1.337 | 0.482 | |
| transverse edge | 1.170 | 1.389 | 0.499 |
| Variant | Stress σy (MPa) on Slab Bottom | Description |
|---|---|---|
| V1 | 1.386 | Basic variant |
| V2 | 1.527 | Missing adjoining dowel |
| V3 | 1.387 | Vertical Translation |
| V4 | 1.387 | Vertical Translation (upwards) 40 mm |
| V5 | 1.386 | Vertical Translation (upwards) 60 mm |
| V6 | 1.397 | Vertical Translation (downwards) 20 mm |
| V7 | 1.412 | Vertical Translation (downwards) 40 mm |
| V8 | 1.425 | Vertical Translation (downwards) 60 mm |
| V9 | 1.387 | Vertical Tilt (away from the force) 20 mm |
| V10 | 1.390 | Vertical Tilt (away from the force) 40 mm |
| V11 | 1.392 | Vertical Tilt (away from the force) 60 mm |
| V12 | 1.385 | Vertical Tilt (towards the force) 20 mm |
| V13 | 1.383 | Vertical Tilt (towards the force) 40 mm |
| V14 | 1.380 | Vertical Tilt (towards the force) 60 mm |
| V15 | 1.405 | Longitudinal Translation (away from the force) 20 mm |
| V16 | 1.402 | Longitudinal Translation (away from the force) 40 mm |
| V17 | 1.478 | Longitudinal Translation (away from the force) 60 mm |
| Variant | Tensile Stress σy (MPa) | Compressive Stress σy (MPa) | Description |
|---|---|---|---|
| V1 | 10.2 | 26.7 | Basic variant |
| V2 | 11.5 | 30.3 | Missing adjoining dowel |
| V3 | 9.2 | 26.4 | Vertical Translation |
| V4 | 9.4 | 27.0 | Vertical Translation (upwards) 40 mm |
| V5 | 9.0 | 26.8 | Vertical Translation (upwards) 60 mm |
| V6 | 10.9 | 26.5 | Vertical Translation (downwards) 20 mm |
| V7 | 12.0 | 27.1 | Vertical Translation (downwards) 40 mm |
| V8 | 12.4 | 25.1 | Vertical Translation (downwards) 60 mm |
| V9 | 9.0 | 23.3 | Vertical Tilt (away from the force) 20 mm |
| V10 | 5.7 | 17.6 | Vertical Tilt (away from the force) 40 mm |
| V11 | 5.5 | 14.8 | Vertical Tilt (away from the force) 60 mm |
| V12 | 10.2 | 23.4 | Vertical Tilt (towards the force) 20 mm |
| V13 | 11.5 | 25.1 | Vertical Tilt (towards the force) 40 mm |
| V14 | 14.2 | 26.6 | Vertical Tilt (towards the force) 60 mm |
| V15 | 9.6 | 23.1 | Longitudinal Translation (away from the force) 20 mm |
| V16 | 9.7 | 26.2 | Longitudinal Translation (away from the force) 40 mm |
| V17 | 8.0 | 21.2 | Longitudinal Translation (away from the force) 60 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grosek, J.; Zuzulova, A.; Brezina, I. Effectiveness of Dowels in Concrete Pavement. Materials 2019, 12, 1669. https://doi.org/10.3390/ma12101669
Grosek J, Zuzulova A, Brezina I. Effectiveness of Dowels in Concrete Pavement. Materials. 2019; 12(10):1669. https://doi.org/10.3390/ma12101669
Chicago/Turabian StyleGrosek, Jiri, Andrea Zuzulova, and Ilja Brezina. 2019. "Effectiveness of Dowels in Concrete Pavement" Materials 12, no. 10: 1669. https://doi.org/10.3390/ma12101669
APA StyleGrosek, J., Zuzulova, A., & Brezina, I. (2019). Effectiveness of Dowels in Concrete Pavement. Materials, 12(10), 1669. https://doi.org/10.3390/ma12101669





