Dependence of Atomic Thickness on Interfacial Conditions and Magnetocrystalline Anisotropy in SmCo5/Sm2Co17 Multilayer
Abstract
1. Introduction
2. Methods
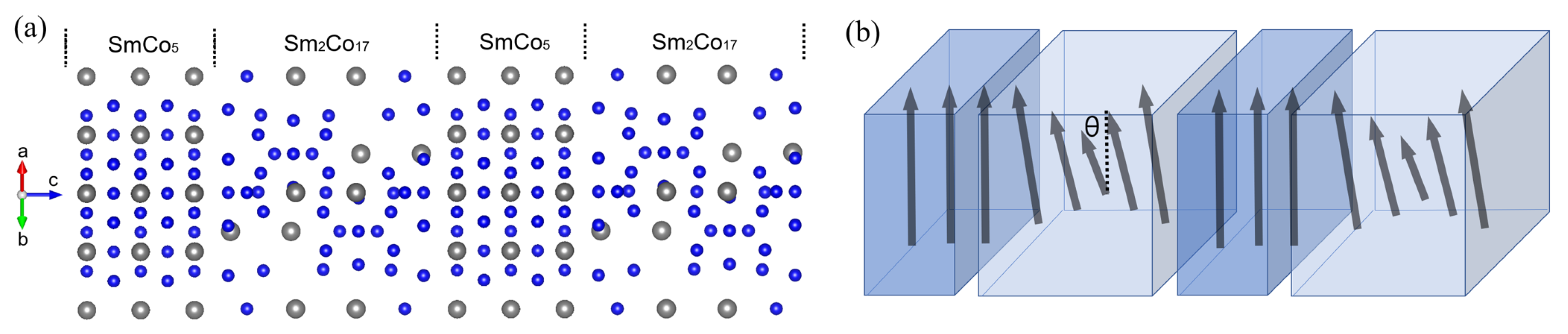
2.1. Atomic Structure
2.2. Exchange Coupling
2.3. Magnetocrystalline Anisotropy Energy
3. Results
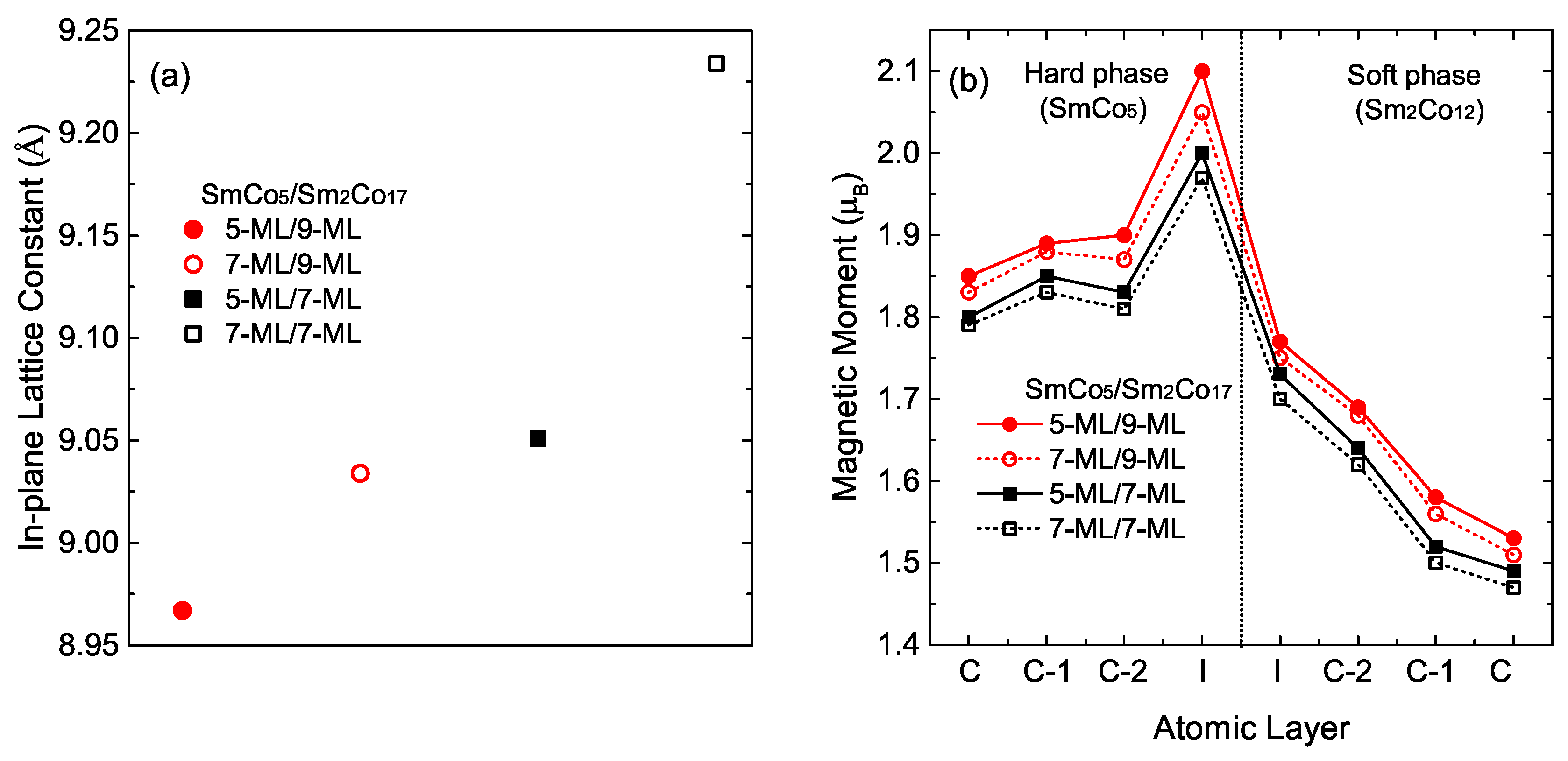
3.1. Atomic Structures & Magnectic Moments
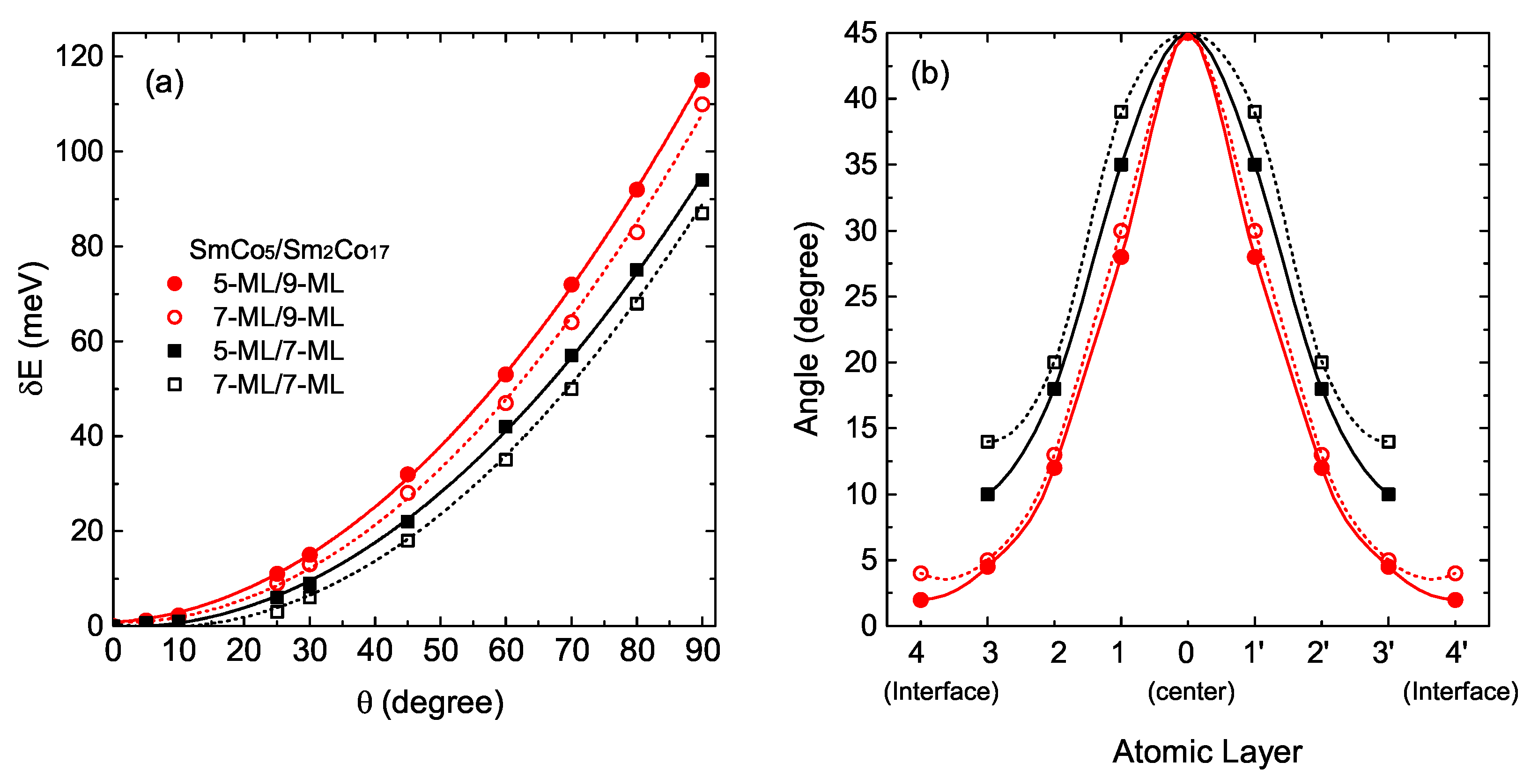
3.2. Exchange Energies
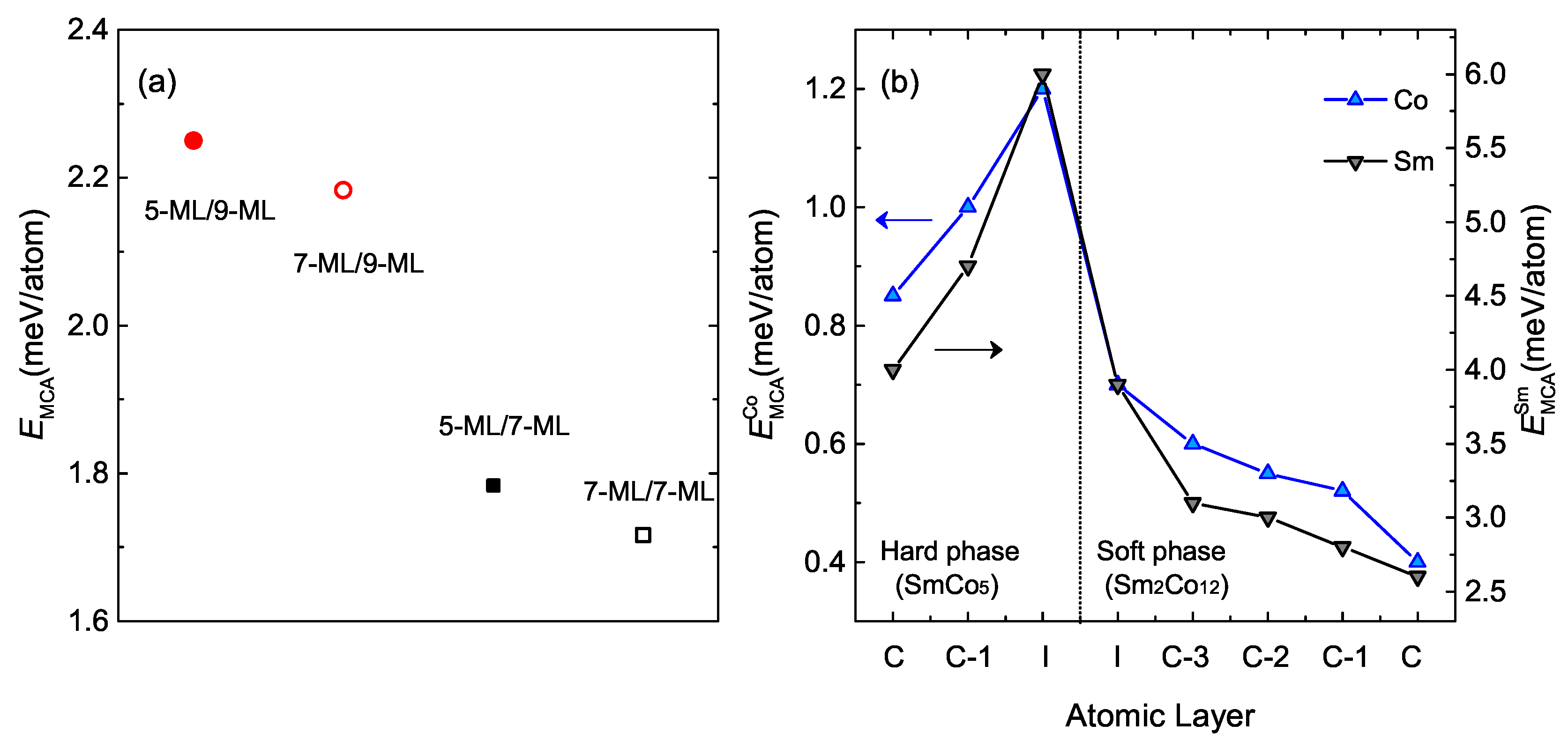
3.3. Magnetocrystalline Anisotropy
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kneller, E.F.; Hawig, R. The exchange-spring magnet: A new material principle for permanent magnets. IEEE Trans. Magn. 1991, 27, 3560–3588. [Google Scholar] [CrossRef]
- Bader, S.D. Colloquium: Opportunities in nanomagnetism. Rev. Mod. Phys. 2006, 78, 1. [Google Scholar] [CrossRef]
- Lopez-Ortega, A.; Estrader, M.; Salazar-Alvarez, G.; Roca, A.G.; Nogues, J. Applications of exchange coupled bi-magnetic hard/soft and soft/hard magnetic core/shell nanoparticles. Phys. Rep. 2015, 553, 1–32. [Google Scholar] [CrossRef]
- Jiang, J.; Bader, S. Rational design of the exchange-spring permanent magnet. J. Phys. Condens. Matter 2014, 26, 064214. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; Sepehri-Amin, H.; Takahashi, Y.; Hono, K. Hard magnetic properties of spacer-layer-tuned NdFeB/Ta/Fe nanocomposite films. Acta Mater. 2015, 84, 405–412. [Google Scholar] [CrossRef]
- Müller, K.H.; Schneider, J.; Handstein, A.; Eckert, D.; Nothnagel, P.; Kirchmayr, H. Comparison of melt-spun Nd4Fe77B19 with neodymium-rich isotropic permanent magnets. In Rapidly Quenched Materials; Elsevier: Amsterdam, The Netherlands, 1991; pp. 151–153. [Google Scholar]
- Eckert, D.; Muller, K.; Handstein, A.; Schneider, J.; Grossinger, R.; Krewenka, R. Temperature dependence of the coercive force in Nd4Fe77B19. IEEE Trans. Magn. 1990, 26, 1834–1836. [Google Scholar] [CrossRef]
- Manaf, A.; Buckley, R.; Davies, H. New nanocrystalline high-remanence Nd-Fe-B alloys by rapid solidification. J. Magn. Magn. Mater. 1993, 128, 302–306. [Google Scholar] [CrossRef]
- Ding, J.; McCormick, P.; Street, R. Remanence enhancement in mechanically alloyed isotropic Sm7Fe93-nitride. J. Magn. Magn. Mater. 1993, 124, 1–4. [Google Scholar] [CrossRef]
- Zheng, B.; Zhang, H.W.; Zhao, S.F.; Chen, J.L.; Wu, G.H. The physical origin of open recoil loops in nanocrystalline permanent magnets. Appl. Phys. Lett. 2008, 93, 182503. [Google Scholar] [CrossRef]
- Zhang, J.; Takahashi, Y.; Gopalan, R.; Hono, K. Sm(Co, Cu)5/Fe exchange spring multilayer films with high energy product. Appl. Phys. Lett. 2005, 86, 122509. [Google Scholar] [CrossRef]
- Skomski, R.; Coey, J. Permanent Magnetism; Institute of Physics Pub.: Bristol, UK, 1999. [Google Scholar]
- Rizal, C.; Kolthammer, J.; Pokharel, R.; Choi, B. Magnetic properties of nanostructured Fe-Co alloys. J. Appl. Phys. 2013, 113, 113905. [Google Scholar] [CrossRef]
- Jekal, S.; Loeffler, J.; Charilaou, M. Pushing the limits of magnetic anisotropy in the Sm-Co system. arXiv, 2018; arXiv:1807.09257. [Google Scholar]
- Jekal, S.Y. Exchange interactions and Curie temperature of Ce-substituted SmCo5. arXiv, 2018; arXiv:1808.00988. [Google Scholar]
- Zhou, J.; Skomski, R.; Chen, C.; Hadjipanayis, G.C.; Sellmyer, D.J. Sm–Co–Cu–Ti high-temperature permanent magnets. Appl. Phys. Lett. 2000, 77, 1514–1516. [Google Scholar] [CrossRef]
- Gutfleisch, O. Controlling the properties of high energy density permanent magnetic materials by different processing routes. J. Phys. D Appl. Phys. 2000, 33, R157. [Google Scholar] [CrossRef]
- Gutfleisch, O.; Willard, M.A.; Brück, E.; Chen, C.H.; Sankar, S.; Liu, J.P. Magnetic materials and devices for the 21st century: stronger, lighter, and more energy efficient. Adv. Mater. 2011, 23, 821–842. [Google Scholar] [CrossRef]
- Handstein, A.; Yan, A.; Martinek, G.; Gutfleisch, O.; Muller, K.H.; Schultz, L. Stability of magnetic properties of Sm2Co17-type magnets at operating temperatures higher than 400°. IEEE Trans. Magn. 2003, 39, 2923–2925. [Google Scholar] [CrossRef]
- Shan, Z.; Liu, J.; Chakka, V.M.; Zeng, H.; Jiang, J. Energy barrier and magnetic properties of exchange-coupled hard-soft bilayer. IEEE Trans. Magn. 2002, 38, 2907–2909. [Google Scholar] [CrossRef]
- Guo, Z.; Jiang, J.; Pearson, J.; Bader, S.; Liu, J. Exchange-coupled Sm–Co/Nd–Co nanomagnets: correlation between soft phase anisotropy and exchange field. Appl. Phys. Lett. 2002, 81, 2029–2031. [Google Scholar] [CrossRef]
- Asti, G.; Solzi, M.; Ghidini, M.; Neri, F.M. Micromagnetic analysis of exchange-coupled hard-soft planar nanocomposites. Phys. Rev. B 2004, 69, 174401. [Google Scholar] [CrossRef]
- Choi, Y.; Jiang, J.; Ding, Y.; Rosenberg, R.; Pearson, J.; Bader, S.; Zambano, A.; Murakami, M.; Takeuchi, I.; Wang, Z.; et al. Role of diffused Co atoms in improving effective exchange coupling in Sm-Co/Fe spring magnets. Phys. Rev. B 2007, 75, 104432. [Google Scholar] [CrossRef]
- Zambano, A.; Oguchi, H.; Takeuchi, I.; Choi, Y.; Jiang, J.; Liu, J.; Lofland, S.; Josell, D.; Bendersky, L.A. Dependence of exchange coupling interaction on micromagnetic constants in hard/soft magnetic bilayer systems. Phys. Rev. B 2007, 75, 144429. [Google Scholar] [CrossRef]
- Sabiryanov, R.; Jaswal, S. Electronic structure and magnetic properties of hard/soft multilayers. J. Magn. Magn. Mater. 1998, 177, 989–990. [Google Scholar] [CrossRef]
- Sabiryanov, R.; Jaswal, S. Magnetic properties of hard/soft composites: SmCo5/Co1−xFex. Phys. Rev. B 1998, 58, 12071. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum espresso: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Steinbeck, L.; Richter, M.; Eschrig, H. Magnetocrystalline anisotropy of RCo5 intermetallics: Itinerant-electron contribution. J. Magn. Magn. Mater. 2001, 226, 1011–1013. [Google Scholar] [CrossRef]
- Larson, P.; Mazin, I.; Papaconstantopoulos, D.A. Calculation of magnetic anisotropy energy in SmCo5. Phys. Rev. B 2003, 67, 214405. [Google Scholar] [CrossRef]
- Larson, P.; Mazin, I.; Papaconstantopoulos, D.A. Effects of doping on the magnetic anisotropy energy in SmCo5−xFex and YCo5−xFex. Phys. Rev. B 2004, 69, 134408. [Google Scholar] [CrossRef]
- Mryasov, O.; Sabiryanov, R.; Freeman, A.; Jaswal, S. Effect of lattice distortions on the competition between the double and superexchange mechanisms in LaMnO3. Phys. Rev. B 1997, 56, 7255. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Q.; Liu, P.J.; Sabirianov, R.F. Dependence of exchange coupling on interfacial conditions in SmCo5/Co system: A first-principles study. J. Nanosci. Nanotechnol. 2008, 8, 3036–3039. [Google Scholar] [CrossRef] [PubMed]
- Yan, A.; Bollero, A.; Gutfleisch, O.; Müller, K.H. Microstructure and magnetization reversal in nanocomposite SmCo5/Sm2Co17 magnets. J. Appl. Phys. 2002, 91, 2192–2196. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jekal, S. Dependence of Atomic Thickness on Interfacial Conditions and Magnetocrystalline Anisotropy in SmCo5/Sm2Co17 Multilayer. Materials 2019, 12, 56. https://doi.org/10.3390/ma12010056
Jekal S. Dependence of Atomic Thickness on Interfacial Conditions and Magnetocrystalline Anisotropy in SmCo5/Sm2Co17 Multilayer. Materials. 2019; 12(1):56. https://doi.org/10.3390/ma12010056
Chicago/Turabian StyleJekal, Soyoung. 2019. "Dependence of Atomic Thickness on Interfacial Conditions and Magnetocrystalline Anisotropy in SmCo5/Sm2Co17 Multilayer" Materials 12, no. 1: 56. https://doi.org/10.3390/ma12010056
APA StyleJekal, S. (2019). Dependence of Atomic Thickness on Interfacial Conditions and Magnetocrystalline Anisotropy in SmCo5/Sm2Co17 Multilayer. Materials, 12(1), 56. https://doi.org/10.3390/ma12010056




