Thin Electric Heating Membrane Constructed with a Three-Dimensional Nanofibrillated Cellulose–Graphene–Graphene Oxide System
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
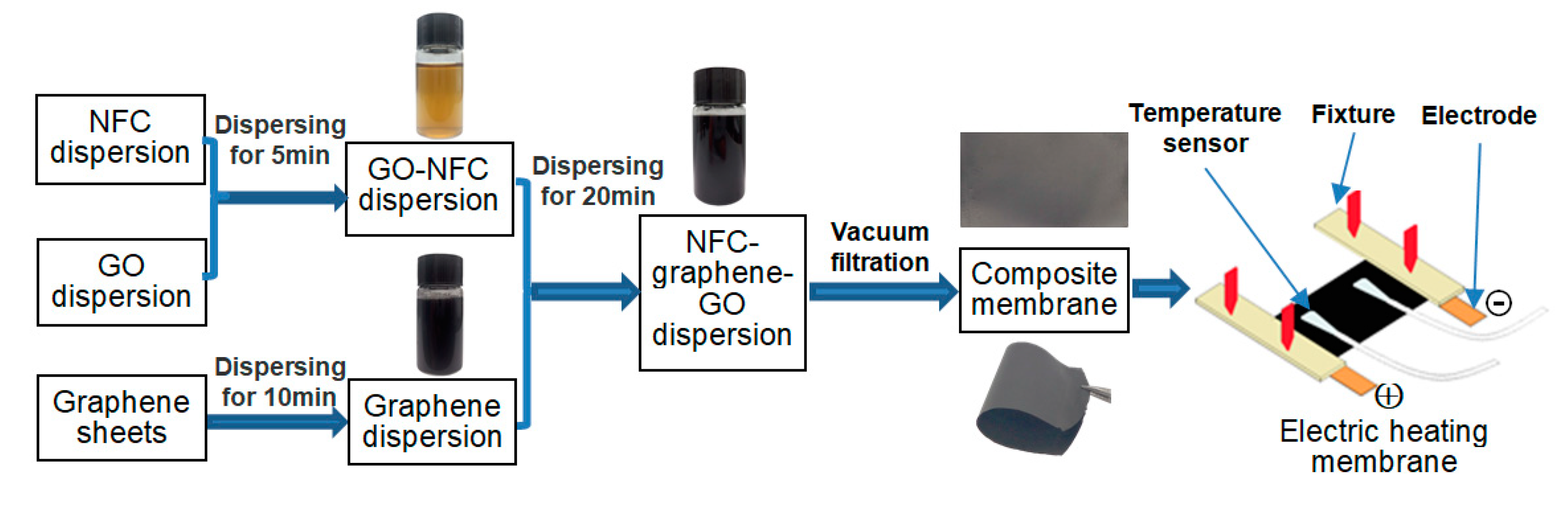
2.2. Preparation of the Composite Membrane
2.3. Electric Heating Membrane and Heating Properties
2.4. Characterization
3. Results and Discussion
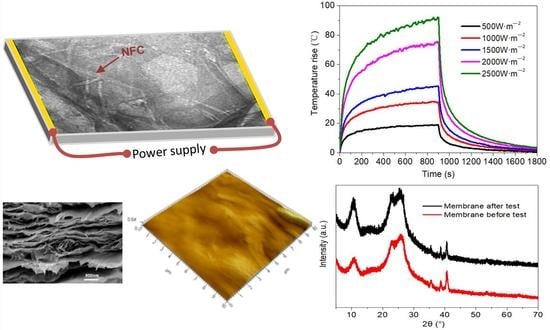
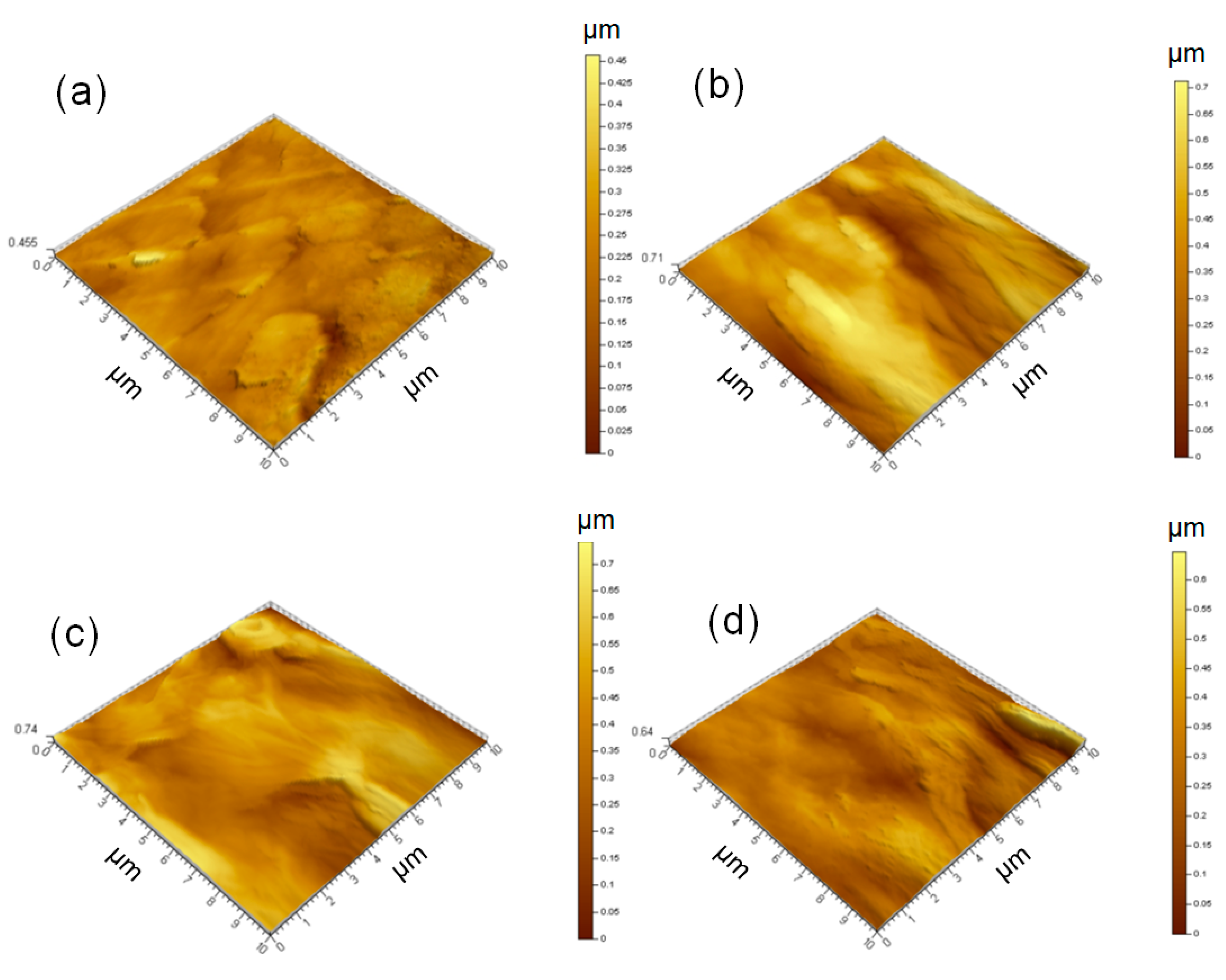
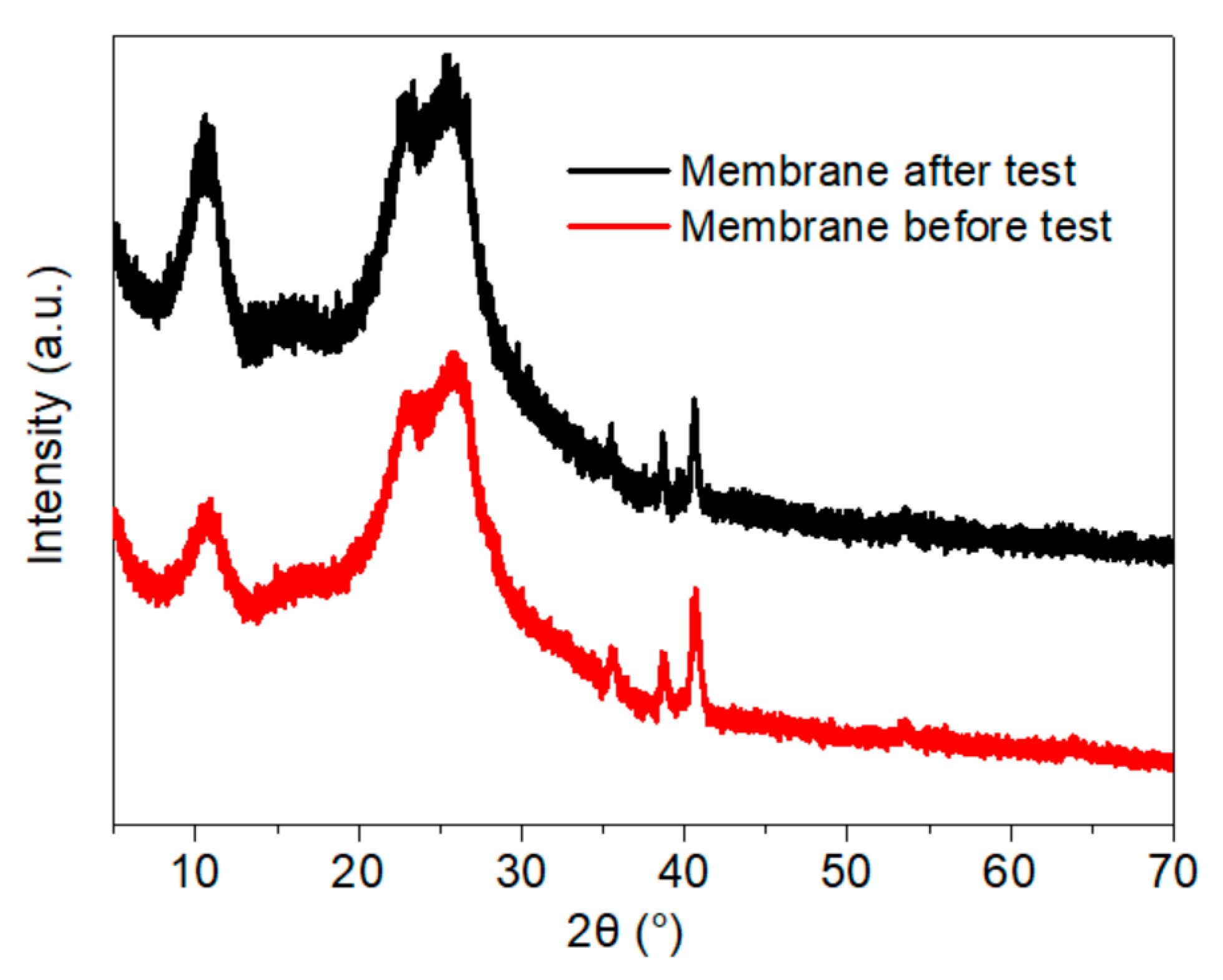
3.1. Morphology and Structure of the Electric Heating Membrane
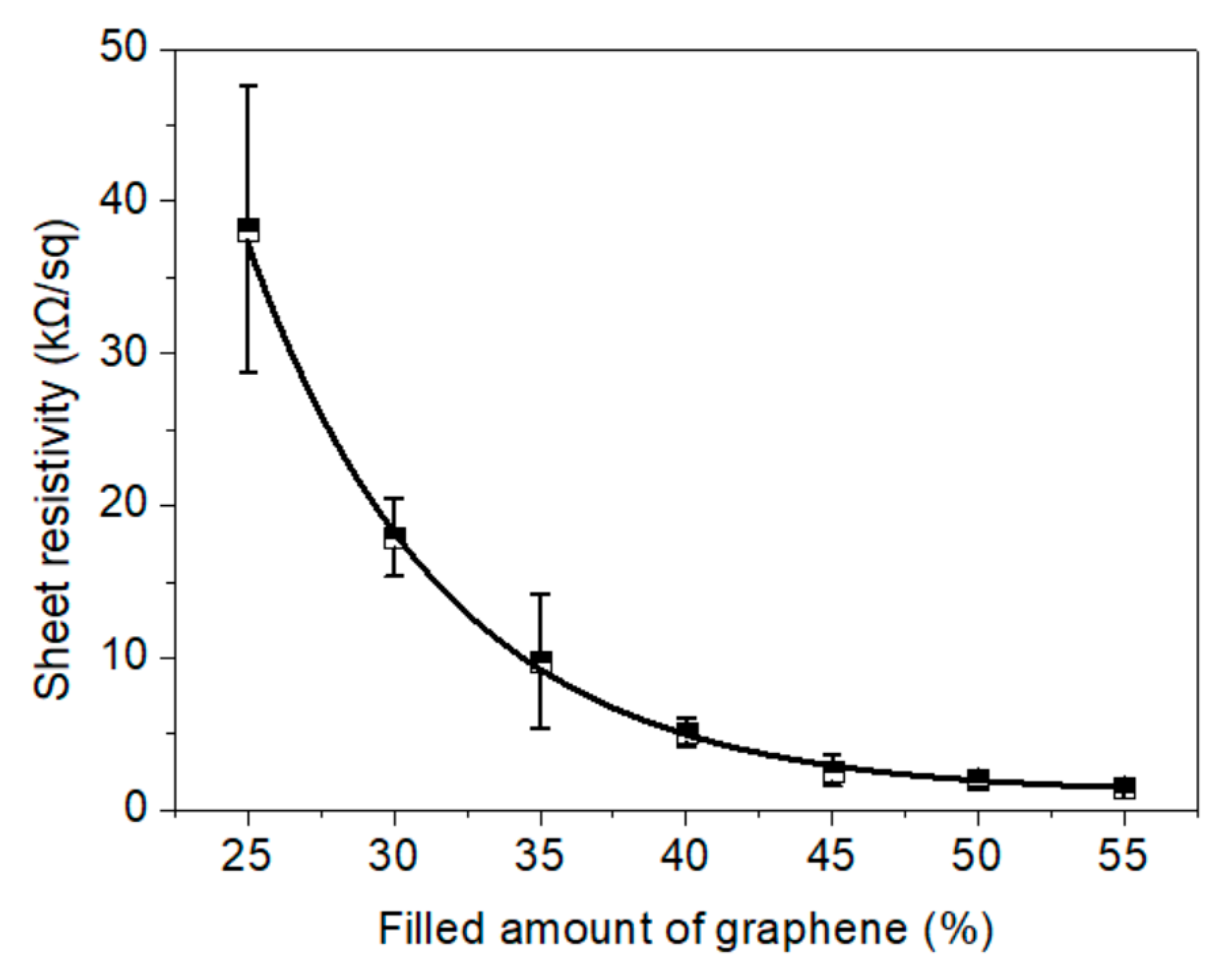
3.2. Conductivity of the Electric Heating Membrane
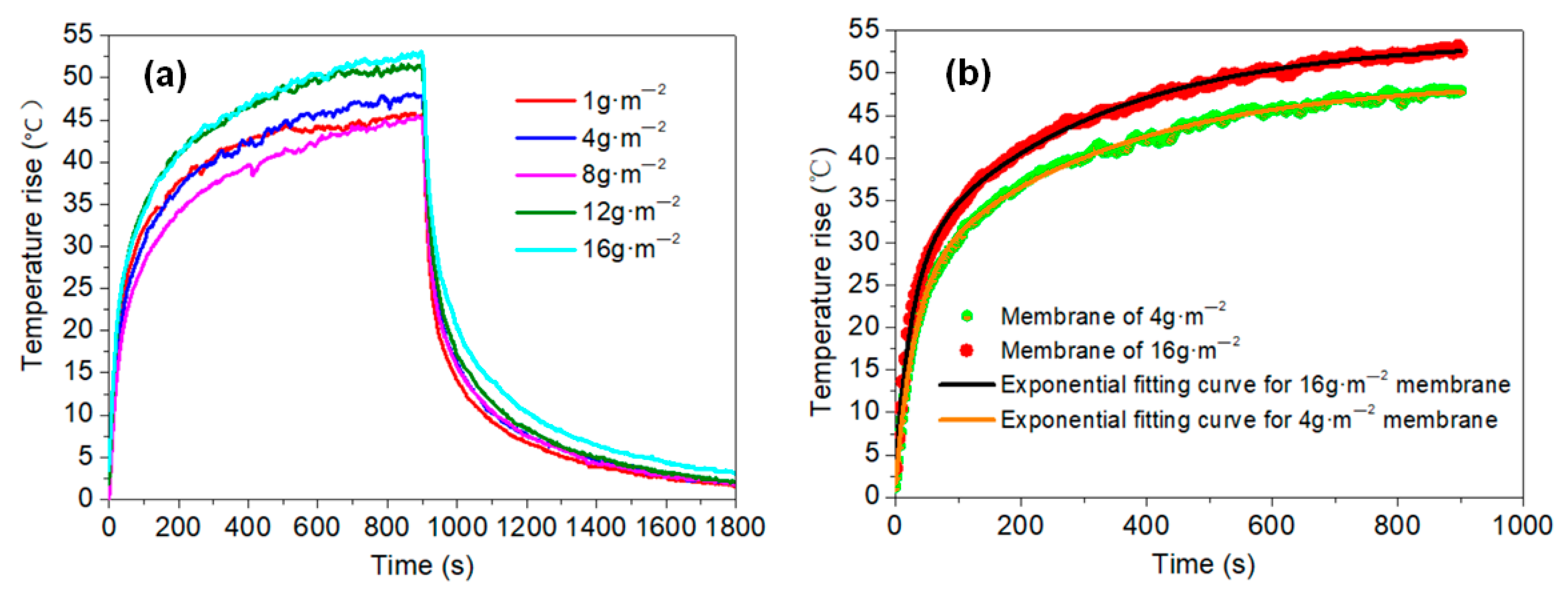
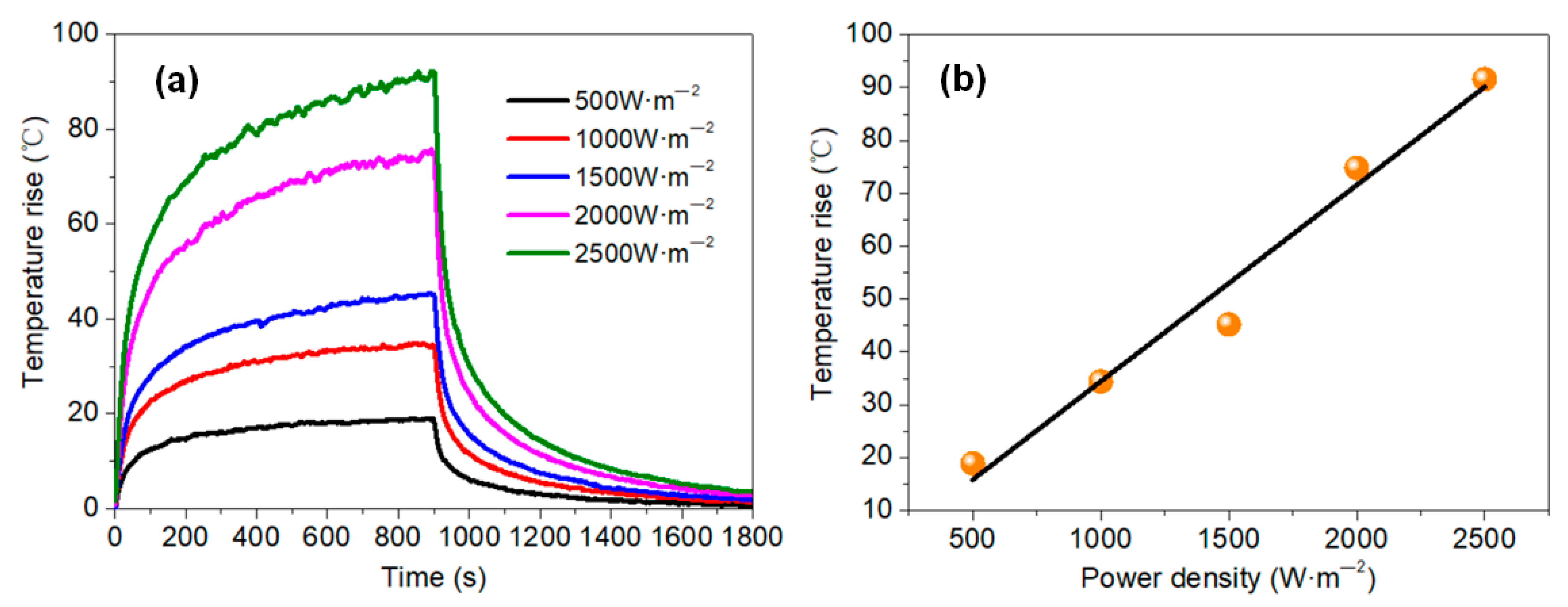
3.3. Electric Heating Property
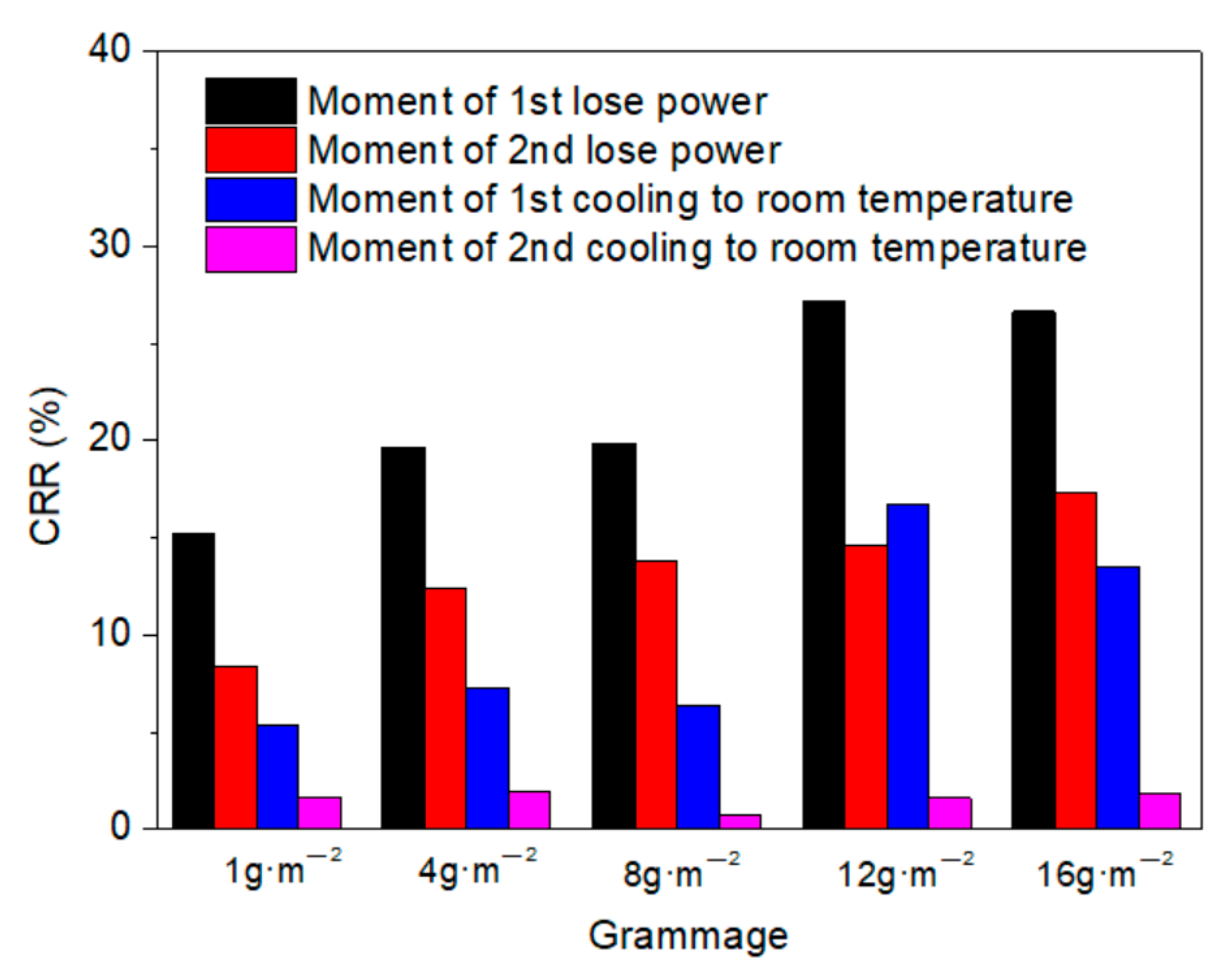
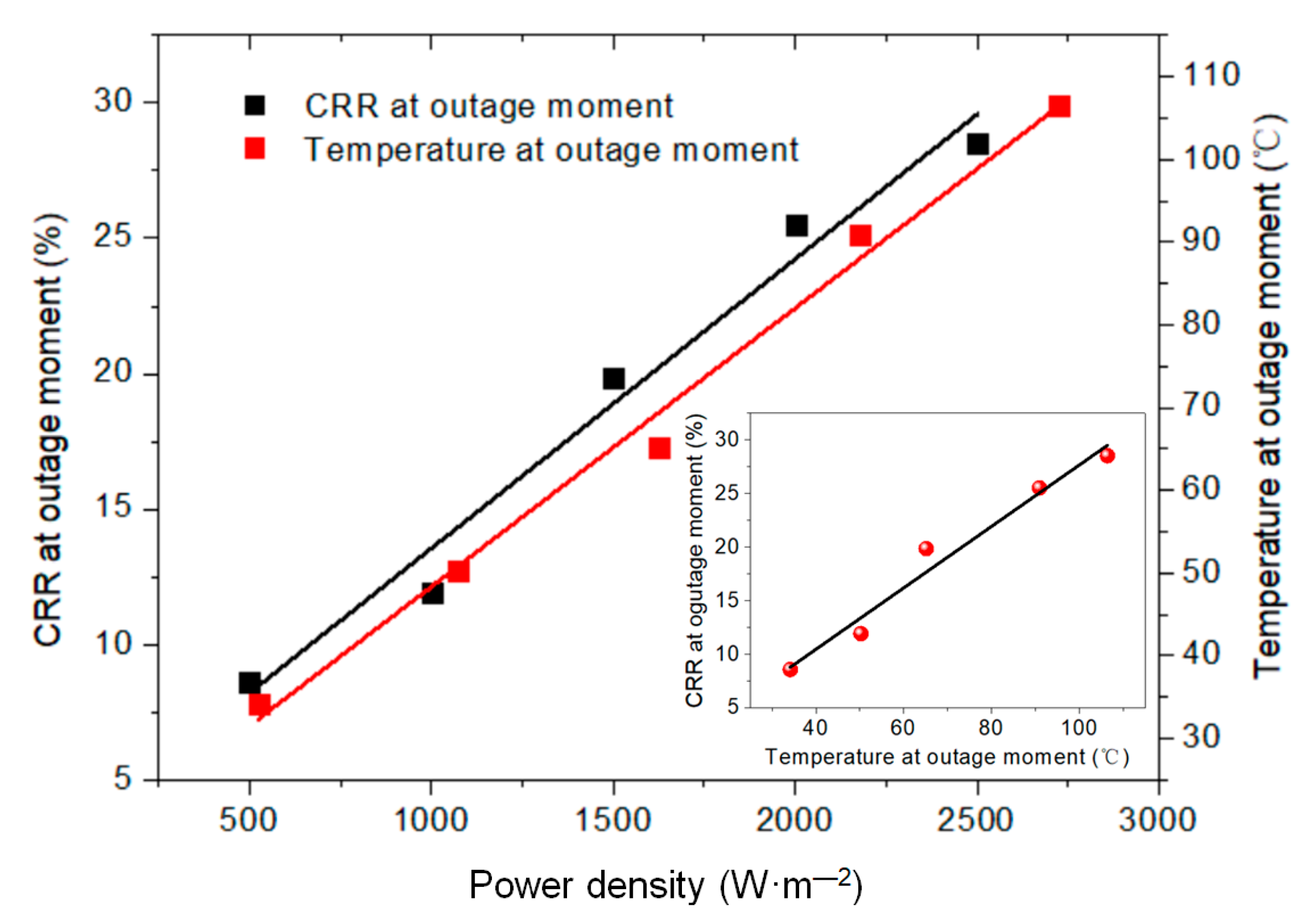
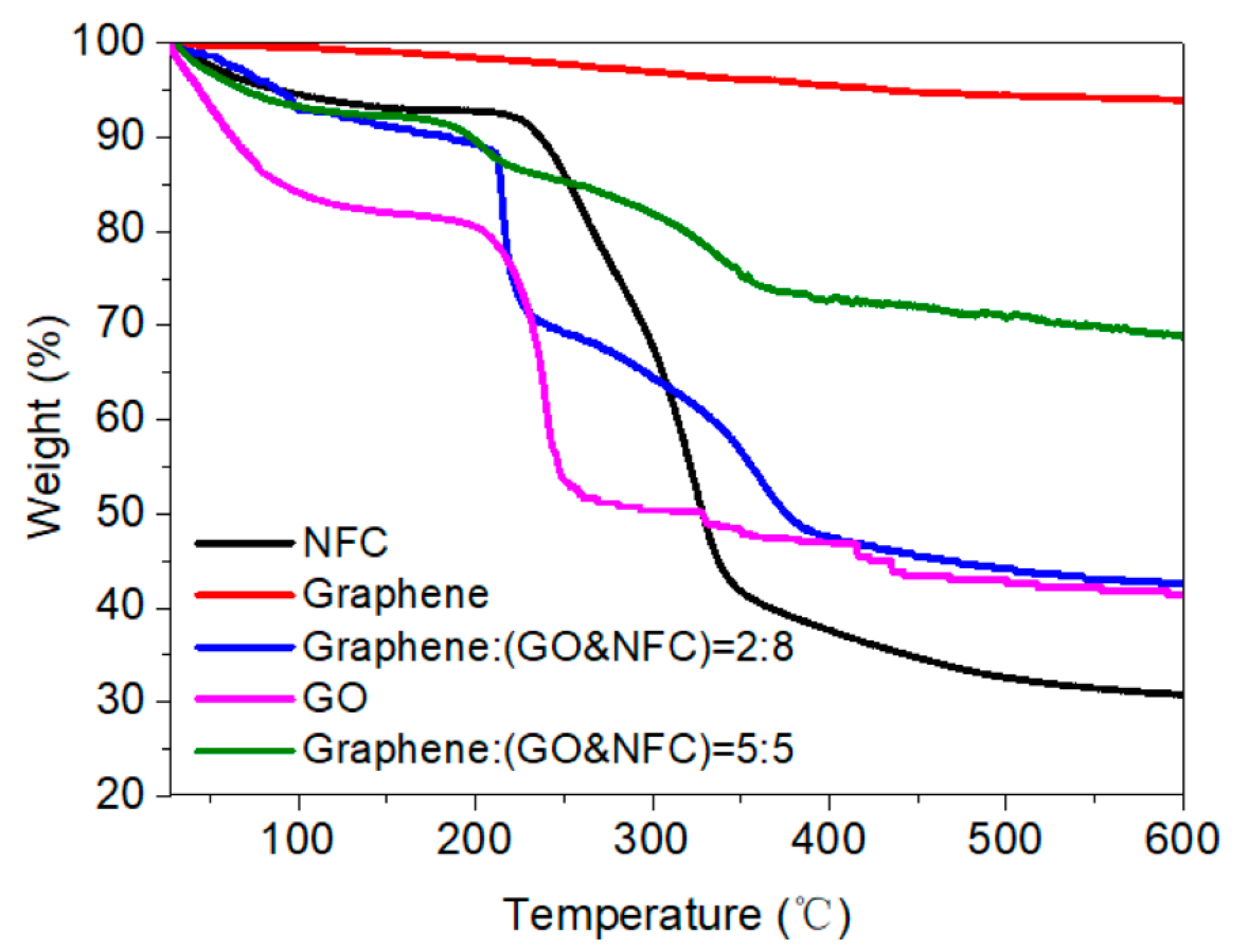
3.4. Thermal Stability
4. Conclusions
- NFC, graphene, and GO were dispersed uniformly and adequately in the aqueous system. The negative charge on the surface of NFC and GO, as well as their high length–diameter and radius–thickness ratio, meant that they formed a crosslinked structure, facilitating the dispersion of graphene and stability of the system. NFC and GO act as a binder, and form bonds between two sheets. Furthermore, the skeletal NFC was lapped across the membrane. The cross-section of the membrane revealed a layered and rough structure, while the surface was smooth and compact. These results indicate that a 3D network had formed in the membrane, generating a certain mechanical and conductive property.
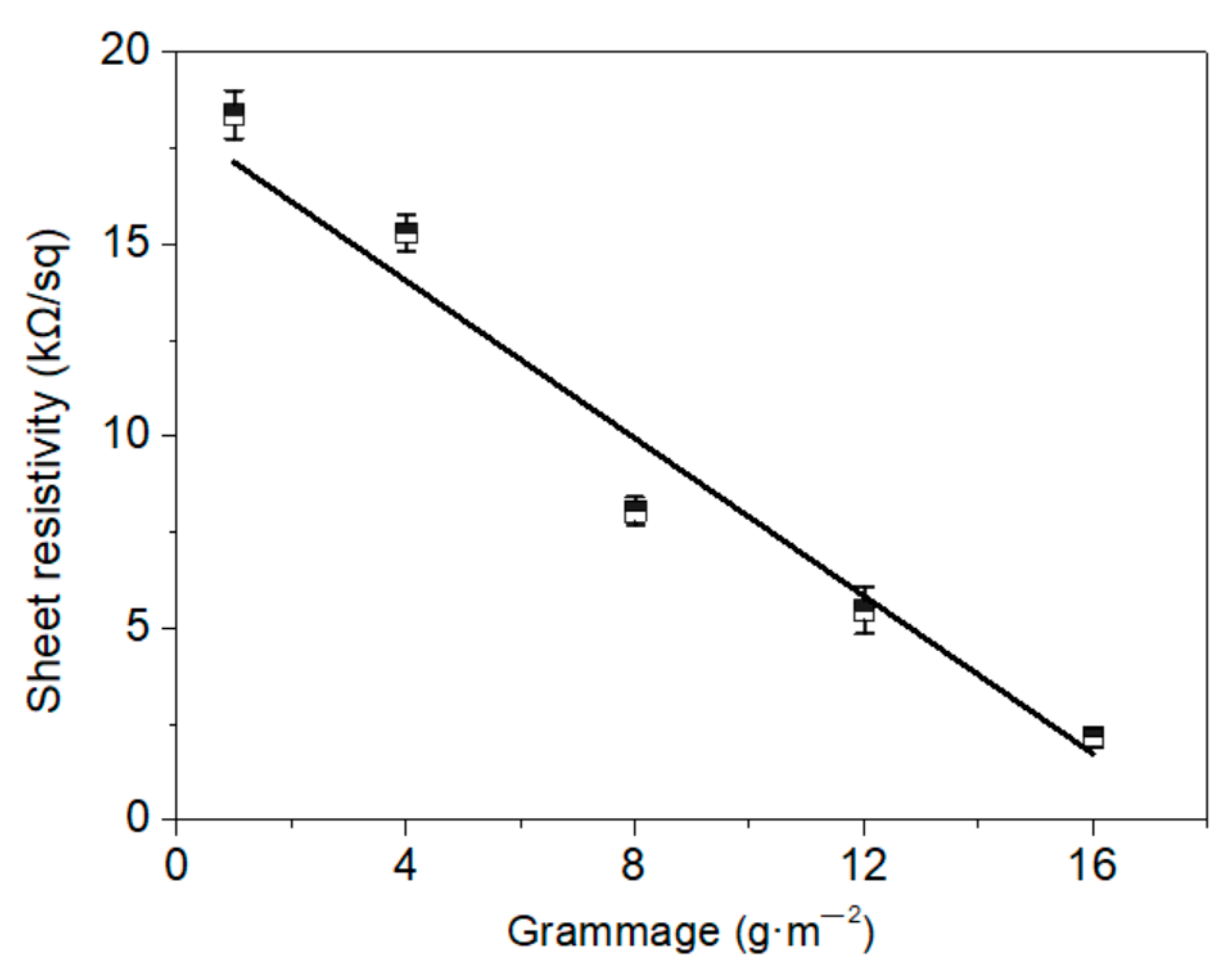
- Graphene sheets with a high aspect ratio contributed toward the enhanced conductivity of the membrane. The sheet resistivity of the electric heating membrane exhibited a downtrend with a significant exponential function as the amount of graphene increased, while there was a high linear relation between the sheet resistivity and grammage. This implies that the conductivity can be controlled for a specific target power and supply voltage, and that NFC and GO disturbed the stacking behavior of the graphene sheet to form the integrated structure.
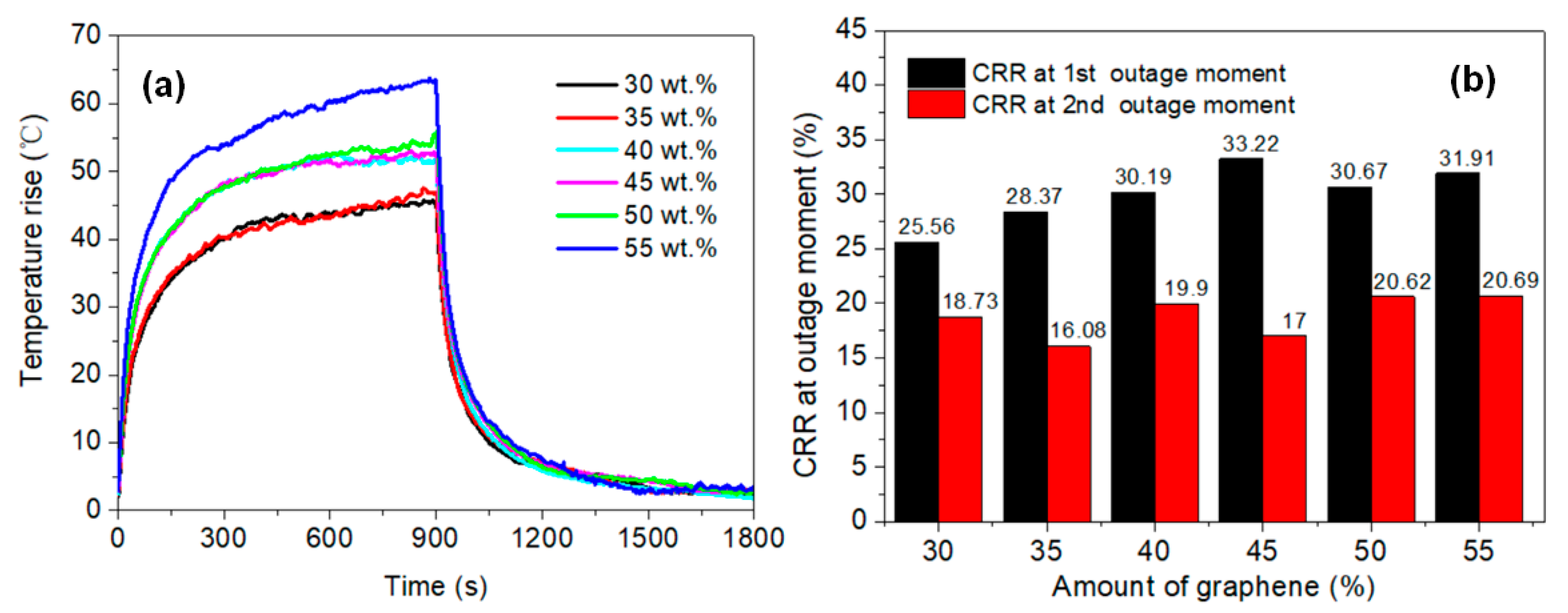
- The temperature rise on the membrane surface was elevated when higher amounts of graphene were added, and increased linearly with the applied power density. Both Joule heating and the electric current led to the decline of membrane resistance. The temperature rose quickly for the initial 300 s and then stabilized, presenting an exponential function trend with high correlation. The heating properties of the membranes did not show significant differences: even when the grammage was decreased from 16 to 1 g·m−2, the membranes showed a stabilized temperature rise of about 52 and 45 °C, respectively, under the same power density of 1500 W·m−2.
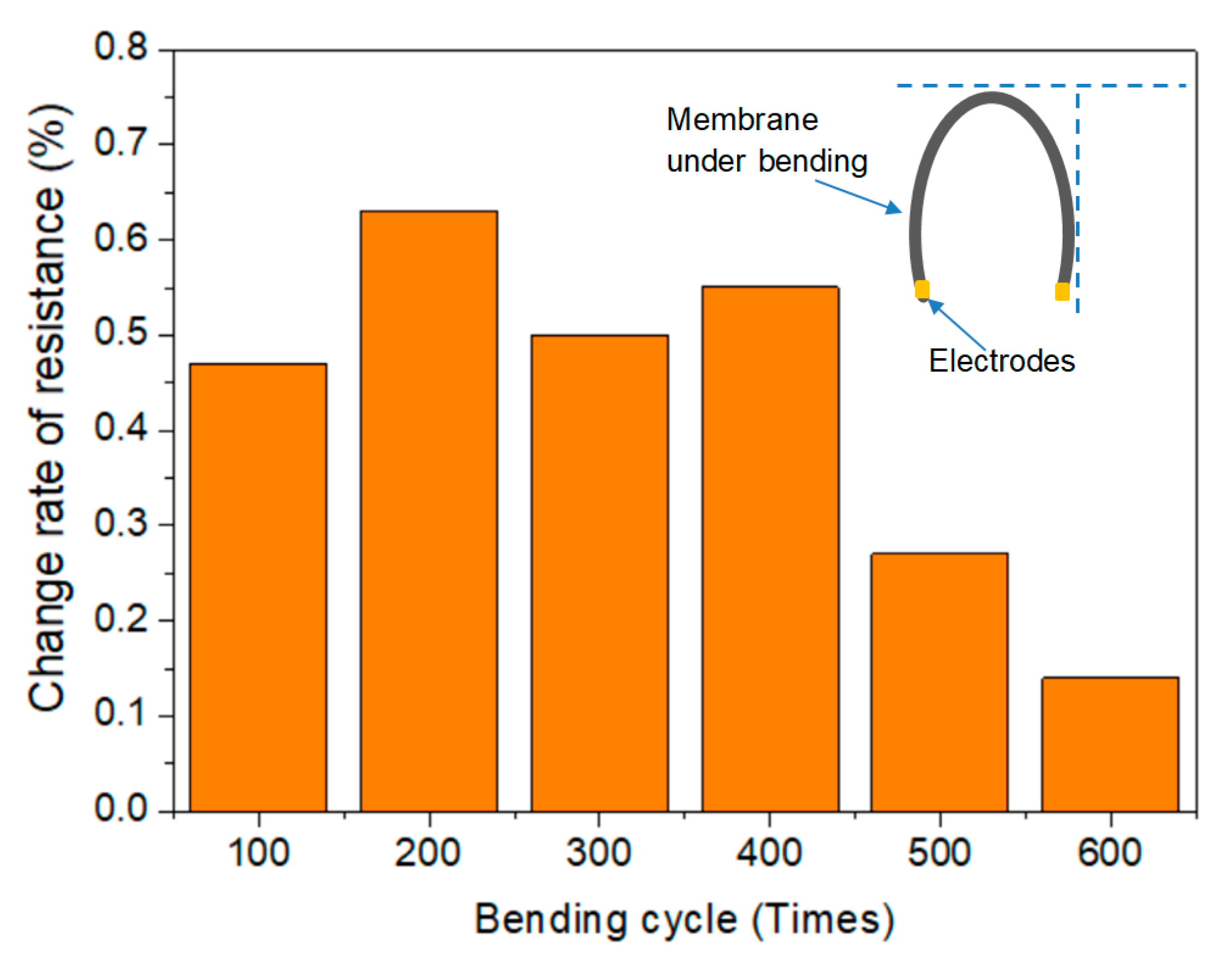
- The thermogravimetric analysis (TGA) results indicated that thermal stability of the membrane was improved due to the crosslinking of NFC and GO. The regularity of the membrane structure was elevated after two heating tests, with regard to the CRR at the moment power was lost and after cooling. The CRR showed suitable relationships with the grammage and graphene content, which will contribute to the control over the actual power in use. However, before further application, additional mechanisms and technologies must be investigated, such as the variation of phase structure induced by Joule heating with a wider range of power and longer working time, the relation between phase structure and thermal radiation, and key technologies for large scale printing or coating.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Fal’Ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Guan, L.Z.; Zhao, L.; Wan, Y.J.; Tang, L.C. Three-dimensional graphene-based polymer nanocomposites: Preparation, properties and applications. Nanoscale 2018, 10, 14788–14811. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.Z.; Wang, K.L.; Zhu, H.W. Recent developments in graphene-based membranes: Structure, mass-transport mechanism and potential applications. Adv. Mater. 2016, 28, 2287–2310. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.G.; Fu, K.K.; Yan, C.Y.; Dai, J.Q.; Chen, Y.N.; Wang, Y.B.; Zhang, B.L.; Hitz, E.; Hu, L.B. Three-dimensional printable high-temperature and high-rate heaters. ACS Nano 2016, 10, 5272–5279. [Google Scholar] [CrossRef] [PubMed]
- Zanjani, J.S.M.; Okan, B.S.; Pappas, P.N.; Galiotis, C.; Menceloglu, Y.Z.; Yildiz, M. Tailoring viscoelastic response, self-heating and deicing properties of carbon-fiber reinforced epoxy composites by graphene modification. Compos. Part A 2018, 106, 1–10. [Google Scholar] [CrossRef]
- Bustillos, J.; Zhang, C.; Boesl, B.; Agarwal, A. Three-dimensional graphene foam-polymer composite with superior deicing efficiency and strength. ACS Appl. Mater. Interfaces 2018, 10, 5022–5029. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, Y.D.; Wu, Q. Effect of graphene coating on the heat transfer performance of a composite anti-/deicing component. Coatings 2017, 7, 158. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, H.T.; Liu, G.; Su, Z.W.; Wu, J.F.; Liu, J.P.; Zhang, X.N.; Chen, Y.Q.; Zhou, W.W. Light-weight, flexible, low-voltage electro-thermal film using graphite nanoplatelets for wearable/smart electronics and deicing devices. J. Alloy. Compd. 2017, 699, 1049–1056. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, X.B.; Chen, J.T.; Zhao, J.P. Large-size graphene microsheets as a protective layer for transparent conductive silver nanowire film heaters. Carbon 2014, 69, 437–443. [Google Scholar] [CrossRef]
- Lee, B.J.; Jeong, G.H. Fabrication of defrost films using graphenes grown by chemical vapor deposition. Curr. Appl. Phys. 2012, 12, S113–S117. [Google Scholar] [CrossRef]
- Sui, D.; Huang, Y.; Huang, L.; Liang, J.J.; Ma, Y.F.; Chen, Y.S. Flexible and transparent electrothermal film heaters based on graphene materials. Small 2011, 7, 3186–3192. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.N.; Fu, K.; Zhu, S.Z.; Luo, W.; Wang, Y.B.; Li, Y.J.; Hitz, E.; Yao, Y.G.; Dai, J.Q.; Wan, J.Y.; et al. Reduced graphene oxide films with ultrahigh conductivity as li-ion battery current collectors. Nano Lett. 2016, 16, 3616–3623. [Google Scholar] [CrossRef] [PubMed]
- Ding, G.M.; Jiao, W.C.; Wang, R.G.; Niu, Y.; Chen, L.Y.; Hao, L.F. Ultrafast, reversible transition of superwettability of graphene network and controllable underwater oil adhesion for oil microdroplet transportation. Adv. Funct. Mater. 2018, 28, 1706686. [Google Scholar] [CrossRef]
- Yan, C.Y.; Wang, J.X.; Kang, W.B.; Cui, M.Q.; Wang, X.; Foo, C.Y.; Chee, K.J.; Lee, P.S. Highly stretchable piezoresistive graphene–nanocellulose nanopaper for strain sensors. Adv. Mater. 2014, 26, 2022–2027. [Google Scholar] [CrossRef] [PubMed]
- Luong, N.D.; Pahimanolis, N.; Hippi, U.; Korhonen, J.T.; Ruokolainen, J.; Johansson, L.S.; Nam, J.D.; Seppala, J. Graphene/cellulose nanocomposite paper with high electrical and mechanical performances. J. Mater. Chem. 2011, 21, 13991–13998. [Google Scholar] [CrossRef]
- Malho, J.M.; Laaksonen, P.; Walther, A.; Ikkala, O.; Linder, M.B. Facile method for stiff, tough, and strong nanocomposites by direct exfoliation of multilayered graphene into native nanocellulose matrix. Biomacromolecules 2012, 13, 1093–1099. [Google Scholar] [CrossRef] [PubMed]
- Blomquist, N.; Engström, A.C.; Hummelgård, M.; Andres, B.; Forsberg, S.; Olin, H. Large-scale production of nanographite by tube-shear exfoliation in water. PLoS ONE 2016, 11, e0154686. [Google Scholar] [CrossRef] [PubMed]
- Fei, F.; Cseri, L.; Szekely, G.; Blanford, C.F. Robust covalently cross-linked polybenzimidazole/graphene oxide membranes for high-flux organic solvent nanofiltration. ACS Appl. Mater. Interfaces 2018, 10, 16140–16147. [Google Scholar] [CrossRef] [PubMed]
- Siró, I.; Plackett, D. Microfibrillated cellulose and new nanocomposite materials: A review. Cellulose 2010, 17, 459–494. [Google Scholar] [CrossRef]
- Andres, B.; Forsberg, S.; Dahlström, C.; Blomquist, N.; Olin, H. Enhanced electrical and mechanical properties of nanographite electrodes for supercapacitors by addition of nanofibrillated cellulose. Phys. Status Solidi B 2014, 251, 2581–2586. [Google Scholar] [CrossRef]
- Carrasco, P.M.; Montes, S.; García, I.; Borghei, M.; Jiang, H.; Odriozola, I.; Cabanero, G.; Ruiz, V. High-concentration aqueous dispersions of graphene produced by exfoliation of graphite using cellulose nanocrystals. Carbon 2014, 70, 157–163. [Google Scholar] [CrossRef]
- Vernnisoglou, E.C.; Giannakopoulou, T.; Todorova, N.; Vaimakis, T.; Boukos, N.; Petridis, D.; Trapalis, C. 2-dimensional clay/reduced graphene oxide ordered heterostructures dispersible in water via a one-step hydrothermal route. J. Nanosci. Nanotechnol. 2018, 18, 4684–4691. [Google Scholar] [CrossRef] [PubMed]
- Taheri, H.; Samyn, P. Effect of homogenization (microfluidization) process parameters in mechanical production of micro- and nanofibrillated cellulose on its rheological and morphological properties. Cellulose 2016, 23, 1221–1238. [Google Scholar] [CrossRef]
- Benhamou, K.; Dufresne, A.; Magnin, A.; Mortha, G.; Kaddami, H. Control of size and viscoelastic properties of nanofibrillated cellulose from palm tree by varying the tempo-mediated oxidation time. Carbohydr. Polym. 2014, 99, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, L.C.; de Araújo, M.M.; de Moraes, A.C.M.; da Silva, D.S.; Ferreira, A.G.; Franqui, L.S.; Martinez, D.S.T.; Alves, O.L. Nanocomposites based on graphene oxide and mesoporous silica nanoparticles: Preparation, characterization and nanobiointeractions with red blood cells and human plasma proteins. Appl. Surf. Sci. 2018, 437, 110–121. [Google Scholar] [CrossRef]
- Kiziltas, E.E.; Kiziltas, A.; Rhodes, K.; Emanetoglu, N.W.; Blumentritt, M.; Gardner, D.J. Electrically conductive nano graphite-filled bacterial cellulose composites. Carbohydr. Polym. 2016, 136, 1144–1151. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.K.; Li, W.; He, Y.; Duan, T. In-situ biopreparation of biocompatible bacterial cellulose/graphene oxide composites pellets. Appl. Surf. Sci. 2015, 338, 22–26. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, D.; Jiu, J.; Nge, T.T.; Sugahara, T.; Nagao, S.; Koga, H.; Nogi, M.; Suganuma, K.; Wang, X.; et al. Electrically conductive bacterial cellulose composite membranes produced by the incorporation of graphite nanoplatelets in pristine bacterial cellulose membranes. Express Polym. Lett. 2013, 7, 756–766. [Google Scholar] [CrossRef]
- Wang, F.Z.; Drzal, L.T.; Qin, Y.; Huang, Z.X. Multifunctional graphene nanoplatelets/cellulose nanocrystals composite paper. Compos. Part B Eng. 2015, 79, 521–529. [Google Scholar] [CrossRef]
- Theivasanthi, T.; Christma, F.L.A.; Toyin, A.J.; Gopinath, S.C.B.; Ravichandran, R. Synthesis and characterization of cotton fiber-based nanocellulose. Int. J. Biol. Macromol. 2017, 109, 832–836. [Google Scholar] [CrossRef] [PubMed]
- Hosseinzadeh, A.; Bidmeshkipour, S.; Abdi, Y.; Arzi, E.; Mohajerzadeh, S. Graphene based strain sensors: A comparative study on graphene and its derivatives. Appl. Surf. Sci. 2018, 448, 71–77. [Google Scholar] [CrossRef]
- Anirudhan, T.S.; Deepa, J.R. Nano-zinc oxide incorporated graphene oxide/nanocellulose composite for the adsorption and photo catalytic degradation of ciprofloxacin hydrochloride from aqueous solutions. J. Colloid Interface Sci. 2017, 490, 343–356. [Google Scholar] [CrossRef] [PubMed]
- Osong, S.H.; Dahlström, C.; Forsberg, S.; Andres, B.; Engstrand, P.; Norgren, S. Nanofibrillated cellulose/nanographite composite films. Cellulose 2016, 23, 2487–2500. [Google Scholar] [CrossRef]
- Cobos, M.; González, B.; Jesús, M.F.; Dolores, M.F. Study on the effect of graphene and glycerol plasticizer on the properties of chitosan-graphene nanocomposites via in situ green chemical reduction of graphene oxide. Int. J. Biol. Macromol. 2018, 5, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Stobinski, L.; Lesiak, B.; Malolepszy, A.; Mazurkiewicz, M.; Mierzwa, B.; Zemek, J.; Jiricek, P.; Bieloshapka, I. Graphene oxide and reduced graphene oxide studied by the XRD, TEM and electron spectroscopy methods. J. Electron Spectrosc. Relat. Phenom. 2014, 195, 145–154. [Google Scholar] [CrossRef]
- Kim, H.; Miura, Y.; Macosko, C.W. Graphene/polyurethane nanocomposites for improved gas barrier and electrical conductivity. Chem. Mater. 2010, 22, 3441–3450. [Google Scholar] [CrossRef]
- Yue, H.J.; Sun, H.J.; Peng, T.J.; Liu, B.; Xie, Y.Y. Evolution of structure and functional groups in the functionalization of graphene oxide with l-cysteine. J. Mol. Struct. 2018, 1163, 449–454. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Yang, J.F.; Zhou, S.Y.; Zhang, W.T.; Chuan, R. Electrical properties of graphene nanoplatelets/ultra-high molecular weight polyethylene composites. J. Mater. Sci. Mater Electron. 2018, 29, 91–96. [Google Scholar] [CrossRef]
- Zhao, S.G.; Luo, D.D.; Zhan, P.F.; Li, G.J.; Dai, K.; Guo, J.; Zheng, G.Q.; Liu, C.T.; Shen, C.Y.; Guo, Z.H. Heating induced negative temperature coefficient effect in conductive graphene/polymer ternary nanocomposites with a segregated and double-percolated structure. J. Mater. Chem. C 2017, 5, 8233–8242. [Google Scholar] [CrossRef]
- NeeIla, N.; Gaddam, V.; Nayak, M.M.; Dinesh, N.S.; Rajanna, K. Scalable fabrication of highly sensitive flexible temperature sensors based on silver nanoparticles coated reduced graphene oxide nanocomposite thin films. Sens. Actuators A Phys. 2017, 268, 173–182. [Google Scholar] [CrossRef]
- Yuan, Q.P.; Fu, F. Application of carbon fiber paper in integrated wooden electric heating composite. BioResources 2015, 9, 5662–5675. [Google Scholar] [CrossRef]
- Yang, S.; Su, C.W.; Song, L.L.; Yuan, Q.P. Composite process and electrothermal properties of a new-type electric heating plywood made with melamine resin adhesive film. BioResources 2017, 12, 8953–8969. [Google Scholar] [CrossRef]





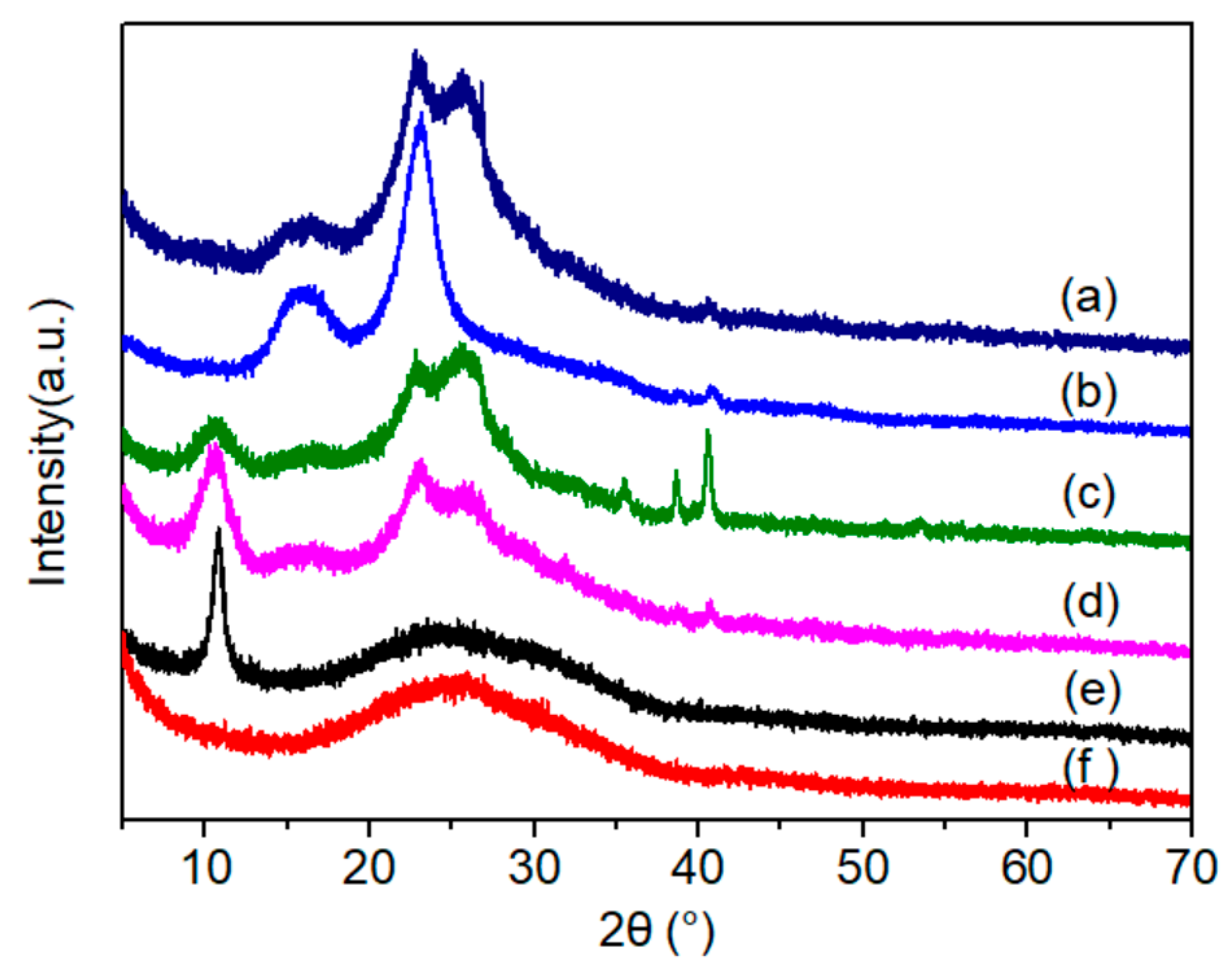

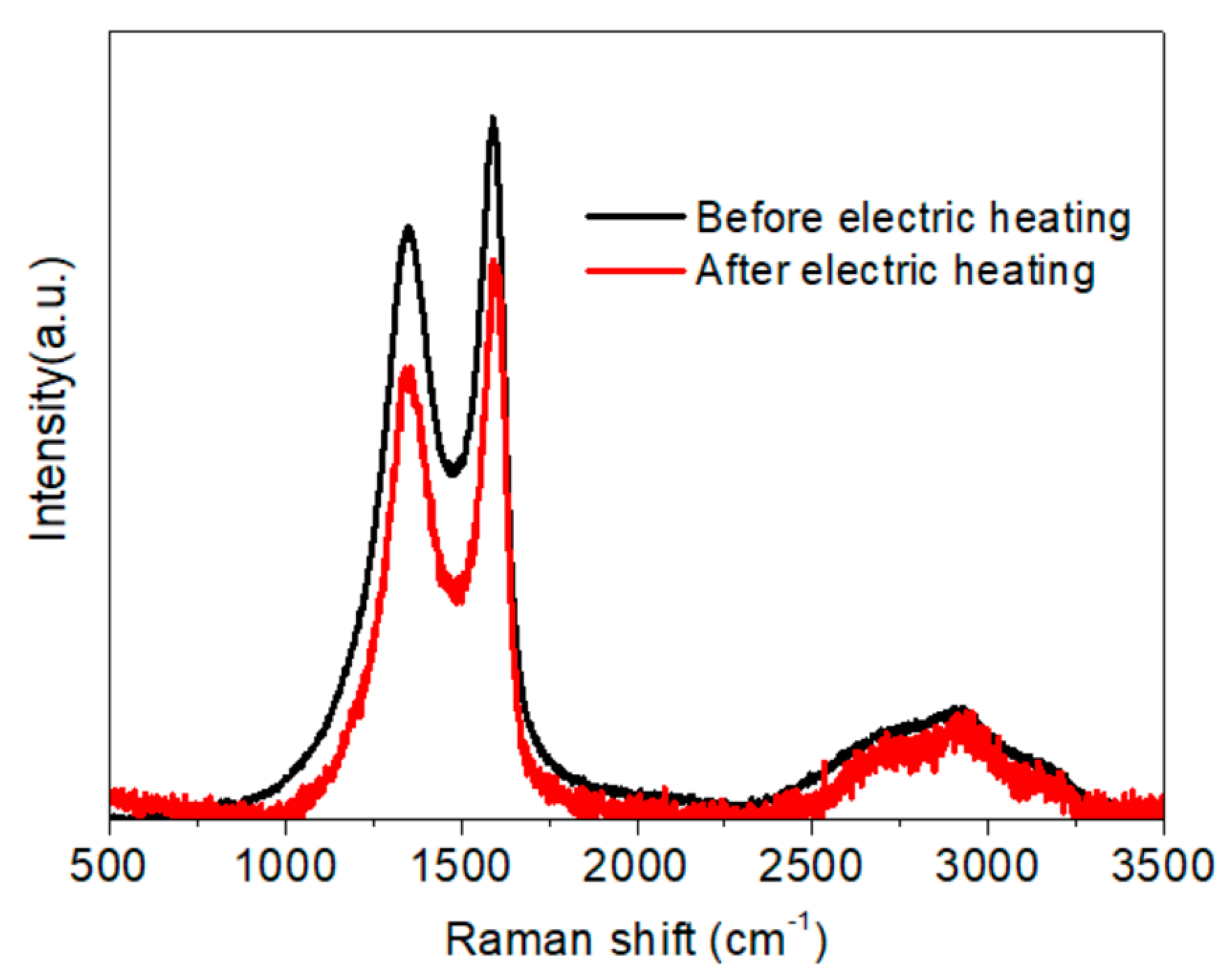
| Samples * | D Peak | 2D Peak | G Peak | ID/IG | I2D/IG | |||
|---|---|---|---|---|---|---|---|---|
| Peak Positions (cm−1) | FWHM of Peak (cm−1) | Peak Positions (cm−1) | FWHM of Peak (cm−1) | Peak Positions (cm−1) | FWHM of Peak (cm−1) | |||
| (a) | 1360.21 | 204.64 | 3861.65 | 387.20 | 1587.76 | 87.28 | 2.03 | 0.66 |
| (b) | 1360.54 | 195.18 | 2854.45 | 409.73 | 1586.30 | 89.14 | 1.88 | 0.70 |
| (c) | 1360.86 | 221.32 | 2821.22 | 437.79 | 1588.42 | 86.81 | 2.26 | 0.78 |
| (d) | 1361.41 | 223.24 | 2826.91 | 430.56 | 1588.27 | 85.91 | 2.27 | 0.77 |
| (e) | 1362.30 | 219.49 | 2835.86 | 434.15 | 1589.08 | 86.15 | 2.19 | 0.83 |
| (f) | 1361.75 | 224.48 | 2807.36 | 473.43 | 1589.96 | 85.85 | 2.27 | 0.88 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, C.; Zhu, Z.; Su, C.; Yang, S.; Yuan, Q. Thin Electric Heating Membrane Constructed with a Three-Dimensional Nanofibrillated Cellulose–Graphene–Graphene Oxide System. Materials 2018, 11, 1727. https://doi.org/10.3390/ma11091727
Shao C, Zhu Z, Su C, Yang S, Yuan Q. Thin Electric Heating Membrane Constructed with a Three-Dimensional Nanofibrillated Cellulose–Graphene–Graphene Oxide System. Materials. 2018; 11(9):1727. https://doi.org/10.3390/ma11091727
Chicago/Turabian StyleShao, Chuang, Zhenyu Zhu, Chuwang Su, Sheng Yang, and Quanping Yuan. 2018. "Thin Electric Heating Membrane Constructed with a Three-Dimensional Nanofibrillated Cellulose–Graphene–Graphene Oxide System" Materials 11, no. 9: 1727. https://doi.org/10.3390/ma11091727
APA StyleShao, C., Zhu, Z., Su, C., Yang, S., & Yuan, Q. (2018). Thin Electric Heating Membrane Constructed with a Three-Dimensional Nanofibrillated Cellulose–Graphene–Graphene Oxide System. Materials, 11(9), 1727. https://doi.org/10.3390/ma11091727