Micro-Tensile Behavior of Mg-Al-Zn Alloy Processed by Equal Channel Angular Pressing (ECAP)
Abstract
:1. Introduction
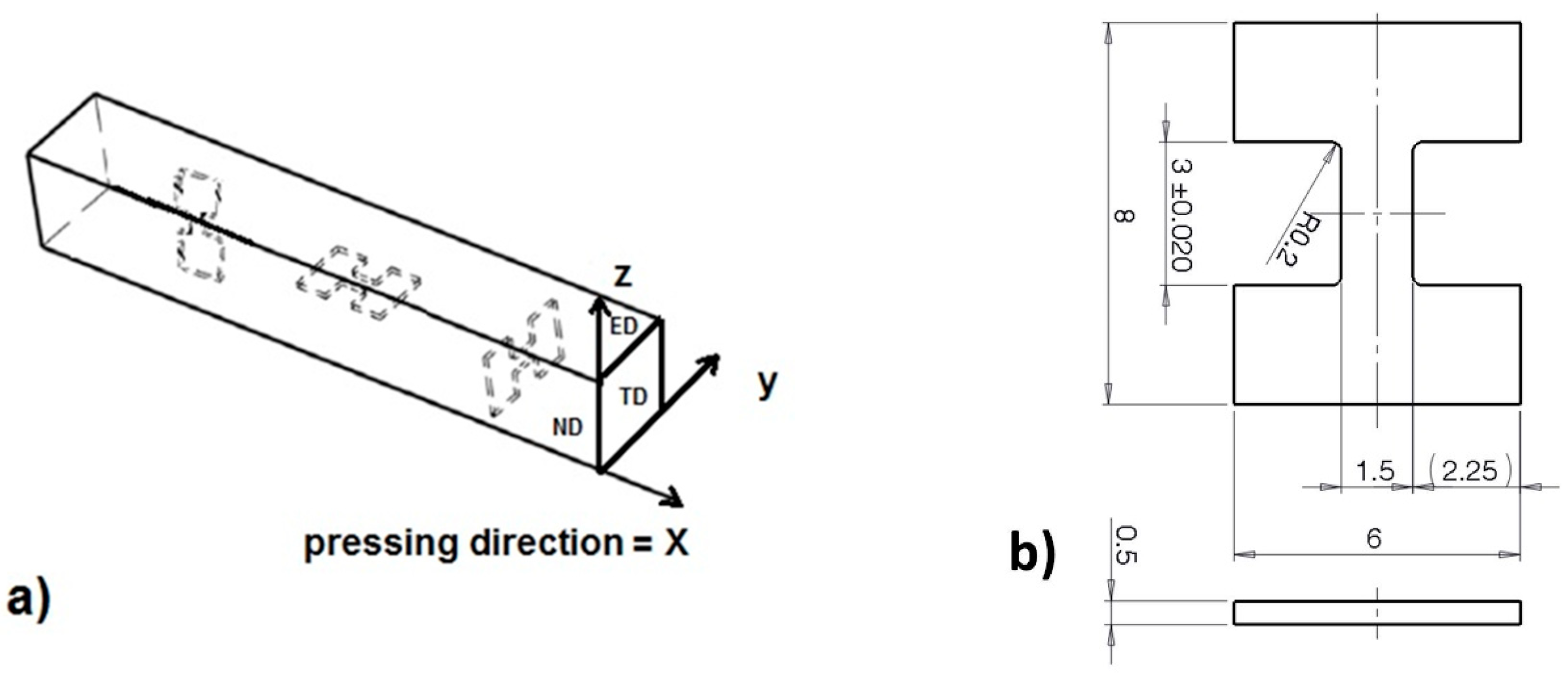
2. Experimental Section
3. Results and Discussion
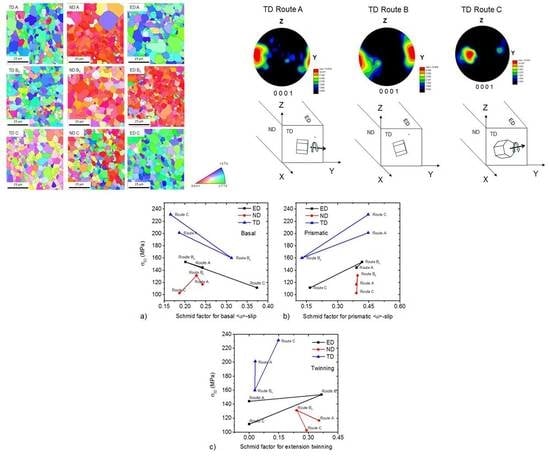
3.1. Initial Microstructure and Texture
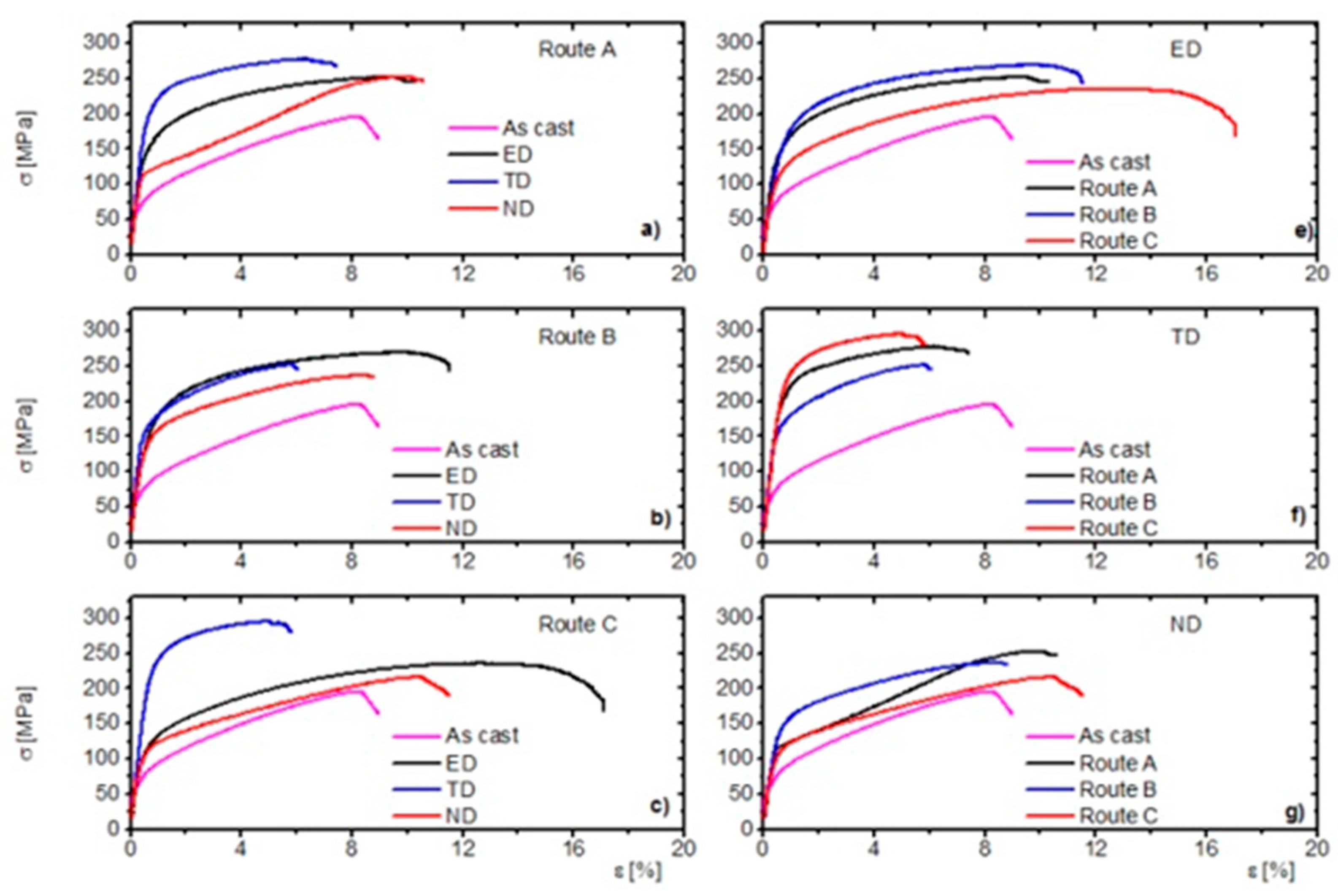
3.2. Mechanical Properties
3.2.1. Influence of the Tensile Direction on Mechanical Properties for the Particular ECAP Routes
3.2.2. Influence of the ECAP Routes on the Mechanical Properties in the Particular Tensile Directions
4. Conclusions
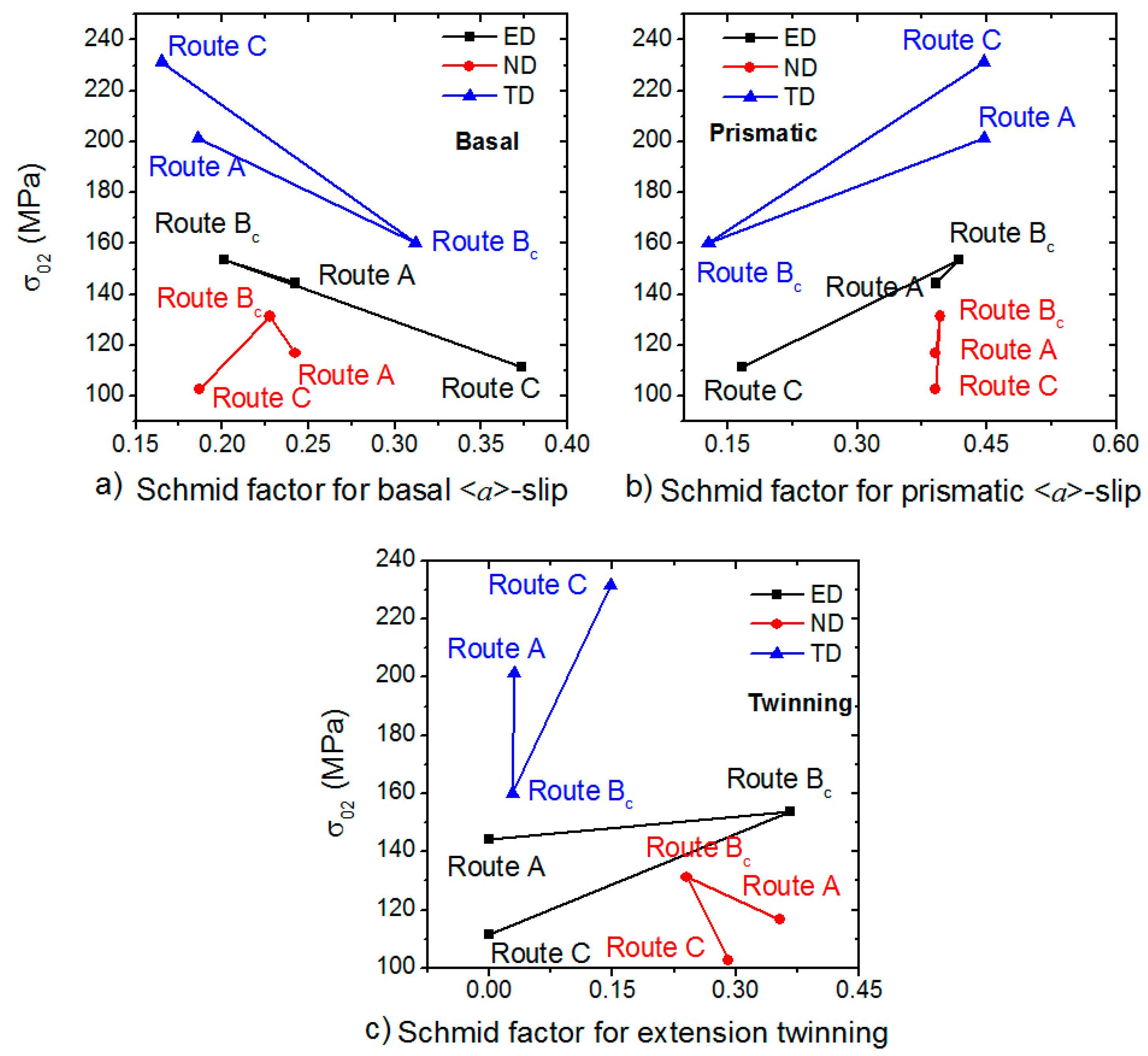
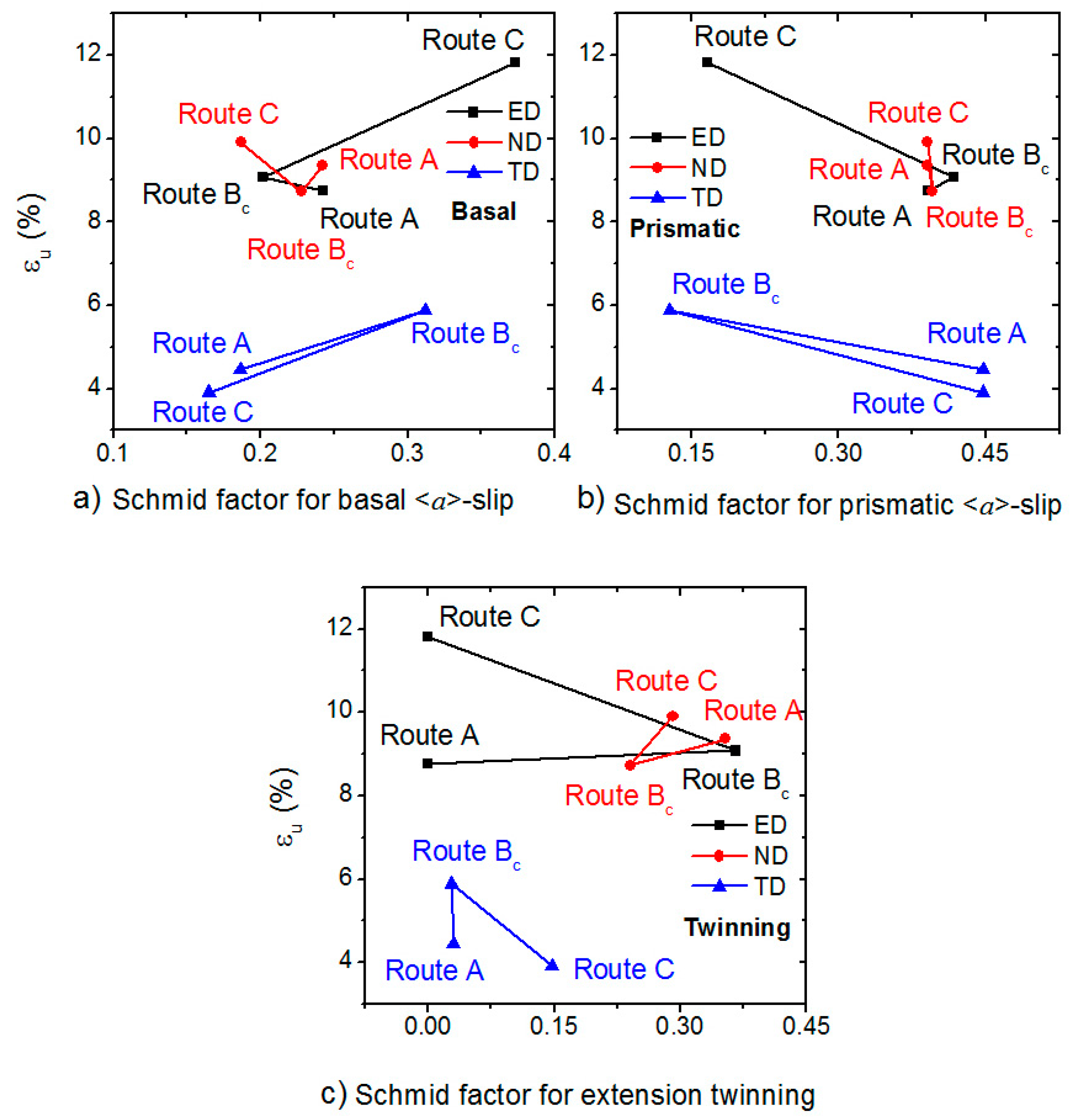
- Influence of the Processing Routes:
- The Schmid factors for the basal <a> slip and extension twinning were foremost responsible for the values of uniform elongation.
- The highest values of yield stress and yield strength were found for samples with the highest Schmid factor for the prismatic <a> and pyramidal <c+a>-slips and the lowest Schmid factor for basal <a> dislocations.
- Influence of the Tensile Direction:
- In ED and TD, the yield stress was determined with the ratio of Schmid factors for basal <a> and prismatic <a> slips. The higher the value, the lower the yield stress. In ND, the twinning activity was significant for all routes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eichenhueller, B.; Egerer, E.; Engel, U. Microforming at elevated temperature—Forming and material behavior. Int. J. Adv. Manuf. Technol. 2007, 33, 119–124. [Google Scholar] [CrossRef]
- Vollertsen, F.; Biermann, D.; Hansen, H.N.; Jawahir, I.S.; Kuzman, K. Size effects in manufacturing of metallic components. CIRP Ann. Manuf. Technol. 2009, 58, 566–587. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Islamgaliev, R.K.; Alexandrov, I.V. Bulk nanostructured materials from severe plastic deformation. Prog. Mater. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- Kim, W.J.; Sa, Y.K. Micro-extrusion of ECAP processed magnesium alloy for production of high strength magnesium micro-gears. Scr. Mater. 2006, 54, 1391–1395. [Google Scholar] [CrossRef]
- Estrin, Y.; Janeček, M.; Raab, G.I.; Valiev, R.Z.; Zi, E. Severe plastic deformation as a means of producing uItra-fine-grained net-shaped micro electro-mechanical systems parts. Metall. Mater. Trans. A 2007, 38A, 1906–1909. [Google Scholar] [CrossRef]
- Horita, Z.; Fujinami, T.; Langdon, T.G. The potential for scaling ECAP: Effect of sample size on grain refinement and mechanical properties. Mater. Sci. Eng. 2001, A318, 34–41. [Google Scholar] [CrossRef]
- Xu, C.; Száraz, Z.; Trojanová, Z.; Lukáč, P.; Langdon, T.G. Evaluating plastic anisotropy in two aluminum alloys processed by equal-channel angular pressing. Mater. Sci. Eng. A 2008, 497, 206–211. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Száraz, Z.; Trojanová, Z.; Lukáč, P.; Langdon, T.G. Significance of twinning in the anisotropic behavior of a magnesium alloy processed by equal-channel angular pressing. Scr. Mater. 2010, 63, 504–507. [Google Scholar] [CrossRef]
- Fu, E.K.Y.; Bellam, H.C.; Qazi, J.I.; Rack, H.J.; Stolyarov, V. Reciprocating-sliding wear of ultra-fine grained Ti-6Al-4V. In Ultrafine Grained Materials; Zhu, Y.T., Ed.; TMS: Warrendale, PA, USA, 2004; p. 547. [Google Scholar]
- Rund, M.; Procházka, R.; Konopík, P.; Džugan, J.; Folgar, H. Investigation of sample-size influence on tensile test results at different strain rates. Procedia Eng. 2015, 114, 410–415. [Google Scholar] [CrossRef]
- Krajňák, T.; Minárik, P.; Gubicza, J.; Máthis, K.; Kužel, R.; Janeček, M. Influence of equal channel angular pressing routes on texture, microstructure and mechanical properties of extruded AX41 magnesium alloy. Mater. Charact. 2017, 123, 282–293. [Google Scholar] [CrossRef]
- Máthis, K.; Rauch, E.F. Microstructural characterization of a fine-grained ultra low carbon steel. Mater. Sci. Eng. A 2007, 462, 248–252. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Langdon, T.G. Grain refinement and mechanical behavior of a magnesium alloy processed by ECAP. J. Mater. Sci. 2010, 45, 4827–4836. [Google Scholar] [CrossRef]
- Beausir, B.S.; Biswas, B.S.; Kim, D.I.; Toth, L.S.; Suwas, S. Analysis of microstructure and texture evolution in pure magnesium during symmetric and asymmetric rolling. Acta Mater. 2009, 57, 5061–5077. [Google Scholar] [CrossRef]
- Krajňák, T.; Minárik, P.; Stráská, J.; Gubicza, J.; Máthis, K.; Janeček, M. Influence of equal channel angular pressing temperature on texture, microstructure and mechanical properties of extruded AX41 magnesium. J. Alloy. Compd. 2017, 705, 273–282. [Google Scholar] [CrossRef]
- Lin, H.K.; Huang, J.C.; Langdon, T.G. Relationship between texture and low temperature superplasticity in an extruded AZ31 Mg alloy processed by ECAP. Mater. Sci. Eng. A 2005, 402, 250–257. [Google Scholar] [CrossRef]
- Yamashita, A.; Horita, Z.; Langdon, T.G. Improving the mechanical properties of magnesium and a magnesium alloy through severe plastic deformation. Mater. Sci. Eng. A 2001, 300, 142–147. [Google Scholar] [CrossRef]
- Ding, S.X.; Lee, W.T.; Chang, C.P.; Chang, L.W.; Kao, P.W. Improvement of strength of magnesium alloy processed by equal channel angular extrusion. Scr. Mater. 2008, 59, 1006–1009. [Google Scholar] [CrossRef]
- Chapuis, A.; Driver, J.H. Temperature dependency of slip and twinning in plane strain compressed magnesium single crystals. Acta Mater. 2011, 59, 1986–1994. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Creep and plasticity of hexagonal polycrystals as related to single-crystal slip. Metall. Mater. Trans. A 1977, 8, 1465–1469. [Google Scholar] [CrossRef]
- Yuan, W.; Mishra, R.S. Grain size and texture effects on deformation behavior of AZ31 magnesium alloy. Mater. Sci. Eng. A 2012, 558, 716–724. [Google Scholar] [CrossRef]
- Bohlen, J.; Dobroň, P.; Swiostek, J.; Letzig, D.; Chmelík, F.; Lukáč, P.; Kainer, K.U. Acoustic emission during stress relaxation of pure magnesium and AZ magnesium alloys. Mater. Sci. Eng. A 2007, 462, 302–306. [Google Scholar] [CrossRef]
- Von Mises, R. Mechanik der festen Körper im plastisch deformablen Zustand. Göttin. Nachr. Math. Phys. 1913, 1, 582–592. [Google Scholar]
- Lukáč, P. Hardening and softening during plastic deformation of hexagonal metals. Czechoslov. J. Phys. 1985, 35, 275–285. [Google Scholar] [CrossRef]
- Agnew, S.R.; Duygulu, O. Plastic anisotropy and the role of non-basal slip in magnesium alloy AZ31B. Int. J. Plast. 2005, 21, 1161–1193. [Google Scholar] [CrossRef]

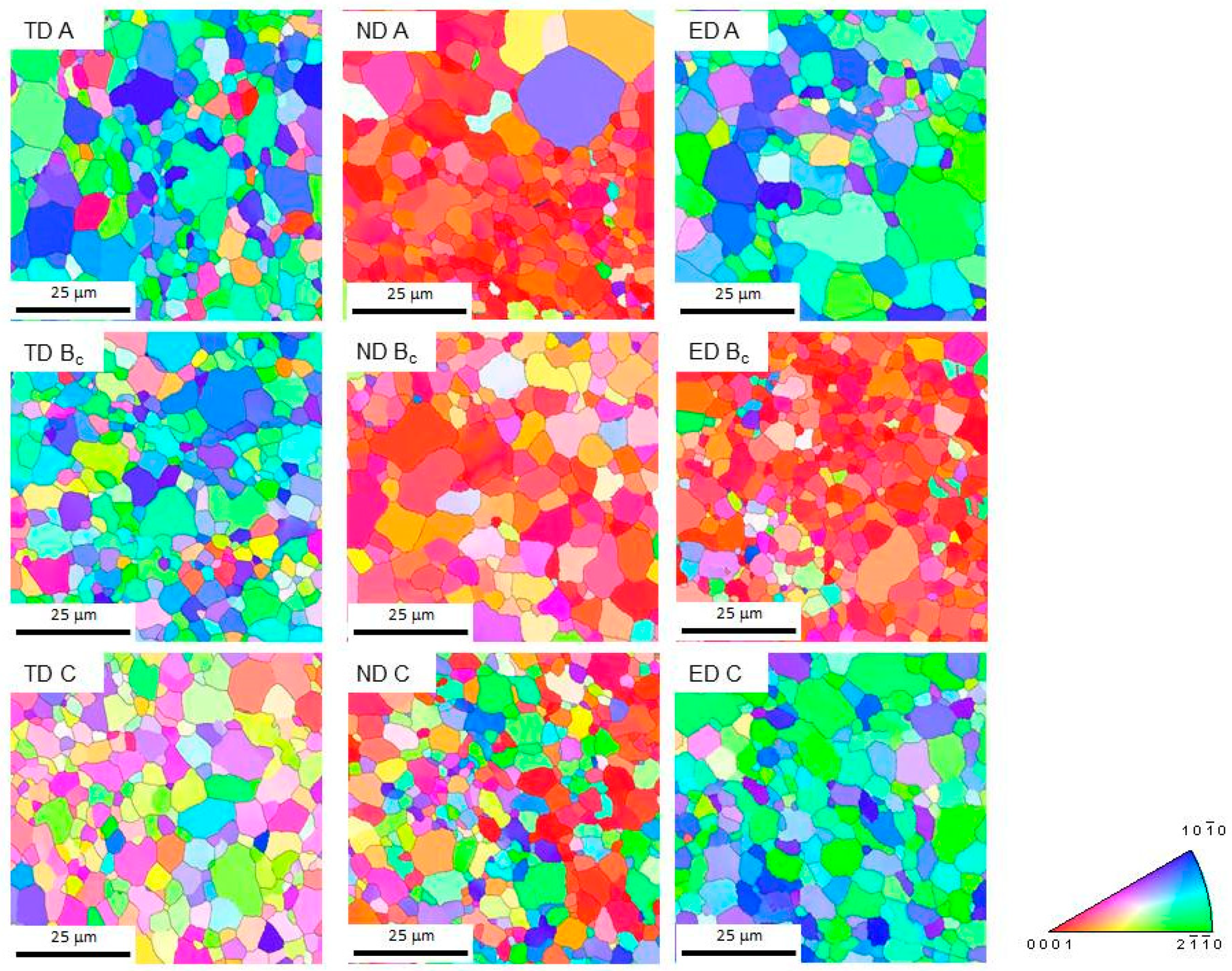
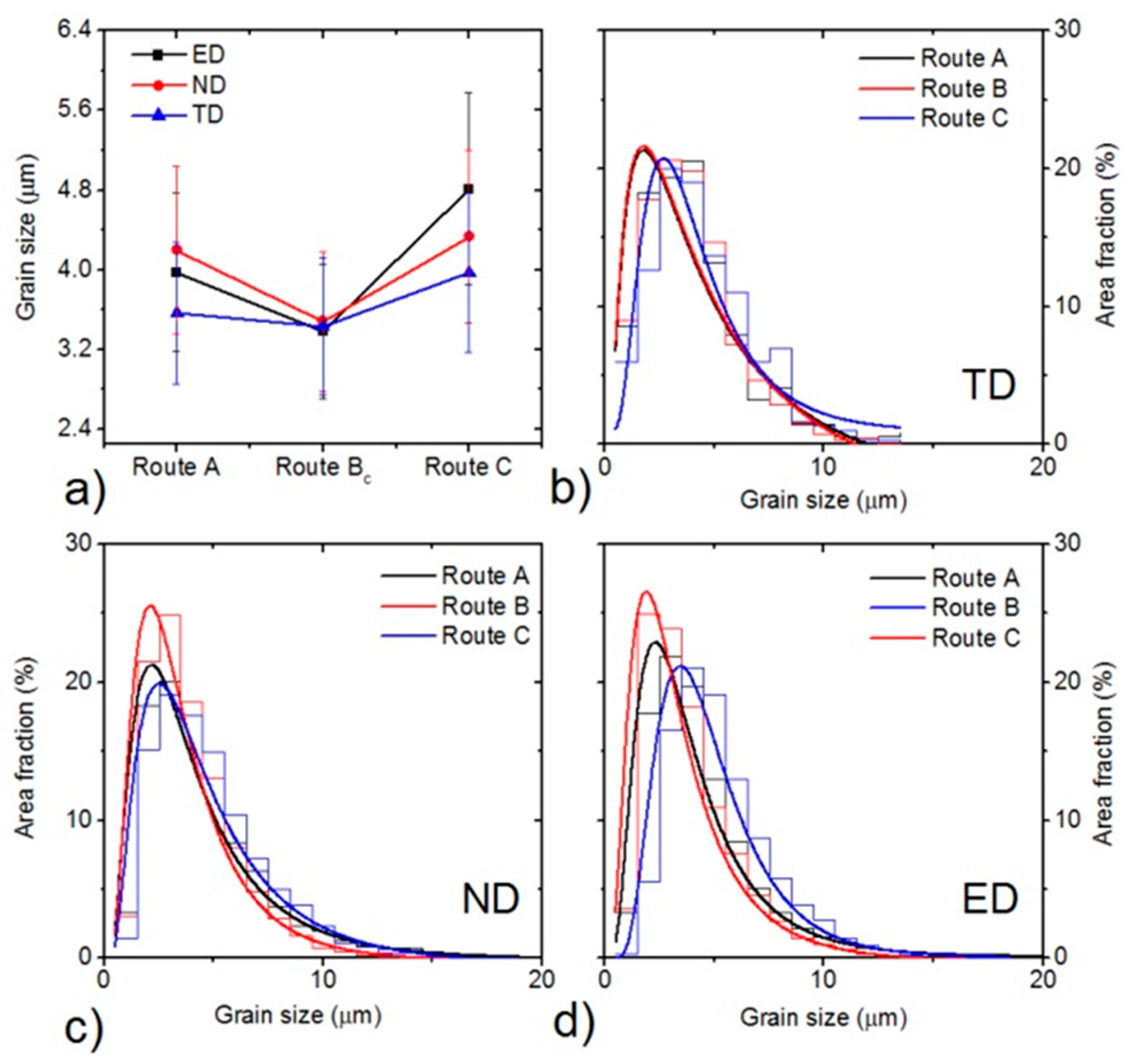
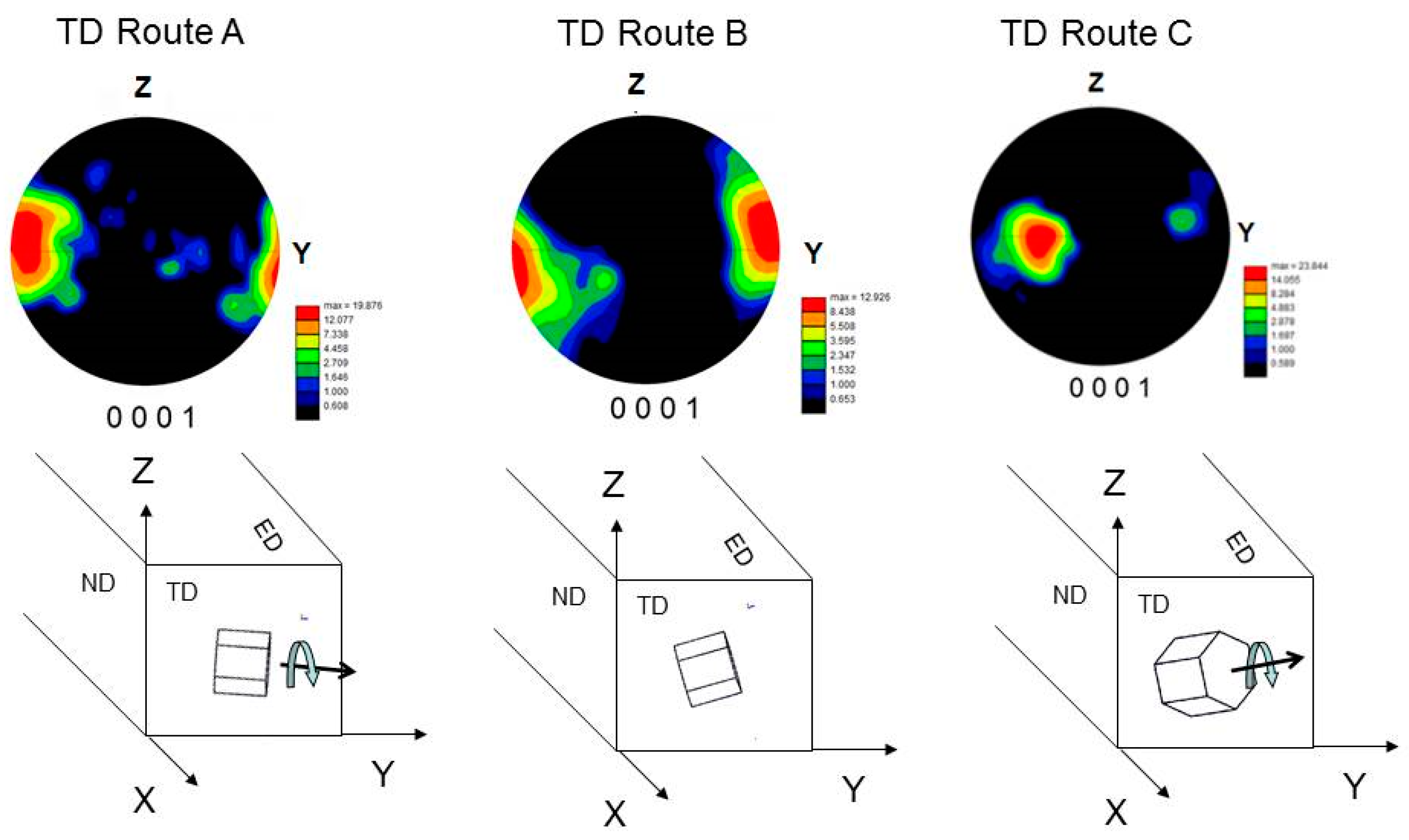
| Route/Plane | TD | ND | ED | |||
|---|---|---|---|---|---|---|
| ECAP Route | Grain Size (µm) | Fraction of HAGBs | Grain Size (µm) | Fraction of HAGBs | Grain Size (µm) | Fraction of HAGBs |
| A | 3.57 | 85.5% | 4.20 | 89.7% | 3.98 | 91.0% |
| BC | 3.43 | 92.1% | 3.48 | 93.8% | 3.37 | 90.2% |
| C | 3.97 | 86.9% | 4.33 | 89.5% | 4.81 | 89.6% |
| Route | Plane | Yield Stress (σ02) | Ultimate Tensile Strength (σmax) | Uniform Elongation (εu) |
|---|---|---|---|---|
| [MPa] | [MPa] | [%] | ||
| Route A | TD | 201 | 275 | 4.4 |
| ND | 117 | 264 | 9.4 | |
| ED | 144 | 253 | 8.8 | |
| Route Bc | TD | 160 | 261 | 5.9 |
| ND | 131 | 242 | 8.7 | |
| Route C | TD | 231 | 295 | 3.9 |
| ND | 103 | 216 | 9.9 | |
| ED | 112 | 236 | 11.8 | |
| Initial | - | 57 | 195 | 8.1 |
| Plane_Route | Basal Slip | Prismatic Slip | Pyramidal <c+a> Slip | Extension Twinning |
|---|---|---|---|---|
| TD_A | 0.19 | 0.45 | 0.44 | 0.03 |
| TD_B | 0.31 | 0.13 | 0.43 | 0.02 |
| TD_C | 0.17 | 0.45 | 0.43 | 0.15 |
| ND_A | 0.24 | 0.39 | 0.42 | 0.35 |
| ND_B | 0.23 | 0.40 | 0.41 | 0.24 |
| ND_C | 0.19 | 0.45 | 0.44 | 0.29 |
| ED_A | 0.32 | 0.17 | 0.43 | 0 |
| ED_B | 0.20 | 0.42 | 0.43 | 0.36 |
| ED_C | 0.37 | 0.22 | 0.38 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Máthis, K.; Köver, M.; Stráská, J.; Trojanová, Z.; Džugan, J.; Halmešová, K. Micro-Tensile Behavior of Mg-Al-Zn Alloy Processed by Equal Channel Angular Pressing (ECAP). Materials 2018, 11, 1644. https://doi.org/10.3390/ma11091644
Máthis K, Köver M, Stráská J, Trojanová Z, Džugan J, Halmešová K. Micro-Tensile Behavior of Mg-Al-Zn Alloy Processed by Equal Channel Angular Pressing (ECAP). Materials. 2018; 11(9):1644. https://doi.org/10.3390/ma11091644
Chicago/Turabian StyleMáthis, Kristián, Michal Köver, Jitka Stráská, Zuzanka Trojanová, Ján Džugan, and Kristýna Halmešová. 2018. "Micro-Tensile Behavior of Mg-Al-Zn Alloy Processed by Equal Channel Angular Pressing (ECAP)" Materials 11, no. 9: 1644. https://doi.org/10.3390/ma11091644
APA StyleMáthis, K., Köver, M., Stráská, J., Trojanová, Z., Džugan, J., & Halmešová, K. (2018). Micro-Tensile Behavior of Mg-Al-Zn Alloy Processed by Equal Channel Angular Pressing (ECAP). Materials, 11(9), 1644. https://doi.org/10.3390/ma11091644