Finite Element Analysis for the Self-Loosening Behavior of the Bolted Joint with a Superelastic Shape Memory Alloy
Abstract
1. Introduction
2. Constitutive Modeling for NiTi SMA under Cyclic Loading
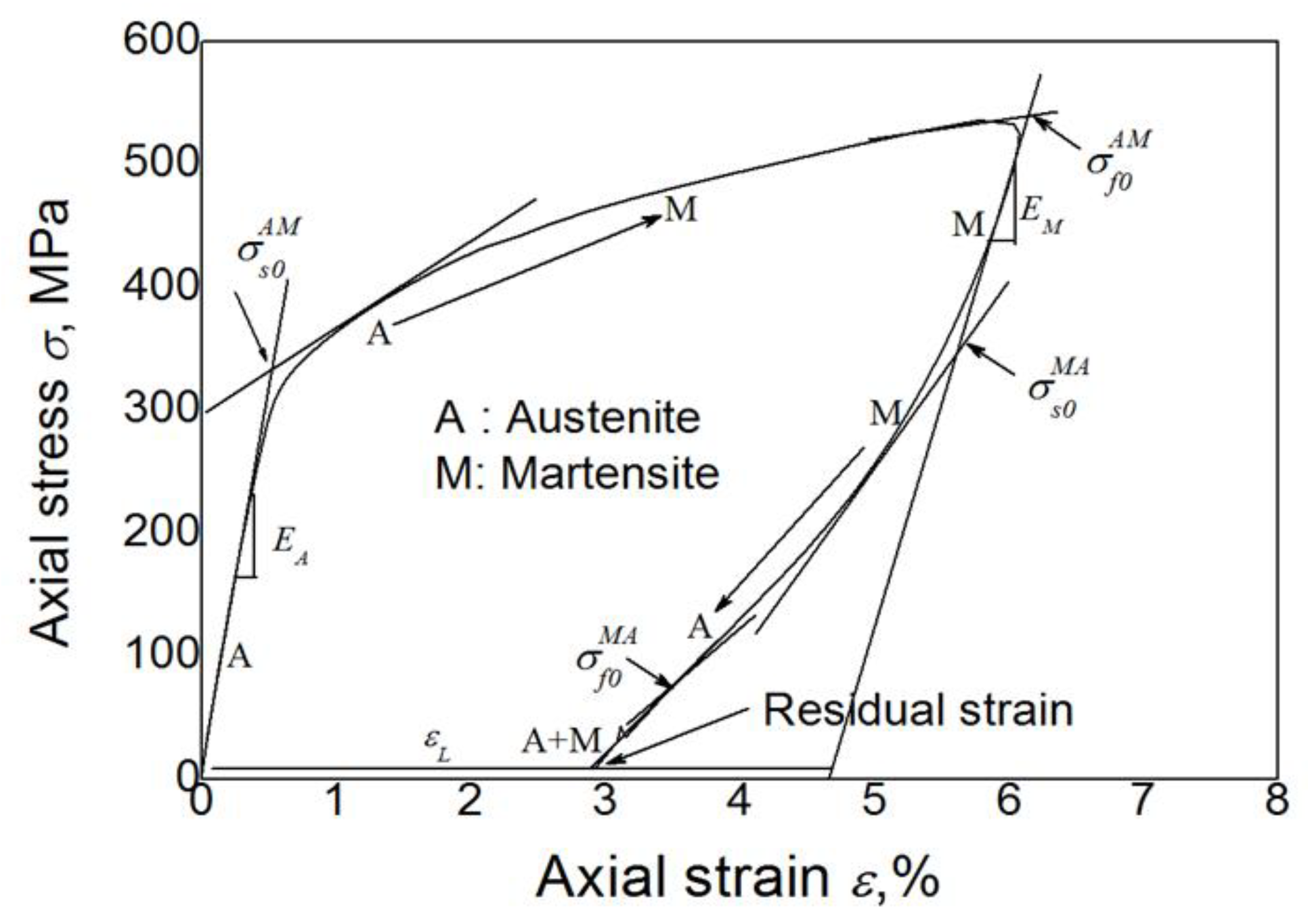
2.1. Constitutive Equation and Internal Variables
- (i)
- Transition to the martensite phaseif and :
- (ii)
- Transition to the austenite phaseif and :where and are the starting and finishing stresses of martensite transition, respectively; and are the slopes for the relation between critical transition stress and temperature, respectively; and are the starting and finishing temperatures of austenite transition, respectively; and are the starting and finishing temperatures of martensite transition, respectively; is the residual volume fraction of martensite transition at the end of transition to the austenite phase; and is the volume fraction of the martensite transition at the end of transition to the martensite phase.
2.2. Evolution Law of Parameters Governed by Accumulated Martensite Volume Fraction
- (i)
- Evolution equation for the residual martensite volume fraction:where is the maximum irreversible residual martensite volume fraction corresponding to the maximum load of the stable cycle phase transition. The material parameter b is to govern the saturation rate of the residual martensite volume fraction . The revised function is introduced in the evolution law and associated with the loading stress level to consider the correlation between that level and the residual martensite fraction, and written aswhere , , and is the value of at the endpoint of the forward transition. The material parameter n is to describe the nonlinear relationship between the residual martensite volume fraction and the loading stress level. It can be found according to Equation 19a that in the forward phase, the value of increases with the increase of the loading stress level in the interval of , and reaches its maximum at the endpoint of the forward transition.
- (ii)
- Evolution law of transition stressDue to incomplete reverse transition during loading cycles, the superelastic NiTi SMA shows the mixture state of the austenite and residual martensite phases. The transition stresses decrease with the increasing of cycle numbers. Thus, according to the experimental observations in [32], the evolution equations in exponential formulation were proposed by [33] to describe the progressive evolution of the transition stresses with increasing cycle numbers from their initial values to stable ones, and are introduced here aswhere , , , and are the transition stresses of the initial cyclic loading, and , , , and are the transition stresses of the stable phase transition. , , , and are the parameters governing the saturated rates of the transition stresses.
2.3. Incremental Formulation of Constitutive Equations
2.4. Finite Element Modeling for the One-Dimensional Bar Element of SMA Ratcheting Behavior
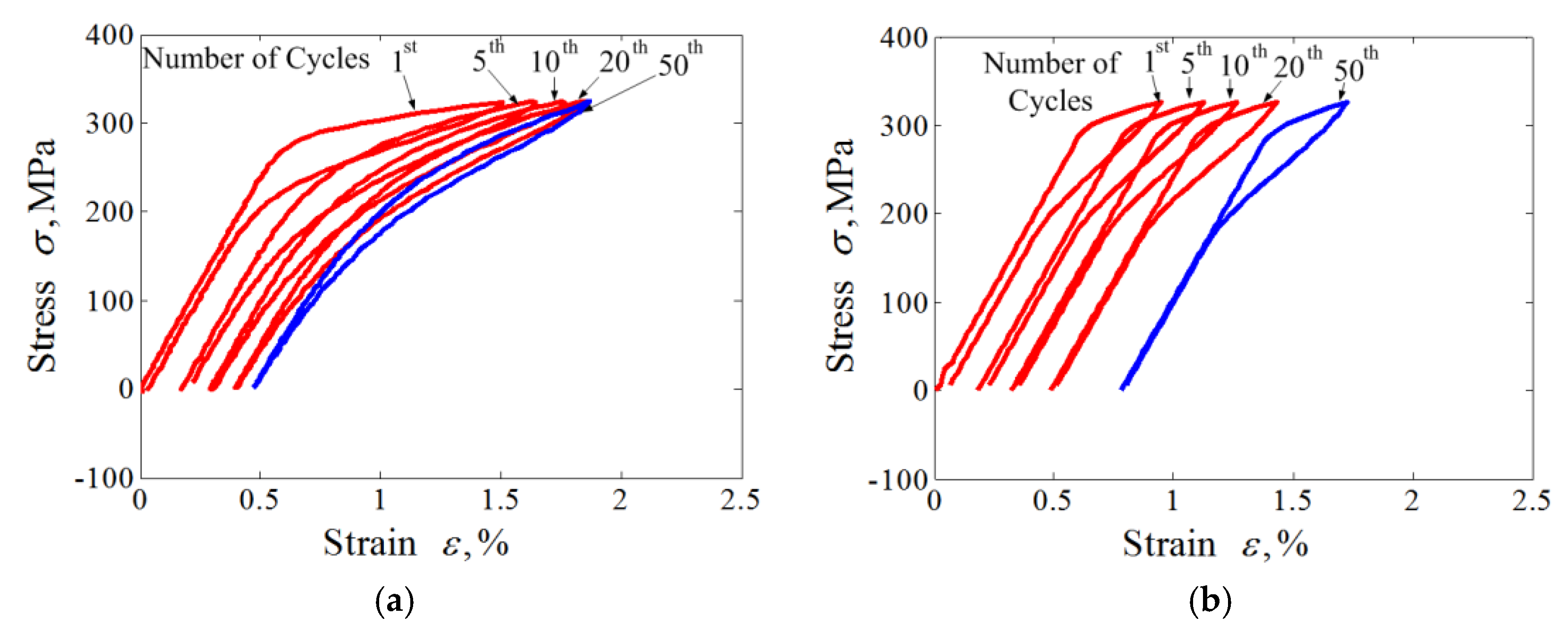
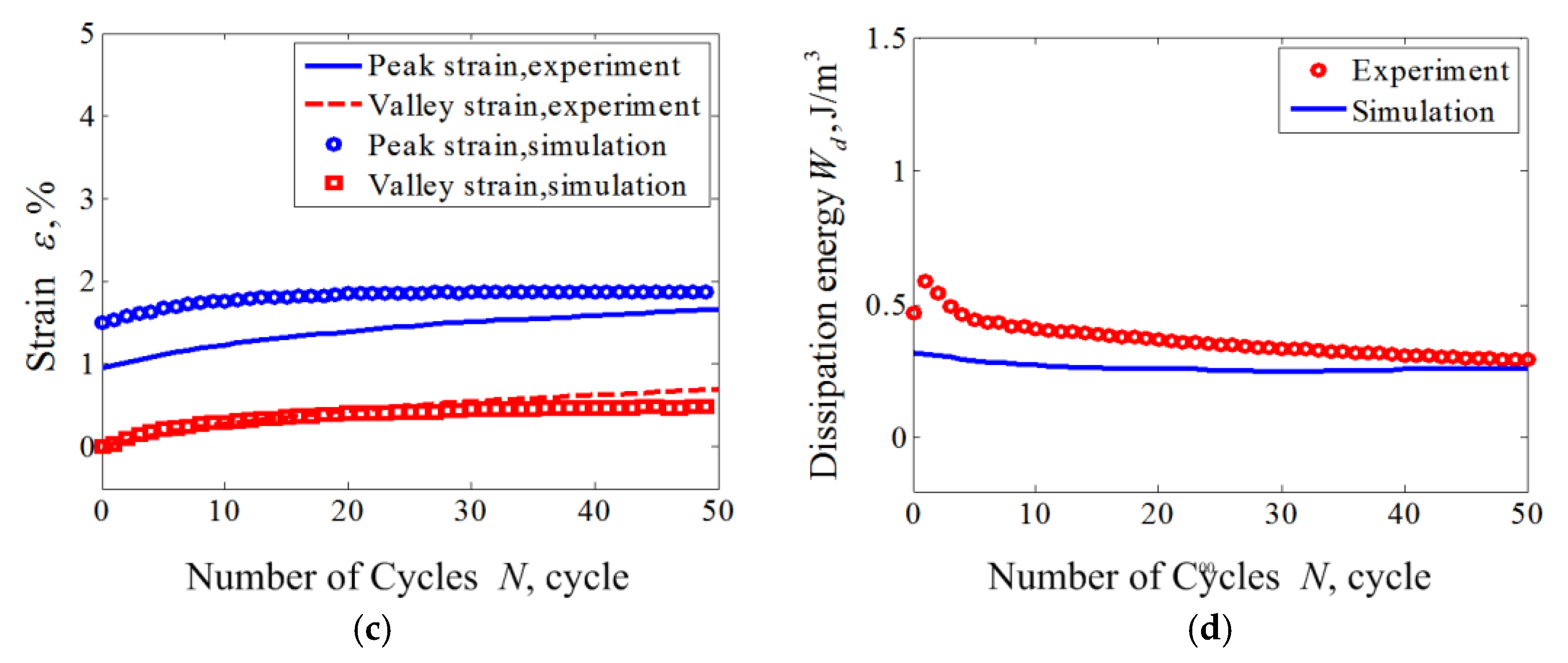
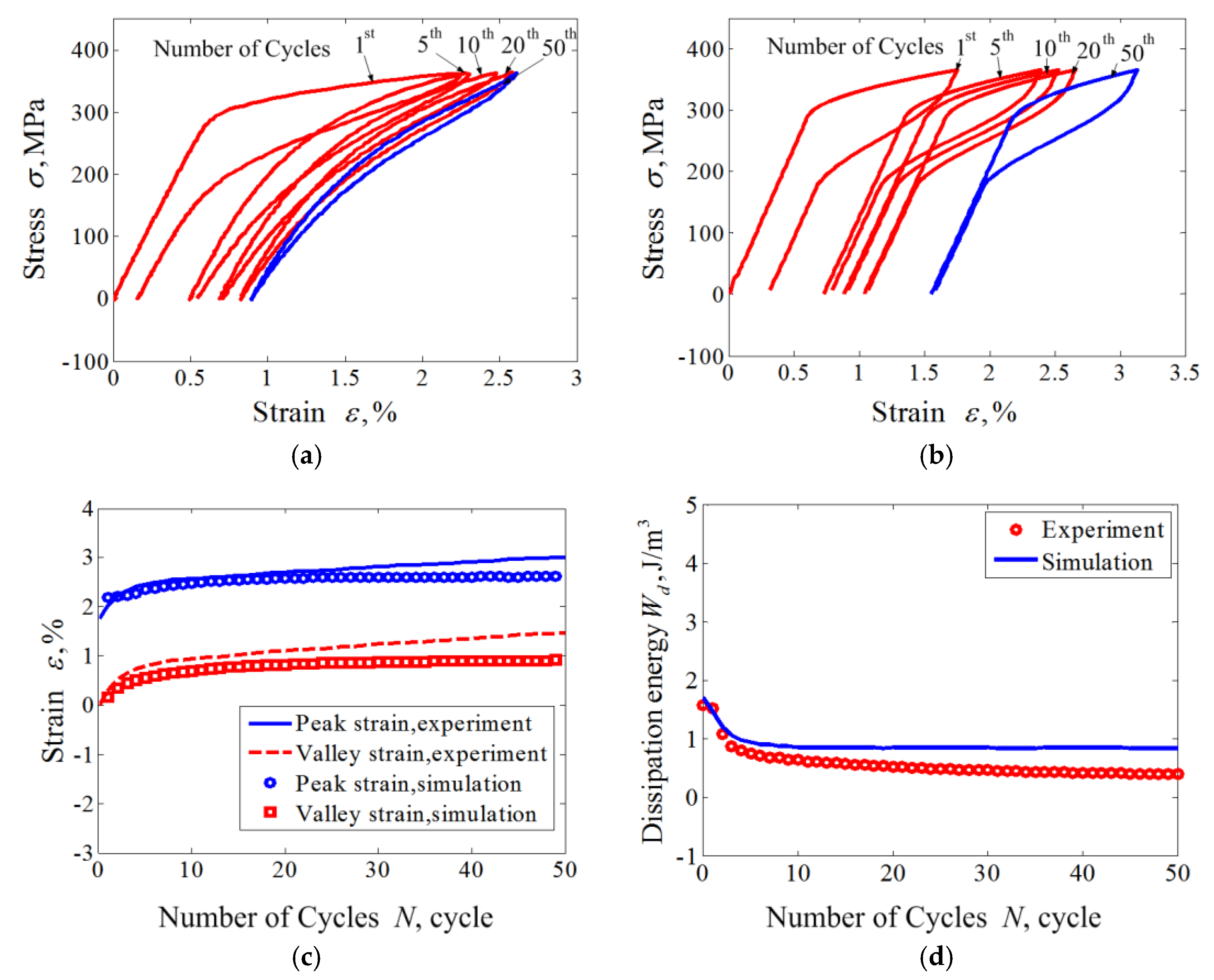
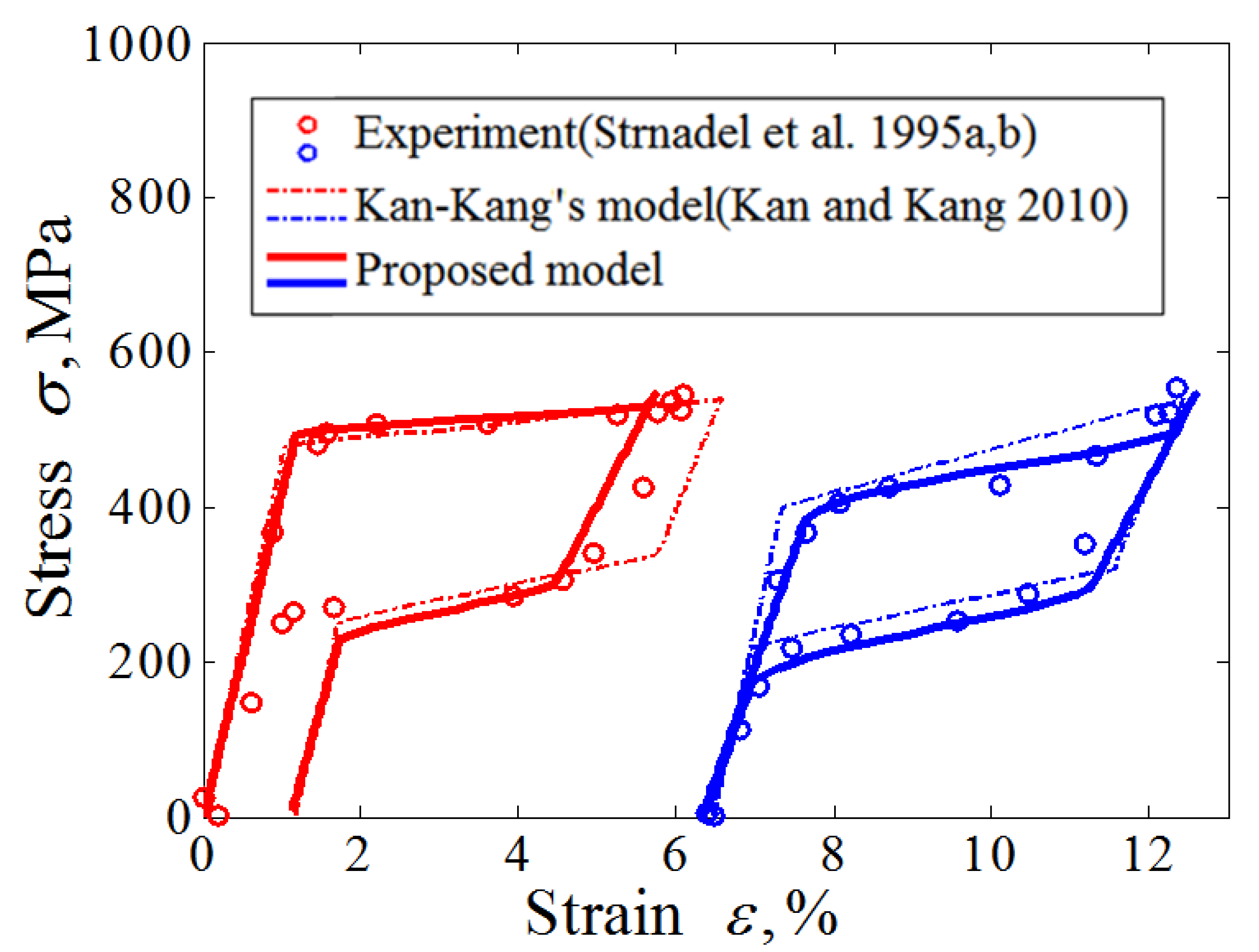
2.5. Numerical Simulation and Model Verification
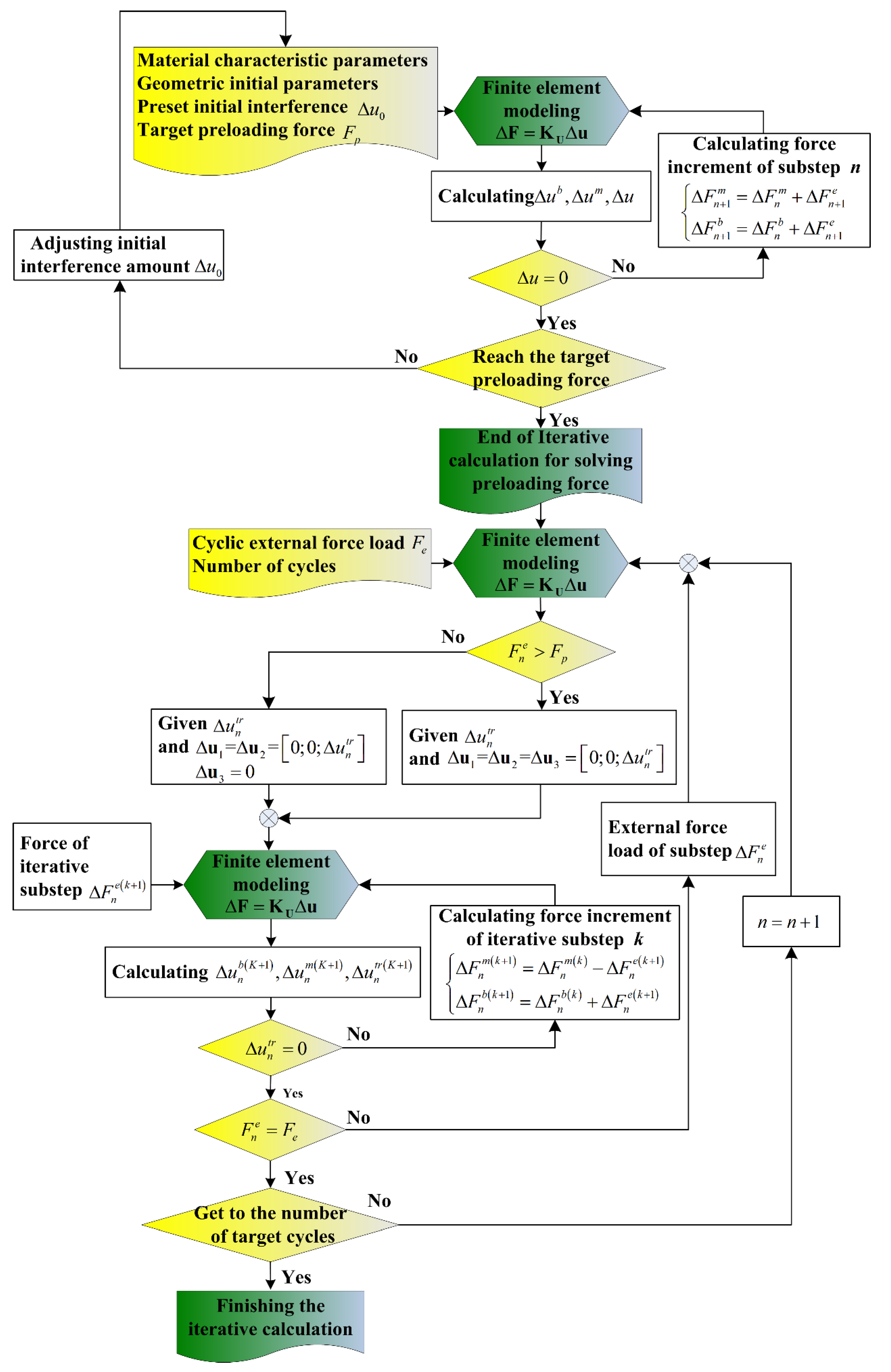
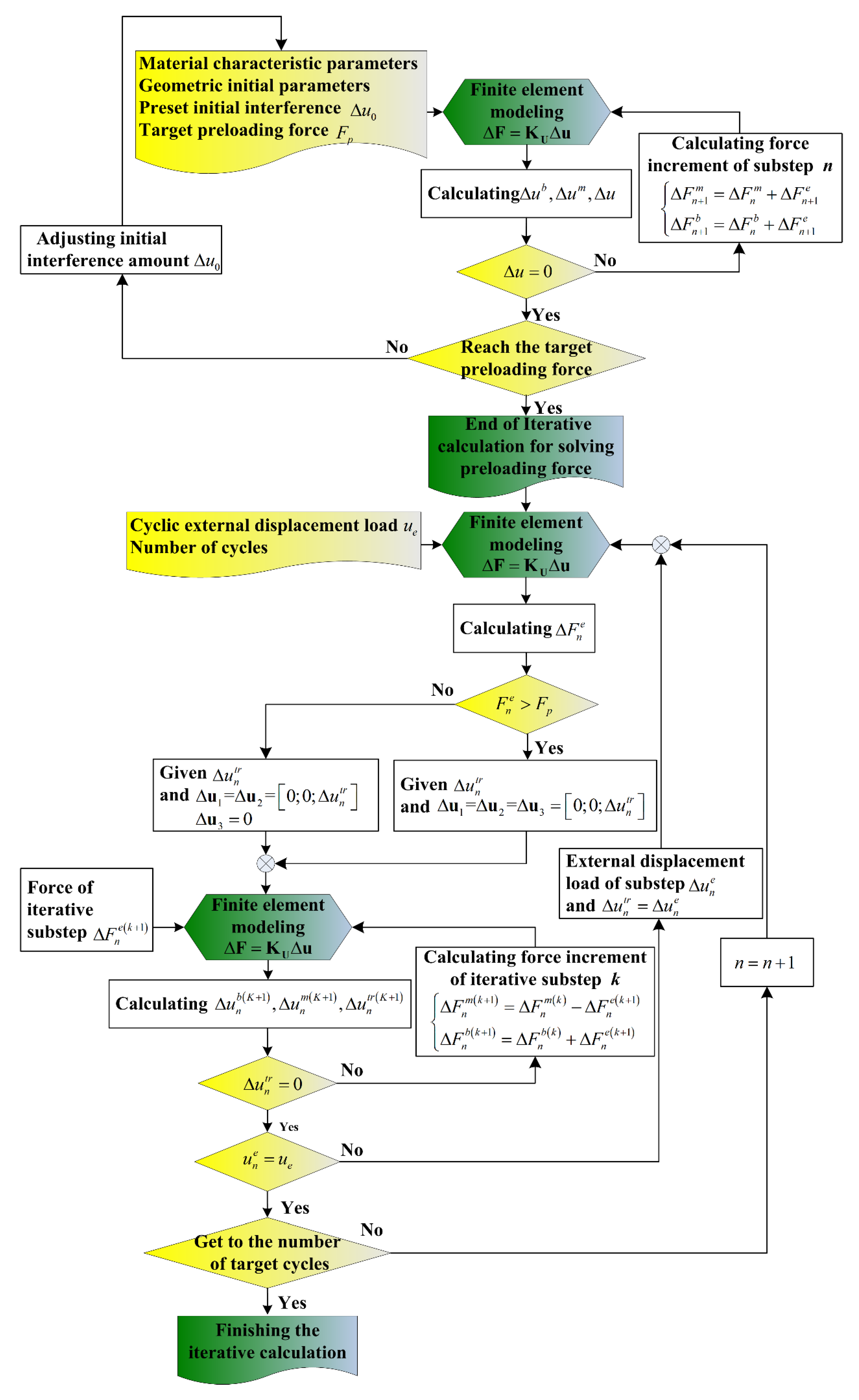
3. Finite Element Modeling for Self-Loosening of the SMA Bolted Joint
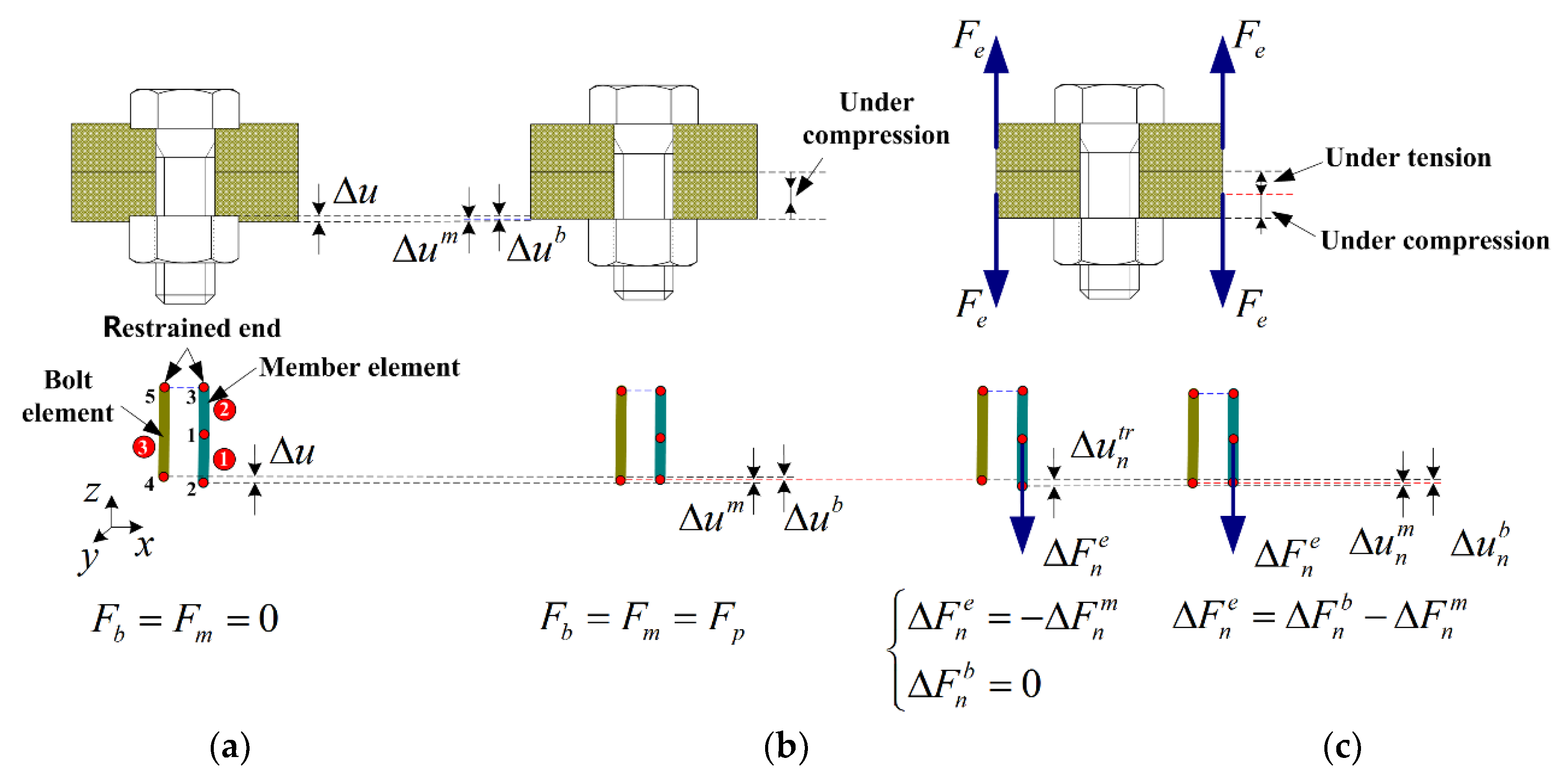
3.1. Finite Element Modeling under Cyclic External Force Load
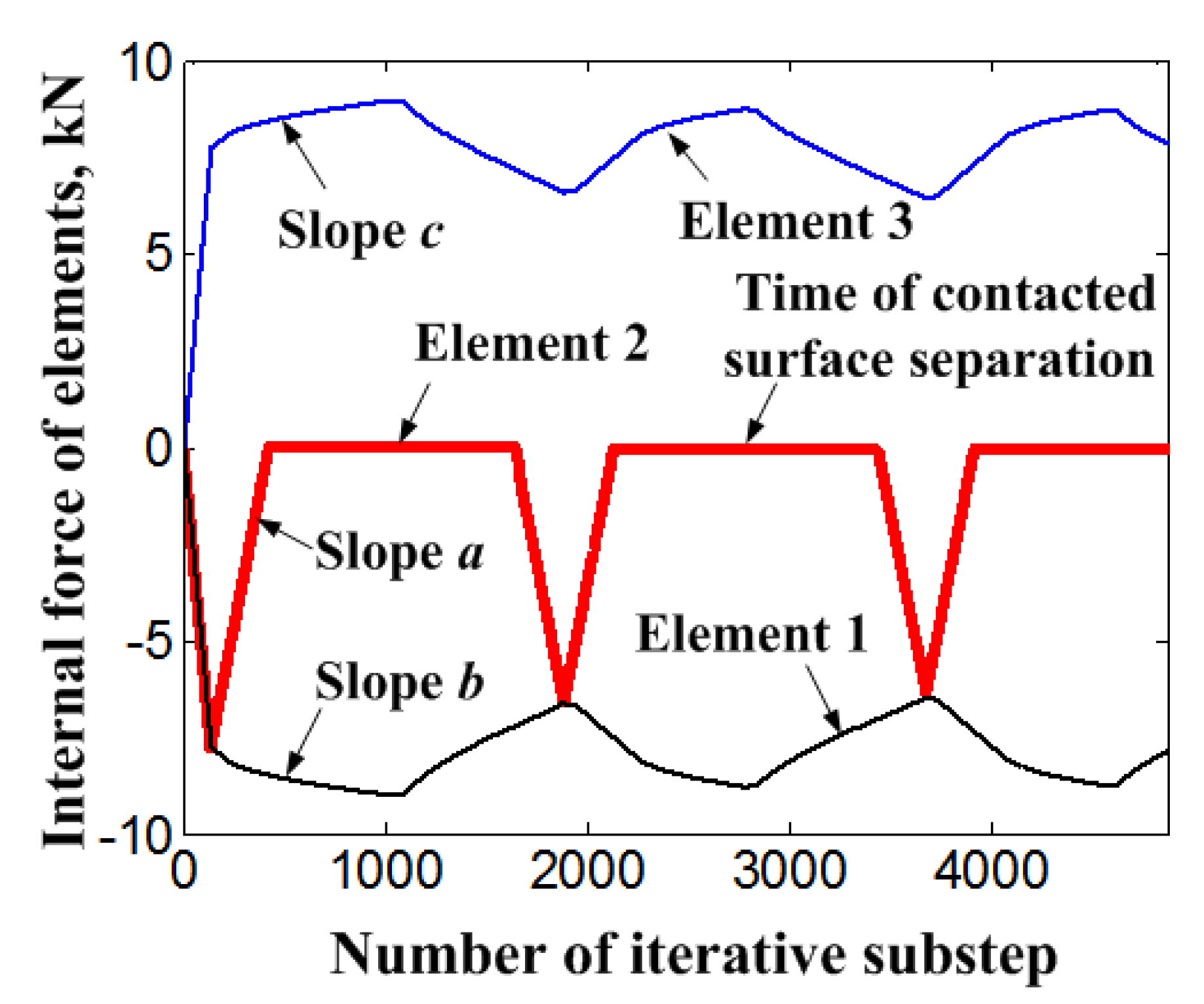
- ①
- As the external load is smaller than the initial preloading force of bolt , the system will satisfy the force equilibrium relationship as .
- ②
- As the external load is larger than the initial preloading force of bolt , is satisfied at this time. Then, the system will satisfy the force equilibrium relationship as . Meanwhile, the constraint at the node 3 is removed and the element 2 is in the state of no stress.
3.2. Finite Element Modeling under Cyclic External Displacement Load
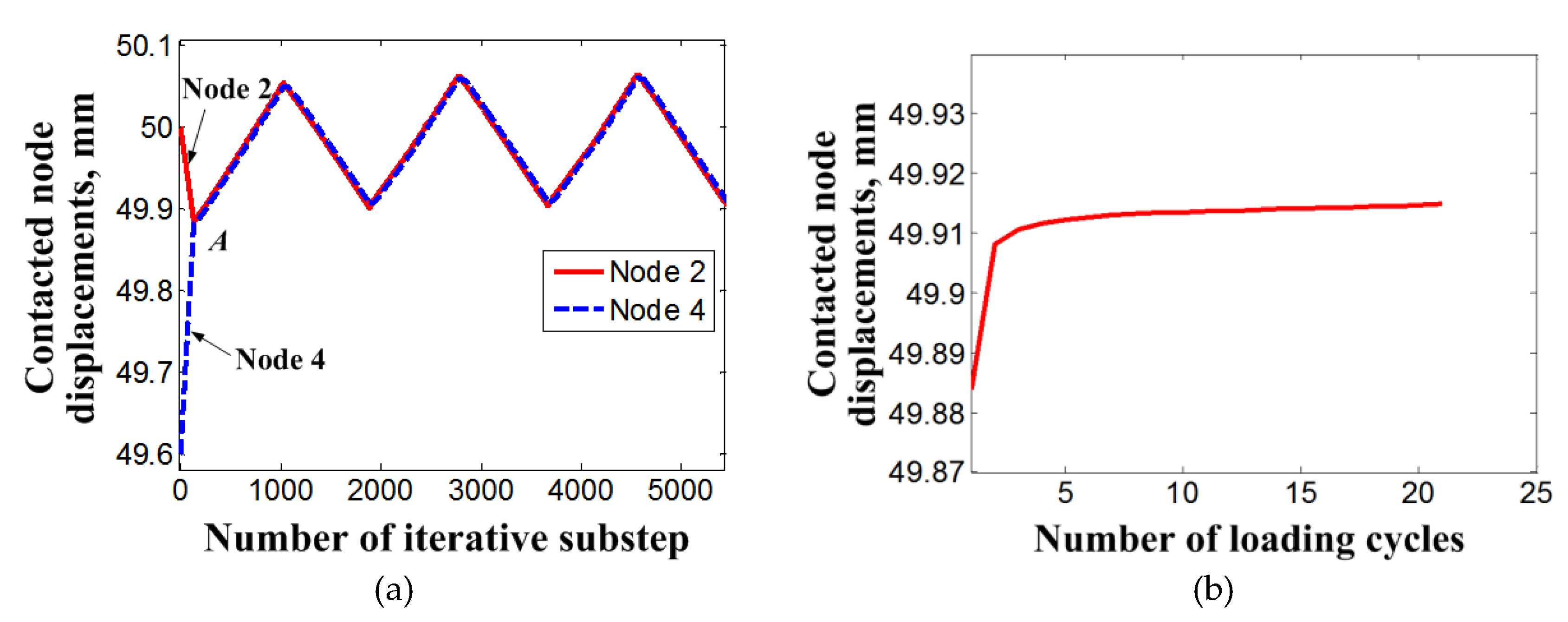
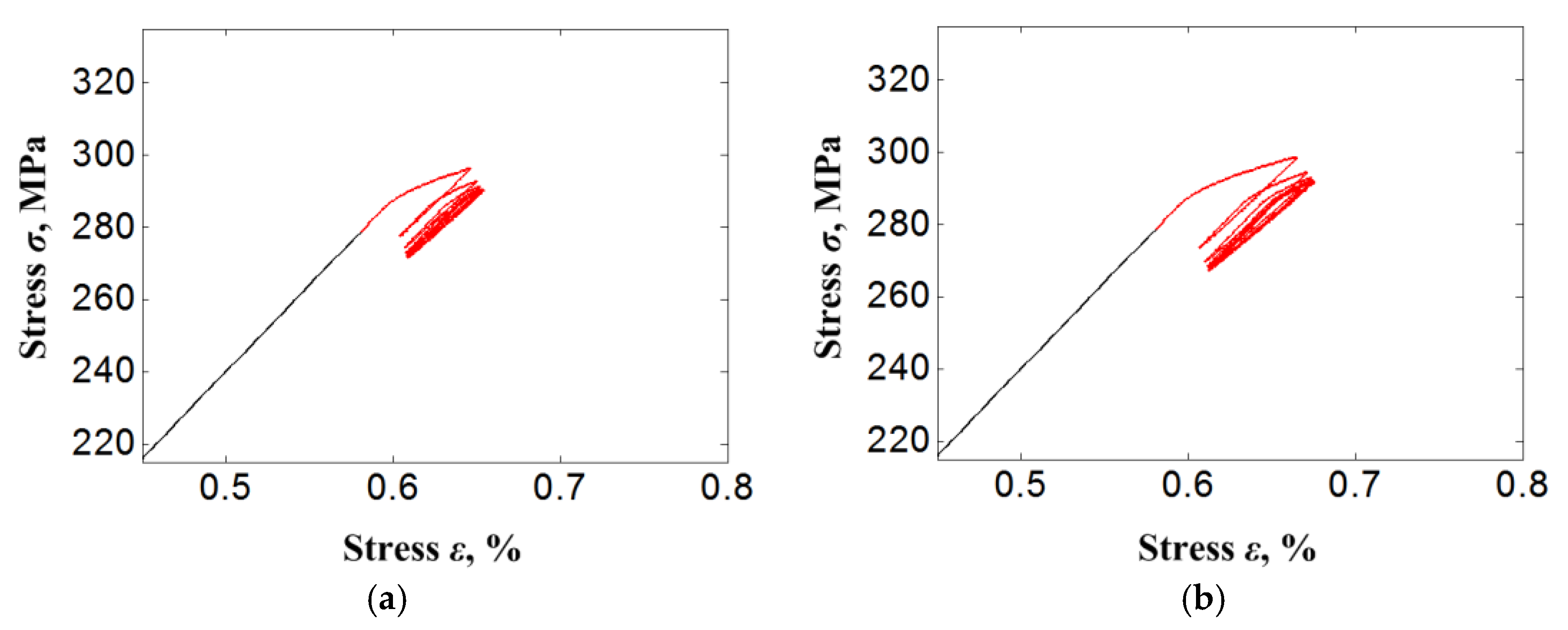
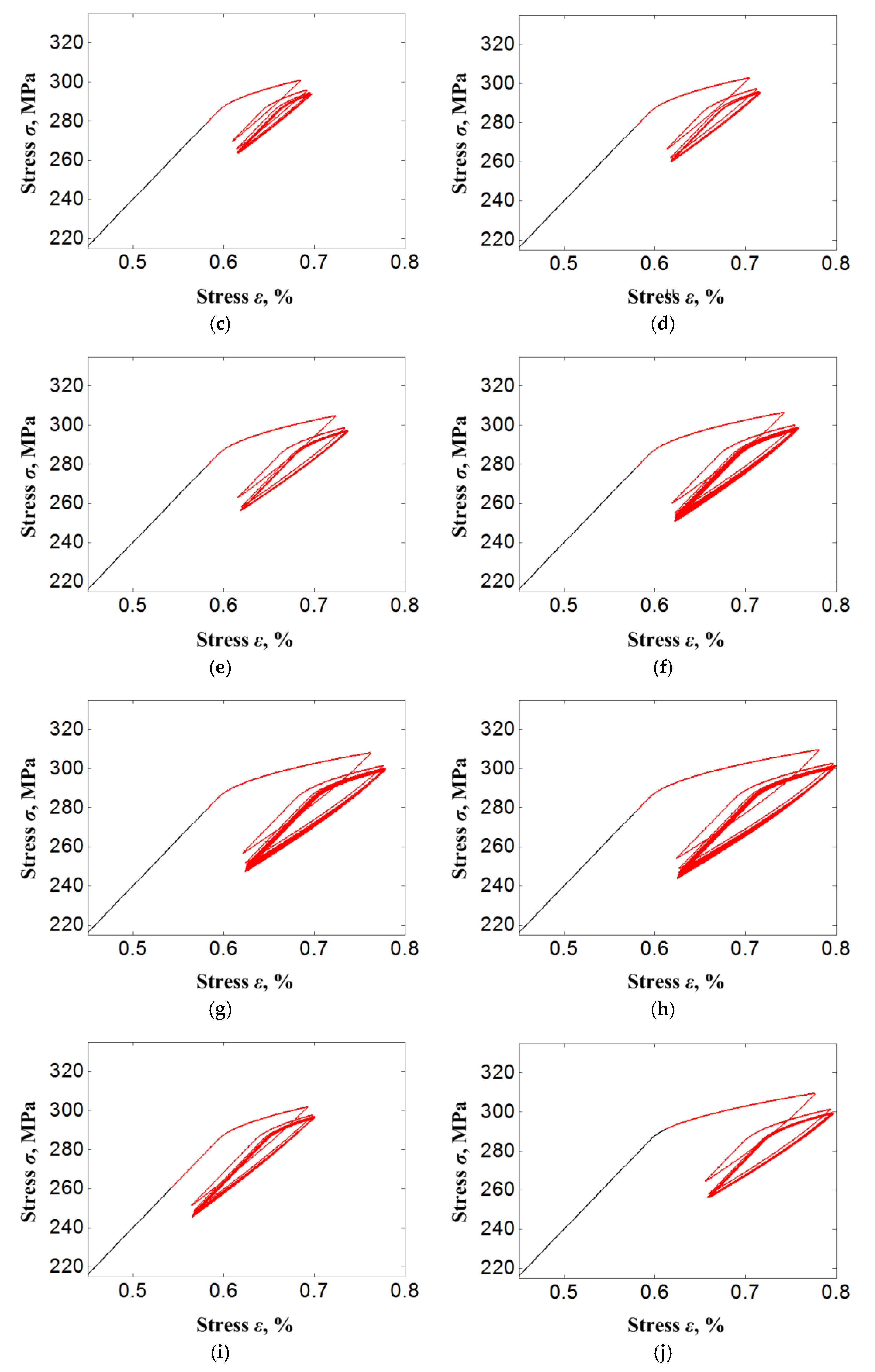
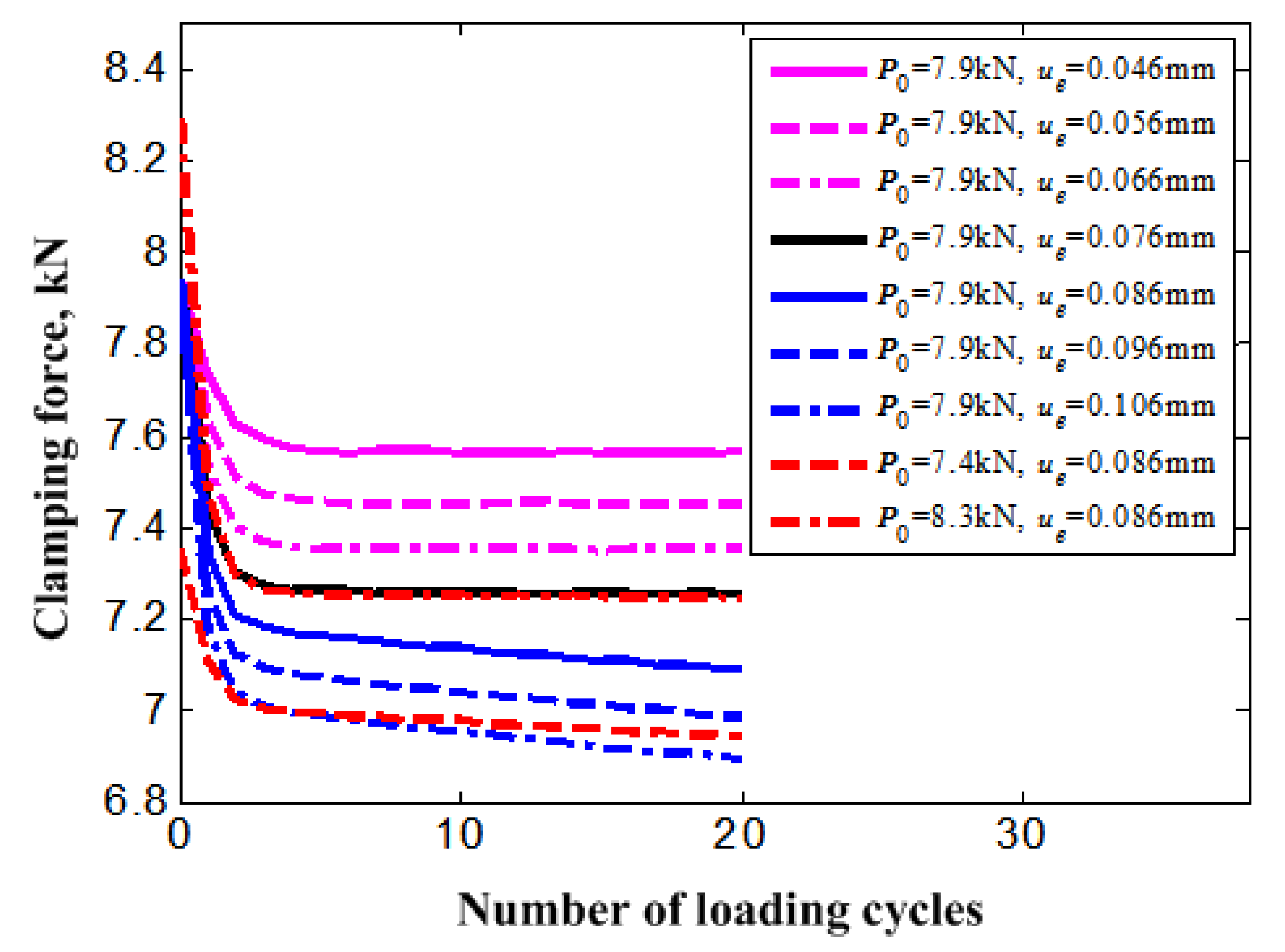
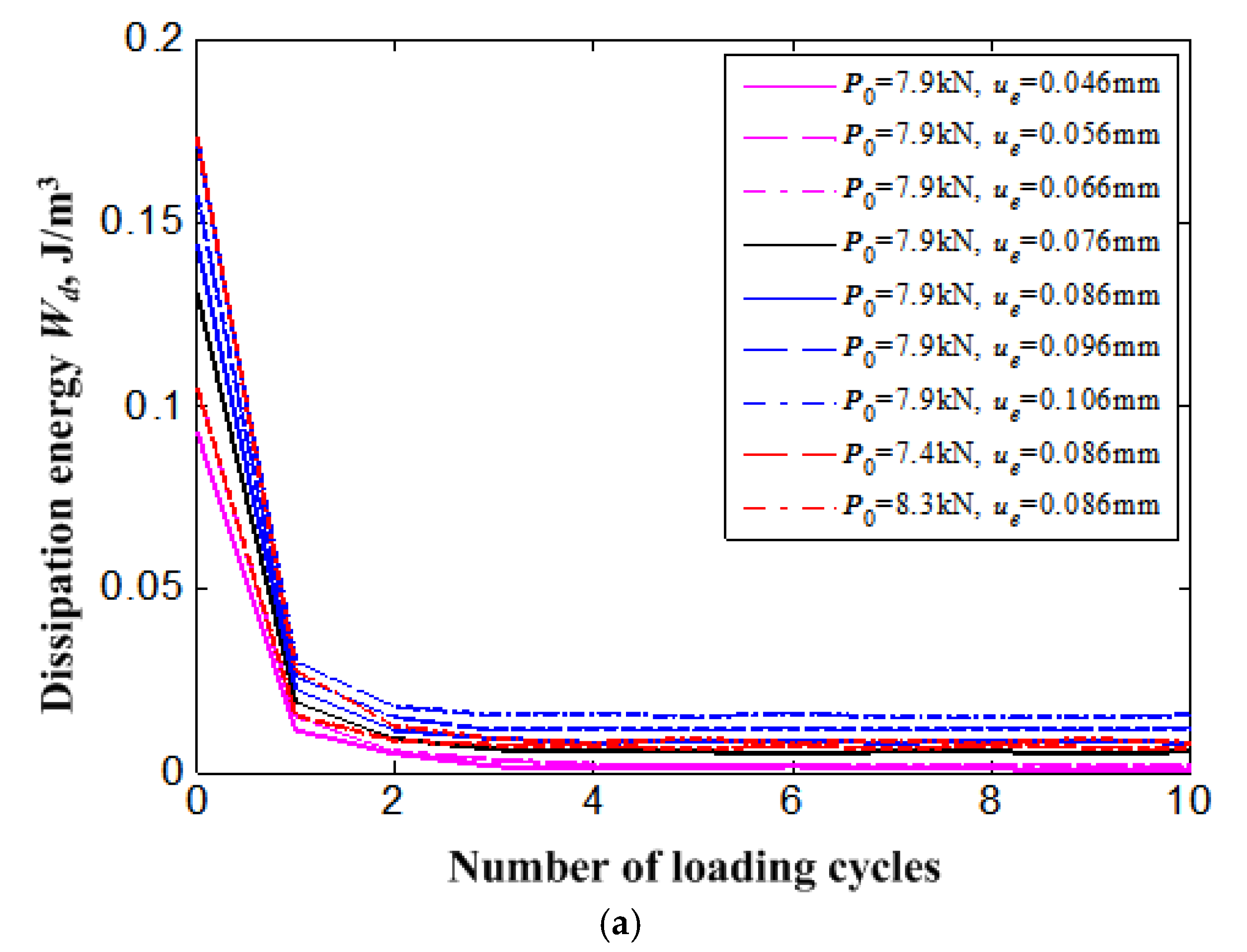
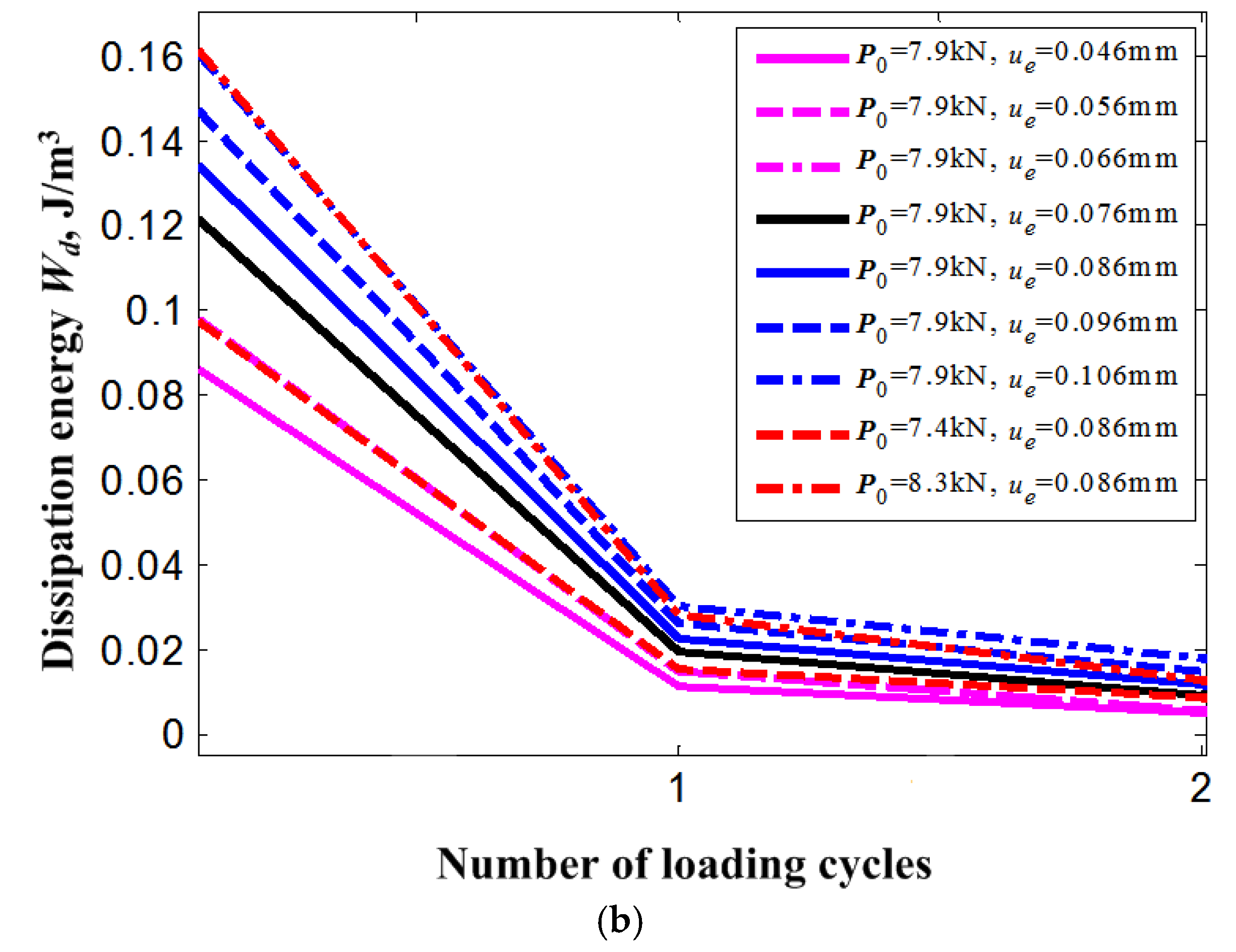
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A.
References
- Bickford, J.H. An Introduction to the Design and Behavior of Bolted Joints, 3rd ed.; Marcel Dekker: New York, NY, USA, 1995; p. 894. [Google Scholar]
- Jiang, X.; Zhu, Y.; Hong, J.; Chen, X.; Zhang, Y. Investigation into the loosening mechanism of bolt in curvic coupling subjected to transverse loading. Eng. Fail. Anal. 2013, 32, 360–373. [Google Scholar] [CrossRef]
- Qin, Z.; Han, Q.; Chu, F. Bolt loosening at rotating joint interface and its influence on rotor dynamics. Eng. Fail. Anal. 2016, 59, 456–466. [Google Scholar] [CrossRef]
- Jiang, Y.Y.; Zhang, M.; Lee, C.H. A study of early stage self-loosening of bolted joints. ASME J. Mech. Des. 2003, 125, 518–526. [Google Scholar] [CrossRef]
- Peairs, D.M.; Park, G.; Inman, D.J. Practical issues of activating self-repairing bolted joints. Smart Mater. Struct. 2004, 13, 1414–1423. [Google Scholar] [CrossRef]
- Faria, C.T.; Junior, V.L.; Inman, D.J. Modeling and experimental aspects of self-healing bolted joint through shape memory alloy actuators. J. Intell. Mater. Syst. Struct. 2011, 22, 1581–1594. [Google Scholar] [CrossRef]
- Ghorashi, M.; Inman, D.J. Shape memory alloy in tension and compression and its application as clamping force actuator in a bolted joint: Part 2 modeling. J. Intell. Mater. Syst. Struct. 2004, 15, 589–600. [Google Scholar] [CrossRef]
- Graesser, E.J.; Cozzarelli, F.A. Shape-memory alloys as new materials for aseismic isolation. J. Eng. Mech. 1991, 117, 2590–2608. [Google Scholar] [CrossRef]
- Tamai, H.; Kitagawa, Y. Pseudoelastic behavior of shape memory alloy wire and its application to seismic resistance member for building. Comput. Mater. Sci. 2002, 25, 218–227. [Google Scholar] [CrossRef]
- Casciati, F.; Faravelli, L. Experimental characterization of a Cu-based shape memory alloy toward its exploitation in passive control devices. J. Phys. IV 2004, 115, 299–306. [Google Scholar]
- Torra, V.; Isalgue, A.; Lovey, F.C.; Martorell, F.; Molina, F.J.; Sade, M.; Tachoire, H. Shape memory alloys: From the physical properties of metastable phase transitions to dampers for civil engineering applications. J. Phys. IV 2004, 113, 85–90. [Google Scholar] [CrossRef]
- Mitchell, D.; Bruneau, M.; Williams, M.; Anderson, D.; Saatcioglu, M.; Sexsmith, R. Performance of bridges in the 1994 Northridge earthquake. Can. J. Civ. Eng. 1995, 22, 415–427. [Google Scholar] [CrossRef]
- Ghannoum, W.M.; Moehle, J.P.; Bozorgnia, Y. Analytical collapse study of lightly confined reinforced concrete frames subjected to northridge earthquake ground motions. J. Earthq. Eng. 2008, 12, 1105–1119. [Google Scholar] [CrossRef]
- Ocel, J.M.; DesRoches, R.; Leon, R.T.; Hess, W.G.; Krumme, R.; Hayes, J.R.; Sweeney, S. Steel beam-column connections using shape memory alloys. ASCE J. Struct. Eng. 2004, 130, 732–740. [Google Scholar] [CrossRef]
- Penar, B.W. Recentering Beam-Column Connections Using Shape Memory Alloys. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2005. [Google Scholar]
- Abolmaali, A.; Treadway, J.; Aswath, P.; Lu, F.K.; McCarthy, E. Hysteresis behavior of T-stub connections with super elastic shape memory fasteners. J. Const. Steel Res. 2006, 62, 831–838. [Google Scholar] [CrossRef]
- Ma, M.; Wilkinson, T.; Cho, C. Feasibility study on a self-centering beam-to-column connection by using the super-elastic behavior of SMAs. Smart Mater. Struct. 2007, 16, 1555–1563. [Google Scholar] [CrossRef]
- Sep’ulveda, J.; Boroschek, R.; Herrera, R.; Moroni, O.; Sarrazin, M. Steel beam-column connection using copper-based shape memory alloy dampers. J. Const. Steel Res. 2008, 64, 429–435. [Google Scholar] [CrossRef]
- Hu, J.W. Seismic Performance Evaluations and Analyses for Composite Moment Frames with Smart SMA PR-CFT Connections. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2008. [Google Scholar]
- Speicher, M.; DesRoches, R.; Leon, R.T. Experimental results of NiTi shape memory alloy (SMA)-based beam-column connection. Eng. Struct. 2011, 33, 2448–2457. [Google Scholar] [CrossRef]
- Hu, J.W.; Choi, E.; Leon, R.T. Design, analysis and application of innovative composite PR connections between steel beams and CFT columns. Smart Mater. Struct. 2011, 20, 1–15. [Google Scholar] [CrossRef]
- Jong-Wan, H.; Won-Sup, H. Design and behavior of recentering beam-to-CFT column connections with super-elastic shape memory alloy fasteners. Int. J. Steel Struct. 2013, 13, 55–69. [Google Scholar]
- Fang, C.; Yam, M.C.; Lam, A.C.; Xie, L. Cyclic performance of extended end-plate connections equipped with shape memory alloy bolts. J. Constr. Steel Res. 2014, 94, 122–136. [Google Scholar] [CrossRef]
- Wang, W.; Chan, T.M.; Shao, H.; Chen, Y. Cyclic behavior of connections equipped with NiTi shape memory alloy and steel tendons between H-shaped beam to CHS column. Eng. Struct. 2015, 88, 37–50. [Google Scholar] [CrossRef]
- Quan, C.; Wang, W.; Chan, T.M.; Khador, M. FE modelling of replaceable I-beam-to-CHS column joints under cyclic loads. J. Constr. Steel Res. 2017, 138, 221–234. [Google Scholar] [CrossRef]
- Wang, W.; Du, X.; Zhang, Y.; Chen, Y. Experimental investigation of beam-through steel frames with self-centering modular panels. ASCE J. Struct. Eng. 2017, 143, 04017006. [Google Scholar] [CrossRef]
- Miyazaki, S.; Otsuka, K.; Suzuki, Y. Transformation pseudoelasticity and deformation behavior in a Ti-50.6 at % Ni alloy. Scripta Metall. 1981, 15, 287–292. [Google Scholar] [CrossRef]
- Miyazaki, S.; Imai, T.; Lgo, Y. Effect of cyclic deformation on the pseudoelasticity characteristics of TiNi alloy. Metall. Trans. 1986, 17, 115–120. [Google Scholar] [CrossRef]
- Strnadel, B.; Ohashi, S.; Ohtsuka, H.; Ishihara, T.; Miyazaki, S. Cyclic stress-strain characteristics of Ti-Ni and Ti-Ni-Cu shape memory alloys. Mater. Sci. Eng. A 1995, 202, 148–156. [Google Scholar] [CrossRef]
- Strnadel, B.; Ohashi, S.; Ohtsuka, H.; Miyazaki, S.; Ishihara, T. Effect of mechanical cycling on the pseudoelasticity characteristics of Ti-Ni and Ti-Ni-Cu alloys. Mater. Sci. Eng. A 1995, 203, 187–196. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W.G. Super-elastic and cyclic response of NiTi SMA at various strain rates and temperatures. Mech. Mater. 2006, 38, 463–474. [Google Scholar] [CrossRef]
- Kang, G.Z.; Kan, Q.H.; Qian, L.M.; Liu, Y.J. Ratcheting deformation of superelastic and shape memory NiTi Alloys. Mech. Mater. 2009, 41, 139–153. [Google Scholar] [CrossRef]
- Kan, Q.; Kang, G. Constitutive model for uniaxial transformation ratchetting of super-elastic NiTi shape memory alloy at room temperature. Int. J. Plast. 2010, 26, 441–465. [Google Scholar] [CrossRef]
- Kan, Q.H.; Kang, G.Z.; Guo, S.J. Finite element implementation of a super-elastic constitutive model for transformation ratchetting of NiTi alloy. Int. J. Comput. Methods. 2012, 9, 1240022. [Google Scholar] [CrossRef]
- Lagoudas, D.C.; Entchev, P.B. Modelling of transformation-induced plasticity and its effect on the behavior of porous shape memory alloys. Part I: Constitutive model for fully dense SMAs. Mech. Mater. 2004, 36, 865–892. [Google Scholar] [CrossRef]
- Brinson, L.C. One dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with nonconstant material functions. J. Intell. Mater. Syst. Str. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Brinson, L.C.; Huang, M.S. Simplifications and comparisons of shape memory alloy constitutive models. J. Intell. Mater. Syst. Str. 1996, 7, 108–114. [Google Scholar] [CrossRef]
- Bekker, A.; Brinson, L.C. Phase diagram based description of the hysteresis behavior of shape memory alloys. Acta Mater. 1998, 46, 3649–3665. [Google Scholar] [CrossRef]
- Yu, C.; Kang, G.; Kan, Q.; Song, D. A micromechanical constitutive model based on crystal plasticity for thermo-mechanical cyclic deformation of NiTi shape memory alloy. Int. J. Plast. 2013, 44, 161–191. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Bui, T.Q.; Truong, T.T.; Trinh, N.A.; Singh, T.Y.; Doan, D.H. Enhanced nodal gradient 3D consecutive-interpolation tetrahedral element (CTH4) for heat transfer analysis. Int. J. Heat Mass Tran. 2016, 103, 14–27. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Bui, T.Q.; Truong, T.T.; Tanaka, S.; Hirose, S. Numerical analysis of 3-D solids and composite structures by an enhanced 8-node hexahedral element. Finite Elem. Anal. Des. 2017, 131, 1–16. [Google Scholar] [CrossRef]
- Jiang, X.J.; Zhu, Y.S.; Hong, J.; Zhu, L.B. Development and validation of an analytical model for stiffness analysis of curvic coupling in tightening. J. Aerospace Eng. 2013, 6, 509–522. [Google Scholar] [CrossRef]
- Jiang, X.J.; Zhu, Y.S.; Hong, J.; Zhu, L.B. Stiffness analysis of curvic coupling in tightening by considering the different bolt structures. J. Aerospace Eng. 2016, 29, 04015076. [Google Scholar] [CrossRef]
- Motosh, N. Determination of joint stiffness in bolted connections. ASME J. Eng. Ind. 1976, 983, 858–861. [Google Scholar] [CrossRef]
- Nassar, S.A.; Abboud, A. An improved stiffness model for bolted joints. J. Mech. Des. 2009, 131, 1–10. [Google Scholar] [CrossRef]
- Hu, J.W. Investigation on the cyclic response of superelastic shape memory alloy (SMA) slit damper devices simulated by quasi-static finite element (FE) analyses. Materials 2014, 7, 1122–1141. [Google Scholar] [CrossRef] [PubMed]
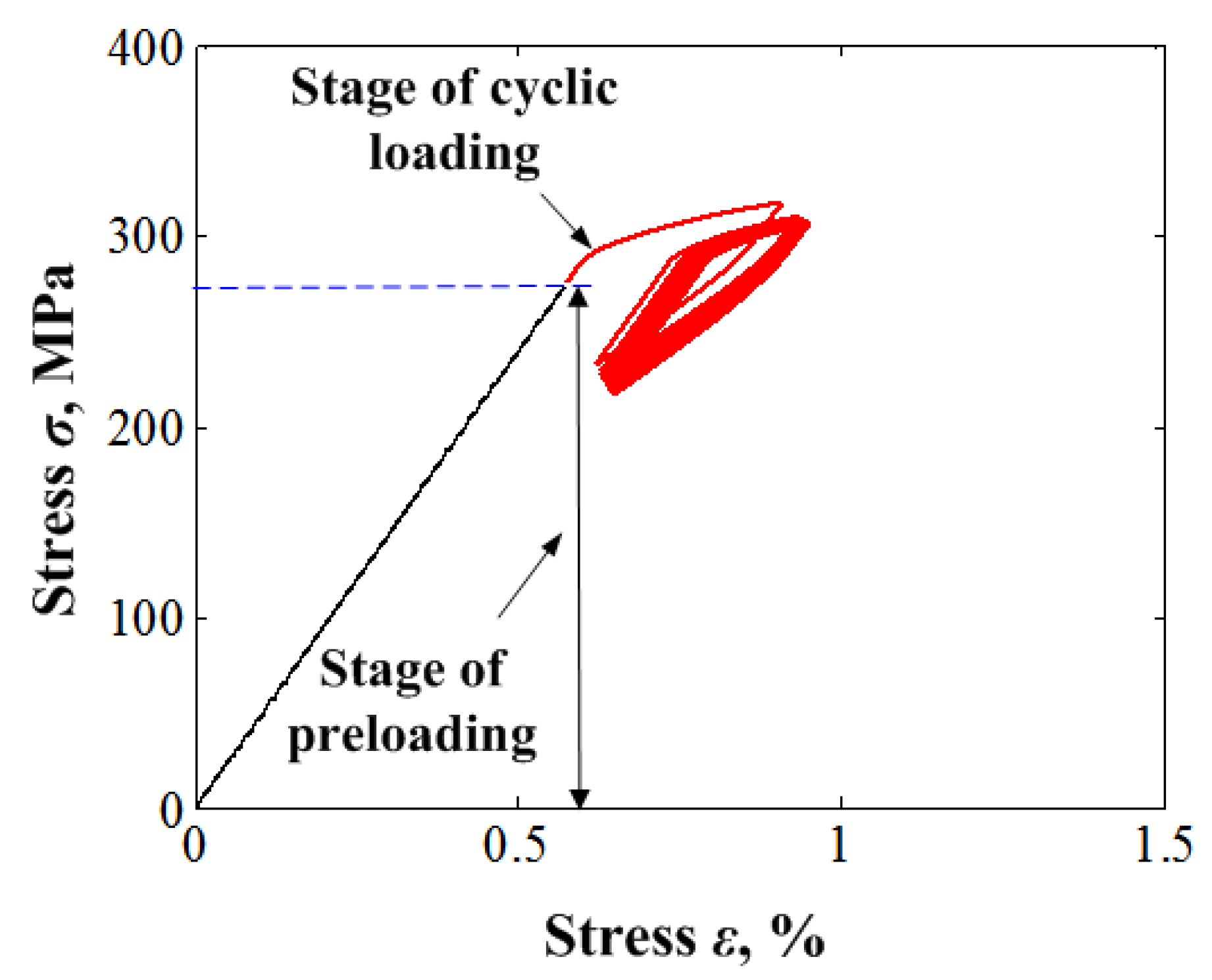
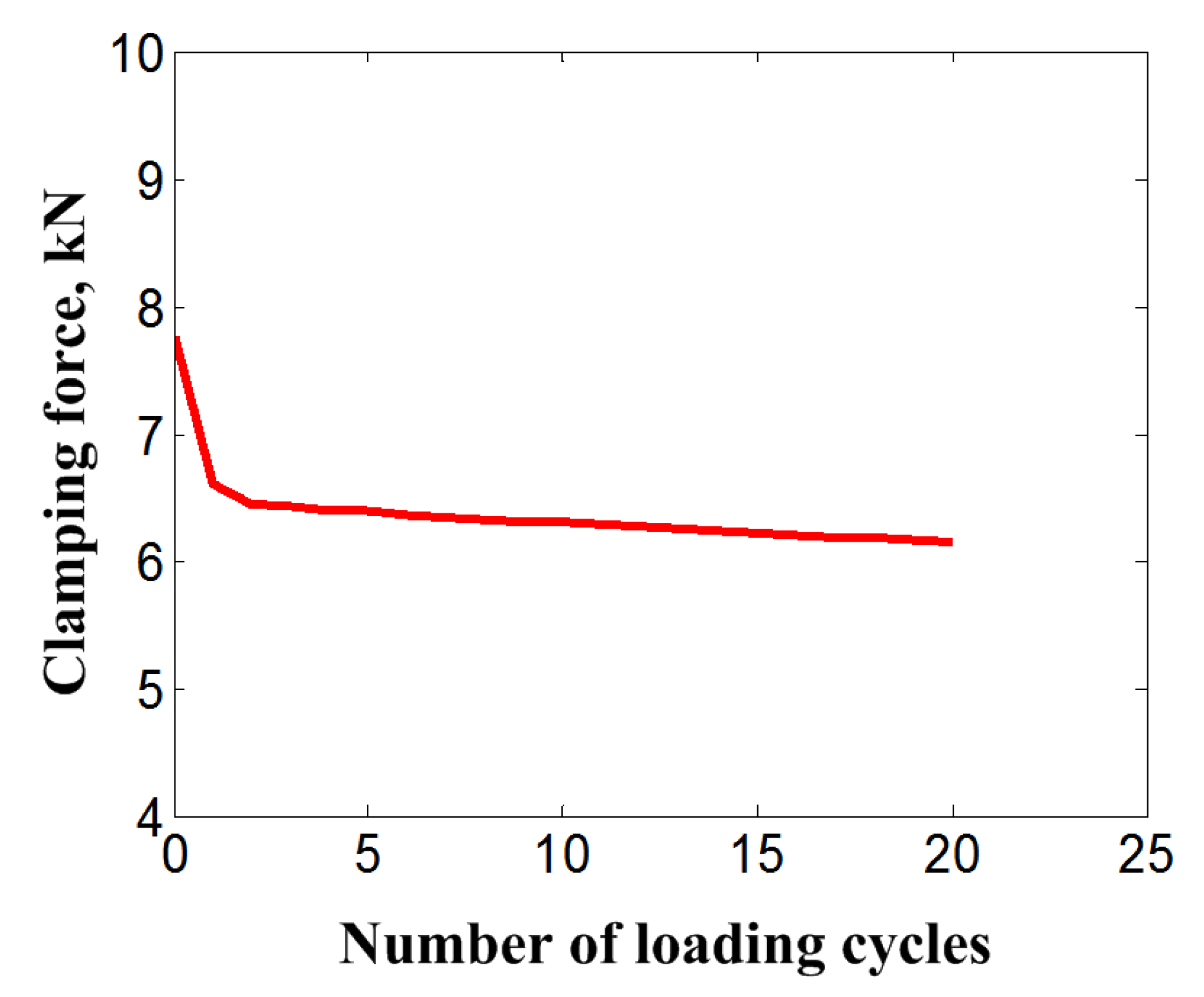
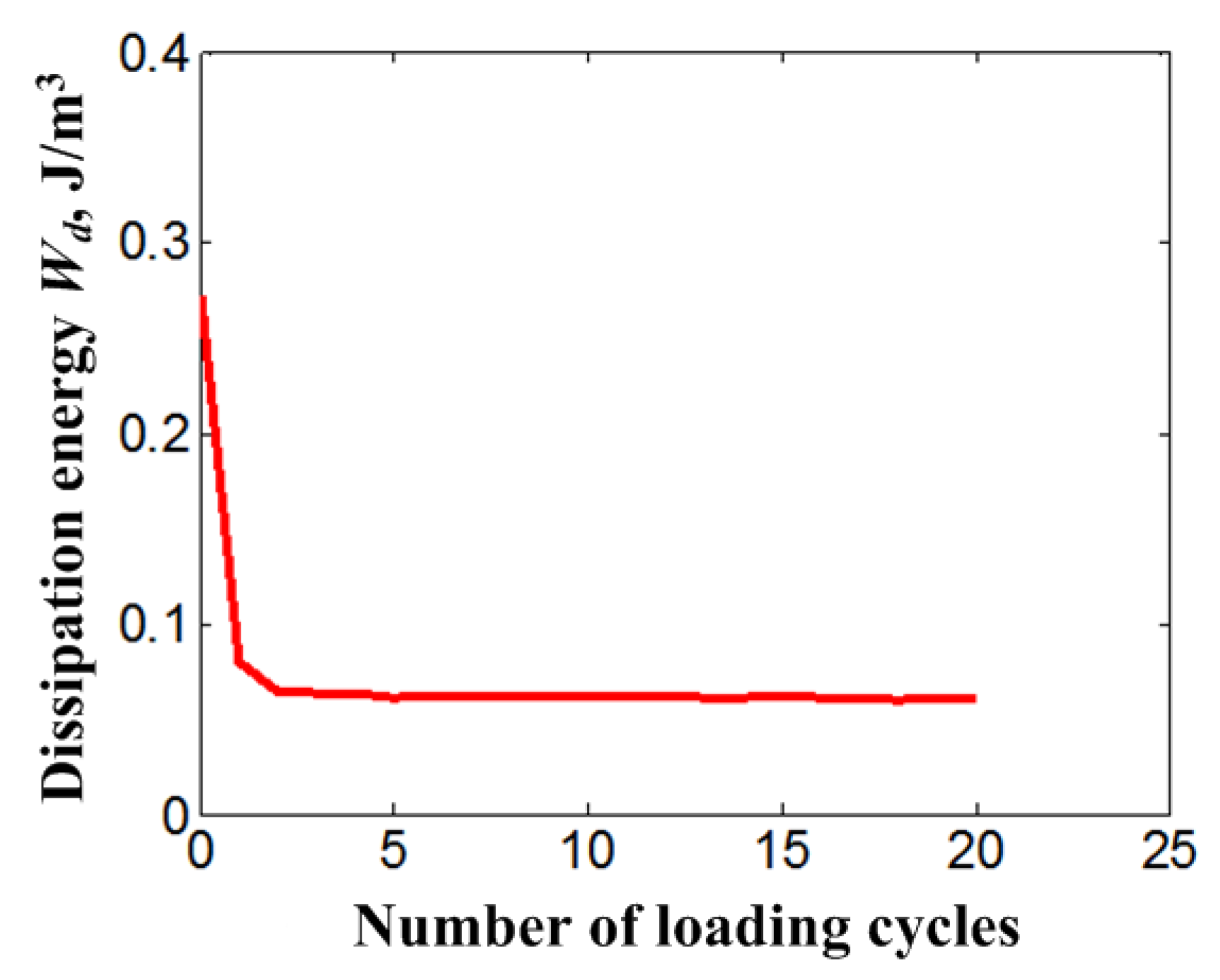
| = 48 GPa | = 35 GPa | = 0.3 | = 0.3 | = 0.063 | = 295 K |
| = 285 MPa | = 458 MPa | = 345 MPa | = 164 MPa | ||
| = 225 MPa | = 458 MPa | = 310 MPa | = 125 MPa; | ||
| = 0.05 | = 0.05 | = 0.05 | = 3 | = 0.84 | = 0.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Huang, J.; Wang, Y.; Li, B.; Du, J.; Hao, P. Finite Element Analysis for the Self-Loosening Behavior of the Bolted Joint with a Superelastic Shape Memory Alloy. Materials 2018, 11, 1592. https://doi.org/10.3390/ma11091592
Jiang X, Huang J, Wang Y, Li B, Du J, Hao P. Finite Element Analysis for the Self-Loosening Behavior of the Bolted Joint with a Superelastic Shape Memory Alloy. Materials. 2018; 11(9):1592. https://doi.org/10.3390/ma11091592
Chicago/Turabian StyleJiang, Xiangjun, Jin Huang, Yongkun Wang, Baotong Li, Jingli Du, and Peng Hao. 2018. "Finite Element Analysis for the Self-Loosening Behavior of the Bolted Joint with a Superelastic Shape Memory Alloy" Materials 11, no. 9: 1592. https://doi.org/10.3390/ma11091592
APA StyleJiang, X., Huang, J., Wang, Y., Li, B., Du, J., & Hao, P. (2018). Finite Element Analysis for the Self-Loosening Behavior of the Bolted Joint with a Superelastic Shape Memory Alloy. Materials, 11(9), 1592. https://doi.org/10.3390/ma11091592







