Buckling Analysis of Vacancy-Defected Graphene Sheets by the Stochastic Finite Element Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Elastic Buckling
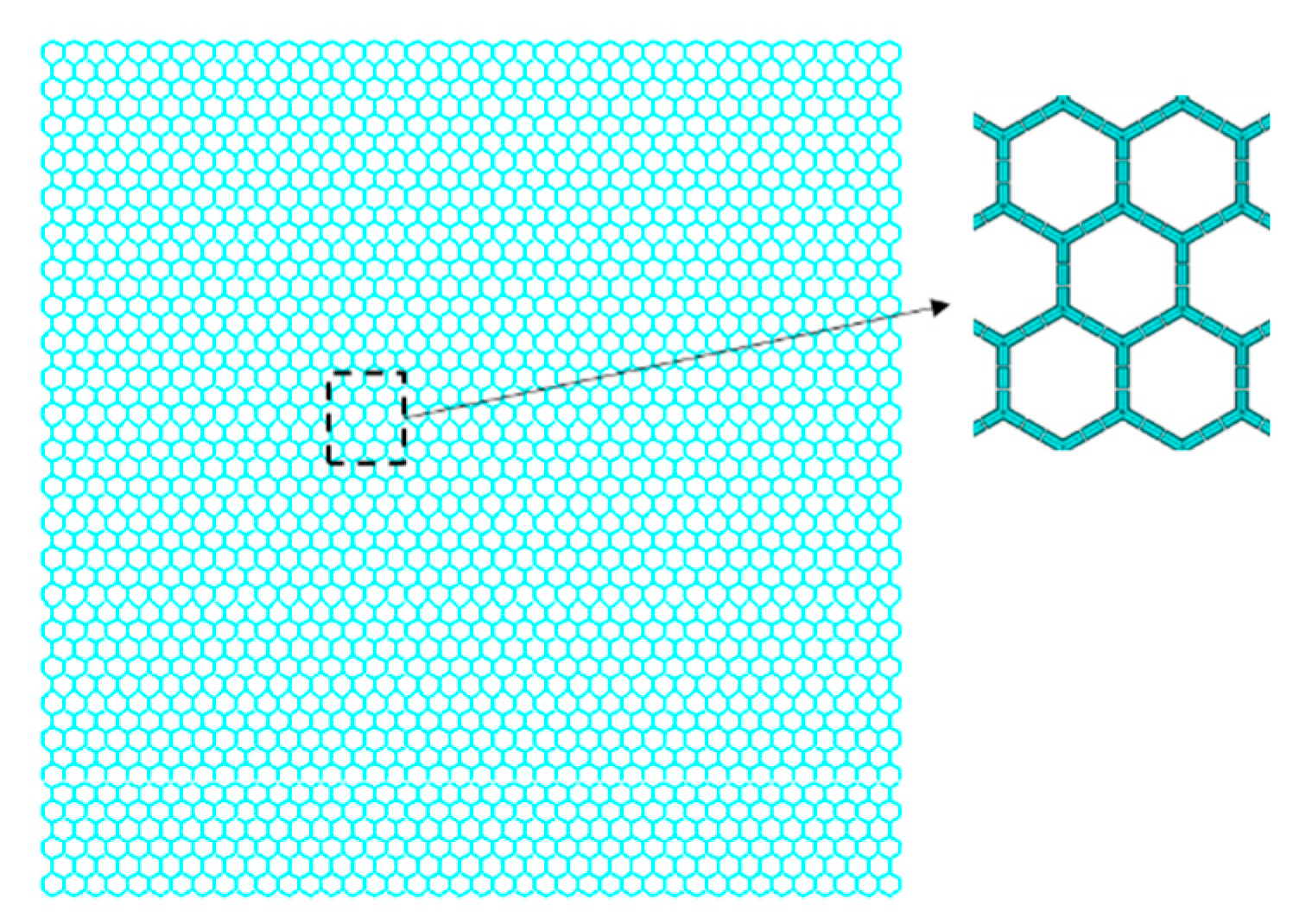
2.2. Graphene Sheets
2.3. Graphene Sheets with Vacancy Defects
3. Results and Discussion
3.1. Probability Analysis
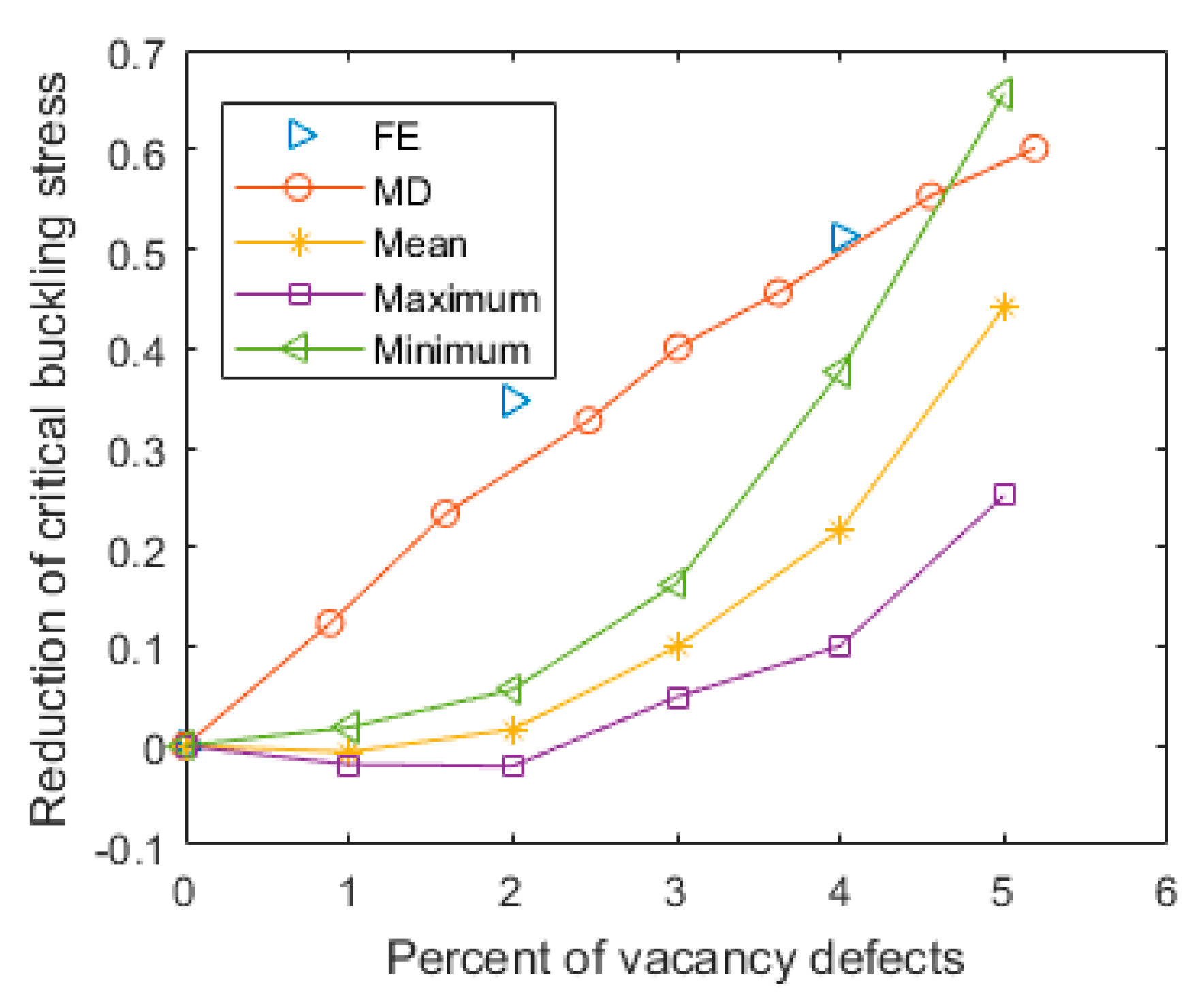
3.2. Comparison and Discussion
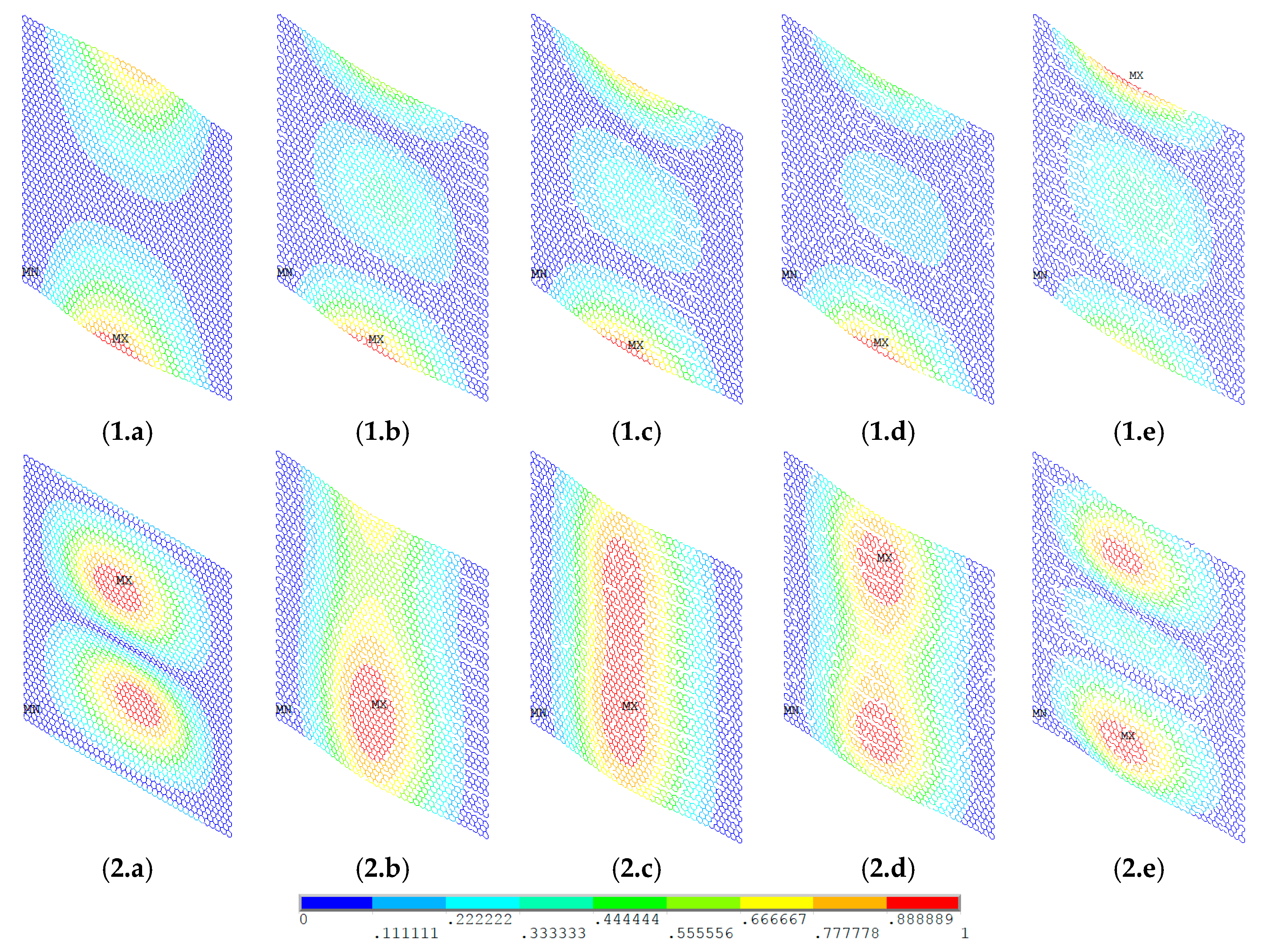
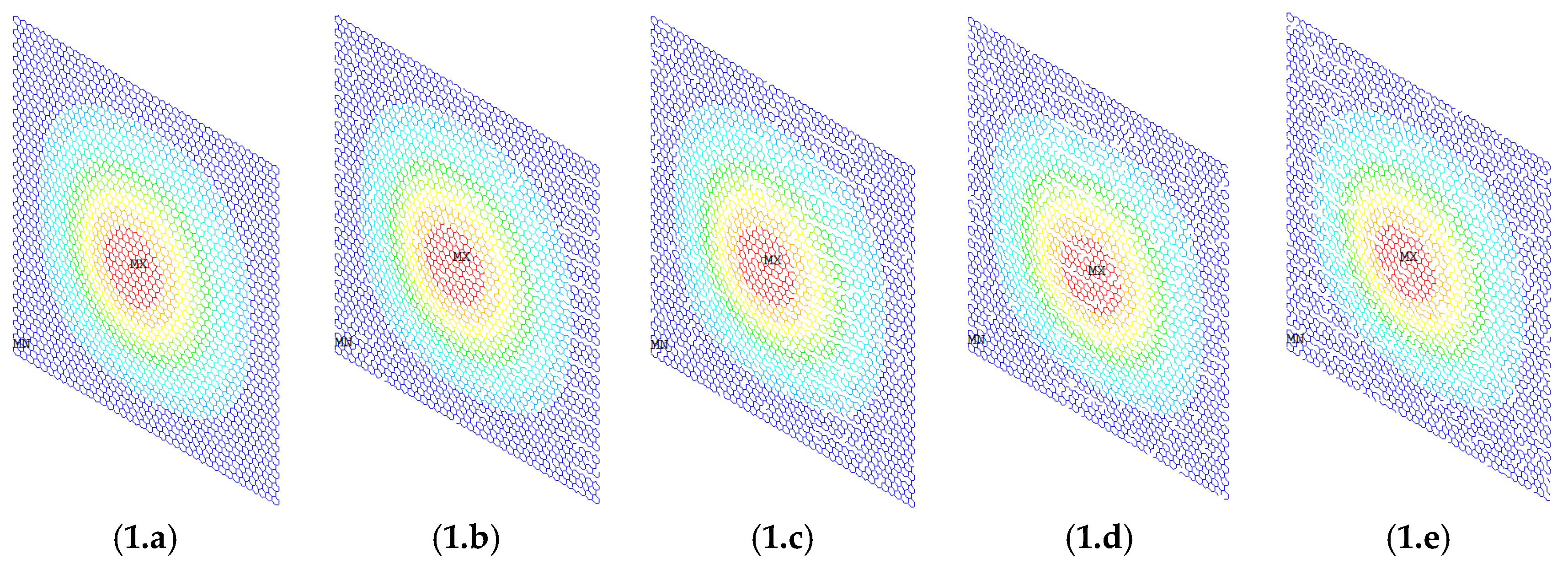
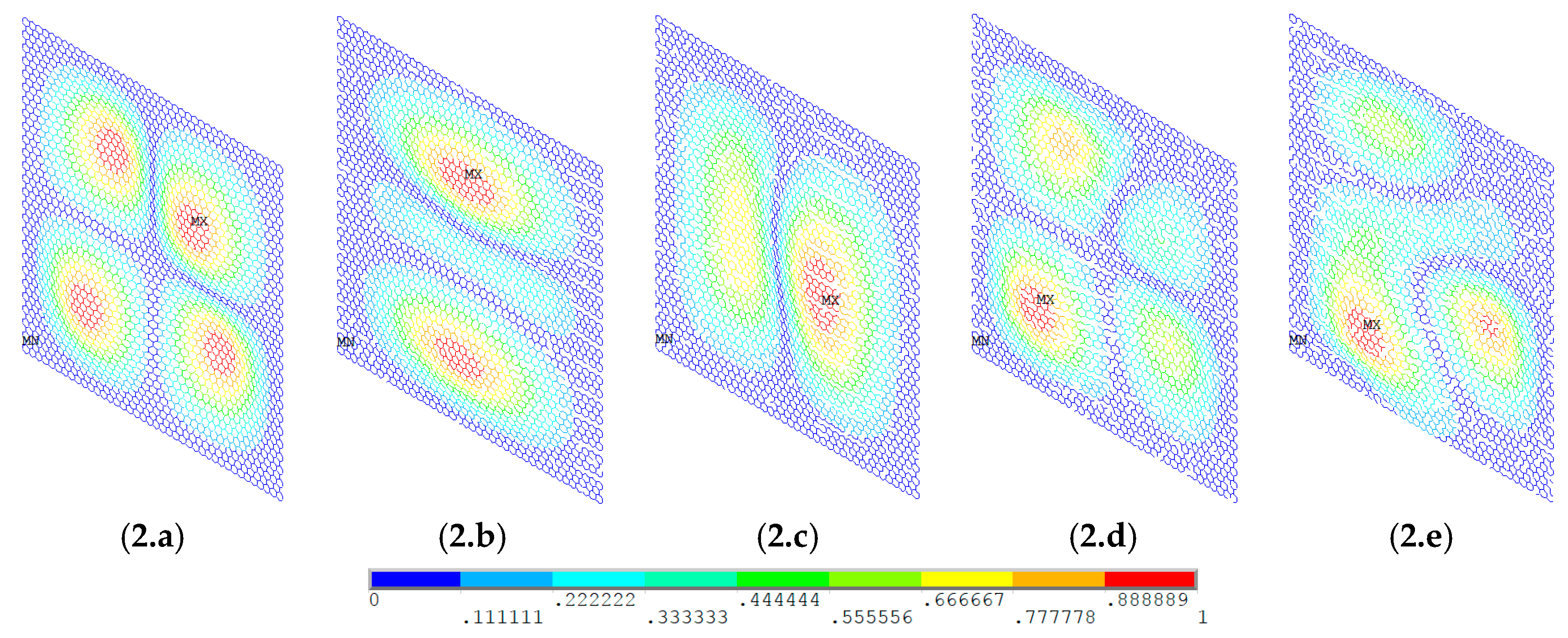
3.3. Displacement Results of Graphene Sheets
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kang, H.; Kulkarni, A.; Stankovich, S.; Ruoff, R.S.; Baik, S. Restoring electrical conductivity of dielectrophoretically assembled graphite oxide sheets by thermal and chemical reduction techniques. Carbon 2009, 47, 1520–1525. [Google Scholar] [CrossRef]
- Bunch, J.S.; Van Der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A.; Ahmadian, M.T.; Naghdabadi, R. Vibrational analysis of single-layered graphene sheets. Nano Technol. 2008, 19, 085702. [Google Scholar] [CrossRef] [PubMed]
- Mielke, S.L.; Troya, D.; Zhang, S.; Li, J.-L.; Xiao, S.; Car, R.; Ruoff, R.S.; Schatz, G.C.; Belytschko, T. The role of vacancy defects and holes in the fracture of carbon nanotubes. Chem. Phys. Lett. 2004, 390, 413–420. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Vatistas, I. Buckling analysis of pristine and defected graphene. Mech. Res. Commun. 2015, 64, 50–56. [Google Scholar] [CrossRef]
- Kim, J.; Reddy, J.N. Analytical solutions for bending, vibration, and buckling of FGM plates using a couple stress-based third-order theory. Compos. Struct. 2013, 103, 86–98. [Google Scholar] [CrossRef]
- Togun, N.; Bağdatli, S.M. Size dependent nonlinear vibration of the tensioned nanobeam based on the modified couple stress theory. Compos. Part B Eng. 2016, 97, 255–262. [Google Scholar] [CrossRef]
- Xu, L.; Ma, T.B.; Hu, Y.Z.; Wang, H. Molecular dynamics simulation of the interlayer sliding behavior in few-layer graphene. Carbon 2012, 50, 1025–1032. [Google Scholar] [CrossRef]
- Ohta, Y.; Okamoto, Y.; Irle, S.; Morokuma, K. Rapid growth of a single-walled carbon nanotube on an iron cluster: Density-functional tight-binding molecular dynamics simulations. Acs Nano 2008, 2, 1437. [Google Scholar] [CrossRef] [PubMed]
- Gillen, R.; Robertson, J. Density functional theory screened-exchange approach for investigating electronical properties of graphene-related materials. Phys. Rev. B 2010, 82, 1303–1307. [Google Scholar] [CrossRef]
- Anjomshoa, A.; Shahidi, A.R.; Hassani, B.; Jomehzadeh, E. Finite element buckling analysis of multi-layered graphene sheets on elastic substrate based on nonlocal elasticity theory. Appl. Math. Model. 2014, 38, 5934–5955. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Sharifpour, F.; Ilkhani, M.R. On the free vibrations of size-dependent closed micro/nano spherical shell based on the modified couple stress theory. Int. J. Mech. Sci. 2016, 115–116, 501–515. [Google Scholar] [CrossRef]
- Xu, W.; Wang, L.; Jiang, J. Strain Gradient Finite Element Analysis on the Vibration of Double-Layered Graphene Sheets. Int. J. Comput. Methods 2016, 13, 1650011. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. ACS Nano 2010, 5, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Jing, N.; Xue, Q.; Ling, C.; Shan, M.; Zhang, T.; Zhou, X.; Jiao, B. Effect of defects on Young’s modulus of graphene sheets a molecular dynamics simulation. RSC Adv. 2012, 2, 9124–9129. [Google Scholar] [CrossRef]
- Xiao, J.R.; Staniszewski, J.; Gillespie, J.W., Jr. Tensile behaviors of graphene sheets and carbon nanotubes with multiple Stone-Wales defects. Mater. Sci. Eng. A 2010, 527, 715–723. [Google Scholar] [CrossRef]
- Ansari, R.; Ajori, S.; Motevalli, B. Mechanical proper-ties of defective single-layered graphene sheets via molecular dynamics simulation. Superlattices Microstruct. 2012, 51, 274–289. [Google Scholar] [CrossRef]
- Namin, S.; Asbaghian, F.; Pilafkan, R. Vibration analy-sis of defective graphene sheets using nonlocal elasticity theory. Phys. E Low Dimens. Syst. Nanostruct. 2017, 93, 257–264. [Google Scholar] [CrossRef]
- Kim, B.; Kim, T.W. Monte Carlo simulation for offshore transportation. Ocean Eng. 2017, 129, 177–190. [Google Scholar] [CrossRef]
- Olsen, B.; Dufek, J. Stabilization effect of fission source in coupled Monte Carlo simulations. Nucl. Eng. Technol. 2017, 49, 1095–1099. [Google Scholar] [CrossRef]
- Leira, B.J.; Næss, A.; Næss, O.E.B. Reliability analysis of corroding pipelines by enhanced Monte Carlo simulation. Int. J. Press. Vessel. Pip. 2016, 144, 11–17. [Google Scholar] [CrossRef]
- Lee, H.; Yoon, C.; Cho, S.; Park, S.H.; Lee, W. The adaptation method in the Monte Carlo simulation for computed tomography. Nucl. Eng. Technol. 2015, 47, 472–478. [Google Scholar] [CrossRef]
- Chu, L.; De Cursi, E.S.; El Hami, A.; Eid, M. Application of Latin Hypercube Sampling Based Kriging Surrogate Models in Reliability Assessment. Sci. J. Appl. Math. Stat. 2015, 3, 6. [Google Scholar] [CrossRef]
- Chu, L.; De Cursi, E.S.; El Hami, A.; Eid, M. Reliability Based Optimization with Metaheuristic Algorithms and Latin Hypercube Sampling Based Surrogate Models. Appl. Comput. Math. 2015, 4, 462–468. [Google Scholar] [CrossRef]
- Wernik, J.M.; Meguid, S.A. Atomistic-based continuum modeling of the nonlinear behavior of carbon nanotubes. Acta Mech. 2010, 212, 167–179. [Google Scholar] [CrossRef]
- Parvaneh, V.; Shariati, M. Effect of defects and loading on prediction of Young’s modulus of SWCNTs. Acta Mech. 2011, 216, 281–289. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harriso, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783. [Google Scholar] [CrossRef]
- Tserpes, K.I. Strength of graphenes containing randomly dispersed vacancies. Acta Mech. 2012, 223, 669–678. [Google Scholar] [CrossRef]
- Belytschko, T.; Xiao, S.P.; Schatz, G.C.; Ruoff, R.S. Atomistic simulations of nanotube fracture. Phys. Rev. B 2002, 65, 235430. [Google Scholar] [CrossRef]
- Lópezpolín, G.; Gómeznavarro, C.; Parente, V.; Guinea, F.; Katsnelson, M.I.; Pérez-Murano, F.; Gómez-Herrero, J. Increasing the elastic modulus of graphene by controlled defect creation. Nat. Phys. 2015, 11, 26–31. [Google Scholar] [CrossRef]
- Sarvi, Z.; Asgari, M.; Shariyat, M.; Googarchin, H.S. Explicit expressions describing elastic properties and buckling load of BN nanosheets due to the effects of vacancy defects. Superlattices Microstruct. 2015, 88, 668–678. [Google Scholar] [CrossRef]
- Parisi, L.; Giugno, R.D.; Deretzis, I.; Angilella, G.G.N.; Magna, A.L. Kinetic Monte Carlo simulations of vacancy evolution in graphene. Mater. Sci. Semicond. Process. 2016, 42, 179–182. [Google Scholar] [CrossRef]
- Trevethan, T.; Latham, C.D.; Heggie, M.I.; Briddon, P.R.; Rayson, M.J. Vacancy diffusion and coalescence in graphene directed by defect strain fields. Nanoscale 2014, 6, 2978–2986. [Google Scholar] [CrossRef] [PubMed]
- Yamaletdinov, R.D.; Ivakhnenko, O.V.; Sedelnikova, O.V.; Shevchenko, S.N.; Pershin, Y.V. Snap-through transition of buckled graphene membranes for memcapacitor applications. Sci. Rep. 2018, 8, 3566. [Google Scholar] [CrossRef] [PubMed]
- Tozzini, V.; Pellegrini, V. Reversible Hydrogen Storage by Controlled Buckling of Graphene Layers. J. Phys. Chem. C 2011, 115, 25523–25528. [Google Scholar] [CrossRef]
- Vubac, N.; Bessa, M.A.; Rabczuk, T.; Liu, W.K. A Multiscale Model for the Quasi-Static Thermo-Plastic Behavior of Highly Cross-Linked Glassy Polymers. Macromolecules 2015, 48, 6713–6723. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Areias, P.M.A.; Rabczuk, T.A. multiscale multisurface constitutive model for the thermo-plastic behavior of polyethylene. Polymer 2016, 105, 327–338. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, W.L.; Wei, D.; Kaxiras, E.; Sodroski, J.G. Graphene Structures at an Extreme Degree of Buckling. ACS Nano 2011, 5, 1395–1400. [Google Scholar] [CrossRef] [PubMed]

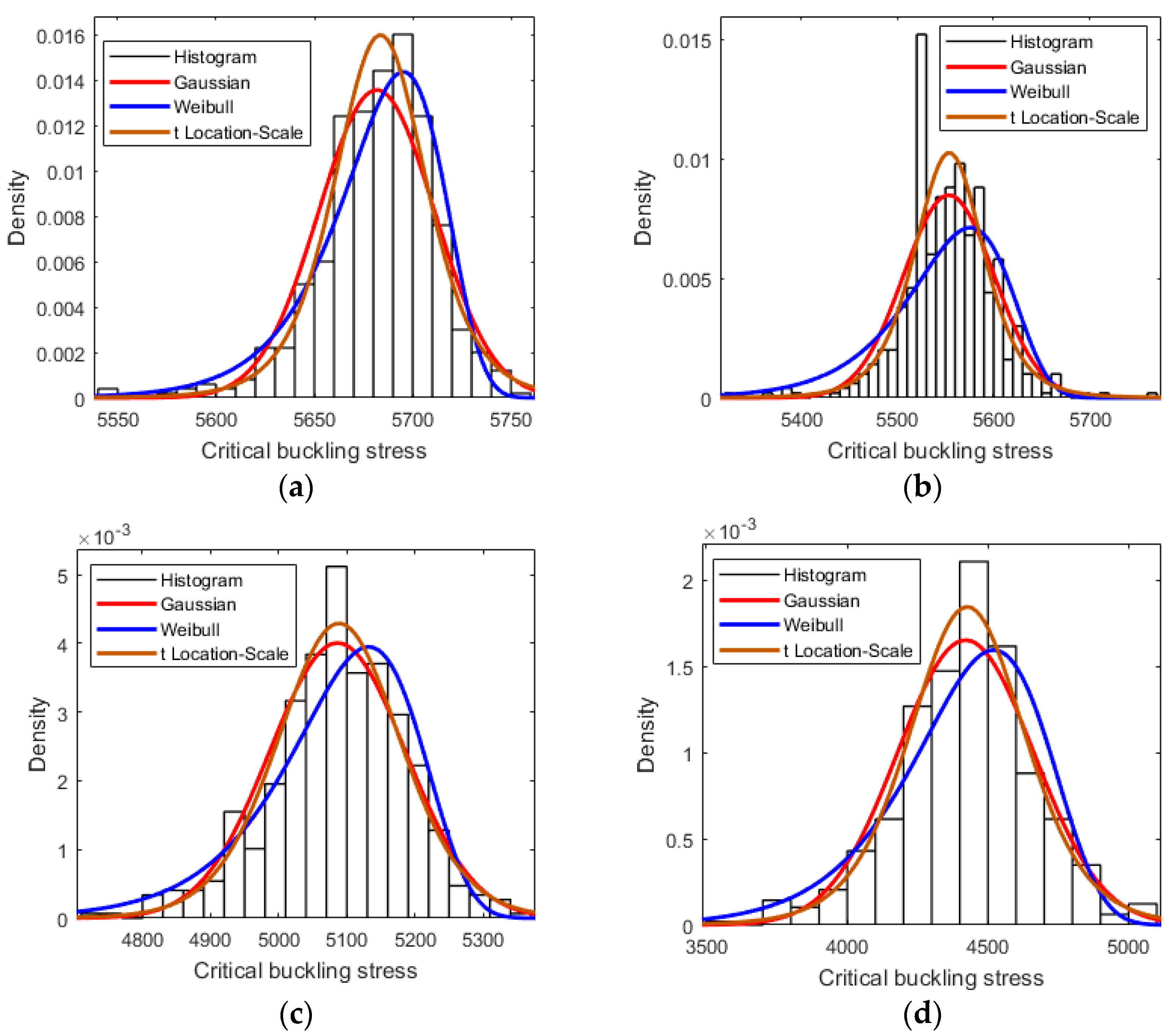
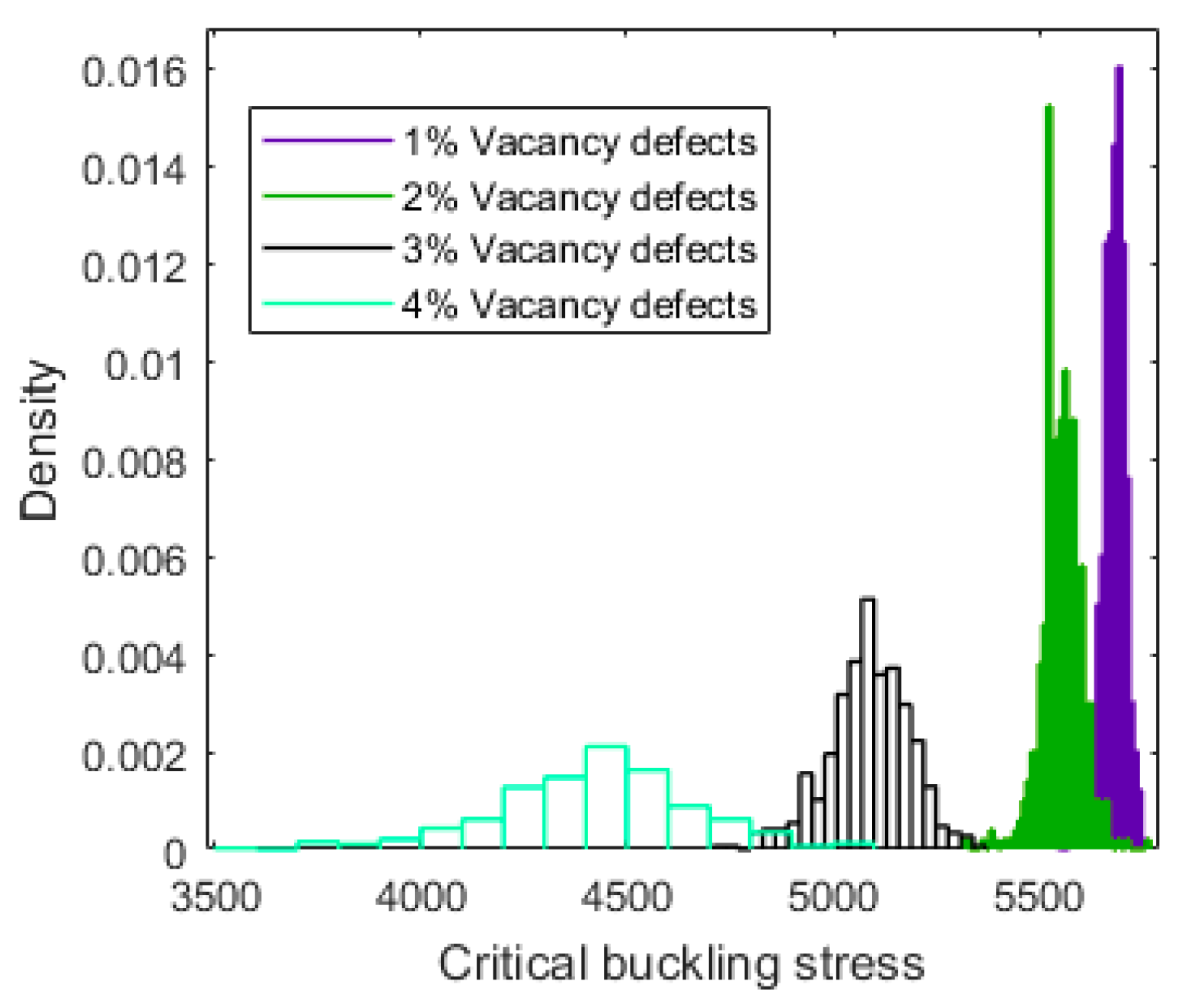
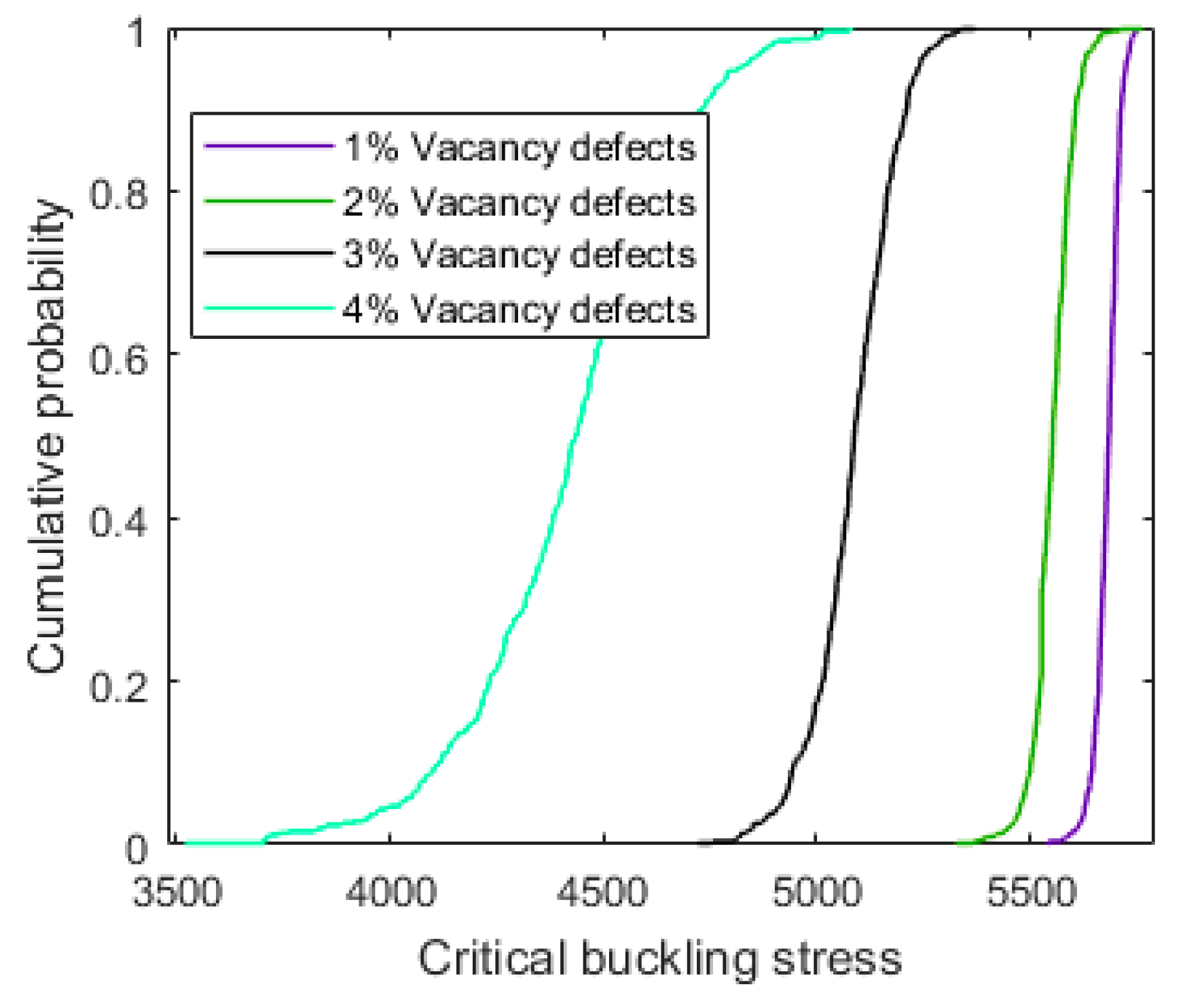

| Per (%) | Mean (THz) | Variance^0.5 | Skewness | Kurtosis |
|---|---|---|---|---|
| 1 | 5.6817 | 0.0294 | −0.0009 | 0.0053 |
| 2 | 5.5534 | 0.0471 | −0.0003 | 0.0056 |
| 3 | 5.0863 | 0.0996 | −0.0004 | 0.0035 |
| 4 | 4.4207 | 0.2416 | −0.0003 | 0.0037 |
| 5 | 3.1576 | 0.4646 | −0.0003 | 0.0029 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, L.; Shi, J.; Ben, S. Buckling Analysis of Vacancy-Defected Graphene Sheets by the Stochastic Finite Element Method. Materials 2018, 11, 1545. https://doi.org/10.3390/ma11091545
Chu L, Shi J, Ben S. Buckling Analysis of Vacancy-Defected Graphene Sheets by the Stochastic Finite Element Method. Materials. 2018; 11(9):1545. https://doi.org/10.3390/ma11091545
Chicago/Turabian StyleChu, Liu, Jiajia Shi, and Shujun Ben. 2018. "Buckling Analysis of Vacancy-Defected Graphene Sheets by the Stochastic Finite Element Method" Materials 11, no. 9: 1545. https://doi.org/10.3390/ma11091545
APA StyleChu, L., Shi, J., & Ben, S. (2018). Buckling Analysis of Vacancy-Defected Graphene Sheets by the Stochastic Finite Element Method. Materials, 11(9), 1545. https://doi.org/10.3390/ma11091545





