Simulation Analysis of Porthole Die Extrusion Process and Die Structure Modifications for an Aluminum Profile with High Length–Width Ratio and Small Cavity
Abstract
1. Introduction
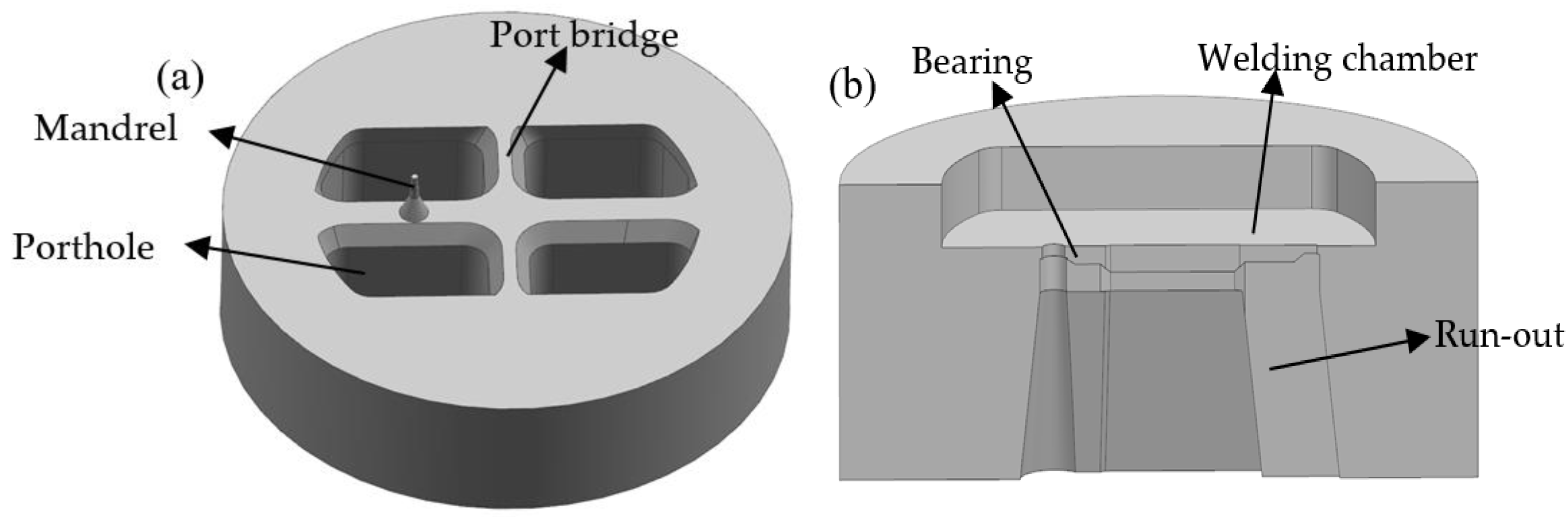
2. Porthole Die Design and Simulation Procedures
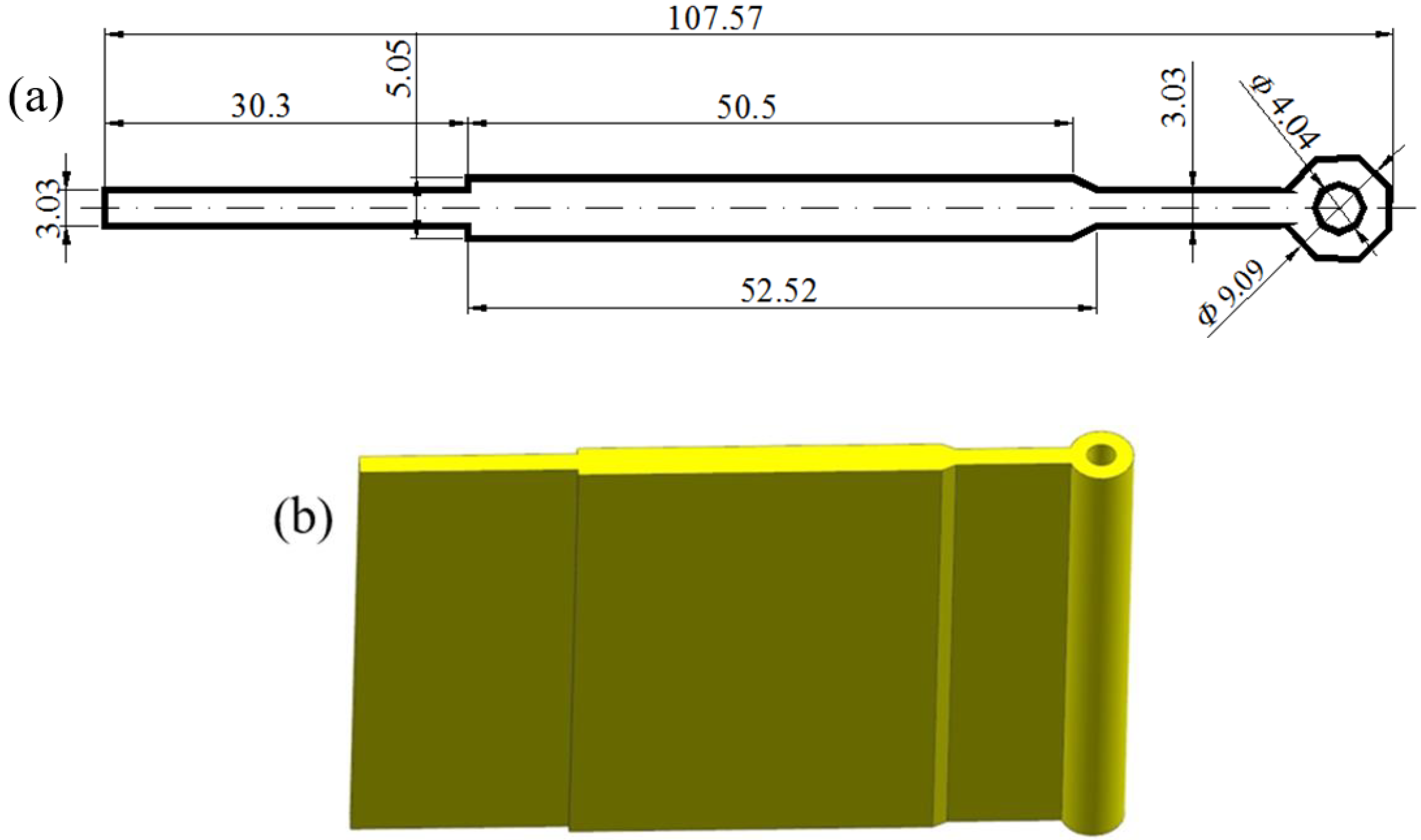
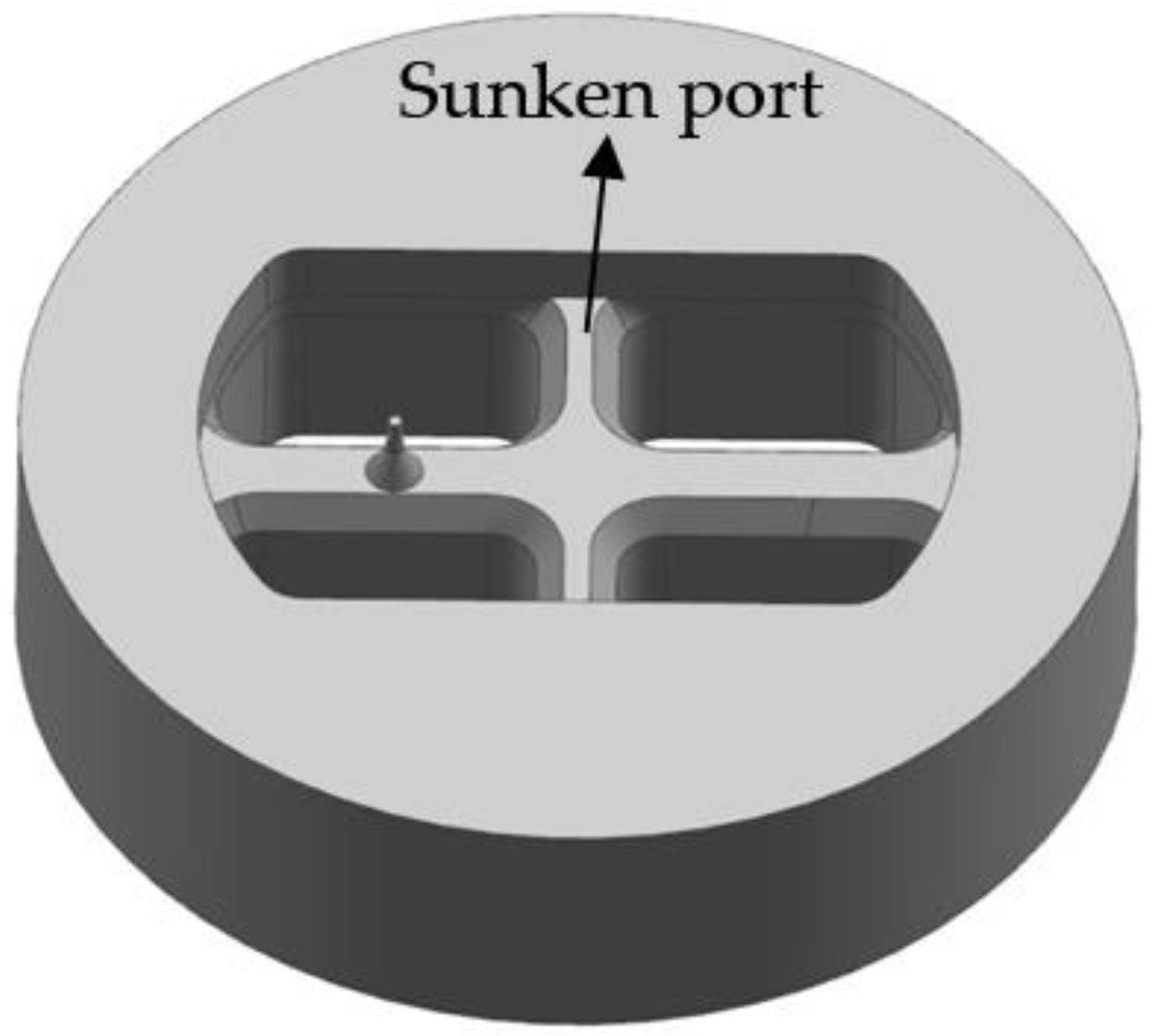
2.1. Traditional Design Scheme and Geometry Modeling
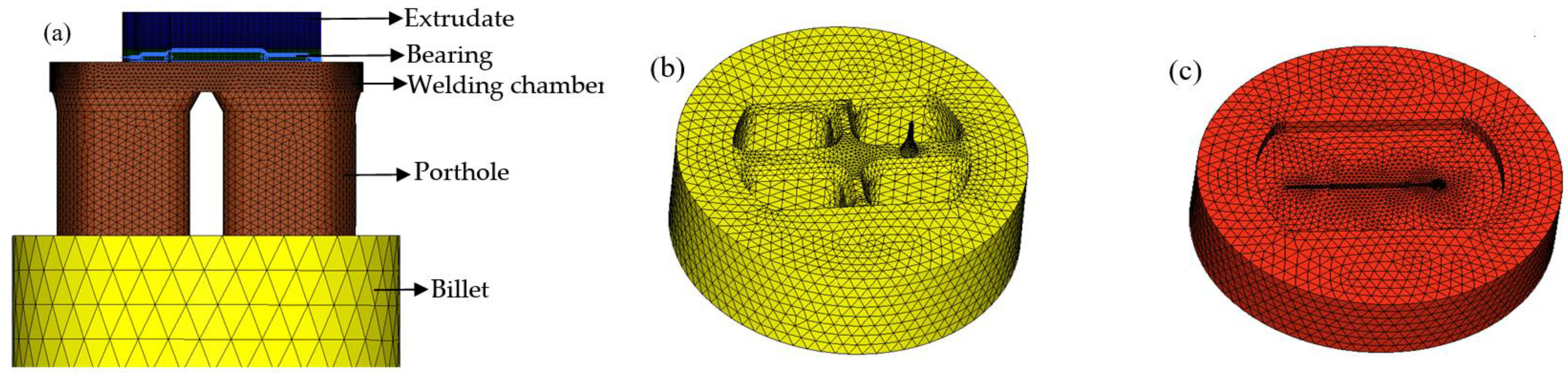
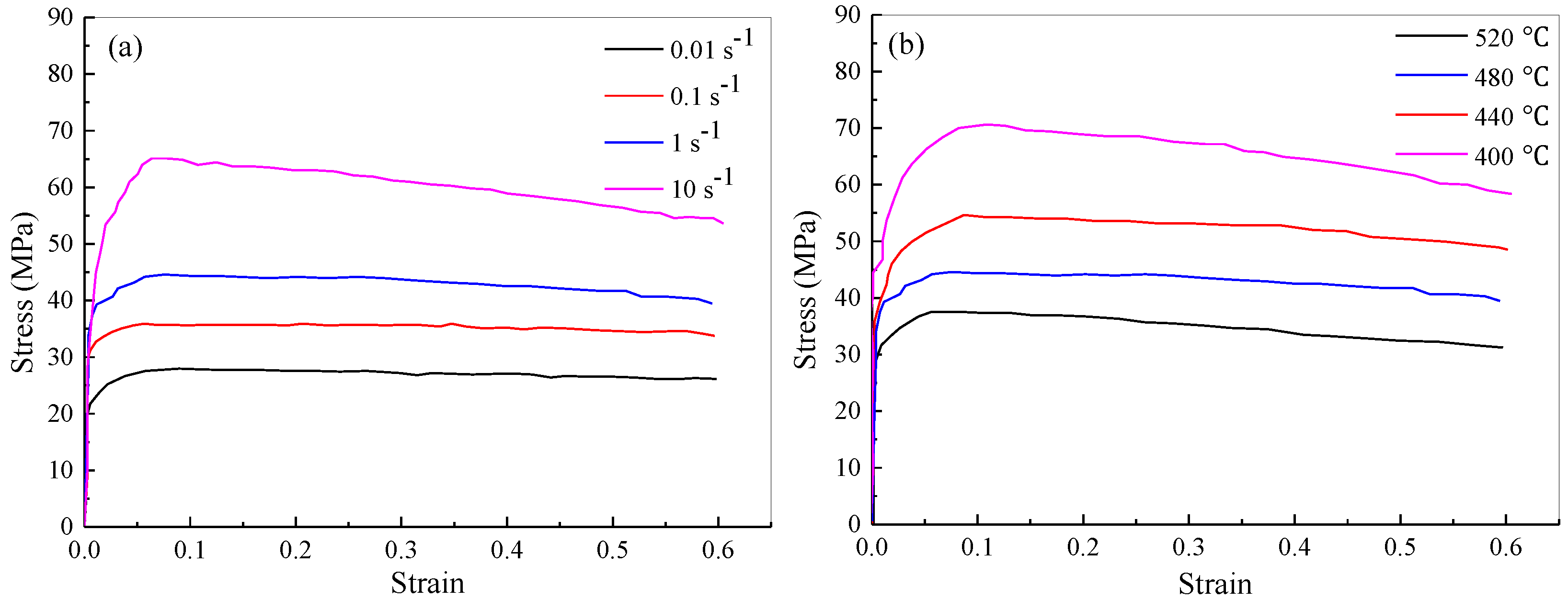
2.2. Establishment of 3D-FE Model
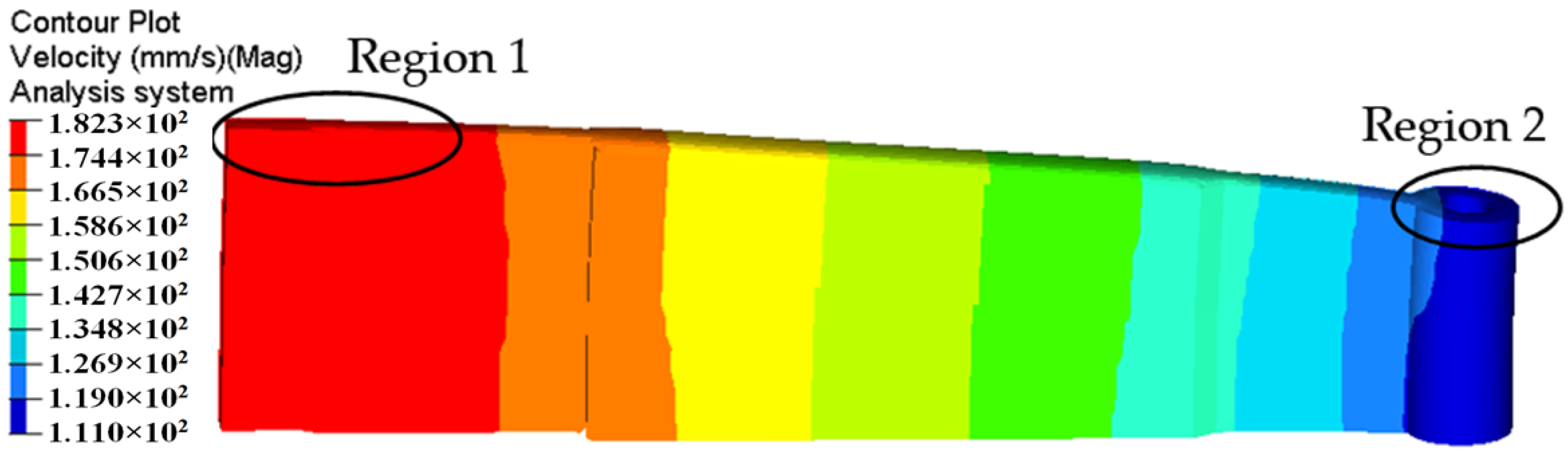
3. FE Simulation of Traditional Die Design
4. Redesign of Porthole Die
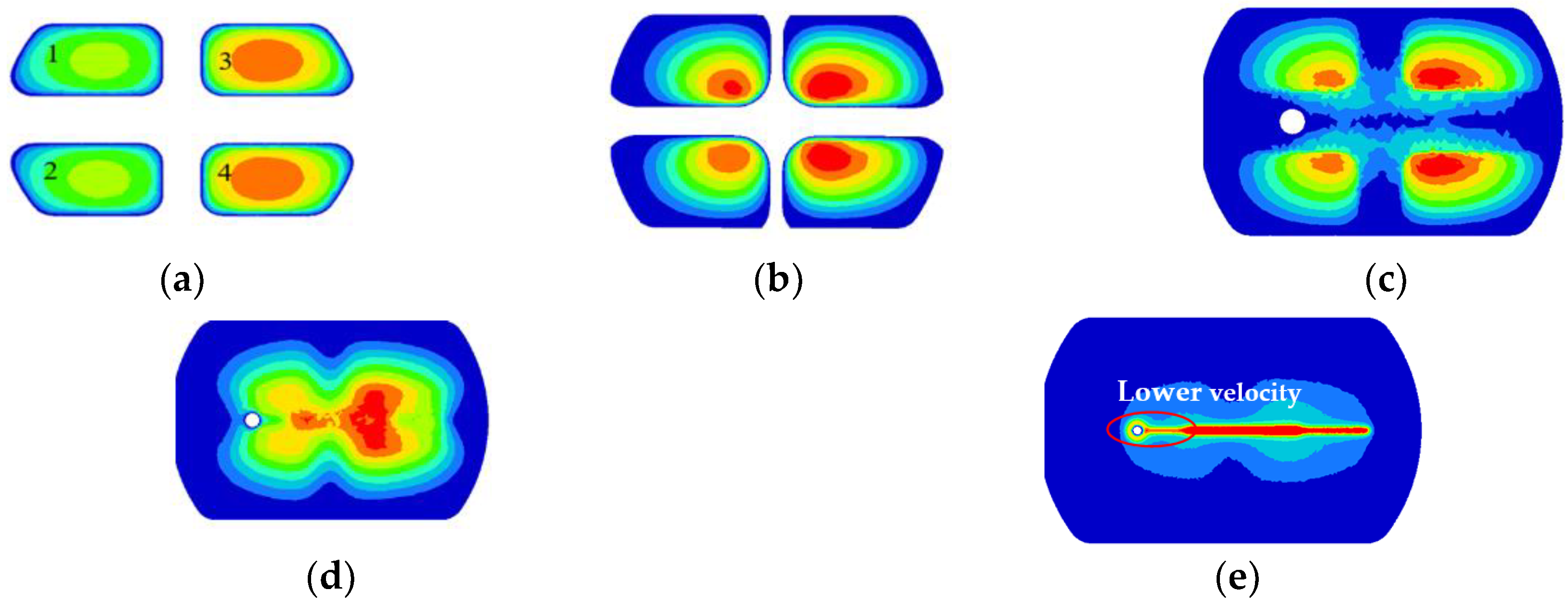
4.1. First Step: Rearranging the Welding Chamber in Upper Die
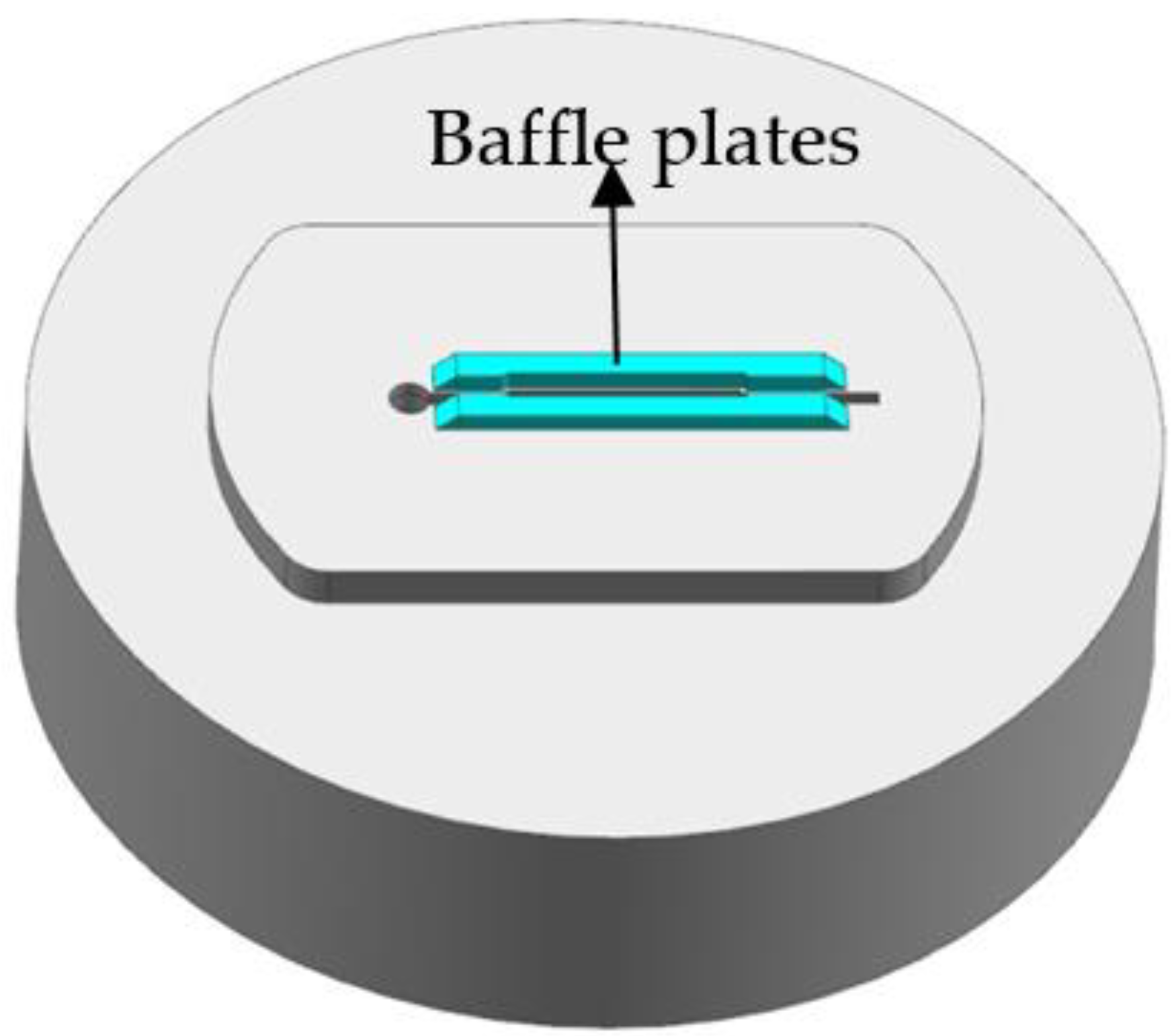
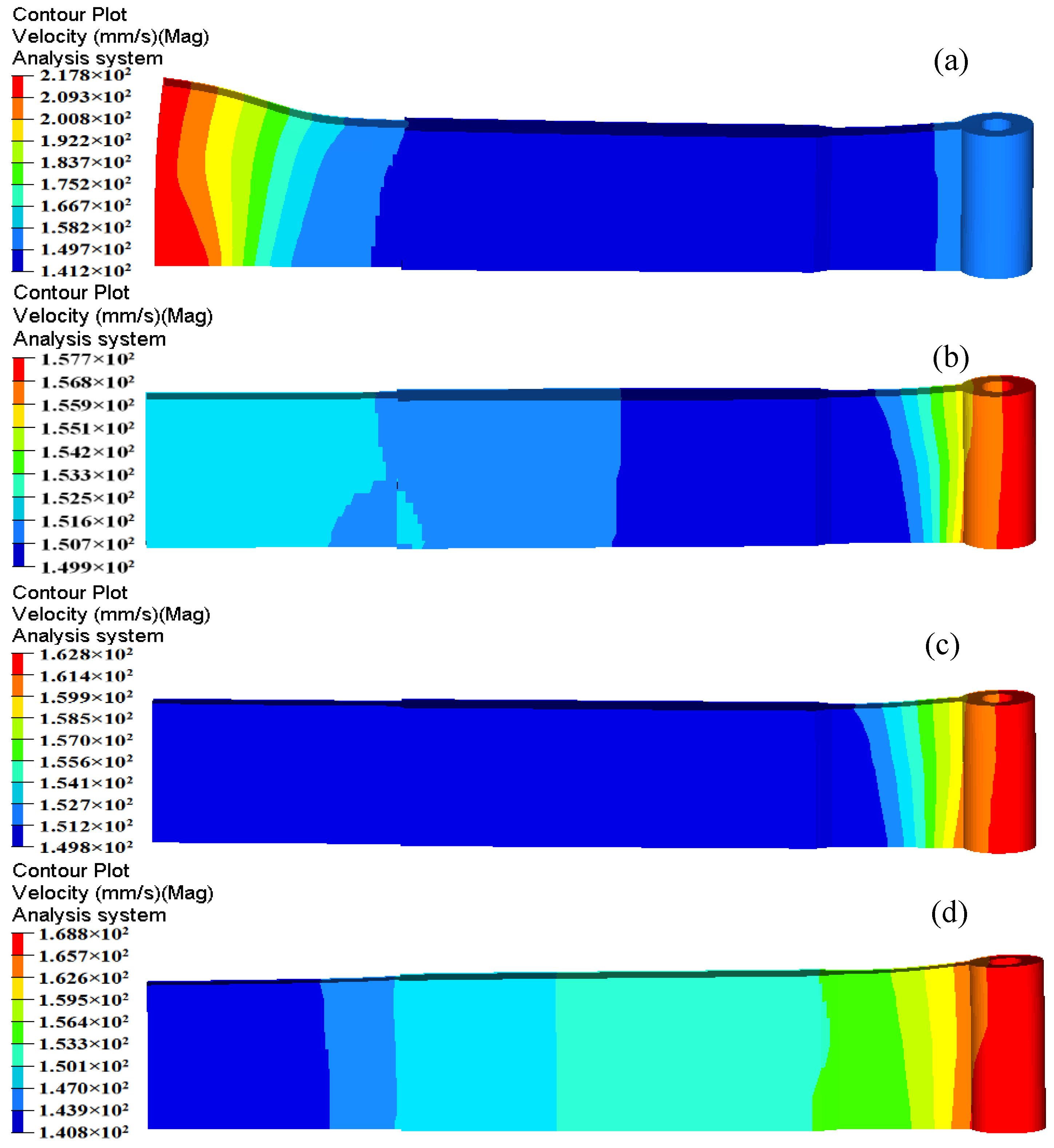
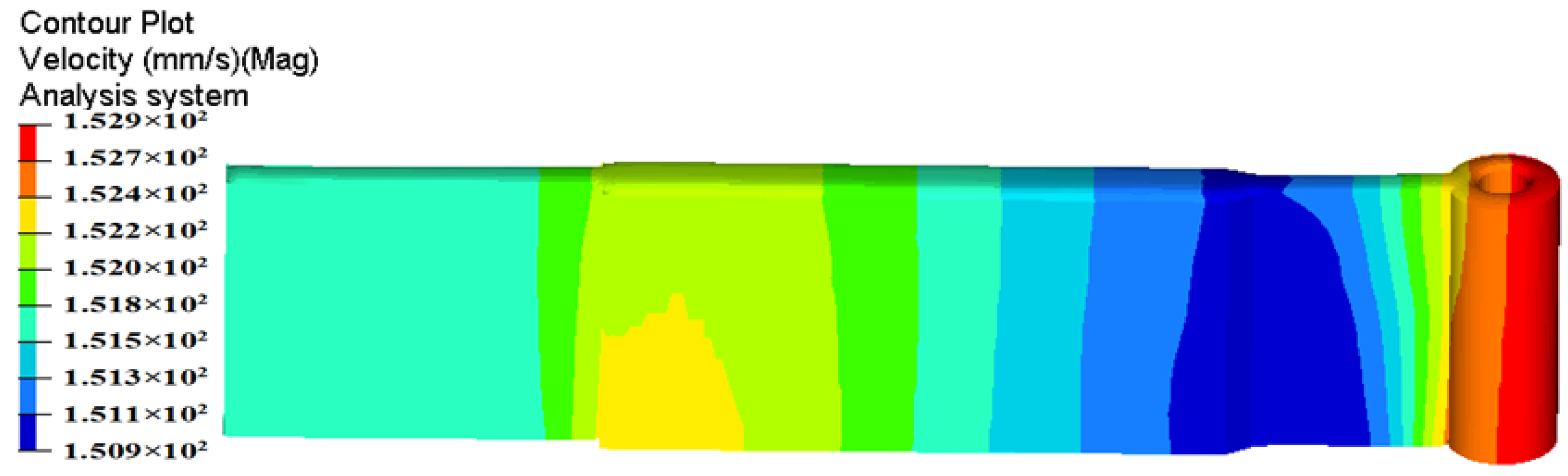
4.2. Second Step: Introducing the Baffle Plates
4.3. Third Step: Adjusting the Die Bearings
5. Comparison between the Initial and Optimal Porthole Dies
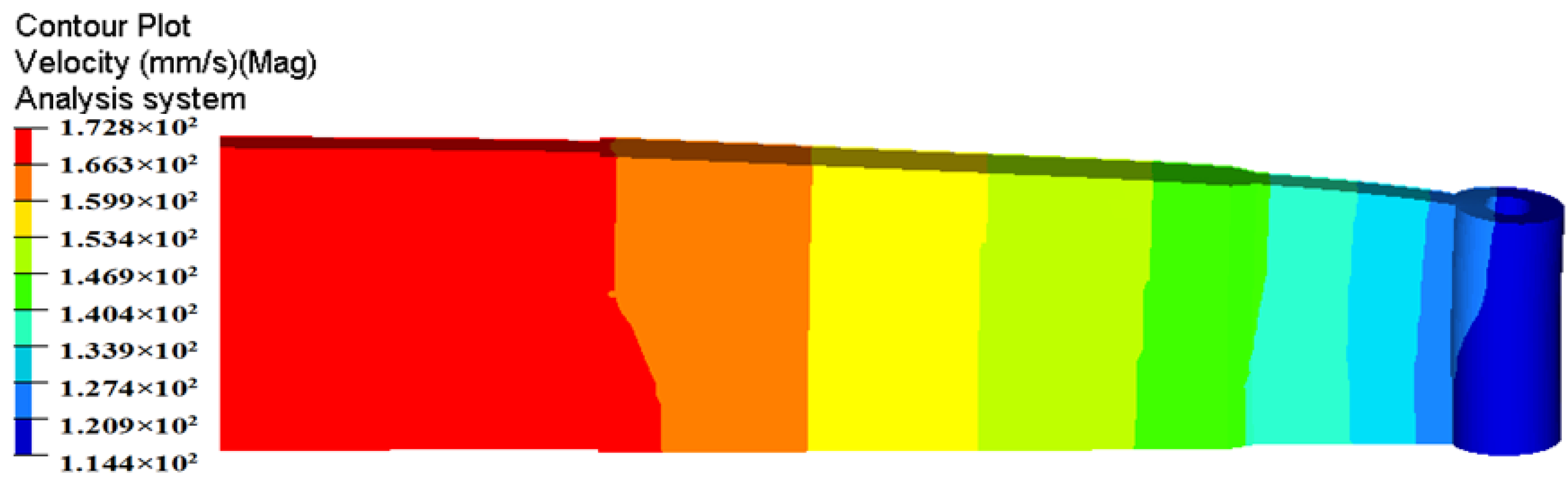
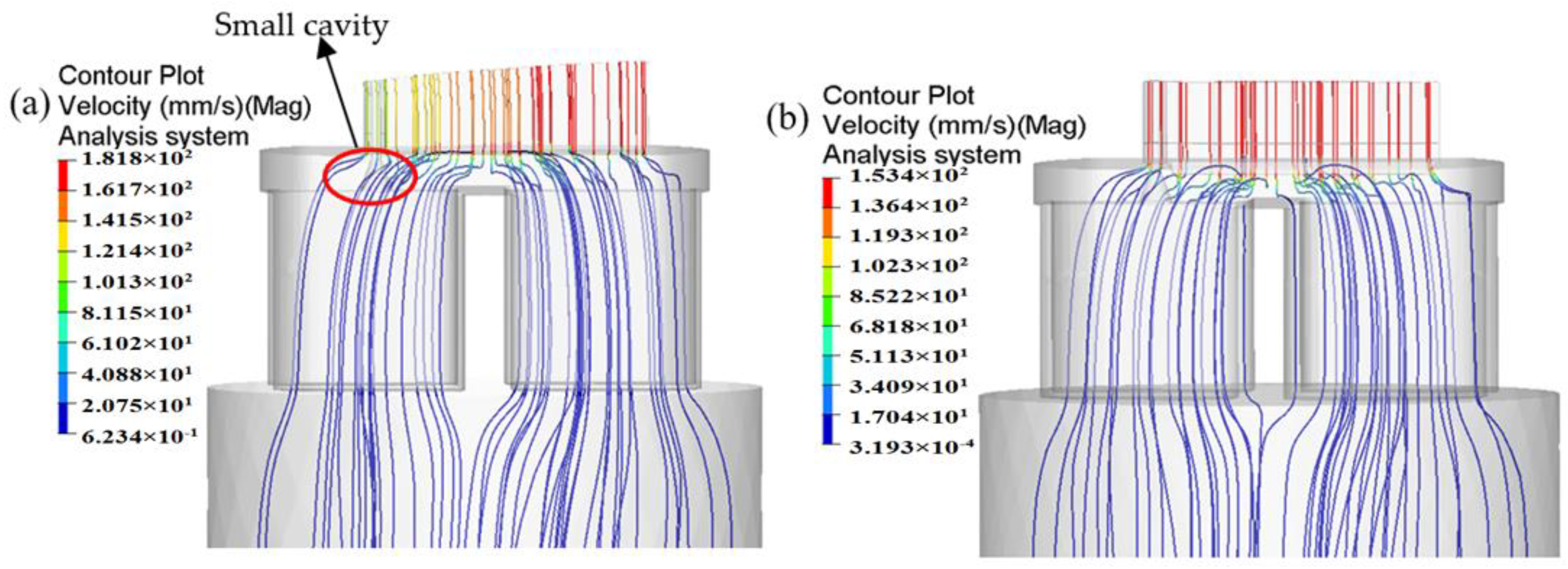
5.1. Metal Flow Pattern
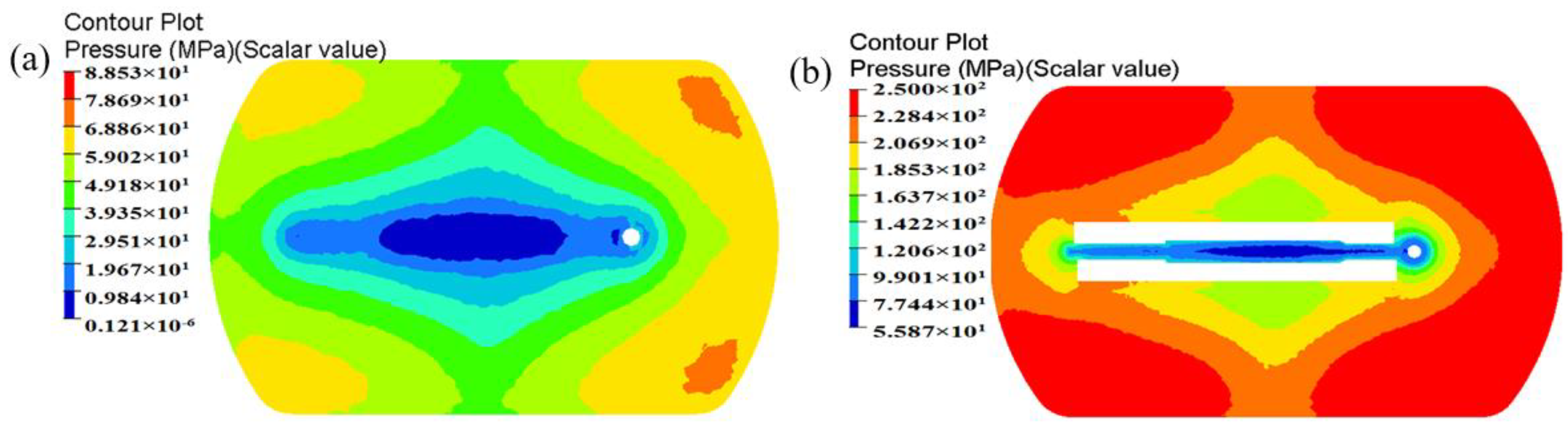
5.2. Welding Pressure
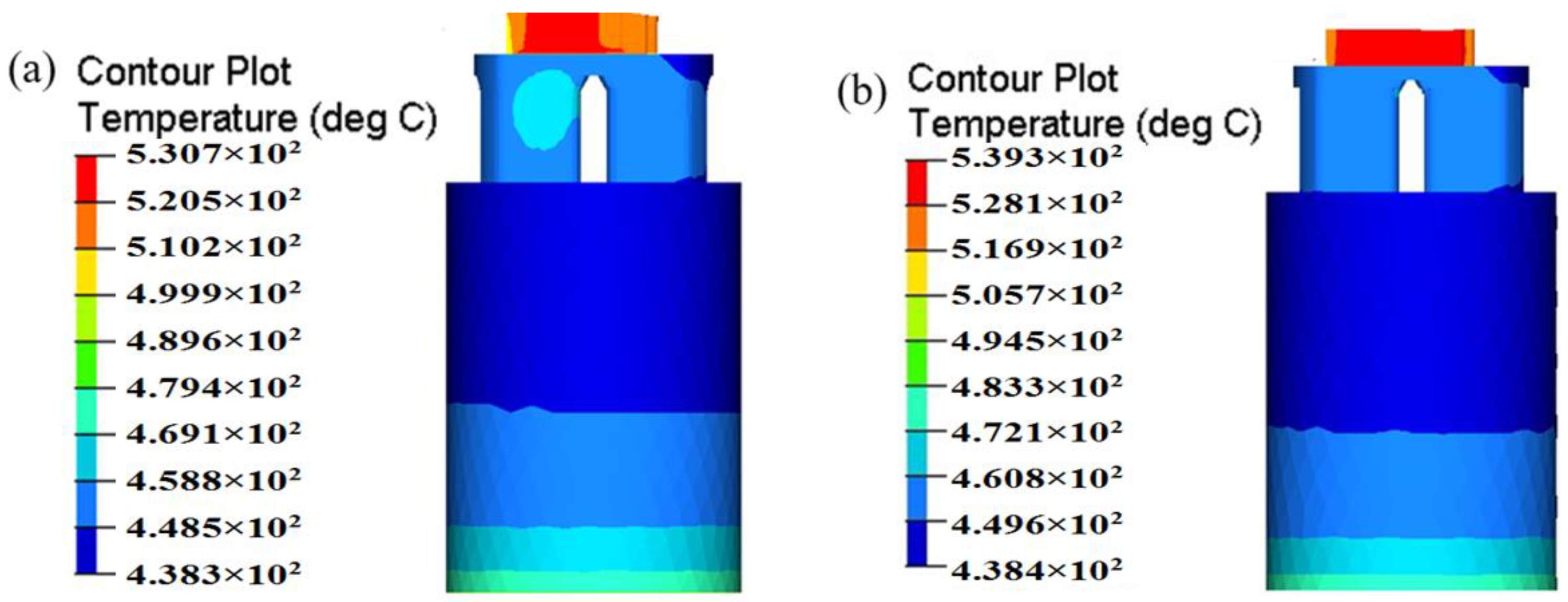
5.3. Temperature Distribution
5.4. Extrusion Load
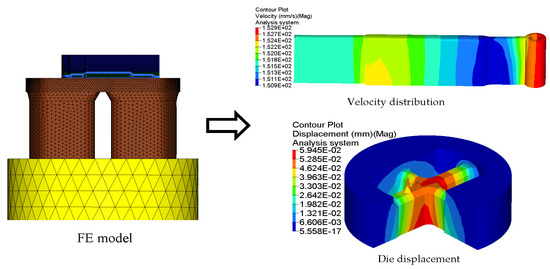
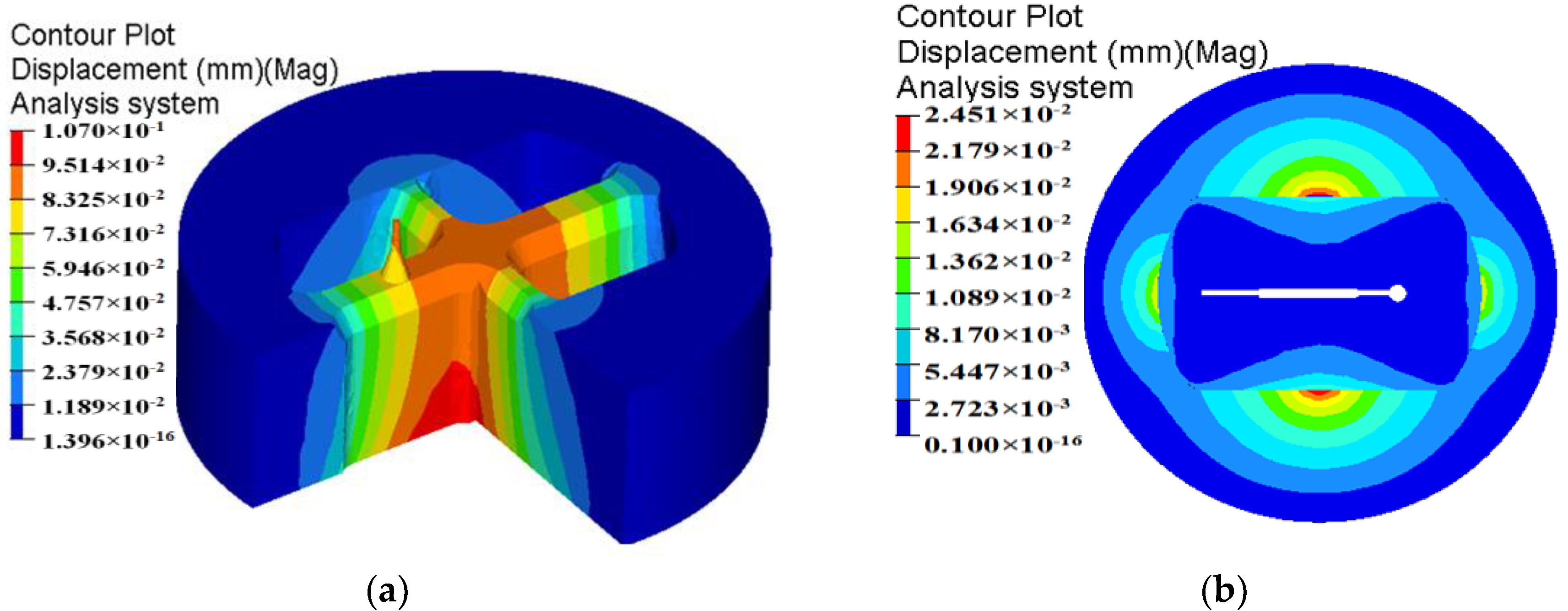
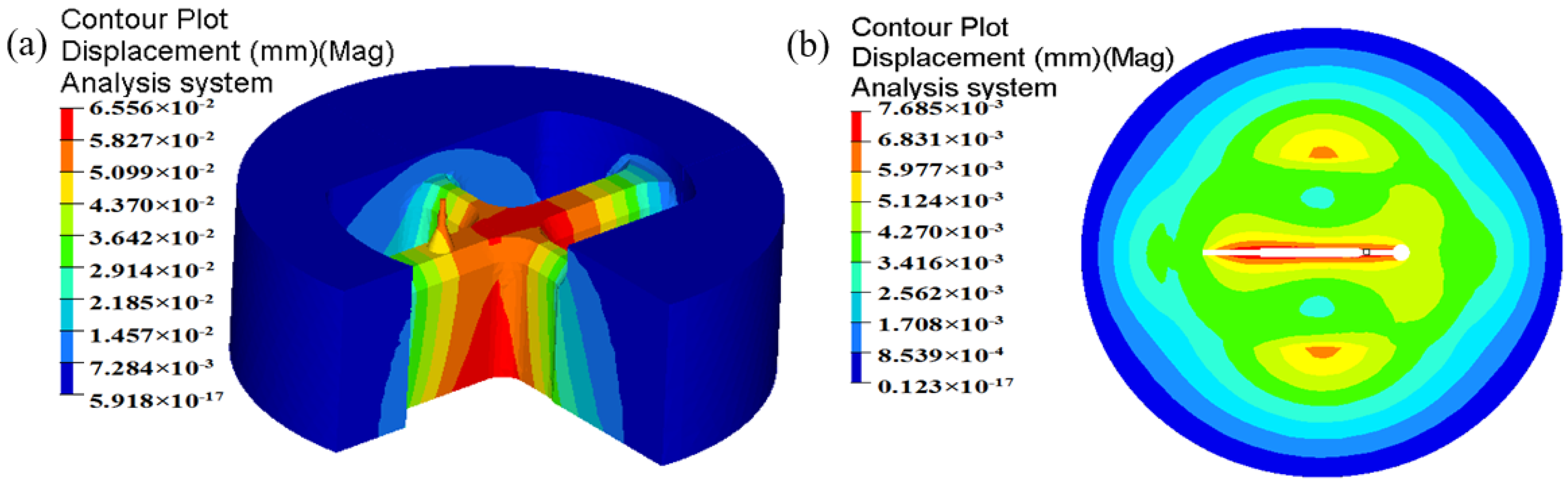
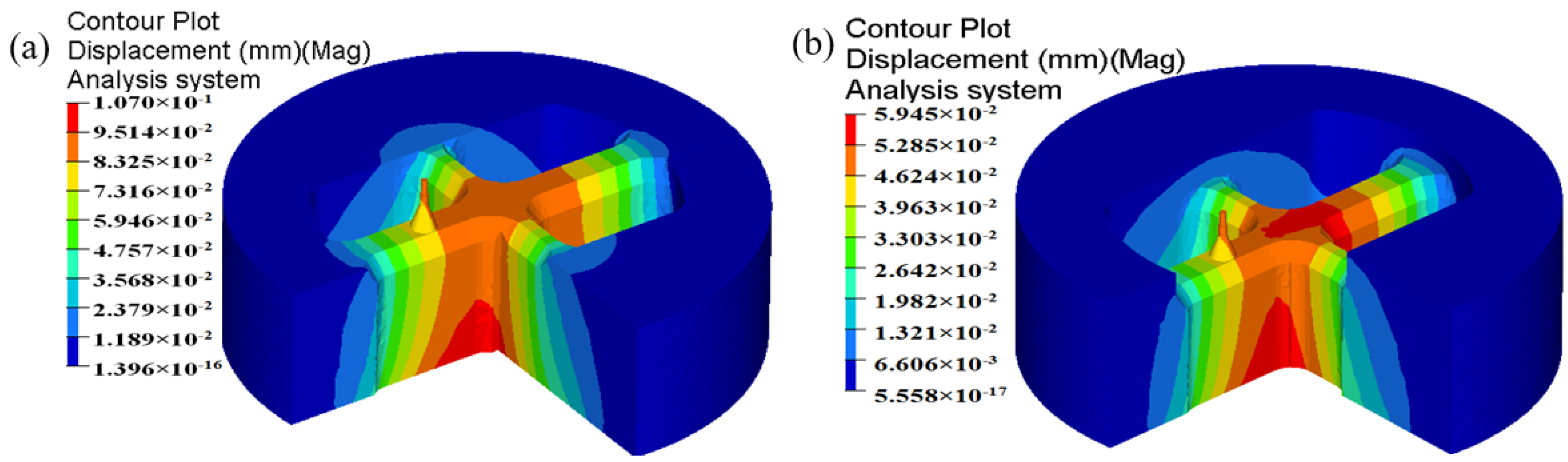
5.5. Die Displacement
6. Experimental Verification
7. Conclusions
- The metal flow behavior in the porthole die at different stages of extrusion process for the initial die scheme is severely not uniform. The SDV at the die exit is 19.63 mm/s. The maximum displacement in the upper die and mandrel are 0.107 and 0.0925 mm, respectively.
- By three steps of die structure modifications, the SDV at the die exit is reduced to 0.448 mm/s. The distortion of the profile is avoided effectively. The mean welding pressure in the welding zones for the optimal die is 197.3 MPa, being 331.72% higher than that of the initial die. The maximum temperature of extrudate at the die exit for the optimal die is 539.3 °C, being 8.6 °C higher than that of the initial die. The maximum displacement in the upper die is decreased from 0.107 to 0.0656 mm, and the mandrel deflection is decreased from 0.0925 to 0.04648 mm.
- The good agreement between the simulation and experimental results shows the modification strategy of porthole die based ALE formulation is practicable and it can provide theoretical guidance for porthole die design of any other similar profiles.
- A design route of porthole die for aluminum profile with a small mandrel is proposed, including sunken port bridges to design the welding chamber in the upper die, increasing the inlet angle of portholes, adding the baffle plates, and adjusting the die bearings.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, Z.; Li, L.; YI, J.; Li, S.; Wang, Z.; Wang, G. Influence of heat treatment conditions on bending characteristics of 6063 aluminum alloy sheets. Trans. Nonferr. Met. Soc. China 2017, 27, 1498–1506. [Google Scholar] [CrossRef]
- Bingöl, S.; Bozacı, A. Experimental and numerical study on the strength of aluminum extrusion welding. Materials 2015, 8, 4389–4399. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhao, G.; Yu, J.; Zhang, W.; Wu, T. Analysis and porthole die design for a multi-hole extrusion process of a hollow, thin-walled aluminum profile. Int. J. Adv. Manuf. Technol. 2014, 74, 383–392. [Google Scholar] [CrossRef]
- Wang, S.T.; Rong, S.L.; Li, H.Y.; Chen, C.H. Optimal die design for three-dimensional porthole extrusion using the Taguchi method. Proc. Inst. Mech. Eng. B J. Eng. 2006, 220, 1005–1009. [Google Scholar] [CrossRef]
- Huang, D.N.; Zhang, Z.H.; Li, J.Y.; Xie, J.X. FEM Analysis of metal flowing behaviors in porthole die extrusion based on the mesh reconstruction technology of the welding process. Int. J. Min. Met. Mater. 2010, 17, 763–769. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Yi, J.; Li, S.; Wang, G. Influence of extrusion speed on the seam weld quality in the porthole die extrusion of AZ31 magnesium alloy tube. Int. J. Adv. Manuf. Technol. 2017, 92, 1039–1052. [Google Scholar] [CrossRef]
- Jo, H.H.; Lee, S.K.; Jung, C.S.; Kim, B.M. A non-steady state FE analysis of Al tubes hot extrusion by a porthole die. J. Mater. Process. Technol. 2006, 173, 223–231. [Google Scholar] [CrossRef]
- Lee, S.K.; Kim, B.M.; Kang, C.G. Effects of chamber shapes of porthole die on elastic deformation and extrusion process in condenser tube extrusion. Mater. Des. 2005, 26, 327–336. [Google Scholar] [CrossRef]
- Donati, L.; Tomesani, L. The effect of die design on the production and seam weld quality of extruded aluminum profiles. J. Mater. Process. Technol. 2005, 164–165, 1025–1031. [Google Scholar] [CrossRef]
- Liu, P.; Xie, S.; Cheng, L. Die structure optimization for a large, multi-cavity aluminum profile using numerical simulation and experiments. Mater. Des. 2012, 36, 152–160. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, G.; Chen, Z.; Chen, H.; Kou, F. Effect of extrusion stem speed on extrusion process for a hollow aluminum profile. Mater. Sci. Eng. B 2012, 177, 1691–1697. [Google Scholar] [CrossRef]
- Sun, X.; Zhao, G.; Zhang, C.; Guan, Y.; Gao, A. Optimal design of second-step welding chamber for a condenser tube extrusion die based on the response surface method and the genetic algorithm. Mater. Manuf. Process. 2013, 28, 823–834. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, G.; Sun, X.; Chen, H.; Gao, B. Optimization design of baffle plates in porthole die for aluminium profile extrusion. Proc. Inst. Mech. Eng. B J. Eng. 2011, 225, 255–265. [Google Scholar] [CrossRef]
- Xue, X.; Vincze, G.; Pereira, A.B.; Pan, J.; Liao, J. Assessment of metal flow balance in multi-output porthole hot extrusion of AA6060 thin-walled profile. Metals 2018, 8, 462. [Google Scholar] [CrossRef]
- Gagliardi, F.; Ciancio, C.; Ambrogio, G. Optimization of porthole die extrusion by Grey-Taguchi relational analysis. Int. J. Adv. Manuf. Technol. 2018, 94, 719–728. [Google Scholar] [CrossRef]
- Ji, H.; Nie, H.; Chen, W.; Ruan, X.; Pan, P.; Zhang, J. Optimization of the extrusion die and microstructure analysis for a hollow aluminum alloy profile. Int. J. Adv. Manuf. Technol. 2017, 93, 3461–3471. [Google Scholar] [CrossRef]
- Koopman, A.J.; Geijselaers, H.J.M.; Huétink, J. Flow front tracking in ALE/Eulerian formulation FEM simulations of aluminium extrusion. Key Eng. Mater. 2017, 367, 39–46. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, I.K.; Jeong, M.S.; Ko, D.C.; Kim, B.M.; Lee, S.K. Development of Porthole Extrusion Die for Improving Welding Pressure in Welding Chamber by Using Numerical Analysis. Trans. Mater. Process. 2017, 26, 115–120. [Google Scholar] [CrossRef]
- Zhou, J.; Li, L.; Duszczyk, J. 3D FEM simulation of the whole cycle of aluminium extrusion throughout the transient state and the steady state using the updated Lagrangian approach. J. Mater. Process. Technol. 2003, 134, 383–387. [Google Scholar] [CrossRef]
- Lou, S.M.; Zhao, G.Q.; Wang, R.; Wu, X. Modeling of aluminum alloy profile extrusion process using finite volume method. J. Mater. Process. Technol. 2008, 206, 481–490. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, G.; Chen, H.; Guan, Y.; Kou, F. Numerical simulation and metal flow analysis of hot extrusion process for a complex hollow aluminum profile. Int. J. Adv. Manuf. Technol. 2012, 60, 101–110. [Google Scholar] [CrossRef]
- He, Z.; Wang, H.; Wang, M.; Li, G. Simulation of extrusion process of complicated aluminium profile and die trial. Trans. Nonferr. Met. Soc. China 2012, 22, 1732–1737. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, G.; Guan, Y.; Gao, A.; Wang, L.; Li, P. Virtual tryout and optimization of the extrusion die for an aluminum profile with complex cross-sections. Int. J. Adv. Manuf. Technol. 2015, 78, 927–937. [Google Scholar] [CrossRef]
- Ranganatha, S.; Kailas, S.V.; Storen, S.; Srivatsan, T.S. Role of temperature on sliding response of aluminum on steel of a hot extrusion. Mater. Manuf. Process. 2007, 23, 29–36. [Google Scholar] [CrossRef]
- Sheppard, T.; Niu, L.; Velay, X. Investigation of metal flow in bridge die extrusion of alloy 6063 and subsequent effect on surface quality and weld seam integrity. Mater. Sci. Technol. 2013, 29, 60–68. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, J.; Duszczyk, J. FE analysis of metal flow and weld seam formation in a porthole die during the extrusion of a magnesium alloy into a square tube and the effect of ram speed on weld strength. J. Mater. Process. Technol. 2008, 200, 185–198. [Google Scholar] [CrossRef]
- Akaret, R. Extrusion Welds Quality Aspects are Now Center Stage. In Proceedings of the 5th International Aluminum Extrusion Technology, ET’92, Chicago, IL, USA, 22–24 May 1992. [Google Scholar]
- Donati, L.; Tomesani, L. The prediction of seam welds quality in aluminum extrusion. J. Mater. Process. Technol. 2004, 53, 366–373. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, G.; Chen, L. Analysis of longitudinal weld seam defects and investigation of solid-state bonding criteria in porthole die extrusion process of aluminum alloy profiles. J. Mater. Process. Technol. 2016, 237, 31–47. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, J.M.; Jo, H.H.; Jo, H.; Kim, B.M. Process analysis and die design in 12 cells condenser tube extrusion of Al3003. J. Mater. Process. Technol. 2008, 201, 53–59. [Google Scholar] [CrossRef]
- Li, L.; Zhang, H.; Zhou, J.; Duszczyk, J. Numerical and experimental study on the extrusion through a porthole die to produce a hollow magnesium profile with longitudinal weld seams. Mater. Des. 2008, 29, 1190–1198. [Google Scholar] [CrossRef]
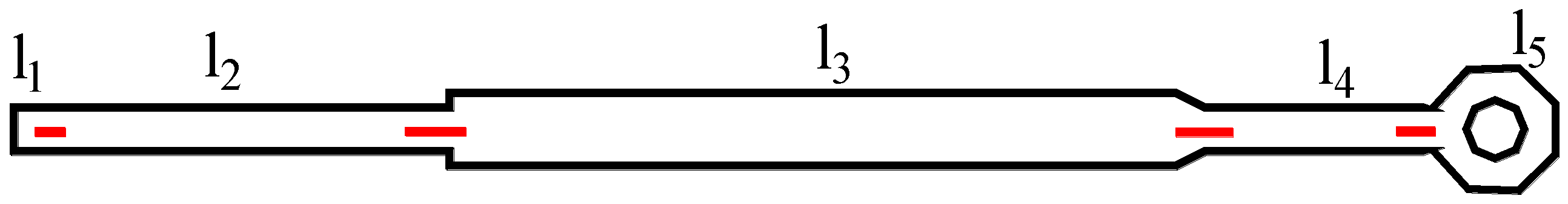



| Physical Properties | AA6063 Aluminum Alloy | AISI H13 Steel |
|---|---|---|
| Density (Kg/m3) | 2700 | 7870 |
| Young’s modulus (MPa) | 68,900 | 210,000 |
| Poisson’s ratio | 0.3 | 0.33 |
| Thermal conductivity (W/(m·K)) | 198 | 24.3 |
| Specific heat (J/(kg·K)) | 900 | 460 |
| Thermal expansion coefficient (1/K) | 1.0 × 10–5 | - |
| Conditions | Values |
|---|---|
| Billet diameter (mm) | 210 |
| Billet length (mm) | 350 |
| Extrusion ratio | 75.8 |
| Extrusion speed (mm/s) | 2 |
| Billet temperature (°C) | 480 |
| Container and die temperature (°C) | 430 |
| Friction coefficient at billet/container and die | Sticking |
| Friction coefficient at billet/die bearing | 0.3 |
| Heat thermal coefficient between billet/container and die (W/(m2·°C)) | 3000 |
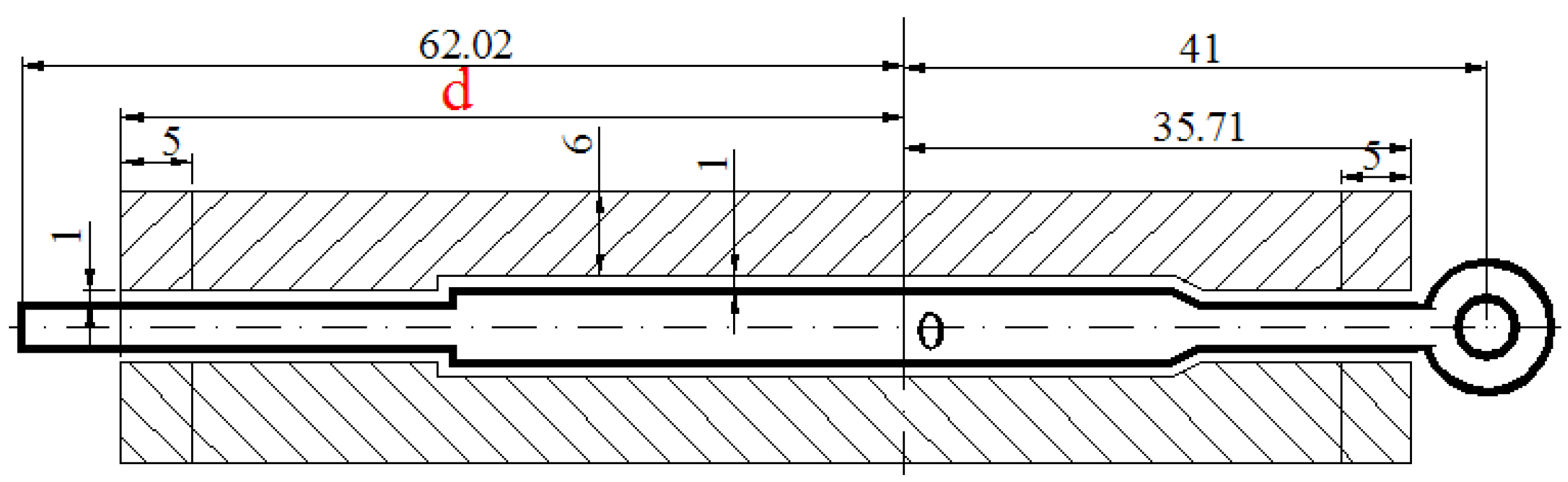
| Design Schemes of Baffle Plates | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Length of d (mm) | 55 | 57.5 | 60 | 65 |
| Max. velocity (mm/s) | 217.8 | 157.7 | 162.8 | 168.8 |
| Min. velocity (mm/s) | 141.2 | 149.9 | 149.8 | 140.8 |
| SDV | 16.266 | 1.892 | 3.656 | 8.825 |
| Displacement of profiles (mm) | 6.657 | 0.927 | 1.499 | 3.318 |
| Position | l1 | l2 | l3 | l4 | l5 |
|---|---|---|---|---|---|
| Initial design (mm) | 2 | 4 | 6.4 | 4.3 | 2.8 |
| Optimal design (mm) | 2.75 | 4.06 | 6.35 | 4.18 | 3.32 |
| Design Schemes | Initial Design | Modification Scheme 1 | Modification Scheme 2 | Modification Scheme 3 |
|---|---|---|---|---|
| Extrusion load (KN) | 10,617.3 | 10,140.6 | 13,718.4 | 13,903.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Li, L.; Li, S.; Yi, J.; Wang, G. Simulation Analysis of Porthole Die Extrusion Process and Die Structure Modifications for an Aluminum Profile with High Length–Width Ratio and Small Cavity. Materials 2018, 11, 1517. https://doi.org/10.3390/ma11091517
Liu Z, Li L, Li S, Yi J, Wang G. Simulation Analysis of Porthole Die Extrusion Process and Die Structure Modifications for an Aluminum Profile with High Length–Width Ratio and Small Cavity. Materials. 2018; 11(9):1517. https://doi.org/10.3390/ma11091517
Chicago/Turabian StyleLiu, Zhiwen, Luoxing Li, Shikang Li, Jie Yi, and Guan Wang. 2018. "Simulation Analysis of Porthole Die Extrusion Process and Die Structure Modifications for an Aluminum Profile with High Length–Width Ratio and Small Cavity" Materials 11, no. 9: 1517. https://doi.org/10.3390/ma11091517
APA StyleLiu, Z., Li, L., Li, S., Yi, J., & Wang, G. (2018). Simulation Analysis of Porthole Die Extrusion Process and Die Structure Modifications for an Aluminum Profile with High Length–Width Ratio and Small Cavity. Materials, 11(9), 1517. https://doi.org/10.3390/ma11091517