Precipitation Characteristics of the Metastable γ″ Phase in a Cu-Ni-Be Alloy
Abstract
:1. Introduction
2. Materials and Methods
3. Results
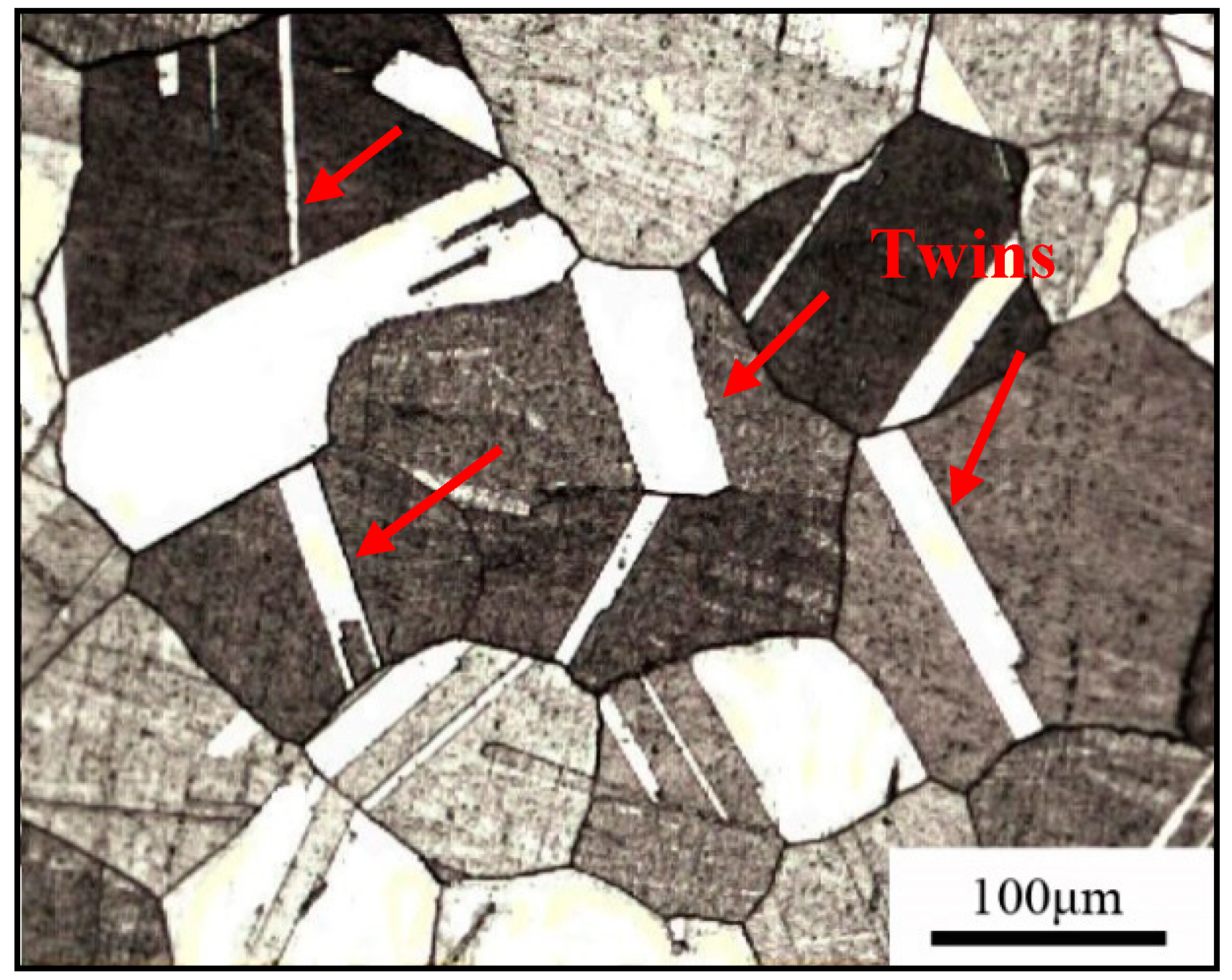
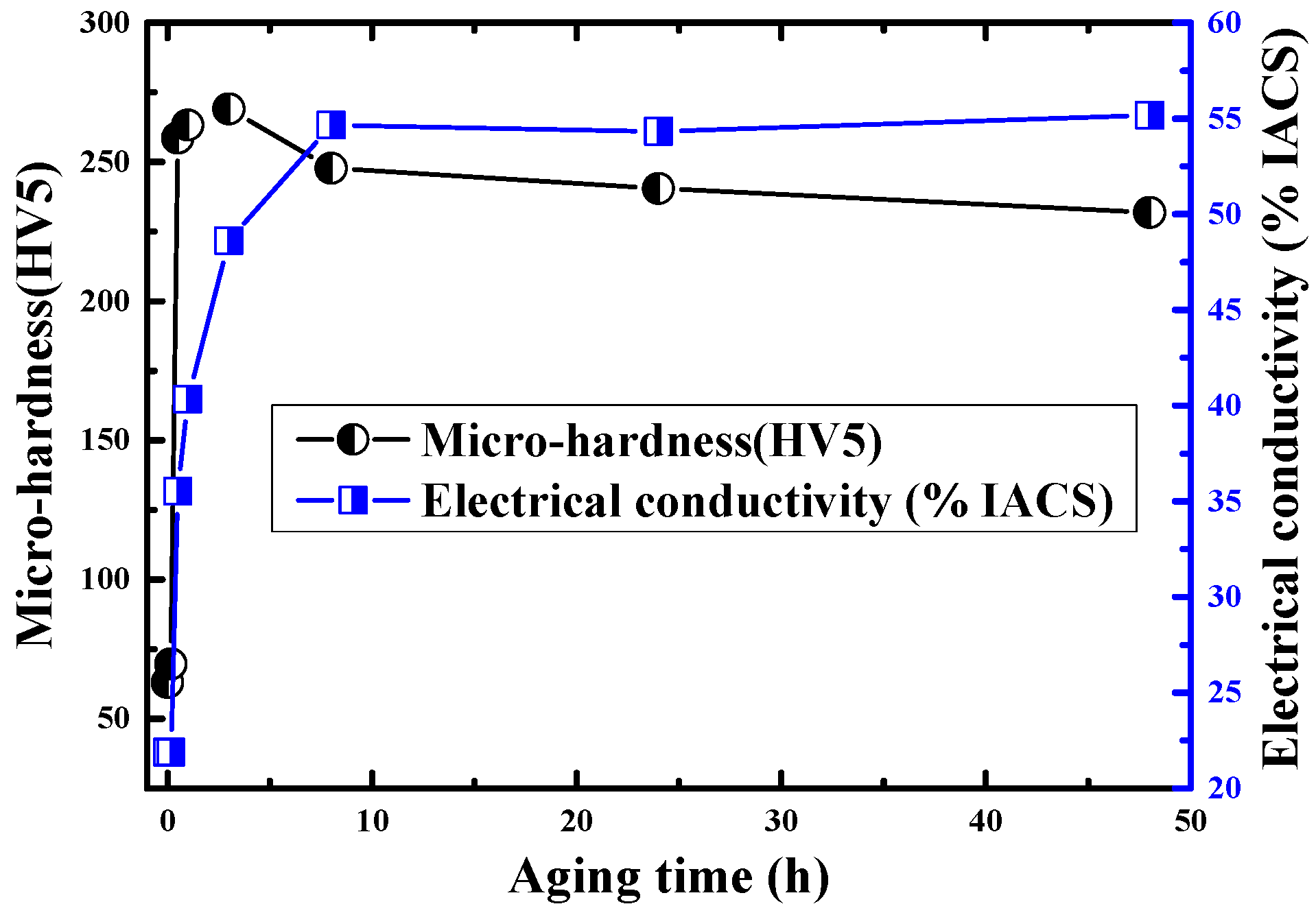
3.1. Metallographic Structure and Performance Analysis
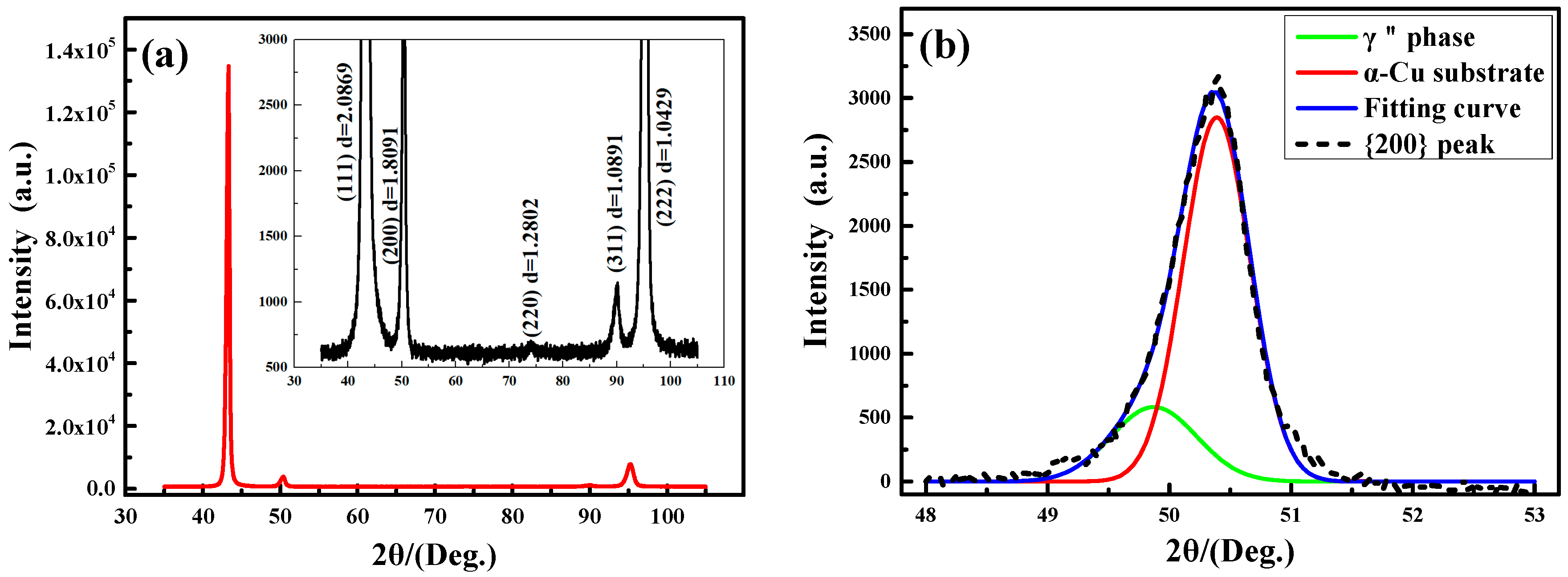
3.2. X-ray Diffraction Analysis
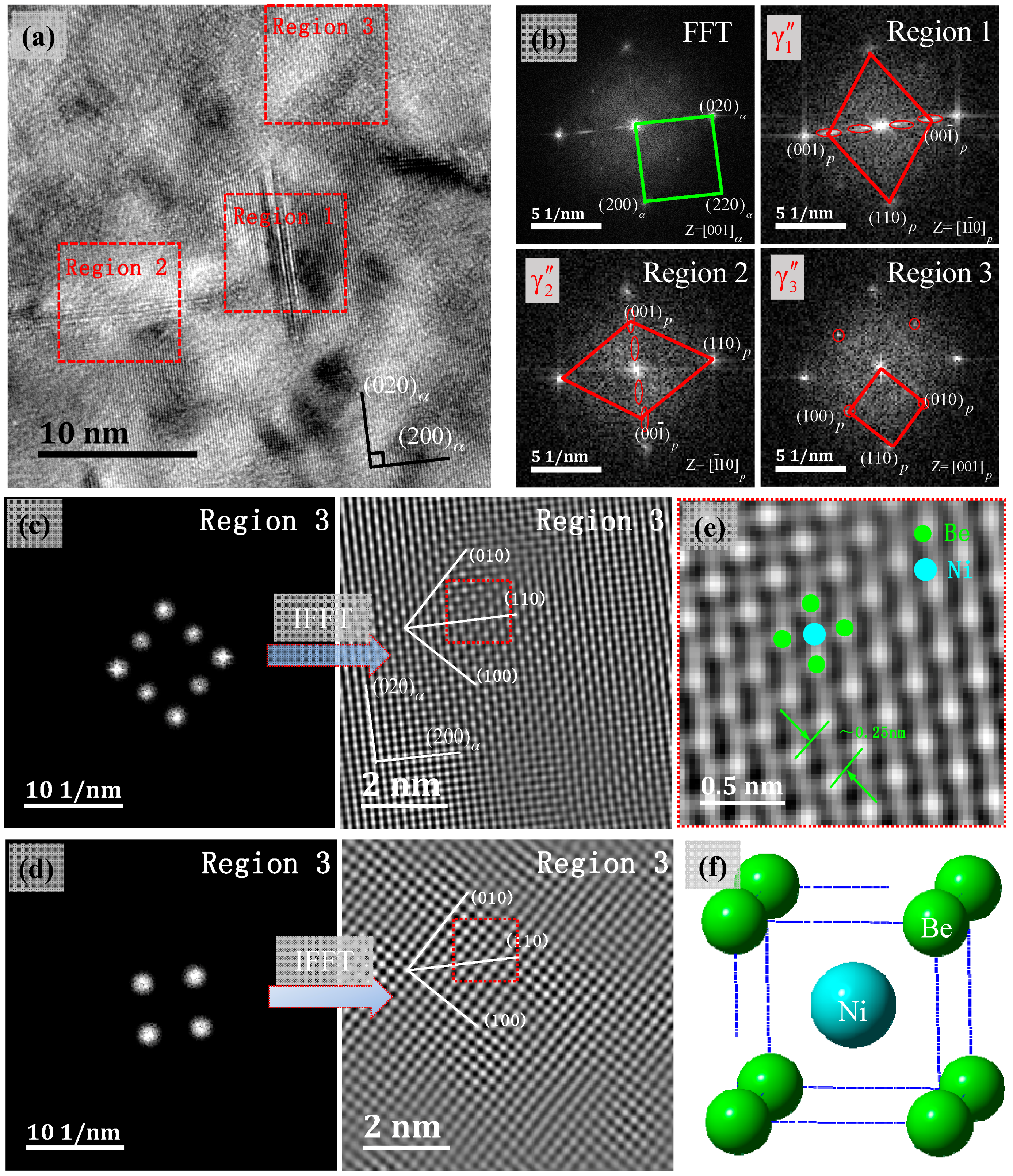
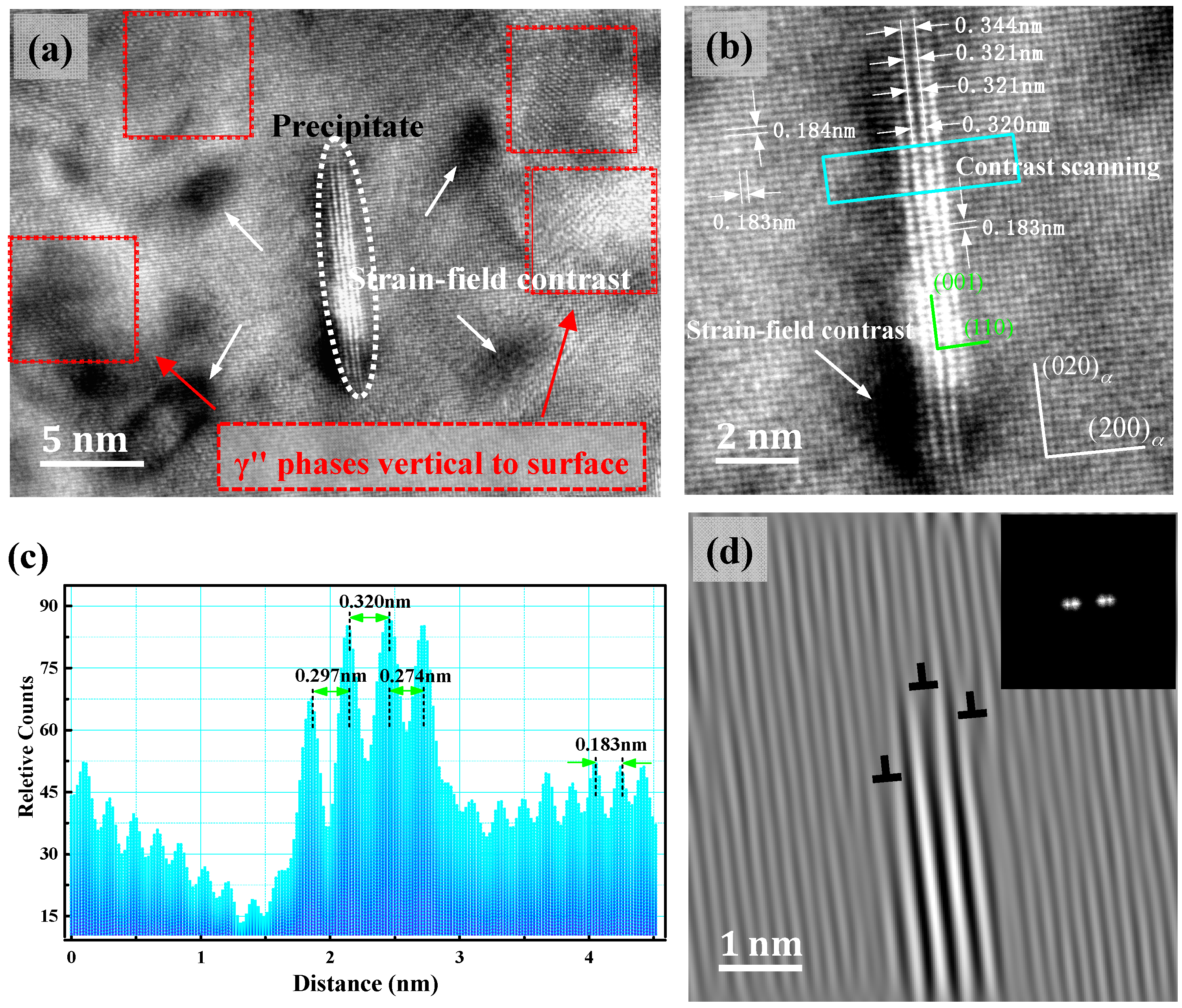
3.3. Precipitated Phase TEM and SADP Analysis
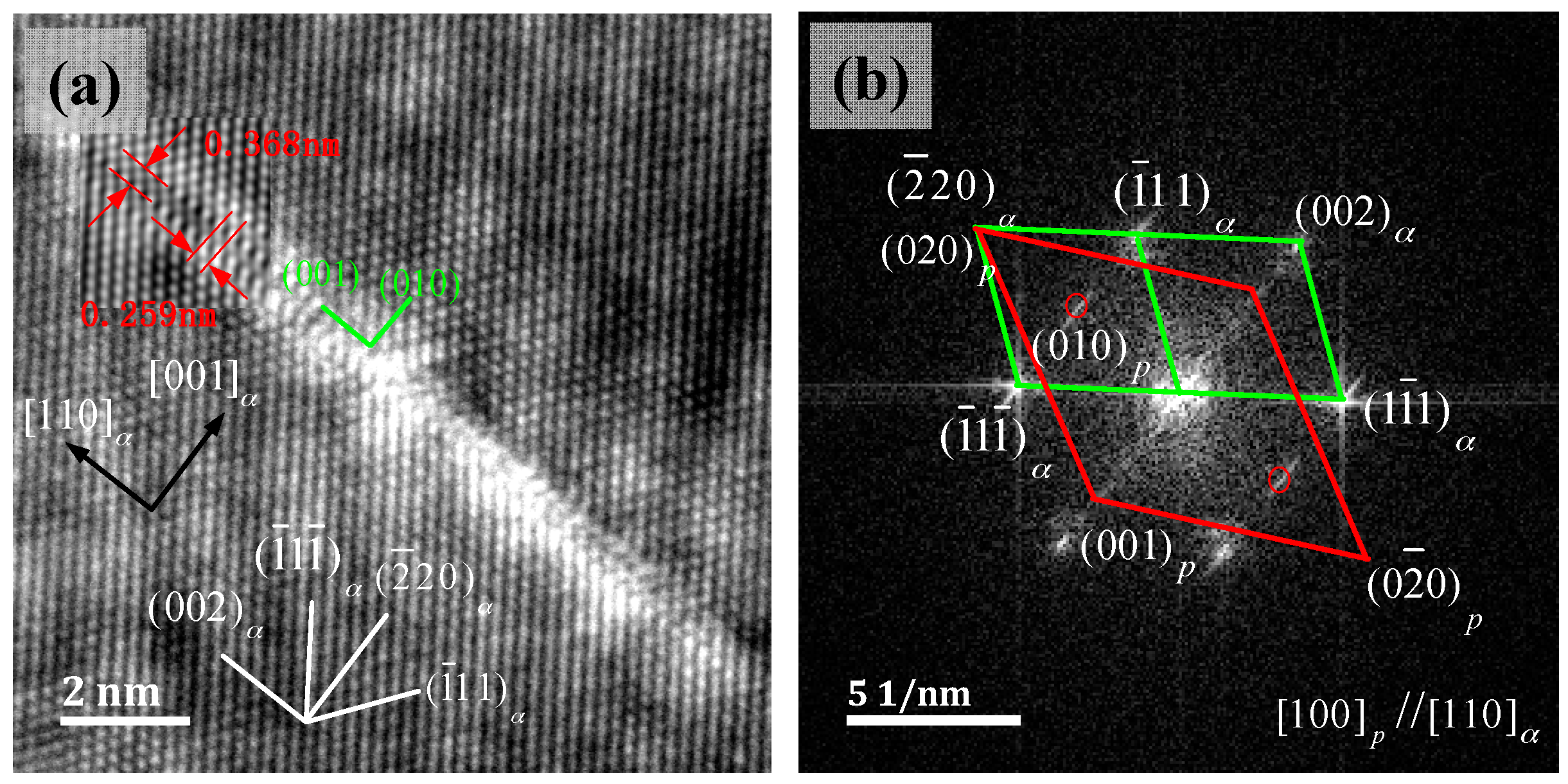
3.4. γ″ Phase HRTEM Structure Analysis
4. Analysis and Discussion
5. Conclusions
- The metastable γ″ phase lattice constants in the present research is a = b = 0.259 ± 0.002 nm, with d(001)p changes in the range of 0.27–0.32 nm. A (001)p diffuse scattering diffraction spot in the reciprocal space is the long trip shape, and with the increase of the metastable phase size, with d(001)P tending to a stable value. Long strip diffraction spots will shrink to a dotted contrast.
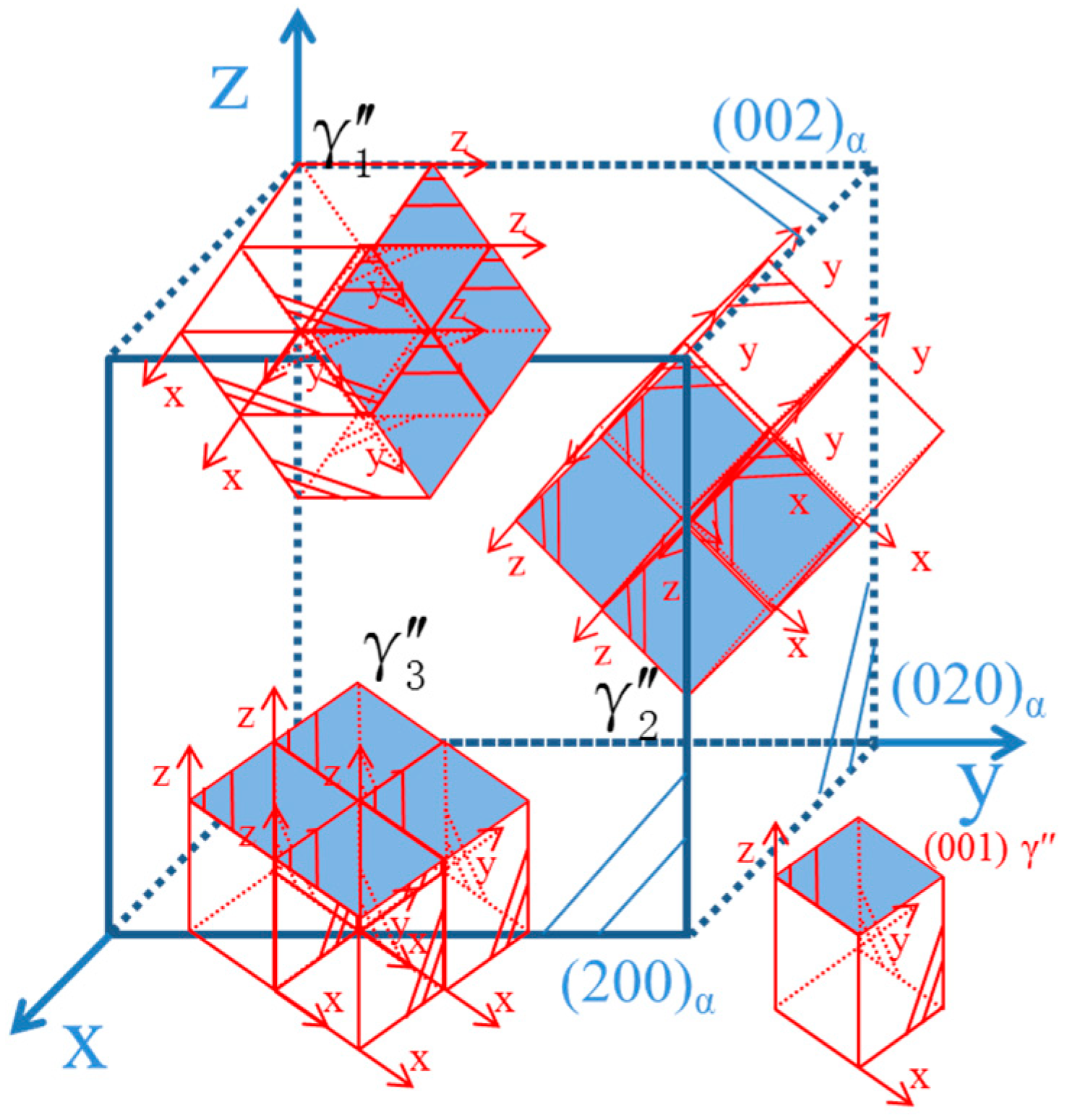
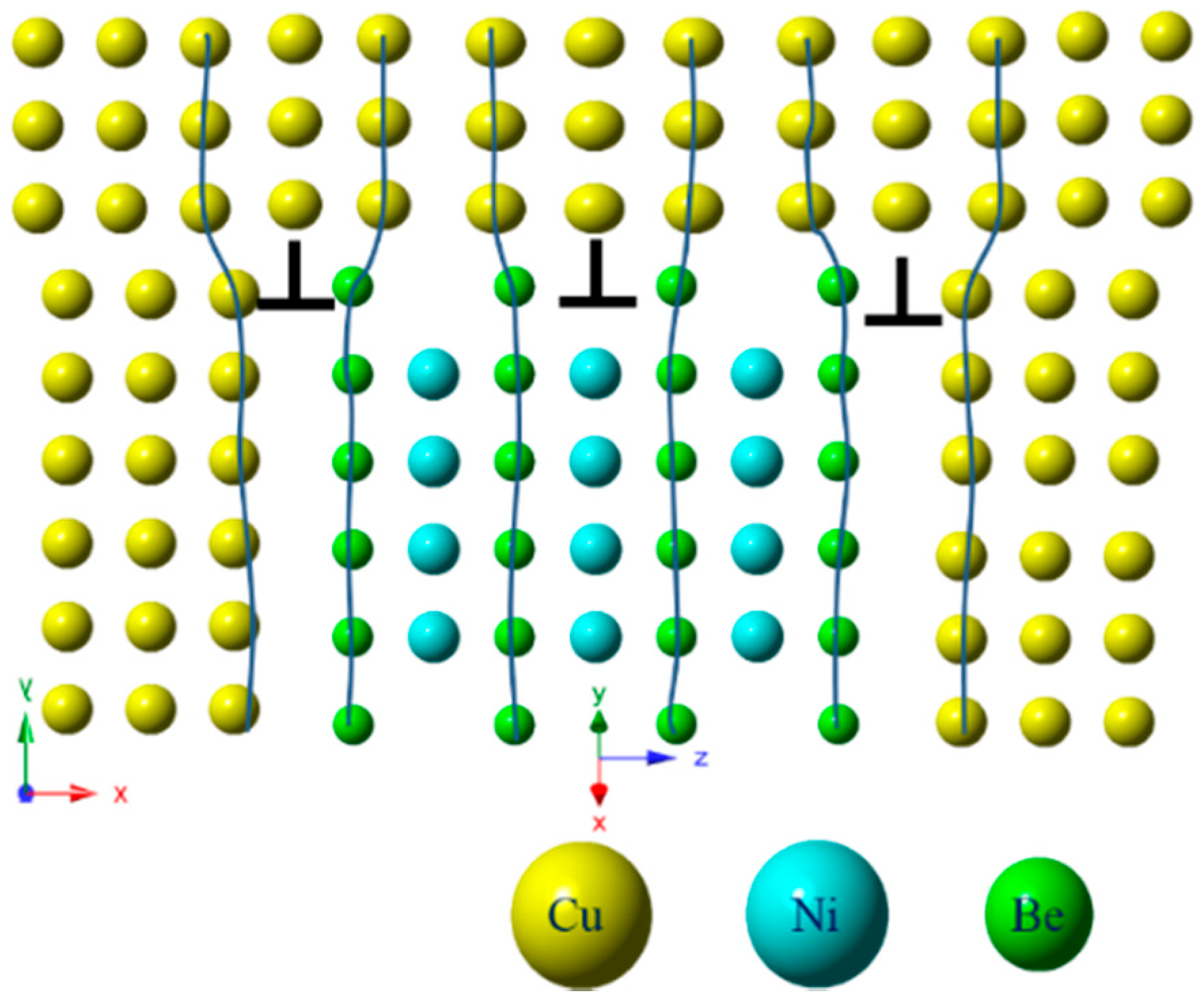
- The orientation relationship between the γ″ phase and the α-Cu matrix is: , which is known as the Bain relation in the FCC/BCC structure. The Habit plane is {001}α. [001]α under the condition of incidence, and there are three forms of the precipitate phase in the matrix, and it is a disc shape. They distribute vertically with each other in the Cu matrix three-dimensional space. Interface mismatches will promote the precipitated phase to form an optimal structure. The γ″ phase prefers to grow along the [110]p direction.
- The Cu-Be and Cu-Ni-Be precipitated phase rule in the alloy precipitation conforms to the interface matching rule of the FCC/BCC structure. In the Cu-Be alloy, along with the aging process, the relationship between the precipitated phase and the matrix transforms from the Bain relationship to N-W, i.e., a habit plane transformation. The Cu-Ni-Be alloy aging precipitation process always maintains the Bain relationship and does not have a habit plane transformation. This depends on the crystallographic constant of the precipitated phase (CuBe, NiBe).
Author Contributions
Funding
Conflicts of Interest
References
- Price, R.J.; Kelly, A. Deformation of age hardened crystals of copper-1.8 wt.% beryllium. Acta Metall. 1963, 11, 915–922. [Google Scholar] [CrossRef]
- Zinkle, S.J. Evaluation of high strength, high conductivity CuNiBe alloys for fusion energy applications. J. Nucl. Mater. 2014, 449, 277–289. [Google Scholar] [CrossRef]
- Kızılaslan, A.; Altınsoy, İ. The mechanism of two-step increase in hardness of precipitation hardened CuCoNiBe alloys and characterization of precipitates. J. Alloy. Compd. 2017, 701, 116–121. [Google Scholar] [CrossRef]
- Tang, Y.; Kang, Y.; Yue, L.; Jiao, X. Mechanical properties optimization of a Cu–Be–Co–Ni alloy by precipitation design. J. Alloy. Compd. 2017, 695, 613–625. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Song, K.X.; Xing, J.D.; Zhang, Y.M. Precipitation behavior and properties of aged Cu-0.23Be-0.84Co alloy. J. Alloy. Compd. 2015, 658, 920–930. [Google Scholar] [CrossRef]
- Yamamoto, S.; Matsui, M.; Murakami, Y. Electron microscopic observation on the precipitation sequence in Cu-Be alloys. Trans. JIM 1971, 12, 159–165. [Google Scholar] [CrossRef]
- Bonfield, W.; Edwards, B.C. Precipitation hardening in Cu 1.81 wt.% Be 0.28 wt.% Co. J. Mater. Sci. 1974, 9, 398–408. [Google Scholar] [CrossRef]
- Rioja, R.J.; Laughlin, D.E. The sequence of precipitation in Cu-2% Be alloys. Acta Metall. 1980, 28, 1301–1313. [Google Scholar] [CrossRef]
- Rotem, A.; Shechtman, D.; Rosen, A. Correlation among microstructure, strength, and electrical conductivity of Cu-Ni-Be alloy. Met. Mater. Trans. A 1988, 19, 2279–2285. [Google Scholar] [CrossRef]
- Yagmur, L.; Duygulu, O.; Aydemir, B. Investigation of metastable γ′ precipitate using HRTEM in aged Cu–Be alloy. Met. Meter. Trans. A 2011, 528, 4147–4151. [Google Scholar] [CrossRef]
- Monzen, R.; Seo, T.; Sakai, T.; Watanabe, C. Precipitation processes in a Cu–0.9 mass% Be single crystal. Mater. Trans. 2006, 47, 2925–2934. [Google Scholar] [CrossRef]
- Geisler, A.H.; Mallery, J.H.; Steigert, F.E. On the mechanism of precipitation in copper-beryllium alloys. JOM 1952, 4, 307–316. [Google Scholar] [CrossRef]
- Watanabe, C.; Monzen, R. Precipitation process in a Cu-Ni-Be alloy. Solid State Phenom. 2011, 172–174, 432–436. [Google Scholar] [CrossRef]
- Khodabakhshi, A.; Abouei, V.; Mortazavi, N.; Razavi, S.H.; Hooshyar, H.; Esmaily, M. Effects of cold working and heat treatment on microstructure and wear behaviour of Cu–Be alloy C17200. Tribol. Mater. Surf. Interfaces 2016, 9, 118–127. [Google Scholar] [CrossRef]
- Watanabe, C. Effect of applied stress on precipitation of Guinier–Preston zones in a Cu–0.9 wt.% Be single crystal. Philos. Mag. Lett. 2005, 85, 603–612. [Google Scholar] [CrossRef]
- Monzen, R.; Okawara, S.; Watanabe, C. Stress-assisted nucleation and growth of γ″ and γ′ precipitates in a Cu–1.2 wt.% Be–0.1 wt.% Co alloy aged at 320 °C. Philos. Mag. 2012, 92, 1826–1843. [Google Scholar] [CrossRef]
- Monzen, R.; Takagawa, Y.; Watanabe, C.; Terada, D.; Tsuji, N. Mechanical properties of precipitation strengthening Cu-base alloys highly deformed by ARB process. Procedia Eng. 2011, 10, 2417–2422. [Google Scholar] [CrossRef]
- Watanabe, C.; Monzen, R.; Ii, S.; Tsuchiya, K. Microstructure and aging behavior of Cu-Be alloy processed by high-pressure torsion. Mater. Sci. Forum 2014, 783–786, 2707–2712. [Google Scholar] [CrossRef]
- Phillips, V.A.; Tanner, L.E. High resolution electron microscope observations on G.P. zones in an aged Cu-1.97wt.% Be crystal. Acta Metall. 1973, 21, 441–448. [Google Scholar] [CrossRef]
- Peng, L.J.; Xiong, B.Q.; Xie, G.L.; Wang, Q.S.; Hong, S.B. Precipitation process and its effects on properties of aging Cu–Ni–Be alloy. Rare Met. 2013, 32, 332–337. [Google Scholar] [CrossRef]
- Shimizu, K.; Mikami, Y.; Mitani, H.; Otsuka, K. Electron microscopy study of the precipitation processes in Cu-2 wt.% Be alloy. Trans. JIM 1971, 12, 206–213. [Google Scholar] [CrossRef]
- Rong, Y.H.; Chen, S.P.; Hu, G.X.; Gao, M.; Wei, R.P. Prediction and characterization of variant electron diffraction patterns for γ″ and δ precipitates in an INCONEL 718 alloy. Metall. Mater. Trans. A 1999, 30, 2297–2303. [Google Scholar] [CrossRef]
- Ota, S.; Muramatsu, N.; Sengoku, K.; Watanabe, C.; Monzen, R. Mechanical and electrical properties and microstructure in Cu-Ni-Be alloys. J. Soc. Mater. Sci. Jpn. 2007, 56, 531–536. [Google Scholar] [CrossRef]
- Anderson, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Monzen, R.; Sakai, T.; Watanabe, C. Metastable precipitates and their misfit strains in a Cu-0.9 wt.% Be Single Crystal. Mater. Sci. Forum 2007, 561, 2297–2300. [Google Scholar] [CrossRef]
- Wilkes, P. Formation of guinier-preston zones in Cu-Be alloys. Acta Metall. 1968, 16, 153–158. [Google Scholar] [CrossRef]
- Almazouzi, A.; Macht, M.; Naundorf, V.V.; Neumann, G. Diffusion of iron and nickel in single-crystalline copper. Phys. Rev. B 1996, 54, 857–863. [Google Scholar] [CrossRef]
- Kelly, P.M.; Zhang, M.X. Edge-to-edge matching—A new approach to the morphology and crystallography of precipitates. Mater. Forum 1999, 23, 41–62. [Google Scholar]
- Zhang, M.X.; Kelly, P.M. Edge-to-edge matching model for predicting orientation relationships and habit planes—The improvements. Scr. Mater. 2005, 52, 963–968. [Google Scholar] [CrossRef]



| Element | Ni | Be | Cu | Impurity |
|---|---|---|---|---|
| Contents (wt.%) | 2.16 | 0.272 | Bal. | ≤0.1 |
| PDF Cards | {111} | Error | {200} | Error | {220} | Error | {311} | Error | {222} | Error |
|---|---|---|---|---|---|---|---|---|---|---|
| PDF#04-0836 | 2.088 | −0.0011 | 1.808 | 0.0011 | 1.278 | 0.0022 | 1.09 | −0.0009 | 1.0436 | −0.0007 |
| PDF#65-9026 | 2.086 | 0.0009 | 1.8065 | 0.0026 | 1.2774 | 0.0028 | 1.0894 | −0.0003 | 1.043 | −0.0001 |
| PDF#65-9743 | 2.083 | 0.0039 | 1.8039 | 0.0052 | 1.2756 | 0.0046 | 1.0878 | 0.0013 | 1.0415 | 0.0014 |
| PDF#70-3038 | 2.0929 | −0.0060 | 1.8125 | −0.0034 | 1.2816 | −0.0014 | 1.093 | −0.0039 | 1.0465 | −0.0026 |
| PDF#70-3039 | 2.086 | 0.0009 | 1.8065 | 0.0026 | 1.2774 | 0.0028 | 1.0894 | −0.0003 | 1.043 | −0.0001 |
| PDF#85-1326 | 2.0871 | −0.0002 | 1.8075 | 0.0016 | 1.2781 | 0.0021 | 1.09 | −0.0009 | 1.0435 | −0.0006 |
| PDF#89-2838 | 2.0872 | −0.0003 | 1.8075 | 0.0016 | 1.2781 | 0.0021 | 1.09 | −0.0009 | 1.0436 | −0.0007 |
| Actual data | 2.0869 | 1.8091 | 1.2802 | 1.0891 | 1.0429 | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Cai, Y.; Sui, Y.; Song, K.; Zhou, Y.; Zou, J. Precipitation Characteristics of the Metastable γ″ Phase in a Cu-Ni-Be Alloy. Materials 2018, 11, 1394. https://doi.org/10.3390/ma11081394
Zhu Z, Cai Y, Sui Y, Song K, Zhou Y, Zou J. Precipitation Characteristics of the Metastable γ″ Phase in a Cu-Ni-Be Alloy. Materials. 2018; 11(8):1394. https://doi.org/10.3390/ma11081394
Chicago/Turabian StyleZhu, Zhiyuan, Yuanfei Cai, Yi Sui, Kexing Song, Yanjun Zhou, and Jiasheng Zou. 2018. "Precipitation Characteristics of the Metastable γ″ Phase in a Cu-Ni-Be Alloy" Materials 11, no. 8: 1394. https://doi.org/10.3390/ma11081394
APA StyleZhu, Z., Cai, Y., Sui, Y., Song, K., Zhou, Y., & Zou, J. (2018). Precipitation Characteristics of the Metastable γ″ Phase in a Cu-Ni-Be Alloy. Materials, 11(8), 1394. https://doi.org/10.3390/ma11081394





