Electromechanical Response of High-Performance Fiber-Reinforced Cementitious Composites Containing Milled Glass Fibers under Tension
Abstract
:1. Introduction
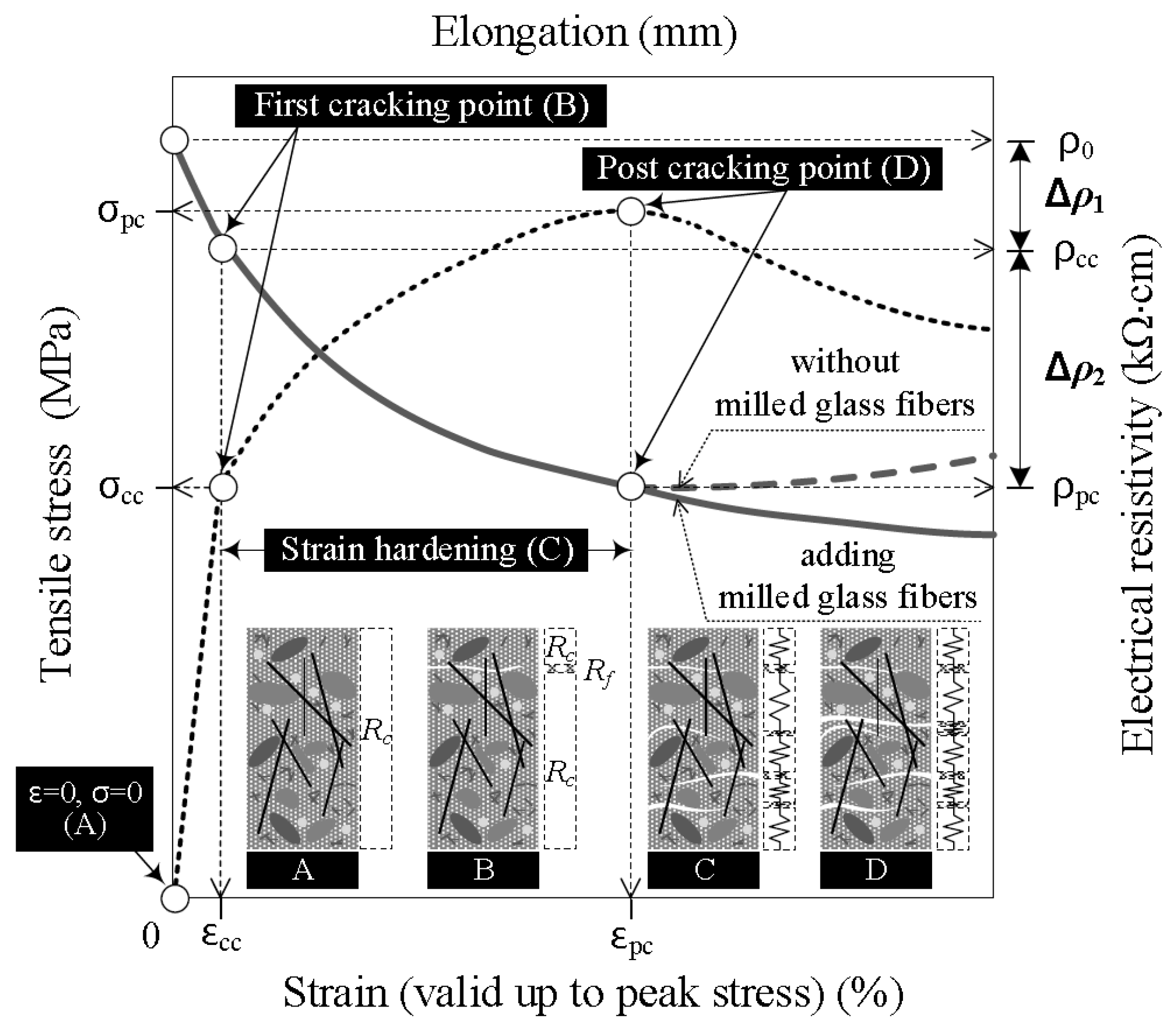
2. Electromechanical Response of HPFRCCs under Tension
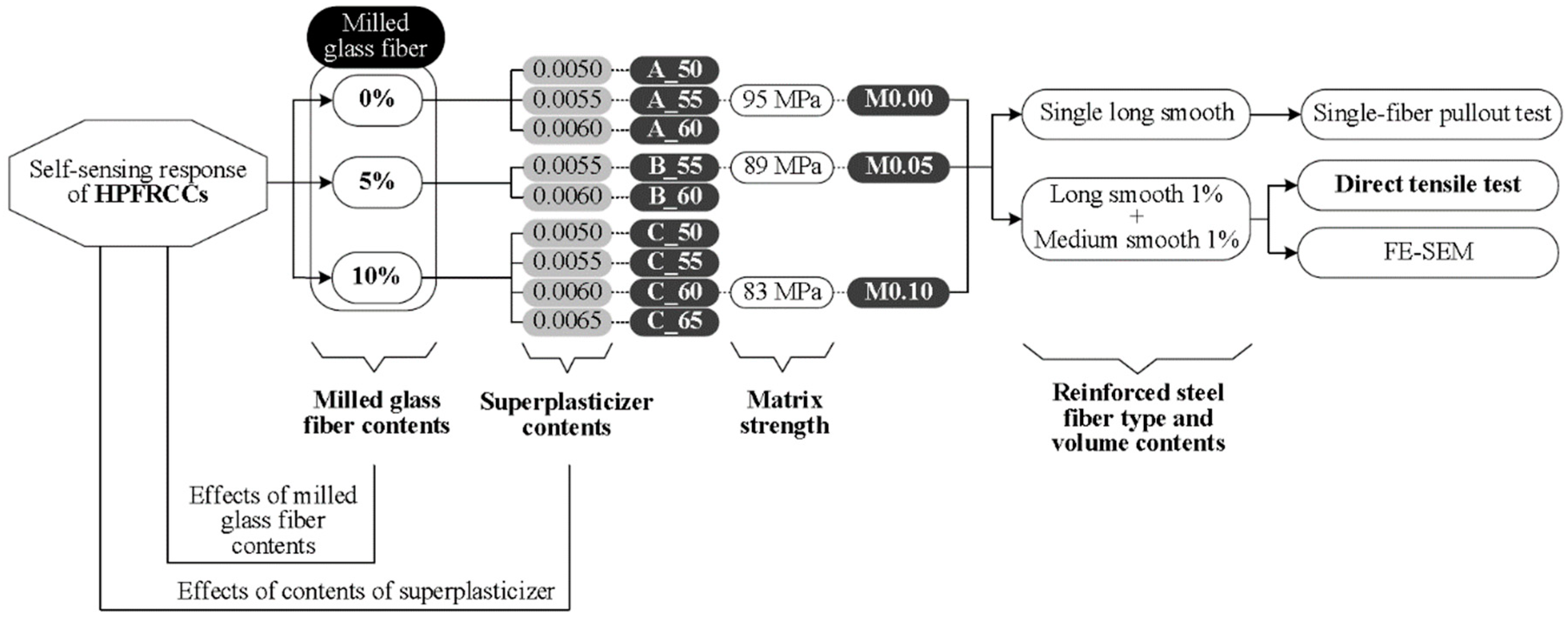
3. Experimental Program
3.1. Materials and Specimen Preparation
3.2. Test Setup and Procedure
4. Results
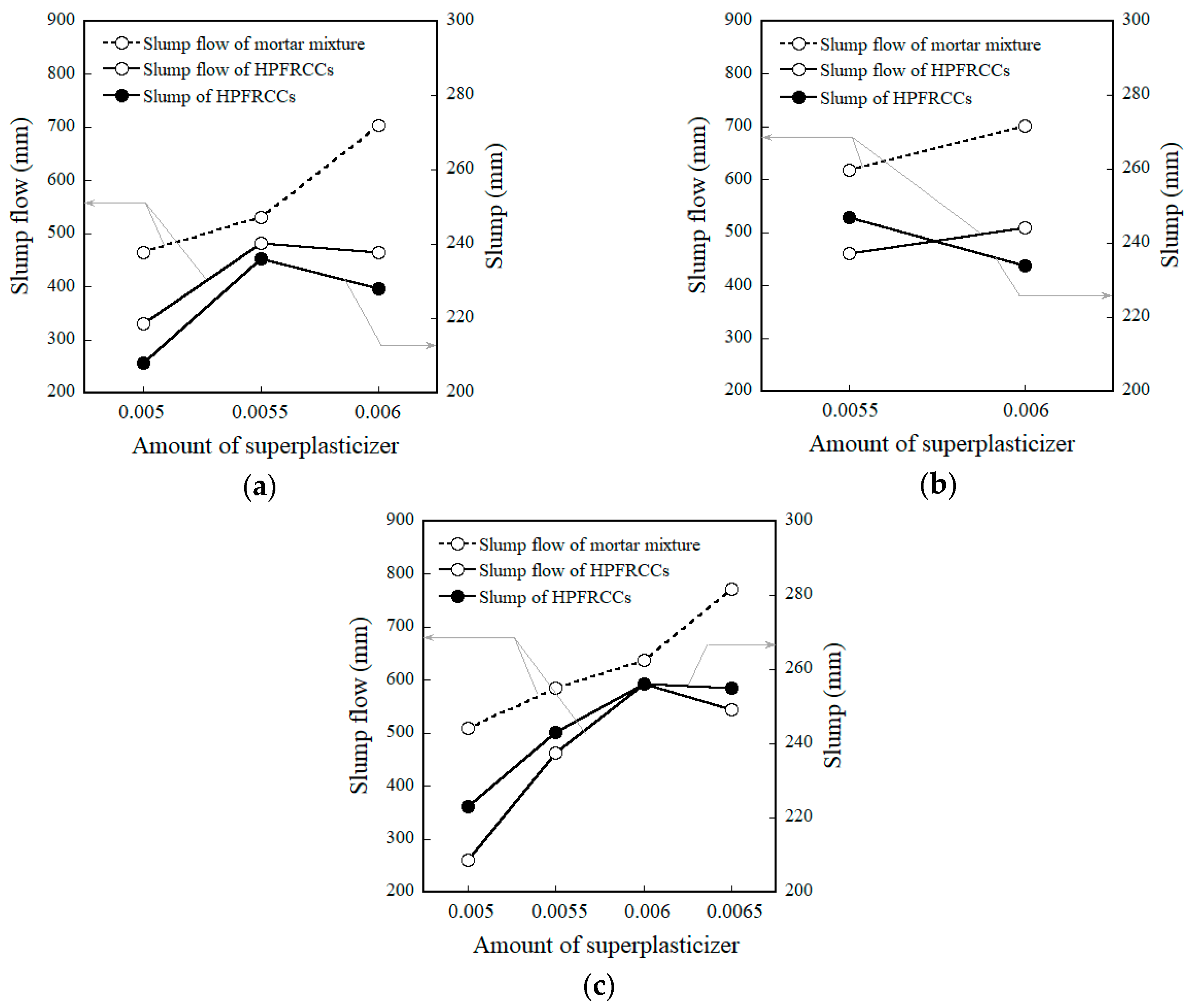
4.1. Slump Flow for Uniform Distribution of Both MGFs and Steel Fibers
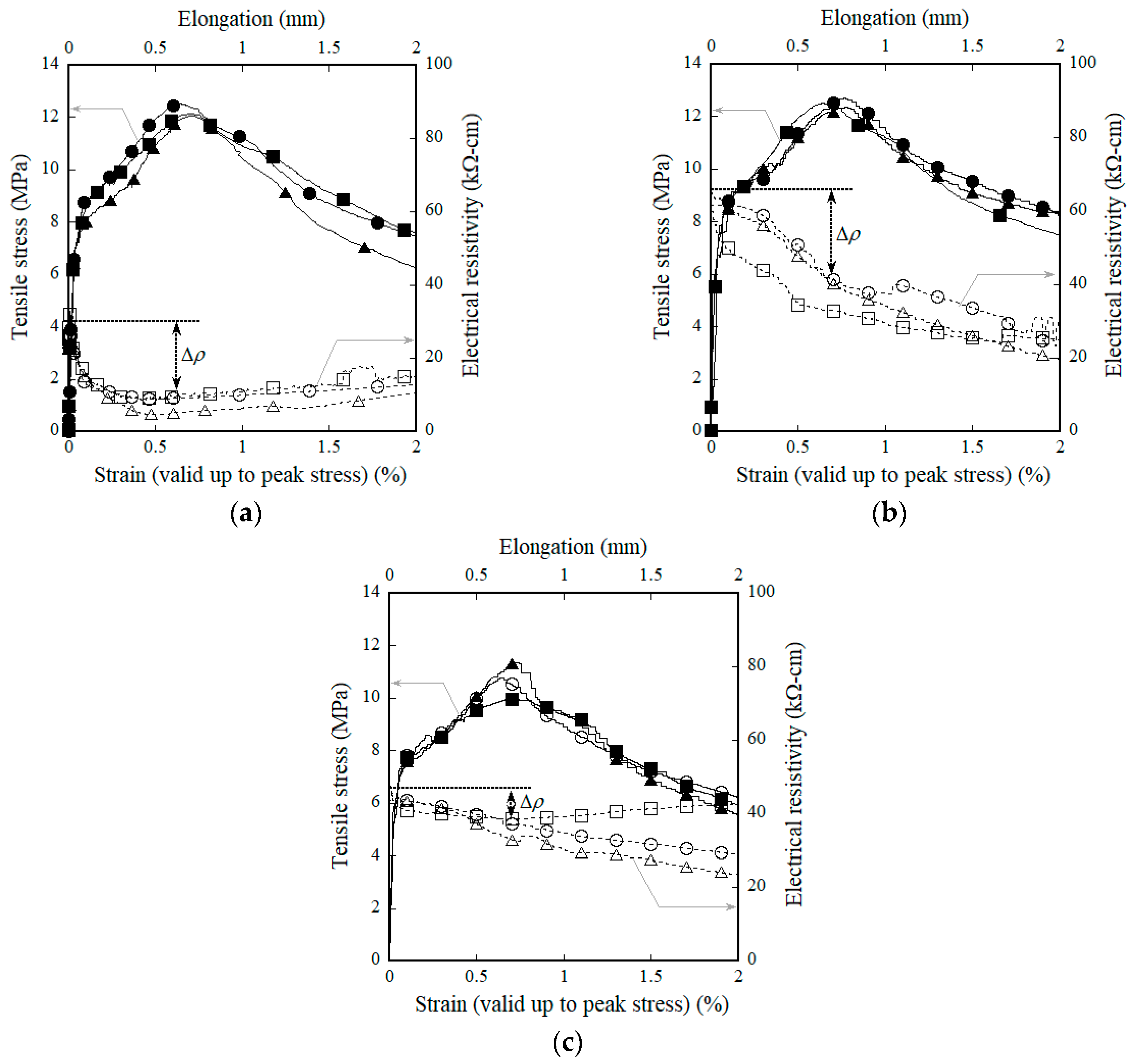
4.2. Influence of MGFs on the Electromechanical Response of HPFRCCs under Tension
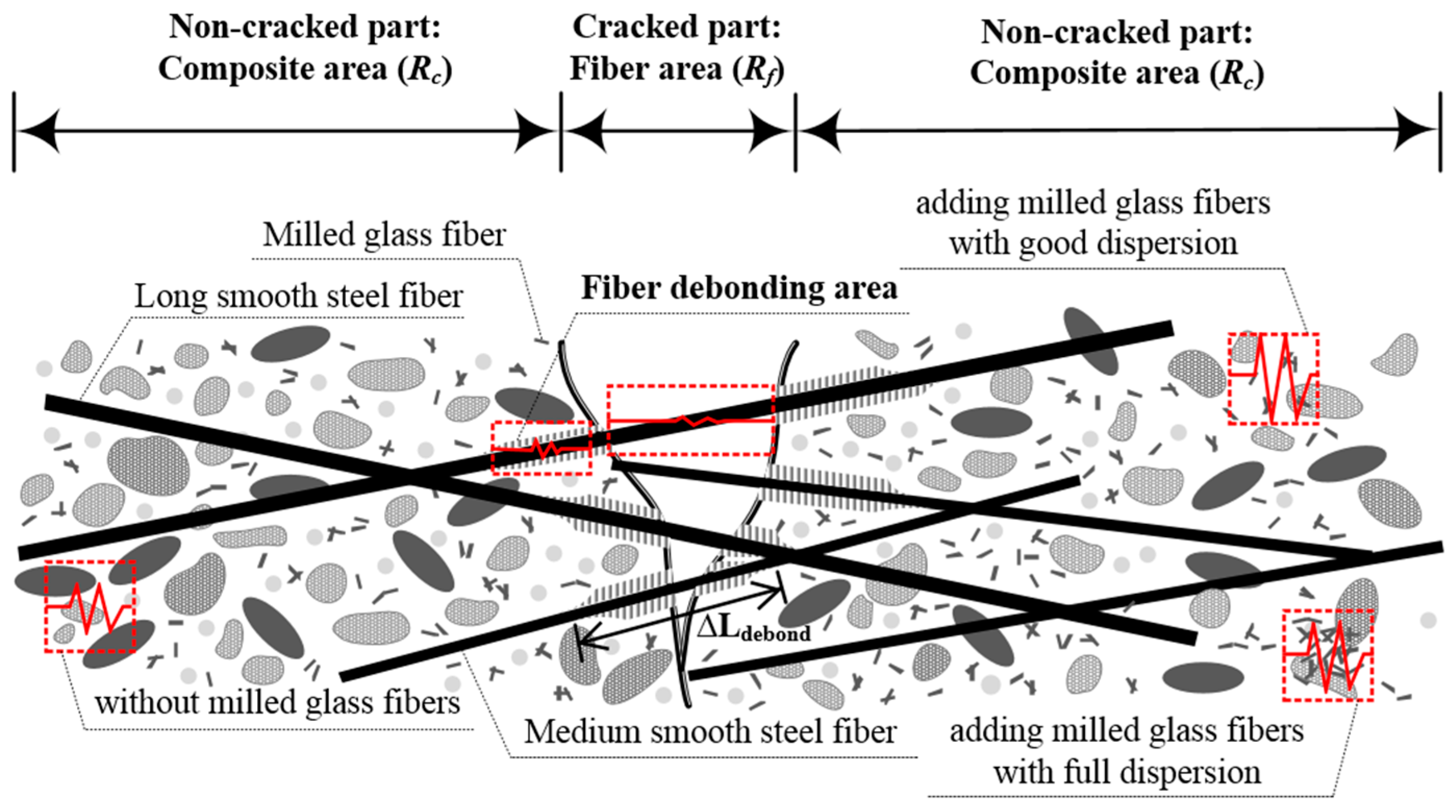
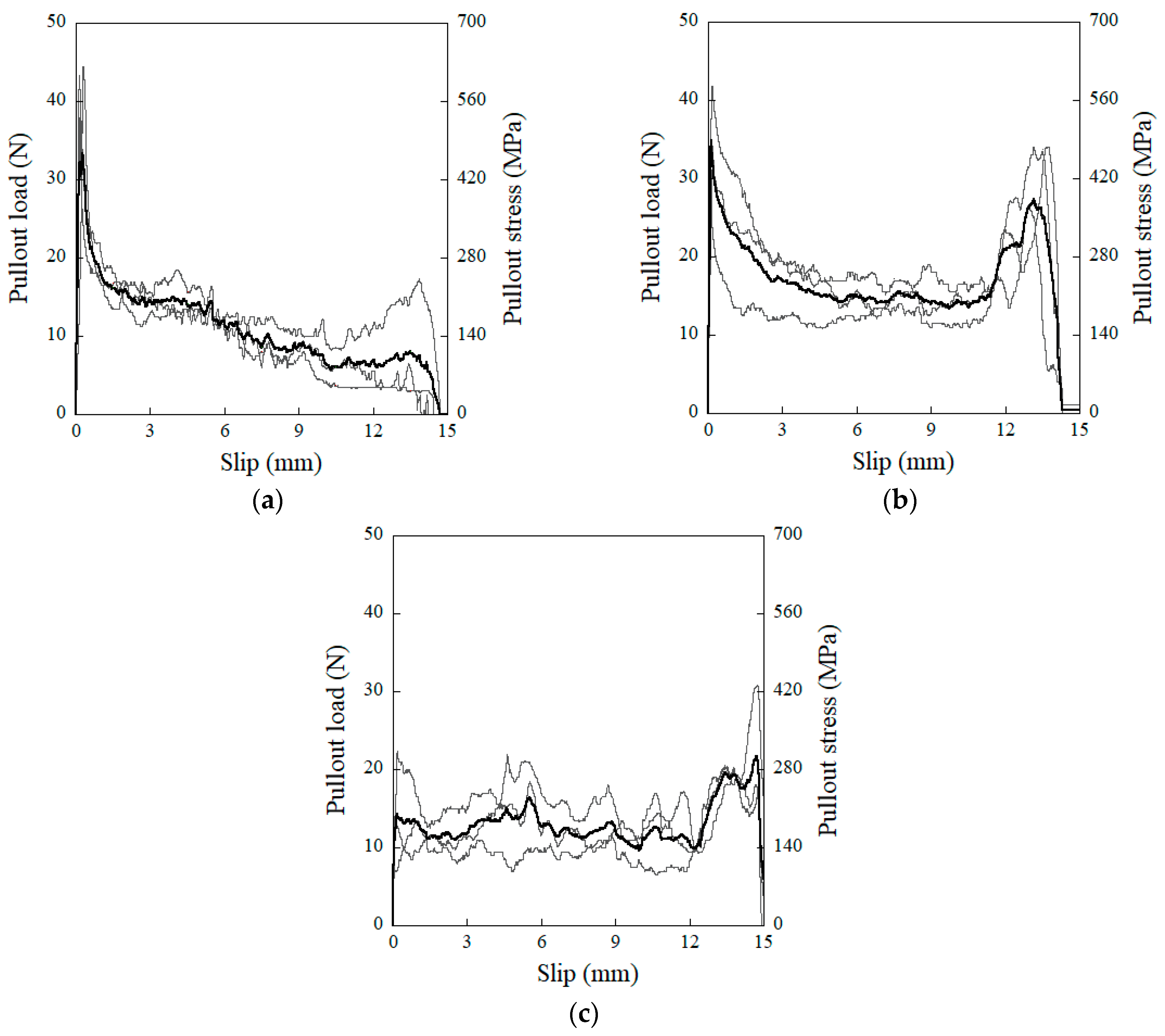
4.3. Influence of MGFs on the Pullout Resistance of Steel Fibers Embedded in Mortar
5. Discussion
6. Conclusions
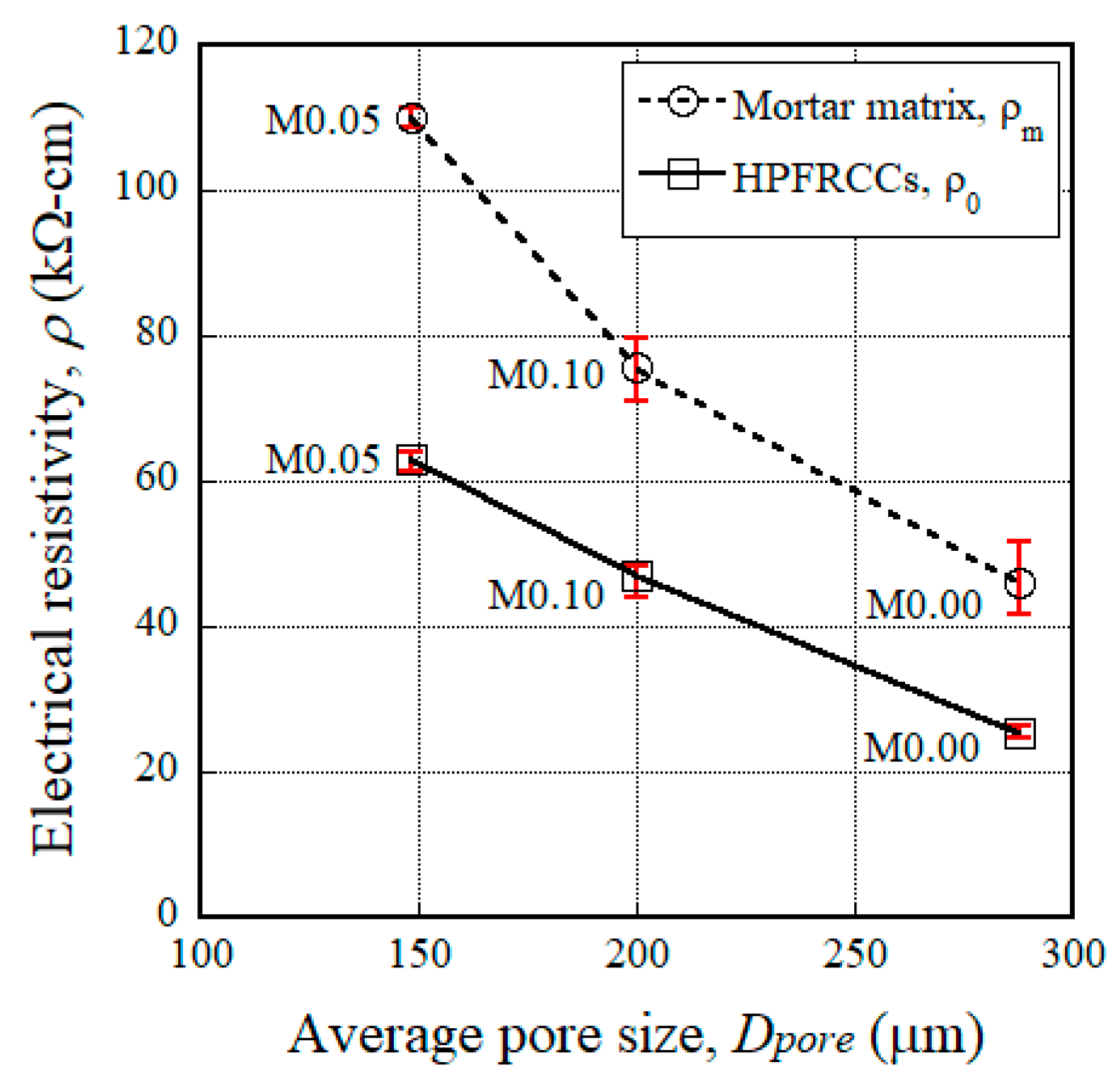
- The addition of MGFs to cement-based composites reduced the size of pores, which is closely related to the electrical resistivity of the composites; the electrical resistivity was the greatest for HPFRCCs containing 5 wt % MGFs.
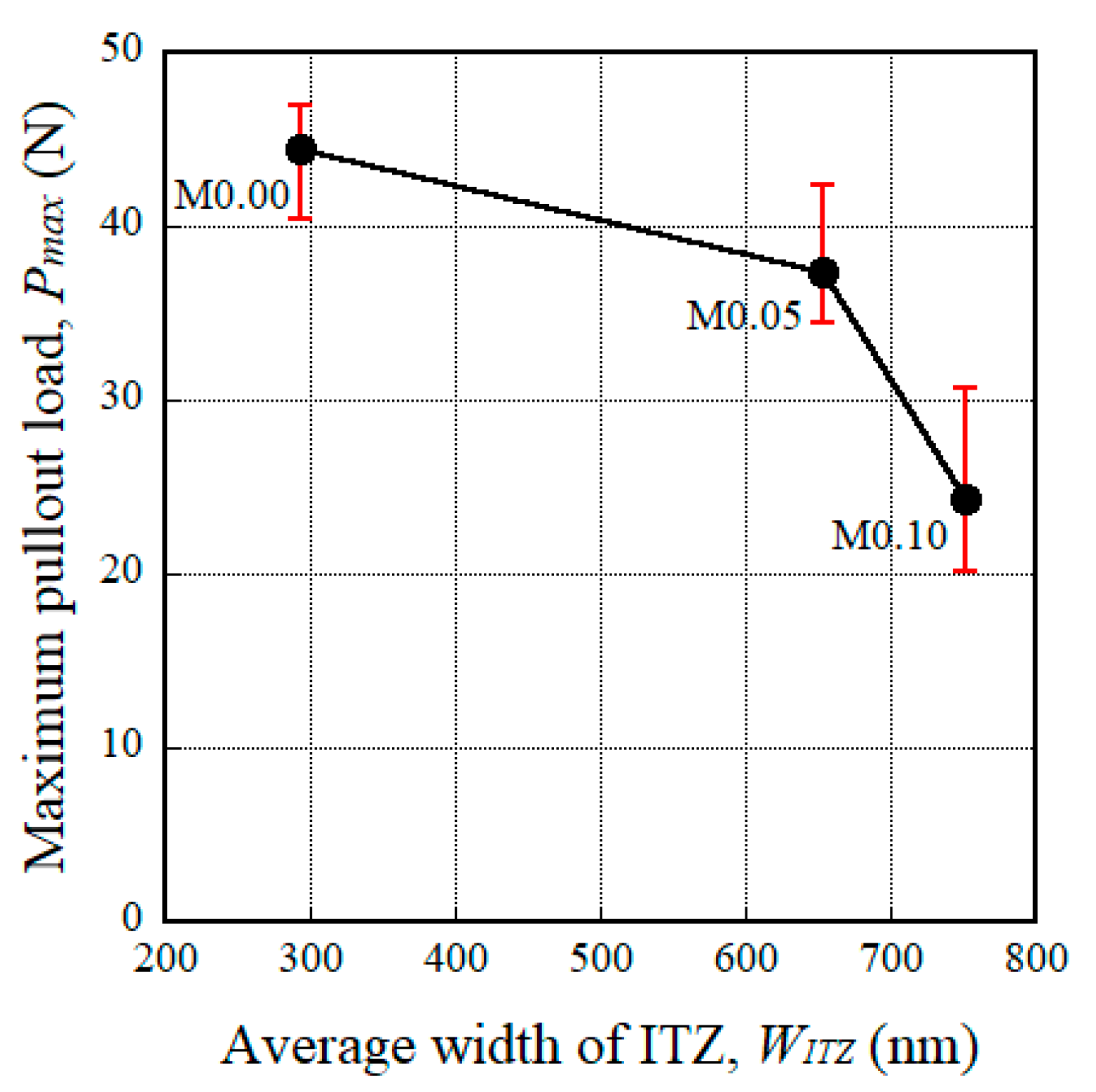
- The maximum pullout load (Pmax) of steel fibers with a 15-mm embedment length decreased from 41.93 to 24.35 N as the amount of MGFs increased from 0 to 10 wt %, because the width of the ITZ (WITZ) increased from 294 to 752 μm.
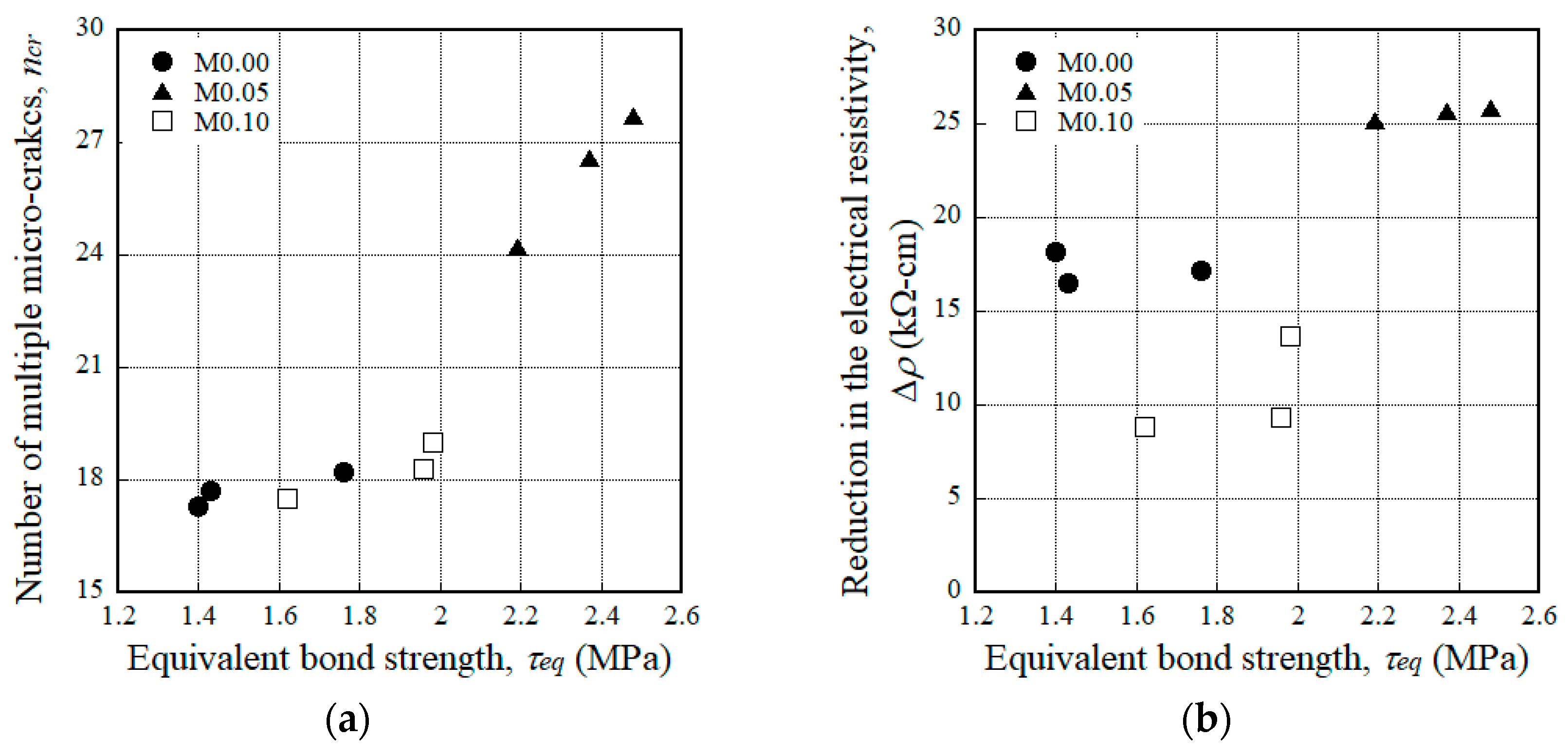
- However, the equivalent bond strength (τeq) of steel fibers, which is closely correlated with the tensile response (especially the number of multiple cracks) of HPFRCCs, increased from 1.53 to 2.35 MPa as the amount of MGFs increased from 0 to 5 wt % owing to the greater accumulation of cementitious material particles attached to the surfaces of steel fibers at the interfacial tunnel.
- The reduction in the electrical resistivity (∆ρ) of HPFRCCs during the strain-hardening response under tension was the greatest with the addition of 5 wt % MGFs to the matrix; this was attributed to the increased electrical resistivity of the mortar matrix due to the generation of a greater number of multiple micro-cracks.
- HPFRCCs containing 5 wt % MGFs generated the largest reduction in the electrical resistivity per crack (∆ρ/ncr) of 1.12 kΩ·cm, i.e., the greatest self-damage sensing capacity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Teomete, E.; Kocyigit, O.I. Tensile strain sensitivity of steel fiber reinforced cement matrix composites tested by split tensile test. Constr. Build. Mater. 2013, 47, 962–968. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Ubertini, F.; Materazzi, A.L. Self-sensing concrete nanocomposites for smart structures. Int. J. Civ. Environ. Eng. 2016, 10, 576–581. [Google Scholar]
- Han, B.; Yu, X.; Ou, J. Self-Sensing Concrete in Smart Structures; Butterworth-Heinemann, Elsevier: Oxford, UK, 2014. [Google Scholar]
- Gupta, S.; Gonzalez, J.G.; Loh, K. Self-sensing concrete enabled by nano-engineered cement-aggregate interfaces. Struct. Health Monit. 2017, 16, 309–323. [Google Scholar] [CrossRef]
- Hoheneder, J.; Flores-Vivian, I.; Lin, Z.; Zilberman, P.; Sobolev, K. The performance of stress-sensing smart fiber reinforced composites in moist and sodium chloride environments. Compos. Part B 2015, 73, 89–95. [Google Scholar] [CrossRef]
- Wittmann, F.H. Observation of and electromechanical effect of hardened cement paste. Cem. Concr. Res. 1973, 3, 601–605. [Google Scholar] [CrossRef]
- Chu, H.Y.; Chen, J.K. The experimental study on the correlation of resistivity and damage for conductive concrete. Cem. Concr. Compos. 2016, 67, 12–19. [Google Scholar] [CrossRef]
- Rana, S.; Subramani, P.; Fangueiro, R.; Correia, A.G. A review on smart self-sensing composite materials for civil engineering applications. AIMS Mater. Sci. 2016, 3, 357–379. [Google Scholar] [CrossRef]
- Xie, P.; Gu, P.; Beaudoin, J.J. Electrical percolation phenomena in cement composites containing conductive fibres. J. Mater. Sci. 1996, 31, 4093–4097. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. Electrical polarization in carbon fiber-reinforced cement. Cem. Concr. Res. 2001, 31, 141–147. [Google Scholar] [CrossRef]
- Toutanji, H.A.; El-Korchi, T.; Katz, R.N. Strength and reliability of carbon-fiber-reinforced cement composites. Cem. Concr. Compos. 1994, 16, 15–21. [Google Scholar] [CrossRef]
- Chen, P.-W.; Chung, D.D.L. Concrete reinforced with up to 0.2 vol% of short carbon fibres. Composites 1993, 24, 33–52. [Google Scholar] [CrossRef]
- Chen, P.-W.; Chung, D.D.L. Low-drying-shrinkage concrete containing carbon fibers. Compos. Part B 1996, 27, 269–274. [Google Scholar] [CrossRef]
- Li, G.Y.; Wang, P.M.; Zhao, X. Pressure-sensitive properties and microstructure of carbon nanotube reinforced cement composites. Cem. Concr. Compos. 2007, 29, 377–382. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Metaxa, Z.S.; Shah, S.P. Highly dispersed carbon nanotube reinforced cement based materials. Cem. Concr. Res. 2010, 40, 1052–1059. [Google Scholar] [CrossRef]
- Nochaiya, T.; Chaipanich, A. Behavior of multi-walled carbon nanotubes on the porosity and microstructure of cement-based-materials. Appl. Surf. Sci. 2011, 257, 1941–1945. [Google Scholar] [CrossRef]
- Al-Rub, R.K.; Ashour, A.I.; Tyson, B.M. On the aspect ratio effect of multi-walled carbon nanotube reinforcements on the mechanical properties of cementitious nanocomposites. Constr. Build. Mater. 2012, 35, 647–655. [Google Scholar] [CrossRef]
- Hu, Y.; Luo, D.; Li, P.; Li, Q.; Sun, G. Fracture toughness enhancement of cement paste with multi-walled carbon nanotubes. Constr. Build. Mater. 2014, 70, 332–338. [Google Scholar] [CrossRef]
- Danoglidis, P.A.; Konsta-Gdoutos, M.S.; Gdoutos, E.E.; Shah, S.P. Strength, energy absorption capability and self-sensing properties of multifunctional carbon nanotube reinforced mortars. Constr. Build. Mater. 2016, 120, 265–274. [Google Scholar] [CrossRef]
- Sanchez, F.; Ince, C. Microstructure and macroscopic properties of hybrid carbon nanofiber/silica fume cement composites. Compos. Sci. Technol. 2009, 69, 1310–1318. [Google Scholar] [CrossRef]
- Hardy, D.K.; Fadden, M.F.; Khattak, M.J.; Khattab, A. Development and characterization of self-sensing CNF HPFRCC. Mater. Struct. 2016, 49, 5327–5342. [Google Scholar] [CrossRef]
- Wang, H.; Gao, X.; Wang, R. The influence of rheological parameters of cement paste on the dispersion of carbon nanofibers and self-sensing performance. Constr. Build. Mater. 2017, 134, 673–683. [Google Scholar] [CrossRef]
- Han, B.; Zhang, L.; Zhang, C.; Wang, Y.; Yu, X.; Ou, J. Reinforcement effect and mechanism of carbon fibers to mechanical and electrically conductive properties of cement-based materials. Constr. Build. Mater. 2016, 125, 479–489. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. Piezoresistivity in continuous carbon fiber cement-matrix composite. Cem. Concr. Res. 1999, 29, 445–449. [Google Scholar] [CrossRef]
- Chung, D.D.L. Electrically conductive cement-based materials. Adv. Cem. Res. 2004, 16, 167–176. [Google Scholar] [CrossRef]
- Garcia-Macias, E.; D’Alessandro, A.; Castro-Triguero, R.; Perez-Mira, D.; Ubertini, F. Micromechanics modeling of the uniaxial strain-sensing property of carbon nanotube cement-matrix composites for SHM applications. Compos. Struct. 2017, 163, 195–215. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Rallini, M.; Ubertini, F.; Materazzi, A.L.; Kenny, J.M. Investigations on scalable fabrication procedures for self-sensing carbon nanotube cement-matrix composites for SHM applications. Cem. Concr. Compos. 2016, 65, 200–213. [Google Scholar] [CrossRef]
- Metaxa, Z.S.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D.; Kourkoulis, S.K. Carbon nanotube reinforced mortar as a sensor to monitor the structural integrity of restored marble epistyles under shear. Procedia Strct. Integr. 2016, 2, 2833–2840. [Google Scholar] [CrossRef]
- Loh, K.J.; Gonzalez, J. Cementitious composites engineered with embedded carbon nanotube thin films for enhanced sensing performance. J. Phys. Conf. Ser. 2015, 628, 012042. [Google Scholar] [CrossRef]
- Sasmal, S.; Ravivarman, N.; Sindu, B.S. Synthesis, characterization and performance of piezo-resistive cementitious nanocomposites. Cem. Concr. Compos. 2017, 75, 10–21. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Aza, C.A. Self sensing carbon nanotube (CNT) and nanofiber (CNF) cementitious composites for real time damage assessment in smart structures. Cem. Concr. Compos. 2014, 53, 162–169. [Google Scholar] [CrossRef]
- Pisello, A.L.; D’Alessandro, A.; Sambuco, S.; Rallini, M.; Uberini, F.; Asdrubli, F.; Materazzi, A.L.; Cotana, F. Multipurpose experimental characterization of smart nanocomposite cement-based materials for thermal-energy efficiency and strain-sensing capability. Sol. Energy Mater. Sol. Cells 2017, 161, 77–88. [Google Scholar] [CrossRef]
- Al-Dahawi, A.; Sarwaty, M.H.; Ozturk, O.; Yildirim, G.; Akin, A.; Sahmaran, M.; Lachemi, M. Electrical percolation threshold of cementitious composites possessing self-sensing functionality incorporating different carbon-based materials. Smart Mater. Struct. 2016, 25, 105005. [Google Scholar] [CrossRef]
- Chung, D.D.L. Carbon materials for structural self-sensing, electromagnetic shielding and thermal interfacing. Carbon 2012, 50, 3342–3353. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. Uniaxial compression in carbon fiber-reinforced cement, sensed by electrical resistivity measurement in longitudinal and transverse directions. Cem. Concr. Res. 2001, 31, 297–301. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. Effect of stress on the electric polarization in cement. Cem. Concr. Res. 2001, 31, 291–295. [Google Scholar] [CrossRef]
- Al-Dahawi, A.; Yildirim, G.; Ozturk, O.; Sahmaran, M. Assessment of self-sensing capability of engineered cementitious composites within the elastic and plastic ranges of cyclic flexural loading. Constr. Build. Mater. 2017, 145, 1–10. [Google Scholar] [CrossRef]
- Muto, N.; Yanagida, H.; Nakatsuji, T.; Sugita, M.; Ohtsuka, Y.; Arai, Y. Design of intelligent materials with self-diagnosing function for preventing fatal fracture. Smart Mater. Struct. 1992, 1, 324–329. [Google Scholar] [CrossRef]
- Chung, D.D.L. Piezoresistive cement-based materials for strain sensing. J. Intell. Mater. Syst. Struct. 2002, 13, 599–609. [Google Scholar] [CrossRef]
- Teomete, E. Transverse strain sensitivity of steel fiber reinforced cement composites tested by compression and split tensile tests. Constr. Build. Mater. 2014, 55, 136–145. [Google Scholar] [CrossRef]
- Song, J.; Nguyen, D.L.; Manathamsombat, C.; Kim, D.J. Effect of fiber volume content on electromechanical behavior of strain-hardening steel-fiber-reinforced cementitious composites. J. Compos. Mater. 2015, 49, 3621–3634. [Google Scholar] [CrossRef]
- Nguyen, D.L.; Song, J.; Manathamsombat, C.; Kim, D.J. Comparative electromechanical damage-sensing behaviors of six strain-hardening steel fiber-reinforced cementitious composites under direct tension. Compos. Part B Eng. 2015, 69, 159–168. [Google Scholar] [CrossRef]
- Kim, D.J.; Kim, M.K. The Damage Self-Sensing Response of Ultra-High-Performance Fiber-Reinforced Concrete in Tension. In Proceedings of the 3rd International Conference on Smart Materials and Structures, Orlando, FL, USA, 20–22 March 2017. [Google Scholar]
- Kim, M.K.; Kim, D.J.; An, Y.-K. Electro-mechanical self-sensing response of ultra-high-performance fiber-reinforced concrete in tension. Compos. Part B Eng. 2018, 134, 254–264. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. A comparative study of steel- and carbon-fibre cement as piezoresistive strain sensors. Adv. Cem. Res. 2003, 15, 119–128. [Google Scholar] [CrossRef]
- Joe, C.D. Cost and Ecological Feasibility of Using Ultra-High Performance Concrete in Highway Bridge Piers. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2016. [Google Scholar]
- Kim, J.J.; Kim, D.J.; Kang, S.T.; Lee, J.H. Influence of sand to coarse aggregate ratio on the interfacial bond strength of steel fibers in concrete for nuclear power plant. Nucl. Eng. Des. 2012, 252, 1–10. [Google Scholar] [CrossRef]
- Szelag, M. The influence of Metakaolinite on the Development of Thermal Cracks in a Cement Matrix. Materials 2018, 11, 520. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, Q.; Zhang, G.; Shi, L.; Dong, J.; Jia, P. A method of detecting the cracks of concrete undergo high-temperature. Constr. Build. Mater. 2018, 162, 345–358. [Google Scholar] [CrossRef]
- Figueiredo, A.D.D.; Ceccato, M.R. Workability analysis of steel fiber reinforced concrete using slump and Ve-Be test. Mater. Res. 2015, 18, 1284–1290. [Google Scholar] [CrossRef]
- Naaman, A.E. High Performance Fiber Reinforced Cement Composites. In Proceedings of the IABSE Symposium on Concrete Structures for the Future, Paris, France, 23–25 September 1987; pp. 371–376. [Google Scholar]
- Kim, D.J.; El-Tawil, S.; Naaman, A.E. Correlation between Single Fiber Pullout Behavior and Tensile Response of FRC Composites with High Strength Steel Fiber. In Proceedings of the Rilem International Workshop on High Performance Fiber Reinforced Cement Composites—HPFRCC5, Mainz, Germany, 10–13 July 2007; Reinhardt, H.W., Naaman, A.E., Eds.; RILEM Publications: Cachan, France, 2007; pp. 67–76. [Google Scholar]
- Monfore, G.E. The Electrical Resistivity of Concrete. J. PCA Res. Dev. Lab. 1968, 10, 35–48. [Google Scholar]
- Teomete, E. The effect of temperature and moisture on electrical resistance, strain sensitivity and crack sensitivity of steel fiber reinforced smart cement composite. Smart Mater. Struct. 2016, 25, 75024–75033. [Google Scholar] [CrossRef]
- El-Enein, S.A.A.; Kotkata, M.F.; Hanna, G.B.; Saad, M.; El Razek, M.M.A. Electrical conductivity of concrete containing silica fume. Cem. Concr. Res. 1995, 25, 1615–1620. [Google Scholar] [CrossRef]
- Bentur, A.; Alexander, M.G. A review of the work of the RILEM TC159-ETC: Engineering of the interfacial transition zone in cementitious composites. Mater. Struct. 2000, 33, 82–87. [Google Scholar] [CrossRef]
- Kong, Y.; Wang, P.; Liu, S.; Zhao, G.; Peng, Y. SEM analysis of the interfacial transition zone between cement-glass powder paste and aggregate of mortar under microwave curing. Materials 2016, 9, 733. [Google Scholar] [CrossRef] [PubMed]





| Series | Cement (Type III) | Milled Glass Fiber | Silica Sand | Fly Ash | Superplasticizer † | Water | f’ck (MPa) | ρm (kΩ·cm) |
|---|---|---|---|---|---|---|---|---|
| M0.00 | 1.0 | 0.00 | 1.0 | 0.15 | 0.005–0.006 (0.0055) | 0.35 | 95 | 45.9 |
| M0.05 | 0.95 | 0.05 | 0.0055–0.006 (0.0055) | 89 | 110.3 | |||
| M0.10 | 0.90 | 0.10 | 0.005–0.0065 (0.006) | 83 | 75.8 |
| Fiber Type | Length, lf (mm) | Diameter, df (mm) | Density (g/cm3) | Tensile Strength (MPa) | Elastic Modulus (GPa) | Aspect Ratio, lf/df |
|---|---|---|---|---|---|---|
| Long smooth steel fiber | 30 | 0.3 | 7.90 | 2447 | 200 | 100 |
| Medium smooth steel fiber | 19.5 | 0.2 | 7.90 | 2942 | 200 | 97.5 |
| Milled glass fiber | 0.3 | 0.0135 | 0.58 | 3367 | 0.76 | 22.2 |
| Chemical Composition | Content (wt %) |
|---|---|
| Silicon dioxide (SiO2) | 54 |
| Calcium oxide (CaO) | 17 |
| Aluminum oxide (Al2O3) | 13 |
| Boron oxide (B2O3) | 6 |
| Magnesium oxide (MgO) | 6 |
| Sodium oxide (Na2O) | 1 |
| Fluorine (F2) | 0.75 |
| Fluorine oxide (F2O3) | 0.75 |
| Titanium oxide (TiO2) | 0.75 |
| Strontium oxide (SrO) | 0.75 |
| Notation | No. | Tensile Strain (%) | Tensile Stress (MPa) | Equivalent Number of Cracks, ncr | ||
|---|---|---|---|---|---|---|
| εcc | εpc | σcc | σpc | |||
| M0.00 | SP1 | 0.024 | 0.64 | 5.6 | 12.5 | 17.7 |
| SP2 | 0.025 | 0.70 | 5.6 | 12.1 | 17.3 | |
| SP3 | 0.025 | 0.70 | 5.5 | 12.1 | 18.2 | |
| Aver.a | 0.025 | 0.68 | 5.6 | 12.2 | 17.7 | |
| STD b | 0.00 | 0.03 | 0.05 | 0.19 | 0.37 | |
| M0.05 | SP1 | 0.030 | 0.76 | 6.1 | 12.7 | 27.7 |
| SP2 | 0.027 | 0.64 | 5.8 | 12.5 | 24.2 | |
| SP3 | 0.028 | 0.77 | 6.2 | 12.4 | 26.6 | |
| Aver. | 0.028 | 0.72 | 6.0 | 12.5 | 26.2 | |
| STD | 0.00 | 0.06 | 0.17 | 0.12 | 1.46 | |
| M0.10 | SP1 | 0.020 | 0.64 | 5.7 | 10.8 | 18.3 |
| SP2 | 0.019 | 0.70 | 4.9 | 10.0 | 17.5 | |
| SP3 | 0.029 | 0.73 | 5.4 | 11.4 | 19.0 | |
| Aver. | 0.023 | 0.69 | 5.3 | 10.7 | 18.3 | |
| STD | 0.00 | 0.04 | 0.33 | 0.57 | 0.61 | |
| Notation | No. | Electrical Resistivity (kΩ·cm) | Reduction in the Electrical Resistivity (kΩ·cm) | Δρ/ncr(kΩ·cm) | ||||
|---|---|---|---|---|---|---|---|---|
| ρ0 | ρcc | ρpc | Δρ | Δρ1 | Δρ2 | |||
| M0.00 | SP1 | 26.25 | 24.13 | 9.12 | 17.13 | 2.12 | 15.01 | 0.94 |
| SP2 | 26.30 | 23.72 | 9.83 | 16.47 | 2.59 | 13.89 | 0.93 | |
| SP3 | 23.67 | 22.08 | 5.47 | 18.20 | 1.58 | 16.61 | 0.95 | |
| Aver. | 25.41 | 23.31 | 8.14 | 17.27 | 2.10 | 15.17 | 0.94 | |
| STD | 1.23 | 0.89 | 1.91 | 0.71 | 0.41 | 1.12 | 0.01 | |
| M0.05 | SP1 | 65.04 | 63.45 | 39.86 | 25.18 | 1.59 | 23.60 | 0.91 |
| SP2 | 60.06 | 55.65 | 34.39 | 25.67 | 4.41 | 21.26 | 1.06 | |
| SP3 | 64.23 | 61.80 | 38.41 | 25.83 | 2.43 | 23.40 | 1.39 | |
| Aver. | 63.11 | 60.30 | 37.55 | 25.56 | 2.81 | 22.75 | 1.12 | |
| STD | 2.18 | 3.36 | 2.31 | 0.28 | 1.18 | 1.06 | 0.20 | |
| M0.10 | SP1 | 47.01 | 44.70 | 38.22 | 8.80 | 2.31 | 6.49 | 0.50 |
| SP2 | 48.02 | 43.73 | 38.66 | 9.36 | 4.29 | 5.07 | 0.54 | |
| SP3 | 46.40 | 43.66 | 32.69 | 13.71 | 2.75 | 10.96 | 0.72 | |
| Aver. | 47.14 | 44.03 | 36.52 | 10.62 | 3.12 | 7.51 | 0.59 | |
| STD | 0.67 | 0.47 | 2.72 | 2.19 | 0.85 | 2.51 | 0.10 | |
| Notation | No. | Maximum Pullout Load, Pmax (N) | Equivalent Bond Strength, τeq (MPa) | Pullout Energy, PW (N·mm) |
|---|---|---|---|---|
| M0.00 | SP1 | 44.50 | 1.40 | 148.54 |
| SP2 | 37.95 | 1.76 | 186.25 | |
| SP3 | 43.35 | 1.43 | 151.93 | |
| Aver. | 41.93 | 1.53 | 162.24 | |
| STD | 2.86 | 0.16 | 17.03 | |
| M0.05 | SP1 | 41.85 | 2.48 | 262.82 |
| SP2 | 34.55 | 2.37 | 251.59 | |
| SP3 | 34.00 | 2.19 | 232.07 | |
| Aver. | 36.80 | 2.35 | 248.83 | |
| STD | 3.58 | 0.12 | 12.70 | |
| M0.10 | SP1 | 30.80 | 1.96 | 207.93 |
| SP2 | 20.25 | 1.62 | 171.45 | |
| SP3 | 22.00 | 1.98 | 209.42 | |
| Aver. | 24.35 | 1.85 | 196.27 | |
| STD | 4.62 | 0.17 | 17.56 |
| Notation | Position No. | Pore Size, Dpore (μm) | Width of the ITZ, WITZ (nm) |
|---|---|---|---|
| M0.00 | Pos.1 | 395 | 239 |
| Pos.2 | 247 | 222 | |
| Pos.3 | 336 | 337 | |
| Pos.4 | 174 | 376 | |
| Aver. | 288 | 294 | |
| STD | 84 | 65 | |
| M0.05 | Pos.1 | 138 | 379 |
| Pos.2 | 148 | 912 | |
| Pos.3 | 169 | 595 | |
| Pos.4 | 138 | 731 | |
| Aver. | 148 | 654 | |
| STD | 13 | 195 | |
| M0.10 | Pos.1 | 215 | 397 |
| Pos.2 | 204 | 171 | |
| Pos.3 | 195 | 1180 | |
| Pos.4 | 187 | 1260 | |
| Aver. | 200 | 752 | |
| STD | 10 | 476 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.K.; Kim, D.J. Electromechanical Response of High-Performance Fiber-Reinforced Cementitious Composites Containing Milled Glass Fibers under Tension. Materials 2018, 11, 1115. https://doi.org/10.3390/ma11071115
Kim MK, Kim DJ. Electromechanical Response of High-Performance Fiber-Reinforced Cementitious Composites Containing Milled Glass Fibers under Tension. Materials. 2018; 11(7):1115. https://doi.org/10.3390/ma11071115
Chicago/Turabian StyleKim, Min Kyoung, and Dong Joo Kim. 2018. "Electromechanical Response of High-Performance Fiber-Reinforced Cementitious Composites Containing Milled Glass Fibers under Tension" Materials 11, no. 7: 1115. https://doi.org/10.3390/ma11071115
APA StyleKim, M. K., & Kim, D. J. (2018). Electromechanical Response of High-Performance Fiber-Reinforced Cementitious Composites Containing Milled Glass Fibers under Tension. Materials, 11(7), 1115. https://doi.org/10.3390/ma11071115




