Mechanical Performance of Multidirectional Buckling-Based Negative Stiffness Metamaterials: An Analytical and Numerical Study
Abstract
1. Introduction
2. Design of Multidirectional Buckling-based Negative Stiffness Metamaterials
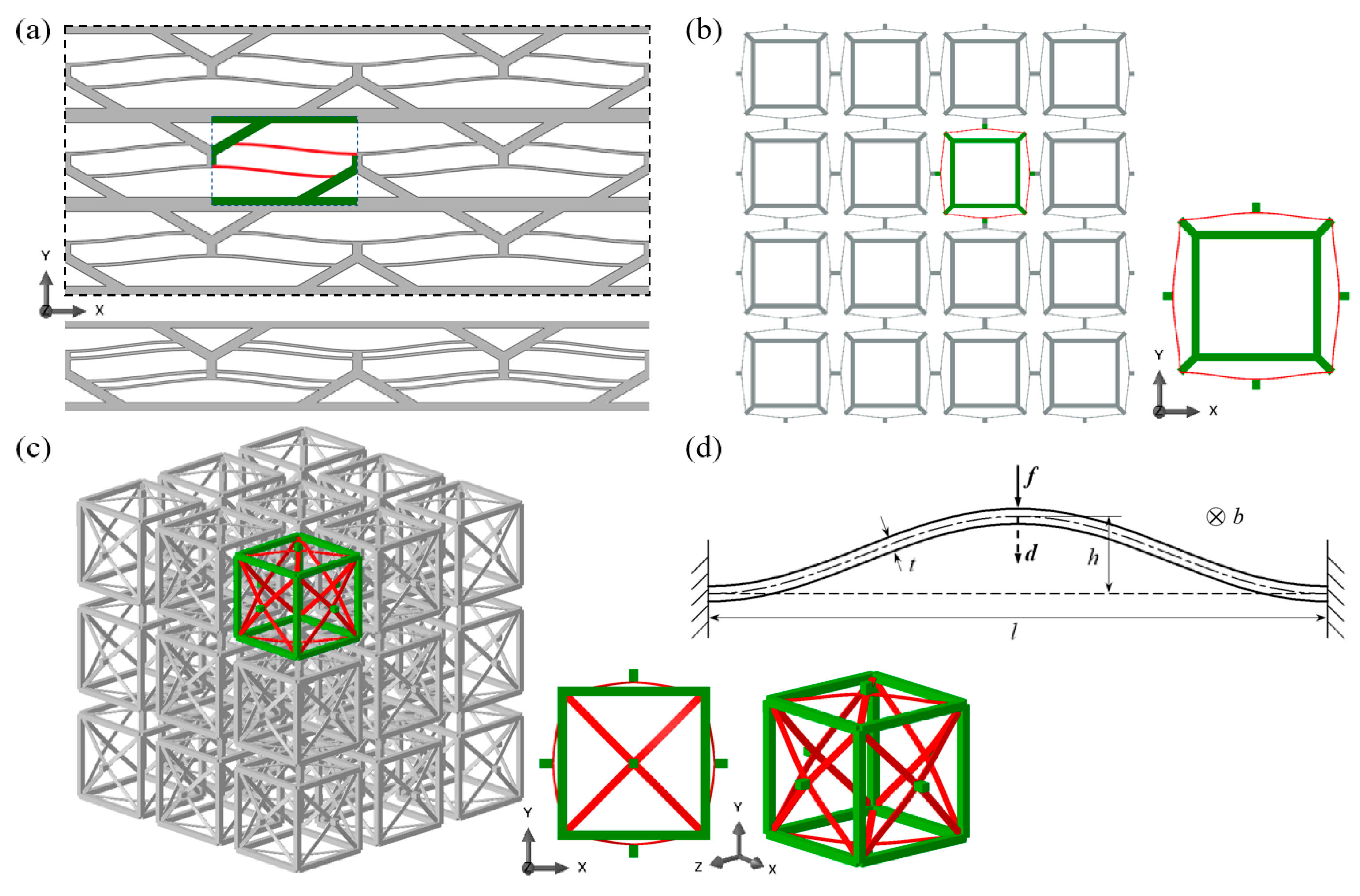
2.1. Multidirectional BNS Metamaterial Designs
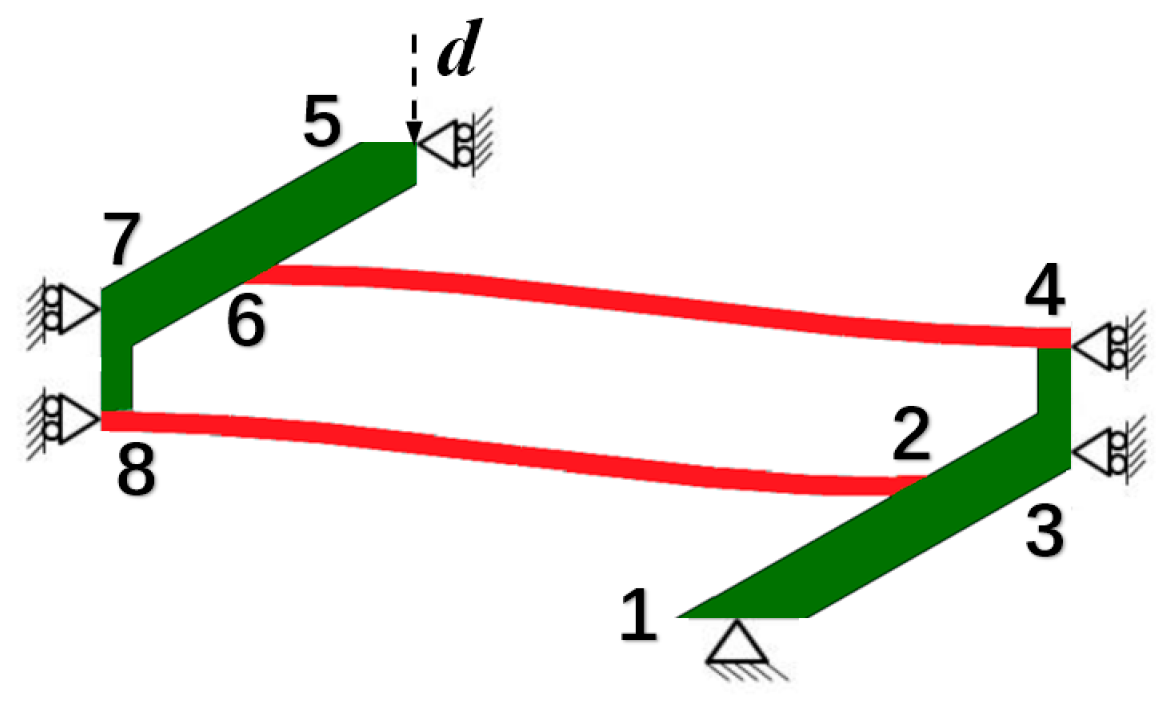
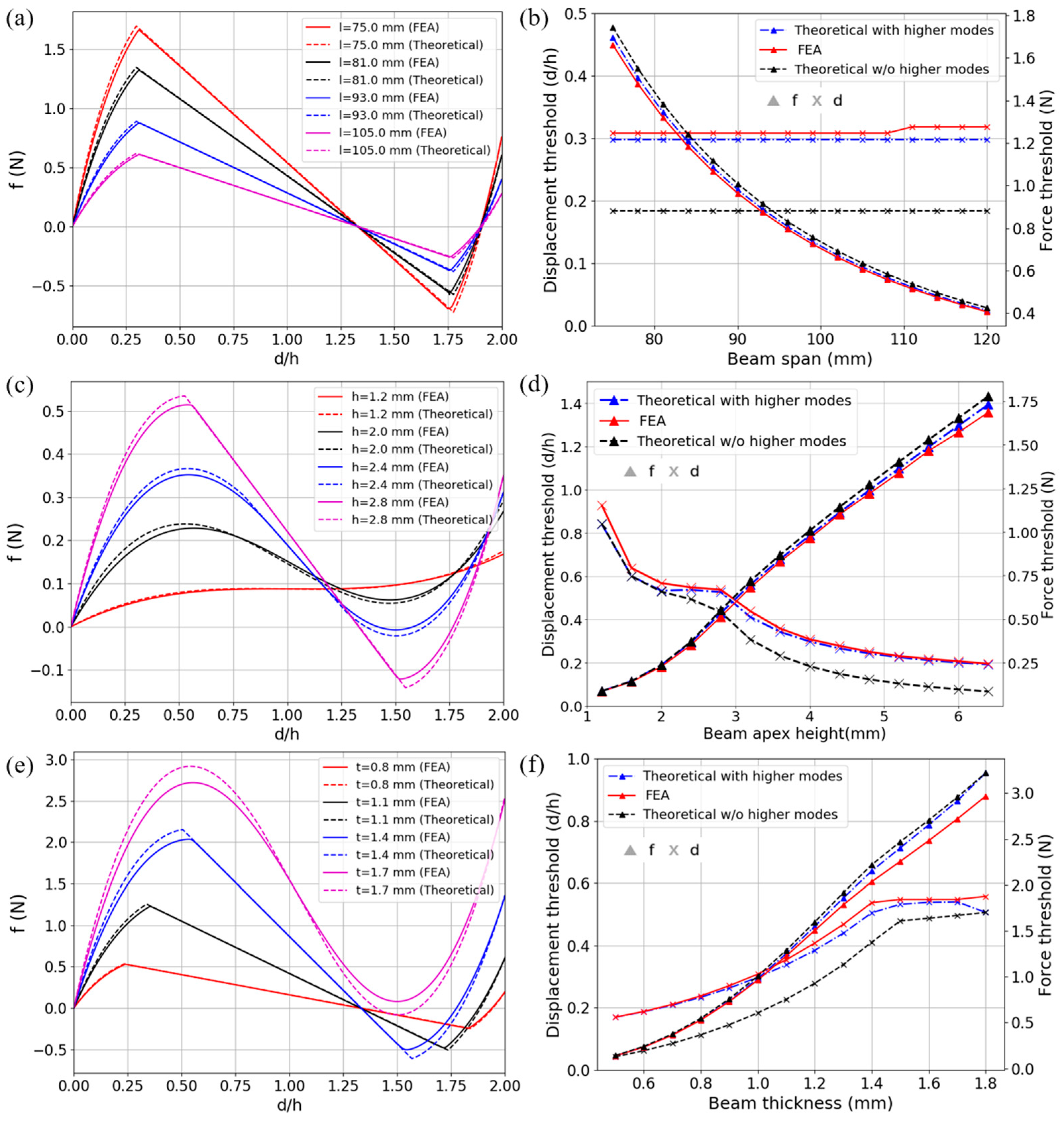
2.2. Parametric Study on the Curved Beam
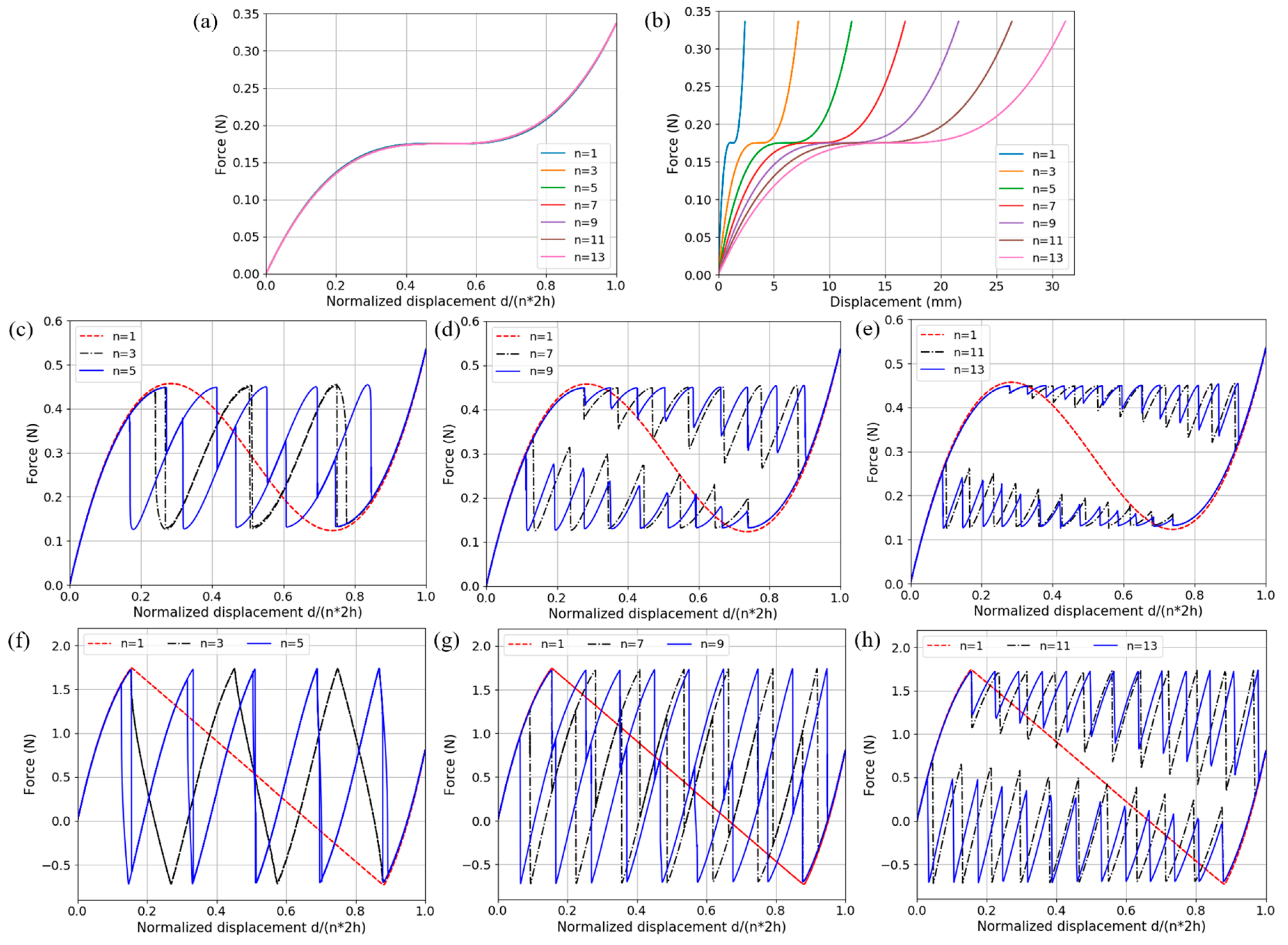
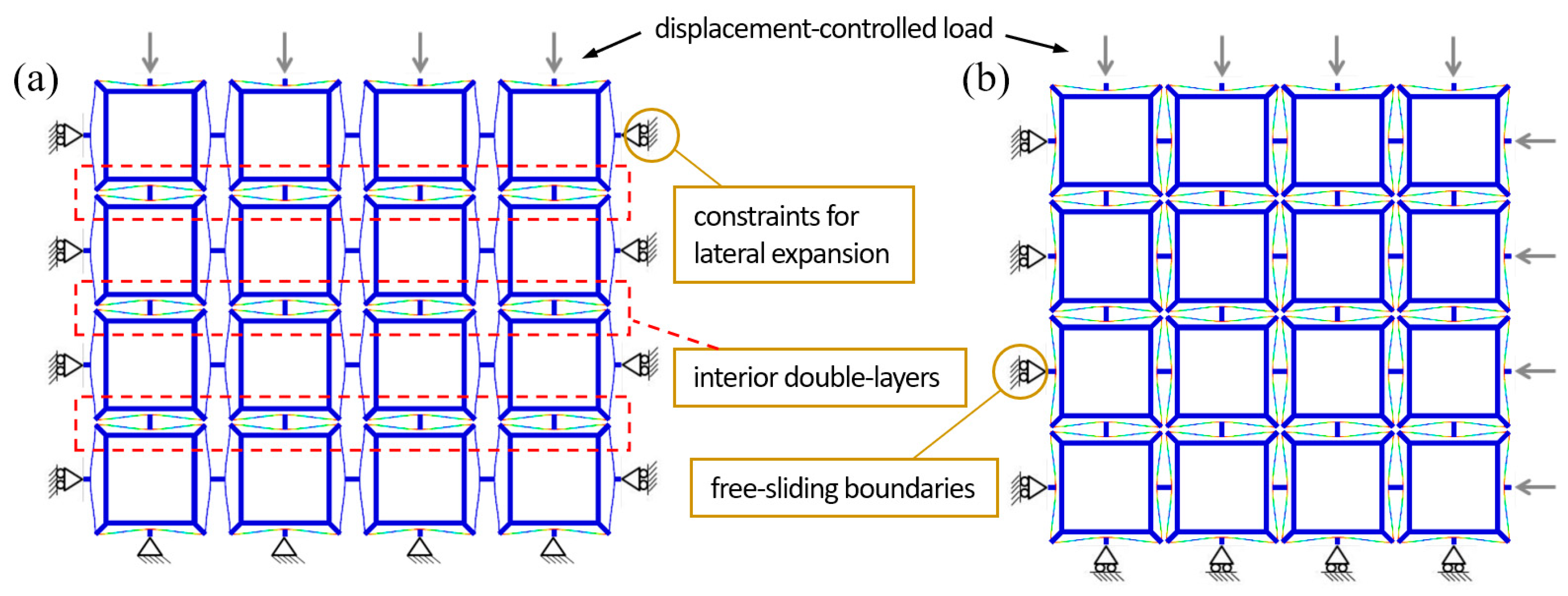
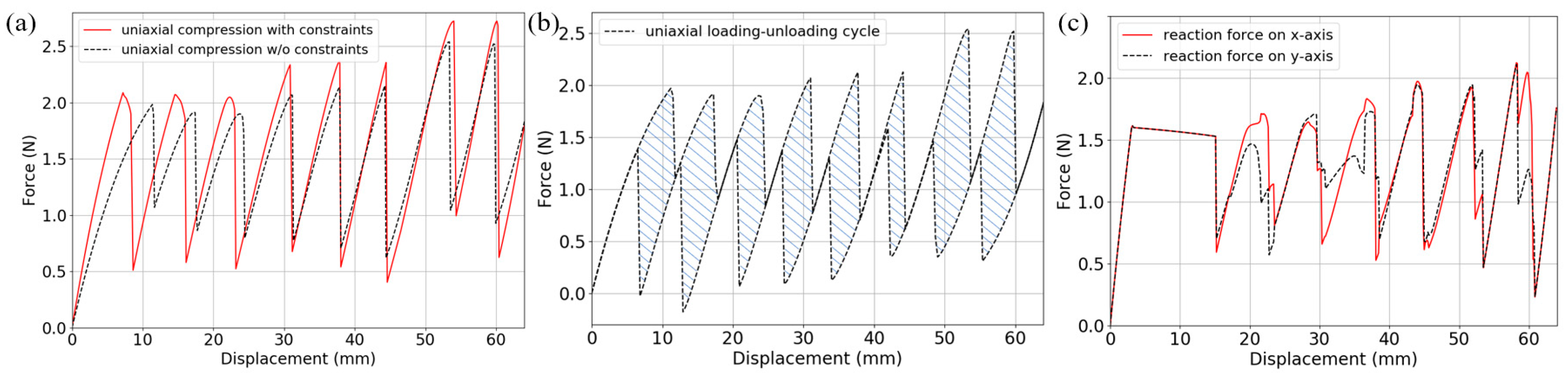
2.3. Multilayer Behaviors of BNS Metamaterials under Uniaxial Quasi-Static Compression
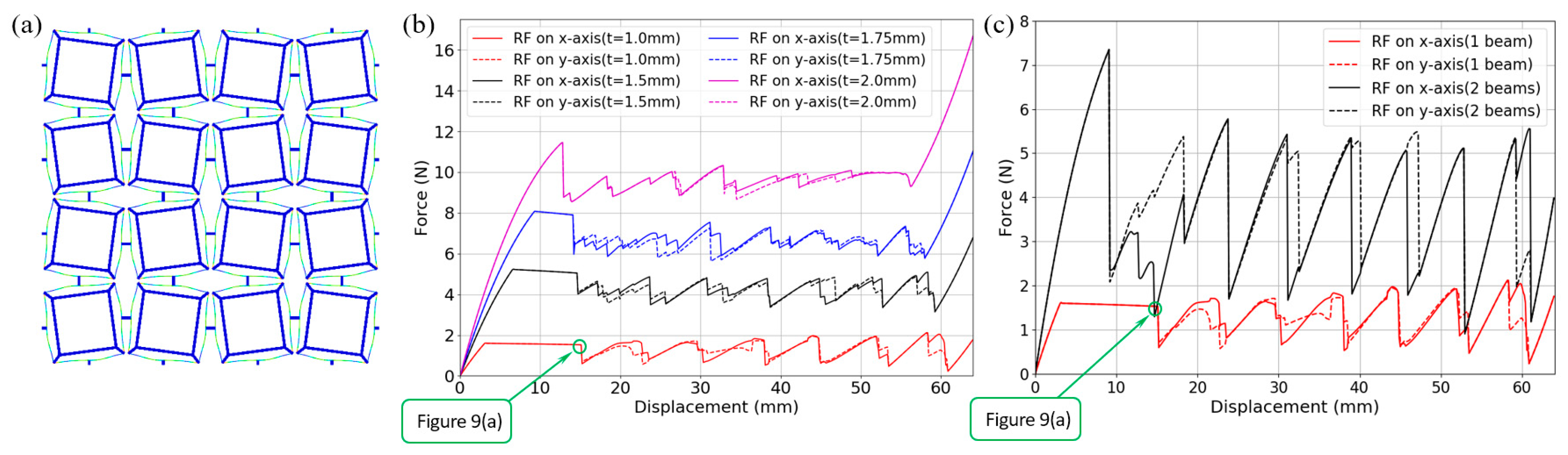
3. Performance of the Bidirectional Buckling-based Negative Stiffness Metamaterial
3.1. Quasi-Static Compression
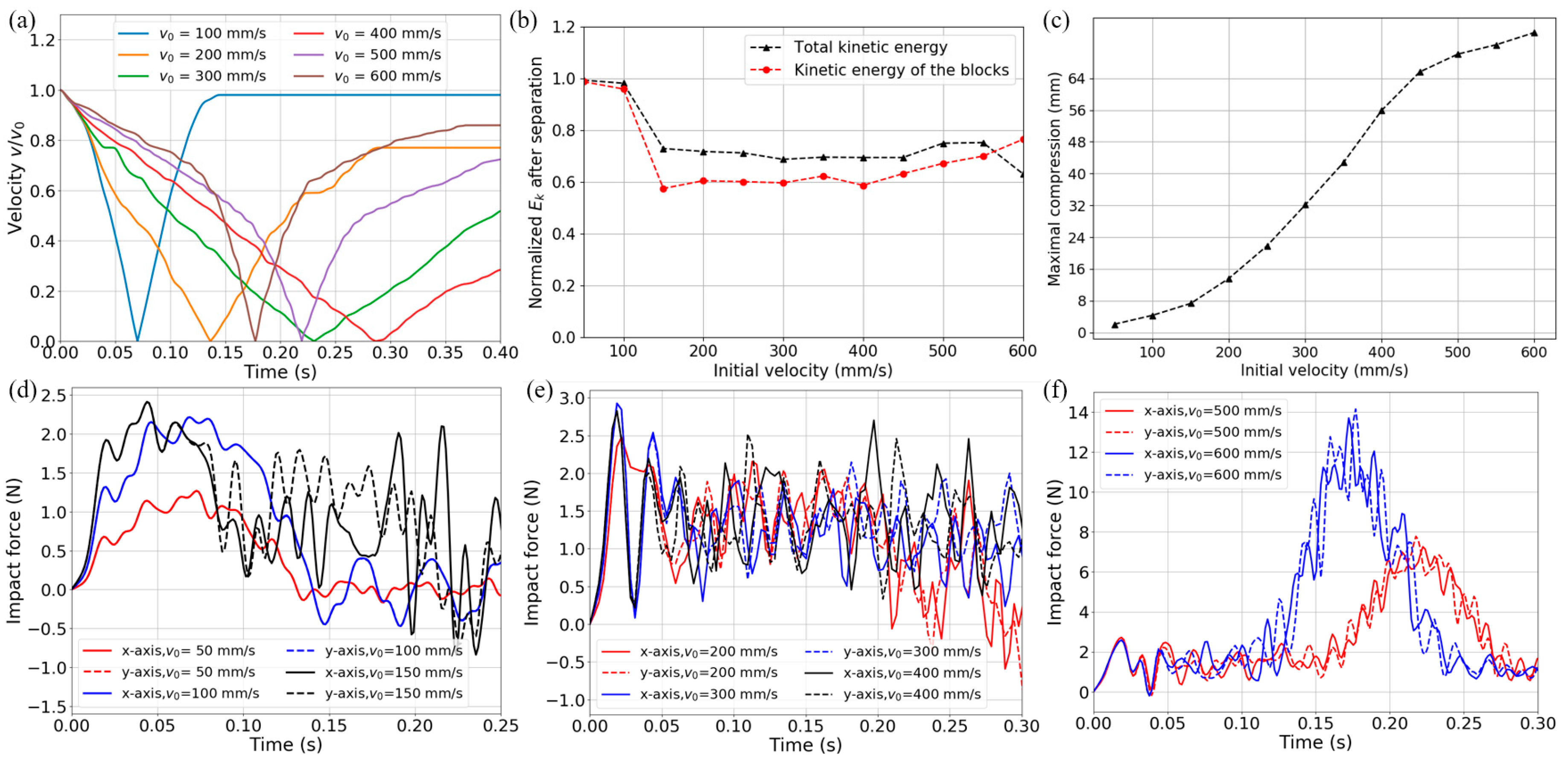
3.2. Transient Dynamic Impact
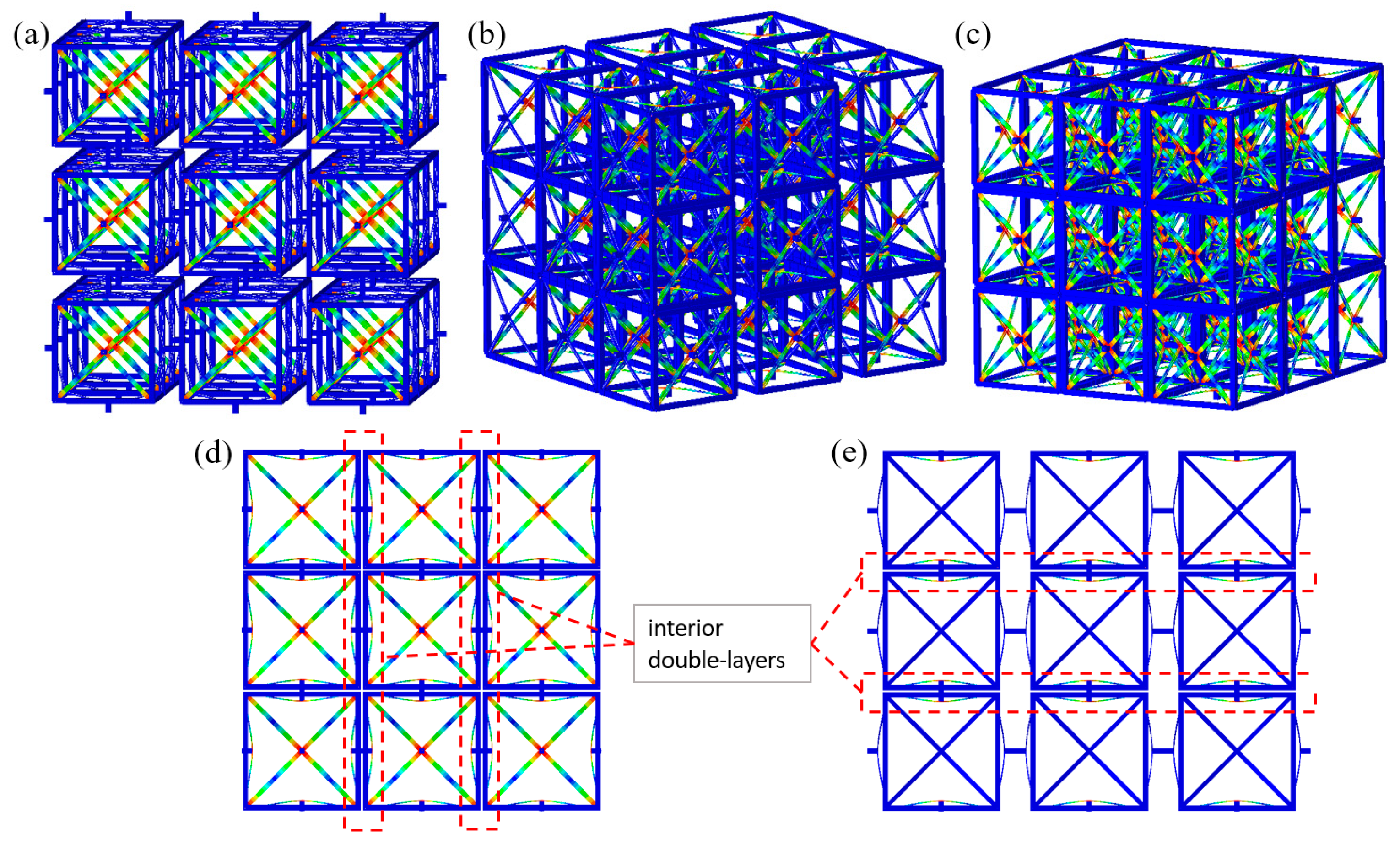
4. Performance of the Tridirectional Buckling-based Negative Stiffness Metamaterial
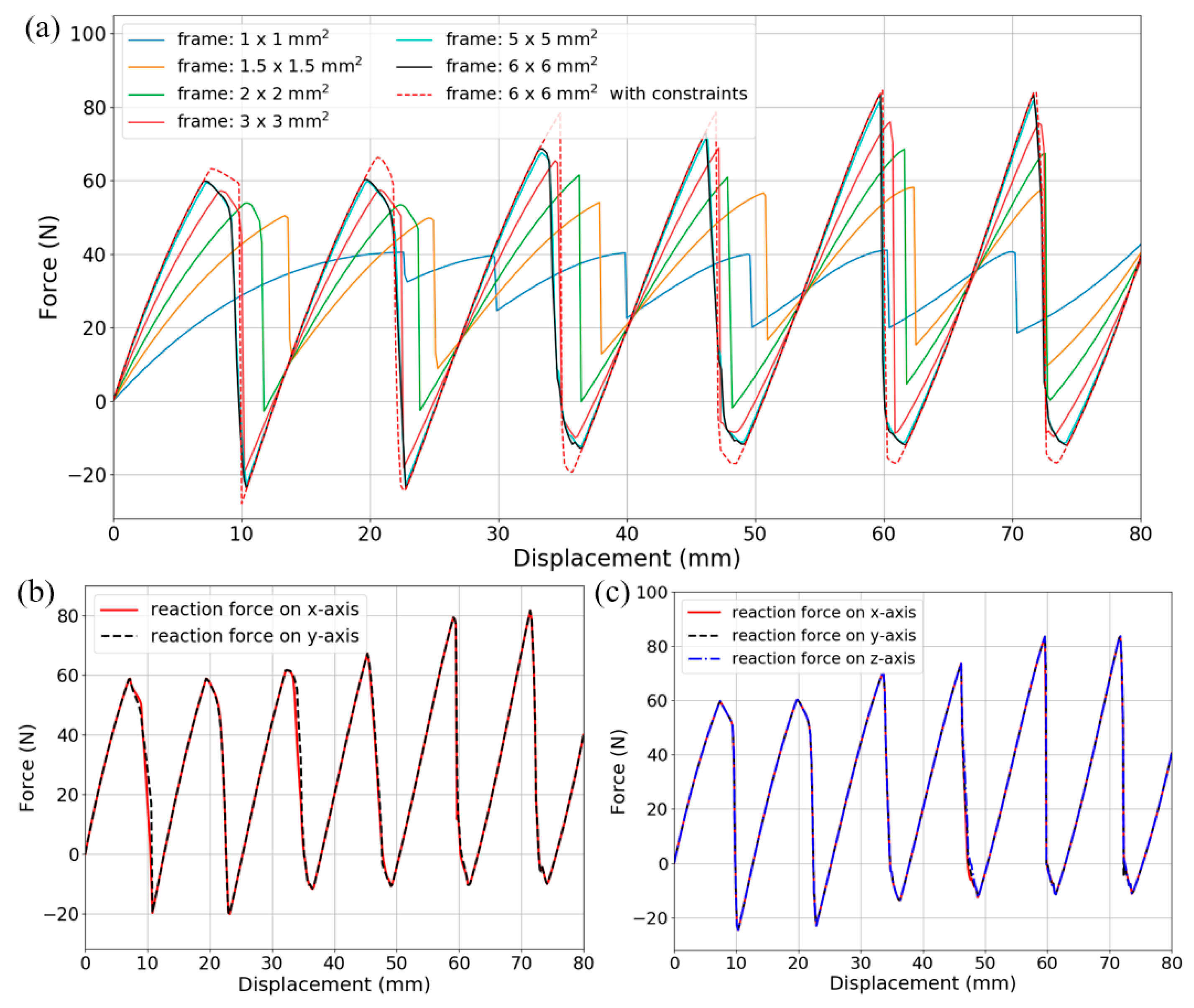
4.1. Quasi-Static Compression
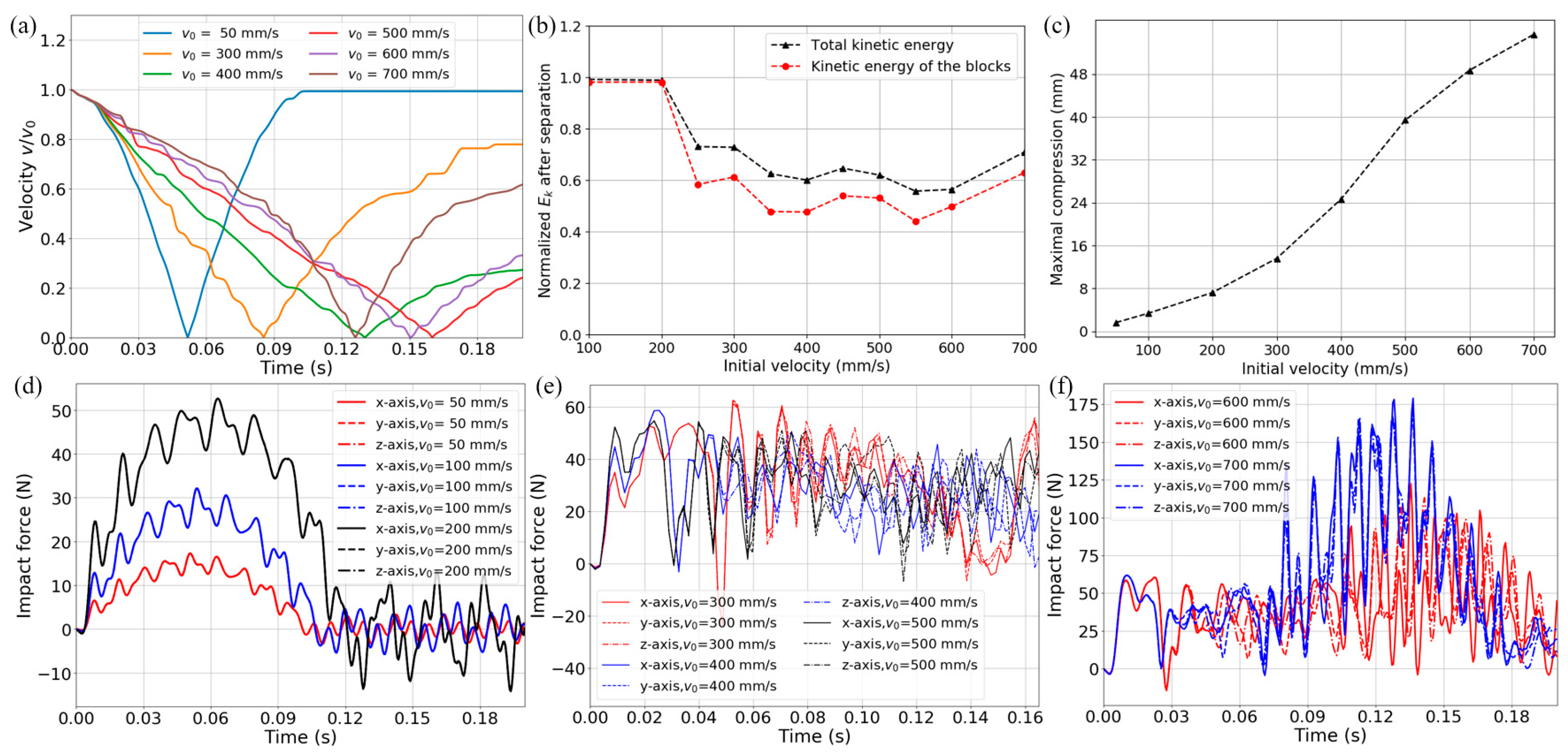
4.2. Transient Dynamic Impact
5. Conclusions
- Geometric parameters of the curved beam are systematically studied in FEA and the results of force-displacement relations show excellent agreement with high-order theoretical solutions. With different parameter combinations, beams of various f-d behaviors can be designed to form BNS metamaterials and structures. In models comprising multiple curved-beam layers, external energy is absorbed via large elastic deformation while reusability is preserved.
- For the bi/tridirectional metamaterial designs, transient impact simulations show that within the load-bearing capacity, impact energy can be absorbed and stored inside the metamaterial/structure and the reaction force never exceeds the buckling force thresholds. Even for extreme impact situations, the force remains below the thresholds before bottom-outs occur.
- To construct all these BNS metamaterials, relatively rigid supporting frames are added besides the curved beams. They have been proved essential to providing boundary conditions for the beams to exhibit negative stiffness behaviors. Therefore, by specially adjusting their geometry and the corresponding rigidity, the overall performance of the metamaterials can be tuned.
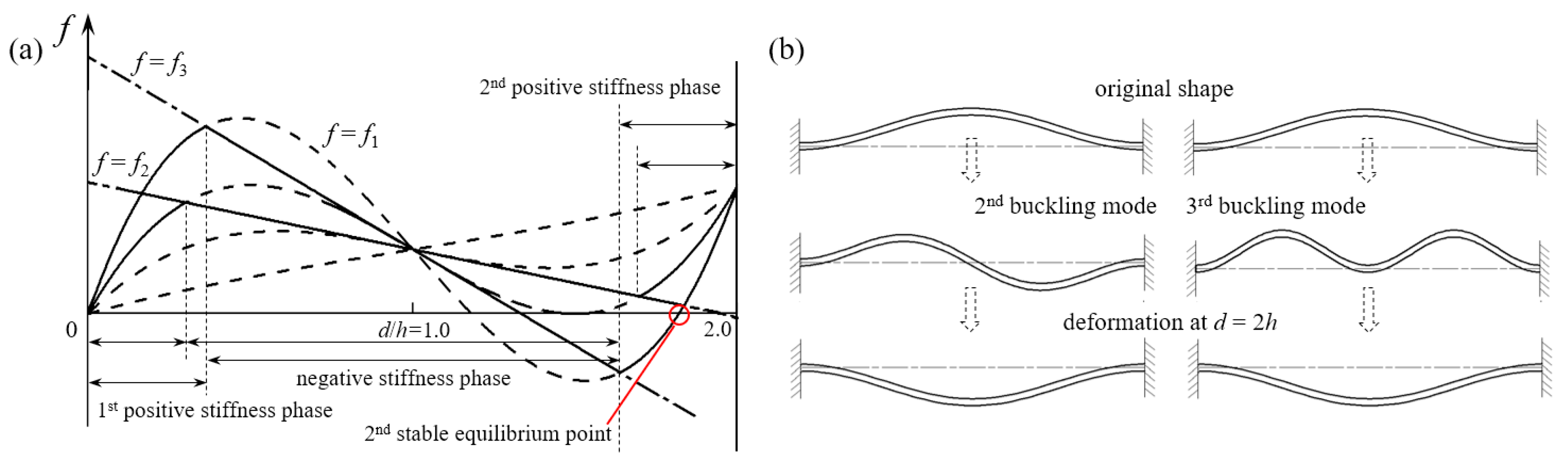
- During the deforming process, if the second mode of the curved beam is not constrained, twisting and rotation at the midpoint may occur and the buckling force threshold will be reduced, which can be favorable or adverse according to different applications. To avoid this from happening, two or more beams can be clamped together at their midpoints.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Li, T.; Chen, Y.; Hu, X.; Li, Y.; Wang, L. Exploiting negative Poisson’s ratio to design 3D-printed composites with enhanced mechanical properties. Mater. Des. 2018, 142, 247–258. [Google Scholar] [CrossRef]
- Mizzi, L.; Mahdi, E.M.; Titov, K.; Gatt, R.; Attard, D.; Evans, K.E.; Grima, J.N.; Tan, J. Mechanical metamaterials with star-shaped pores exhibiting negative and zero Poisson’s ratio. Mater. Des. 2018, 146, 28–37. [Google Scholar] [CrossRef]
- Babaee, S.; Shim, J.; Weaver, J.C.; Chen, E.R.; Patel, N.; Bertoldi, K. 3D Soft Metamaterials with Negative Poisson’s Ratio. Adv. Mater. 2013, 25, 5044–5049. [Google Scholar] [CrossRef] [PubMed]
- Fu, M.; Liu, F.; Hu, L. A novel category of 3D chiral material with negative Poisson’s ratio. Compos. Sci. Technol. 2018, 160, 111–118. [Google Scholar] [CrossRef]
- Wang, X.T.; Wang, B.; Li, X.W.; Ma, L. Mechanical properties of 3D re-entrant auxetic cellular structures. Int. J. Mech. Sci. 2017, 131, 396–407. [Google Scholar] [CrossRef]
- Xie, Y.M.; Yang, X.; Shen, J.; Yan, X.; Ghaedizadeh, A.; Rong, J.; Huang, X.; Zhou, S. Designing orthotropic materials for negative or zero compressibility. Int. J. Solids Struct. 2014, 51, 4038–4051. [Google Scholar] [CrossRef]
- Lakes, R.S.; Lee, T.; Bersie, A.; Wang, Y.C. Extreme damping in composite materials with negative-stiffness inclusions. Nature 2001, 410, 565–567. [Google Scholar] [CrossRef] [PubMed]
- Nicolaou, Z.G.; Motter, A.E. Mechanical metamaterials with negative compressibility transitions. Nat. Mater. 2012, 11, 608–613. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Farag, A.; Pasini, D. Routes to program thermal expansion in three-dimensional lattice metamaterials built from tetrahedral building blocks. J. Mech. Phys. Solids 2018, 117, 54–87. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Li, T.; Cao, S.; Wang, L. Hoberman-sphere-inspired lattice metamaterials with tunable negative thermal expansion. Compos. Struct. 2018, 189, 586–597. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, S.; Wang, Y.; Zhang, C. Topology optimization of anisotropic broadband double-negative elastic metamaterials. J. Mech. Phys. Solids 2017, 105, 54–80. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Wang, Y.; Wang, W.; Zhang, B.; Gai, X. Membrane acoustic metamaterial absorbers with magnetic negative stiffness. J. Acoust. Soc. Am. 2017, 141, 840–846. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R.S.; Drugan, W.J. Dramatically stiffer elastic composite materials due to a negative stiffness phase? J. Mech. Phys. Solids 2002, 50, 979–1009. [Google Scholar] [CrossRef]
- Wang, Y.C.; Ludwigson, M.; Lakes, R.S. Deformation of extreme viscoelastic metals and composites. Mater. Sci. Eng. A 2004, 370, 41–49. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lakes, R.S. Extreme thermal expansion, piezoelectricity, and other coupled field properties in composites with a negative stiffness phase. J. Appl. Phys. 2001, 90, 6458–6465. [Google Scholar] [CrossRef]
- Eijk, J.V.; Dijksman, J.F. Plate spring mechanism with constant negative stiffness. Mech. Mach. Theory 1979, 14, 1–9. [Google Scholar] [CrossRef]
- Huang, X.; Liu, X.; Sun, J.; Zhang, Z.; Hua, H. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: A theoretical and experimental study. J. Sound Vib. 2014, 333, 1132–1148. [Google Scholar] [CrossRef]
- Guell Izard, A.; Fabian Alfonso, R.; McKnight, G.; Valdevit, L. Optimal design of a cellular material encompassing negative stiffness elements for unique combinations of stiffness and elastic hysteresis. Mater. Des. 2017, 135, 37–50. [Google Scholar] [CrossRef]
- Liu, F.; Theodossiades, S.; McFarland, D.M.; Vakakis, A.F.; Bergman, L.A. Tailoring Strongly Nonlinear Negative Stiffness. J. Mech. Des. 2013, 136, 24501. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Y.; Zhou, J.; Lou, J. On the analytical and experimental assessment of the performance of a quasi-zero-stiffness isolator. J. Vib. Control 2013, 20, 2314–2325. [Google Scholar] [CrossRef]
- Bertoldi, K. Harnessing Instabilities to Design Tunable Architected Cellular Materials. Annu. Rev. Mater. Res. 2017, 47, 51–61. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Tran, P.; Ngo, T.D.; Xie, Y.M. Design and characterisation of a tuneable 3D buckling-induced auxetic metamaterial. Mater. Des. 2018, 139, 336–342. [Google Scholar] [CrossRef]
- Vangbo, M. An analytical analysis of a compressed bistable buckled beam. Sens. Actuators A 1998, 69, 212–216. [Google Scholar] [CrossRef]
- Qiu, J.; Lang, J.H.; Slocum, A.H. A centrally-clamped parallel-beam bistable MEMS mechanism. In Proceedings of the 14th IEEE International Conference on Micro Electro Mechanical Systems, Interlaken, Switzerland, 25 January 2001; pp. 353–356. [Google Scholar] [CrossRef]
- Qiu, J.; Lang, J.H.; Slocum, A.H. A Curved-Beam Bistable Mechanism. J. Microelectromech. Syst. 2004, 13, 137–146. [Google Scholar] [CrossRef]
- Cazottes, P.; Fernandes, A.N.; Pouget, J.; Hafez, M. Bistable Buckled Beam: Modeling of Actuating Force and Experimental Validations. J. Mech. Des. 2009, 131, 101001. [Google Scholar] [CrossRef]
- Klatt, T.; Haberman, M.; Seepersad, C. Selective laser sintering of negative stiffness mesostructures for recoverable, nearly-ideal shock isolation. In Proceedings of the 24th International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 12–14 August 2013; pp. 1010–1022. [Google Scholar]
- Correa, D.M.; Klatt, T.; Cortes, S.; Haberman, M.; Kovar, D.; Seepersad, C. Negative stiffness honeycombs for recoverable shock isolation. Rapid Prototyp. J. 2015, 21, 193–200. [Google Scholar] [CrossRef]
- Fulcher, B.A.; Shahan, D.W.; Haberman, M.R.; Seepersad, C.C.; Wilson, P.S. Analytical and Experimental Investigation of Buckled Beams as Negative Stiffness Elements for Passive Vibration and Shock Isolation Systems. J. Vib. Acoust. 2014, 136, 31009. [Google Scholar] [CrossRef]
- Correa, D.; Bostwick, K.; Wilson, P.S.; Haberman, M.; Seepersad, C.C. Mechanical Impact Performance of Additively Manufactured Negative Stiffness Honeycombs. In Proceedings of the 26th International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 10–12 August 2015; pp. 1422–1433. [Google Scholar]
- Correa, D.M. Design and Evaluation of Negative Stiffness Honeycombs for Recoverable Shock Isolation. Master Thesis, The University of Texas at Austin, Austin, TX, USA, 2015. [Google Scholar]
- Rafsanjani, A.; Akbarzadeh, A.; Pasini, D. Snapping Mechanical Metamaterials under Tension. Adv. Mater. 2015, 27, 5931–5935. [Google Scholar] [CrossRef] [PubMed]
- Restrepo, D.; Mankame, N.D.; Zavattieri, P.D. Phase transforming cellular materials. Extreme Mech. Lett. 2015, 4, 52–60. [Google Scholar] [CrossRef]
- Frenzel, T.; Findeisen, C.; Kadic, M.; Gumbsch, P.; Wegener, M. Tailored Buckling Microlattices as Reusable Light-Weight Shock Absorbers. Adv. Mater. 2016, 28, 5865–5870. [Google Scholar] [CrossRef] [PubMed]
- Shan, S.; Kang, S.H.; Raney, J.R.; Wang, P.; Fang, L.; Candido, F.; Lewis, J.A.; Bertoldi, K. Multistable Architected Materials for Trapping Elastic Strain Energy. Adv. Mater. 2015, 27, 4296–4301. [Google Scholar] [CrossRef] [PubMed]
- Goldsberry, B.M.; Haberman, M.R. Negative stiffness honeycombs as tunable elastic metamaterials. J. Appl. Phys. 2018, 123, 91711. [Google Scholar] [CrossRef]
- Nadkarni, N.; Daraio, C.; Kochmann, D.M. Dynamics of periodic mechanical structures containing bistable elastic elements: From elastic to solitary wave propagation. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 23204. [Google Scholar] [CrossRef] [PubMed]
- Puglisi, G.; Truskinovsky, L. Mechanics of a discrete chain with bi-stable elements. J. Mech. Phys. Solids 2000, 48, 1–27. [Google Scholar] [CrossRef]
- Benichou, I.; Givli, S. The hidden ingenuity in titin structure. Appl. Phys. Lett. 2011, 98, 91904. [Google Scholar] [CrossRef]
- Benichou, I.; Givli, S. Structures undergoing discrete phase transformation. J. Mech. Phys. Solids 2013, 61, 94–113. [Google Scholar] [CrossRef]
- Che, K.; Yuan, C.; Wu, J.; Qi, H.J.; Meaud, J. Three-Dimensional-Printed Multistable Mechanical Metamaterials with a Deterministic Deformation Sequence. J. Appl. Mech. 2016, 84, 11004. [Google Scholar] [CrossRef]
- Findeisen, C.; Hohe, J.; Kadic, M.; Gumbsch, P. Characteristics of mechanical metamaterials based on buckling elements. J. Mech. Phys. Solids 2017, 102, 151–164. [Google Scholar] [CrossRef]
- Liu, J.; Qin, H.; Liu, Y. Dynamic behaviors of phase transforming cellular structures. Compos. Struct. 2018, 184, 536–544. [Google Scholar] [CrossRef]
- Florijn, B.; Coulais, C.; Van, H.M. Programmable mechanical metamaterials. Phys. Rev. Lett. 2014, 113, 175503. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.H.; Hong, M.S.; Kim, Y.Y. Adjoining of negative stiffness and negative density bands in an elastic metamaterial. Appl. Phys. Lett. 2016, 108, 93501. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Pasini, D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extreme Mech. Lett. 2016, 9, 291–296. [Google Scholar] [CrossRef]
- Hewage, T.A.M.; Alderson, K.L.; Alderson, A.; Scarpa, F. Double-Negative Mechanical Metamaterials Displaying Simultaneous Negative Stiffness and Negative Poisson’s Ratio Properties. Adv. Mater. 2016, 28, 10323–10332. [Google Scholar] [CrossRef] [PubMed]
- Duoss, E.B.; Weisgraber, T.H.; Hearon, K.; Zhu, C.; Small, W.; Metz, T.R.; Vericella, J.J.; Barth, H.D.; Kuntz, J.D.; Maxwell, R.S.; et al. Three-Dimensional Printing of Elastomeric, Cellular Architectures with Negative Stiffness. Adv. Funct. Mater. 2014, 24, 4905–4913. [Google Scholar] [CrossRef]
- Prasad, J.; Diaz, A.R. Synthesis of Bistable Periodic Structures Using Topology Optimization and a Genetic Algorithm. J. Mech. Des. 2005, 128, 1298–1306. [Google Scholar] [CrossRef]
- Prasad, J.; Diaz, A.R. Viscoelastic material design with negative stiffness components using topology optimization. Struct. Multidiscip. Optim. 2009, 38, 583–597. [Google Scholar] [CrossRef]
- Correa, D.M.; Seepersad, C.C.; Haberman, M.R. Mechanical design of negative stiffness honeycomb materials. Integr. Mater. Manuf. Innov. 2015, 4, 1–11. [Google Scholar] [CrossRef]
- Overvelde, J.T.B.; Shan, S.; Bertoldi, K. Compaction through Buckling in 2D Periodic, Soft and Porous Structures: Effect of Pore Shape. Adv. Mater. 2012, 24, 2337–2342. [Google Scholar] [CrossRef] [PubMed]
- Ghaedizadeh, A.; Shen, J.; Ren, X.; Xie, Y. Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity. Materials 2016, 9, 54. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.M.; Zhang, J.; Yu, T.X. Collapse of periodic planar lattices under uniaxial compression, part II: Dynamic crushing based on finite element simulation. Int. J. Impact Eng. 2009, 36, 1231–1241. [Google Scholar] [CrossRef]
| Parameter Name | Minimum | Maximum | Interval | Unit |
|---|---|---|---|---|
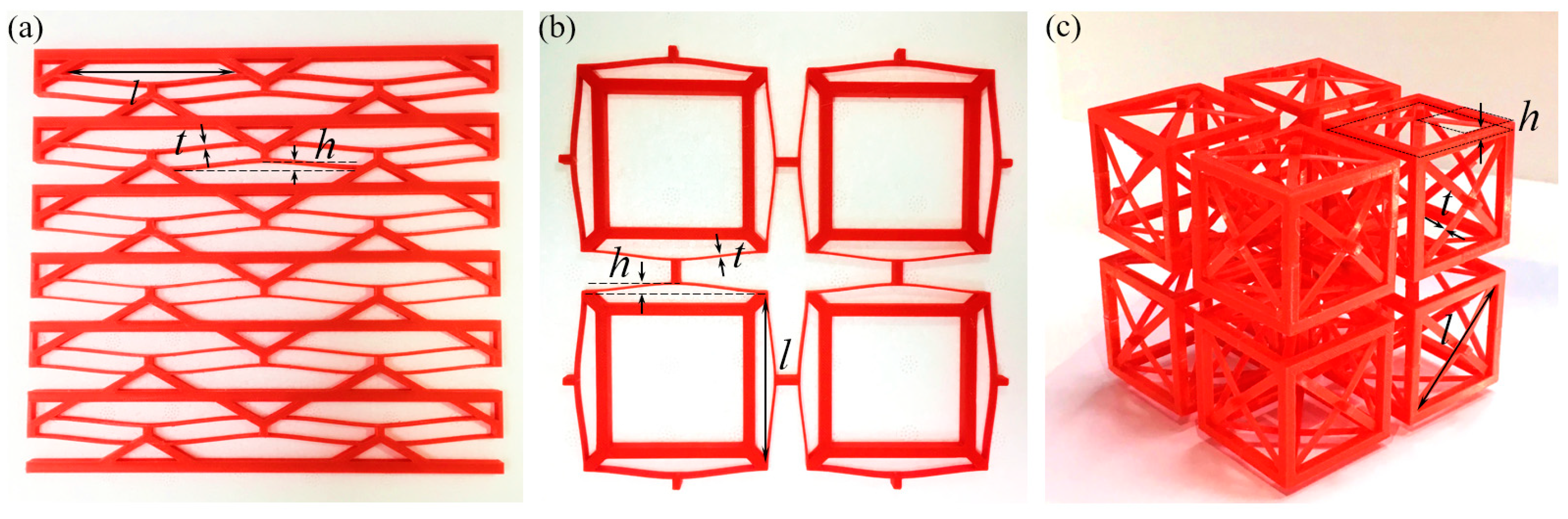
| Beam span l | 75 | 120 | 3 | mm |
| Beam apex height h | 1.2 | 6.4 | 0.4 | mm |
| Beam thickness tbm 1 | 0.5 | 1.8 | 0.1 | mm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, C.; Yang, D.; Qin, H. Mechanical Performance of Multidirectional Buckling-Based Negative Stiffness Metamaterials: An Analytical and Numerical Study. Materials 2018, 11, 1078. https://doi.org/10.3390/ma11071078
Ren C, Yang D, Qin H. Mechanical Performance of Multidirectional Buckling-Based Negative Stiffness Metamaterials: An Analytical and Numerical Study. Materials. 2018; 11(7):1078. https://doi.org/10.3390/ma11071078
Chicago/Turabian StyleRen, Chenhui, Deqing Yang, and Haoxing Qin. 2018. "Mechanical Performance of Multidirectional Buckling-Based Negative Stiffness Metamaterials: An Analytical and Numerical Study" Materials 11, no. 7: 1078. https://doi.org/10.3390/ma11071078
APA StyleRen, C., Yang, D., & Qin, H. (2018). Mechanical Performance of Multidirectional Buckling-Based Negative Stiffness Metamaterials: An Analytical and Numerical Study. Materials, 11(7), 1078. https://doi.org/10.3390/ma11071078




