Development of Perovskite-Type Materials for Thermoelectric Application
Abstract
1. Introduction
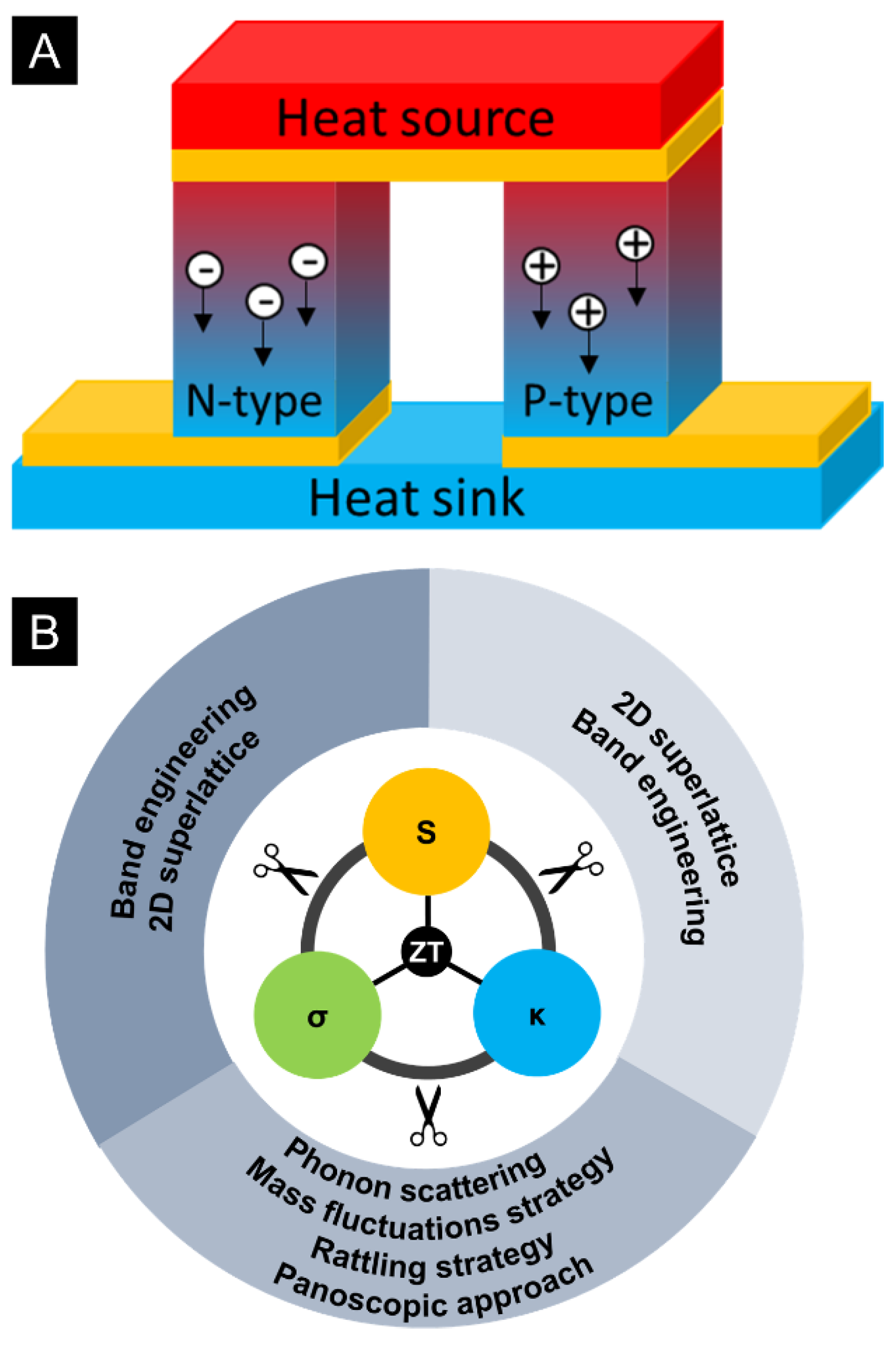
1.1. Thermoelectrics (TE)
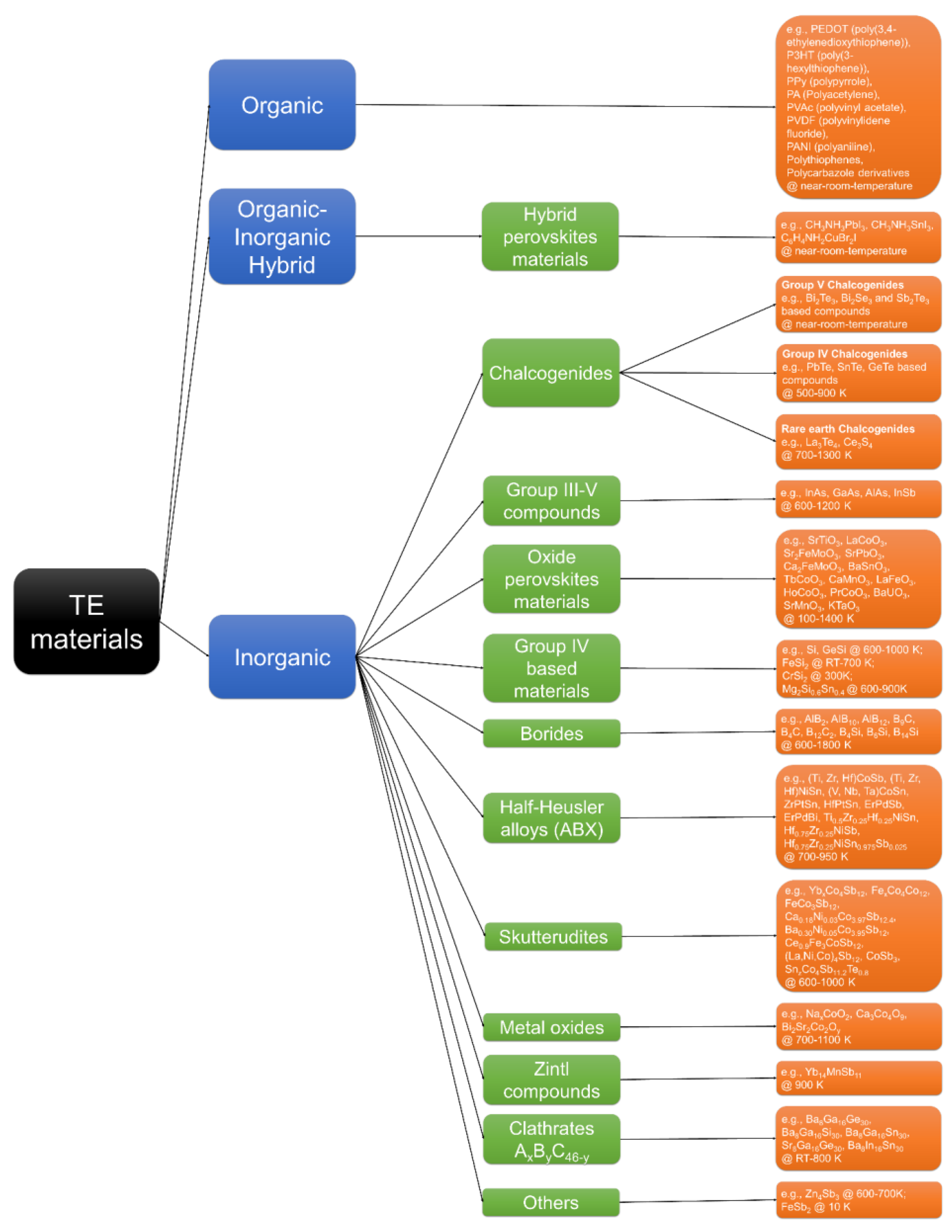
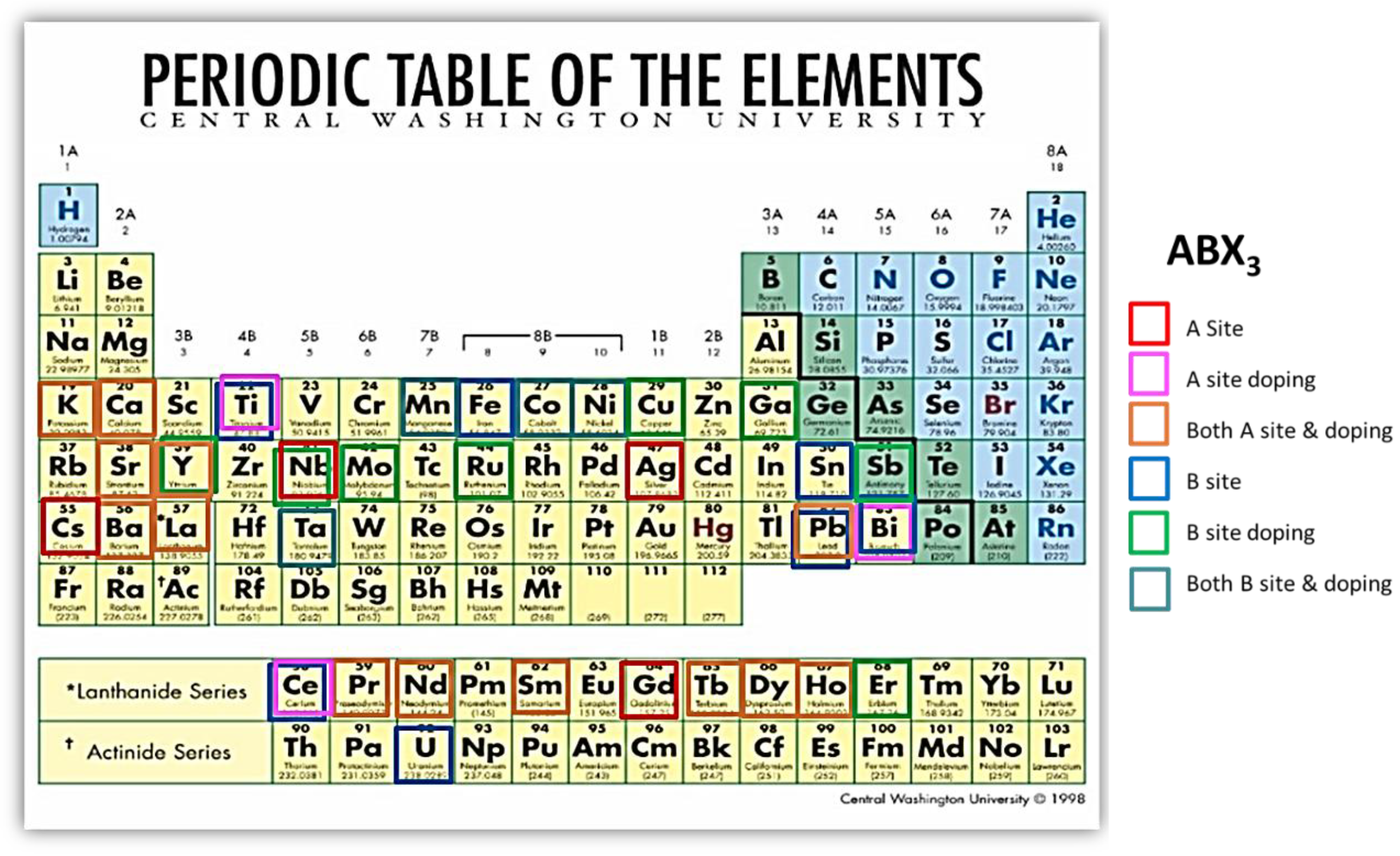
1.2. Perovskite Materials
2. Oxide Perovskites
2.1. Titanium (Ti) as B-Site (ATiO3)
2.1.1. Enhancing Electrical Conductivity
2.1.2. Decoupling Electrical Conductivity and Seebeck Coefficient
2.1.3. Reducing Thermal Conductivity
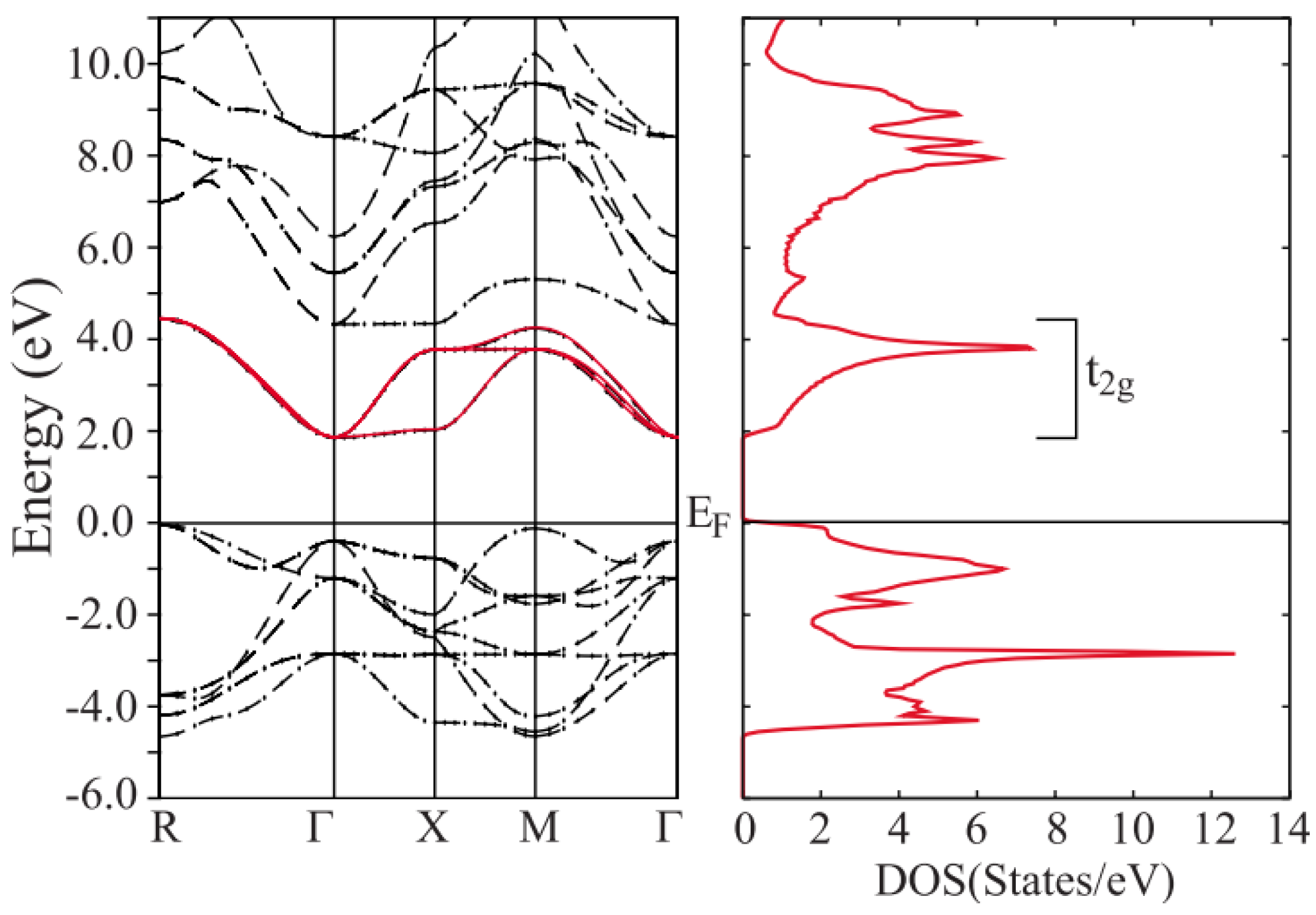
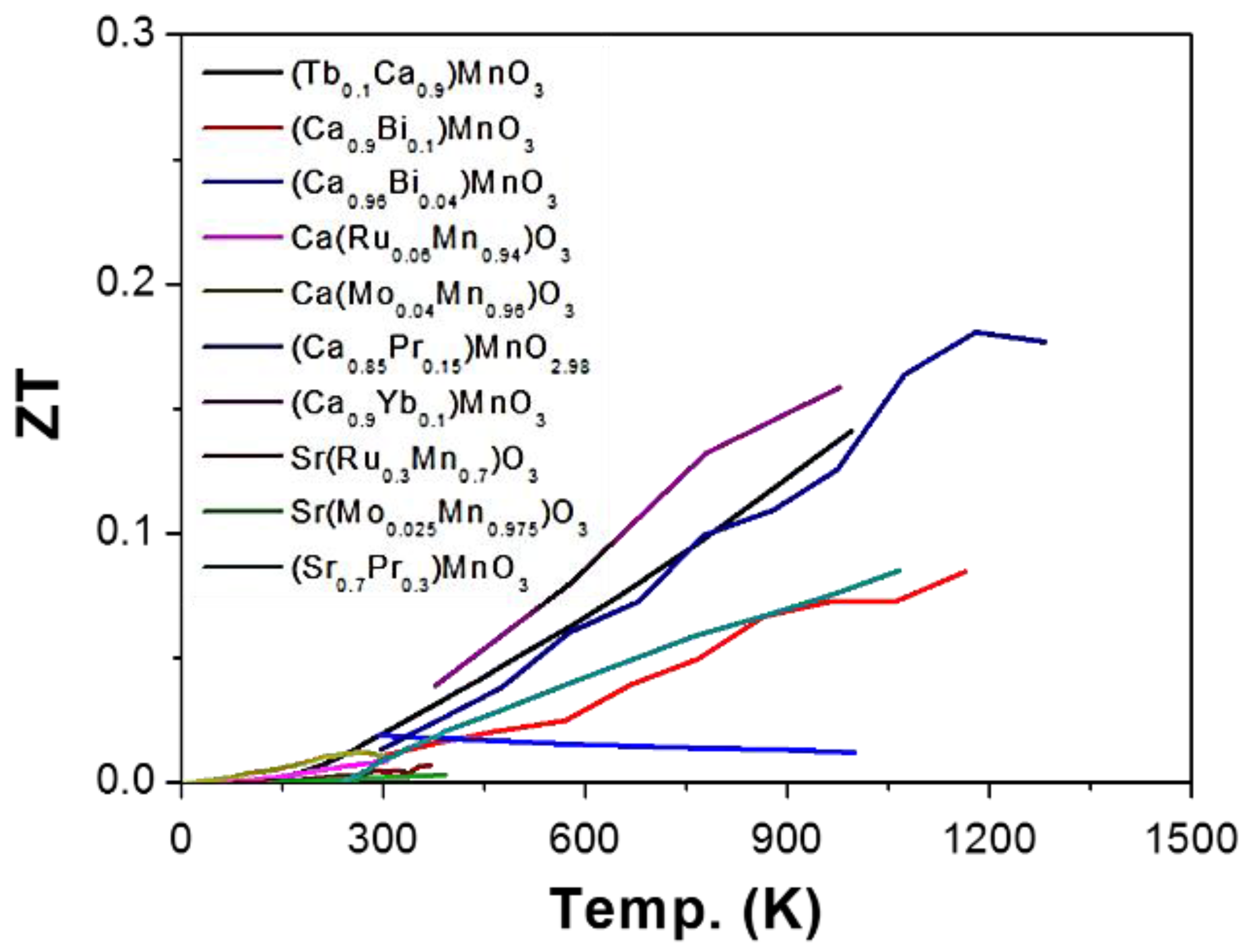
2.2. Manganese (Mn) as B-Site (AMnO3)
2.2.1. Enhancing Electrical Conductivity
2.2.2. Reducing Thermal Conductivity
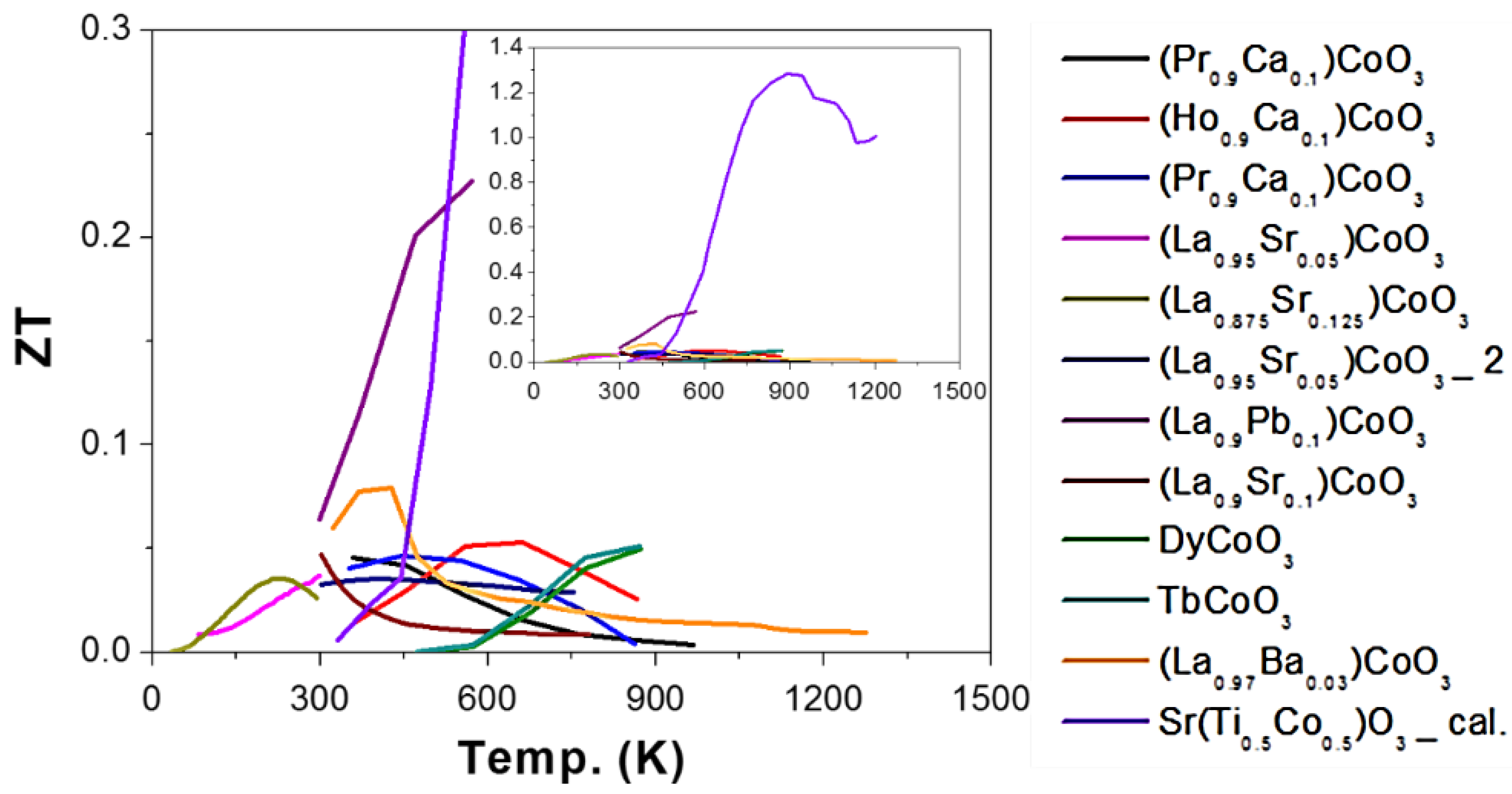
2.3. Cobalt (Co) as B-Site (ACoO3)
2.3.1. Chemical Doping in A-Site
2.3.2. Chemical Doping in B-Site
2.3.3. Reducing Thermal Conductivity
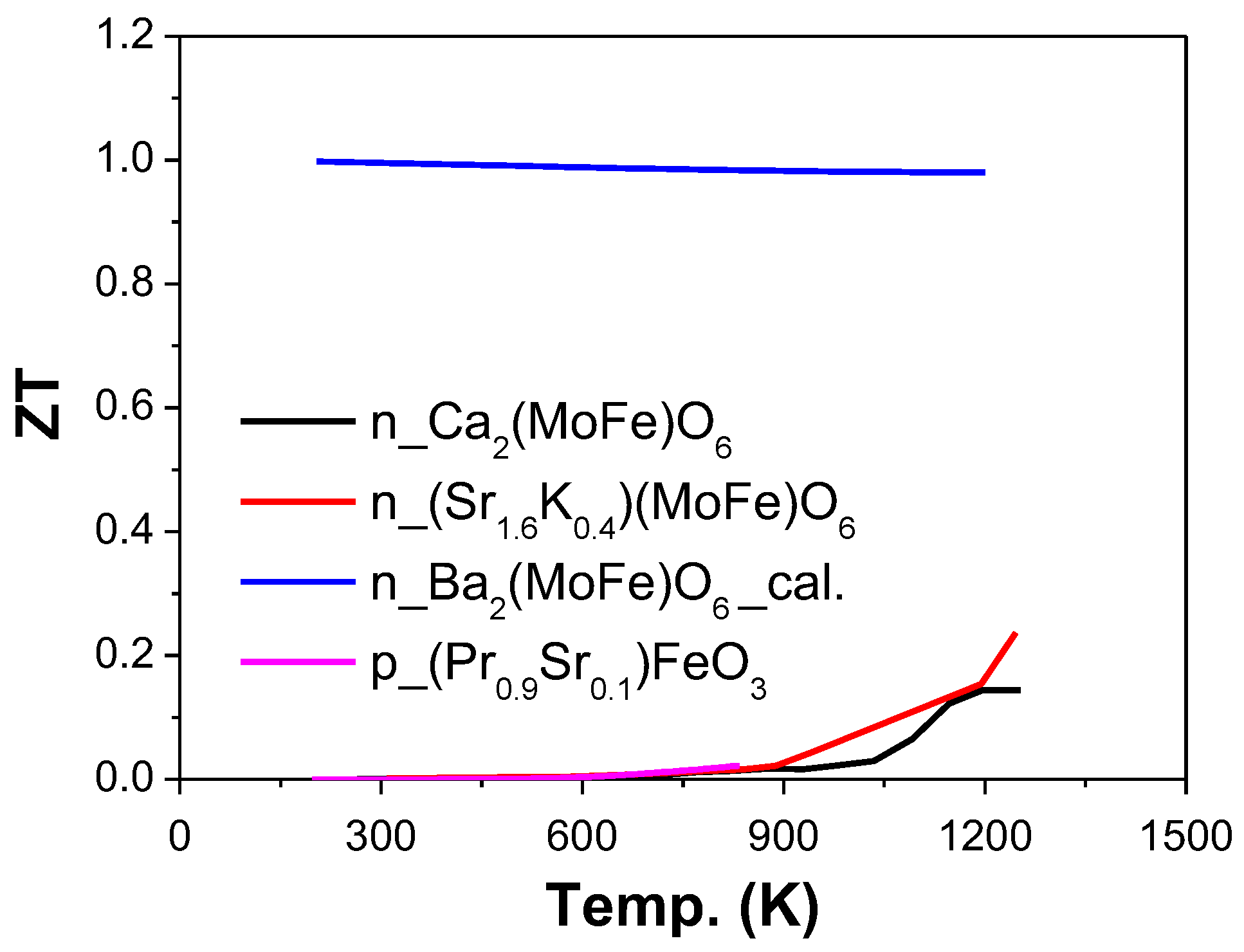
2.4. Other Elements, Including Iron (Fe), Nickel (Ni), Tin (Sn), Lead (Pb), Bismuth (Bi), Molybdenum (Mo), Ruthenium (Ru), and Uranium (U) as B-Site (ABO3)
2.4.1. Fe as B-Site (AFeO3)
2.4.2. Ni as B-Site (ANiO3)
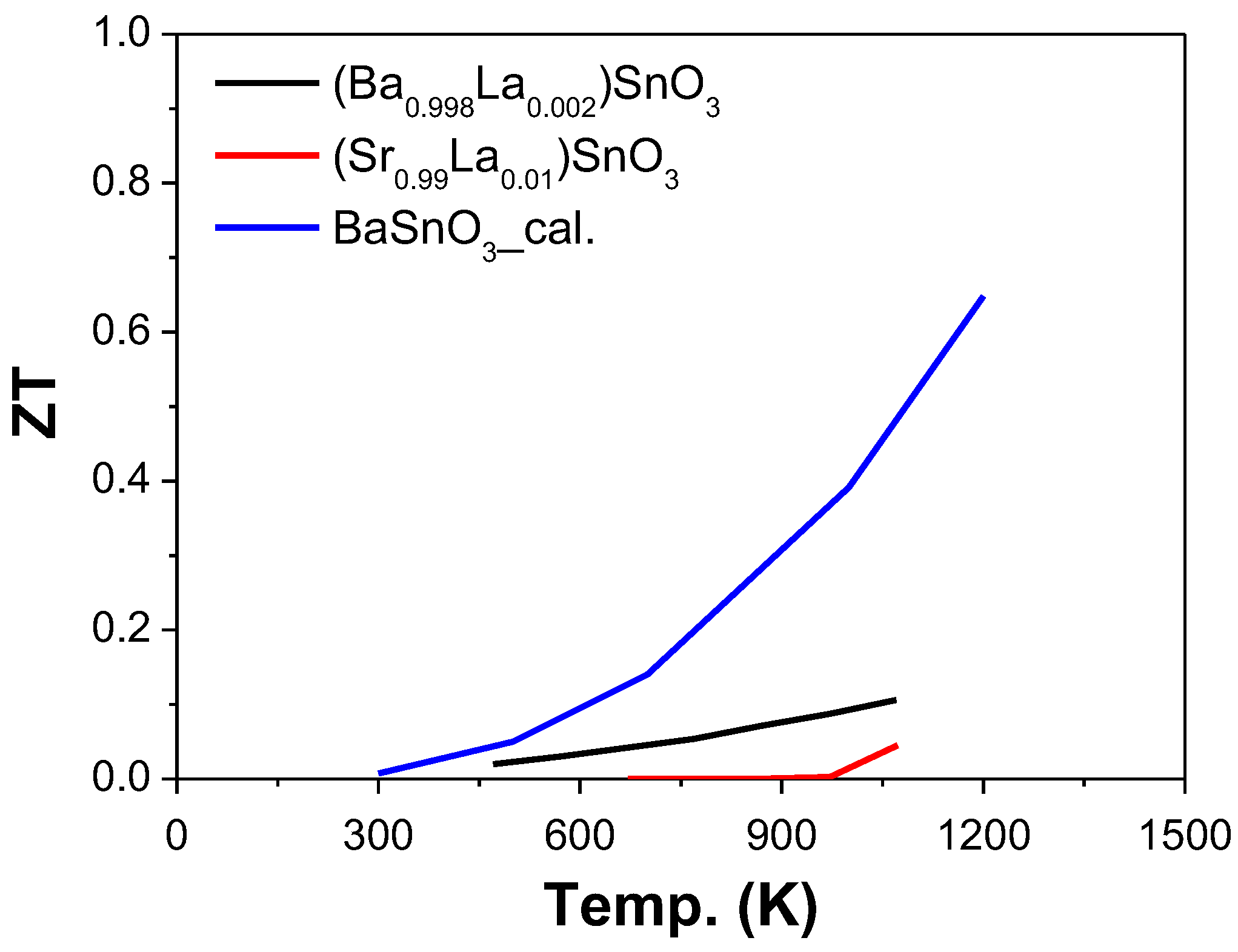
2.4.3. Sn as B-Site (ASnO3)
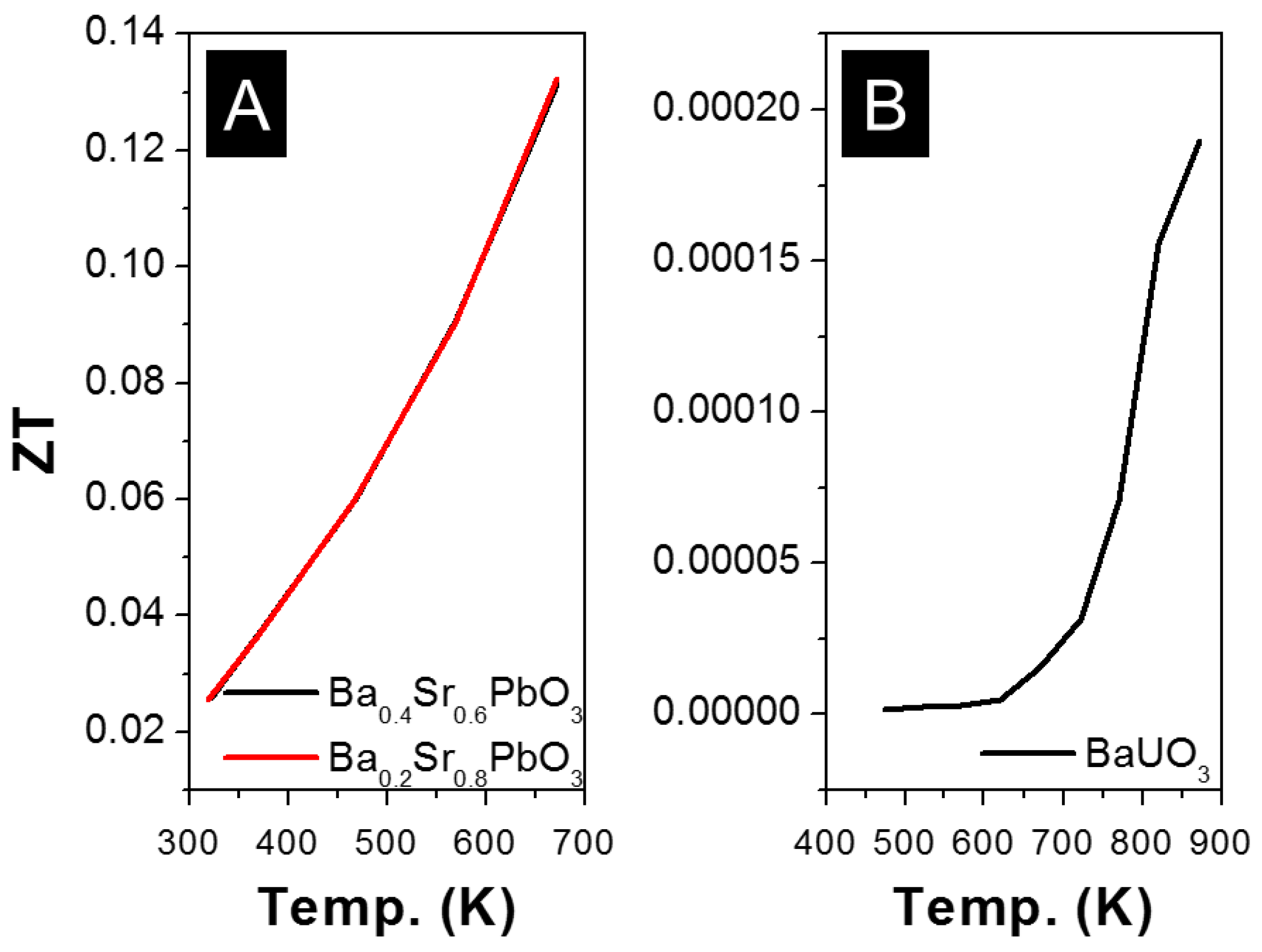
2.4.4. Pb as B-Site (APbO3)
2.4.5. Bi as B-Site (ABiO3)
2.4.6. Mo as B-Site (AMoO3)
2.4.7. Ru as B-Site (ARuO3)
2.4.8. U as B-Site (AUO3)
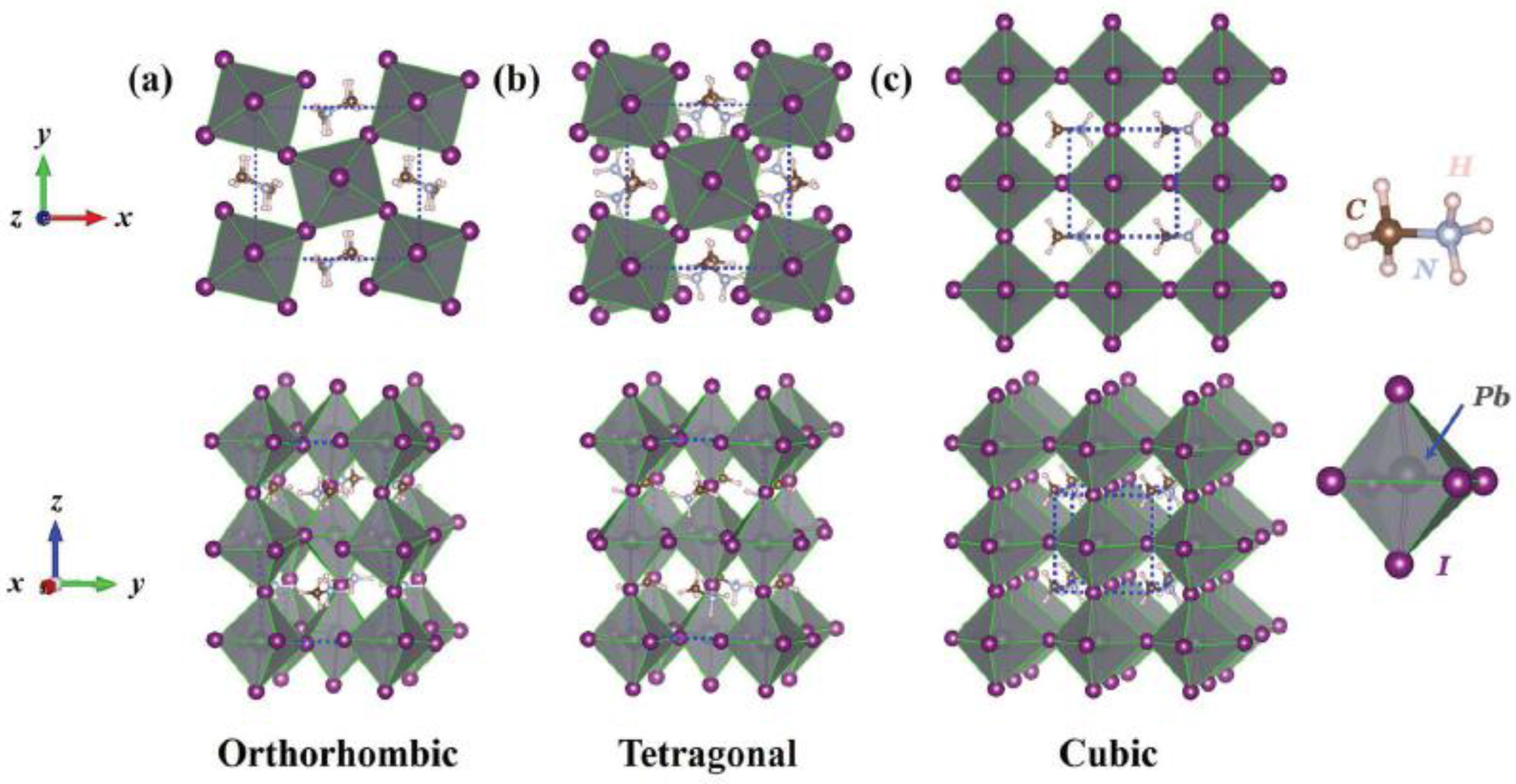
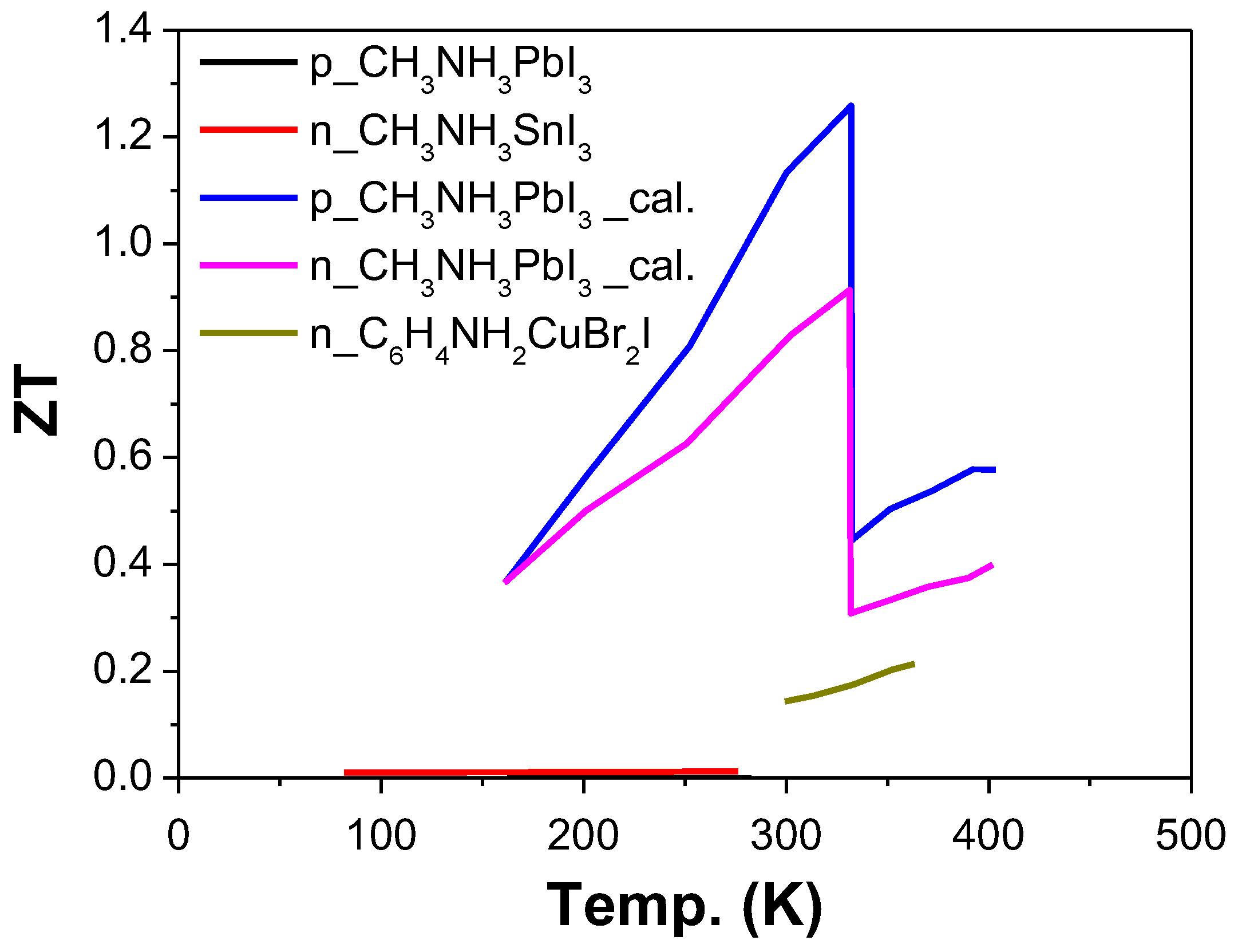
3. Hybrid Perovskites
4. Conclusions and Outlook
Funding
Conflicts of Interest
References
- Zebarjadi, M.; Esfarjani, K.; Dresselhaus, M.S.; Ren, Z.F.; Chen, G. Perspectives on thermoelectrics: From fundamentals to device applications. Energy Environ. Sci. 2012, 5, 5147–5162. [Google Scholar] [CrossRef]
- Nolas, G.S.; Sharp, J.; Goldsmid, H.J. Thermoelectrics; Springer Series in MATERIALS SCIENCE; Springer: Berlin/Heidelberg, Germany, 2001; Volume 45, pp. 59–109. ISBN 978-3-642-07451-6. [Google Scholar]
- Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and Old Concepts in Thermoelectric Materials. Angew. Chem. Int. Ed. 2009, 48, 8616–8639. [Google Scholar] [CrossRef] [PubMed]
- Snyder, G.J.; Ursell, T.S. Thermoelectric Efficiency and Compatibility. Phys. Rev. Lett. 2003, 91, 148301. [Google Scholar] [CrossRef] [PubMed]
- McGrail, B.T.; Sehirlioglu, A.; Pentzer, E. Polymer composites for thermoelectric applications. Angew. Chem. Int. Ed. 2015, 54, 1710–1723. [Google Scholar] [CrossRef] [PubMed]
- Russ, B.; Glaudell, A.; Urban, J.J.; Chabinyc, M.L.; Segalman, R.A. Organic thermoelectric materials for energy harvesting and temperature control. Nat. Rev. Mater. 2016, 1, 16050. [Google Scholar] [CrossRef]
- Nielsch, K.; Bachmann, J.; Kimling, J.; Böttner, H. Thermoelectric Nanostructures: From Physical Model Systems towards Nanograined Composites. Adv. Energy Mater. 2011, 1, 713–731. [Google Scholar] [CrossRef]
- He, J.; Kanatzidis, M.G.; Dravid, V.P. High performance bulk thermoelectrics via a panoscopic approach. Mater. Today 2013, 16, 166–176. [Google Scholar] [CrossRef]
- Alam, H.; Ramakrishna, S. A review on the enhancement of figure of merit from bulk to nano-thermoelectric materials. Nano Energy 2013, 2, 190–212. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Lan, Y.; Minnich, A.J.; Chen, G.; Ren, Z. Enhancement of Thermoelectric Figure-of-Merit by a Bulk Nanostructuring Approach. Adv. Funct. Mater. 2010, 20, 357–376. [Google Scholar] [CrossRef]
- Kanatzidis, M.G. Nanostructured Thermoelectrics: The New Paradigm? Chem. Mater. 2010, 22, 648–659. [Google Scholar] [CrossRef]
- Zhang, Y.; Snedaker, M.L.; Birkel, C.S.; Mubeen, S.; Ji, X.; Shi, Y.; Liu, D.; Liu, X.; Moskovits, M.; Stucky, G.D. Silver-Based Intermetallic Heterostructures in Sb2Te3 Thick Films with Enhanced Thermoelectric Power Factors. Nano Lett. 2012, 12, 1075–1080. [Google Scholar] [CrossRef] [PubMed]
- Meng, B.C.; Liu, C.; Fan, S. A Promising Approach to Enhanced Thermoelectric Properties Using Carbon Nanotube Networks. Adv. Mater. 2010, 22, 535–539. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Ge, J.; Lin, Z.; Feng, X.; Wang, X.; Lu, H.; Yanga, Y.; Qiu, F. Environmental Science energy scattering at the organic—Inorganic semiconductor interface. Energy Environ. Sci. 2012, 5, 8351–8358. [Google Scholar] [CrossRef]
- Faleev, S.V.; Leonard, F. Theory of enhancement of thermoelectric properties of materials with nanoinclusions. Phys. Rev. B 2008, 77, 214304. [Google Scholar] [CrossRef]
- Yang, J.; Yip, H.-L.; Jen, A.K.-Y. Rational Design of Advanced Thermoelectric Materials. Adv. Energy Mater. 2013, 3, 549–565. [Google Scholar] [CrossRef]
- LaLonde, A.D.; Pei, Y.; Wang, H.; Jeffrey Snyder, G. Lead telluride alloy thermoelectrics. Mater. Today 2011, 14, 526–532. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, M.; Lee, K.-H.; Lee, C.-M.; Lee, H.-K.; Choa, Y.; Myung, N.V. Electrodeposition of Compact Tellurium Thick Films from Alkaline Baths. J. Electrochem. Soc. 2017, 164, D82–D87. [Google Scholar] [CrossRef]
- Wu, T.; Lee, H.-K.; Myung, N.V. Electrodeposition of Dense Lead Telluride Thick Films in Alkaline Solutions. J. Electrochem. Soc. 2016, 163, D801–D808. [Google Scholar] [CrossRef]
- Snyder, G.J.; Lim, J.R.; Huang, C.-K.; Fleurial, J.-P. Thermoelectric microdevice fabricated by a MEMS-like electrochemical process. Nat. Mater. 2003, 2, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Rostek, R.; Stein, N.; Boulanger, C. A review of electroplating for V-VI thermoelectric films: From synthesis to device integration. J. Mater. Res. 2015, 30, 2518–2543. [Google Scholar] [CrossRef]
- Massaro, M.; Dumay, J.; Bagnoli, C. Where there is a will there is a way. J. Intellect. Cap. 2015, 16, 490–517. [Google Scholar] [CrossRef]
- Bubnova, O.; Khan, Z.U.; Malti, A.; Braun, S.; Fahlman, M.; Berggren, M.; Crispin, X. Optimization of the thermoelectric figure of merit in the conducting polymer poly(3,4-ethylenedioxythiophene). Nat. Mater. 2011, 10, 429–433. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Qiu, F.; Lin, Z. Towards high-performance polymer-based thermoelectric materials. Energy Environ. Sci. 2013, 6, 1352–1361. [Google Scholar] [CrossRef]
- Shi, W.; Chen, J.; Xi, J.; Wang, D.; Shuai, Z. Search for Organic Thermoelectric Materials with High Mobility: The Case of 2,7-Dialkyl[1]benzothieno[3,2-b][1]benzothiophene Derivatives. Chem. Mater. 2014, 26, 2669–2677. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y.; Xu, W.; Zhu, D. Organic Thermoelectric Materials: Emerging Green Energy Materials Converting Heat to Electricity Directly and Efficiently. Adv. Mater. 2014, 26, 6829–6851. [Google Scholar] [CrossRef] [PubMed]
- Taroni, P.J.; Hoces, I.; Stingelin, N.; Heeney, M.; Bilotti, E. Thermoelectric materials: A brief historical survey from metal junctions and inorganic semiconductors to organic polymers. Isr. J. Chem. 2014, 54, 534–552. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, F.; Di, C.-A.A.; Yan, T.-W.W.; Zou, Y.; Zhou, X.; Zhu, D.; Wang, J.-Y.Y.; Pei, J. Toward High Performance n -Type Thermoelectric Materials by Rational Modification of BDPPV Backbones. J. Am. Chem. Soc. 2015, 137, 6979–6982. [Google Scholar] [CrossRef] [PubMed]
- Kroon, R.; Mengistie, D.A.; Kiefer, D.; Hynynen, J.; Ryan, J.D.; Yu, L.; Müller, C. Thermoelectric plastics: From design to synthesis, processing and structure–property relationships. Chem. Soc. Rev. 2016, 45, 6147–6164. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Xu, W.; Zhu, D. Recent advances in organic polymer thermoelectric composites. J. Mater. Chem. C 2017, 5, 4350–4360. [Google Scholar] [CrossRef]
- Cowen, L.M.; Atoyo, J.; Carnie, M.J.; Baran, D.; Schroeder, B.C. Review—Organic Materials for Thermoelectric Energy Generation. ECS J. Solid State Sci. Technol. 2017, 6, N3080–N3088. [Google Scholar] [CrossRef]
- Filippetti, A.; Caddeo, C.; Delugas, P.; Mattoni, A. Appealing Perspectives of Hybrid Lead-Iodide Perovskites as Thermoelectric Materials. J. Phys. Chem. C 2016, 120, 28472–28479. [Google Scholar] [CrossRef]
- Lee, C.; Hong, J.; Stroppa, A.; Whangbo, M.-H.; Shim, J.H. Organic–inorganic hybrid perovskites ABI3 (A = CH3NH3, NH2CHNH2; B = Sn, Pb) as potential thermoelectric materials: A density functional evaluation. RSC Adv. 2015, 5, 78701–78707. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Wang, J.; Xu, L.; Hu, B. An extremely high power factor in Seebeck effects based on a new n-type copper-based organic/inorganic hybrid C6H4NH2 CuBr2I film with metal-like conductivity. J. Mater. Chem. A 2017, 5, 13834–13841. [Google Scholar] [CrossRef]
- Wood, C. Materials for thermoelectric energy conversion. Inst. Phys. 1988, 51, 459–539. [Google Scholar] [CrossRef]
- Szczech, J.R.; Higgins, J.M.; Jin, S. Enhancement of the thermoelectric properties in nanoscale and nanostructured materials. J. Mater. Chem. 2011, 21, 4037–4055. [Google Scholar] [CrossRef]
- Choi, W.S.; Yoo, H.K.; Ohta, H. Polaron transport and thermoelectric behavior in la-doped SrTio3. thin films with elemental vacancies. Adv. Funct. Mater. 2015, 25, 799–804. [Google Scholar] [CrossRef]
- Roy, P.; Waghmare, V.; Maiti, T. Environmentally friendly BaxSr2−xTiFeO6 double perovskite with enhanced thermopower for high temperature thermoelectric power generation. RSC Adv. 2016, 6, 54636–54643. [Google Scholar] [CrossRef]
- Mehdizadeh Dehkordi, A.; Bhattacharya, S.; Darroudi, T.; Graff, J.W.; Schwingenschlögl, U.; Alshareef, H.N.; Tritt, T.M. Large thermoelectric power factor in Pr-doped SrTiO3−δ ceramics via grain-boundary-induced mobility enhancement. Chem. Mater. 2014, 26, 2478–2485. [Google Scholar] [CrossRef]
- Zhang, M.; Park, H.; Kim, J.; Park, H.; Wu, T.; Kim, S.; Park, S.-D.; Choa, Y.; Myung, N.V. Thermoelectric Properties of Ultralong Silver Telluride Hollow Nanofibers. Chem. Mater. 2015, 27, 5189–5197. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, M.; Lee, K.-H.; Kim, S.; Choa, Y.; Myung, N.V. Synthesis of Tellurium Heterostructures by Galvanic Displacement Reaction of Zinc in Alkaline Baths. Electrochim. Acta 2014, 150, 298–307. [Google Scholar] [CrossRef]
- Wu, T.; Myung, L.Y.; Zhang, M.; Lee, K.-H.; Lee, Y.L.; Lim, H.-R.; Kim, B.S.; Choa, Y.-H.; Myung, N.V. Size Controlled Synthesis of Tellurium Nanorices by Galvanic Displacement Reaction of Aluminum. Electrochim. Acta 2015, 176, 1382–1392. [Google Scholar] [CrossRef]
- Sahu, A.; Russ, B.; Su, N.C.; Forster, J.D.; Zhou, P.; Cho, E.S.; Ercius, P.; Coates, N.E.; Segalman, R.A.; Urban, J.J. Bottom-up design of de novo thermoelectric hybrid materials using chalcogenide resurfacing. J. Mater. Chem. A 2017, 5, 3346–3357. [Google Scholar] [CrossRef]
- Du, Y.; Shen, S.Z.; Cai, K.; Casey, P.S. Research progress on polymer-inorganic thermoelectric nanocomposite materials. Prog. Polym. Sci. 2012, 37, 820–841. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y.; Liang, Z. Solution processed organic thermoelectrics: Towards flexible thermoelectric modules. Energy Environ. Sci. 2015, 8, 401–422. [Google Scholar] [CrossRef]
- De Trizio, L.; Manna, L. Forging Colloidal Nanostructures via Cation Exchange Reactions. Chem. Rev. 2016, 116, 10852–10887. [Google Scholar] [CrossRef] [PubMed]
- Moon, G.D.; Ko, S.; Min, Y.; Zeng, J.; Xia, Y.; Jeong, U. Chemical transformations of nanostructured materials. Nano Today 2011, 6, 186–203. [Google Scholar] [CrossRef]
- Terasaki, I.; Sasago, Y.; Uchinokura, K. Large thermoelectric power in NaCo2O4 single crystals. Phys. Rev. B 1997, 56, R12685–R12687. [Google Scholar] [CrossRef]
- Funahashi, R.; Matsubara, I.; Sodeoka, S. Thermoelectric properties of Bi2Sr2Co2Ox polycrystalline materials. Appl. Phys. Lett. 2000, 76, 2385–2387. [Google Scholar] [CrossRef]
- Masset, A.C.; Michel, C.; Maignan, A.; Hervieu, M.; Toulemonde, O.; Studer, F.; Raveau, B.; Hejtmanek, J. Misfit-layered cobaltite with an anisotropic giant magnetoresistance: Ca3Co4O9. Phys. Rev. B 2000, 62, 166–175. [Google Scholar] [CrossRef]
- Ohtaki, M.; Araki, K.; Yamamoto, K. High thermoelectric performance of dually doped ZnO ceramics. J. Electron. Mater. 2009, 38, 1234–1238. [Google Scholar] [CrossRef]
- Gao, P.; Grätzel, M.; Nazeeruddin, M.K. Organohalide lead perovskites for photovoltaic applications. Energy Environ. Sci. 2014, 7, 2448–2463. [Google Scholar] [CrossRef]
- Yin, W.-J.; Yang, J.-H.; Kang, J.; Yan, Y.; Wei, S.-H. Halide perovskite materials for solar cells: A theoretical review. J. Mater. Chem. A 2015, 3, 8926–8942. [Google Scholar] [CrossRef]
- Kagan, C.R. Organic-Inorganic Hybrid Materials as Semiconducting Channels in Thin-Film Field-Effect Transistors. Science 1999, 286, 945–947. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Lin, S. Anisotropic and Ultralow Phonon Thermal Transport in Organic–Inorganic Hybrid Perovskites: Atomistic Insights into Solar Cell Thermal Management and Thermoelectric Energy Conversion Efficiency. Adv. Funct. Mater. 2016, 26, 5297–5306. [Google Scholar] [CrossRef]
- Ravichandran, J.; Siemons, W.; Oh, D.W.; Kardel, J.T.; Chari, A.; Heijmerikx, H.; Scullin, M.L.; Majumdar, A.; Ramesh, R.; Cahill, D.G. High-temperature thermoelectric response of double-doped SrTiO3 epitaxial films. Phys. Rev. B 2010, 82, 165126. [Google Scholar] [CrossRef]
- Onoda, M.; Tsukahara, S. The upper limit of thermoelectric power factors in the metal–band-insulator crossover of the perovskite-type oxygen deficient system SrTiO3−δ/2. J. Phys. Condens. Matter 2011, 23, 45604. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Fan, Y.; Nomura, N.; Kikuchi, K.; Wang, L.; Jiang, W.; Kawasaki, A. Graphene promoted oxygen vacancies in perovskite for enhanced thermoelectric properties. Carbon 2017, 112, 169–176. [Google Scholar] [CrossRef]
- Jalan, B.; Stemmer, S. Large Seebeck coefficients and thermoelectric power factor of La-doped SrTiO3 thin films. Appl. Phys. Lett. 2010, 97, 2008–2011. [Google Scholar] [CrossRef]
- Moos, R.; Gnudi, A.; Härdtl, K.H. Thermopower of Sr1−xLaxTiO3 ceramics. J. Appl. Phys. 1995, 78, 5042–5047. [Google Scholar] [CrossRef]
- Muta, H.; Kurosaki, K.; Yamanaka, S. Thermoelectric properties of rare earth doped SrTiO3. J. Alloys Compd. 2003, 350, 292–295. [Google Scholar] [CrossRef]
- Muta, H.; Kurosaki, K.; Yamanaka, S. Thermoelectric properties of reduced and La-doped single-crystalline SrTiO3. J. Alloys Compd. 2005, 392, 306–309. [Google Scholar] [CrossRef]
- Liu, J.; Wang, C.L.; Su, W.B.; Wang, H.C.; Zheng, P.; Li, J.C.; Zhang, J.L.; Mei, L.M. Enhancement of thermoelectric efficiency in oxygen-deficient Sr1−xLaxTiO3−δ ceramics. Appl. Phys. Lett. 2009, 95, 162110. [Google Scholar] [CrossRef]
- Ohta, S.; Nomura, T.; Ohta, H.; Koumoto, K. High-temperature carrier transport and thermoelectric properties of heavily La- Or Nb-doped SrTiO3 single crystals. J. Appl. Phys. 2005, 97, 034106. [Google Scholar] [CrossRef]
- Onoda, M.; Goto, I. Correlation and phonon effects for the electronic transport and thermoelectric power factors in the metal–band-insulator crossover of perovskite-type titanates. J. Phys. Condens. Matter 2009, 21, 435603. [Google Scholar] [CrossRef] [PubMed]
- Sugahara, T.; Ohtaki, M. Structural and semiconductor-to-metal transitions of double-perovskite cobalt oxide Sr2−xLaxCoTiO6−δ with enhanced thermoelectric capability. Appl. Phys. Lett. 2011, 99, 62107. [Google Scholar] [CrossRef]
- Ohta, S.; Nomura, T.; Ohta, H.; Hirano, M.; Hosono, H.; Koumoto, K. Large thermoelectric performance of heavily Nb-doped SrTiO3 epitaxial film at high temperature. Appl. Phys. Lett. 2005, 87, 092108. [Google Scholar] [CrossRef]
- Nasir Khan, M.; Kim, H.T.; Minami, H.; Uwe, H. Thermoelectric properties of niobium doped hexagonal barium titanate. Mater. Lett. 2001, 47, 95–101. [Google Scholar] [CrossRef]
- Kolodiazhnyi, T.; Petric, A.; Niewczas, M.; Bridges, C.; Safa-Sefat, A.; Greedan, J.E. Thermoelectric power, Hall effect, and mobility of n-type BaTiO3. Phys. Rev. B 2003, 68, 85205. [Google Scholar] [CrossRef]
- Obara, H.; Yamamoto, A.; Lee, C.H.; Kobayashi, K.; Matsumoto, A.; Funahashi, R. Thermoelectric properties of Y-doped polycrystalline SrTiO3. Jpn. J. Appl. Phys. 2004, 43, L540. [Google Scholar] [CrossRef]
- Muta, H.; Kurosaki, K.; Yamanaka, S. Thermoelectric properties of doped BaTiO3-SrTiO3 solid solution. J. Alloys Compd. 2004, 368, 22–24. [Google Scholar] [CrossRef]
- Muta, H.; Ieda, A.; Kurosaki, K.; Yamanaka, S. Substitution effect on the thermoelectric properties of alkaline earth titanate. Mater. Lett. 2004, 58, 3868–3871. [Google Scholar] [CrossRef]
- Okuda, T.; Nakanishi, K.; Miyasaka, S.; Tokura, Y. Large thermoelectric response of metallic perovskites: Sr1−xLaxTiO3(0 < x <0.1). Phys. Rev. B 2001, 63, 113104. [Google Scholar] [CrossRef]
- Ohta, H.; Kim, S.; Mune, Y.; Mizoguchi, T.; Nomura, K.; Ohta, S.; Nomura, T.; Nakanishi, Y.; Ikuhara, Y.; Hirano, M.; et al. Giant thermoelectric Seebeck coefficient of a two-dimensional electron gas in SrTiO3. Nat. Mater. 2007, 6, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Ohta, S.; Ohta, H.; Koumoto, K. Grain Size Dependence of Thermoelectric Performance of Nb-Doped SrTiO3 Polycrystals. J. Ceram. Soc. Jpn. 2006, 114, 102–105. [Google Scholar] [CrossRef]
- Kato, K.; Yamamoto, M.; Ohta, S.; Muta, H.; Kurosaki, K.; Yamanaka, S.; Iwasaki, H.; Ohta, H.; Koumoto, K. The effect of Eu substitution on thermoelectric properties of SrTi0.8Nb0.2O3. J. Appl. Phys. 2007, 102, 116107. [Google Scholar] [CrossRef]
- Cui, Y.; Salvador, J.R.; Yang, J.; Wang, H.; Amow, G.; Kleinke, H. Thermoelectric properties of heavily doped n-type SrTiO3 bulk materials. J. Electron. Mater. 2009, 38, 1002–1007. [Google Scholar] [CrossRef]
- Lee, S.; Yang, G.; Wilke, R.H.T.; Trolier-Mckinstry, S.; Randall, C.A. Thermopower in highly reduced n-type ferroelectric and related perovskite oxides and the role of heterogeneous nonstoichiometry. Phys. Rev. B 2009, 79, 134110. [Google Scholar] [CrossRef]
- Usui, H.; Shibata, S.; Kuroki, K. Origin of coexisting large Seebeck coefficient and metallic conductivity in the electron doped SrTiO3 and KTaO3. Phys. Rev. B 2010, 81, 205121. [Google Scholar] [CrossRef]
- Filippetti, A.; Delugas, P.; Verstraete, M.J.; Pallecchi, I.; Gadaleta, A.; Marré, D.; Li, D.F.; Gariglio, S.; Fiorentini, V. Thermopower in oxide heterostructures: The importance of being multiple-band conductors. Phys. Rev. B 2012, 86, 195301. [Google Scholar] [CrossRef]
- Delugas, P.; Filippetti, A.; Verstraete, M.J.; Pallecchi, I.; Marré, D.; Fiorentini, V. Doping-induced dimensional crossover and thermopower burst in Nb-doped SrTiO3 superlattices. Phys. Rev. B 2013, 88, 045310. [Google Scholar] [CrossRef]
- Okuda, T.; Hata, H.; Eto, T.; Nishina, K.; Kuwahara, H.; Nakamura, M.; Kajimoto, R. Effects of Mn substitution on the thermoelectric properties of the electron-doped perovskite Sr1−xLaxTiO3. J. Phys. Conf. Ser. 2014, 568, 22035. [Google Scholar] [CrossRef]
- Choi, W.S.; Ohta, H.; Lee, H.N. Thermopower enhancement by fractional layer control in 2D oxide superlattices. Adv. Mater. 2014, 26, 6701–6705. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Singh, D.J. Thermoelectric properties of n-type SrTiO3. APL Mater. 2016, 4, 104803. [Google Scholar] [CrossRef]
- Roy, P.; Bose, I.; Maiti, T. Synthesis and characterization of Sr2TiMO6 (M = Fe,Co) double perovskites for high temperature thermoelectric applications. Integr. Ferroelectr. 2016, 174, 34–42. [Google Scholar] [CrossRef]
- Saxena, M.; Tanwar, K.; Maiti, T. Environmental friendly Sr2TiMoO6 double perovskite for high temperature thermoelectric applications. Scr. Mater. 2017, 130, 205–209. [Google Scholar] [CrossRef]
- Ohkubo, I.; Mori, T. Comparative Study of Exchange–Correlation Functional and Potential for Evaluating Thermoelectric Transport Properties in d 0 Perovskite Oxides. J. Phys. Soc. Jpn. 2017, 86, 74705. [Google Scholar] [CrossRef]
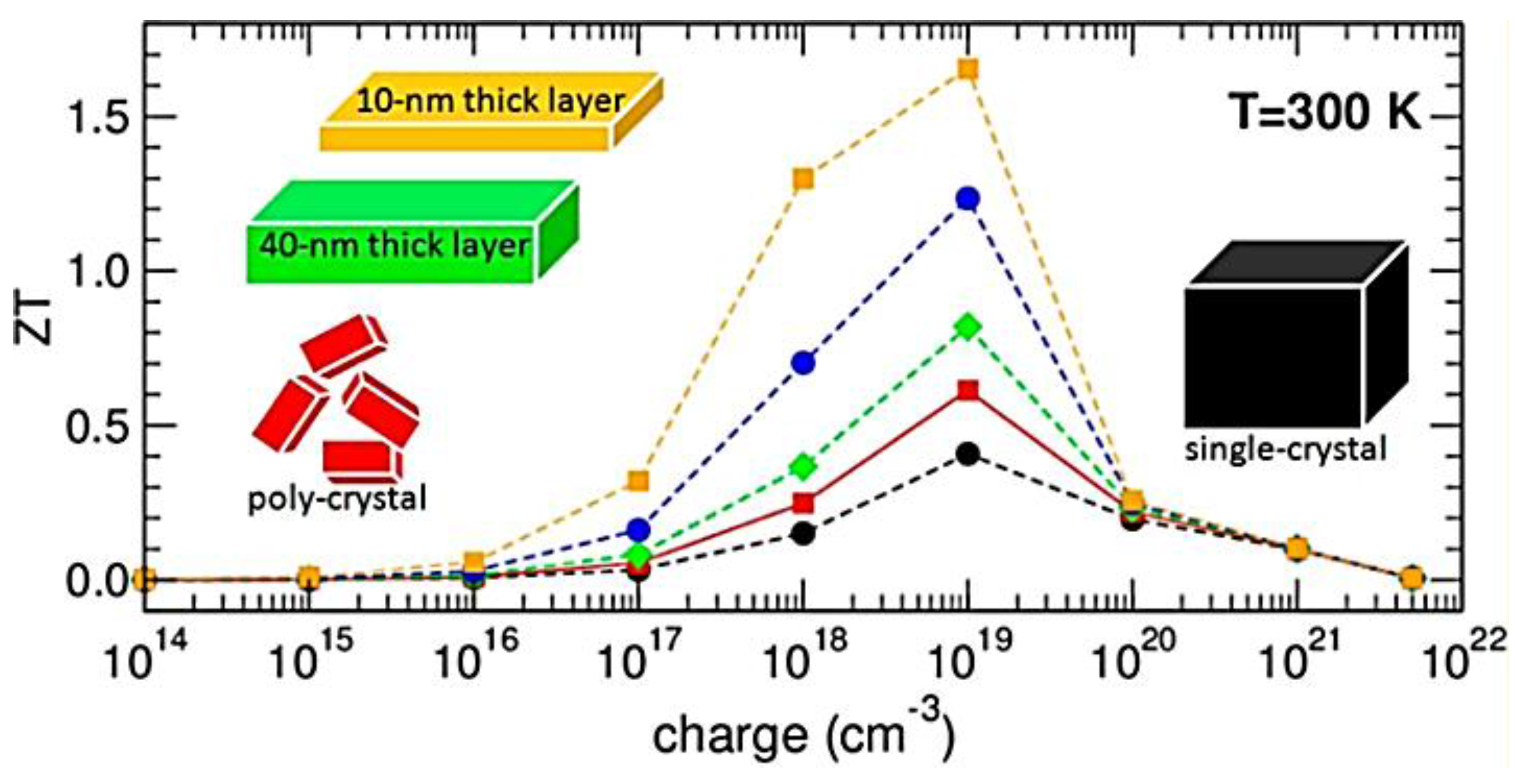
- Kahaly, M.U.; Ozdogan, K.; Schwingenschlögl, U. Half-metallic perovskite superlattices with colossal thermoelectric figure of merit. J. Mater. Chem. A 2013, 1, 8406–8410. [Google Scholar] [CrossRef]
- Kobayashi, T.; Takizawa, H.; Endo, T.; Sato, T.; Shimada, M.; Taguchi, H.; Nagao, M. Metal-insulator transition and thermoelectric properties in the system (R1−xCax)MnO3−δ (R: Tb, Ho, Y). J. Solid State Chem. 1991, 92, 116–129. [Google Scholar] [CrossRef]
- Ohtaki, M.; Koga, H.; Tokunaga, T.; Eguchi, K.; Arai, H. Electrical Transport Properties and High-Temperature Thermoelectric Performance of (Ca0.9M0.1)MnO3 (M = Y, La, Ce, Sm, In, Sn, Sb, Pb, Bi). J. Solid State Chem. 1995, 120, 105–111. [Google Scholar] [CrossRef]
- Hashimoto, S.; Iwahara, H. Study on the structural and electrical properties of Sr1−xCexMnO3−a (x = 0.1, 0.3) perovskite oxide. Mater. Res. Bull. 2000, 35, 2253–2262. [Google Scholar] [CrossRef]
- Vecherskii, S.I.; Konopel’ko, M.A.; Esina, N.O.; Batalov, N.N. Transport Properties of Ca1–xMnO3–d + xCeO2 (0 < x ≤ 0.15) Mixtures. Inorg. Mater. 2002, 38, 1270–1276. [Google Scholar]
- Cong, B.T.; Tsuji, T.; Thao, P.X.; Thanh, P.Q.; Yamamura, Y. High-temperature thermoelectric properties of Ca1−xPrxMnO3−δ (0 ≤ x < 1). Phys. B Condens. Matter 2004, 352, 18–23. [Google Scholar] [CrossRef]
- Flahaut, D.; Mihara, T.; Funahashi, R.; Nabeshima, N.; Lee, K.; Ohta, H.; Koumoto, K. Thermoelectrical properties of A-site substituted Ca1−xRexMnO3 system. J. Appl. Phys. 2006, 100, 84911. [Google Scholar] [CrossRef]
- Park, K.; Lee, G.W.; Jung, J.; Kim, S.-J.; Lim, Y.-S.; Choi, S.-M.; Seo, W.-S. Thermoelectric Properties of Ca1−x−yDyxCeyMnO3 for Power Generation. J. Nanosci. Nanotechnol. 2011, 11, 7176–7179. [Google Scholar] [CrossRef] [PubMed]
- Nakatsugawa, H.; Kubota, M.; Saito, M. Thermoelectric and magnetic properties of Pr1−xSrxMnO3 (0.1 < x < 0.7). Mater. Trans. 2015, 56, 864–871. [Google Scholar]
- Hejtmánek, J.; Jirák, Z.; Maryško, M.; Martin, C.; Maignan, a.; Hervieu, M.; Raveau, B. Interplay between transport, magnetic, and ordering phenomena in Sm1−xCaxMnO3. Phys. Rev. B 1999, 60, 14057–14065. [Google Scholar] [CrossRef]
- Martin, C.; Maignan, A.; Hervieu, M.; Raveau, B.; Hejtmanek, J. Electron doping in CaMnO3 induced by Mo for Mn substitution: An efficient route to orbital and charge ordering. Phys. Rev. B 2001, 63, 100406. [Google Scholar] [CrossRef]
- Gutierrez, D.; Peña, O.; Duran, P.; Moure, C. Crystal structure, electrical conductivity and Seebeck coefficient of Y(Mn,Ni)O3 solid solution. J. Eur. Ceram. Soc. 2002, 22, 567–572. [Google Scholar] [CrossRef]
- Maignan, A.; Hébert, S.; Pi, L.; Pelloquin, D.; Martin, C.; Michel, C.; Hervieu, M.; Raveau, B. Perovskite manganites and layered cobaltites: Potential materials for thermoelectric applications. Cryst. Eng. 2002, 5, 365–382. [Google Scholar] [CrossRef]
- Maignan, A.; Martin, C.; Autret, C.; Hervieu, M.; Raveau, B.; Hejtmanek, J. Structural–magnetic phase diagram of Mo-substituted CaMnO3: Consequences for thermoelectric power properties. J. Mater. Chem. 2002, 12, 1806–1811. [Google Scholar] [CrossRef]
- Xu, G.; Funahashi, R.; Matsubara, I.; Shikano, M.; Zhou, Y. High-temperature Thermoelectric Properties of the Ca1−xBixMnO3 System. J. Mater. Res. 2002, 17, 1092–1095. [Google Scholar] [CrossRef]
- Pi, L.; Hébert, S.; Martin, C.; Maignan, A.; Raveau, B. Comparison of CaMn1−xRuxO3 and CaMn1−yMoyO3 perovskites. Phys. Rev. B 2003, 67, 244301–244307. [Google Scholar] [CrossRef]
- Xu, G.; Funahashi, R.; Pu, Q.; Liu, B.; Tao, R.; Wang, G.; Ding, Z. High-temperature transport properties of Nb and Ta substituted CaMnO3 system. Solid State Ion. 2004, 171, 147–151. [Google Scholar] [CrossRef]
- Miclau, M.; Hébert, S.; Retoux, R.; Martin, C. Influence of A-site cation size on structural and physical properties in Ca1−xSrxMn0.96Mo0.04O3: A comparison of the and 0.6 compounds. J. Solid State Chem. 2005, 178, 1104–1111. [Google Scholar] [CrossRef]
- Bocher, L.; Aguirre, M.H.; Logvinovich, D.; Shkabko, A.; Robert, R.; Trottmann, M.; Weidenkaff, A. CaMn1−xNbxO3 (x ≤ 0.08) Perovskite-Type Phases As Promising New High-Temperature n-Type Thermoelectric Materials. Inorg. Chem. 2008, 47, 8077–8085. [Google Scholar] [CrossRef] [PubMed]
- Kolesnik, S.; Dabrowski, B.; Chmaissem, O. Structural and physical properties of SrMn1−xRuxO3 perovskites. Phys. Rev. B 2008, 78, 214425. [Google Scholar] [CrossRef]
- Choi, S.-M.; Lim, C.-H.; Seo, W.-S. Thermoelectric Properties of the Ca1−xRxMnO3 Perovskite System (R: Pr, Nd, Sm) for High-Temperature Applications. J. Electron. Mater. 2011, 40, 551–556. [Google Scholar] [CrossRef]
- Suzuki, T.; Sakai, H.; Taguchi, Y.; Tokura, Y. Thermoelectric properties of electron-doped SrMnO3 single crystals with perovskite structure. J. Electron. Mater. 2012, 41, 1559–1563. [Google Scholar] [CrossRef]
- Kawakami, H.; Saito, M.; Takemoto, H.; Yamamura, H.; Isoda, Y.; Shinohara, Y. Thermoelectric Properties of Perovskite-type Oxide Ca-Mn-O System in Relation to A-site Vacancies. Mater. Trans. 2013, 54, 1818–1822. [Google Scholar] [CrossRef]
- Kim, C.M.; Seo, J.W.; Choi, S.-M.; Seo, W.-S.; Lee, S.; Lim, Y.S.; Park, K. Structural and thermoelectric properties of n-type Sr1−xTixMnO3−δ perovskite system. Electron. Mater. Lett. 2015, 11, 276–281. [Google Scholar] [CrossRef]
- Moon, J.-W.; Seo, W.-S.; Okabe, H.; Okawa, T.; Koumoto, K. Ca-doped RCoO3 (R = Gd, Sm, Nd, Pr) as thermoelectric materials. J. Mater. Chem. 2000, 10, 2007–2009. [Google Scholar] [CrossRef]
- Moon, J.W.; Masuda, Y.; Seo, W.S.; Koumoto, K. Influence of ionic size of rare-earth site on the thermoelectric properties of RCoO3-type perovskite cobalt oxides. Mater. Sci. Eng. 2001, 85, 70–75. [Google Scholar] [CrossRef]
- Hashimoto, H.; Kusunose, T.; Sekino, T. Influence of ionic sizes of rare earths on thermoelectric properties of perovskite-type rare earth cobalt oxides RCoO3 (R = Pr, Nd, Tb, Dy). J. Alloys Compd. 2009, 484, 246–248. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Bhide, V.G.; Mott, N.F. Hopping conduction in La1–xSrxCoO3 and Nd1–xSrxCoO3. Philos. Mag. 1975, 32, 1277–1282. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Parkash, O. Anderson transitions in Ln1−xSrxCoO3(Ln = Pr or Nd). Philos. Mag. 1977, 35, 37–41. [Google Scholar] [CrossRef]
- Señarís-Rodríguez, M.A.; Goodenough, J.B. LaCoO3 Revisited. J. Solid State Chem. 1995, 116, 224–231. [Google Scholar] [CrossRef]
- Señarís-Rodríguez, M.A.; Goodenough, J.B. Magnetic and Transport Properties of the System La1−xSrxCoO3−δ (0 < x ≤ 0.50). J. Solid State Chem. 1995, 118, 323–336. [Google Scholar]
- Kobayashi, Y.; Murata, S.; Asai, K.; Tranquada, J.M.; Shirane, G.; Kohn, K. Magnetic and transport properties of LaCo1−xNixO3-comparison with La1−xSrxCoO3. J. Phys. Soc. Jpn. 1999, 68, 1011–1017. [Google Scholar] [CrossRef]
- Moon, J.-W.; Masuda, Y.; Seo, W.-S.; Koumoto, K. Ca-doped HoCoO3 as p-type oxide thermoelectric material. Mater. Lett. 2001, 48, 225–229. [Google Scholar] [CrossRef]
- Berggold, K.; Kriener, M.; Zobel, C.; Reichl, A.; Reuther, M.; Müller, R.; Freimuth, A.; Lorenz, T. Thermal conductivity, thermopower, and figure of merit of La1−xSrxCoO3. Phys. Rev. B 2005, 72, 155116. [Google Scholar] [CrossRef]
- Andrbulakis, J.; Migiakis, P.; Giapintzakis, J. La0.95Sr0.05Coo3: An efficient room-temperature thermoelectric oxide. Appl. Phys. Lett. 2004, 84, 1099–1101. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.M.; Chen, T.L.; Chen, L.D. Thermoelectric and transport properties of La0.95Sr0.05CoO3. J. Cryst. Growth 2006, 286, 1–5. [Google Scholar] [CrossRef]
- Zhou, A.J.; Zhu, T.J.; Zhao, X.B. Thermoelectric properties of perovskite oxides La1−xSrxCoO3 prepared by polymerlized complex method. J. Mater. Sci. 2008, 43, 1520–1524. [Google Scholar] [CrossRef]
- He, T.; Chen, J.; Calvarese, T.G.; Subramanian, M.A. Thermoelectric properties of La1−xAxCoO3 (A = Pb, Na). Solid State Sci. 2006, 8, 467–469. [Google Scholar] [CrossRef]
- Inagoya, A.; Sawaki, D.; Horiuchi, Y.; Urata, S.; Funahashi, R.; Terasaki, I. Thermoelectric module made of perovskite cobalt oxides with large thermopower. J. Appl. Phys. 2011, 110, 123712. [Google Scholar] [CrossRef]
- Kun, R.; Populoh, S.; Karvonen, L.; Gumbert, J.; Weidenkaff, A.; Busse, M. Structural and thermoelectric characterization of Ba substituted LaCoO3 perovskite-type materials obtained by polymerized gel combustion method. J. Alloys Compd. 2013, 579, 147–155. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.-J.; Zhang, Q.; Li, Y.; Liu, H.-T. Electrical transport and thermoelectric properties of Ni-doped perovskite-type YCo1−xNixO3 (0 ≤ x ≤ 0.07) prepared by sol-gel process. Chin. Phys. B 2013, 22, 57201. [Google Scholar] [CrossRef]
- Zhou, A.J.; Zhu, T.J.; Zhao, X.B. Thermoelectric properties of perovskite-type oxide La1−xSr xCoO3 (x = 0, 0.1) prepared by solid state reactions. Mater. Sci. Eng. B 2006, 128, 174–178. [Google Scholar] [CrossRef]
- Robert, R.; Bocher, L.; Sipos, B.; Döbeli, M.; Weidenkaff, A. Ni-doped cobaltates as potential materials for high temperature solar thermoelectric converters. Prog. Solid State Chem. 2007, 35, 447–455. [Google Scholar] [CrossRef]
- Iwasaki, K.; Ito, T.; Nagasaki, T.; Arita, Y.; Yoshino, M.; Matsui, T. Thermoelectric properties of polycrystalline La1−xSrxCoO3. J. Solid State Chem. 2008, 181, 3145–3150. [Google Scholar] [CrossRef]
- Zhou, A.J.; Zhu, T.J.; Zhao, X.B.; Chen, H.Y.; Müller, E. Fabrication and thermoelectric properties of perovskite-type oxide La1−xSrxCoO3 (x = 0, 0.1). J. Alloys Compd. 2008, 449, 105–108. [Google Scholar] [CrossRef]
- Mizusaki, J.; Sasamoto, T.; Cannon, W.R.; Bowen, H.K. Electronic Conductivity, Seebeck Coefficient, and Defect Structure of La1−xSrxFeO3 (x = 0.l, 0.25). J. Am. Ceram. Soc. 1983, 66, 247–252. [Google Scholar] [CrossRef]
- Nakatsugawa, H.; Saito, M.; Okamoto, Y. High-Temperature Thermoelectric Properties of Perovskite-Type Pr0.9Sr0.1Mn1−xFexO3 (0 ≤ x ≤ 1). J. Electron. Mater. 2017, 46, 3262–3272. [Google Scholar] [CrossRef]
- Iijima, M.; Murayama, N. High Temperature Thermoelectric Properties of La1−xSrxFeO3 (0 < x < 1). In Proceedings of the 17th Internaltional Conference on Thermoelectrics, Nagoya, Japan, 28 May 1998. [Google Scholar]
- Sugahara, T.; Van Nong, N.; Ohtaki, M. Structure and thermoelectric properties of Ca2−xSrxFeMoO6 (0 ≤ x ≤ 0.3) double-perovskite oxides. Mater. Chem. Phys. 2012, 133, 630–634. [Google Scholar] [CrossRef]
- Sugahara, T.; Araki, T.; Ohtaki, M.; Suganuma, K. Structure and thermoelectric properties of double-perovskite oxides: Sr2−xKFeMoO6. J. Ceram. Soc. Jpn. 2012, 120, 211–216. [Google Scholar] [CrossRef]
- Sahnoun, O.; Bouhani-Benziane, H.; Sahnoun, M.; Driz, M. Magnetic and thermoelectric properties of ordered double perovskite Ba2FeMoO6. J. Alloys Compd. 2017, 714, 704–708. [Google Scholar] [CrossRef]
- Tak, J.Y.; Choi, S.M.; Seo, W.S.; Cho, H.K. Thermoelectric properties of a doped LaNiO3 perovskite system prepared using a spark-plasma sintering process. Electron. Mater. Lett. 2013, 9, 513–516. [Google Scholar] [CrossRef]
- Parkash, O.; Kumar, D.; Srivastav, K.K.; Dwivedi, R.K. Electrical conduction behaviour of cobalt substituted BaSnO3. J. Mater. Sci. 2001, 6, 5805–5810. [Google Scholar] [CrossRef]
- Hadjarab, B.; Bouguelia, A.; Trari, M. Synthesis, physical and photo electrochemical characterization of La-doped SrSnO3. J. Phys. Chem. Solids 2007, 68, 1491–1499. [Google Scholar] [CrossRef]
- Yasukawa, M.; Kono, T.; Ueda, K.; Yanagi, H.; Wng Kim, S.; Hosono, H. Thermoelectric properties and figure of merit of perovskite-type Ba1−xLaxSnO3 with x = 0.002–0.008. Solid State Commun. 2013, 172, 49–53. [Google Scholar] [CrossRef]
- Yasukawa, M.; Ueda, K.; Fujitsu, S.; Hosono, H. Thermoelectric properties and figure of merit of perovskite-type Sr1−xLaxSnO3 ceramics. Ceram. Int. 2017, 43, 9653–9657. [Google Scholar] [CrossRef]
- Li, J.; Ma, Z.; Sa, R.; Wu, K. Improved thermoelectric power factor and conversion efficiency of perovskite barium stannate. RSC Adv. 2017, 7, 32703–32709. [Google Scholar] [CrossRef]
- Yasukawa, M.; Murayama, N. High-temperature thermoelectric properties of the oxide material: Ba1−xSrxPbO3 (x = 0 − 0.6). J. Mater. Sci. Lett. 1997, 16, 1731–1734. [Google Scholar] [CrossRef]
- Yasukawa, M.; Murayama, N. A promising oxide material for high-temperature thermoelectric energy conversion: Ba1−xSrxPbO3 solid solution system. Mater. Sci. Eng. B 1998, 54, 64–69. [Google Scholar] [CrossRef]
- Yasukawa, M.; Kono, T. Bi doping effect on the thermoelectric properties of perovskite-type Sr0.7Ba0.3PbO3. Solid State Commun. 2008, 146, 458–461. [Google Scholar] [CrossRef]
- Sera, M.; Kondoh, S.; Sato, M. Thermoelectric power of superconducting BaKBiO with Perovskite structure. Solid State Commun. 1988, 68, 647–648. [Google Scholar] [CrossRef]
- Yasukawa, M.; Shiga, Y.; Kono, T. Electrical conduction and thermoelectric properties of perovskite-type BaBi1-xSbxO3. Solid State Commun. 2012, 152, 964–967. [Google Scholar] [CrossRef]
- Kurosaki, K.; Oyama, T.; Muta, H.; Uno, M.; Yamanaka, S. Thermoelectric properties of perovskite type barium molybdate. J. Alloys Compd. 2004, 372, 65–69. [Google Scholar] [CrossRef]
- Oba, A.; Kamishima, K.; Kakizaki, K.; Hiratsuka, N. Substitution effect on thermoelectric properties of double Perovskite Sr2FeMoO6. Trans. Mater. Res. Soc. Jpn. 2012, 37, 267–270. [Google Scholar] [CrossRef]
- Maekawa, T.; Kurosaki, K.; Muta, H.; Uno, M.; Yamanaka, S. Thermoelectric properties of perovskite type strontium ruthenium oxide. J. Alloys Compd. 2005, 387, 56–59. [Google Scholar] [CrossRef]
- Aguirre, M.H.; Logvinovich, D.; Bocher, L.; Robert, R.; Ebbinghaus, S.G.; Weidenkaff, A. High-temperature thermoelectric properties of Sr2RuYO6 and Sr2RuErO6 double perovskites influenced by structure and microstructure. Acta Mater. 2009, 57, 108–115. [Google Scholar] [CrossRef]
- Takahashi, R.; Okazaki, R.; Yasui, Y.; Terasaki, I.; Sudayama, T.; Nakao, H.; Yamasaki, Y.; Okamoto, J.; Murakami, Y.; Kitajima, Y. High-temperature thermoelectric properties of the double-perovskite ruthenium oxide (Sr1−xLax)2ErRuO6. J. Appl. Phys. 2012, 112, 073714. [Google Scholar] [CrossRef]
- Mahmood, A.; Ramay, S.M.; Rafique, H.M.; Al-Zaghayer, Y.; Khan, S.U.-D. First-principles study of electronic, optical and thermoelectric properties in cubic perovskite materials AgMO3 (M = V, Nb, Ta). Mod. Phys. Lett. B 2014, 28, 1450077. [Google Scholar] [CrossRef]
- Sakai, A.; Kanno, T.; Yotsuhashi, S.; Adachi, H.; Tokura, Y. Thermoelectric properties of electron-doped KTaO3. Jpn. J. Appl. Phys. 2009, 48, 970021–970024. [Google Scholar] [CrossRef]
- Kurosaki, K.; Matsuda, T.; Uno, M.; Kobayashi, S.; Yamanaka, S. Thermoelectric properties of BaUO3. J. Alloys Compd. 2001, 319, 271–275. [Google Scholar] [CrossRef]
- Röder-Roith, U.; Rettig, F.; Sahner, K.; Röder, T.; Janek, J.; Moos, R. Perovskite-type proton conductor for novel direct ionic thermoelectric hydrogen sensor. Solid State Ion. 2011, 192, 101–104. [Google Scholar] [CrossRef]
- Mettan, X.; Pisoni, R.; Matus, P.; Pisoni, A.; Jaćimović, J.; Náfrádi, B.; Spina, M.; Pavuna, D.; Forró, L.; Horváth, E. Tuning of the Thermoelectric Figure of Merit of CH3NH3MI3 (M = Pb,Sn) Photovoltaic Perovskites. J. Phys. Chem. C 2015, 119, 11506–11510. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, D.; Shuai, Z. Doping optimization of organic-inorganic hybrid perovskite CH3NH3PbI3 for high thermoelectric efficiency. Synth. Met. 2017, 225, 108–114. [Google Scholar] [CrossRef]
- Guo, S.-D.; Wang, J.-L. Potential thermoelectric materials CsMI3 (M = Sn and Pb) in perovskite structures from first-principles calculations. RSC Adv. 2016, 6, 101552–101559. [Google Scholar] [CrossRef]
- Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.; Muto, A.; Vashaee, D.; et al. High-Thermoelectric Performance of Nanostructured Bismuth Antimony Telluride Bulk Alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Sun, T.; Sim, D.; Peng, H.; Wang, H.; Fan, S.; Hng, H.H.; Ma, J.; Boey, F.Y.C.; Li, S.; et al. Sb2Te3 Nanoparticles with Enhanced Seebeck Coefficient and Low Thermal Conductivity. Chem. Mater. 2010, 22, 3086–3092. [Google Scholar] [CrossRef]
- Sumithra, S.; Takas, N.J.; Misra, D.K.; Nolting, W.M.; Poudeu, P.F.P.; Stokes, K.L. Enhancement in Thermoelectric Figure of Merit in Nanostructured Bi2Te3 with Semimetal Nanoinclusions. Adv. Energy Mater. 2011, 1, 1141–1147. [Google Scholar] [CrossRef]
- Moos, R.; Menesklou, W.; Hardtl, K.H. Hall mobility of undoped n-type conducting strontium titanate single crystals between 19 K and 1373 K. Appl. Phys. A 1995, 61, 389–395. [Google Scholar] [CrossRef]
- Moos, R.; Härdtl, K.H. Electronic transport properties of Sr1−xLaxTiO3 ceramics. J. Appl. Phys. 1996, 80, 393–400. [Google Scholar] [CrossRef]
- Fukuyado, J.; Narikiyo, K.; Akaki, M.; Kuwahara, H.; Okuda, T. Thermoelectric properties of the electron-doped perovskites Sr1−xCaxTi1−yNbyO3. Phys. Rev. B 2012, 85, 075112. [Google Scholar] [CrossRef]
- Baniecki, J.D.; Ishii, M.; Aso, H.; Kurihara, K.; Ricinschi, D. Density functional theory and experimental study of the electronic structure and transport properties of La, V, Nb, and Ta doped SrTiO3. J. Appl. Phys. 2013, 113, 13701. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science 2008, 321, 554–557. [Google Scholar] [CrossRef] [PubMed]
- Hsu, K.F.; Loo, S.; Guo, F.; Chen, W.; Dyck, J.S.; Uher, C.; Hogan, T.; Polychroniadis, E.K.; Kanatzidis, M.G. Cubic AgPbmSbTe2+m: Bulk Thermoelectric Materials with High Figure of Merit. Science 2004, 303, 818–821. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Zebarjadi, M.; Wang, H.; Lukas, K.; Wang, H.; Wang, D.; Opeil, C.; Dresselhaus, M.; Chen, G.; Ren, Z. Enhancement of Thermoelectric Properties by Modulation-Doping in Silicon Germanium Alloy Nanocomposites. Nano Lett. 2012, 12, 2077–2082. [Google Scholar] [CrossRef] [PubMed]
- Dualeh, A.; Gao, P.; Seok, S.I.; Nazeeruddin, M.K.; Grätzel, M. Thermal Behavior of Methylammonium Lead-Trihalide Perovskite Photovoltaic Light Harvesters. Chem. Mater. 2014, 26, 6160–6164. [Google Scholar] [CrossRef]

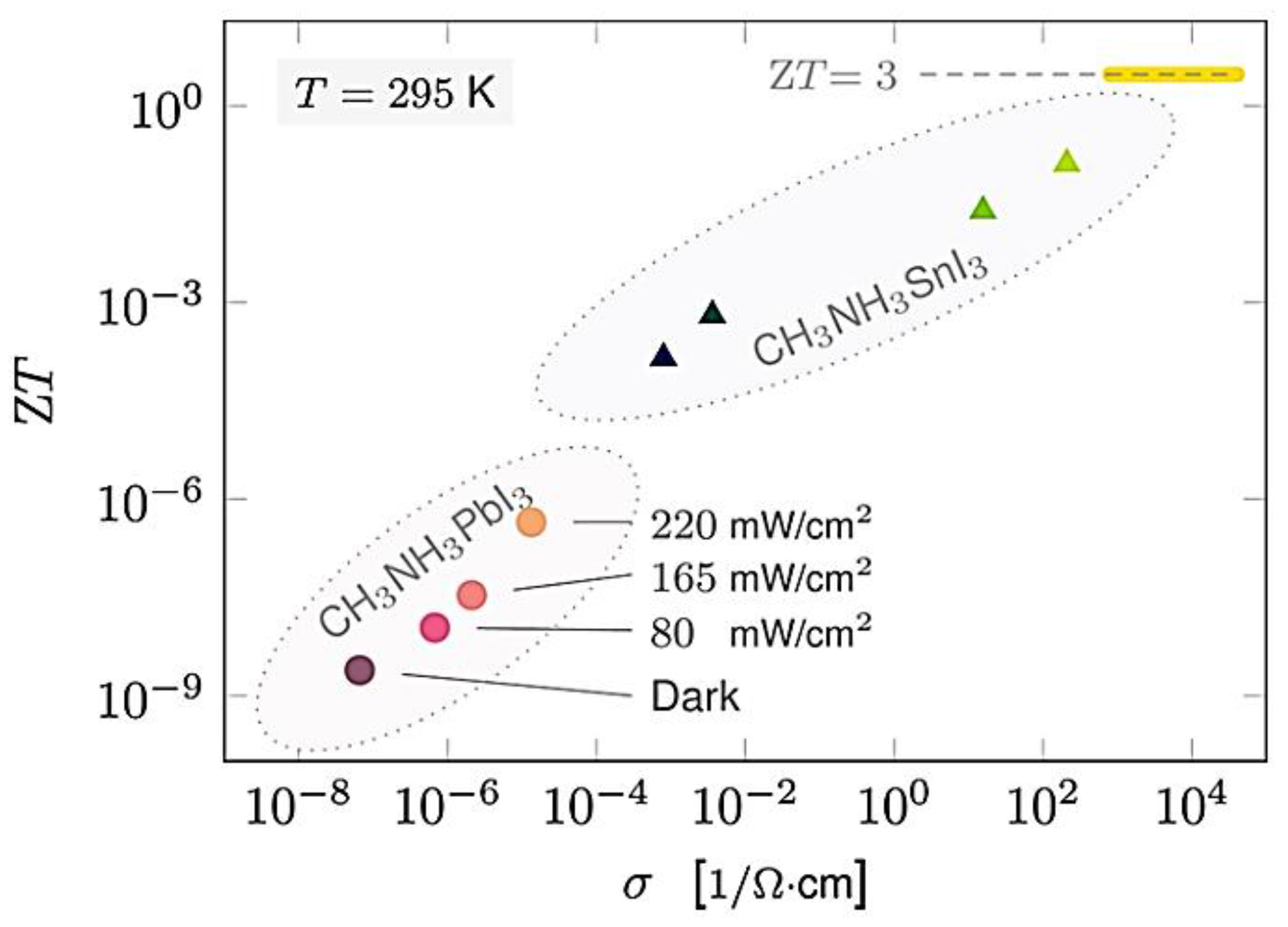
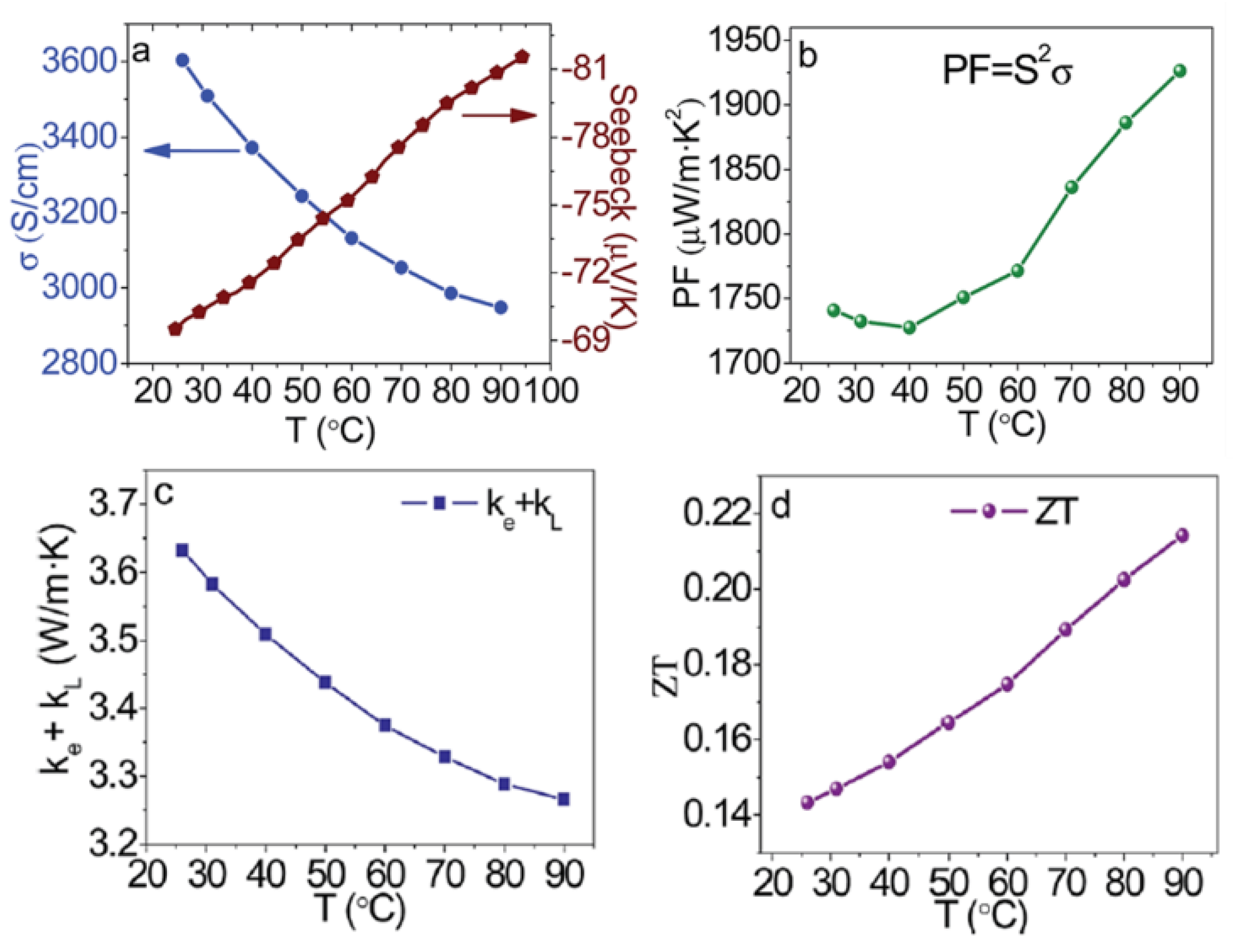
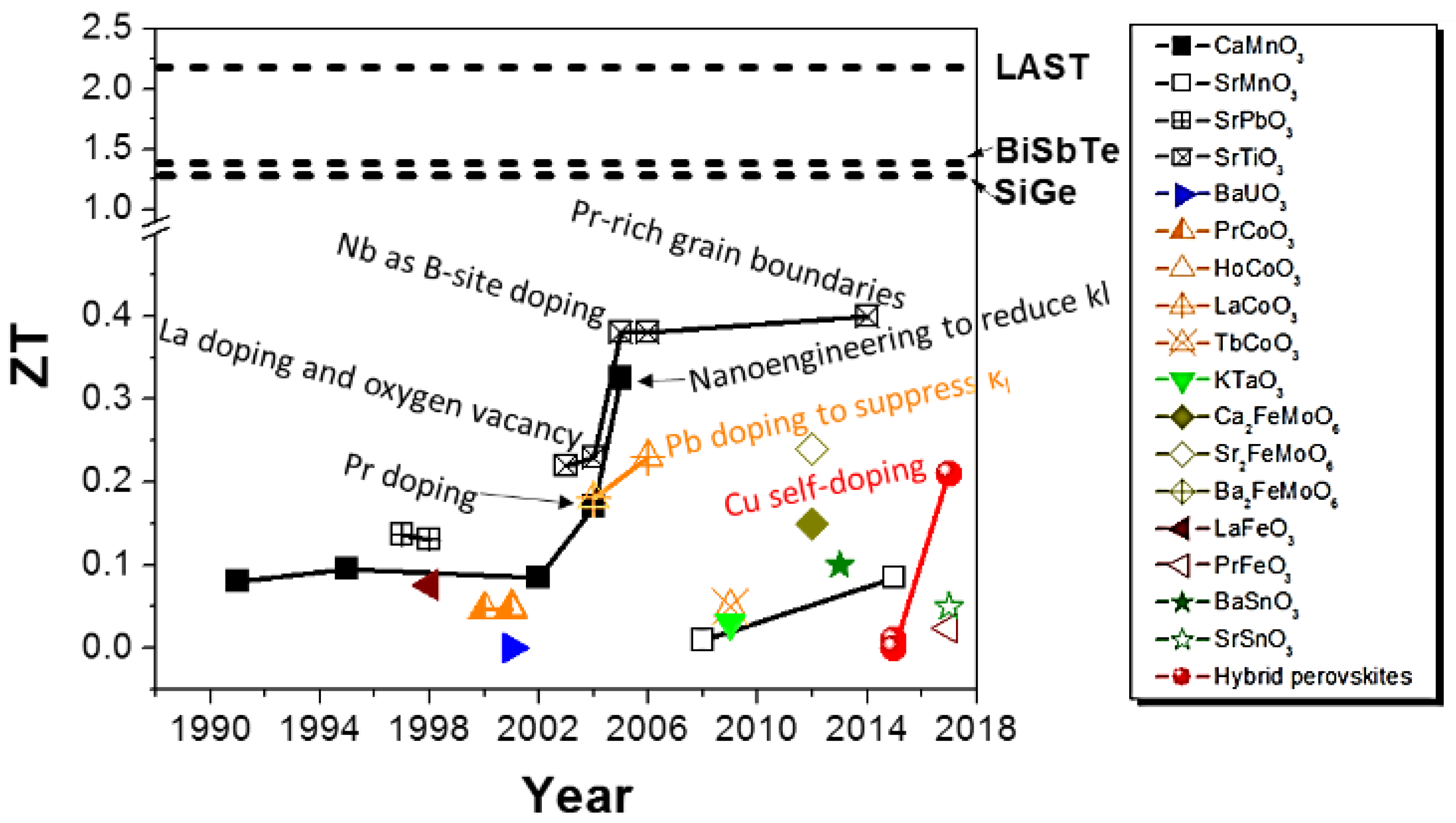
| Ref. | Materials | Seebeck (µV·K−1) | Electrical Conductivity (S·cm−1) | Thermal Conductivity (W·m−1·K−1) | Power Factor (µW·K−2·m−1) | ZT | Measure Temp. (K) |
|---|---|---|---|---|---|---|---|
| [38] | La-Doped SrTiO3 | −260 | 298 | ||||
| [57] | Sr0.85La0.15TiO3 | 175 | 400 | 3 | 0.28 | 873 | |
| [58] | SrTiO3 | 210 | 250 | 200 | 300 | ||
| [59] | reduced graphene oxide—SrTiO3 | −380 | 30 | 0.09 | 760 | ||
| [40] | Sr0.875Pr0.125TiO3 | −80 | 3700 | 0.4 | 323 | ||
| [60] | La-doped SrTiO3 | 980 | 0.39 | 298 | |||
| [61] | Sr0.9La0.1TiO3 | −250 | 1000 | ||||
| [62] | Sr0.9Dy0.1TiO3 R = (La, Sm, Gd, Dy, Y) | −160 | 500 | 2.7 | 0.22 | 573 | |
| [63] | Sr0.95La0.05TiO3 | 250 | 150 | 4.2 | 800 | 0.15 | 780 |
| [64] | Sr0.9La0.1TiO3 | −225 | 300 | 3.2 | 0.21 | 750 | |
| [65] | La-doped SrTiO3 | −300 | 80 | 3.1 | 0.27 | 1073 | |
| [66] | Sr0.96Ce0.04TiO3 | −65 | 300 | ||||
| Sr0.98La0.02TiO3 | −138 | 300 | |||||
| [67] | Sr2CoTiO6 | 60 | 10 | 1200 | |||
| [68] | Sr(Ti0.8Nb0.2)O3 | −200 | 3.5 | 1300 | 0.37 | 1000 | |
| [69] | BaNb0.01Ti0.99O3 | −640 | 290 | ||||
| [70] | BaTiO3 | −550 | 300 | ||||
| [71] | Sr0.9Y0.1TiO3 | −130 | 120 | 420 | |||
| [72] | Ba0.3Sr0.6La0.1TiO3 | −110 | 4.4 | 0.13 | 420 | ||
| [73] | Sr0.45Ca0.45La0.1TiO3 | −195 | 250 | 3.7 | 0.22 | 850 | |
| [74] | Sr0.98La0.02TiO3 | −260 | 500 | 11 | 0.09 | 298 | |
| [75] | SrTiO3/SrTi0.8Nb0.2O3/SrTiO3 | −850 | 1400 | 12 | 2.4 | 300 | |
| [76] | Sr(Ti0.8Nb0.2)O3 | 3 | 0.35 | 1000 | |||
| [77] | Sr0.2Eu0.8Ti0.8Nb0.2O3 | 170 | 0.5 | 1000 | |||
| [78] | SrTi0.9Ta0.1O3 | −175 | 300 | 4.4 | 0.17 | 752 | |
| [79] | BaTiO3 | −620 | 0.17 | 300 | |||
| [80] | PbTiO3 | 110 | 300 | ||||
| BaTiO3 | 110 | 300 | |||||
| SrTiO3 | 100 | 300 | |||||
| [81] | SrTiO3 | −500 | 300 | ||||
| [82] | Nb-doped SrTiO3 | −540 | 1200 | ||||
| [83] | Sr0.95La0.05Ti0.98Mn0.02O3 | −150 | 833 | 3.9 | 20 | 0.15 | 300 |
| [84] | La0.25Sr0.75TiO3 | 450 | 300 | ||||
| [85] | n-type SrTiO3 | 300 | 0.7 | 1400 | |||
| [86] | Sr2TiFeO6 | 280 | 1.2 | 10 | 1130 | ||
| Sr2TiCoO6 | 60 | 20 | 5.4 | 750 | |||
| [39] | Ba0.25Sr1.75FeTiO6 | 800 | 15 | 1123 | |||
| [87] | Sr2TiMoO6 | −10.8 | 960 | 11 | 1223 | ||
| [88] | SrTiO3 | −150 | 1000 | ||||
| [89] | SrTi0.5Co0.5O3 | 200 | 1.36 | 800 | |||
| [90] | (Tb0.1Ca0.9)MnO3 | −140 | −0.18 | 0.13 | 950 | ||
| (Ho0.1Ca0.9)MnO3 | −110 | −0.18 | 0.08 | 950 | |||
| (Y0.1Ca0.9)MnO3 | −130 | −0.2 | 0.15 | 950 | |||
| [91] | (Ca0.9Bi0.1)MnO3 | 80 | 10 | 4 | 0.095 | 1173 | |
| [92] | Sr0.9Ce0.1MnO3 | 180 | 100 | 1273 | |||
| [93] | CaMnO3 | −520 | 667 | ||||
| [94] | Ca0.85Pr0.15MnO2.98 | −130 | 111 | 1.5 | 0.17 | 1100 | |
| [95] | Ca0.9Yb0.1MnO3 | −150 | 133 | 1.6 | 0.16 | 970 | |
| [96] | Ca0.8Dy0.2MnO3 | −135 | 270 | 510 | 1073 | ||
| [97] | Pr0.3Sr0.7MnO3 | −75 | 250 | 1.6 | 0.085 | 1073 | |
| [98] | Sm0.25Ca0.75MnO3 | −380 | 65 | ||||
| [99] | CaMn0.88Mo0.12O3 | −240 | 0.011 | 100 | |||
| [100] | YNi0.3Mn0.7O3 | 90 | 357 | ||||
| [101] | SrMnO3 | −110 | 50 | 300 | |||
| [102] | CaMn0.85Mo0.15O3 (Sm0.2Ca0.8MnO3, Pr0.15Sr0.85MnO3) | −270 | 10−4 | 0.6 | 80 | ||
| [103] | Ca0.96Bi0.04MnO3 | −170 | 66.7 | 3.6 | 300 | 0.086 | 1000 |
| [104] | CaMn0.96Mo0.04O3 | −90 | 3.4 | 0.012 | 270 | ||
| CaMn0.94Ru0.06O3 | −140 | 5.4 | 0.0085 | 330 | |||
| [105] | CaMn0.98Ta0.02O3 | −190 | 29 | 0.05 | 1000 | ||
| CaMn0.98Nb0.02O3 | −205 | 1000 | |||||
| [106] | Ca0.4Sr0.6Mn0.96Mo0.04O3 | −110 | 50 | 220 | |||
| [107] | CaMn0.98Nb0.02O3 | −255 | 31 | 0.32 | 1050 | ||
| [108] | SrMn0.7Ru0.3O3 | −40 | 50 | 1.8 | 0.01 | 370 | |
| [109] | Ca0.9Nd0.1MnO3 | −150 | 160 | 398 | 1123 | ||
| [110] | Sr(Mn0.975Mo0.025)O3 | −120 | 0.13 | 5 | 0.003 | 400 | |
| [111] | Ca0.8Nd0.2MnO3 | −62 | 280 | 1.3 | 0.17 | 873 | |
| [112] | Sr0.9Ti0.1MnO3 | −340 | 2.25 | 25 | 800 | ||
| [113] | (Pr0.9Ca0.1)CoO3 | 106 | 220 | 1.9 | 0.047 | 358 | |
| [114] | Pr0.9Ca0.1CoO3 [RCoO3 (R = Pr, Nd, Sm, Gd, Dy, Ho)] | 125 | 220 | 1.6 | 0.046 | 450 | |
| [115] | TbCoO3 DyCoO3 | 80 | 200 | 1.6 | 0.05 | 873 | |
| [116] | Nd0.95Sr0.05CoO3 | 130 | 400 | ||||
| [117] | Nd0.99Sr0.01CoO3 | 300 | 290 | ||||
| Pr0.99Sr0.01CoO3 | 450 | 270 | |||||
| [118] | LaCoO3 | 1200 | 100 | ||||
| [119] | La0.975Sr0.025CoO3 | 280 | 300 | ||||
| [120] | La0.95Sr0.05CoO3 | 720 | 100 | 280 | |||
| [121] | Ho0.9Ca0.1CoO3 | 220 | 20 | 0.75 | 0.051 | 573 | |
| [122] | La0.875Sr0.125CoO3 | 100 | 6 | 0.035 | 230 | ||
| [123] | La0.95Sr0.05CoO3 | 720 | 20 | 0.037 | 0.18 | 300 | |
| [124] | La0.95Sr0.05CoO3 | 170 | 1.2 | 0.033 | 300 | ||
| [125] | La0.9Sr0.1CoO3 | 120 | 1.5 | 0.046 | 300 | ||
| [126] | La0.9Pb0.1CoO3 | 110 | 333 | 0.8 | 0.23 | 575 | |
| [127] | Nd0.995Ca0.005CoO3 | 500 | 1.1 | 300 | |||
| LaCo0.99Mn0.01O3 | −200 | 300 | |||||
| [128] | La0.97Ba0.03CoO3 | 80 | 40 | 80 | 0.08 | 420 | |
| [129] | YCo0.98Ni0.02O3 | 900 | 300 | ||||
| [130] | LaCoO3 | 600 | 0.067 | 300 | |||
| La0.98Sr0.02CoO3 | 350 | 0.3 | 300 | ||||
| La0.99Ce0.01CoO3 | −300 | 0.03 | 300 | ||||
| LaCo0.995Ga0.005O3 | 480 | 300 | |||||
| LaCo0.995Ti0.005O3 | −200 | 300 | |||||
| [131] | LaCo0.92Ni0.08O2.9 | 220 | 33.3 | 0.35 | 0.2 | 300 | |
| [132] | La0.94Sr0.06CoO3 | 180 | 2 | 0.048 | 300 | ||
| [133] | La0.9Sr0.1CoO3 | 0.046 | 300 | ||||
| [134] | La0.9Sr0.1FeO3 | 380 | 1173 | ||||
| [135] | Pr0.9Sr0.1FeO3 | 140 | 0.8 | 0.024 | 850 | ||
| [136] | La0.95Sr0.05FeO3 | 230 | 1.8 | 0.076 | 1273 | ||
| [137] | Ca2FeMoO6 | −108 | 300 | 3.2 | 0.14 | 1250 | |
| Ca1.9Sr0.1FeMoO6 | −110 | 250 | 3.0 | 0.14 | 1250 | ||
| Ca1.8Sr0.2FeMoO6 | −100 | 260 | 2.8 | 0.14 | 1250 | ||
| [138] | Sr1.6K0.4FeMoO6 | −48 | 3.1 | 450 | 0.24 | 1250 | |
| [139] | Ba2FeMoO6 | −1350 | 0.995 | 300 | |||
| [140] | LaNi0.8Cu0.2O3 | −26 | 600 | 40 | 600 | ||
| [141] | BaSn0.99Co0.01O3 | 1000 | 700 | ||||
| [142] | Sr0.98La0.02SnO3 | −80 | 0.03 | 300 | |||
| [143] | Ba0.998La0.002SnO3 | −170 | 150 | 4 | 0.1 | 1073 | |
| [144] | Sr0.99La0.01SnO3 | −80 | 1.5 | 3.6 | 120 | 0.05 | 1073 |
| [145] | BaSnO3 | −130 | 300 | 3.4 | 1400 | 0.65 | 1200 |
| [146] | Ba0.4Sr0.6PbO3 | 125 | 250 | 2 | 0.13 | 673 | |
| [147] | Ba0.2Sr0.8PbO3 | −190 | 79 | 1.8 | 0.13 | 680 | |
| [148] | Sr0.7Ba0.3Pb0.99Bi0.01O3 | −70 | 390 | 900 | |||
| [149] | Ba0.77K0.23BiO3 | 3.2 | 10 | 290 | |||
| [150] | BaBi0.9Sb0.1O3 | 260 | 10 | 850 | |||
| [151] | BaMoO3 | −30 | 0.015 | 1000 | |||
| [152] | Sr1.4Ba0.6Fe0.8Mo0.8Mn0.2V0.2O6 | −58 | 316 | 83.2 | 973 | ||
| [153] | SrRuO3 | 36 | 5.3 | 0.03 | 1200 | ||
| [154] | Sr2RuYO6 | −250 | 1200 | ||||
| Sr2RuErO6 | −250 | 1200 | |||||
| [155] | (Sr0.95La0.05)2RuErO6 | −160 | 0.001 | 800 | |||
| [156] | AgNbO3 | 700 −500 | 800 | ||||
| AgTaO3 | 710 | 800 | |||||
| [157] | K0.991Ba0.009TaO3 | 200 | 333 | 0.03 | 300 | ||
| [88] | KTaO3 | −280 | 1000 | ||||
| [158] | BaUO3 | −170 | 0.1 | 0.8 | 0.0002 | 880 | |
| [159] | BaCe0.95Y0.05O3 | −220 | 873 | ||||
| [35] | C6H4NH2CuBr2I | −82 | 2950 | 3.25 | 0.21 | 363 | |
| [33] | CH3NH3PbI3-n-type | −238 | 160 | 0.1 | 8.4 | 0.61 | 300 |
| p-type | 181 | 94 | 0.06 | 3.1 | 0.25 | 300 | |
| n-type | −362 | 89 | 0.145 | 10.5 | 1.61 | 600 | |
| p-type | 295 | 41 | 0.06 | 3.6 | 0.71 | 600 | |
| n-type | −428 | 68 | 0.151 | 11.3 | 2.56 | 800 | |
| p-type | 358 | 25 | 0.04 | 3.3 | 1.08 | 800 | |
| [160] | CH3NH3SnI3 | 720 | 0.001 | 0.08 | 0.01 | 295 | |
| CH3NH3PbI3 | 700 | 10−7 | 0.5 | 10−7 | 295 | ||
| [34] | (MA)PbI3 | 200 | 0.44 | 298 | |||
| (MA)SnI3 | 200 | 0.44 | 298 | ||||
| (FA)PbI3 | 100 | 0.43 | 298 | ||||
| (FA)SnI3 | 150 | 0.35 | 298 | ||||
| [161] | CH3NH3PbI3-n-type | 80 | 1.2 | 0.9 | 330 | ||
| CH3NH3PbI3-p-type | 50 | 1 | 1.25 | 330 | |||
| [162] | CsSnI3 | 0.18 | 0.63 | 1000 | |||
| CsPbI3 | 0.1 | 0.64 | 1000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Gao, P. Development of Perovskite-Type Materials for Thermoelectric Application. Materials 2018, 11, 999. https://doi.org/10.3390/ma11060999
Wu T, Gao P. Development of Perovskite-Type Materials for Thermoelectric Application. Materials. 2018; 11(6):999. https://doi.org/10.3390/ma11060999
Chicago/Turabian StyleWu, Tingjun, and Peng Gao. 2018. "Development of Perovskite-Type Materials for Thermoelectric Application" Materials 11, no. 6: 999. https://doi.org/10.3390/ma11060999
APA StyleWu, T., & Gao, P. (2018). Development of Perovskite-Type Materials for Thermoelectric Application. Materials, 11(6), 999. https://doi.org/10.3390/ma11060999







