Seebeck Coefficient of Thermocouples from Nickel-Coated Carbon Fibers: Theory and Experiment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Etching Process
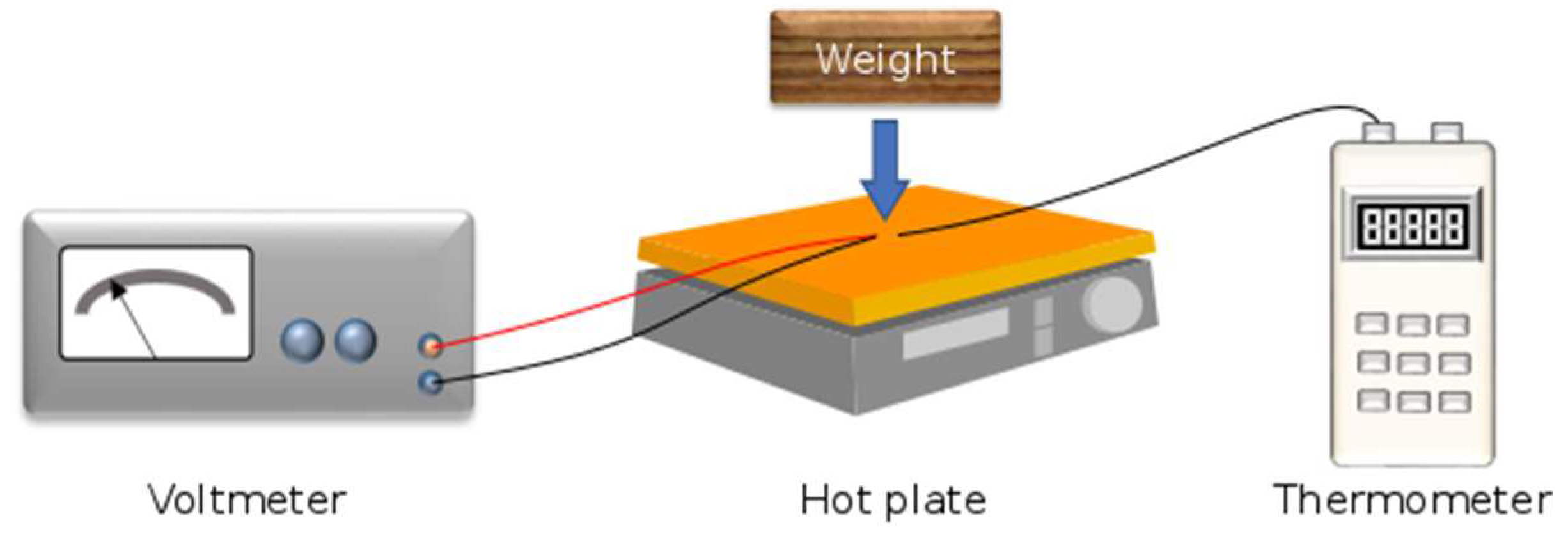
2.3. Seebeck Coefficient Measurement
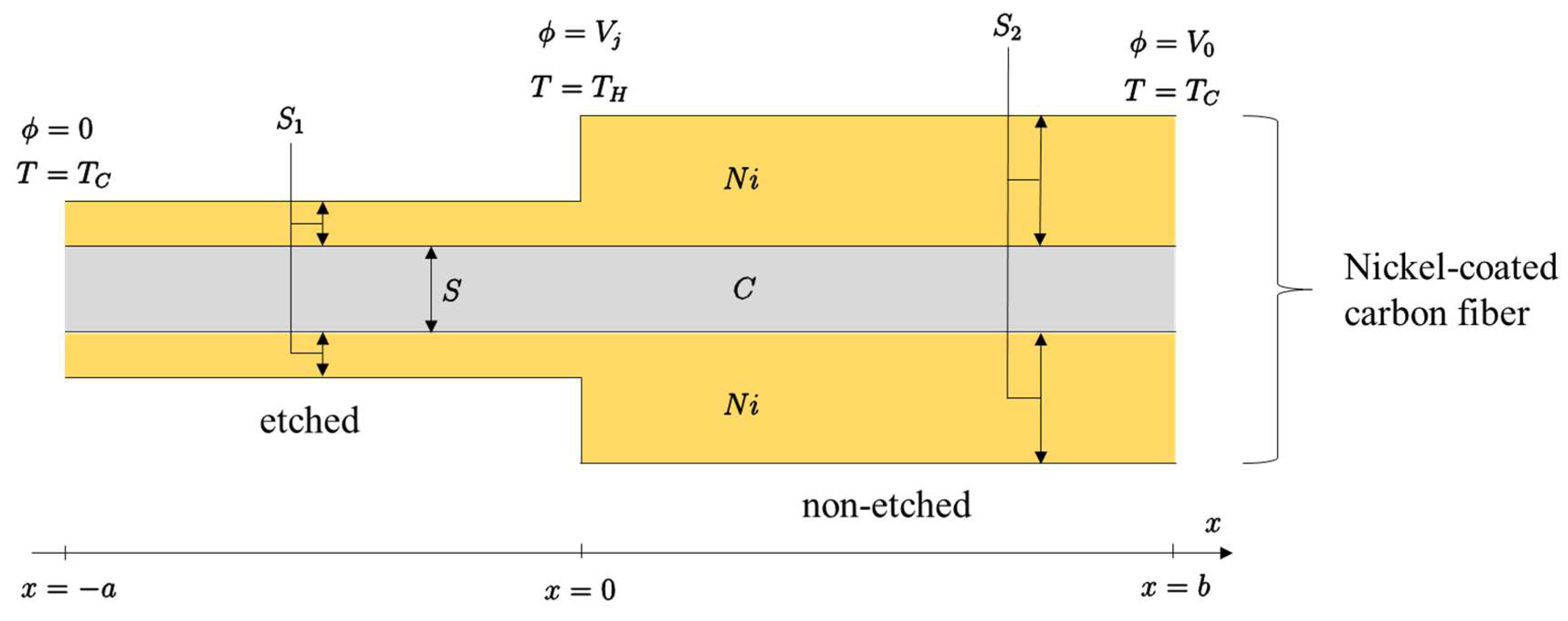
2.4. Theoretical Analysis
3. Results and Discussion
3.1. Microscopic Observation after Etching Process
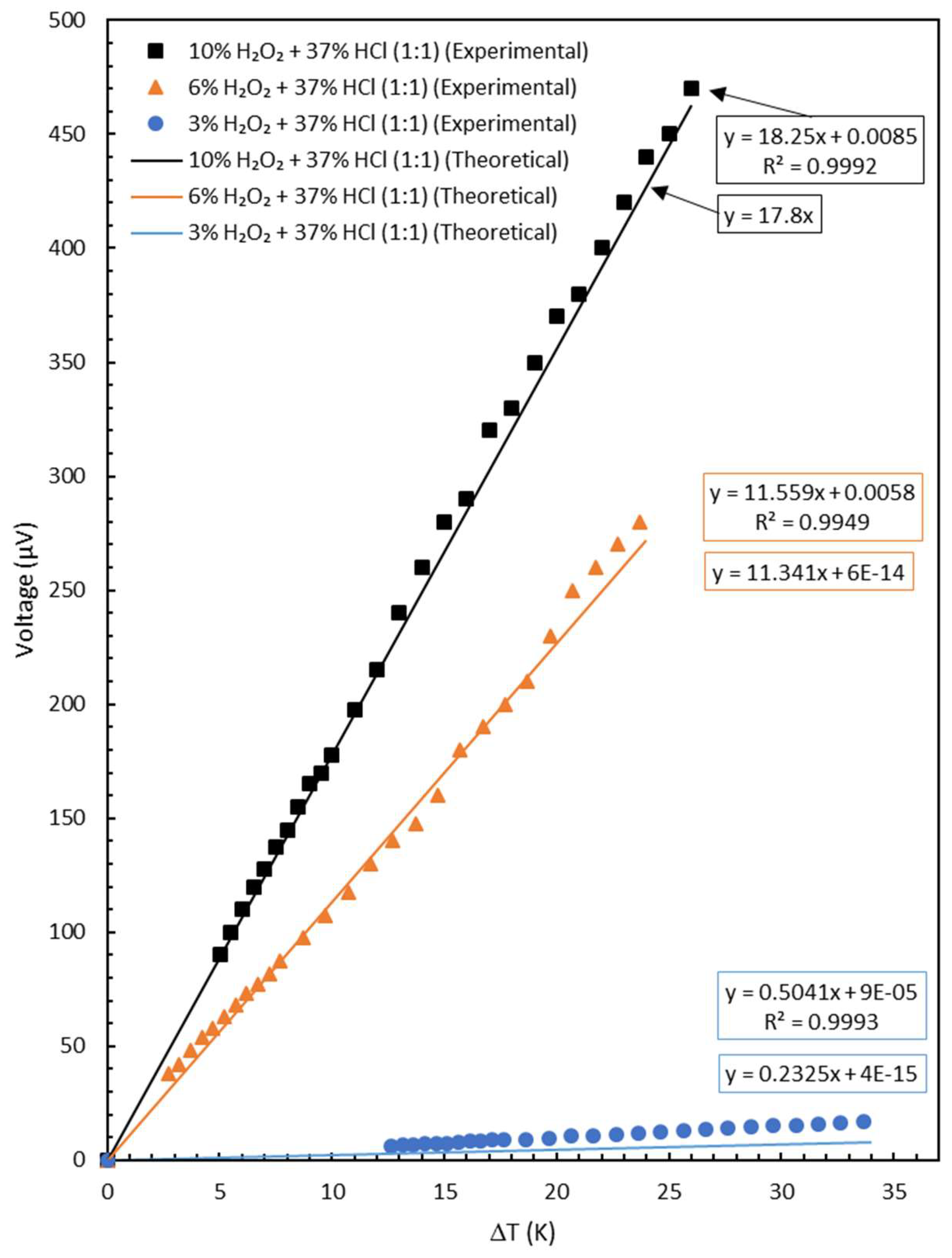
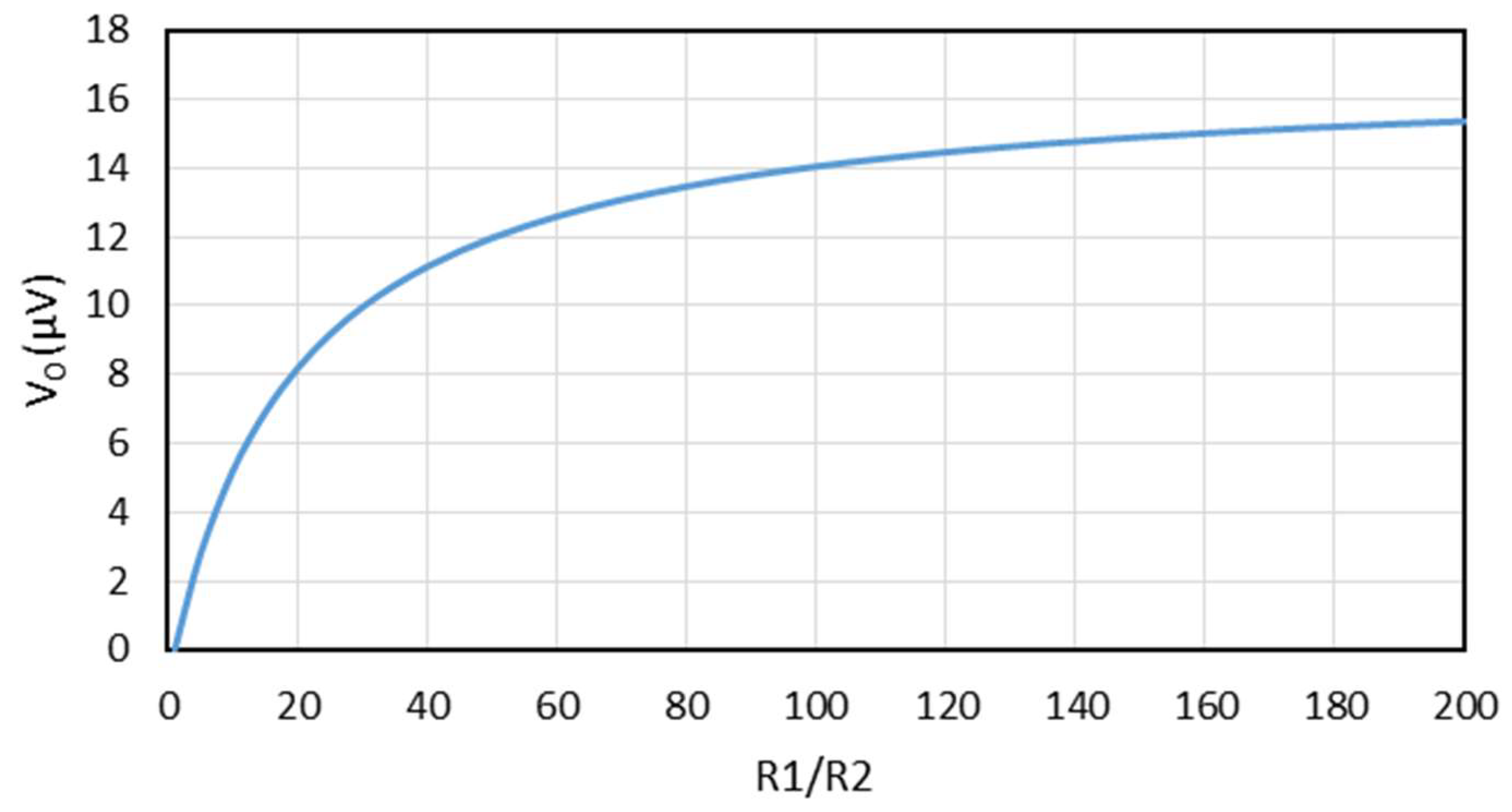
3.2. Comparison between Experiment and Theory
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, C.; Kim, K.M.; Kim, K.J.; Lepró, X.; Spinks, G.M.; Baughman, R.H.; Kim, S.J. Improvement of system capacitance via weavable superelastic biscrolled yarn supercapacitors. Nat. Commun. 2016, 7, 13811. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Leng, T.; Zhu, M.; Zhang, X.; Chen, J.; Chang, K.; Aqeeli, M.; Geim, A.K.; Novoselov, K.S.; Hu, Z. Highly Flexible and Conductive printed graphene for wireless wearable communications applications. Sci. Rep. 2015, 5, 18298. [Google Scholar] [CrossRef] [PubMed]
- Uchida, K.; Takahashi, S.; Harii, K.; Ieda, J.; Koshibae, W.; Ando, K.; Maekawa, S.; Saitoh, E. Observation of the spin Seebeck effect. Nature 2008, 455, 778–781. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, S.; Frydrysiak, M. Initial research into the structure and working conditions of textile thermocouples. Fibres Text. East. Eur. 2009, 77, 84–88. [Google Scholar]
- Gidik, H.; Bedek, G.; Dupont, D. Developing thermophysical sensors with textile auxiliary wall. In Smart Textiles and Their Applications; Woodhead Publishing: Cambridge, MA, USA, 2016; pp. 423–453. [Google Scholar]
- Alexander, R. Jones The Application of Temperature Sensors Into Fabric Substrates. Master’s Thesis, Kansas State University, Manhattan, KS, USA, 2011. [Google Scholar]
- Dupont, D.; Godts, P.; Leclercq, D. Design of textile heat flowmeter combining evaporation phenomena. Text. Res. J. 2006, 76, 772–776. [Google Scholar] [CrossRef]
- Gidik, H.; Bedek, G.; Dupont, D.; Codau, C. Impact of the textile substrate on the heat transfer of a textile heat flux sensor. Sens. Actuators A Phys. 2015, 230, 25–32. [Google Scholar] [CrossRef]
- Hertleer, C.; Bedek, G.; Dupont, D. A Textile-Based Heat Flux Sensor. In Proceedings of the VI International Technical Textiles Congress, Izmir, Turkey, 14–16 October 2015. [Google Scholar]
- Meng, C.; Liu, C.; Fan, S. A promising approach to enhanced thermoelectric properties using carbon nanotube networks. Adv. Mater. 2010, 22, 535–539. [Google Scholar] [CrossRef] [PubMed]
- Esfarjani, K.; Zebarjadi, M.; Kawazoe, Y. Thermoelectric properties of a nanocontact made of two-capped single-wall carbon nanotubes calculated within the tight-binding approximation. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73. [Google Scholar] [CrossRef]
- Mahmoud, L.; Abdul Samad, Y.; Alhawari, M.; Mohammad, B.; Liao, K.; Ismail, M. Combination of PVA with graphene to improve the seebeck coefficient for thermoelectric generator applications. J. Electron. Mater. 2015, 44, 420–424. [Google Scholar] [CrossRef]
- Hardianto, A.; Hertleer, C.; Mey, G.; De Langenhove, L. Van Removing nickel from nickel-coated carbon fibers. IOP Conf. Ser. Mater. Sci. Eng. 2017, 254, 72010. [Google Scholar] [CrossRef]
- Wróbel, I.C.; Knockaert, J.; Mey, G. De Shielding the electromagnetic waves by inserting conductive lightweight materials into woven curtains. J. Fash. Technol. Text. Eng. 2017, 1–4. [Google Scholar] [CrossRef]
- TIBTECH Innovations Properties Table of Stainless Steel, Metals and Other Conductive Materials. Available online: http://www.tibtech.com/conductivity.php (accessed on 1 February 2018).
- Bejan, A. Advanced Engineering Thermodynamics, 3rd ed.; Wiley: Hoboken, NJ, USA, 2006; ISBN 0471677639. [Google Scholar]
- McGhee, J.; Korczynski, J.; Henderson, I.; Kulesza, W. Scientific Metrology; ACGM Lodart S.A.: Lódz, Poland, 1998; ISBN 83-904299-9-3. [Google Scholar]


| Parameter | Description |
|---|---|
| Raw material | Carbon |
| Liner density [tex] | 1420 tex |
| Coating | 0.25 µm of Ni |
| No. of filaments | 1200 |
| Filament diameter [µm] | 7.5 incl. Coating |
| Density [g/cm3] | 2.70 |
| Twist [tpm, type] | 0 |
| Linear electrical resistance [Ω/m] | 2.2667 |
| Commercial name | Tenax®-J HTS40 |
| Etching Condition | Linear Electrical Resistance [Ω/m] |
|---|---|
| Non-etched | 2.2667 |
| 3% H2O2 + 37% HCl (1:1) | 2.8667 |
| 6% H2O2 + 37% HCl (1:1) | 31.533 |
| 10% H2O2 + 37% HCl (1:1) | 45.933 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hardianto, H.; De Mey, G.; Ciesielska-Wrόbel, I.; Hertleer, C.; Van Langenhove, L. Seebeck Coefficient of Thermocouples from Nickel-Coated Carbon Fibers: Theory and Experiment. Materials 2018, 11, 922. https://doi.org/10.3390/ma11060922
Hardianto H, De Mey G, Ciesielska-Wrόbel I, Hertleer C, Van Langenhove L. Seebeck Coefficient of Thermocouples from Nickel-Coated Carbon Fibers: Theory and Experiment. Materials. 2018; 11(6):922. https://doi.org/10.3390/ma11060922
Chicago/Turabian StyleHardianto, Hardianto, Gilbert De Mey, Izabela Ciesielska-Wrόbel, Carla Hertleer, and Lieva Van Langenhove. 2018. "Seebeck Coefficient of Thermocouples from Nickel-Coated Carbon Fibers: Theory and Experiment" Materials 11, no. 6: 922. https://doi.org/10.3390/ma11060922
APA StyleHardianto, H., De Mey, G., Ciesielska-Wrόbel, I., Hertleer, C., & Van Langenhove, L. (2018). Seebeck Coefficient of Thermocouples from Nickel-Coated Carbon Fibers: Theory and Experiment. Materials, 11(6), 922. https://doi.org/10.3390/ma11060922






