Percent Reduction in Transverse Rupture Strength of Metal Matrix Diamond Segments Analysed via Discrete-Element Simulations
Abstract
:1. Introduction
2. Materials and Experimental Details
2.1. Fabrication of Diamond Segments
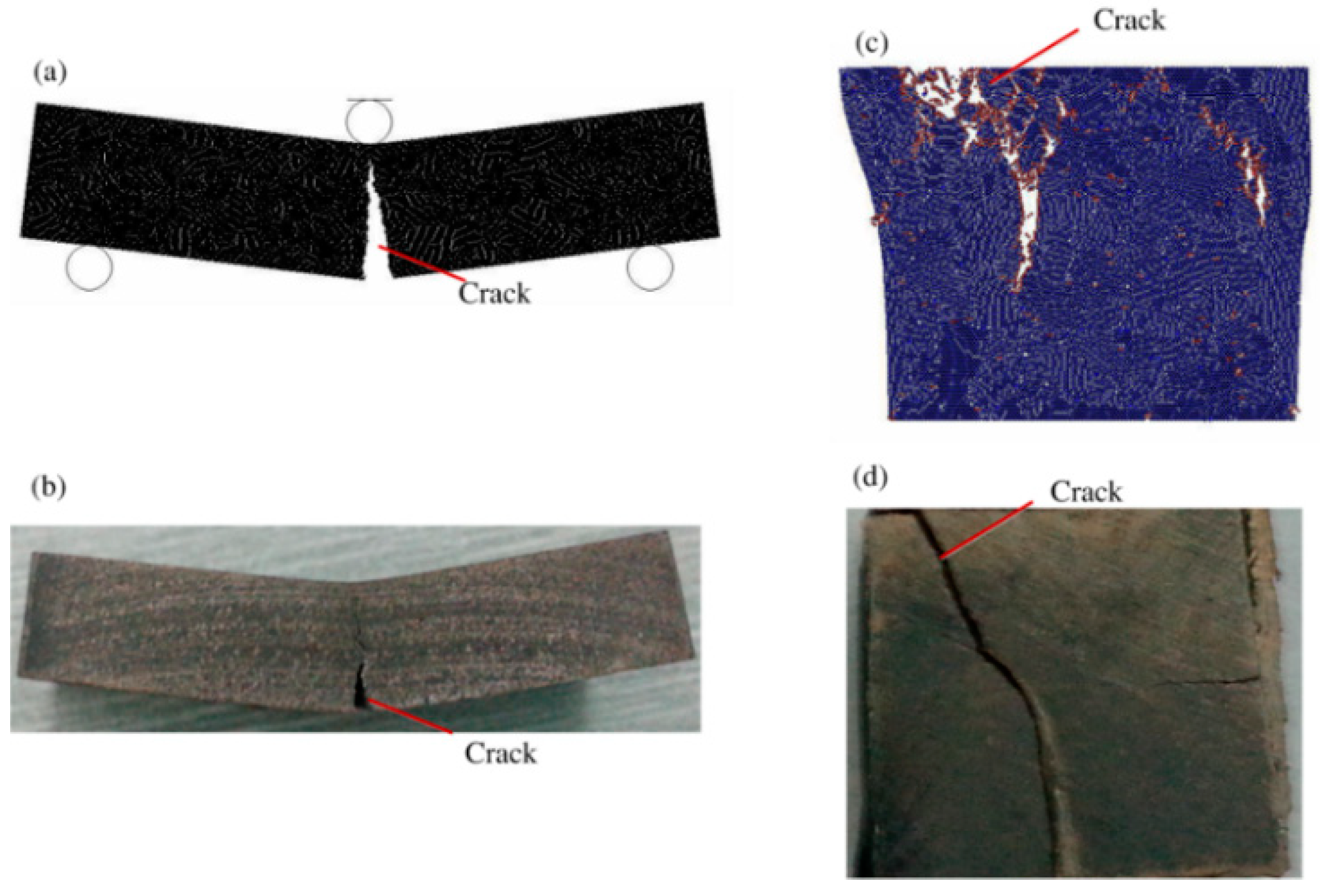
2.2. The Three-Point Bending Tests and Compression Tests
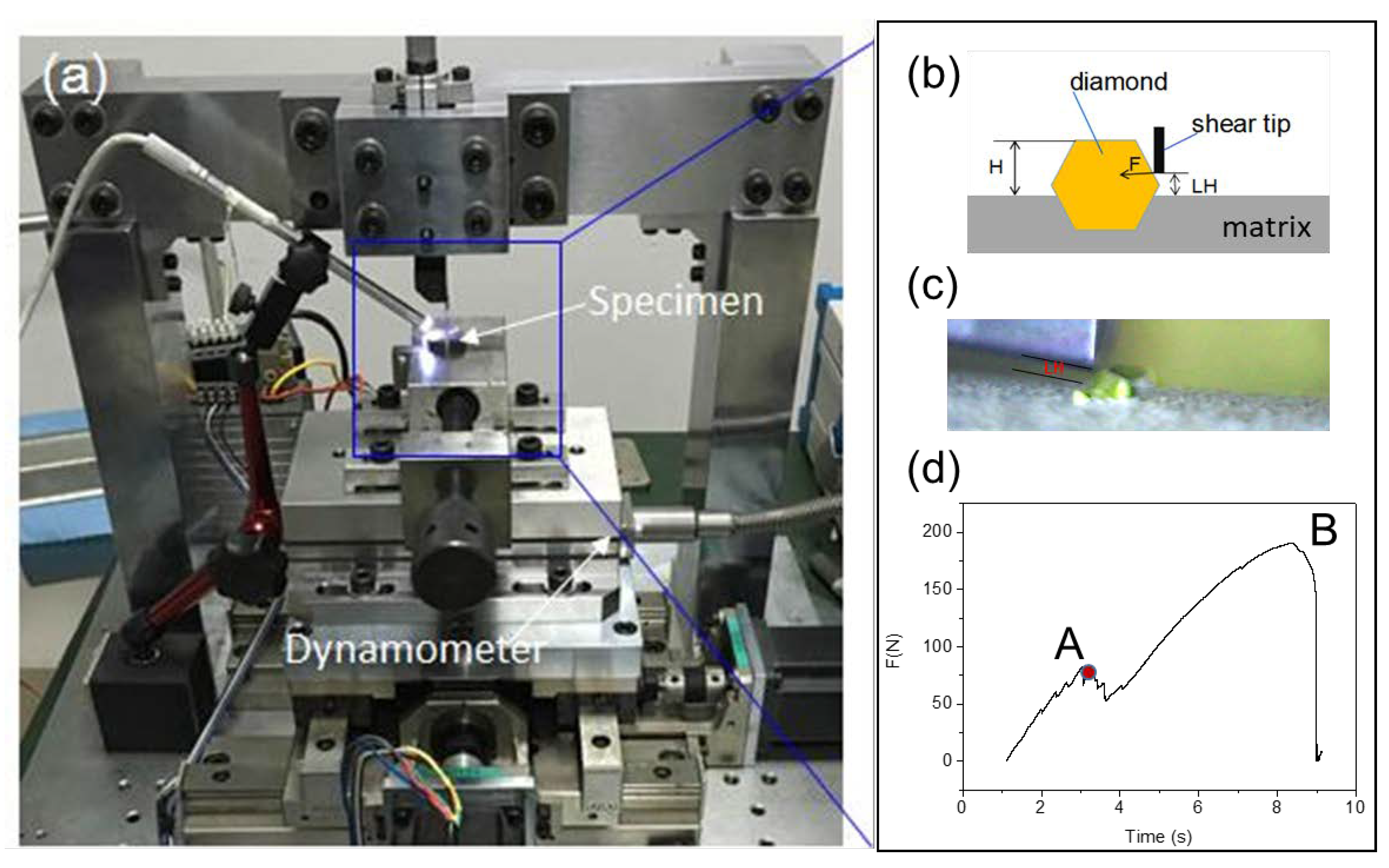
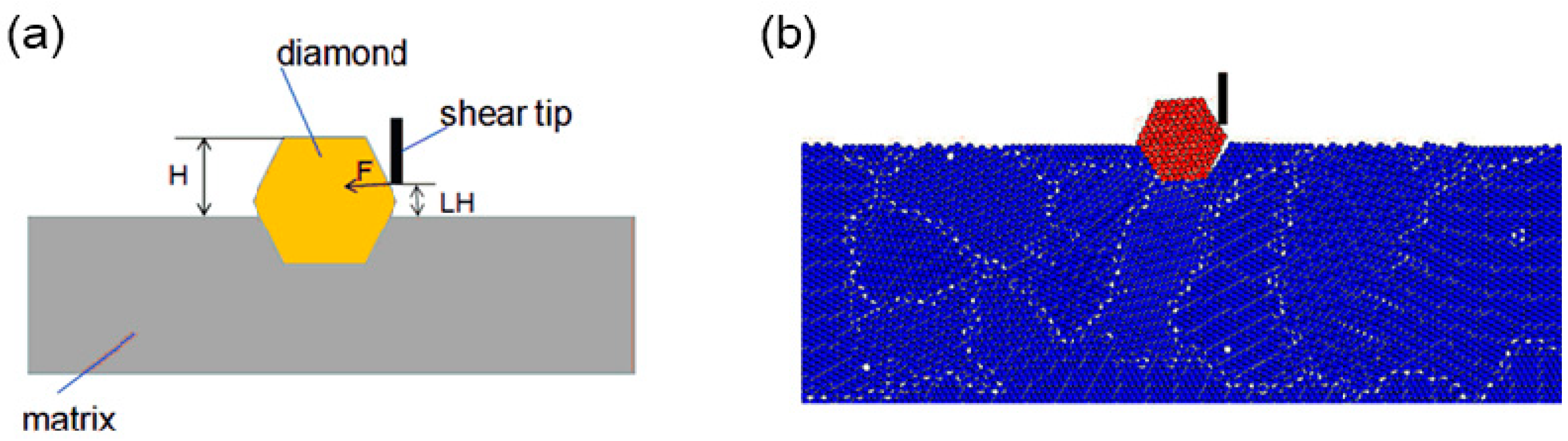
2.3. Single Grit Shearing Test
3. Establishment, Calibration, and Verification of Discrete-Element Model
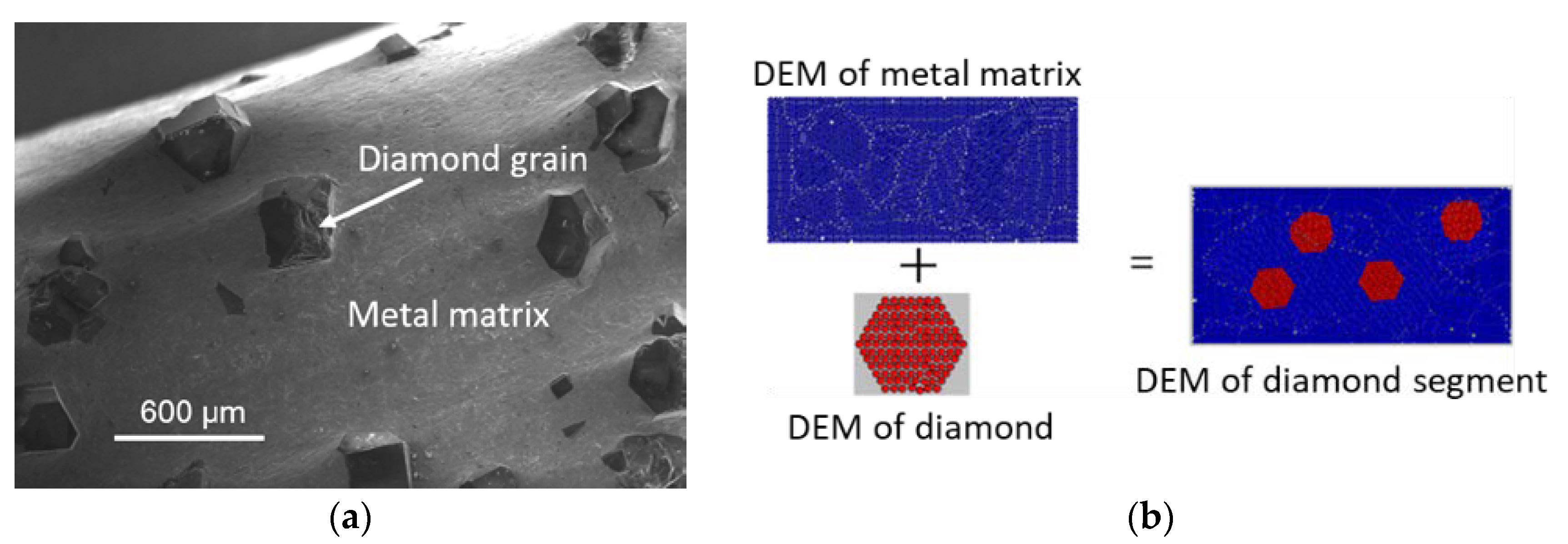
3.1. Discrete-Element Model of Metal Matrix
3.2. Discrete-Element Model of Diamond
3.3. Discrete-Element Model of the Diamond Segment
3.4. Verification of Discrete-Element Model of the Diamond Segment
4. Simulation of Percent Reduction of TRS
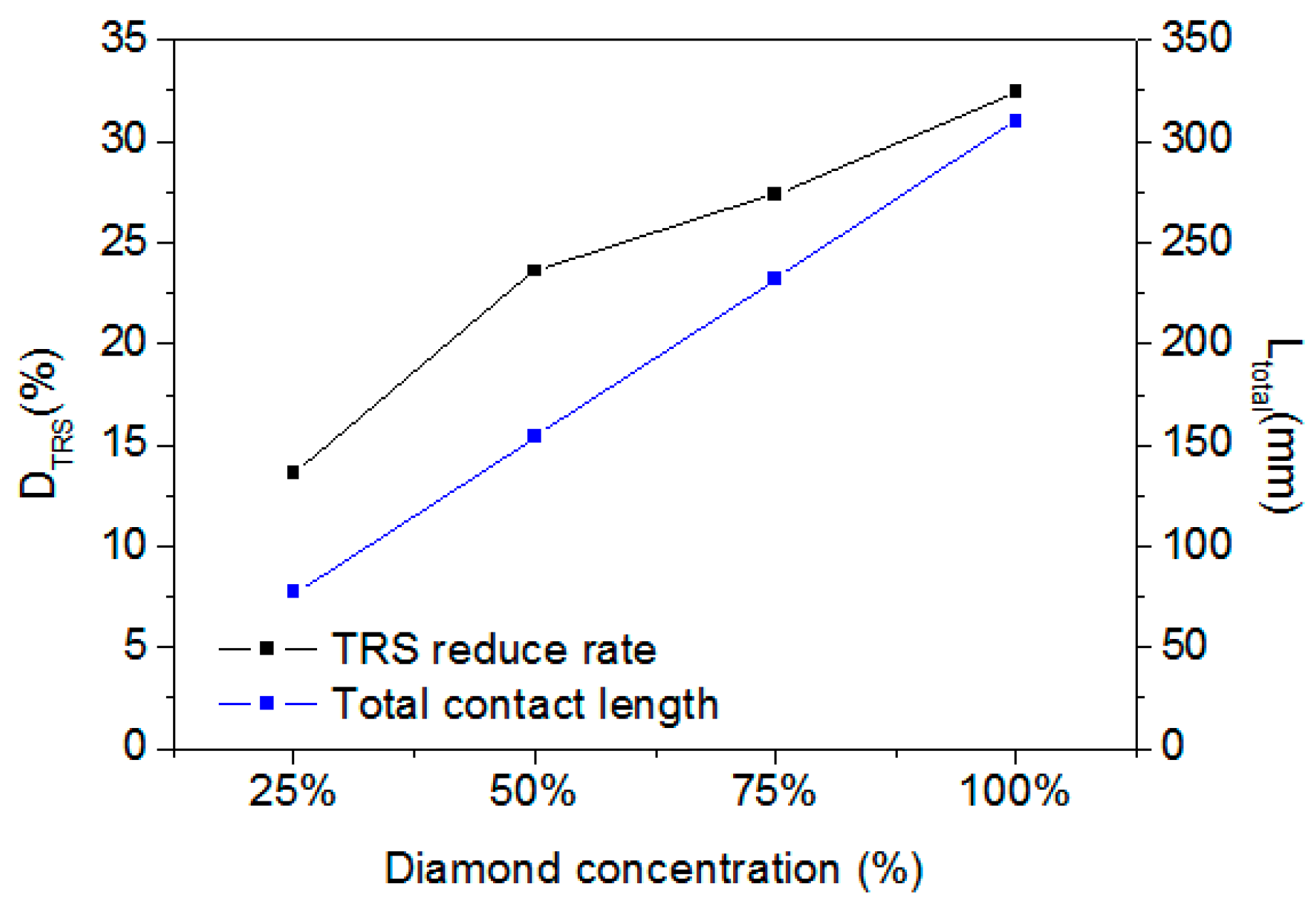
4.1. Effect of Diamond Concentration
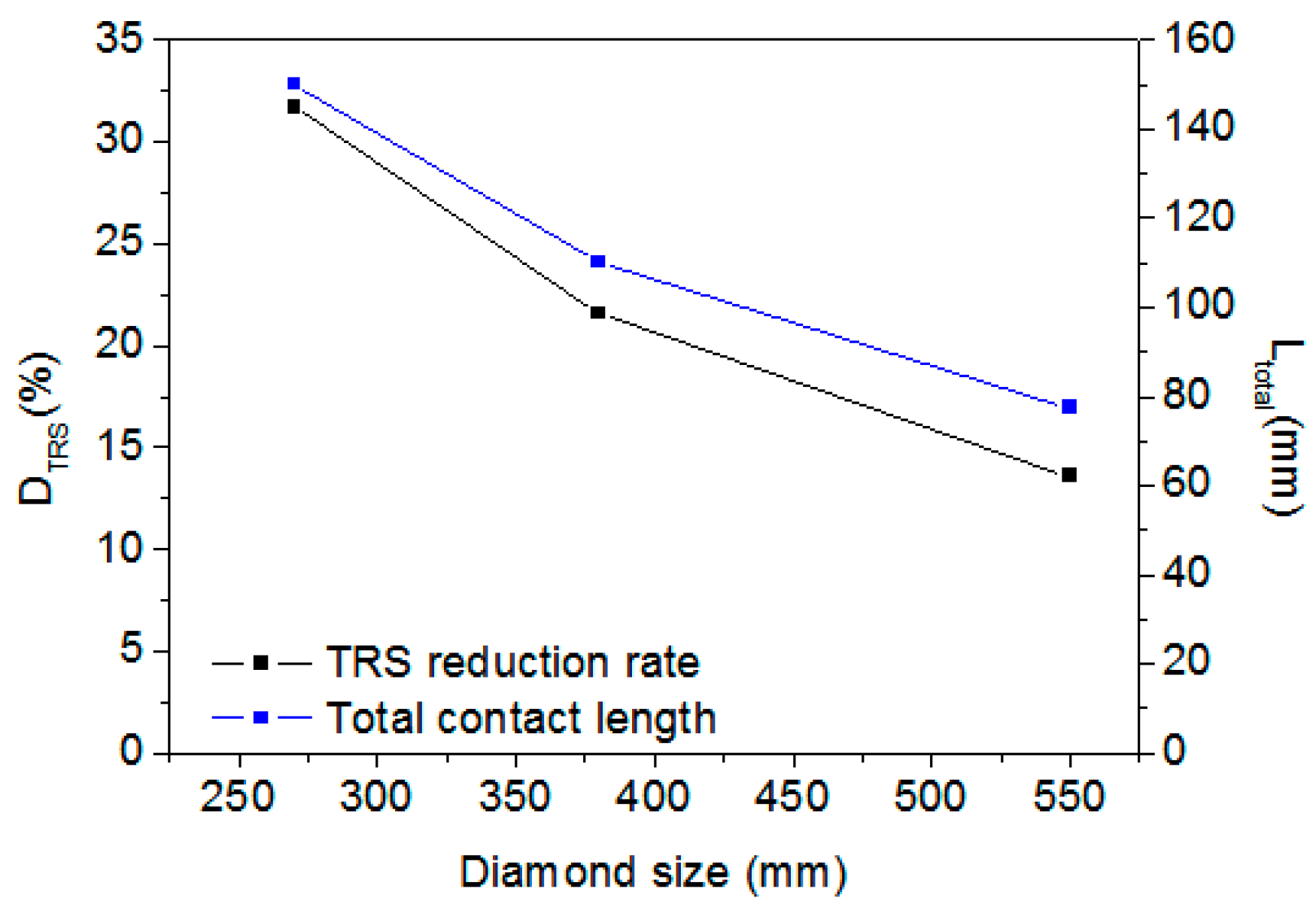
4.2. Effect of Diamond-Grain Size
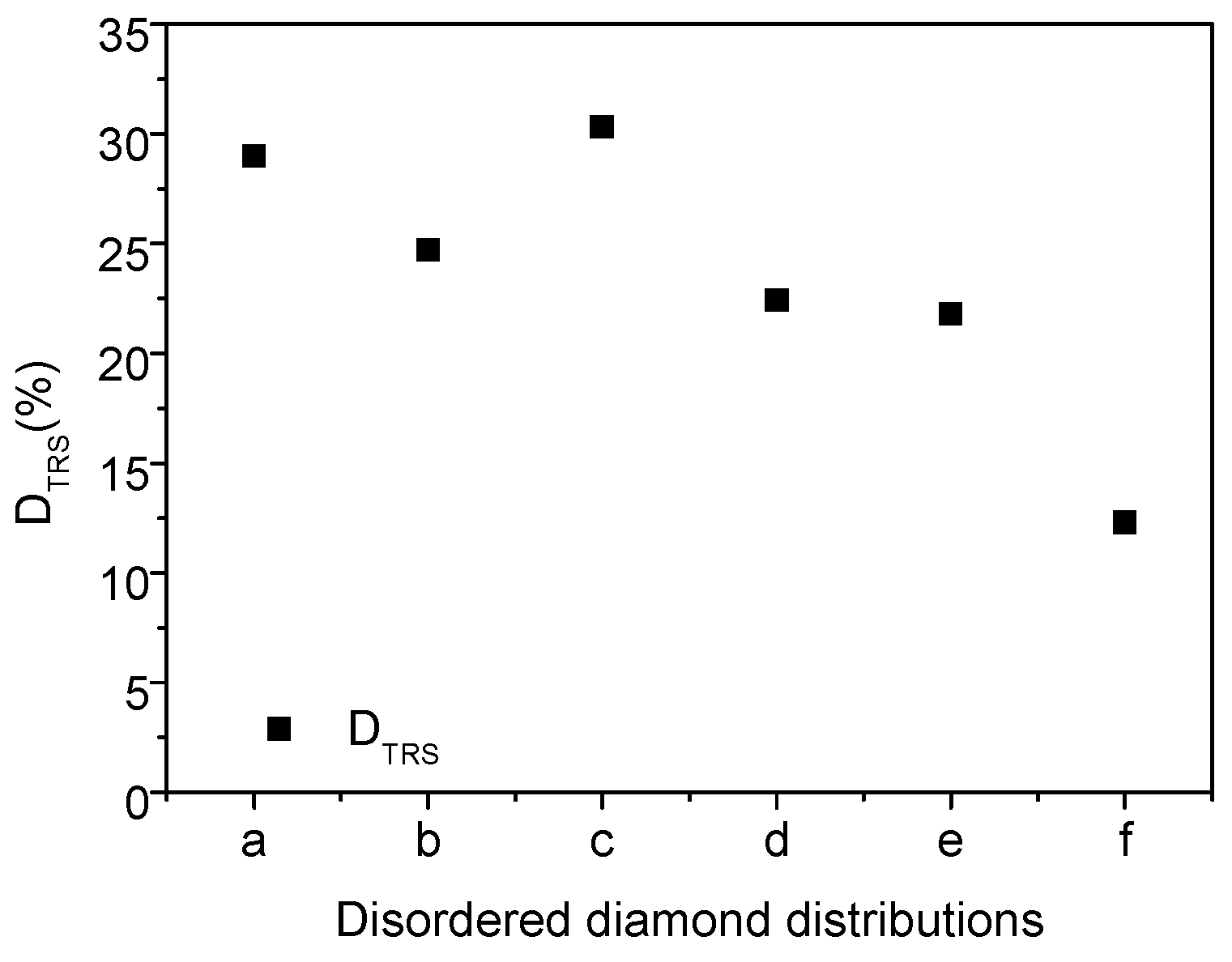
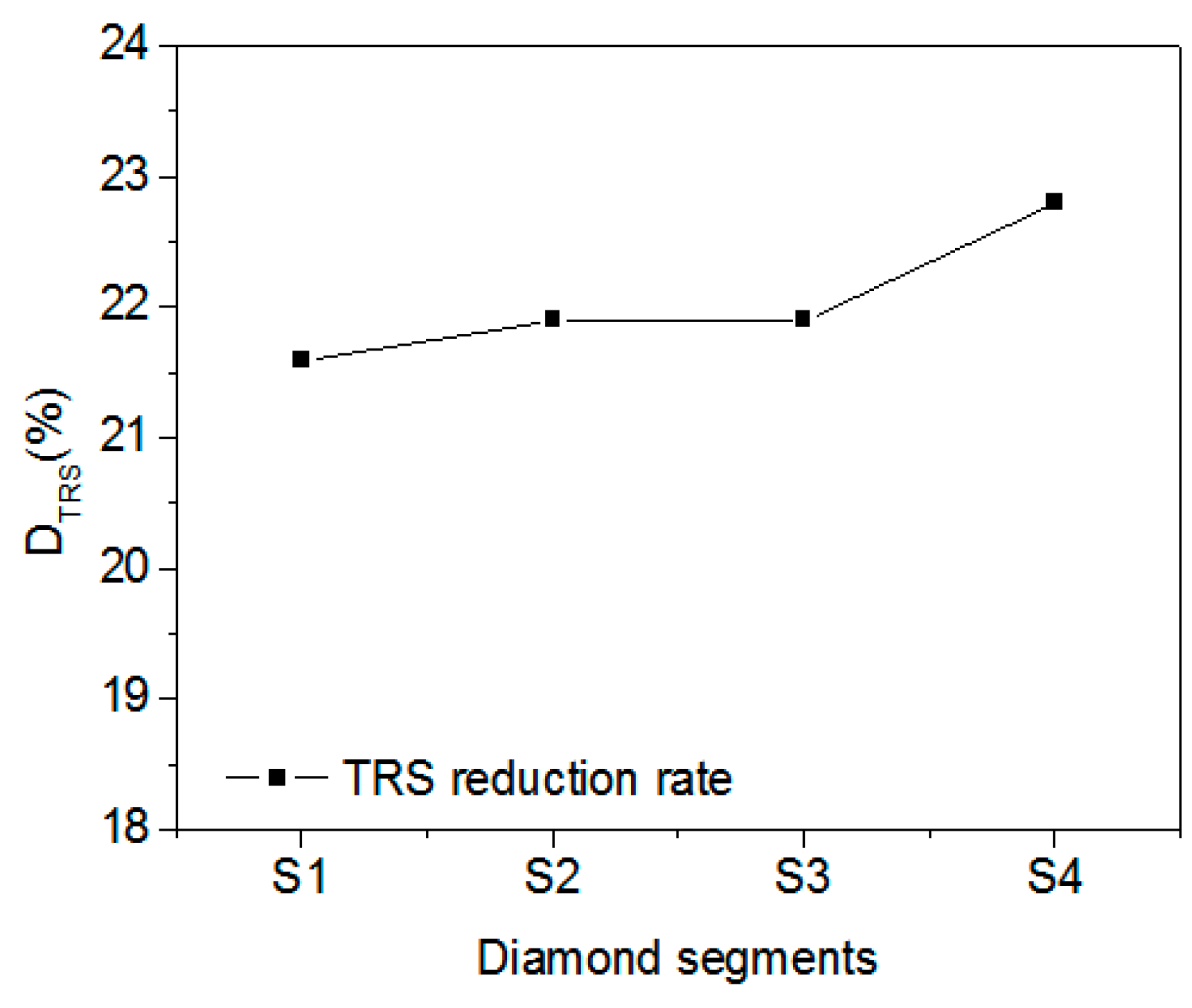
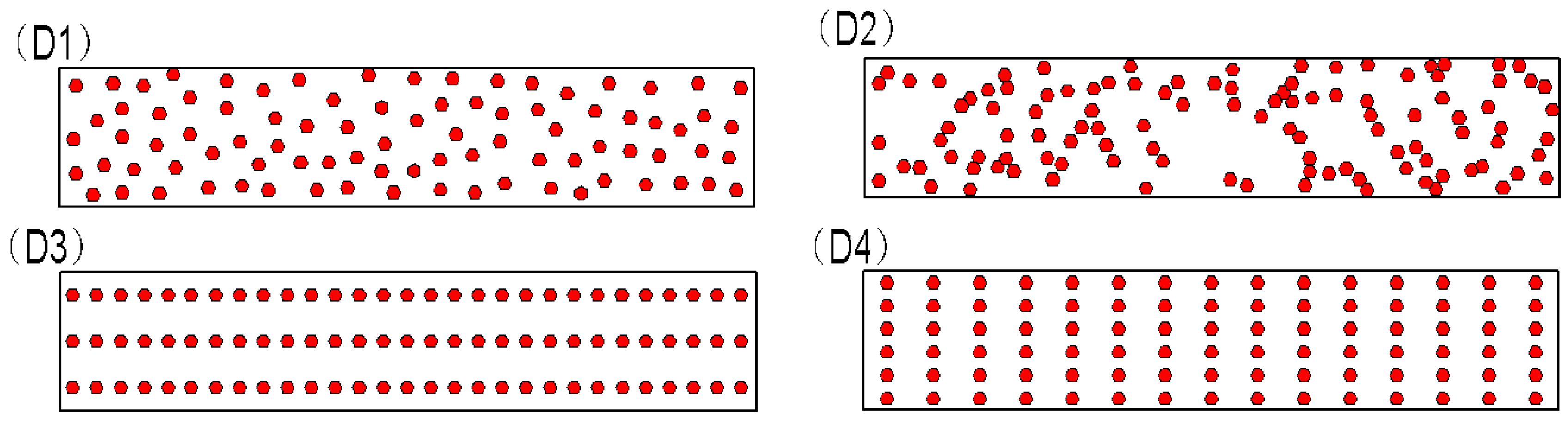
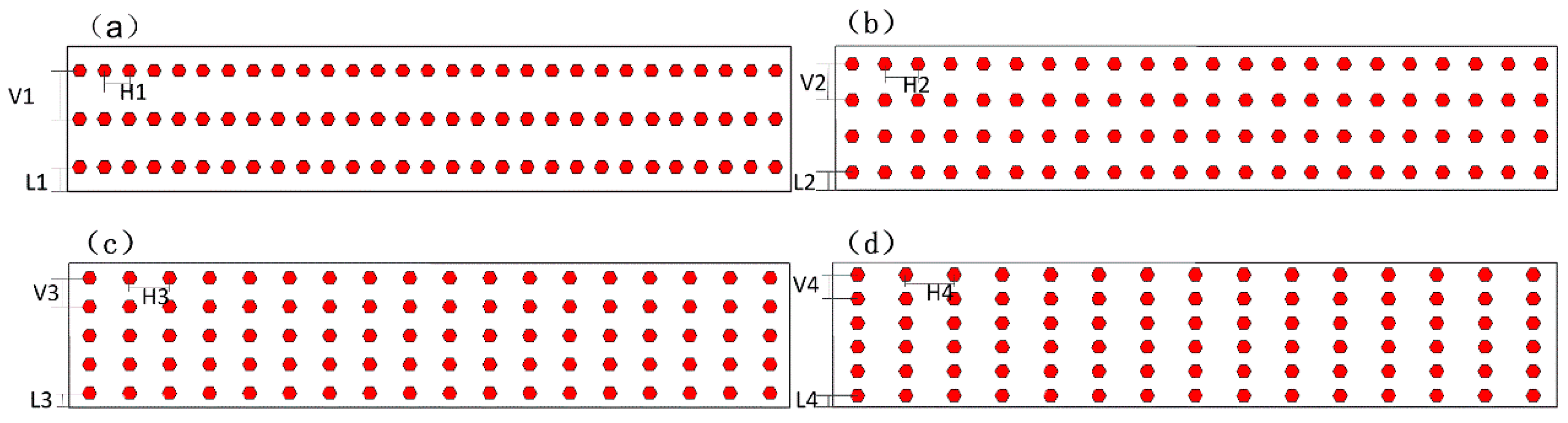
4.3. Effect of Diamond Distribution
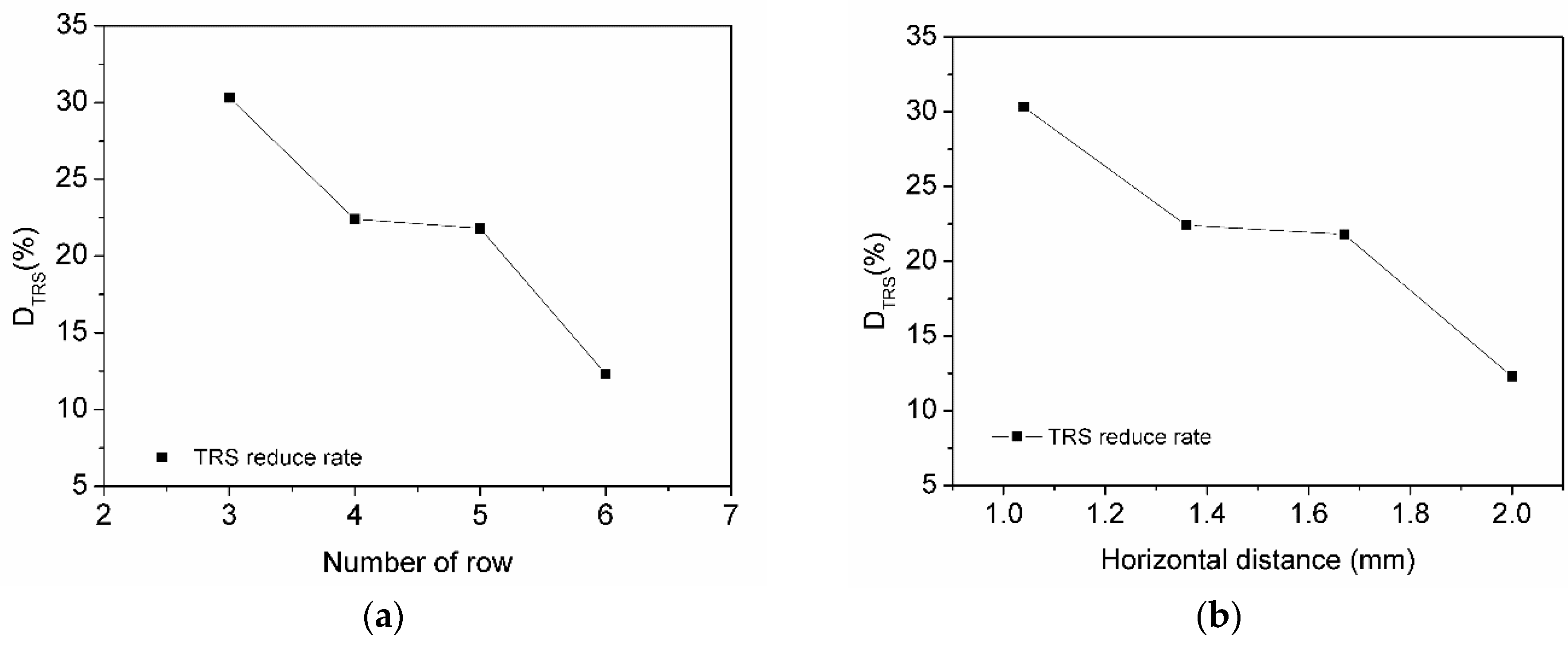
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Abyzov, A.M.; Shakhov, F.M.; Averkin, A.I.; Nikolaev, V.I. Mechanical properties of a diamond—Copper composite with high thermal conductivity. Mater. Des. 2015, 87, 527–539. [Google Scholar] [CrossRef]
- Oliveiral, F.A.C.; Anjinho, C.A.; Coelho, A. PM materials selection: The key for improvedperformance of diamond tools. Met. Powder Rep. 2017, 72, 339–344. [Google Scholar] [CrossRef]
- Yu, Y.Q.; Xu, X.P. Improvement on the performance of diamond segments for rock sawing, part 1: Effects of segment components. Key Eng. Mater. 2003, 250, 46–53. [Google Scholar] [CrossRef]
- Xu, X.P.; Tie, X.R.; Wu, H.R. The effects of a Ti coating on the performance of metal-bonded diamond composites containing rare earth. Int. J. Refract. Met. Hard Mater. 2007, 25, 244–249. [Google Scholar] [CrossRef]
- Dai, Q.L.; Luo, C.B.; Xu, X.P.; Wang, Y.C. Effects of rare earth and sintering temperature on the transverse rupture strength of Fe-based diamond composites. J. Mater. Process. Technol. 2002, 129, 427–430. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive large scale movements in blocky rock systems. Proc. Int. Symp. Rock Fract. 1971, 2, 129–136. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. Discrete numerical model for granular assemblies. Geothechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Hunt, S.P.; Meyers, A.G.; Louchnikov, V. Modelling the Kaiser effect and deformation rate analysis in sandstone using the discrete element method. Comput. Geotech. 2006, 30, 611–621. [Google Scholar] [CrossRef]
- Frédéric, S.H.; Donzé, V.; Daudeville, L. Discrete element modeling of concrete submitted to dynamic loading at high strain rates. Comput. Struct. 2004, 82, 2509–2524. [Google Scholar]
- Tan, Y.; Yang, D.; Sheng, Y. Discrete element method (DEM) modeling of fracture and damage in the machining process of polycrystalline SiC. J. Eur. Ceram. Soc. 2009, 29, 1029–1037. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. PFC2D (Particle Flow Code in 2-Dimensions); Version 3.10; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2004. [Google Scholar]
- Ostanin, I.; Ballarini, R.; Potyond, D.; Dumitric, T. A distinct element method for large scale simulations of carbon nanotube assemblies. J. Mech. Phys. Solids 2013, 61, 762–782. [Google Scholar] [CrossRef]
- Benvenuti, L.; Kloss, C.; Pirker, S. Identification of DEM simulation parameters by Artificial Neural Networks and bulk experiments. Powder Technol. 2016, 291, 456–465. [Google Scholar] [CrossRef]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Rajeev, S. Discrete Element Modeling of Silicon Nitride Ceramics. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2009. [Google Scholar]
- Field, J. The mechanical and strength properties of diamond. Rep. Prog. Phys. Phys. Soc. 2012, 75, 126–135. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, L.J.; Guerold, S.B.; Marcello, F. Processing and characterization of impregnated diamond cutting tools using a ferrous metal matrix. Int. J. Refract. Metals Hard Mater. 2007, 25, 328–335. [Google Scholar] [CrossRef]
- Zhao, X.J.; Duan, L. A Review of the Diamond Retention Capacity of Metal Bond Matrices. Metals 2018, 8, 307. [Google Scholar] [CrossRef]


| Mechanical Properties | Co-Based Metal Matrix (Segment without Diamonds) | ||
|---|---|---|---|
| Experimental Results | Simulation Results | Error | |
| UCS/MPa | 1681 | 1842 | 9.6% |
| Ec/GPa | 13.8 | 12.8 | 7.2% |
| TRS/MPa | 1120 | 1046 | 4.2% |
| Mechanical Properties | Values from [16] | Values Simulated by DEM Model |
|---|---|---|
| Young’s modulus Ec (GPa) | 900–1000 | 940 |
| Poisson’s ratio γ | 0.069–0.12 | 0.095 |
| UCS (MPa) | 4500–5800 | 4853 |
| Exposure Height (µm) | Critical Force of Shearing Test, F (N) | Error (%) | |
|---|---|---|---|
| By Experiment (N) | By Simulation (N) | ||
| 230 | 70.5 | 71.1 | 0.9 |
| 280 | 67.3 | 68 | 1.0 |
| Values of Microcosmic Parameters | |||
|---|---|---|---|
| Matrix | Diamond | Diamond/Matrix Boundary | |
| Particle density (kg/m3) | 8900 | 3500 | / |
| Particle contactmodulus, Ec (GPa) | 1.3 × e10 | 3 × e11 | / |
| Particle stiffnessratio, kn/ks | 1 | 1 | / |
| Particle friction coefficient | 0.8 | 0.1 | / |
| Isotropics Stress, (Pa) | −2.0 × e7 | −5.0 × e7 | / |
| Radius multiplier of parallel bond | 1 | 1 | 1 |
| Elasticity modulus of parallel bond (Pa) | 1.3 × e9 | 11 × e11 | 4 × e7 |
| Normal strength of parallel bond (Pa) | 3 × e8 | 1 × e10 | 4 × e3 |
| Shear strength of parallel bond (Pa) | 3 × e8 | 1 × e10 | 4 × e3 |
| Normal strength of contact bond (Pa) | 6 × e7 | / | 5 × e3 |
| Shear strength of contact bond (Pa) | 6 × e7 | / | 5 × e3 |
| Diamond Size (US Mesh) | Concentration (%) | TRS | Ec | ||||
|---|---|---|---|---|---|---|---|
| Simulation (MPa) | Experiment (MPa) | Error (%) | Simulation (N) | Experiment (N) | Error (%) | ||
| 30/40 | 50 | 743 | 786 | 5.5 | 17.4 | 15.9 | 9.4 |
| Diamond Segments | Number of Diamonds with Given Grain Size | Total Contact Length (mm) | Diamond Concentration (%) | DTRS (%) | ||
|---|---|---|---|---|---|---|
| 550 µm | 380 µm | 270 µm | ||||
| S1 | 0 | 92 | 0 | 110 | 25 | 21.6 |
| S2 | 29 | 31 | 32 | 110 | 29.7 | 22.0 |
| S3 | 23 | 32 | 37 | 110 | 29.7 | 22.0 |
| S4 | 43 | 0 | 49 | 110 | 32 | 22.8 |
| Diamond Distribution | TRS (MPa) | Percent TRS Reduction (%) |
|---|---|---|
| D1 | 788 | 24.7 |
| D2 | 734 | 29.8 |
| D3 | 729 | 30.3 |
| D4 | 916 | 12.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Huang, G.; Tan, Y.; Yu, Y.; Guo, H.; Xu, X. Percent Reduction in Transverse Rupture Strength of Metal Matrix Diamond Segments Analysed via Discrete-Element Simulations. Materials 2018, 11, 1048. https://doi.org/10.3390/ma11061048
Chen X, Huang G, Tan Y, Yu Y, Guo H, Xu X. Percent Reduction in Transverse Rupture Strength of Metal Matrix Diamond Segments Analysed via Discrete-Element Simulations. Materials. 2018; 11(6):1048. https://doi.org/10.3390/ma11061048
Chicago/Turabian StyleChen, Xiuyu, Guoqin Huang, Yuanqiang Tan, Yiqing Yu, Hua Guo, and Xipeng Xu. 2018. "Percent Reduction in Transverse Rupture Strength of Metal Matrix Diamond Segments Analysed via Discrete-Element Simulations" Materials 11, no. 6: 1048. https://doi.org/10.3390/ma11061048
APA StyleChen, X., Huang, G., Tan, Y., Yu, Y., Guo, H., & Xu, X. (2018). Percent Reduction in Transverse Rupture Strength of Metal Matrix Diamond Segments Analysed via Discrete-Element Simulations. Materials, 11(6), 1048. https://doi.org/10.3390/ma11061048






