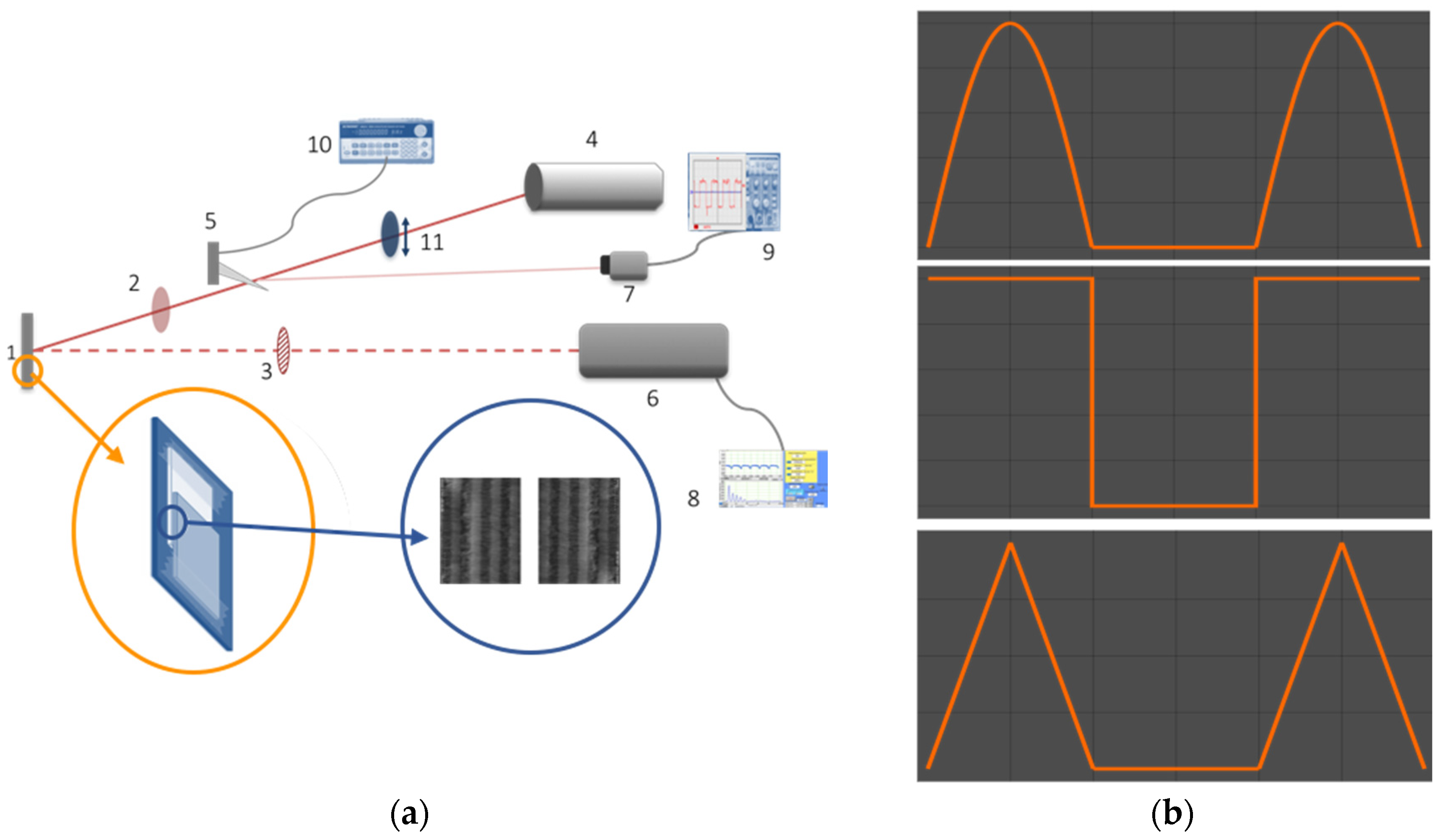
1. Introduction
The use of light concepts such as radiation pressure and optical tweezers to spatially manipulate micro-objects or to levitate viruses, bacteria, cells, and subcellular organisms have been around since the 1970s [
1,
2]. Currently, there is a fast development of electromagnetic wave driven micro motors [
3] where the radiation pressure is too small to activate such devices [
4]. However, some resonance principles can be used to notably increase the force, for instance in waveguides made of lossless dielectric blocks or Bragg waveguides [
5,
6,
7]. Due to the vast range of optical properties that can be obtained by the design of a photonic crystal, the creation of devices derived from the application of these properties has increased [
8,
9,
10,
11]. An interesting application using photonic crystals is the confinement of an incident electric field that allows the emergence of electromagnetic forces on the surface of the layers inside the photonic crystal [
4,
12]. Recently, we realized such application using one-dimensional photonic crystals (1D-PC) based on Porous Silicon (Psi) multilayers to create a dynamical system capable of performing oscillations such as a forced oscillation. In this application, an oscillation is imposed upon the system by an external source (vibrator) at a certain frequency [
13,
14,
15]. The photonic crystal structures known as photodynes were activated with modulated laser light. Light modulation was achieved with a mechanical chopper and a wave generator. Square waveforms were used at different duty cycles and light intensities. Under these conditions, the photonic structure, amplitude and frequency were measured. From these measurements and with the help of a theoretical model, a pendulum in a viscous frictional medium acted upon by a force of constant magnitude, the induced electromagnetic force was estimated. The obtained values are of the order of a few
to hundredths of
. Notwithstanding these remarkable results, we would like to emphasize that we did not explore the influence of the external signal modulation waveform and frequency on the performance (amplitude and oscillation frequency) of the photonic oscillators.
In this paper, the experimental details for the fabrication of photonic crystals and its characterization are described and the measurement of the photonic crystal oscillations is presented. Then, the theoretical model that describes the oscillations is analyzed. Subsequently, the comparison between the theoretical analysis and the experimental results is shown. Finally, some conclusions are given.
3. Results
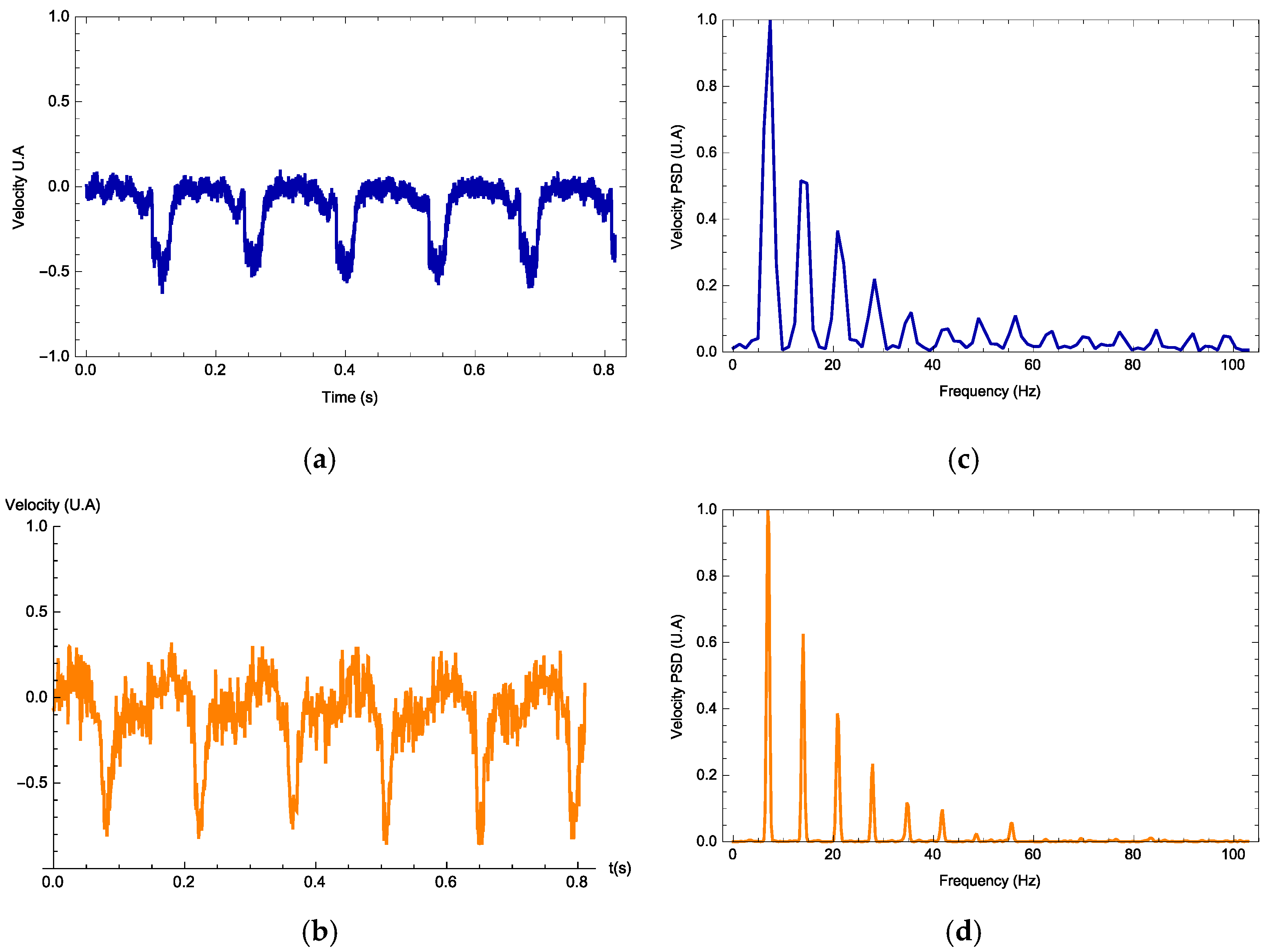
The vibrometer software interface provides the data containing the maximum displacement and velocity, velocity time series and its Fourier spectrum along with its mean frequency and harmonics. In all experiments, the vibrometer gives the velocity profile as a signal measured in volts. For each signal waveform, the parameters
h,
, and
are free parameters and Equation (1) is calculated. In
Figure 4,
Figure 5 and
Figure 6, we observe three examples (one for each waveform) on how the photodyne velocity oscillates. Both theory and experimental results are compared. In general, the theory can predict correctly the velocity waveform and the number of harmonics present on the Fourier Power Spectral Density. In all examples, the best value for
was 1.98 m/s
2 while
h and
took different values in each example.
Based on the experimental data and the theoretical model, it is possible to know for each frequency which type of signal is the best to optimize the displacement of the photodyne.
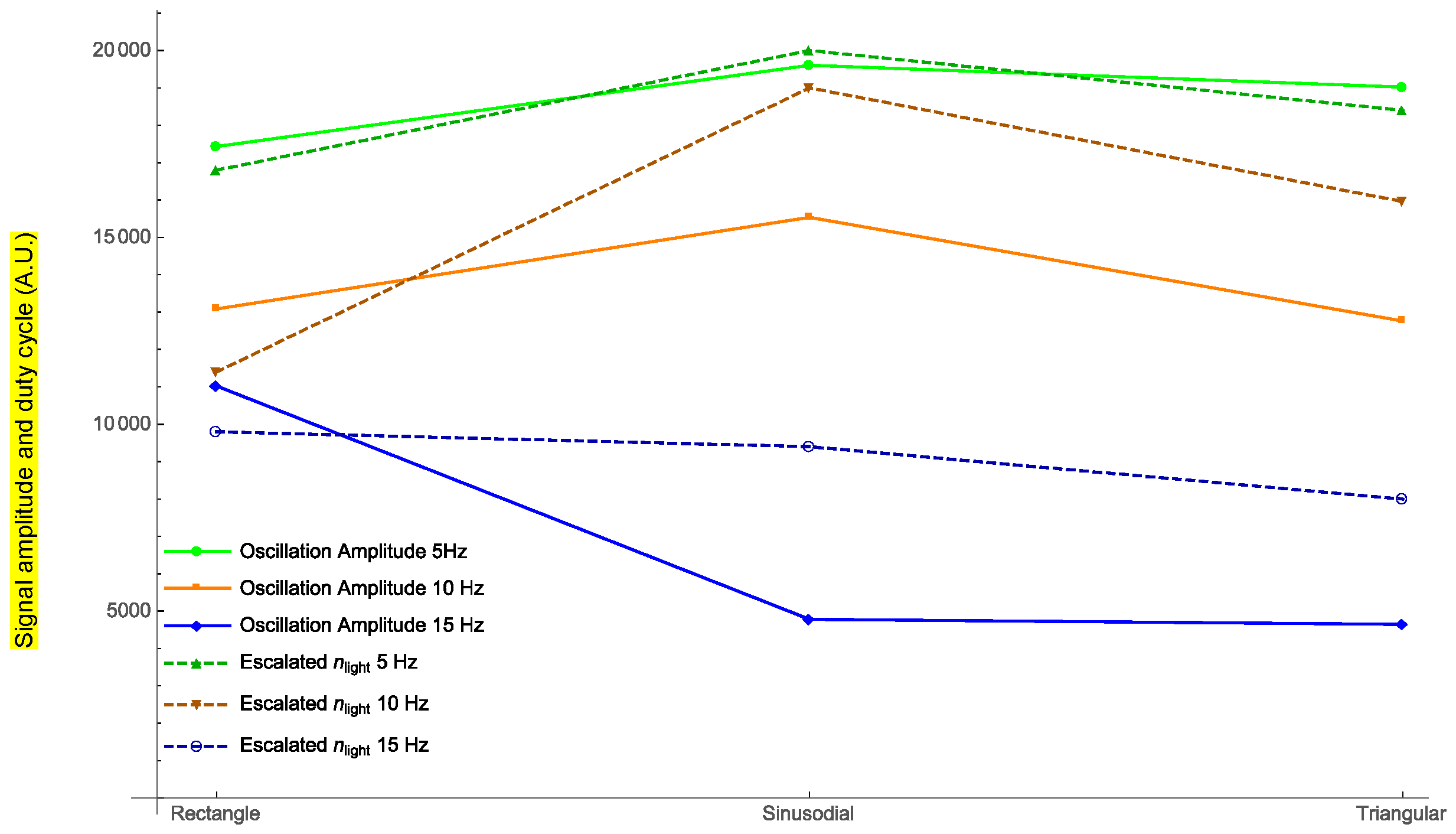
In
Figure 7, the amplitude of the oscillations for three different external frequencies is plotted for each signal waveform. Dashed lines show the duty cycle of the light obtained for each case (
nlight has been normalized for the representation).
The maximum mechanical power of the oscillation movement has been calculated by multiplying the maximum experimental velocity times the calculated electromagnetic force. In
Figure 8, the maximum mechanical power of the oscillations for three different external frequencies are plotted for each signal waveform.
4. Discussion and Conclusions
Electromagnetic forces due to an incident electromagnetic field are induced within a photonic device known as a photodyne. Photodynes are based on one-dimensional photonic crystals arranged in a microcavity or double juxtaposed cantilever configuration. These electromagnetic forces become evident when the photodyne starts to vibrate. The oscillatory movement has been experimentally recorded and modeled theoretically. For each of the wave signals used, the frequency that optimizes the displacement has been found. As it can be seen in
Figure 7, for the external frequency value of 5 Hz, the photodyne displacement achieved by using the sinusoidal signal is 2.75% greater than the triangular signal and 11% greater than the rectangular signal. For the external frequency of 10 Hz, the best option was a sinusoidal waveform which gave 16% higher displacement than the rectangular signal and 18% higher than the triangular signal. Nonetheless, for an external frequency of 15 Hz, the best option was the rectangular form, in which case the displacement amplitudes of the sinusoidal and triangular forms were 15% lower. The interesting results shown in
Figure 4,
Figure 5 and
Figure 6 are the harmonic results. Some have large harmonic output and some have very small harmonic results. The mean reason for this is the duty cycle variation. As it increases, the number of mechanical modes is also incremented. If this parameter is not properly controlled, it may induce that the number of harmonic varies as well. The damping of the oscillations also influences how high the harmonic amplitude is going to be. Experimentally the damping is not easy to control because it depends on many nonlinearities such as the initial cavity size, surface uniformity and even the nature of the input waveform.
The highest amplitude displacement correlates with the highest theoretical duty cycle parameter value for the three frequencies and all waveforms, (0.5, 0.5 and 0.49 for the external frequencies of 5 Hz, 10 Hz, and 15 Hz, respectively). This could be because, the longer the sample is illuminated, the more modes have the opportunity to couple as the dynamic cavity moves. In addition, the maximum mechanical power has the same correlation as the duty cycle parameter against the external frequencies and waveforms (see
Figure 8). This result could be taken as a starting point to make a more exhaustive analysis in the future. The data obtained can be implemented in the experimental design and thus optimize the oscillations of the photodyne.
The largest difference between the amplitudes of the oscillation obtained theoretically and experimentally is 2.83%. Taking into account that the theoretical model has been optimized, not only to reproduce the amplitude of the movement, but also the harmonics of each signal, it is a good fit between both results. Another important parameter is the acceleration of the photodyne movement. The values found for the largest displacements were and for the external frequencies , and , respectively. These values of the acceleration are the highest obtained in the experiment for each frequency. Finally, once this type of new photonic structure is optimized, we can think of integrating them in more complicated devices such as a sensor. This is because the photodynes are based on porous silicon and some gas or liquid can be introduced inside the pores that would change the refractive indices, thereby modifying the electromagnetic force that can be generated. Thus, when the photodyne is operating, the vibrometer would detect a change in the oscillation amplitude according to the properties of the inserted material. Additionally, in the future, we would like to further explore the dangling defect condition on the force generation; that is, the impact of the inhomogeneous distribution of the air gap between both Psi multilayer foils on the creation of electromagnetic forces. We would like to determine the relationship between pumping light shapes from the chopper and charge displacement relaxation times within the multilayers.
Another important point to discuss is that, at the optical frequencies of this work, the external field should be able to excite phonon modes whereby Guided acoustic wave Brillouin scattering (GAWBS) could raise. These GAWBs should be naturally related to the mechanical effects reported in this paper. Nonetheless, for the transversal dimension of a photodyne (approximately 2 mm), the transversal sound speed of silicon (5800 m/s), the air sound speed (340 m/s) and the maximum porosity of the multilayers (88%), we can estimate GAWBS mechanical frequencies. Porous silicon sound speed would be 995.2 m/s (340 × 0.88 + 5800 × 0.12), thus 995.2/2 × 10
−3 equals 497,600 Hz, almost half a MHz. These range of frequencies are in the correct range found elsewhere in photonic crystals [
17,
18] and they could be 0.5 × 10
6 faster that the frequencies we found in our experiments. Moreover, since GAWBS is a thermal effect [
18], in the past, we have done some control experiments to rule out heating effects from laser illumination. To measure the influence of laser fluctuations and temperature changes on the possible generation of mechanical oscillations in our device, a laser illuminated one photodyne device for five minutes and the vibrometer measured any possible oscillation. The result only showed a 1/
fa noise signal with no peaks within the frequency band of interest (1 Hz–64 Hz), thus if GAWBS were presented they could certainly produce some mechanical oscillations but clearly it was not the case [
15]. Finally, it is known that GAWBS could modulate the existence of localized photonic states [
17] and, since the electromagnetic force is always maximized when a localized state is excited, a photodyne with no localized states could not maximize the electromagnetic force. Nevertheless, theoretical calculations showed that the electromagnetic force is still high (500 times higher than any current optical tweezer) even in the case where there are no localized states. Consequently, from all these arguments, GAWBS cannot explain the nature of the oscillations we have found in this work and in the past [
13,
14,
15] but they may contribute as noise within our measurements. For future work, experimental studies on measuring GAWBS could be included. This can be interesting for sensor applications since the GAWBS peaks are highly sensitive to strain and temperature.
Finally, in every oscillator, it is essential to estimate the phase noise within the oscillation output signal. The easiest way to do it is using an oscillation signal that only contains a single frequency. In the past, we have created self-oscillators (where there is only one oscillation frequency) using exactly the same configuration and experimental setup. Phase noise can be estimated using the power spectral density of the oscillation signal (frequency domain) and the temporal jitter of the same signal (temporal domain). If we use the frequency domain, the phase noise is found as the ratio of the noise power in a 1 Hz bandwidth and the total signal power. Using the power spectral density of a self-oscillation experiment (see
Supplementary Materials), the phase noise was estimated with a value of −7.17 dB/Hz @ 20.8 Hz. In the time domain, we used 20 successive measurements of the period of the self-oscillator (see
Supplementary Materials). If the measurements contain only random jitter elements, the distribution of these elements would be a Gaussian and the RMS jitter would be given by the value of one standard deviation. Then, the phase noise can be approximated by
[
19], where
is the oscillation frequency,
is the RMS jitter and
is the frequency interval for the full width at half maximum, which can be obtained from the power spectral density. Bear in mind that this phase noise approximation is valid only if its value is almost constant within such frequency interval. We used a one-sample Kolmogorov–Smirnov test to verify that a Gaussian distribution described the jitter elements. The test was passed with a probability of 94%. We found that
,
rad/s and
. Using these values, the phase noise is −8.51 dB/Hz @ 20.8 Hz, which is of the same order of magnitude as the value found in the frequency domain. We do not expect this value to be that different from our current experiments, but, in the future, we would like to measure the phase noise more precisely and determine the different sources of noise by means of a spectrum analyzer and with better experimental controls.