The Effects of Excess Co on the Phase Composition and Thermoelectric Properties of Half-Heusler NbCoSb
Abstract
:1. Introduction
2. Experimental Procedures
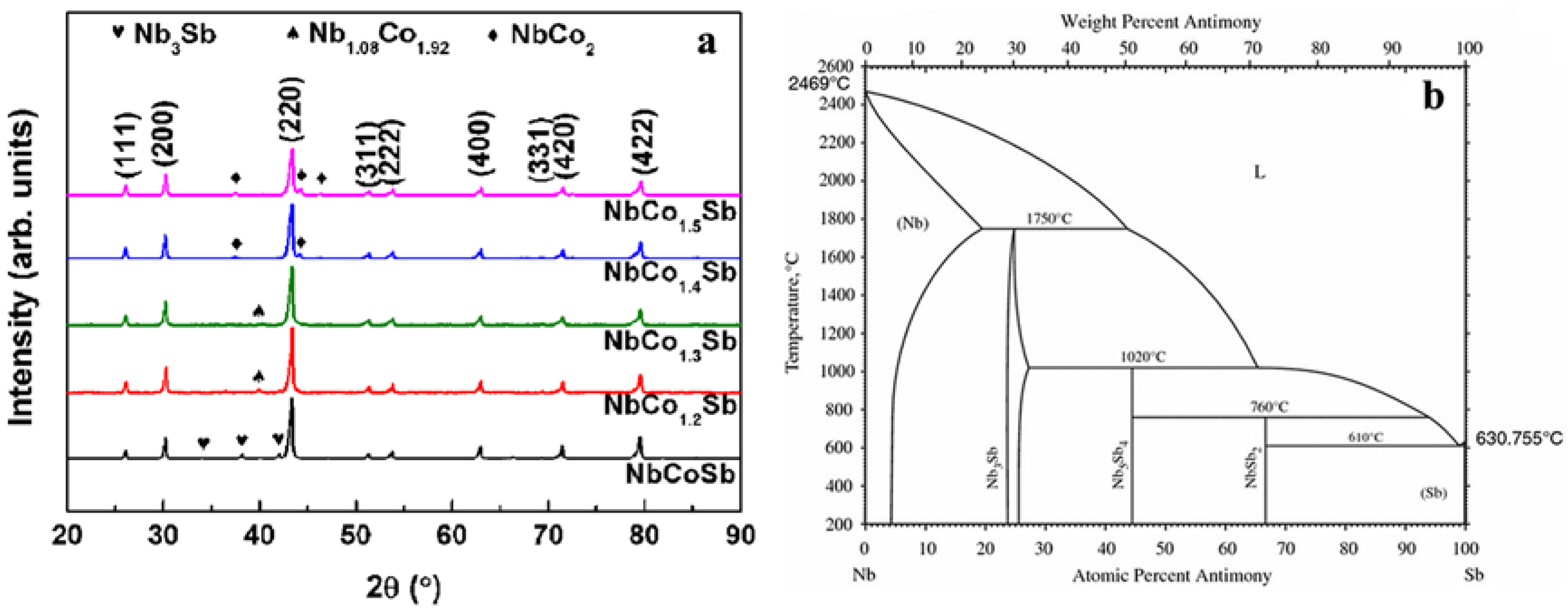
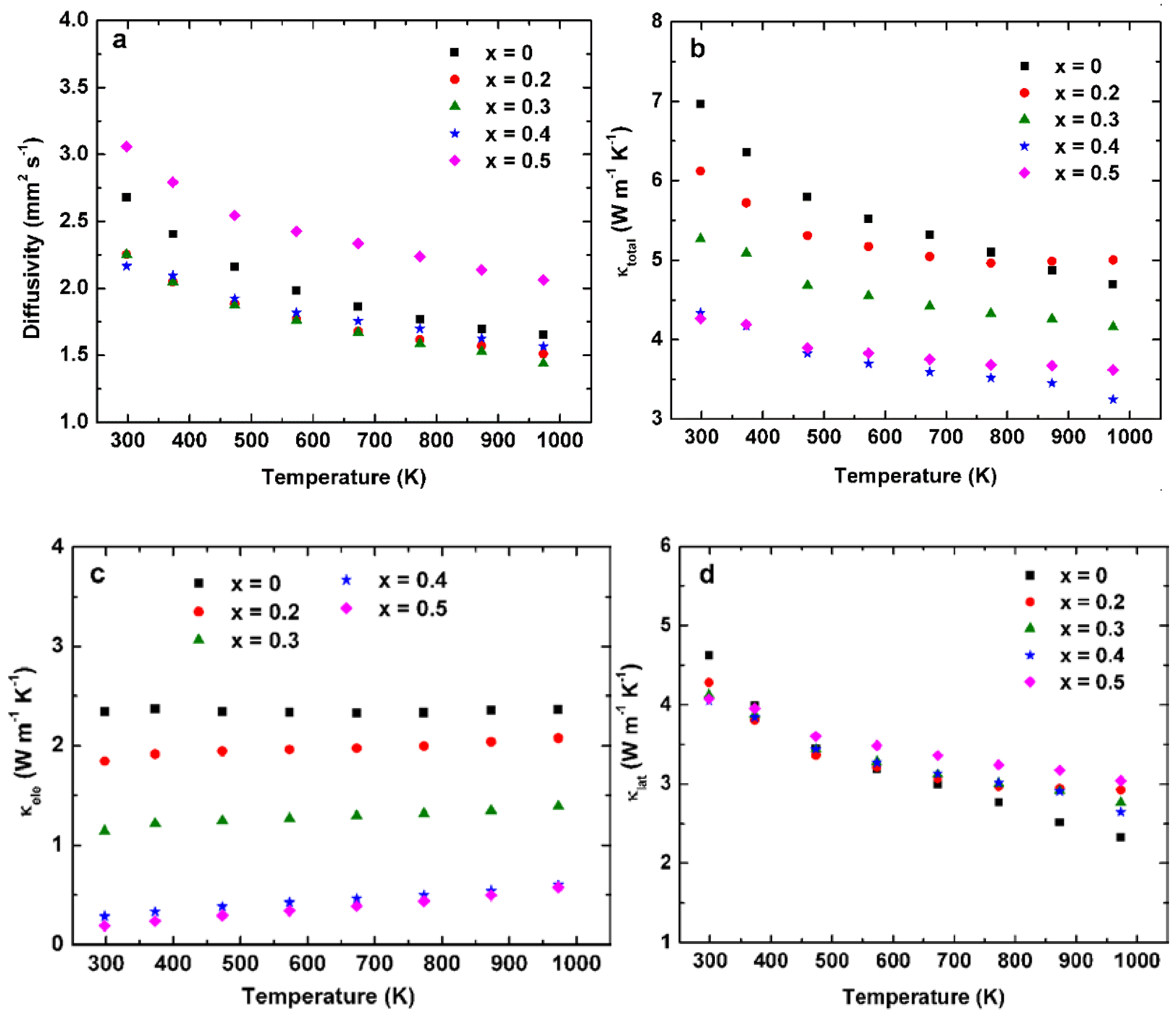
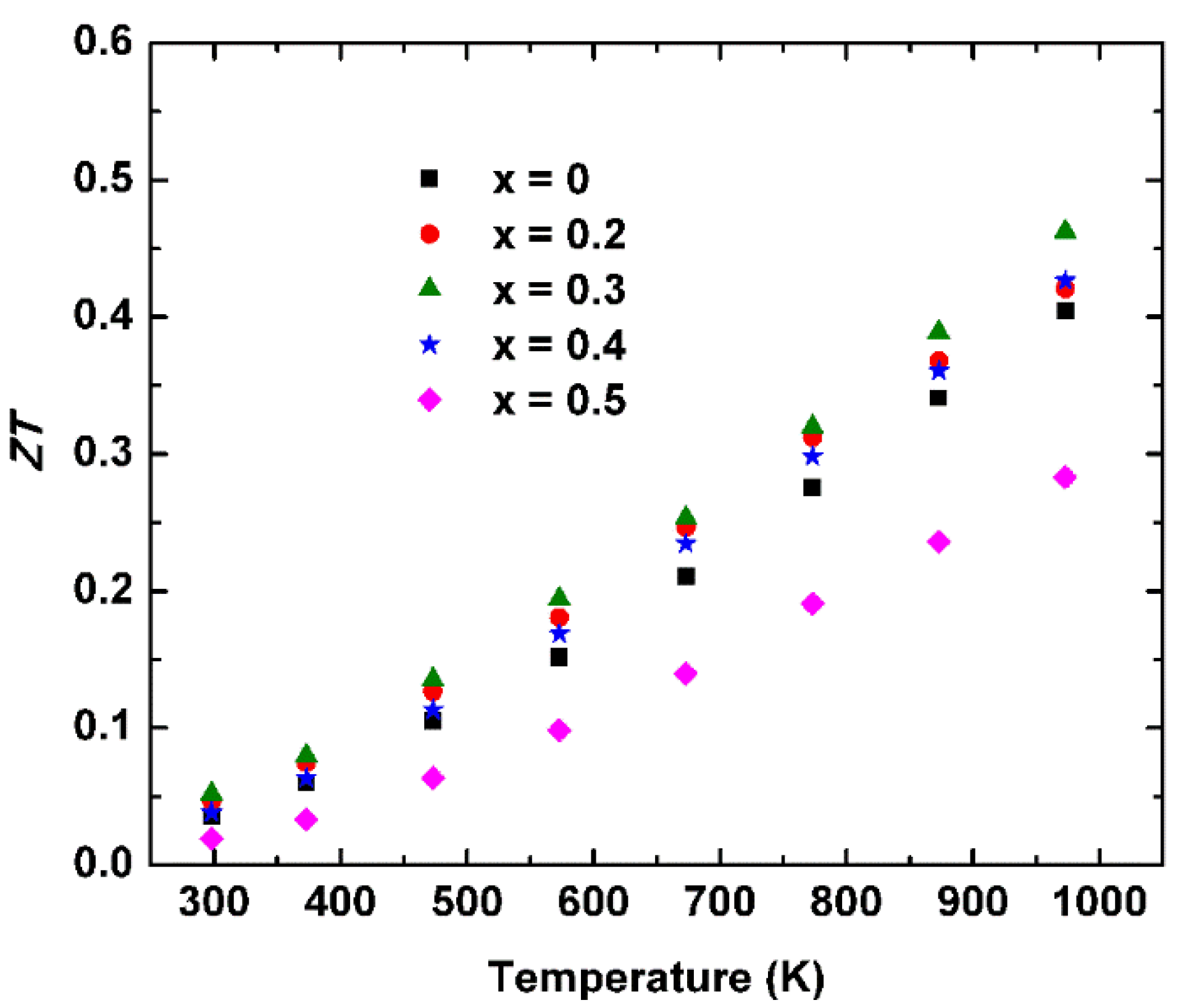
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mao, J.; Wu, Y.X.; Song, S.W.; Shuai, J.; Liu, Z.H.; Pei, Y.Z.; Ren, Z.F. Anomalous electrical conductivity of n-type Te-doped Mg3.2Sb1.5Bi0.5. Mater. Today Phys. 2017, 3, 1–6. [Google Scholar] [CrossRef]
- Ioffe, A.F. Semiconductor Thermoelements and Thermoelectric Cooling; Infosearch: London, UK, 1957. [Google Scholar]
- Goldsmid, H.J. Thermoelectric Refrigeration; Plenum Press: New York, NY, USA, 1964. [Google Scholar]
- Lin, S.Q.; Li, W.; Li, S.S.; Zhang, X.Y.; Chen, Z.W.; Xu, Y.D.; Chen, Y.; Pei, Y.Z. High thermoelectric performance of Ag9GaSe6 enabled by low cutoff frequency of acoustic phonons. Joule 2017, 1, 816–830. [Google Scholar] [CrossRef]
- Wu, Y.X.; Li, W.; Faghaninia, A.; Chen, Z.W.; Li, J.; Zhang, X.Y.; Gao, B.; Lin, S.Q.; Zhou, B.Q.; Jain, A.; et al. Promising thermoelectric performance in van der Waals layered SnSe2. Mater. Today Phys. 2017, 3, 127–136. [Google Scholar] [CrossRef]
- Rogl, G.; Rogl, P. How nanoparticles can change the figure of merit, ZT, and mechanical properties of skutterudites. Mater. Today Phys. 2017, 3, 48–69. [Google Scholar] [CrossRef]
- Zhang, Q.; Chere, E.K.; McEnaney, K.; Yao, M.L.; Cao, F.; Ni, Y.Z.; Chen, S.; Opeil, C.; Chen, G.; Ren, Z.F. Enhancement of thermoelectric performance of n-type PbSe by Cr doping with optimized carrier concentration. Adv. Energy Mater. 2015, 5, 1401977. [Google Scholar] [CrossRef]
- Berry, T.; Fu, C.G.; Auffermann, G.; Fecher, G.H.; Schnelle, W.; Sanchez, F.S.; Yue, Y.; Liang, H.; Felser, C. Enhancing thermoelectric performance of TiNiSn half-Heusler compounds via modulation doping. Chem. Mater. 2017, 29, 7042–7048. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Y.M.; He, J.; Tritt, T.M.; Poon, S.J. High thermoelectric figure of merit by resonant dopant in half-Heusler alloys. AIP Adv. 2017, 7, 065208. [Google Scholar] [CrossRef]
- Silpawilawan, W.; Kurosaki, K.; Ohishi, Y.; Muta, H.; Yamanaka, S. FeNbSb p-type half-Heusler compound: beneficial thermomechanical properties and high-temperature stability for thermoelectrics. J. Mater. Chem. C 2017, 5, 6677–6681. [Google Scholar] [CrossRef]
- Zeier, W.G.; Anand, S.; Huang, L.H.; He, R.; Zhang, H.; Ren, Z.F.; Wolverton, C.; Snyder, G.J. Using the 18-electron rule to understand the nominal 19-electron half-Heusler NbCoSb with Nb vacancies. Chem. Mater. 2017, 29, 1210–1217. [Google Scholar] [CrossRef]
- He, R.; Zhu, H.T.; Sun, J.Y.; Mao, J.; Reith, H.; Schierning, S.C.G.; Nielsch, K.; Ren, Z.F. Improved thermoelectric performance of n-type half-Heusler MCo1−xNixSb (M = Hf, Zr). Mater. Today Phys. 2017, 1, 24–30. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.M.; Huang, L.H.; Chen, S.; Dahal, H.; Wang, D.Z.; Ren, Z.F. Synthesis and thermoelectric properties of n-type half-Heusler compound VCoSb with valence electron count of 19. J. Alloy Compd. 2016, 654, 321–326. [Google Scholar] [CrossRef]
- Huang, L.H.; Wang, Y.M.; Shuai, J.; Zhang, H.; Yang, S.Q.; Zhang, Q.Y.; Ren, Z.F. Thermal conductivity reduction by isoelectronic elements V and Ta for partial substitution of Nb in half-Heusler Nb(1−x)/2V(1−x)/2TaxCoSb. RSC Adv. 2015, 5, 102469–102476. [Google Scholar] [CrossRef]
- Zhu, T.J.; Fu, C.G.; Liu, X.H.; Liu, Y.T.; Zhao, X.B. High efficiency half-Heusler thermoelectric materials for energy harvesting. Adv. Energy Mater. 2015, 5, 1500588. [Google Scholar] [CrossRef]
- Dow, H.S.; Kim, W.S.; Shin, W.H. Effect of C and N addition on thermoelectric properties of TiNiSn half-Heusler compounds. Materials 2018, 11, 262. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.G.; Zhu, T.J.; Liu, Y.T.; Xie, H.H.; Zhao, X.B. Band engineering of high performance p-type FeNbSb based half-Heusler thermoelectric materials for figure of merit zT > 1. Energy Environ. Sci. 2015, 8, 216–220. [Google Scholar] [CrossRef]
- Fu, C.G.; Bai, S.Q.; Liu, Y.T.; Tang, Y.S.; Chen, L.D.; Zhao, X.B.; Zhu, T.J. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.H.; He, R.; Chen, S.; Zhang, H.; Dahal, K.; Zhou, H.Q.; Wang, H.; Zhang, Q.Y.; Ren, Z.F. A new n-type half-Heusler thermoelectric material NbCoSb. Mater. Res. Bull. 2015, 70, 773–778. [Google Scholar] [CrossRef]
- Chai, Y.W.; Oniki, T.; Kimura, Y. Microstructure and thermoelectric properties of a ZrNi1.1Sn half-Heusler alloy. Acta Mater. 2015, 85, 290–300. [Google Scholar] [CrossRef]
- Chai, Y.W.; Oniki, T.; Kenjo, T.; Kimura, Y. The effect of an isoelectronic Ti-Zr substitution on Heusler nanoprecipitation and the thermoelectric properties of a (Ti0.2,Zr0.8)Ni1.1Sn half-Heusler alloy. J. Alloy Compd. 2016, 662, 566–577. [Google Scholar] [CrossRef]
- Pei, Y.Z.; Wang, H.; Snyder, G.J. Band engineering of thermoelectric materials. Adv. Mater. 2012, 24, 6125–6135. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.H.; Wang, Y.M.; Mao, J.; Geng, H.Y.; Shuai, J.; Wang, Y.X.; He, R.; Cai, W.; Sui, J.H.; Ren, Z.F. Lithium doping to enhance thermoelectric performance of MgAgSb with weak electron–phonon coupling. Adv. Energy Mater. 2016, 6, 1502269. [Google Scholar] [CrossRef]
- Liu, X.H.; Zhu, T.J.; Wang, H.; Hu, L.P.; Xie, H.H.; Jiang, G.Y.; Snyder, G.J.; Zhao, X.B. Low electron scattering potentials in high performance Mg2Si0.45Sn0.55 based thermoelectric solid solutions with band convergence. Adv. Energy Mater. 2013, 3, 1238–1244. [Google Scholar] [CrossRef]
- Pei, Y.Z.; Gibbs, Z.M.; Gloskovskii, A.; Balke, B.; Zeier, W.G. Optimum carrier concentration in n-type PbTe thermoelectrics. Adv. Energy Mater. 2014, 4, 1400486. [Google Scholar] [CrossRef]
- Huang, L.H.; Zhang, Q.Y.; Wang, Y.M.; He, R.; Shuai, J.; Zhang, J.J.; Wang, C.; Ren, Z.F. The effect of Sn doping on thermoelectric performance of n-type half-Heusler NbCoSb. Phys. Chem. Chem. Phys. 2017, 19, 25683–25690. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.Z.; Cao, B.L.; Li, S.M.; Liu, N.; Shen, J.W.; Li, S.; Jian, J.K.; Gu, L.; Pei, Y.Z.; Snyder, G.J.; et al. Engineering the thermoelectric transport in half-Heusler materials through a bottom-up nanostructure synthesis. Adv. Energy Mater. 2017, 7, 1700446. [Google Scholar] [CrossRef]
- Ohno, S.; Aydemir, U.; Amsler, M.; Pöhls, J.H.; Chanakian, S.; Zevalkink, A.; White, M.A.; Bux, S.K.; Wolverton, C.; Snyder, G.J. Achieving zT >1 in inexpensive zintl phase Ca9Zn4+xSb9 by phase boundary mapping. Adv. Funct. Mater. 2017, 27, 1606361. [Google Scholar] [CrossRef]


| Nominal Composition | Lattice Parameter (nm) | Density (g cm−3) | Relative Density (%) | |
|---|---|---|---|---|
| Theoretical | Experimental | |||
| NbCoSb | 0.5890 | 8.893 | 8.329 | 93.66 |
| NbCo1.2Sb | 0.5893 | 9.262 | 8.345 | 90.10 |
| NbCo1.3Sb | 0.5895 | 9.443 | 8.637 | 91.46 |
| NbCo1.4Sb | 0.5896 | 9.634 | 8.310 | 86.26 |
| NbCo1.5Sb | 0.5897 | 9.817 | 8.342 | 84.98 |
| Nominal Composition | RH | nH (1021 cm−3) | μH (cm2 V−1 s−1) | Edef (eV) |
|---|---|---|---|---|
| NbCoSb | −1.03 | 6.04 | 3.62 | 18.86 |
| NbCo1.2Sb | −1.21 | 5.16 | 3.45 | 18.21 |
| NbCo1.3Sb | −2.01 | 3.11 | 3.68 | 21.93 |
| NbCo1.4Sb | −2.66 | 2.35 | 1.34 | 30.71 |
| NbCo1.5Sb | −2.27 | 2.75 | 0.74 | 41.38 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Wang, J.; Chen, X.; He, R.; Shuai, J.; Zhang, J.; Zhang, Q.; Ren, Z. The Effects of Excess Co on the Phase Composition and Thermoelectric Properties of Half-Heusler NbCoSb. Materials 2018, 11, 773. https://doi.org/10.3390/ma11050773
Huang L, Wang J, Chen X, He R, Shuai J, Zhang J, Zhang Q, Ren Z. The Effects of Excess Co on the Phase Composition and Thermoelectric Properties of Half-Heusler NbCoSb. Materials. 2018; 11(5):773. https://doi.org/10.3390/ma11050773
Chicago/Turabian StyleHuang, Lihong, Junchen Wang, Xi Chen, Ran He, Jing Shuai, Jianjun Zhang, Qinyong Zhang, and Zhifeng Ren. 2018. "The Effects of Excess Co on the Phase Composition and Thermoelectric Properties of Half-Heusler NbCoSb" Materials 11, no. 5: 773. https://doi.org/10.3390/ma11050773
APA StyleHuang, L., Wang, J., Chen, X., He, R., Shuai, J., Zhang, J., Zhang, Q., & Ren, Z. (2018). The Effects of Excess Co on the Phase Composition and Thermoelectric Properties of Half-Heusler NbCoSb. Materials, 11(5), 773. https://doi.org/10.3390/ma11050773





