A Tensile Specimen of Tailor Rolled Blanks with Equal Probability in Yield and Its Mechanical Behavior Analysis
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Experimental Material
2.2. Experimental Method
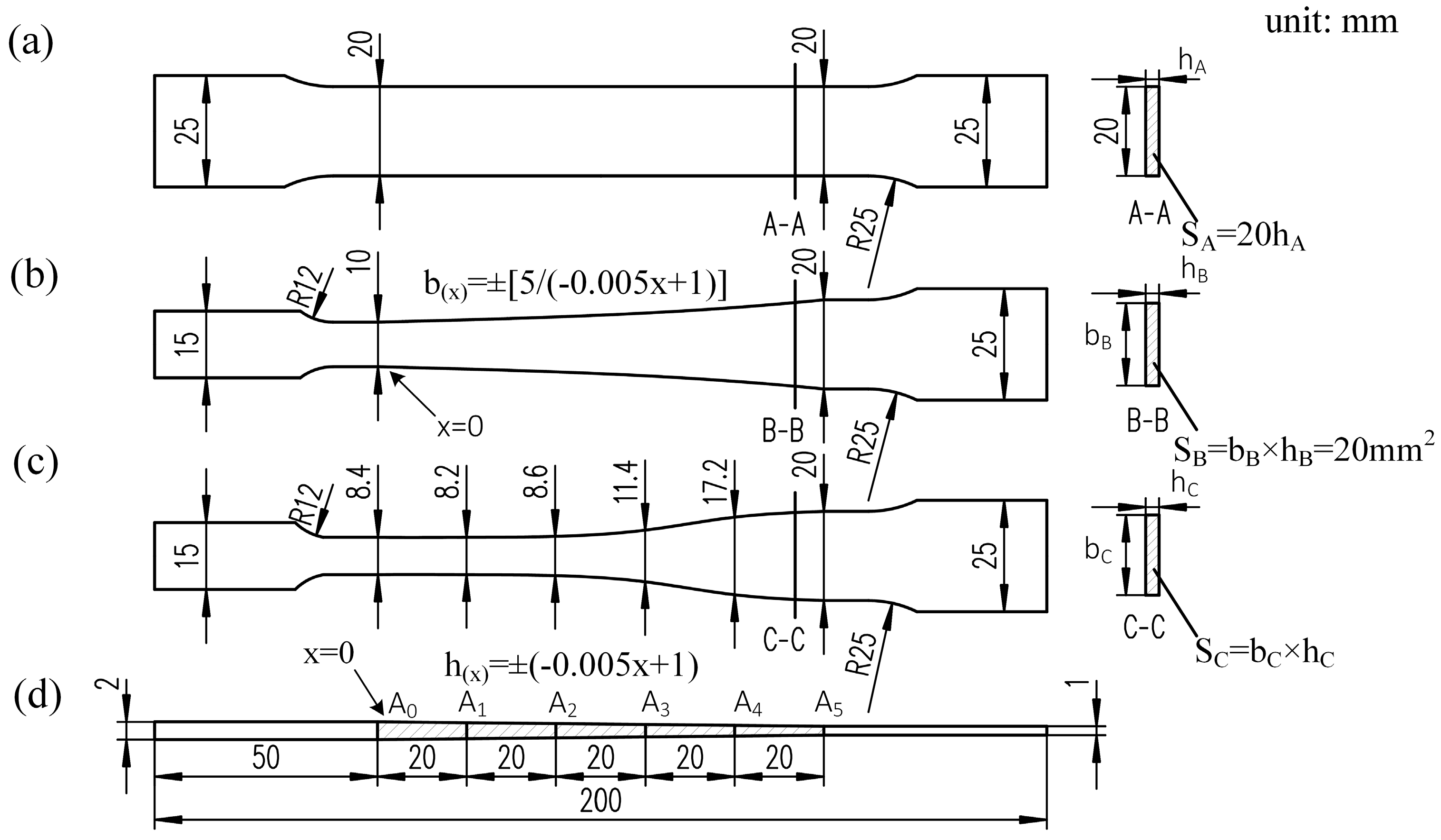
3. Design a New Type of Tensile Specimen for TRB
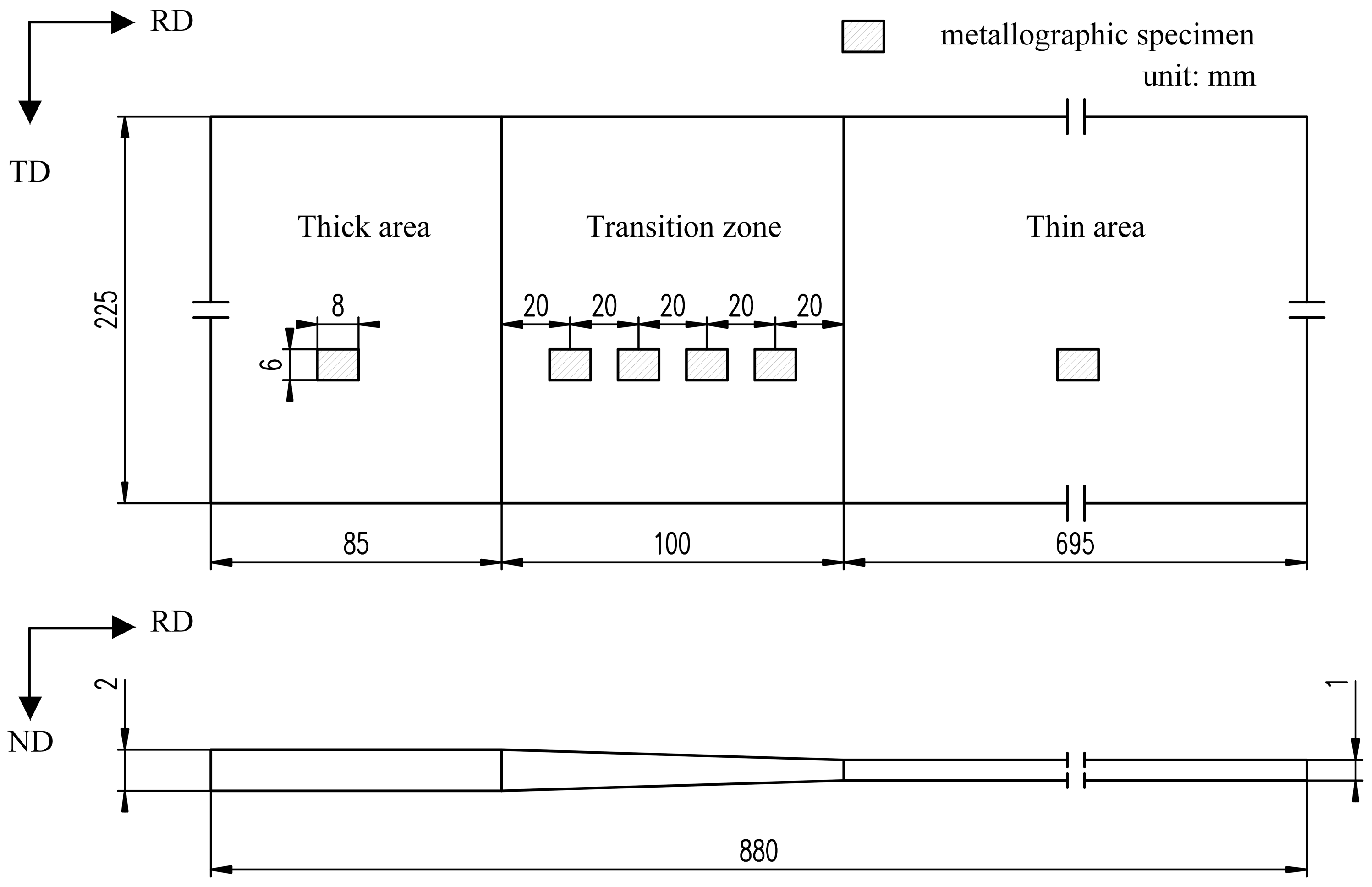
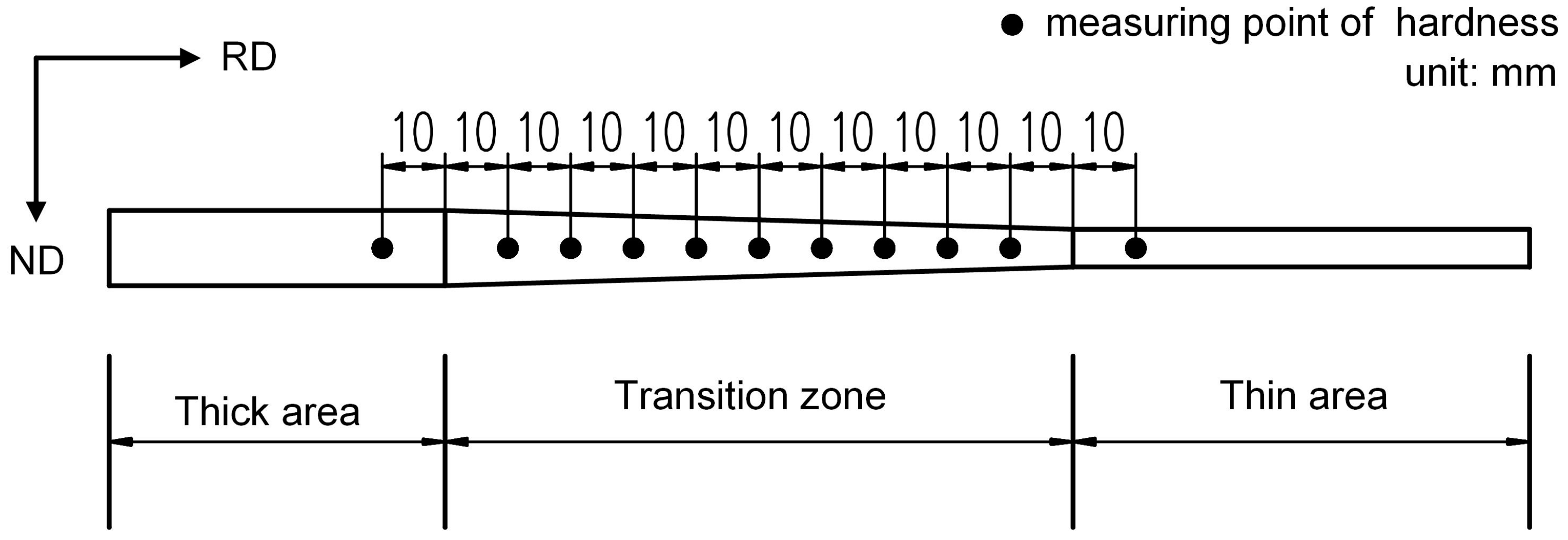
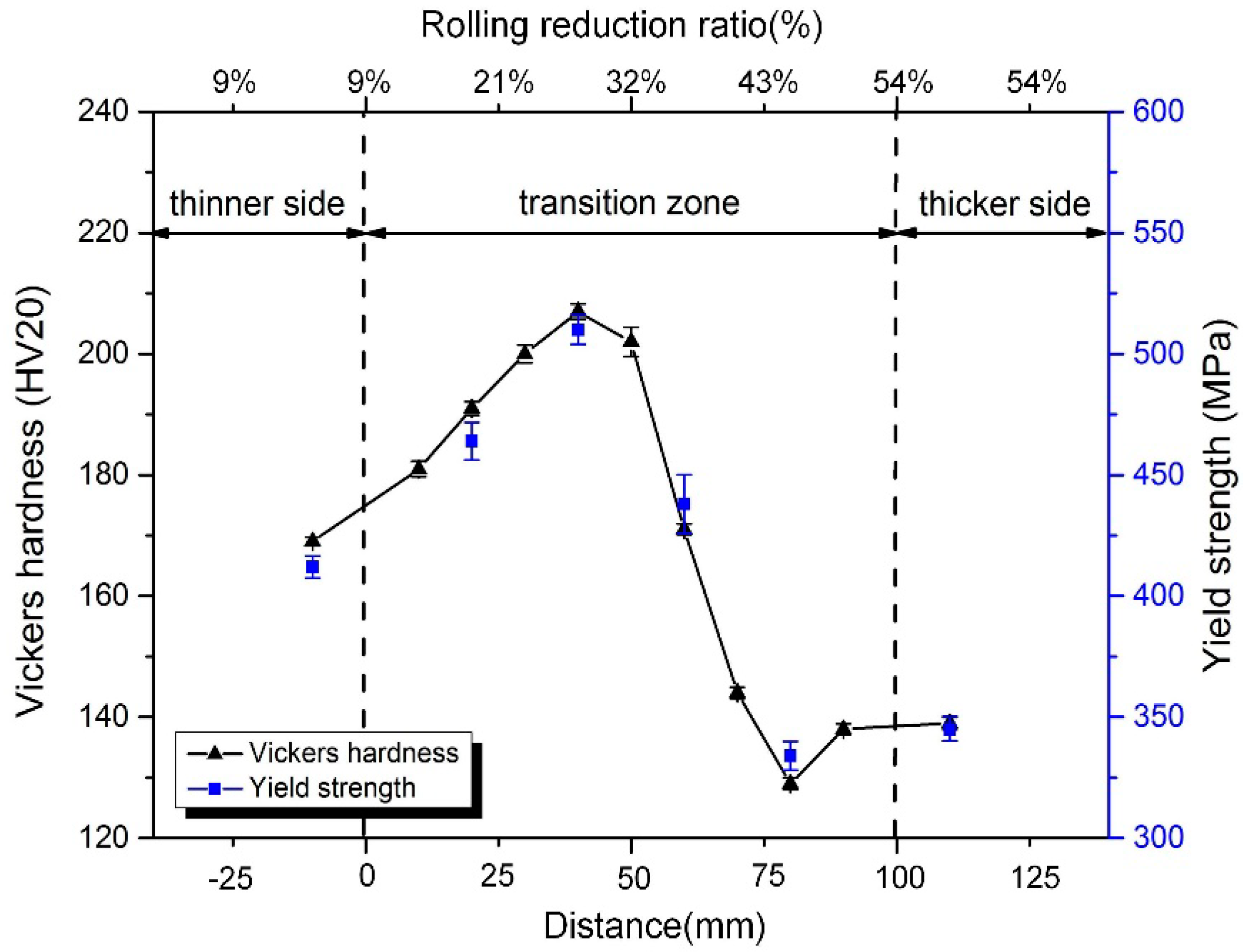
3.1. Microstructure and Mechanical Properties Distribution of TRB along Rolling Direction
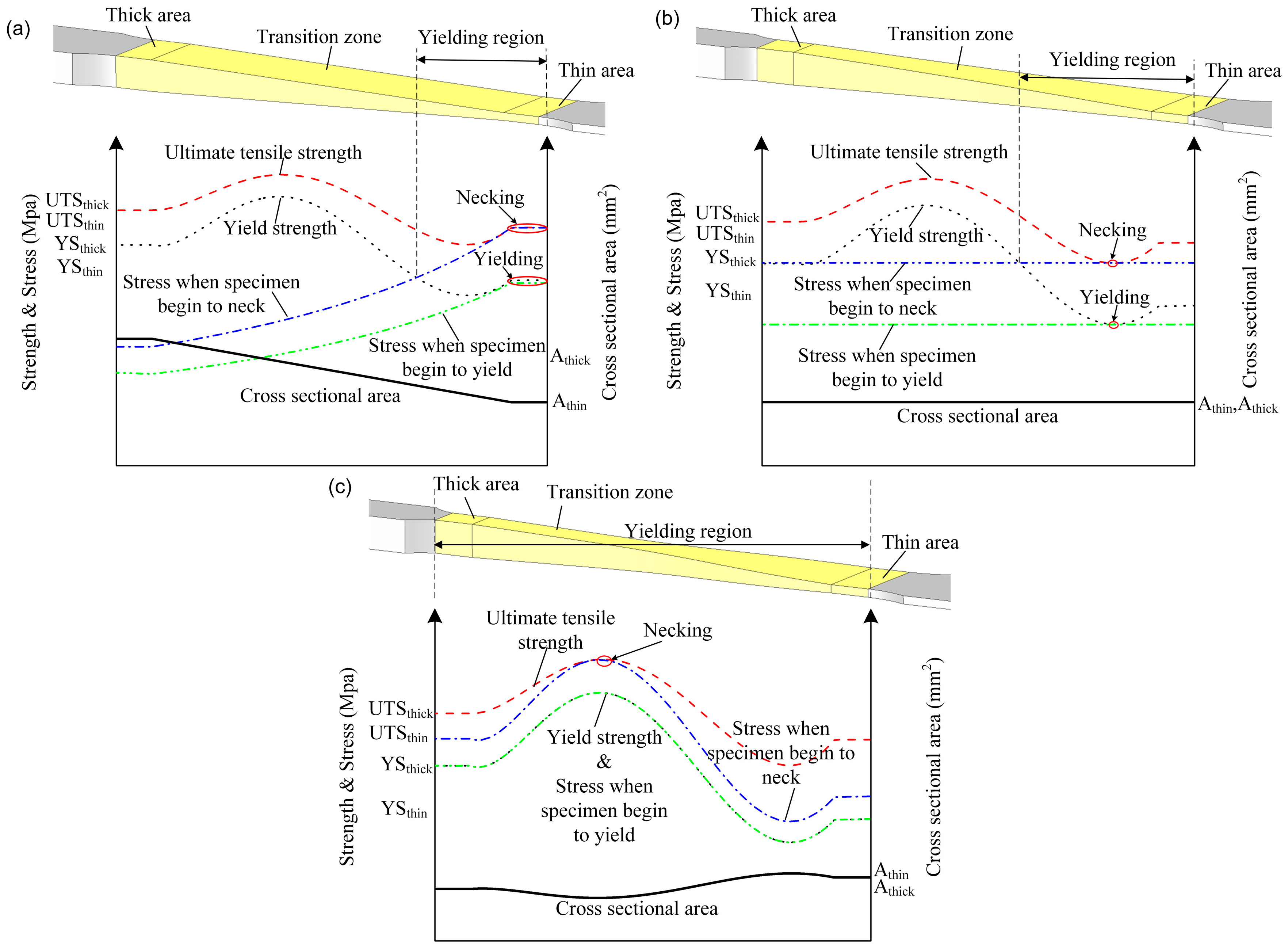
3.2. Design Philosophy for TRB Tensile Specimen
3.3. Specimen Design and Preparation
4. Results and Discussion
4.1. Experimental Results and Discussion
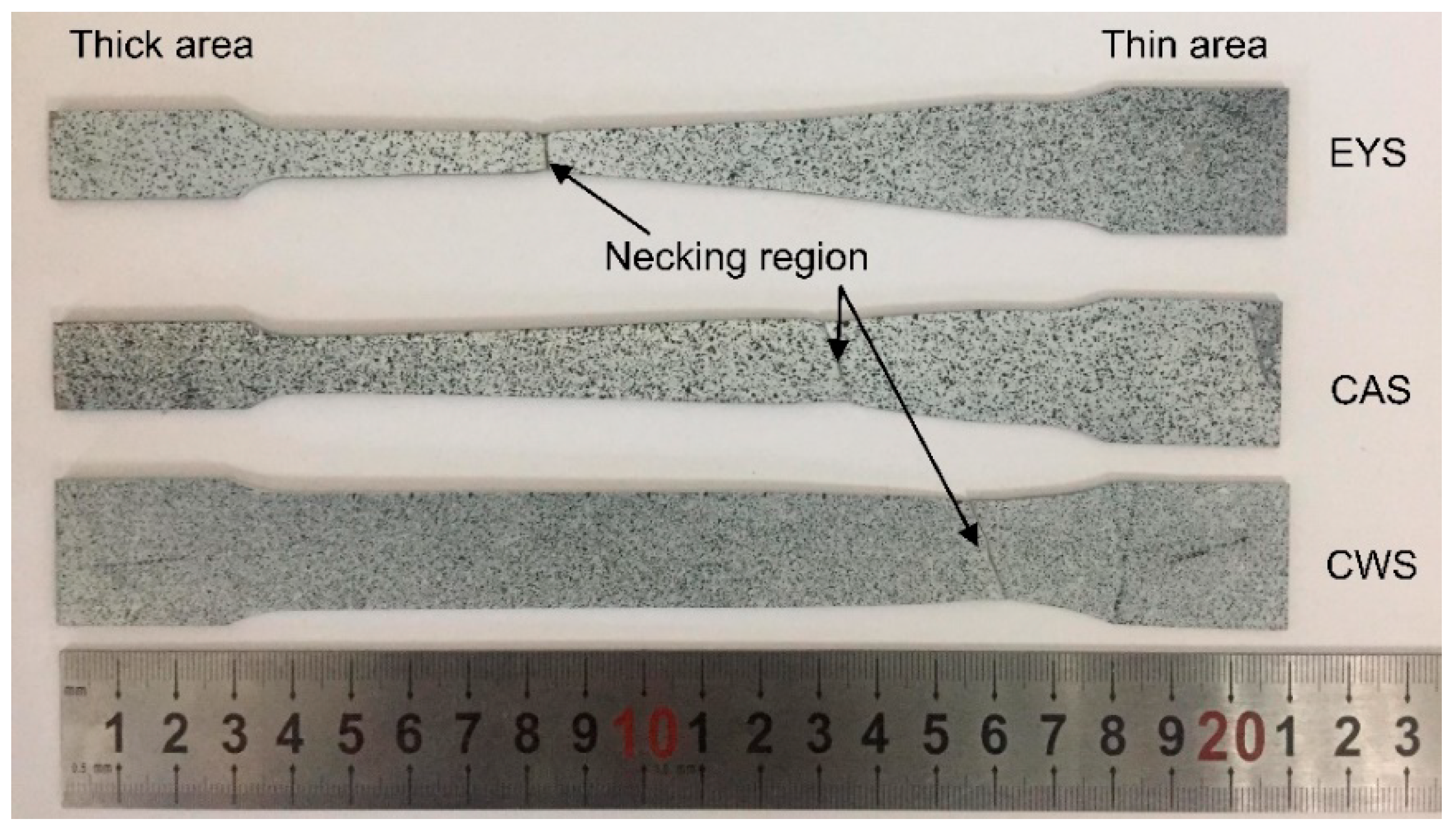
4.1.1. Observation of TRB Specimens
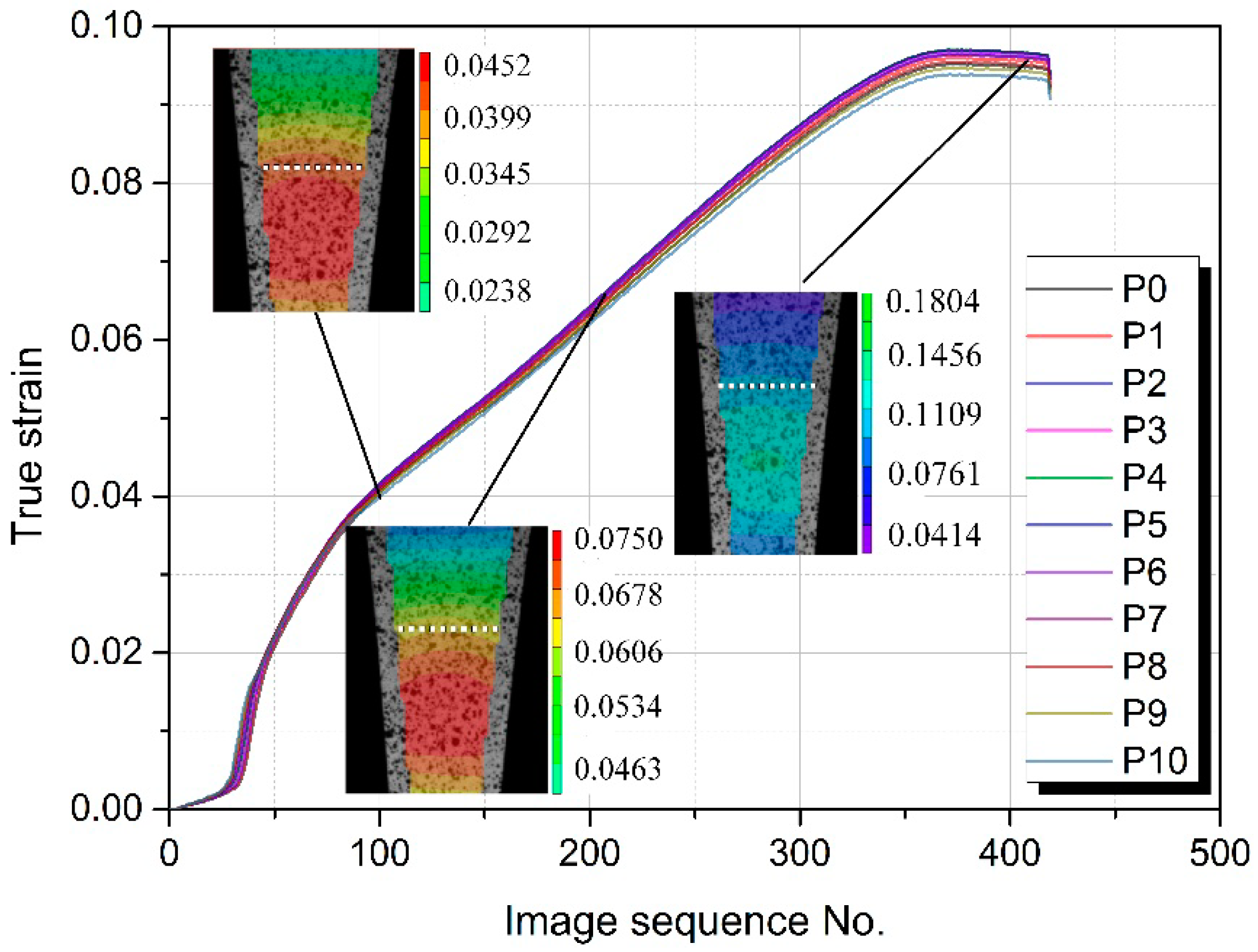
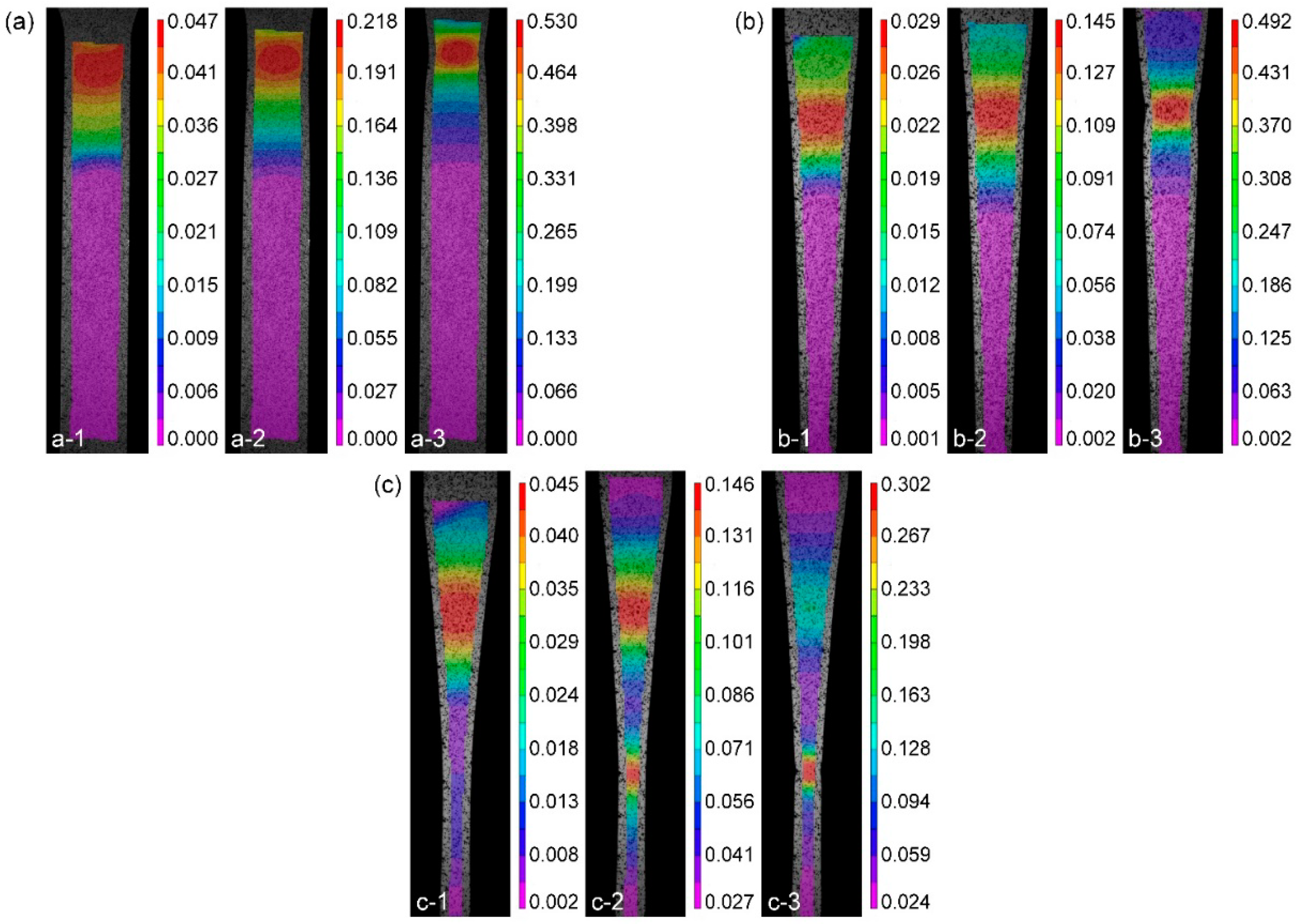
4.1.2. Strain Distribution of TRB Specimens
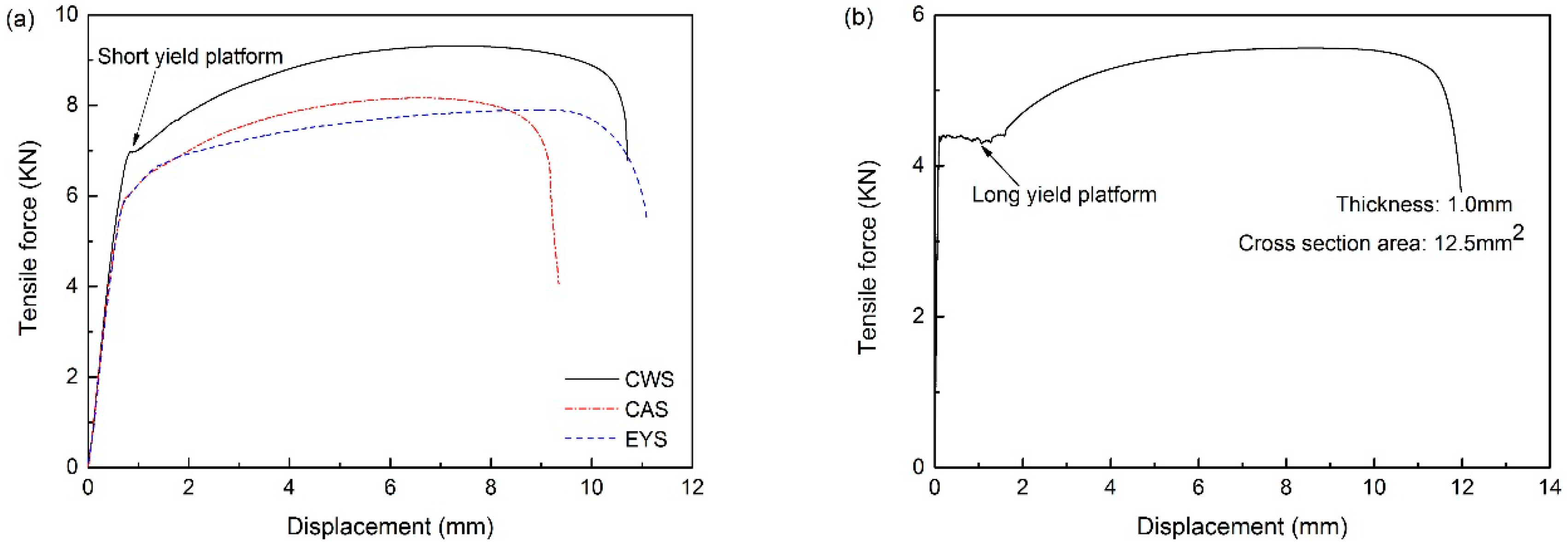
4.1.3. Force-Displacement Curves of Specimens
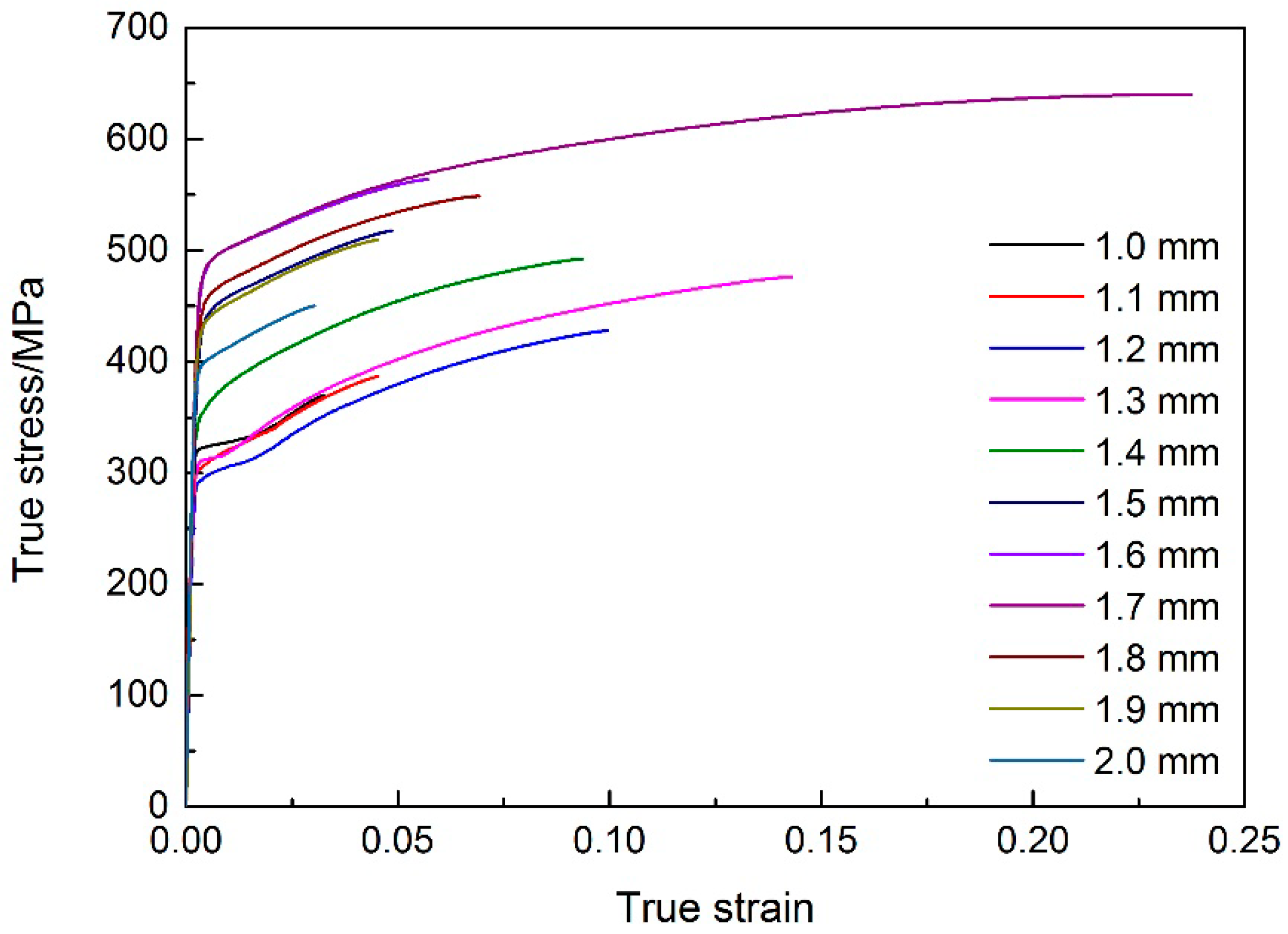
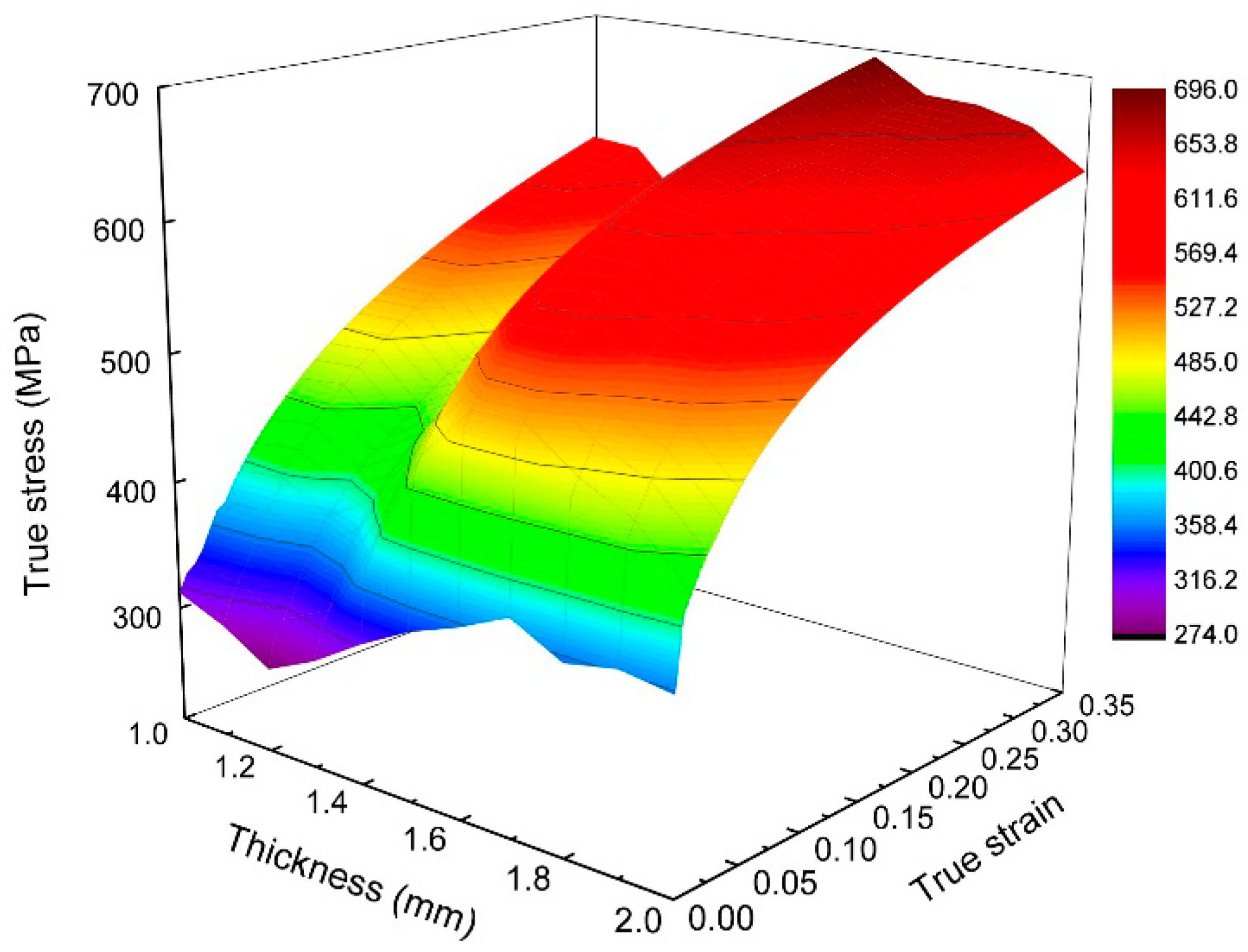
4.1.4. The True Stress-Strain Curve of Metal in TRB
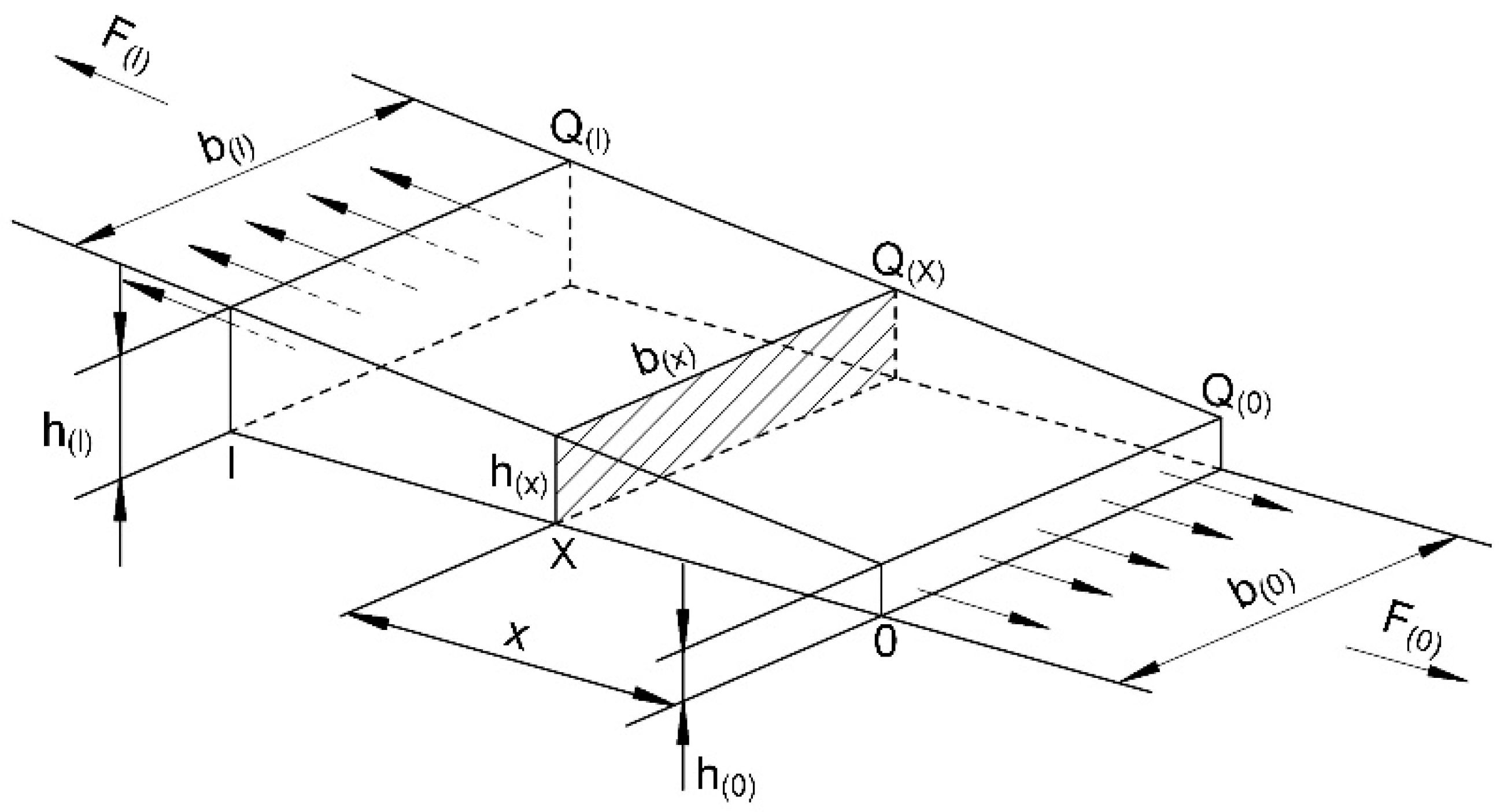
- Measure the original width b0 and the original thickness h0 of the cross section;
- The width bt (t = 0, 1, 2 s, …) and thickness ht of the cross section at time t can be calculated by
4.2. Numerical Analysis and Discussion
4.2.1. Finite Element Model
4.2.2. Simulation Results and Comparison
5. Conclusions
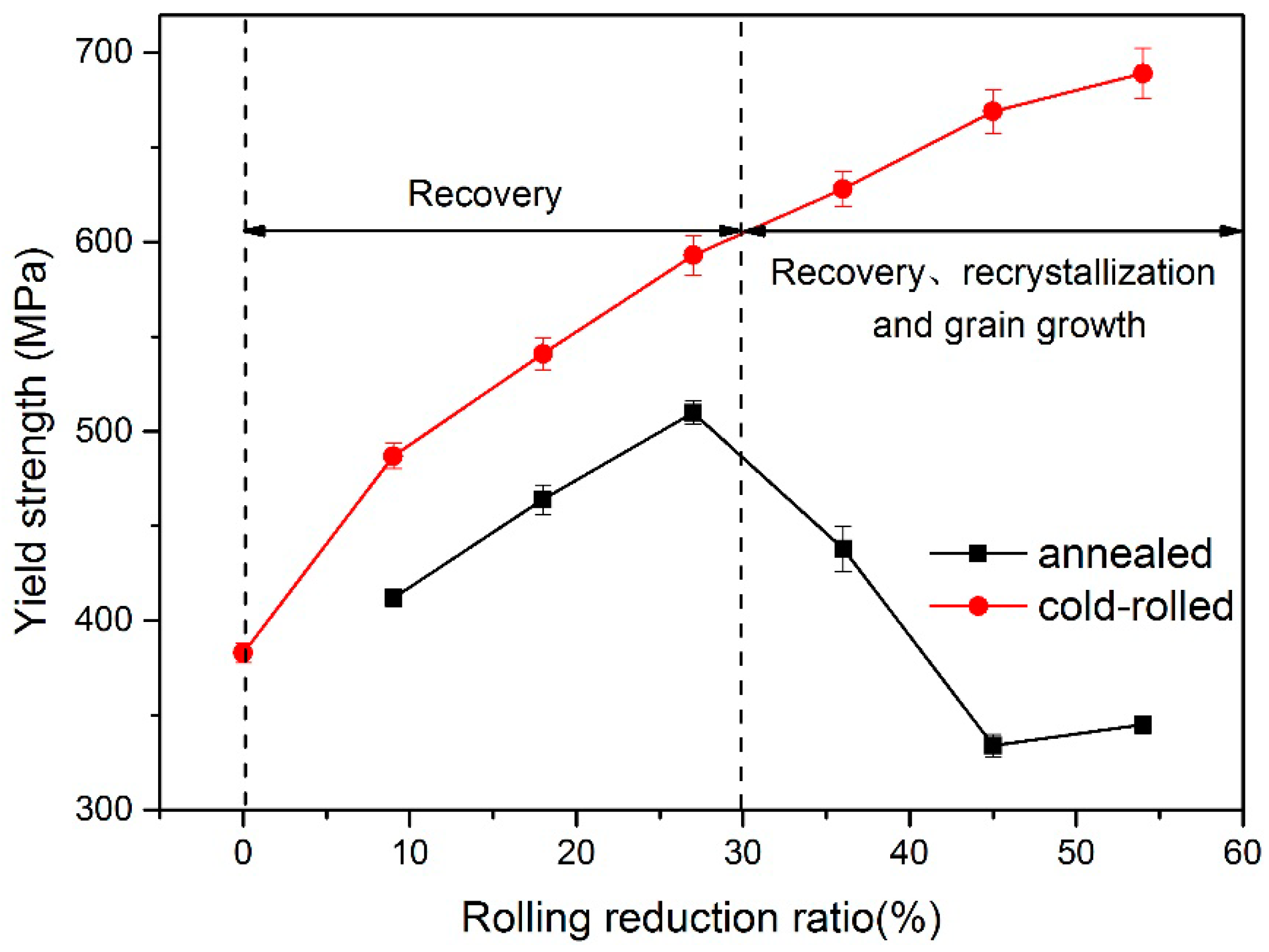
- Under the combined influence of work-hardening and annealing softening, the mechanical properties of TRB vary along the rolling direction. The hardness and strength of annealed TRB increase first and then decrease with the increase of the rolling reduction ratio, reaching the maximum value at a reduction ratio of 27%;
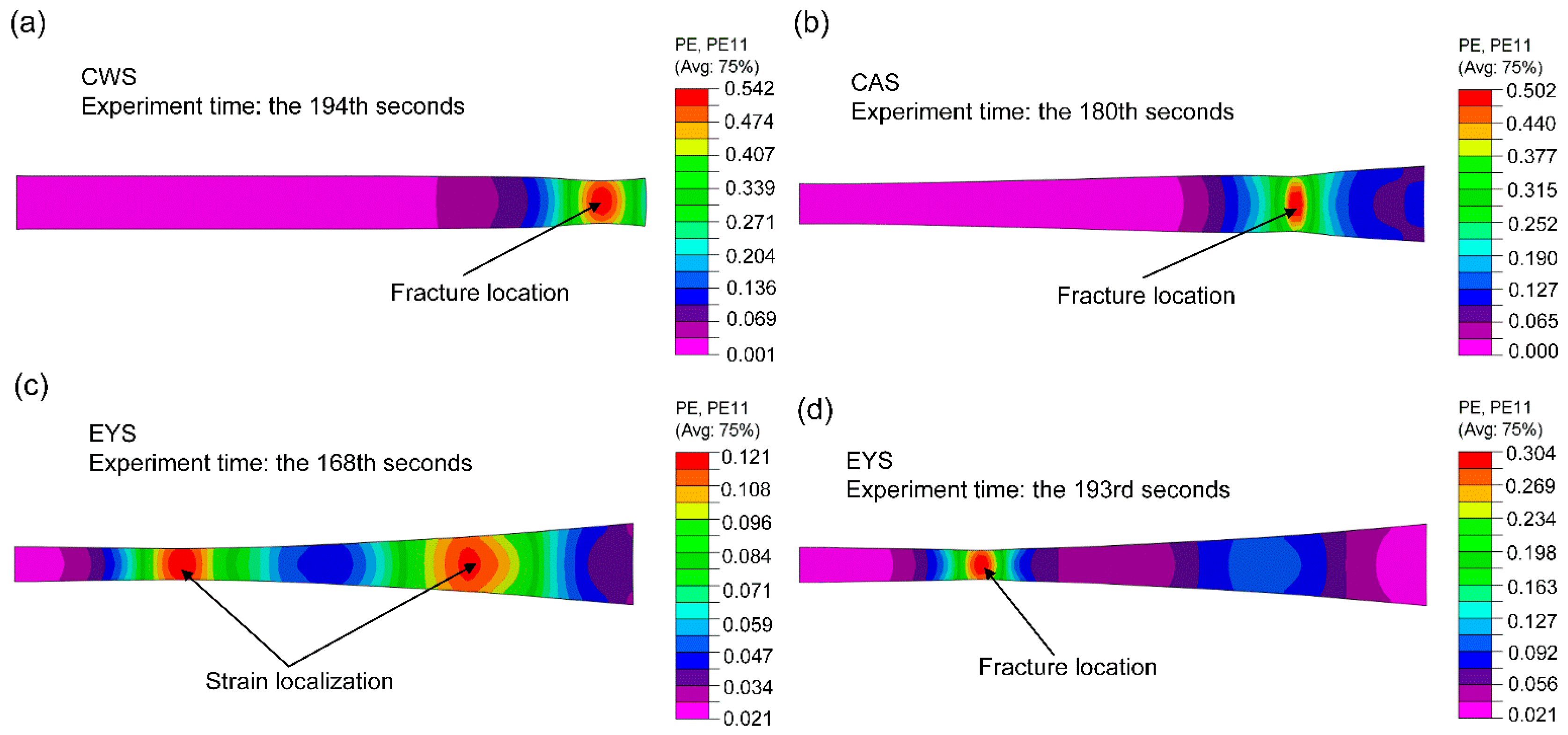
- The variation index of the major strain distributions on the cross section of EYS ranges from 1.24% to 3.46%, which is lower than 5%. This indicates that the strains on the cross section of the specimen are uniform during the test and the effect of modified geometry on the strain distribution can be negligible;
- After tensile tests, the elongation of a reduced section of EYS is 9.3%, which is 5% and 19% higher than that of CWS (8.9%) and CAS (7.8%), respectively. In addition, the elongation of the transition zone of EYS is 11%, which is 124% and 39% higher than that of CWS (4.9%) and CAS (7.9%). The plastic deformation of EYS is more sufficient;
- The length strain fields of specimens during the deformation process were measured by the DIC method. It is noted that the difference between the maximum and minimum strains in EYS before fracture is 0.275, while that in CWS and CAS are 0.53 and 0.49, respectively. The strain distribution of EYS is more homogeneous compared with the other two types of specimens;
- There is a long yield plateau in the force-displacement curve of the constant-thickness blank, while a short yield plateau can be observed in the force-displacement curve of CWS and no yield plateau can be observed in the force-displacement curve of CAS and EYS;
- On the basis of data obtained by the DIC method in a uniaxial tensile test, the true stress-strain curves of metal in 11 different cross sections of TRB were calculated. A material model of TRB was constructed and then implemented into the FE simulations of uniaxial tensile tests;
- The strain distribution of numerical and experimental results are similar and the fracture locations and strain localization are predicted accurately in the FE simulations. The error between the elongation of the specimen after fracture obtained by experiment and FE ranges from 9.51% to 13.06%. It can be concluded that the FE results are in good agreement with the experimental results. Thus, the applicability of the material model was verified.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Merklein, M.; Johannes, M.; Lechner, M.; Andreas, K. A review on tailored blanks—Production, applications and evaluation. J. Mater. Process. Technol. 2014, 214, 151–164. [Google Scholar] [CrossRef]
- Liu, X.H. Prospects for variable gauge rolling: Technology, theory and application. J. Iron Steel Res. Int. 2011, 18, 1–7. [Google Scholar] [CrossRef]
- Kopp, R.; Wiedner, C.; Meyer, A. Flexibly rolled sheet metal and its use in sheet metal forming. Adv. Mater. Res. 2005, 6, 81–92. [Google Scholar] [CrossRef]
- Kim, H.W.; Lim, C.Y. Annealing of flexible-rolled Al–5.5 wt % Mg alloy sheets for auto body application. Mater. Design 2010, 31, S71–S75. [Google Scholar] [CrossRef]
- Meyer, A.; Wietbrock, B.; Hirt, G. Increasing of the drawing depth using tailor rolled blanks—Numerical and experimental analysis. Int. J. Mach. Tools Manuf. 2008, 48, 522–531. [Google Scholar] [CrossRef]
- Kleiner, M.; Krux, R.; Homberg, W. High-pressure sheet metal forming of large scale structures from sheets with optimised thickness distribution. Steel Res. Int. 2005, 76, 177–181. [Google Scholar] [CrossRef]
- Chatti, S.; Kleiner, M. Manufacturing of profiles for lightweight structures. In Proceedings of the 10th International ESAFORM Conference on Material Forming, American Institute of Physics, Melville, NY, USA, 18–20 April 2007; pp. 584–589. [Google Scholar]
- Urban, M.; Krahn, M.; Hirt, G.; Kopp, R. Numerical research and optimisation of high pressure sheet metal forming of tailor rolled blanks. J. Mater. Process. Technol. 2006, 177, 360–363. [Google Scholar] [CrossRef]
- Lu, R.H.; Liu, X.H.; Chen, S.D.; Hu, X.L.; Liu, L.Z. Axial crashing analysis for tailor rolled square tubes with axially graded both wall thickness and material strength. Thin Walled Struct. 2017, 117, 10–24. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, X.H.; Liu, L.Z.; Hu, P.; Wu, J.L. Study on nonuniform deformation of tailor rolled blank during uniaxial tension. Acta Metall. Sin. 2015, 28, 1198–1204. [Google Scholar] [CrossRef]
- Shafiei, E.; Dehghani, K. Tensile behavior of tailor rolled blanks with longitudinal thickness transition zone: Introducing a new tensile specimen. Vacuum 2017, 143, 71–86. [Google Scholar] [CrossRef]
- Cui, Z.X.; Tan, Y.C. Metallurgy and Heat Treatment, 2nd ed.; China Machine Press: Beijing, China, 2007; pp. 194–208. ISBN 978-7-111-01796-7. (In Chinese) [Google Scholar]
- Tabor, D. A simple theory of static and dynamic hardness. Proc. R. Soc. Lond. A 1948, 192, 247–274. [Google Scholar] [CrossRef]
- Lai, M.O.; Lim, K.B. On the prediction of tensile properties from hardness tests. J. Mater. Sci. 1991, 26, 2031–2036. [Google Scholar] [CrossRef]
- Pavlina, E.J.; van Tyne, C.J. Correlation of yield strength and tensile strength with hardness for steels. J. Mater. Eng. Perform. 2008, 17, 888–893. [Google Scholar] [CrossRef]
- Busby, J.T.; Hash, M.C.; Was, G.S. The relationship between hardness and yield stress in irradiated austenitic and ferritic steels. J. Nucl. Mater. 2005, 336, 267–278. [Google Scholar] [CrossRef]
- Zhang, P.; Li, S.X.; Zhang, Z.F. General relationship between strength and hardness. Mater. Sci. Eng. A 2011, 529, 62–73. [Google Scholar] [CrossRef]
- Zhao, K.M.; Chun, B.K.; Lee, J.K. Finite element analysis of tailor-welded blanks. Finite Elem. Anal. Des. 2001, 37, 117–130. [Google Scholar] [CrossRef]




| Specimen | Elongation of Reduced Section (%) | Elongation of Transition Zone (%) |
|---|---|---|
| CWS | 8.9 | 4.9 |
| CAS | 7.8 | 7.9 |
| EYS | 9.3 | 11.0 |
| Thickness (mm) | Strength Coefficient: K (MPa) | Tensile Strain Hardening Exponent: n |
|---|---|---|
| 1.0 | 742.00 | 0.21 |
| 1.1 | 731.00 | 0.20 |
| 1.2 | 679.14 | 0.20 |
| 1.3 | 703.18 | 0.19 |
| 1.4 | 747.52 | 0.17 |
| 1.5 | 790.23 | 0.14 |
| 1.6 | 770.65 | 0.11 |
| 1.7 | 755.32 | 0.11 |
| 1.8 | 758.00 | 0.12 |
| 1.9 | 745.35 | 0.12 |
| 2.0 | 727.00 | 0.14 |
| Specimen | Elongation of the Specimens after Fracture (mm) | Error (%) | |
|---|---|---|---|
| Experiments | Simulations | ||
| CWS | 10.72 | 9.70 | −9.51 |
| CAS | 9.26 | 9.00 | −2.81 |
| EYS | 11.10 | 9.65 | −13.06 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Liu, X.; Liu, L. A Tensile Specimen of Tailor Rolled Blanks with Equal Probability in Yield and Its Mechanical Behavior Analysis. Materials 2018, 11, 693. https://doi.org/10.3390/ma11050693
Zhang S, Liu X, Liu L. A Tensile Specimen of Tailor Rolled Blanks with Equal Probability in Yield and Its Mechanical Behavior Analysis. Materials. 2018; 11(5):693. https://doi.org/10.3390/ma11050693
Chicago/Turabian StyleZhang, Sijia, Xianghua Liu, and Lizhong Liu. 2018. "A Tensile Specimen of Tailor Rolled Blanks with Equal Probability in Yield and Its Mechanical Behavior Analysis" Materials 11, no. 5: 693. https://doi.org/10.3390/ma11050693
APA StyleZhang, S., Liu, X., & Liu, L. (2018). A Tensile Specimen of Tailor Rolled Blanks with Equal Probability in Yield and Its Mechanical Behavior Analysis. Materials, 11(5), 693. https://doi.org/10.3390/ma11050693





