Core Level Spectra of Organic Molecules Adsorbed on Graphene
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
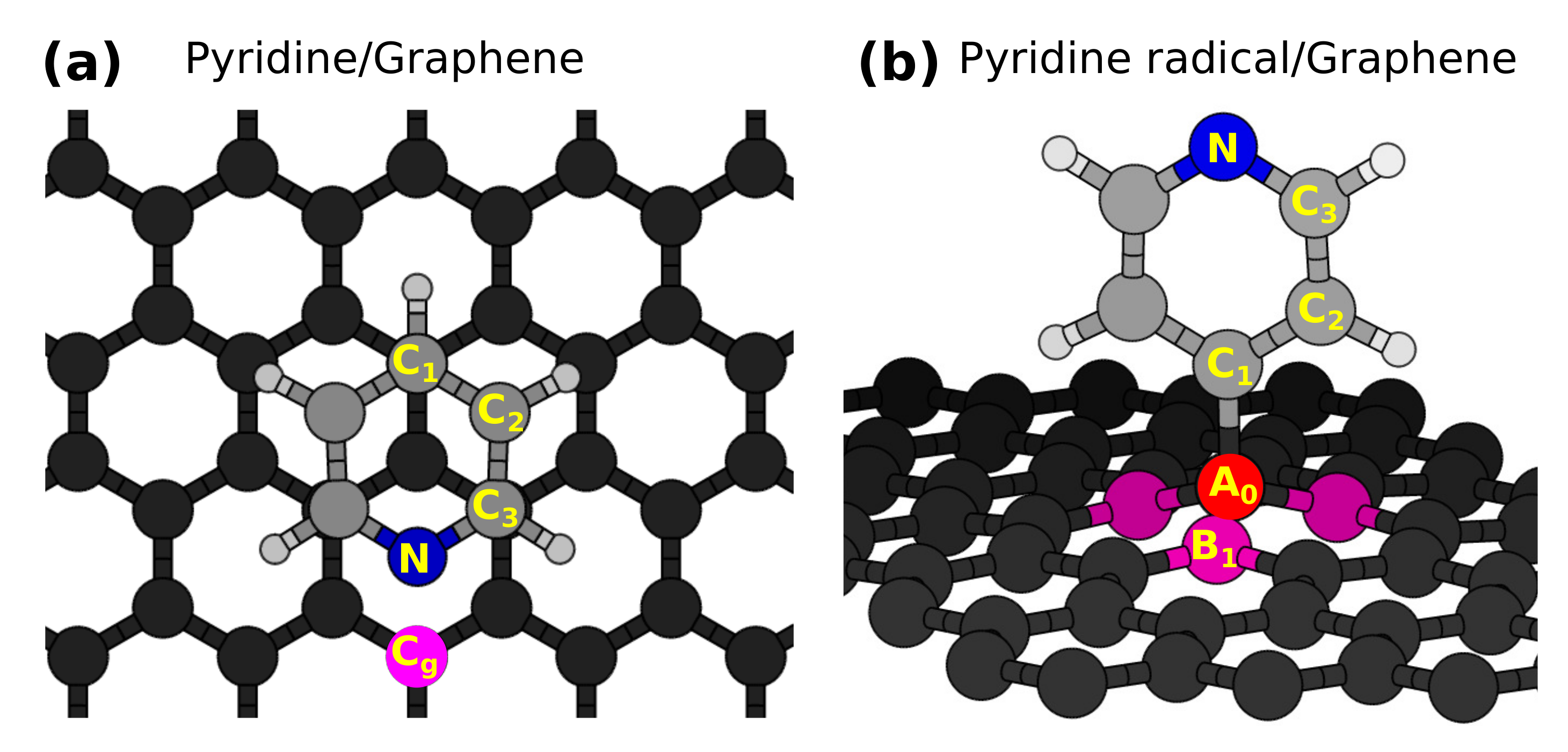
3.1. Adsorption Configurations
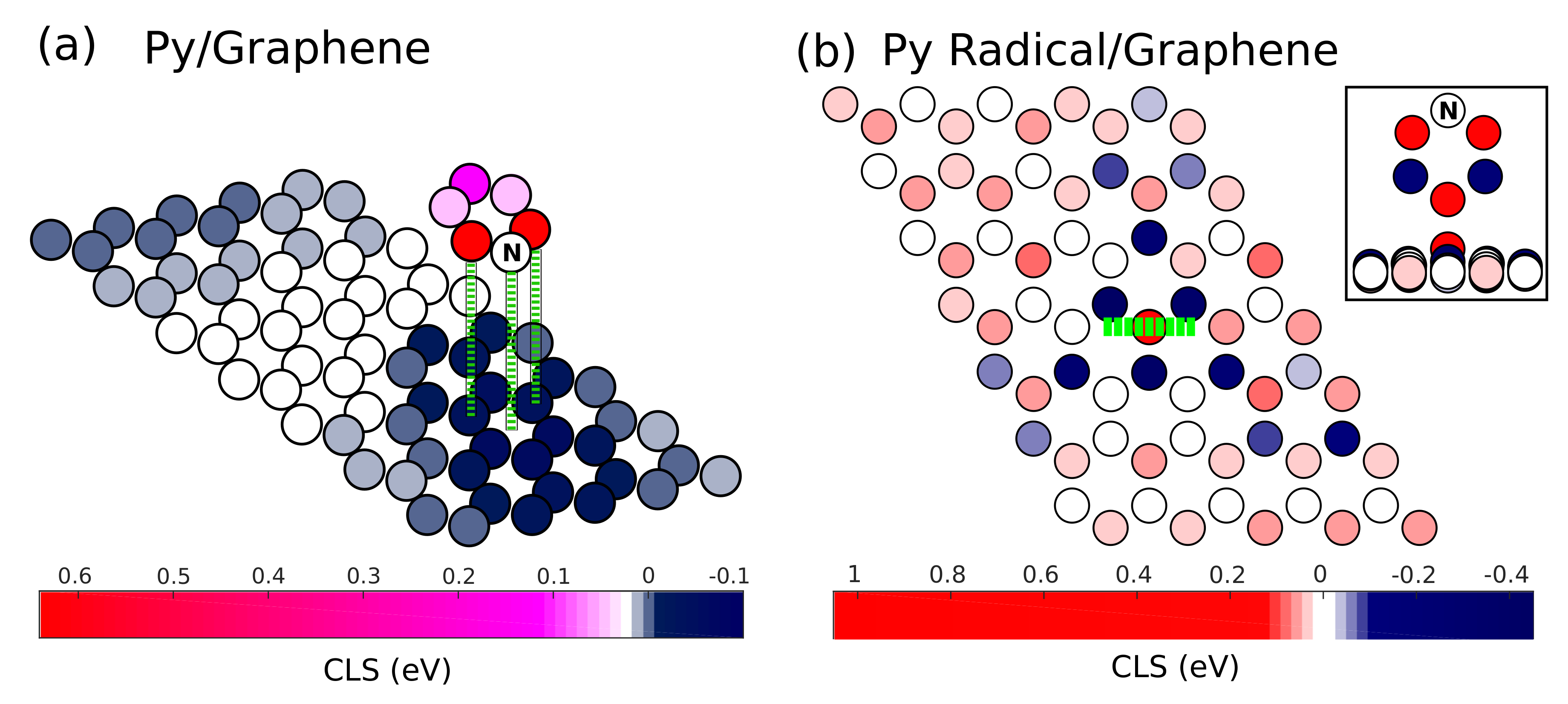
3.2. X-Ray Photoemission
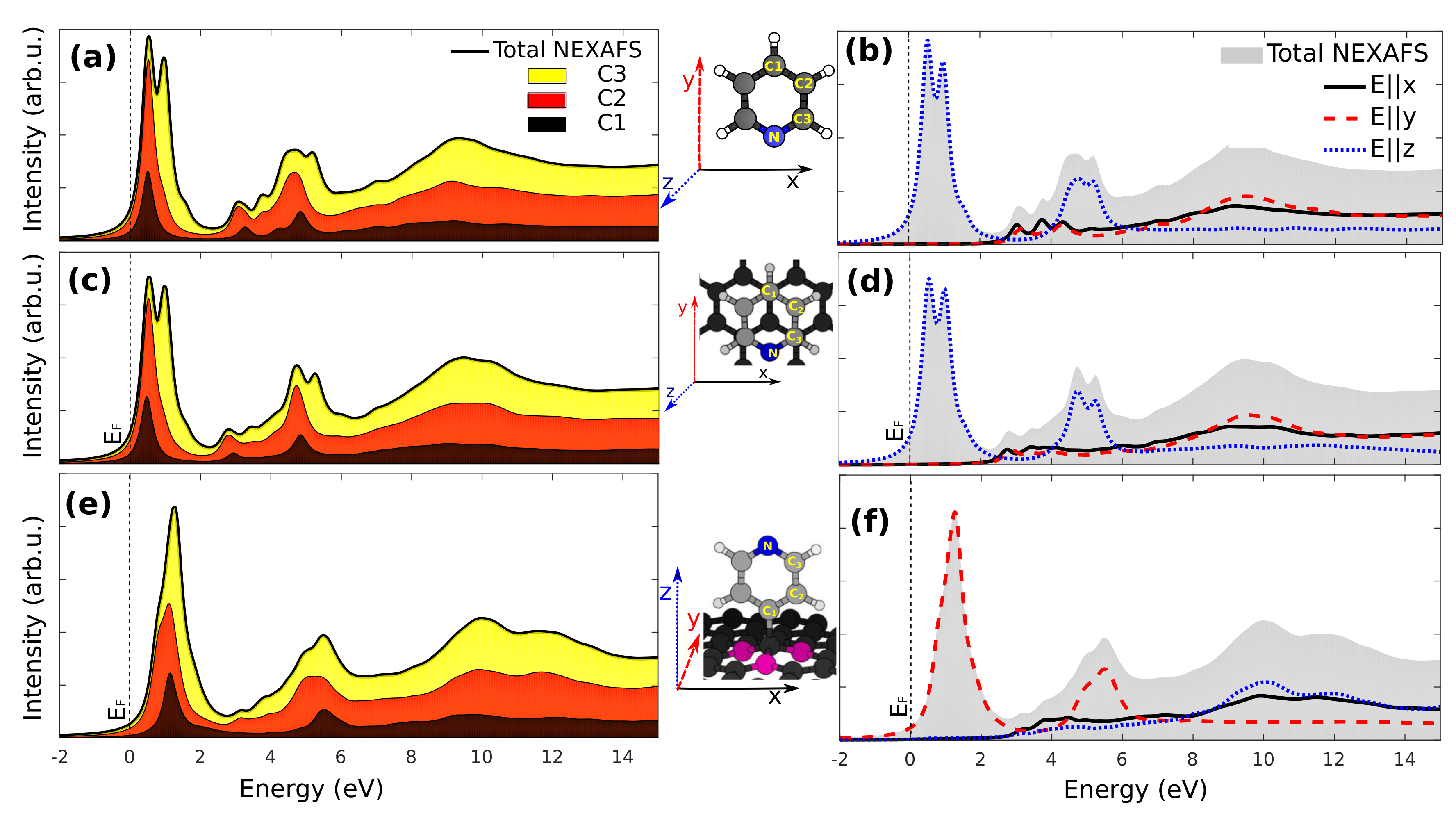
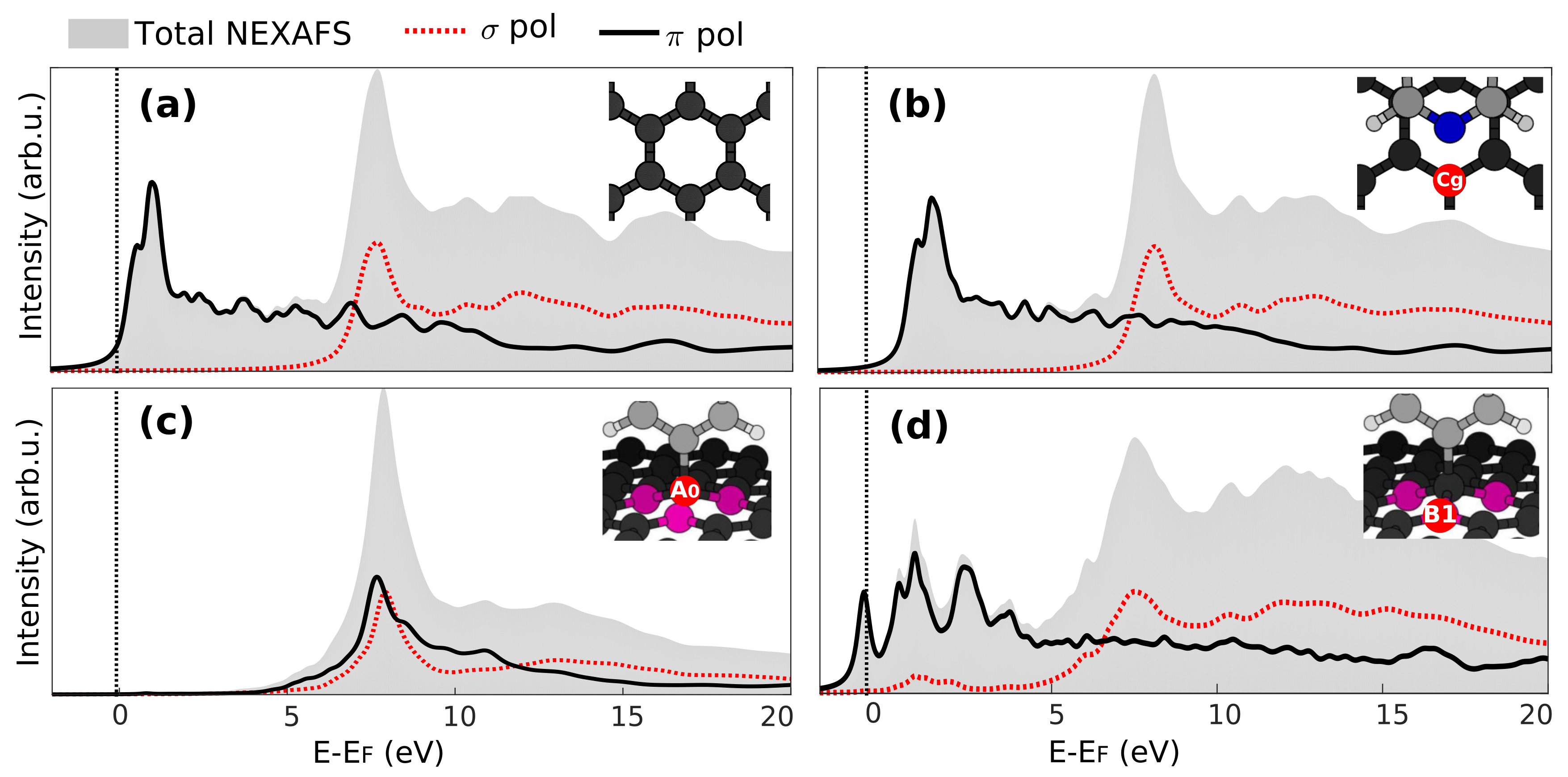
3.3. X-Ray Absorption
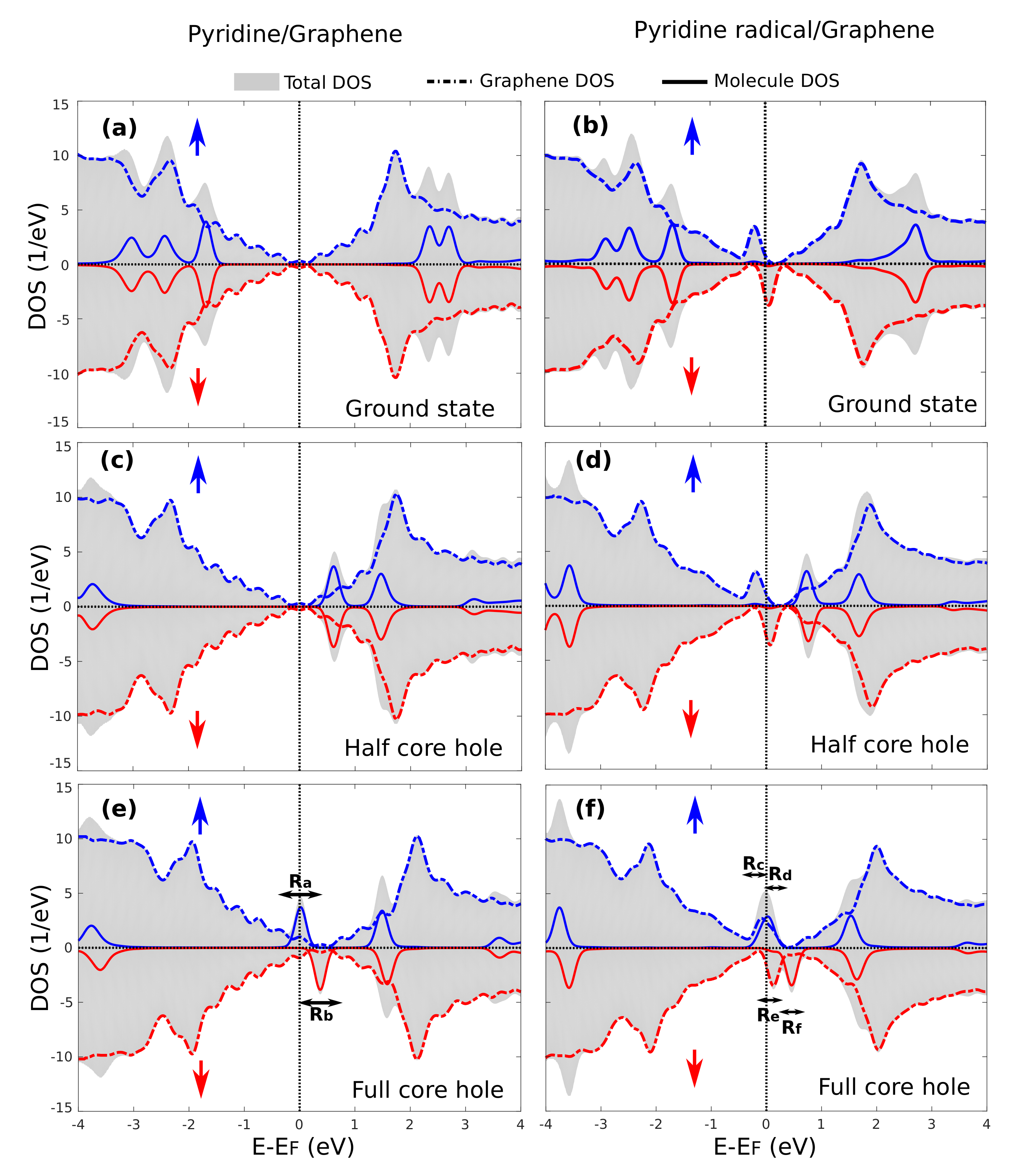
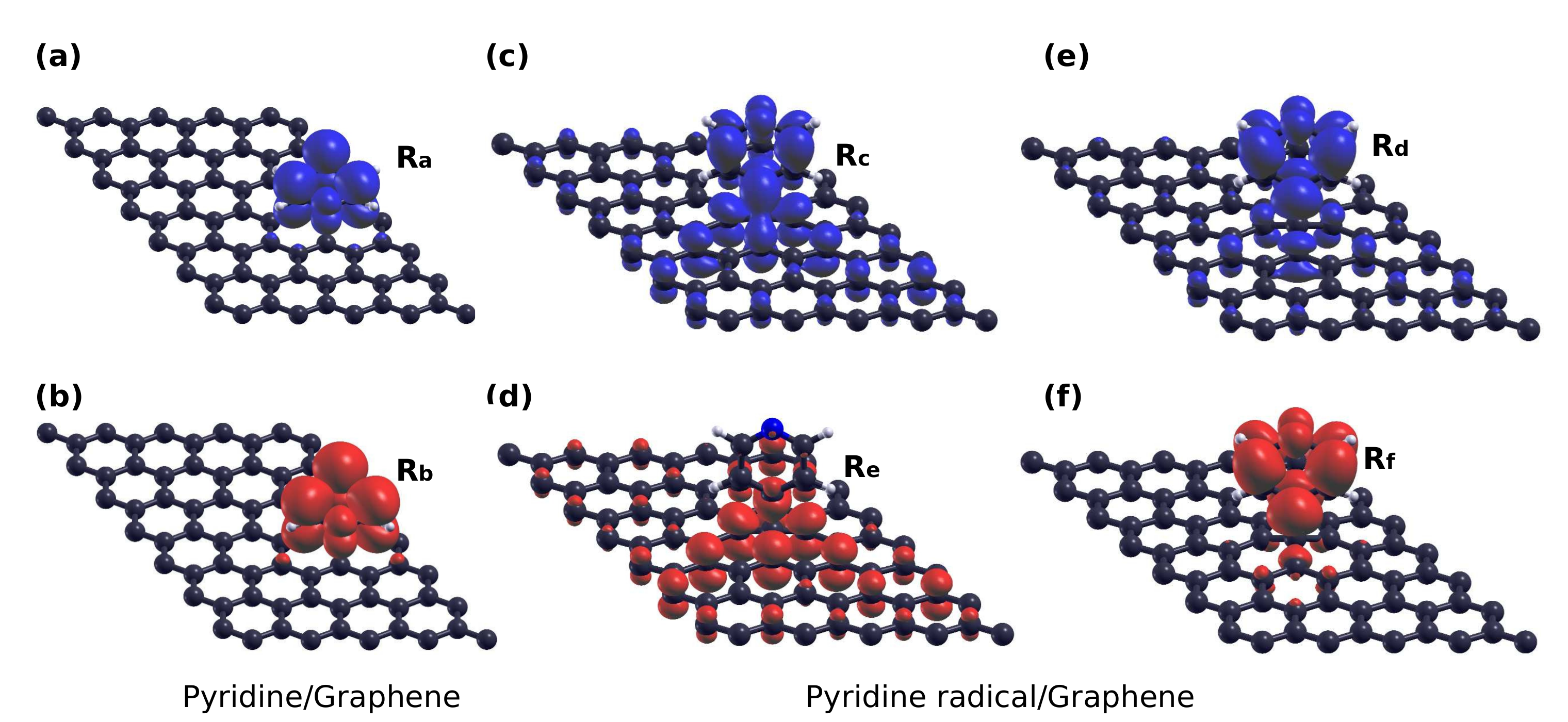
3.4. Core-Excited Electronic and Magnetic Properties
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FCH | Full Core Hole |
| HCH | Half Core Hole |
| CLS | Core Level Shift |
| BE | Binding Energy |
References
- Novoselov, K.S. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Katsnelson, M.I. Graphene: Carbon in two dimensions. Mater. Today 2007, 10, 20–27. [Google Scholar] [CrossRef]
- Gunlycke, D.; Lawler, H.M.; White, C.T. Room-temperature ballistic transport in narrow graphene strips. Phys. Rev. B 2007, 75, 085418. [Google Scholar] [CrossRef]
- Solís-Fernández, P.; Bissett, M.; Ago, H. Synthesis, structure and applications of graphene-based 2D heterostructures. Chem. Soc. Rev. 2017, 46, 4572–4613. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, J.; Castro Neto, A.H.; Guinea, F.; Peres, N.M.R. Transmission through a biased graphene bilayer barrier. Phys. Rev. B 2007, 76, 165416. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Novoselov, K.S.; Geim, A.K. Chiral tunnelling and the Klein paradox in graphene. Nat. Phys. 2006, 2, 620–625. [Google Scholar] [CrossRef]
- Sojoudi, H.; Baltazar, J.; Tolbert, L.M.; Henderson, C.L.; Graham, S. Creating Graphene p–n Junctions Using Self-Assembled Monolayers. ACS Appl. Mater. Interfaces 2012, 4, 4781–4786. [Google Scholar] [CrossRef] [PubMed]
- Schwierz, F. Graphene transistors. Nat. Nanotechnol. 2010, 5, 487–496. [Google Scholar] [CrossRef] [PubMed]
- Sood, A.K.; Lund, I.; Puri, Y.R.; Efstathiadis, H.; Haldar, P.; Dhar, N.K.; Lewis, J.; Dubey, M.; Zakar, E.; Polla, D.L.; et al. Review of Graphene Technology and Its Applications for Electronic Devices. In Graphene-New Trends and Developments; InTech: London, UK, 2015. [Google Scholar]
- Bokdam, M.; Khomyakov, P.A.; Brocks, G.; Zhong, Z.; Kelly, P.J. Electrostatic Doping of Graphene through Ultrathin Hexagonal Boron Nitride Films. Nano Lett. 2011, 11, 4631–4635. [Google Scholar] [CrossRef] [PubMed]
- Bokdam, M.; Khomyakov, P.A.; Brocks, G.; Kelly, P.J. Field effect doping of graphene in metal|dielectric| graphene heterostructures: A model based upon first-principles calculations. Phys. Rev. B 2013, 87, 075414. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Zhang, L.; Yoon, Y.; Weber, P.K.; Wang, H.; Guo, J.; Dai, H. N-doping of graphene through electrothermal reactions with ammonia. Science 2009, 324, 768–771. [Google Scholar] [CrossRef] [PubMed]
- Lherbier, A.; Blase, X.; Niquet, Y.M.; Triozon, F.; Roche, S. Charge Transport in Chemically Doped 2D Graphene. Phys. Rev. Lett. 2008, 101, 036808. [Google Scholar] [CrossRef] [PubMed]
- Martins, T.B.; Miwa, R.H.; da Silva, A.J.R.; Fazzio, A. Electronic and Transport Properties of Boron-Doped Graphene Nanoribbons. Phys. Rev. Lett. 2007, 98, 196803. [Google Scholar] [CrossRef] [PubMed]
- Panchakarla, L.S.; Subrahmanyam, K.S.; Saha, S.K.; Govindaraj, A.; Krishnamurthy, H.R.; Waghmare, U.V.; Rao, C.N.R. Synthesis, Structure, and Properties of Boron- and Nitrogen-Doped Graphene. Adv. Mater. 2009, 21, 4726–4730. [Google Scholar] [CrossRef]
- Georgakilas, V.; Otyepka, M.; Bourlinos, A.B.; Chandra, V.; Kim, N.; Kemp, K.C.; Hobza, P.; Zboril, R.; Kim, K.S. Functionalization of Graphene: Covalent and Non-Covalent Approaches, Derivatives and Applications. Chem. Rev. 2012, 112, 6156–6214. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Yan, M. Covalent Functionalization of Graphene with Reactive Intermediates. Acc. Chem. Res. 2013, 46, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Englert, J.M.; Dotzer, C.; Yang, G.; Schmid, M.; Papp, C.; Gottfried, J.M.; Steinrück, H.P.; Spiecker, E.; Hauke, F.; Hirsch, A. Covalent bulk functionalization of graphene. Nat. Chem. 2011, 3, 279–286. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Fratesi, G.; Brivio, G.P. Graphene magnetism induced by covalent adsorption of aromatic radicals. Phys. Chem. Chem. Phys. 2014, 17, 2210–2215. [Google Scholar] [CrossRef] [PubMed]
- Ravikumar, A.; Baby, A.; Lin, H.; Brivio, G.P.; Fratesi, G. Femtomagnetism in graphene induced by core level excitation of organic adsorbates. Sci. Rep. 2016, 6, 24603. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.J.D.; McLendon, G.L.; Nozik, A.J.; Schmickler, W.; Willig, F. Surface Electron Transfer Processes; Wiley-VCH: Weinheim, Germany, 1995. [Google Scholar]
- Morrison, S.R. Electrochemistry at Semiconductor and Oxidized Metal Electrodes; Springer: New York, NY, USA, 1980. [Google Scholar]
- Finklea, H.O. Semiconductor Electrodes; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Heller, A. Conversion of sunlight into electrical power and photoassisted electrolysis of water in photoelectrochemical cells. Acc. Chem. Res. 1981, 14, 154–162. [Google Scholar] [CrossRef]
- Hannappel, T.; Burfeindt, B.; Storck, W.; Willig, F. Measurement of Ultrafast Photoinduced Electron Transfer from Chemically Anchored Ru-Dye Molecules into Empty Electronic States in a Colloidal Anatase TiO2 Film. J. Phys. Chem. B 1997, 101, 6799–6802. [Google Scholar] [CrossRef]
- Ehlert, C.; Unger, W.E.S.; Saalfrank, P. C K-edge NEXAFS spectra of graphene with physical and chemical defects: A study based on density functional theory. Phys. Chem. Chem. Phys. 2014, 16, 14083–14095. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.S.; Tao, Y.T.; Hsu, Y.J.; Wei, D.H.; Wu, Y.S. Molecular Orientation of Evaporated Pentacene Films on Gold: Alignment Effect of Self-Assembled Monolayer. Langmuir 2005, 21, 2260–2266. [Google Scholar] [CrossRef] [PubMed]
- Solomon, J.L.; Madix, R.J.; Stöhr, J. Orientation and absolute coverage of benzene, aniline, and phenol on Ag(110) determined by NEXAFS and XPS. Surf. Sci. 1991, 255, 12–30. [Google Scholar] [CrossRef]
- Fratesi, G.; Lanzilotto, V.; Floreano, L.; Brivio, G.P. Azimuthal Dichroism in Near-Edge X-ray Absorption Fine Structure Spectra of Planar Molecules. J. Phys. Chem. C 2013, 117, 6632–6638. [Google Scholar] [CrossRef]
- Brühwiler, P.A.; Karis, O.; Mårtensson, N. Charge-transfer dynamics studied using resonant core spectroscopies. Rev. Mod. Phys. 2002, 74, 703–740. [Google Scholar] [CrossRef]
- Adak, O.; Kladnik, G.; Bavdek, G.; Cossaro, A.; Morgante, A.; Cvetko, D.; Venkataraman, L. Ultrafast Bidirectional Charge Transport and Electron Decoherence at Molecule/Surface Interfaces: A Comparison of Gold, Graphene, and Graphene Nanoribbon Surfaces. Nano Lett. 2015, 15, 8316–8321. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Brivio, G.P.; Trioni, M.I. The adiabatic molecule–metal surface interaction: Theoretical approaches. Rev. Mod. Phys. 1999, 71, 231–265. [Google Scholar] [CrossRef]
- Pehlke, E.; Scheffler, M. Evidence for site-sensitive screening of core holes at the Si and Ge(001) surface. Phys. Rev. Lett. 1993, 71, 2338–2341. [Google Scholar] [CrossRef] [PubMed]
- Slater, J.C.; Johnson, K.H. Self-Consistent-Field Xα Cluster Method for Polyatomic Molecules and Solids. Phys. Rev. B 1972, 5, 844–853. [Google Scholar] [CrossRef]
- Triguero, L.; Pettersson, L.G.M.; Ågren, H. Calculations of near-edge X-ray-absorption spectra of gas-phase and chemisorbed molecules by means of density-functional and transition-potential theory. Phys. Rev. B 1998, 58, 8097–8110. [Google Scholar] [CrossRef]
- Ugolotti, A.; Harivyasi, S.S.; Baby, A.; Dominguez, M.; Pinardi, A.L.; López, M.F.; Martín-Gago, J.Á.; Fratesi, G.; Floreano, L.; Brivio, G.P. Chemisorption of Pentacene on Pt(111) with a Little Molecular Distortion. J. Phys. Chem. C 2017, 121, 22797–22805. [Google Scholar] [CrossRef]
- Perera, S.D.; Urquhart, S.G. Systematic Investigation of π–π Interactions in Near-Edge X-ray Fine Structure (NEXAFS) Spectroscopy of Paracyclophanes. J. Phys. Chem. A 2017, 121, 4907–4913. [Google Scholar] [CrossRef] [PubMed]
- Leetmaa, M.; Ljungberg, M.P.; Lyubartsev, A.; Nilsson, A.; Pettersson, L.G.M. Theoretical approximations to X-ray absorption spectroscopy of liquid water and ice. J. Electron. Spectrosc. Relat. Phenom. 2010, 177, 135–157. [Google Scholar] [CrossRef]
- Fratesi, G.; Lanzilotto, V.; Stranges, S.; Alagia, M.; Brivio, G.P.; Floreano, L. High resolution NEXAFS of perylene and PTCDI: A surface science approach to molecular orbital analysis. Phys. Chem. Chem. Phys. 2014, 16, 14834–14844. [Google Scholar] [CrossRef] [PubMed]
- Diller, K.; Maurer, R.J.; Müller, M.; Reuter, K. Interpretation of X-ray absorption spectroscopy in the presence of surface hybridization. J. Chem. Phys. 2017, 146, 214701. [Google Scholar] [CrossRef] [PubMed]
- Santos, E.J.G.; Ayuela, A.; Sánchez-Portal, D. Universal magnetic properties of sp 3-type defects in covalently functionalized graphene. New J. Phys. 2012, 14, 043022. [Google Scholar] [CrossRef]
- Zhang, W.; Nefedov, A.; Naboka, M.; Cao, L.; Wöll, C. Molecular orientation of terephthalic acid assembly on epitaxial graphene: NEXAFS and XPS study. Phys. Chem. Chem. Phys. 2012, 14, 10125–10131. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.; Huang, C.; Kim, M.; Safron, N.; Arnold, M.; Wong, B.; Gopalan, P.; Himpsel, F. Orientation of a monolayer of dipolar molecules on graphene from X-ray absorption spectroscopy. Langmuir 2014, 30, 2559–2565. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Wang, S.Y.; Hu, J.; Song, X.N.; Zhou, Y.; Wang, C.K. Theoretical N K-edge NEXAFS spectroscopy study for configuration of a dipolar molecule on graphene. Mater. Chem. Phys. 2018, 207, 309–314. [Google Scholar] [CrossRef]
- Voloshina, E.; Ovcharenko, R.; Shulakov, A.; Dedkov, Y. Theoretical description of X-ray absorption spectroscopy of the graphene-metal interfaces. J. Chem. Phys. 2013, 138, 154706. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Rappe, A.M.; Rabe, K.M.; Kaxiras, E.; Joannopoulos, J.D. Optimized pseudopotentials. Phys. Rev. B 1990, 41, 1227–1230. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Elias, D.C.; Nair, R.R.; Mohiuddin, T.M.G.; Morozov, S.V.; Blake, P.; Halsall, M.P.; Ferrari, A.C.; Boukhvalov, D.W.; Katsnelson, M.I.; Geim, A.K.; et al. Control of Graphene’s Properties by Reversible Hydrogenation: Evidence for Graphane. Science 2009, 323, 610–613. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, N.; Fink, R.; Hieringer, W. Assignment of near-edge X-ray absorption fine structure spectra of metalloporphyrins by means of time-dependent density-functional calculations. J. Chem. Phys. 2010, 133, 054703. [Google Scholar] [CrossRef] [PubMed]
- Kolczewski, C.; Püttner, R.; Plashkevych, O.; Ågren, H.; Staemmler, V.; Martins, M.; Snell, G.; Schlachter, A.S.; Sant’Anna, M.; Kaindl, G.; et al. Detailed study of pyridine at the C 1s and N 1s ionization thresholds: The influence of the vibrational fine structure. J. Chem. Phys. 2001, 115, 6426–6437. [Google Scholar] [CrossRef]
- Gougoussis, C.; Calandra, M.; Seitsonen, A.P.; Mauri, F. First-principles calculations of X-ray absorption in a scheme based on ultra-soft pseudopotentials: From α-quartz to high-Tc compounds. Phys. Rev. B 2009, 80, 075102. [Google Scholar] [CrossRef]
- Lanczos, C. Solution of Systems of Linear Equations by Minimized Iterations. J. Res. Natl. Bur. Stand. 1952, 49, 33. [Google Scholar] [CrossRef]
- García-Gil, S.; García, A.; Ordejón, P. Calculation of core level shifts within DFT using pseudopotentials and localized basis sets. Eur. Phys. J. B 2018, 85, 239. [Google Scholar] [CrossRef]
- Casolo, S.; Løvvik, O.M.; Martinazzo, R.; Tantardini, G.F. Understanding adsorption of hydrogen atoms on graphene. J. Chem. Phys. 2009, 130, 054704. [Google Scholar] [CrossRef] [PubMed]
- Cvetko, D.; Fratesi, G.; Kladnik, G.; Cossaro, A.; Brivio, G.P.; Venkataraman, L.; Morgante, A. Ultrafast electron injection into photo-excited organic molecules. Phys. Chem. Chem. Phys. 2016, 18, 22140–22145. [Google Scholar] [CrossRef] [PubMed]
- Bavdek, G.; Cossaro, A.; Cvetko, D.; Africh, C.; Blasetti, C.; Esch, F.; Morgante, A.; Floreano, L. Pentacene Nanorails on Au(110). Langmuir 2008, 24, 767–772. [Google Scholar] [CrossRef] [PubMed]
| Atom Site | Gas Phase | Pyridine/Graphene | Pyridine Radical/Graphene |
|---|---|---|---|
| (CLS) (eV) | CLS (CLS) (eV) | CLS (CLS) (eV) | |
| C1 | (−0.02) | 0.26 (−0.06) | 0.18 (0.02) |
| C2 | (−0.29) | 0.04 (−0.28) | −0.19 (−0.35) |
| C3 | (0.30) | 0.64 (0.31) | 0.50 (0.34) |
| C | - | −0.06 (−0.38) | - |
| A | - | - | 1.03 (0.87) |
| B | - | - | −0.42 (−0.59) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ravikumar, A.; Brivio, G.P.; Fratesi, G. Core Level Spectra of Organic Molecules Adsorbed on Graphene. Materials 2018, 11, 518. https://doi.org/10.3390/ma11040518
Ravikumar A, Brivio GP, Fratesi G. Core Level Spectra of Organic Molecules Adsorbed on Graphene. Materials. 2018; 11(4):518. https://doi.org/10.3390/ma11040518
Chicago/Turabian StyleRavikumar, Abhilash, Gian Paolo Brivio, and Guido Fratesi. 2018. "Core Level Spectra of Organic Molecules Adsorbed on Graphene" Materials 11, no. 4: 518. https://doi.org/10.3390/ma11040518
APA StyleRavikumar, A., Brivio, G. P., & Fratesi, G. (2018). Core Level Spectra of Organic Molecules Adsorbed on Graphene. Materials, 11(4), 518. https://doi.org/10.3390/ma11040518





