Related Structure Characters and Stability of Structural Defects in a Metallic Glass
Abstract
:1. Introduction
2. Materials and Methods
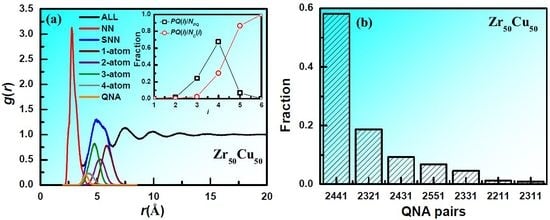
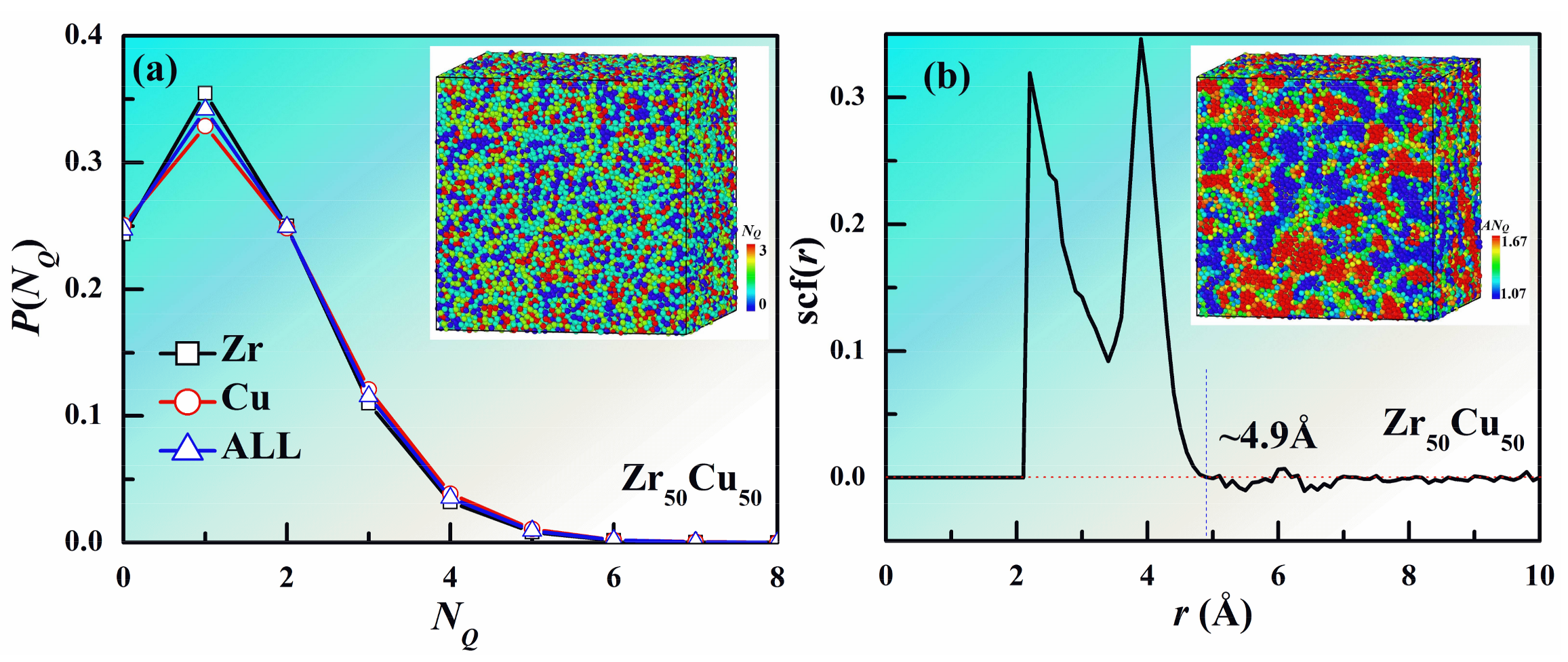
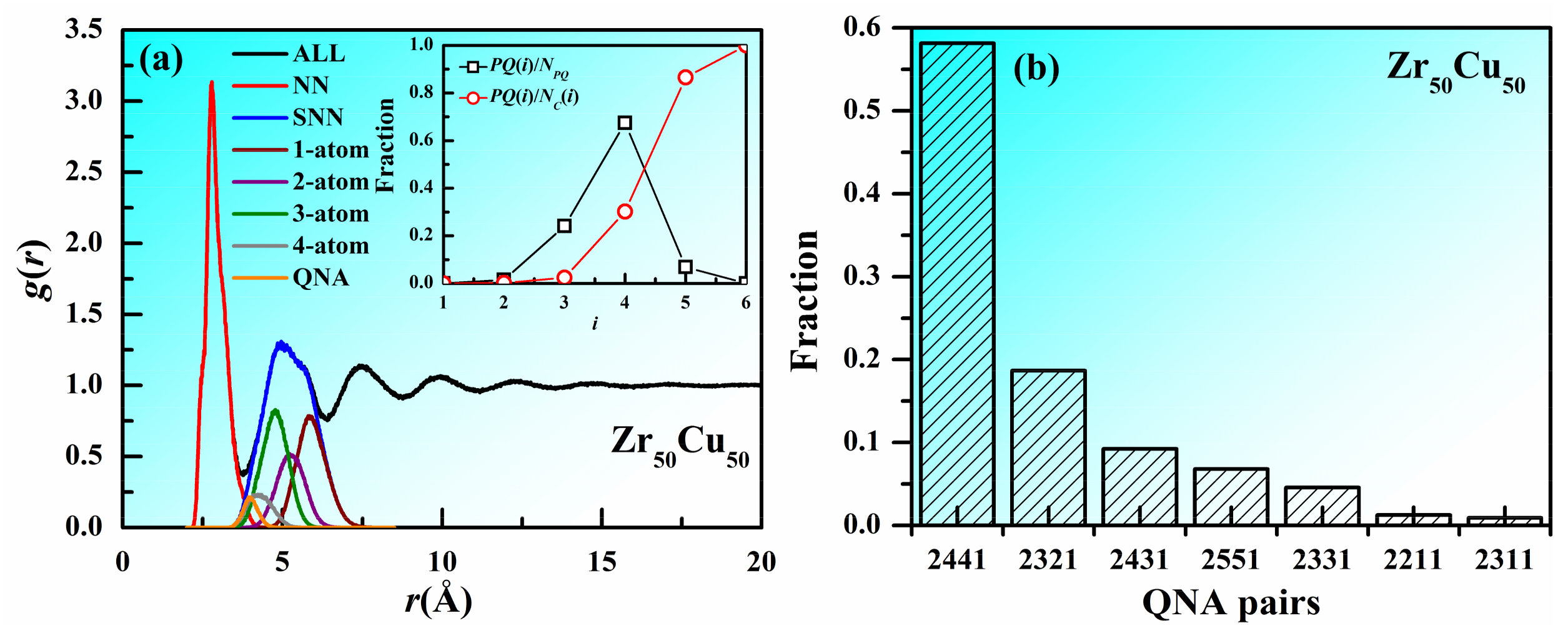
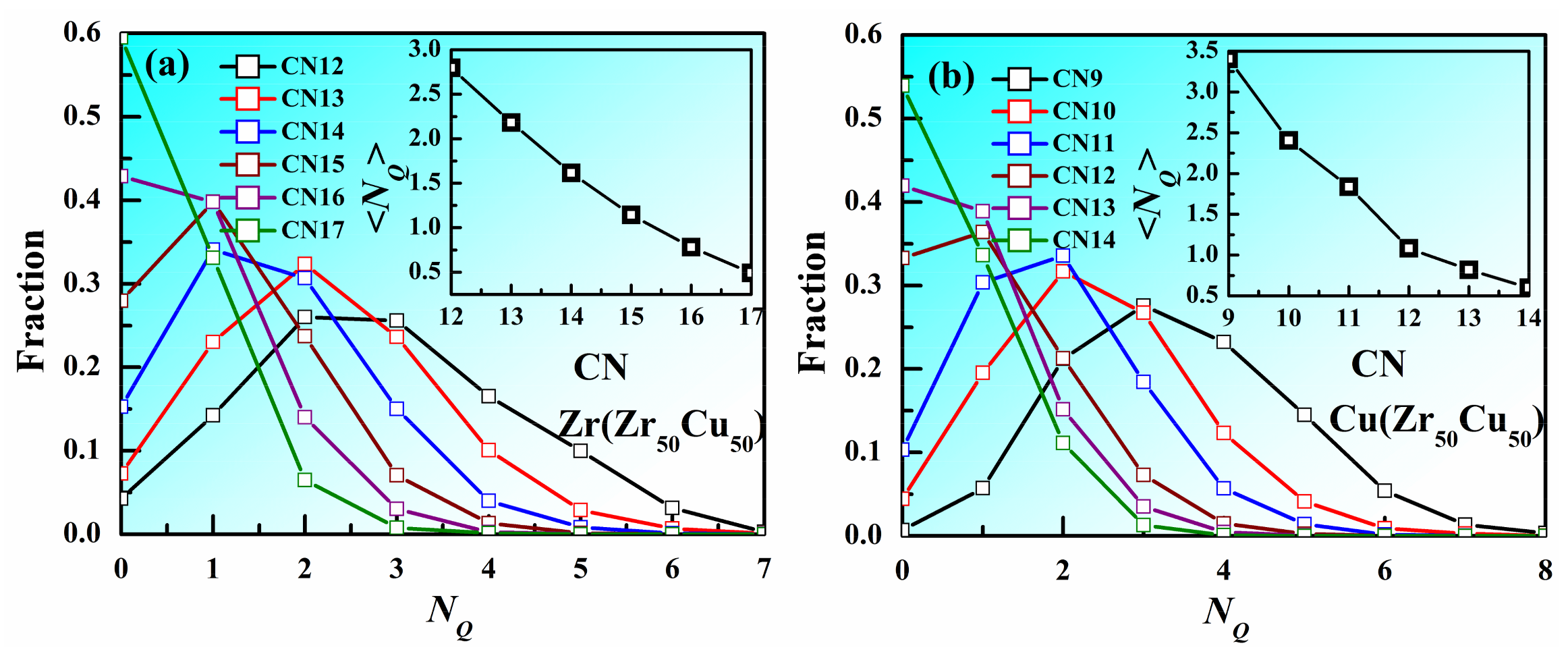
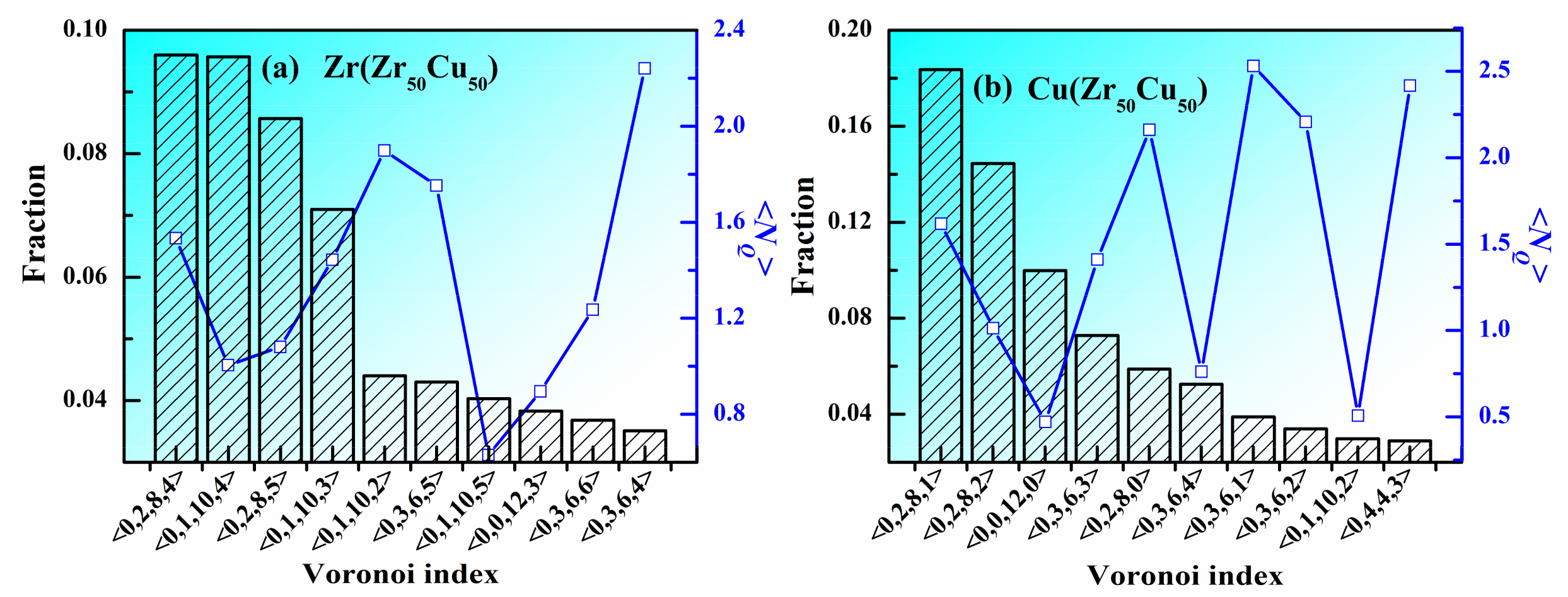
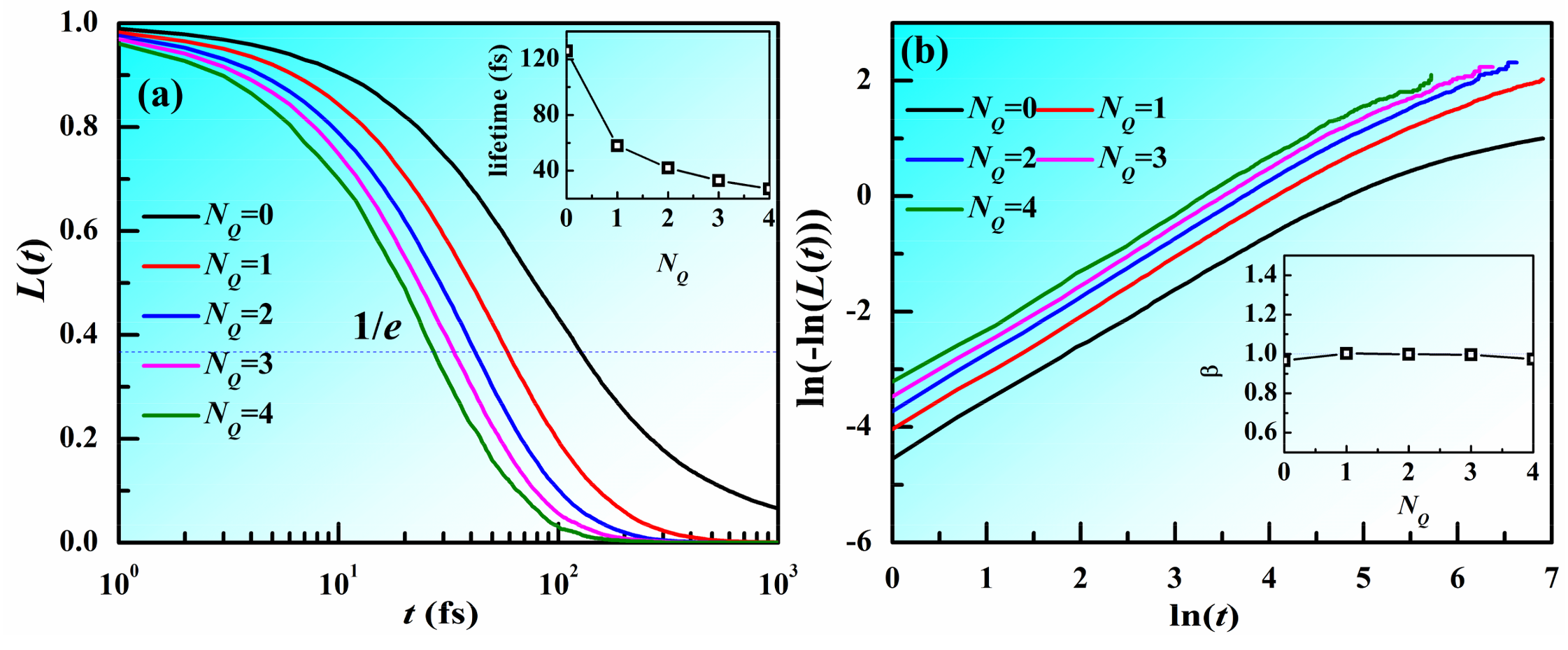
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hufnagel, T.C.; Schuh, C.A.; Falk, M.L. Deformation of metallic glasses: Recent developments in theory, simulations, and experiments. Acta Mater. 2016, 109, 375–393. [Google Scholar] [CrossRef]
- Chen, T.-H.; Tsai, C.-K. The microstructural evolution and mechanical properties of Zr-based metallic glass under different strain rate compressions. Material 2015, 8, 1831–1840. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Q.; Ma, E. Atomic-level structure and structure-property relationship in metallic glasses. Prog. Mater. Sci. 2011, 56, 379–473. [Google Scholar] [CrossRef]
- Wang, W.H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 2012, 57, 487–656. [Google Scholar] [CrossRef]
- Ghidelli, M.; Gravier, S.; Blandin, J.J.; Djemia, P.; Mompiou, F.; Abadias, G.; Raskin, J.P.; Pardoen, T. Extrinsic mechanical size effects in thin ZrNi metallic glass films. Acta Mater. 2015, 90, 232–241. [Google Scholar] [CrossRef]
- Ghidelli, M.; Idrissi, H.; Gravier, S.; Blandin, J.-J.; Raskin, J.-P.; Schryvers, D.; Pardoen, T. Homogeneous flow and size dependent mechanical behavior in highly ductile Zr65Ni35 metallic glass films. Acta Mater. 2017, 131, 246–259. [Google Scholar] [CrossRef]
- Cheng, Y.; Peng, C.; Zhang, Z.; Wang, P.; Yuan, S.; Wang, L. Plastic deformation of pressured metallic glass. Materials 2017, 10, 1361. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.L.; Li, M.Z.; Wang, W.H. Structural signature of plastic deformation in metallic glasses. Phys. Rev. Lett. 2011, 106, 135503. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.J.; Xu, Y.; Hui, X.; Lu, Z.P.; Li, F.; Chen, G.L.; Lu, J.; Liu, C.T. Metallic liquids and glasses: Atomic order and global packing. Phys. Rev. Lett. 2010, 105, 155501. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Lu, J.; Liu, C.; Wang, Q.; Yang, Y. Atomistic free-volume zones and inelastic deformation of metallic glasses. Nat. Mater. 2010, 9, 619–623. [Google Scholar] [CrossRef] [PubMed]
- Nagel, C.; Rätzke, K.; Schmidtke, E.; Wolff, J.; Geyer, U.; Faupel, F. Free-volume changes in the bulk metallic glass Zr46.7Ti8.3Cu7.5Ni10Be27.5 and the undercooled liquid. Phys. Rev. B 1998, 57, 10224. [Google Scholar] [CrossRef]
- Chen, L.Y.; Setyawan, A.D.; Kato, H.; Inoue, A.; Zhang, G.Q.; Saida, J.; Wang, X.D.; Cao, Q.P.; Jiang, J.Z. Free-volume-induced enhancement of plasticity in a monolithic bulk metallic glass at room temperature. Scr. Mater. 2008, 59, 75–78. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Xu, J. Free volume gradient effect on mechanical properties of metallic glasses. Scr. Mater. 2017, 130, 12–16. [Google Scholar] [CrossRef]
- Ding, J.; Patinet, S.; Falk, M.L.; Cheng, Y.; Ma, E. Soft spots and their structural signature in a metallic glass. Proc. Natl. Acad. Sci. USA 2014, 111, 14052–14056. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.L.; Li, M.Z.; Wang, W.H.; Wang, C.Z.; Ho, K.M. Effect of local structures and atomic packing on glass forming ability in CuxZr100−x metallic glasses. Appl. Phys. Lett. 2010, 96, 021901. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, B.; Bai, H.; Wang, W. Evolution of hidden localized flow during glass-to-liquid transition in metallic glass. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.H. Correlation between relaxations and plastic deformation, and elastic model of flow in metallic glasses and glass-forming liquids. J. Appl. Phys. 2011, 110, 053521. [Google Scholar]
- Pan, S.P.; Feng, S.D.; Qiao, J.W.; Wang, W.M.; Qin, J.Y. Correlation between local structure and dynamic heterogeneity in a metallic glass-forming liquid. J. Alloys Compd. 2016, 664, 65–70. [Google Scholar] [CrossRef]
- Pan, S.P.; Feng, S.D.; Wang, L.M.; Qiao, J.W.; Niu, X.F.; Dong, B.S.; Wang, W.M.; Qin, J.Y. Structural disorder in metallic glass-forming liquids. Sci. Rep. 2016, 6, 27708. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Feng, S.; Qiao, J.; Niu, X.; Wang, W.; Qin, J. Correlation between initial structure and athermal quasi-static compressive deformation in a metallic glass. J. Alloys Compd. 2017, 699, 274–277. [Google Scholar] [CrossRef]
- Feng, S.D.; Chan, K.C.; Chen, S.H.; Zhao, L.; Liu, R.P. The role of configurational disorder on plastic and dynamic deformation in Cu64Zr36 metallic glasses: A molecular dynamics analysis. Sci. Rep. 2017, 7, 40969. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Q.; Ma, E.; Sheng, H.W. Atomic level structure in multicomponent bulk metallic glass. Phys. Rev. Lett. 2009, 102, 245501. [Google Scholar] [CrossRef] [PubMed]
- Medvedev, N. The algorithm for three-dimensional Voronoi polyhedra. J. Comput. Phys. 1986, 67, 223–229. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, X.; Feng, S.; Pan, S. Related Structure Characters and Stability of Structural Defects in a Metallic Glass. Materials 2018, 11, 468. https://doi.org/10.3390/ma11040468
Niu X, Feng S, Pan S. Related Structure Characters and Stability of Structural Defects in a Metallic Glass. Materials. 2018; 11(4):468. https://doi.org/10.3390/ma11040468
Chicago/Turabian StyleNiu, Xiaofeng, Shidong Feng, and Shaopeng Pan. 2018. "Related Structure Characters and Stability of Structural Defects in a Metallic Glass" Materials 11, no. 4: 468. https://doi.org/10.3390/ma11040468
APA StyleNiu, X., Feng, S., & Pan, S. (2018). Related Structure Characters and Stability of Structural Defects in a Metallic Glass. Materials, 11(4), 468. https://doi.org/10.3390/ma11040468