Energy Absorption Capacity in Natural Fiber Reinforcement Composites Structures
Abstract
:1. Introduction
2. Materials and Specimens
3. Experimental Set-Up
3.1. Quasi-Static Testing
3.2. Dynamic Testing
3.3. Evaluation of Experiments
4. Results
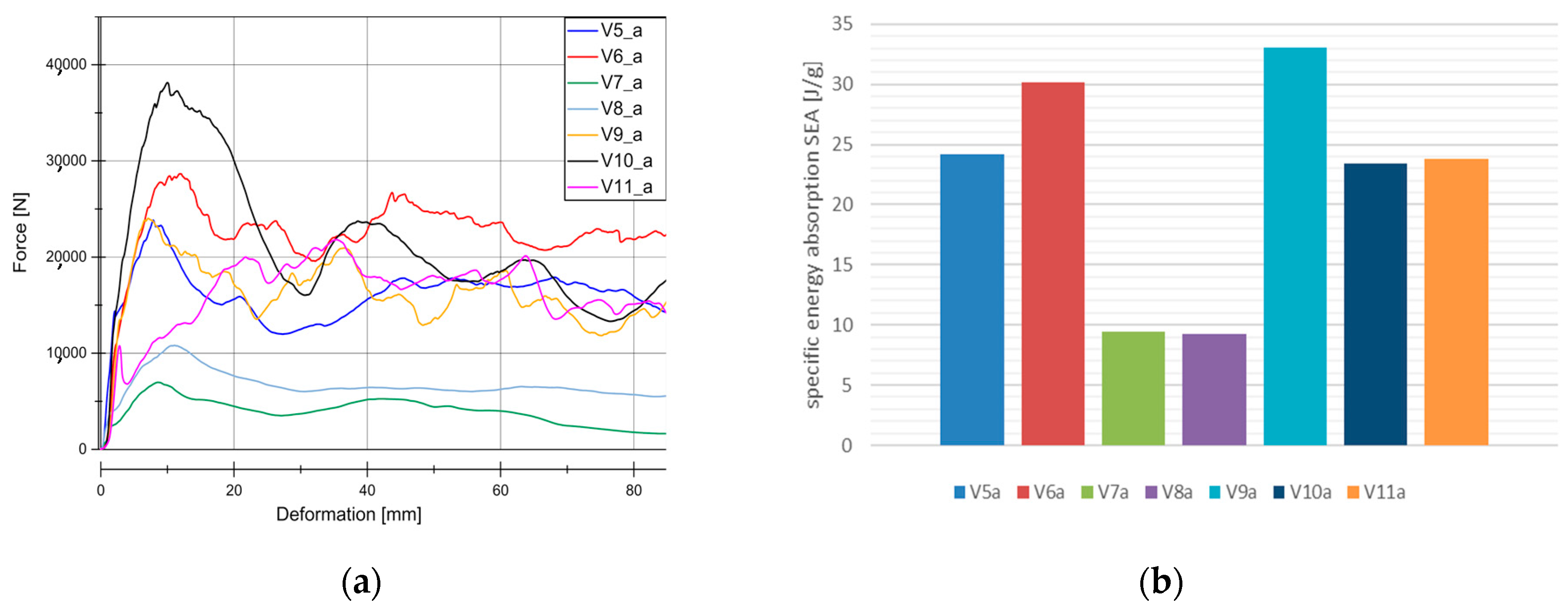
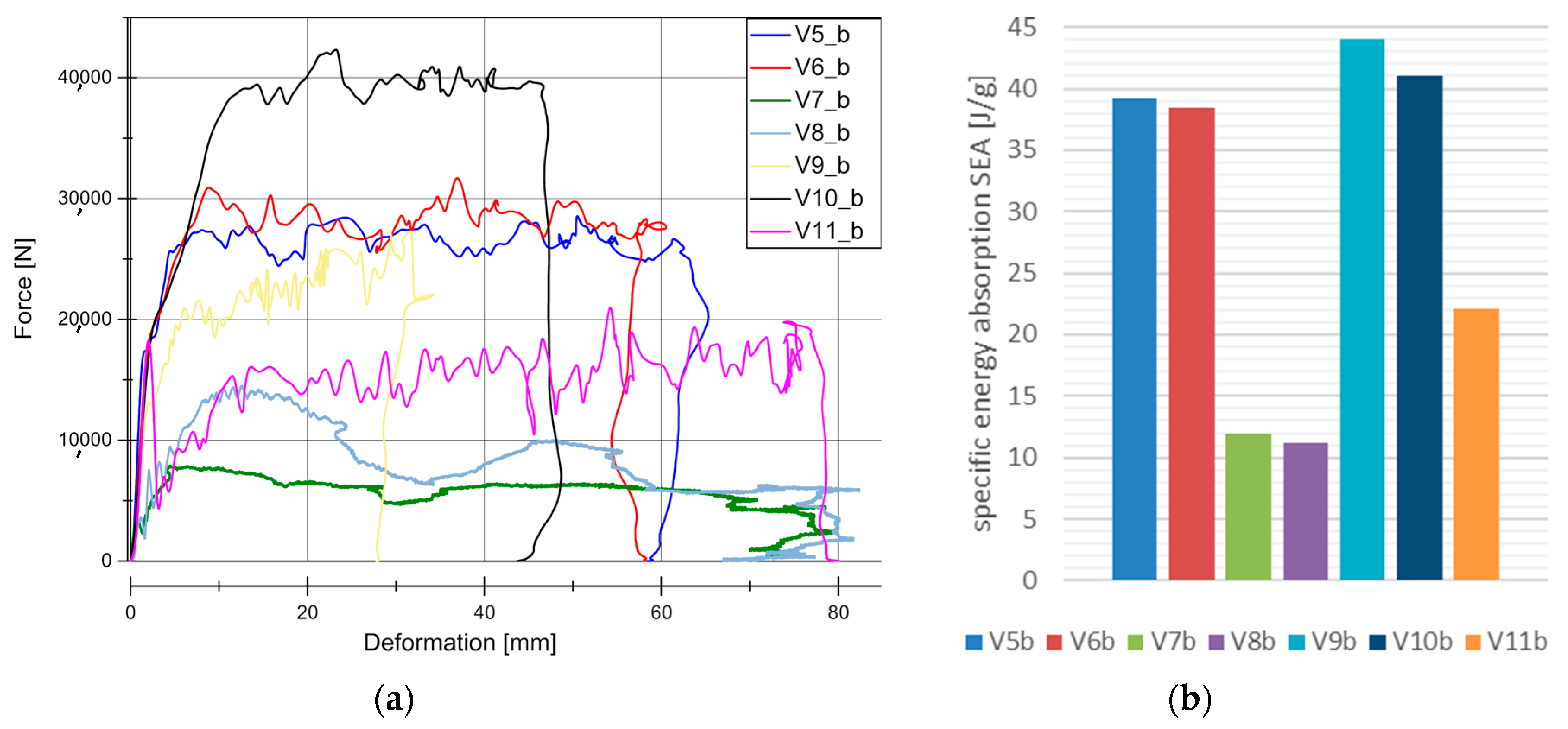
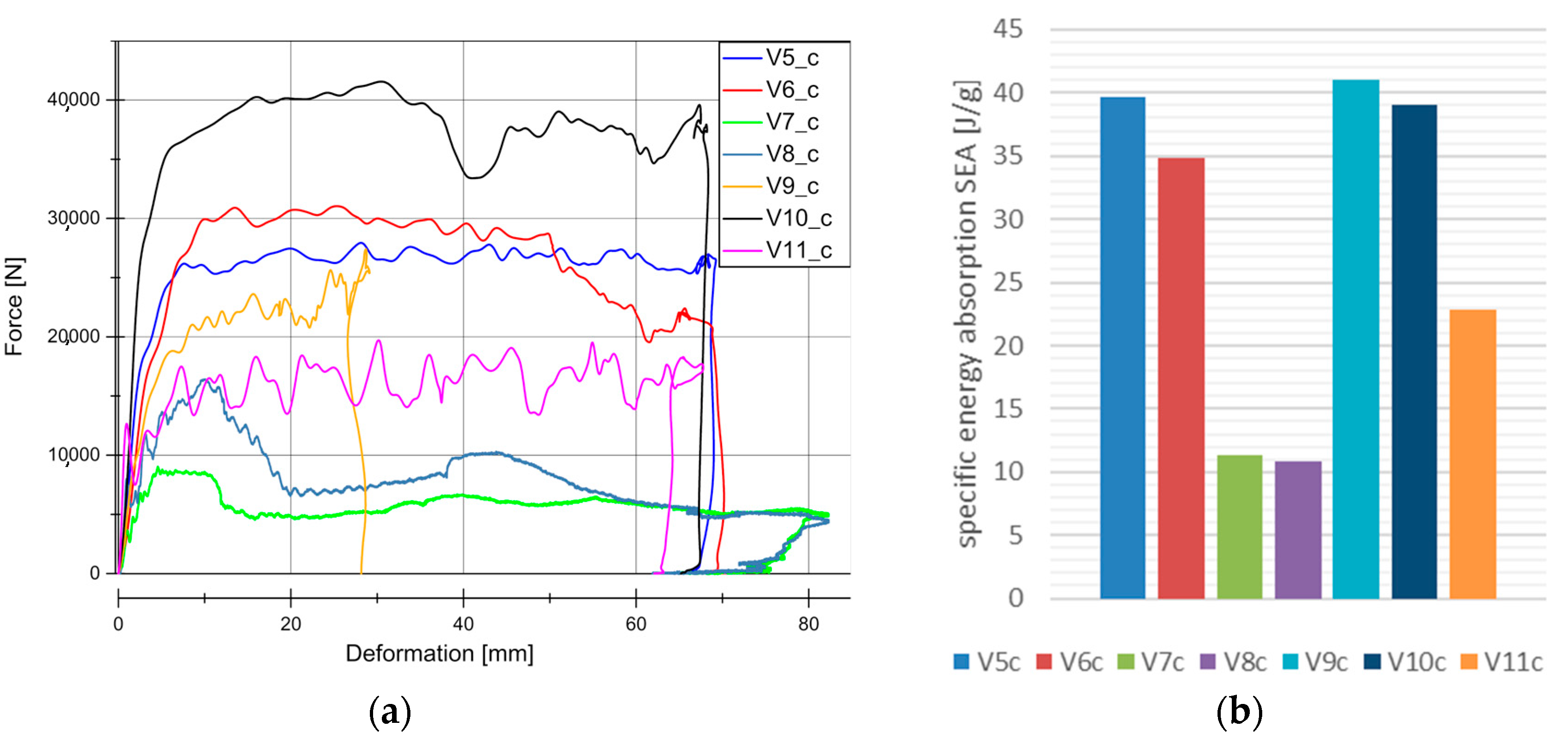
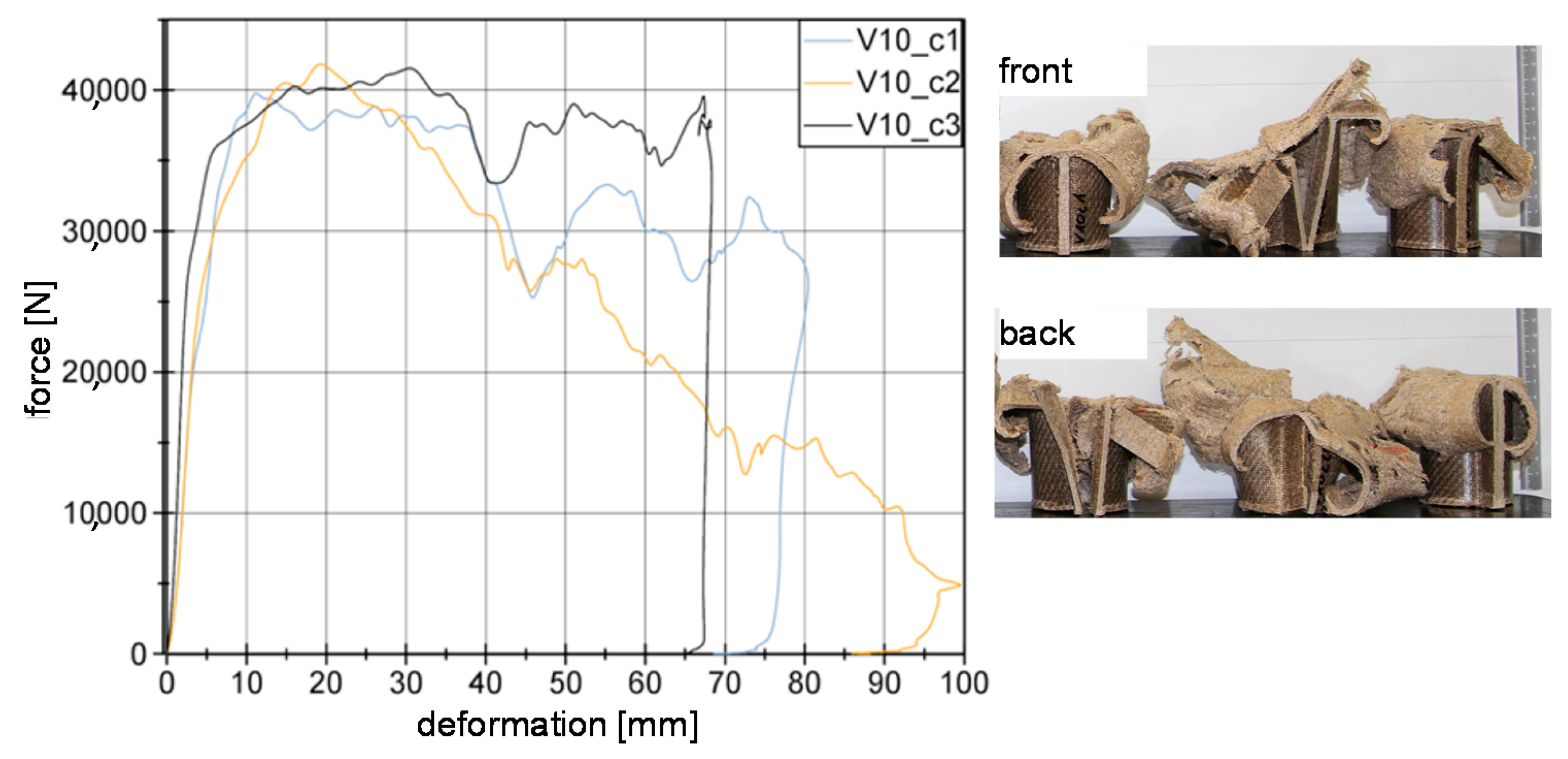
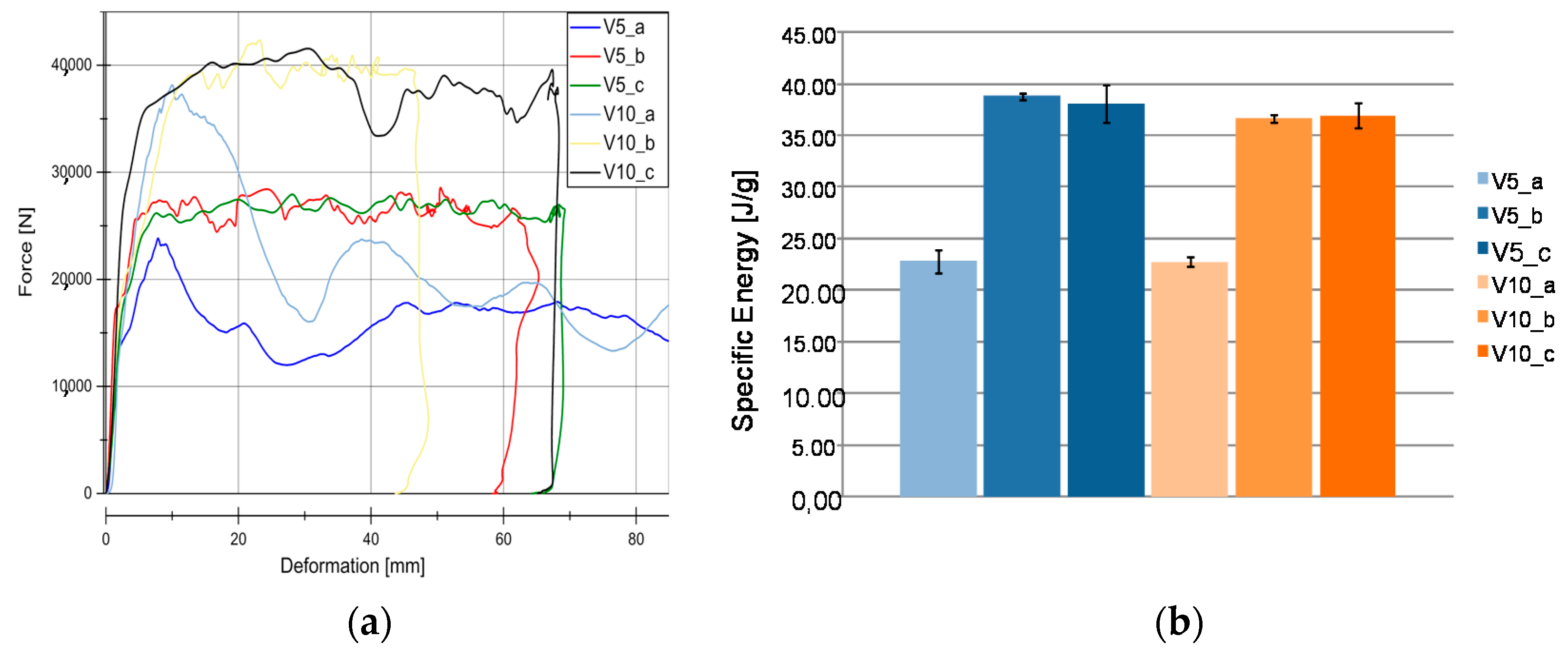
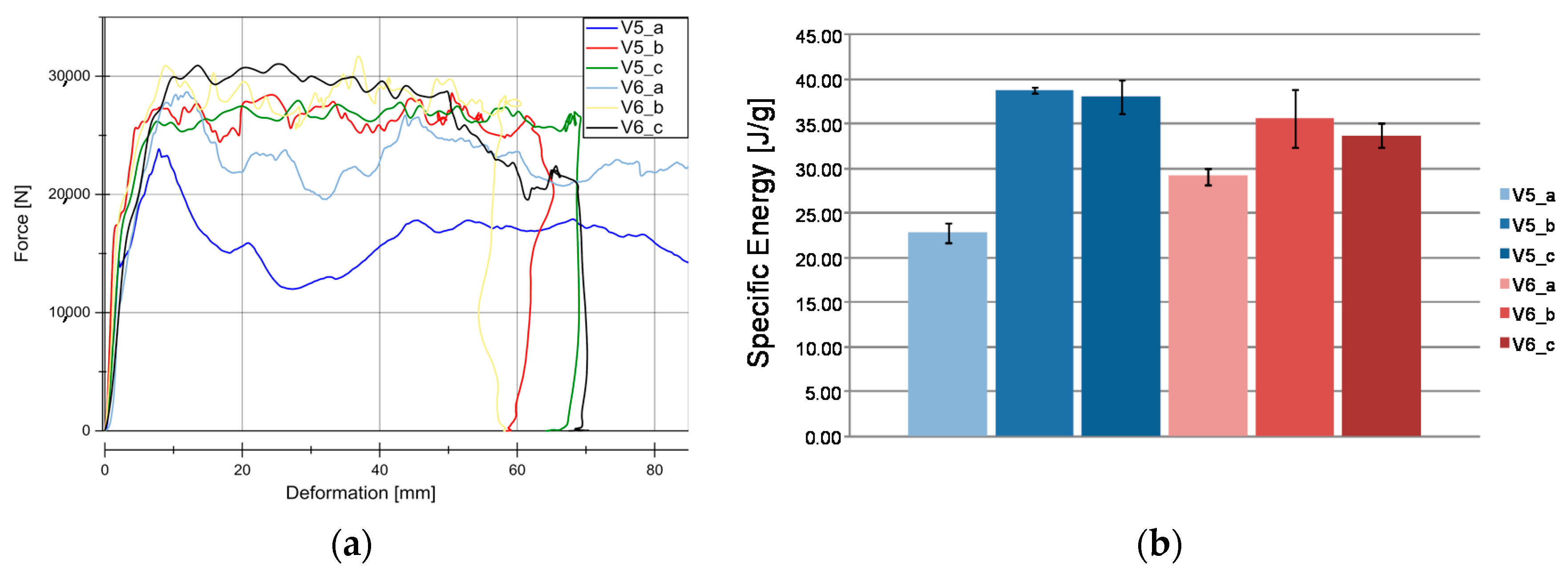
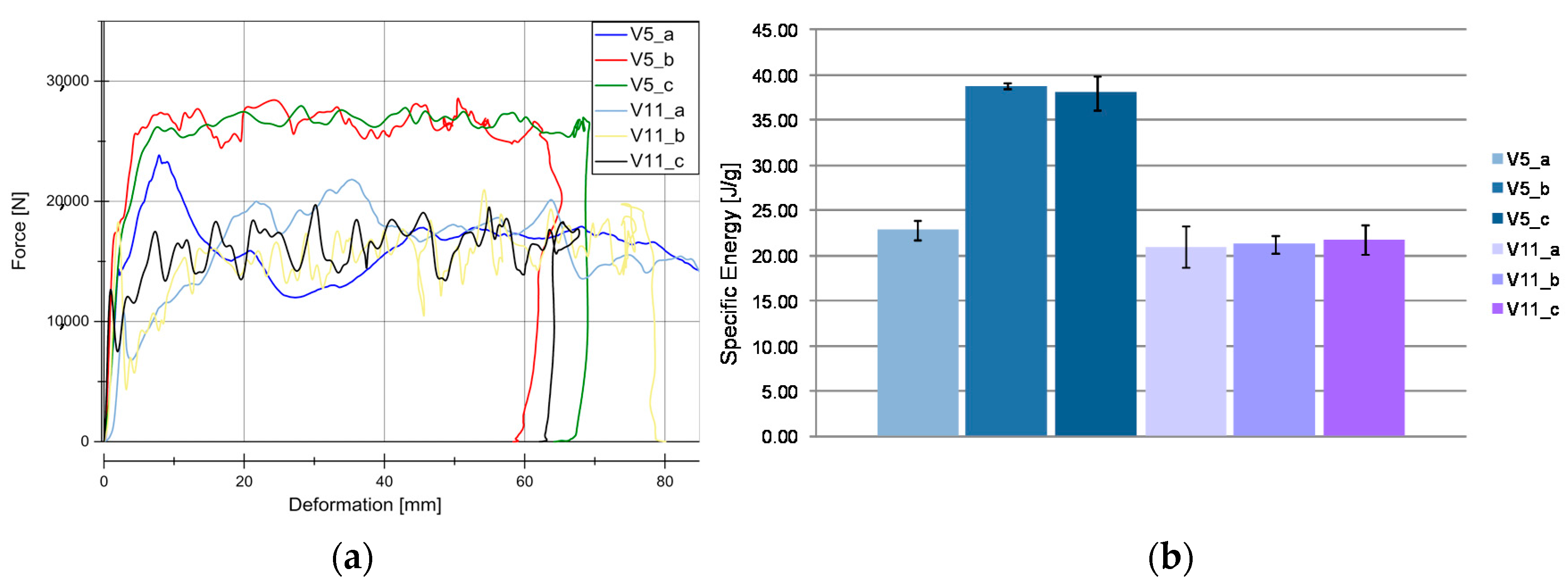
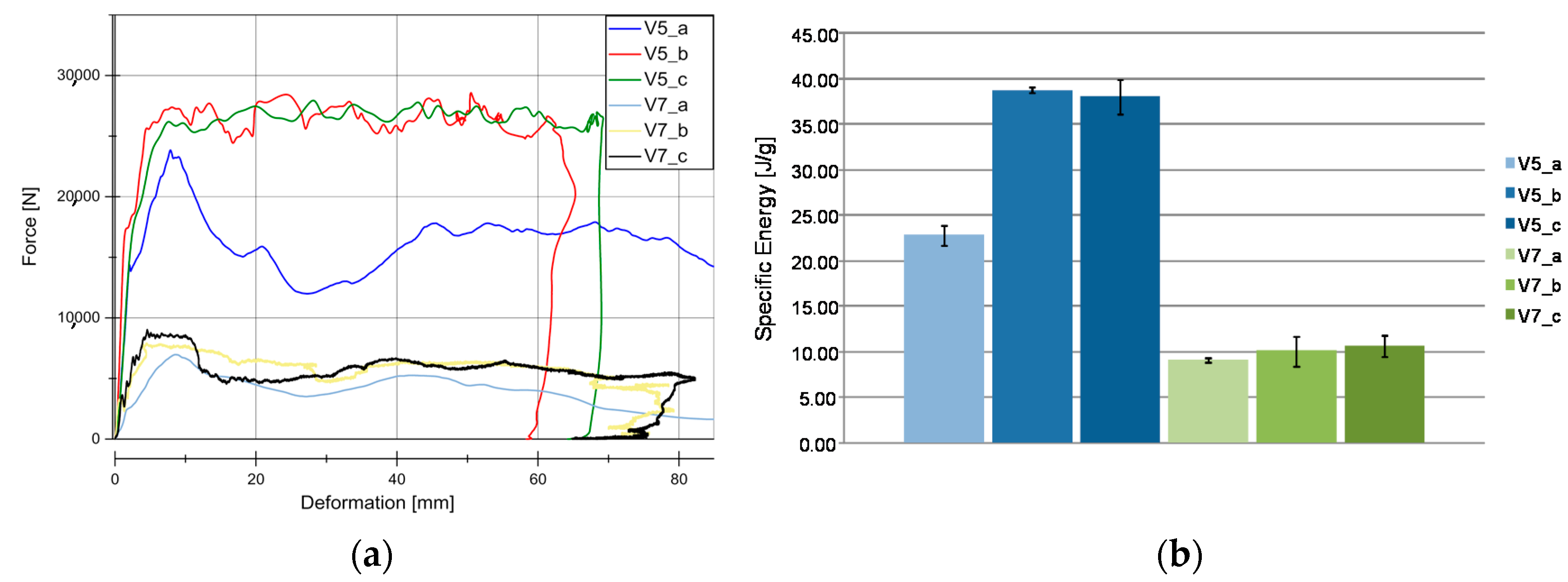
4.1. Quasi-Static Results
4.2. Dynamic Results
5. Discussion
5.1. Loading Rate Influence to Material Behaviour
5.2. Wall Thickness Influence to Material Behavior
5.3. Weave Configuration Influence to Material Behavior
5.4. Reinforcement Textile Material Influence in SEA Results
5.5. Matrix Type Influence in Material Behavior
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bek, M. Directive 2005/64/EC of the European Parliament and of the Council of 26 October 2005 on the Type-Approval of Motor Vehicles with Regard to their Reusability, Recyclability and Recoverability and Amending Council; Directive 70/156/EEC; OJ L 310; EU Publications: Luxembourg, 2005; pp. 10–27. [Google Scholar]
- Yan, L.; Chouw, N.; Jayaraman, K. Flax fibre and its composites—A review. Compos. Part B Eng. 2014, 56, 296–317. [Google Scholar] [CrossRef]
- Nassiopoulos, E.; Njuguna, J. Thermo-mechanical performance of poly(laxtic acid)/flax fibre-reinforced biocomposites. Mater. Des. 2015, 66, 473–485. [Google Scholar] [CrossRef]
- Garkhail, S.K.; Heimenrath, R.W.H.; Peijs, T. Mechanical properties of natural-fibremat-reinforced thermoplastics based on flax fibres and polypropylene. Appl. Compos. Mater. 2000, 7, 351–372. [Google Scholar] [CrossRef]
- Stevens, C.; Müssig, J. Industrial Applications of Natural Fibres: Structure, Properties and Technical Applications; Wiley: Chichester, UK, 2010; ISBN 978-0-470-69501-1. [Google Scholar]
- Lampke, T. Beitrag zur Charakterisierung Naturfaserverstärkter Verbundwerkstoffe mit Hochpolymerer Matrix. Lehrstuhl für Verbund werkstoffe. Ph.D. Thesis, IVW, Kaiserslautern, Germany, 23 October 2001. [Google Scholar]
- Yan, L.; Chouw, N. Crashworthiness characteristics of flax fiber reinforced epoxy tubes for energy absorption application. Mater. Des. 2013, 53, 629–640. [Google Scholar] [CrossRef]
- Wambua, P.; Ivens, J.; Verpoest, I. Natural fibres: Can they replace the glass in fiber reinforced plastics? Compos. Sci. Technol. 2003, 63, 1259–1264. [Google Scholar] [CrossRef]
- Rodriguez, E.; Petruci, R.; Puglia, D.; Kenny, J.M.; Zquez, A.V. Characterization of composites based on natural and glass fibers obtained by vacuum infusion. J. Compos. Mater. 2005, 39, 265–283. [Google Scholar] [CrossRef]
- Eshkoor, R.A.; Oshkovr, S.A.; Sulong, A.B.; Zulkifli, R.; Ariffin, A.K.; Azhari, C.H. Effect of trigger configuration on the crashworthiness characteristics of natural silk epoxy composite tubes. Compos. Part B Eng. 2013, 55, 5–10. [Google Scholar] [CrossRef]
- Ataollahi, S.; Taher, S.T.; Eshkoor, R.A.; Ariffin, A.K.; Azhari, C.H. Energy absorption and failure response of silk/epoxy composite square tubes: Experimental. Compos. Part B Eng. 2012, 43, 542–548. [Google Scholar] [CrossRef]
- Meredith, J.; Ebsworth, R.; Coles, S.R.; Wood, B.M.; Kirwan, K. Natural fibre composite energy absorption structures. Compos. Sci. Technol. 2012, 72, 211–217. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N.; Jayaraman, K. Effect of triggering and polyurethane foam-filler on axial crushing of natural flax/epoxy composite tubes. Mater. Des. 2014, 56, 528–541. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N.; Jayaraman, K. Lateral crushing of empty and polyurethane-foam filled natural flax fabric reinforced epoxy composite tubes. Compos. Part B Eng. 2014, 63, 15–26. [Google Scholar] [CrossRef]
- Yan, L.; Wang, B.; Kasal, B. Can Plant-Based Natural Flax replace Basalt and E-Glas for Fiber_Reinforced Polymer Tubular Energy Absorbers? A Comparative Study on Quasi-Static Axial Crushing. Front. Mater. 2017, 4, 42. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Gassan, J.; Zhang, W. Impact properties of natural fiber-reinforced expoxy foams. J. Cell. Plast. 1999, 33, 550–562. [Google Scholar] [CrossRef]
- Siengchin, S. Impact, thermal and mechanical properties of high density polyethylene/flax/SiO2 composites: Effect of flax reinforcing structures. J. Reinf. Plast. Compos. 2012, 31, 959–966. [Google Scholar] [CrossRef]
- Siengchin, S.; Pohl, T.; Medina, L.; Meitschang, P. Structure and properties of flax/poyactide/alumina nanocomposites. J. Reinf. Plast. Compos. 2013, 32, 23–33. [Google Scholar] [CrossRef]
- Liang, S.; Guillaumat, L.; Gnig, P.B. Impact behavior of flax/epoxy composite plates. Int. J. Impact. Eng. 2015, 80, 56–64. [Google Scholar] [CrossRef]
- Bax, B.; Müssig, J. Impact and tensile properties of PLA/Cordenka and PLA/flax composites. Comp. Sci. Technol. 2008, 68, 1601–1607. [Google Scholar] [CrossRef]
- Meredith, J.; Coles, S.R.; Powe, R.; Collings, E.; Cozien-Cazuc, S.; Weager, B.; Müssig, J.; Kirwan, K. On the static and dynamic properties of flax and Cordenka epoxy composites. Compos. Sci. Technol. 2013, 80, 31–38. [Google Scholar] [CrossRef]
- Neitzel, M.; Mitshang, P. Handbuch Verbundwerkstoffe; Carl Hanser Verlag: Berlin, Germany, 2004; ISBN 3-446-22041-0. [Google Scholar]
- Dehn, A. Experimentelle Untersuchung und Numerische Simulation des Crashverhaltens Gewebeverstärkter Thermoplaste unter Temperatureinfluss. Ph.D. Thesis, IVW, Kaiserslautern, Germany, 1 November 2001. [Google Scholar]
- Farley, G.L.; Jones, R.M. Crushing Characteristics of Continuous Fiber Reinforced Composites Tubes. J. Compos. Mater. 1992, 26, 37–50. [Google Scholar] [CrossRef]
- Farley, G.L. Effect of Specimen Geometry on the Energy Absorption Capability of Composite Materials. J. Compos. Mater. 1886, 20, 390–400. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Hamada, H. Energy Absorption Characteristic of Crash Worthy Structural Composite Materials. Key Eng. Mater. 1998, 141–143, 585–620. [Google Scholar] [CrossRef]

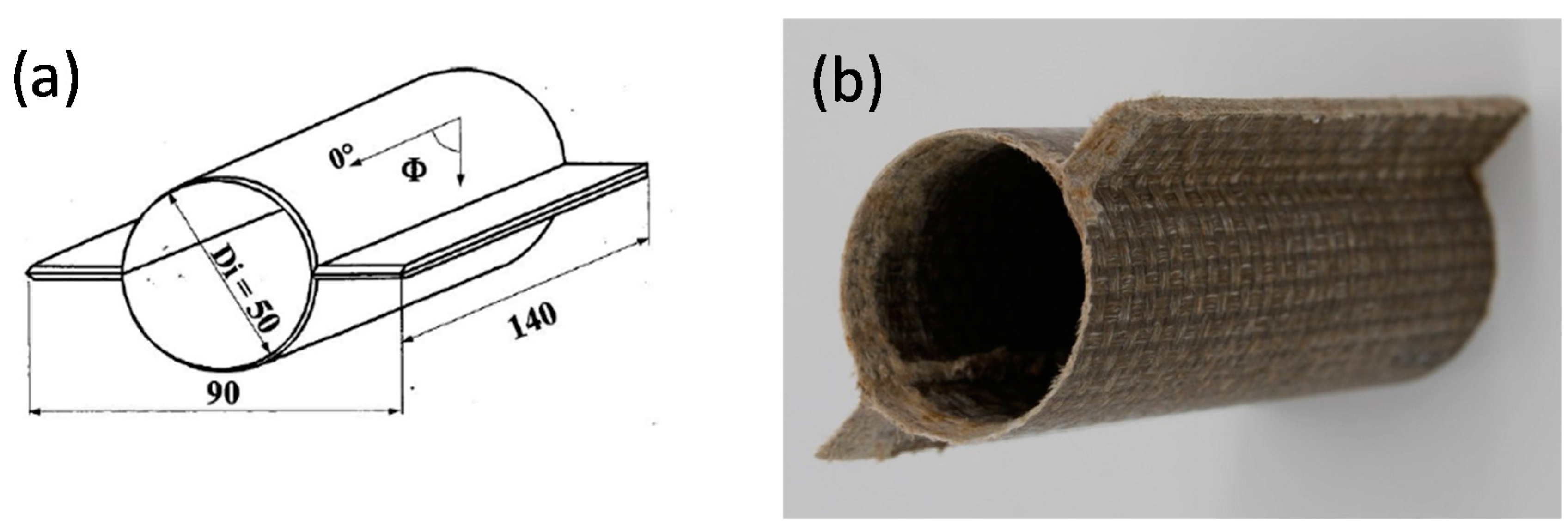










| Material Composition | Thickness (m) | Vf (–) | Area Density (g/mm2) | Modulus of Elasticity (N/mm2) | Ultimate Tensile Strength (N/mm2) | Ultimate Elongation (%) | |
|---|---|---|---|---|---|---|---|
| V5 | 4 Twill + 5 PLA | 2.4 | 0.5 | 3027.2 | 8711.4 +/− 278.8 | 73.8 +/− 2.2 | 1.66 +/− 0.13 |
| V6 | 4 Hopsack + 5 PLA | 2.7 | 0.54 | 3481.0 | 10289.0 +/− 206.8 | 88.5 +/− 2.5 | 1.63 +/− 0.10 |
| V7 | 4 Twill + 5 HD-PE | 2.2 | 0.55 | 2382.3 | 4348.8 +/− 58.9 | 58.9 +/− 1.3 | 3.06 +/− 0.25 |
| V8 | 6 Twill + 7 HD-PE | 3.15 | 0.57 | 3457.8 | 4554.1 +/− 350.9 | 61.7 +/− 0.9 | 3.12 +/− 0.34 |
| V9 | 2 comingled Hopsack/PLA | 1.75 | - | 2248.8 | 7329.5 +/− 214.4 | 37.2 +/− 3.9 | 0.83 +/− 0.19 |
| V10 | 6 Twill + 7 PLA | 3.5 | 0.51 | 4379.8 | 9278.8 +/− 298.7 | 83.4 +/− 2.3 | 1.59 +/− 0.22 |
| V11 | 1 Vlies + 7 PLA | 2.95 | 0.28 | 3333.9 | - | - | - |
| PLA | - | - | 0 | 309.6 | 3223.0 +/− 136.2 | 49.3 +/− 2.1 | 1.8 +/− 0.03 |
| HDPE | - | - | 0 | 188.3 | 943.5 +/− 15.5 | 21.1 +/− 0.3 | 10.13 +/− 0.29 |
| Synthetic Material | Density (g/cm3) | E-Modulus (GPa) | Tensile Strength (MPa) | Breakage Strain (%) | Tg (°C) | Ts (°C) | Typ |
|---|---|---|---|---|---|---|---|
| HD-PE | 0.95–0.97 | 0.55–1.1 | 20–37 | 10–1200 | −3 | 117 | TP |
| PP | 0.9–0.91 | 1.2–1.7 | 30–70 | 10–600 | −20 | −28 | TP |
| PVC | 1.3–1.6 | 2.4–4.1 | 40–60 | 40–80 | 77 | 157 | TP |
| Polyester | 1.1–1.4 | 1.3–4.5 | 45–85 | 1–5 | 67 | - | TS |
| Epoxid | 1.2–1.4 | 2.1–4.5 | 40–85 | 2–7 | 107 | - | TS |
| PLA | 1.21 | 3.3 | 30 | 2.5 | 37–67 | 127–177 | TP Bio |
| PHB | 1.18 | 3.5 | 40 | 5–8 | 2 | 137–177 | TP Bio |
| Material | Mean Mass (g) | St dev. |
|---|---|---|
| V5 | 91.3 | 1.6 |
| V6 | 104.5 | 0.9 |
| V7 | 72.1 | 0.8 |
| V8 | 107.0 | 0.9 |
| V9 | 68.4 | 0.6 |
| V10 | 131.7 | 1.6 |
| V11 | 96.2 | 1.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Alba, E.; Schmeer, S.; Díaz, F. Energy Absorption Capacity in Natural Fiber Reinforcement Composites Structures. Materials 2018, 11, 418. https://doi.org/10.3390/ma11030418
López-Alba E, Schmeer S, Díaz F. Energy Absorption Capacity in Natural Fiber Reinforcement Composites Structures. Materials. 2018; 11(3):418. https://doi.org/10.3390/ma11030418
Chicago/Turabian StyleLópez-Alba, Elías, Sebastian Schmeer, and Francisco Díaz. 2018. "Energy Absorption Capacity in Natural Fiber Reinforcement Composites Structures" Materials 11, no. 3: 418. https://doi.org/10.3390/ma11030418
APA StyleLópez-Alba, E., Schmeer, S., & Díaz, F. (2018). Energy Absorption Capacity in Natural Fiber Reinforcement Composites Structures. Materials, 11(3), 418. https://doi.org/10.3390/ma11030418







