Preparation and Dielectric Properties of SiC/LSR Nanocomposites for Insulation of High Voltage Direct Current Cable Accessories
Abstract
:1. Introduction
2. Materials and Methods
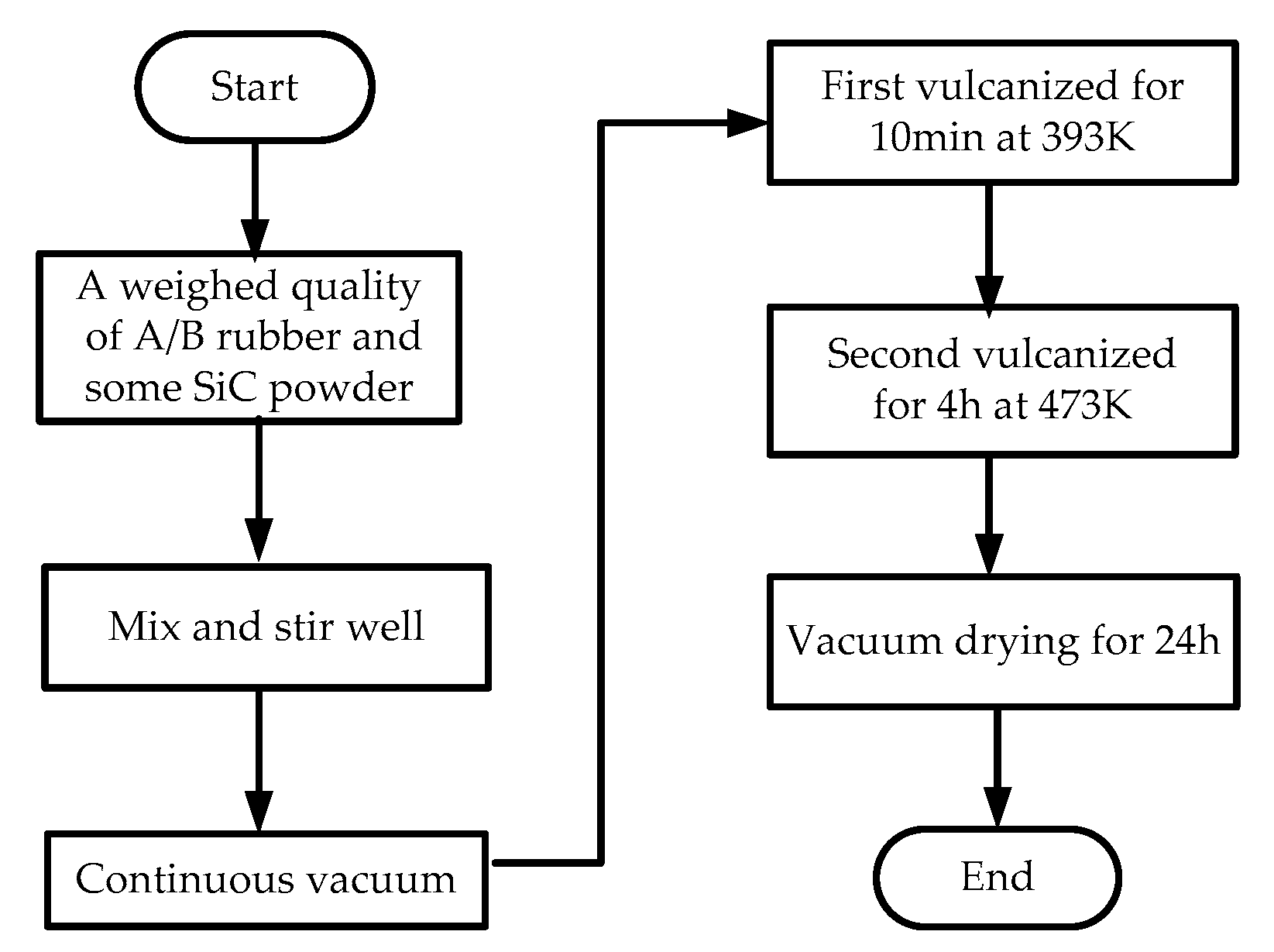
2.1. Sample Preparation
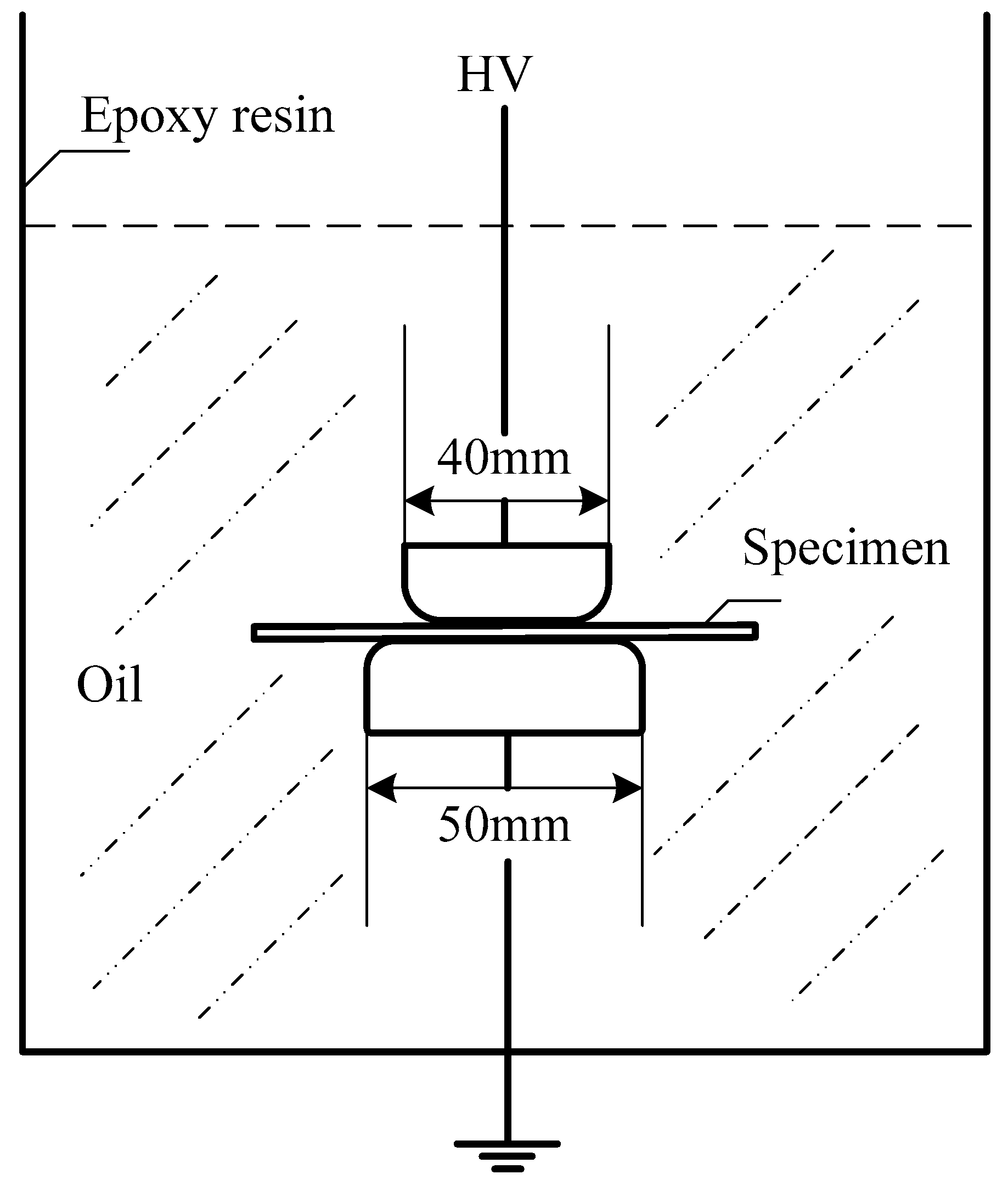
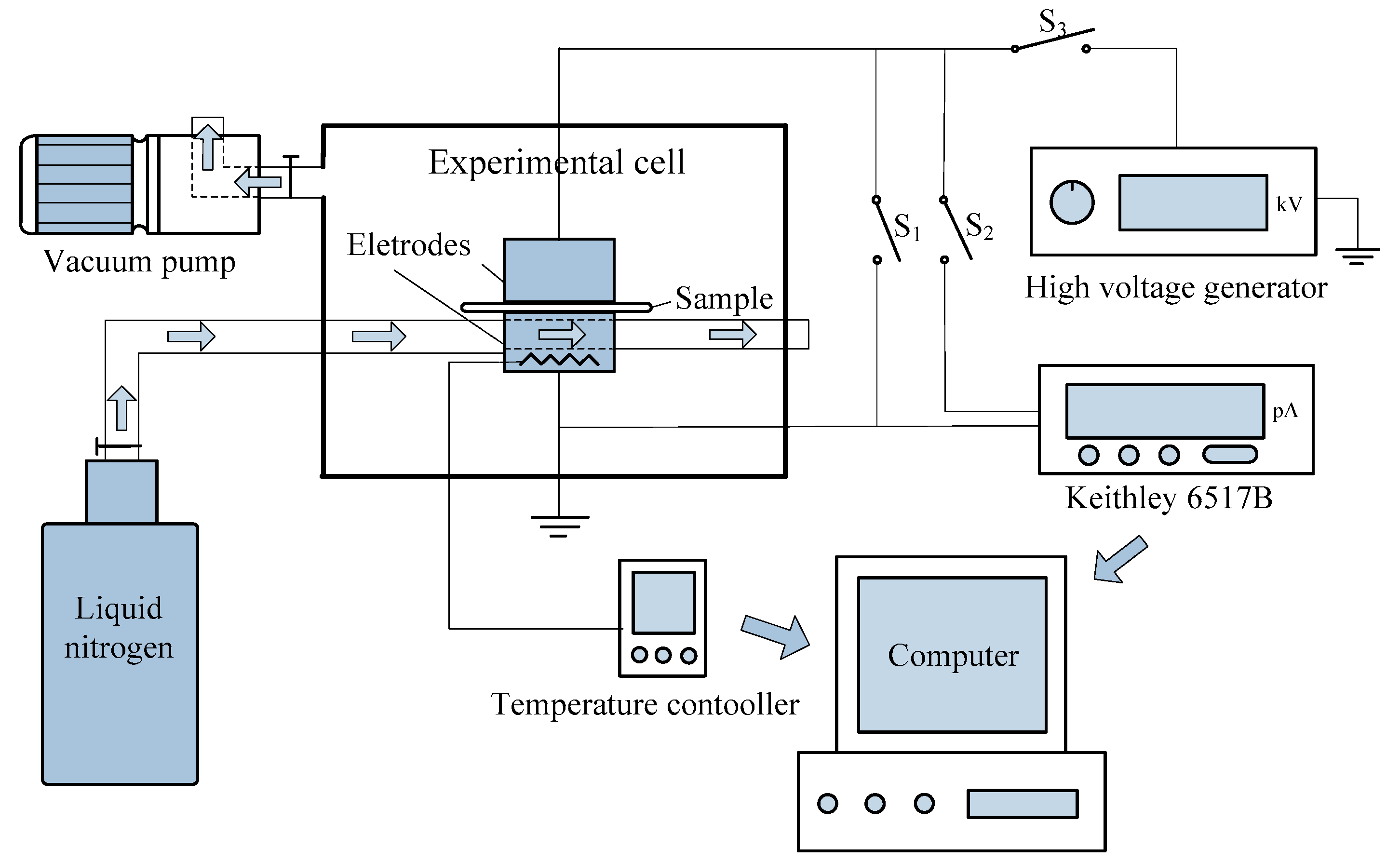
2.2. Dielectric Properties
3. Results and Discussion
3.1. Microstructure
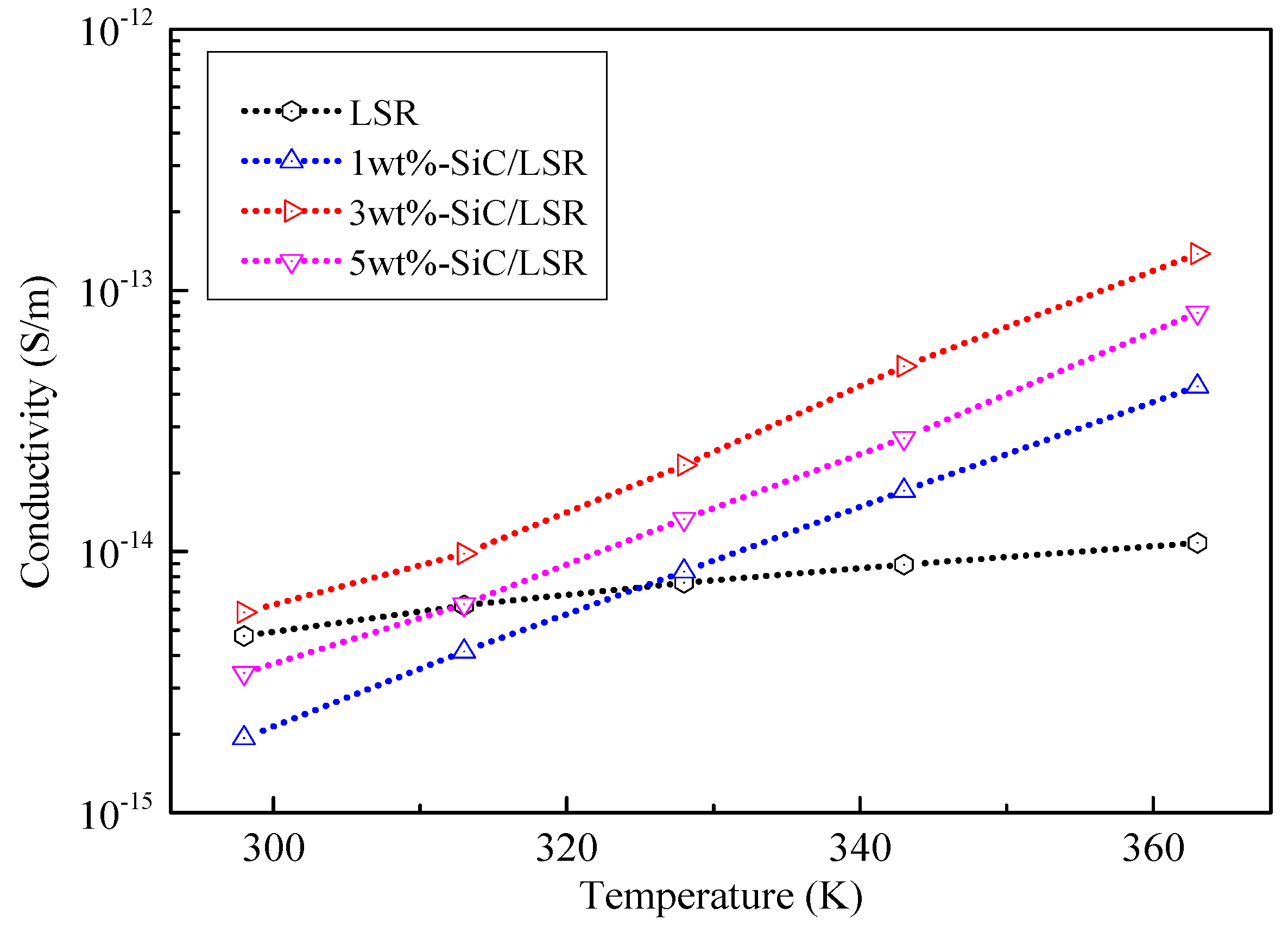
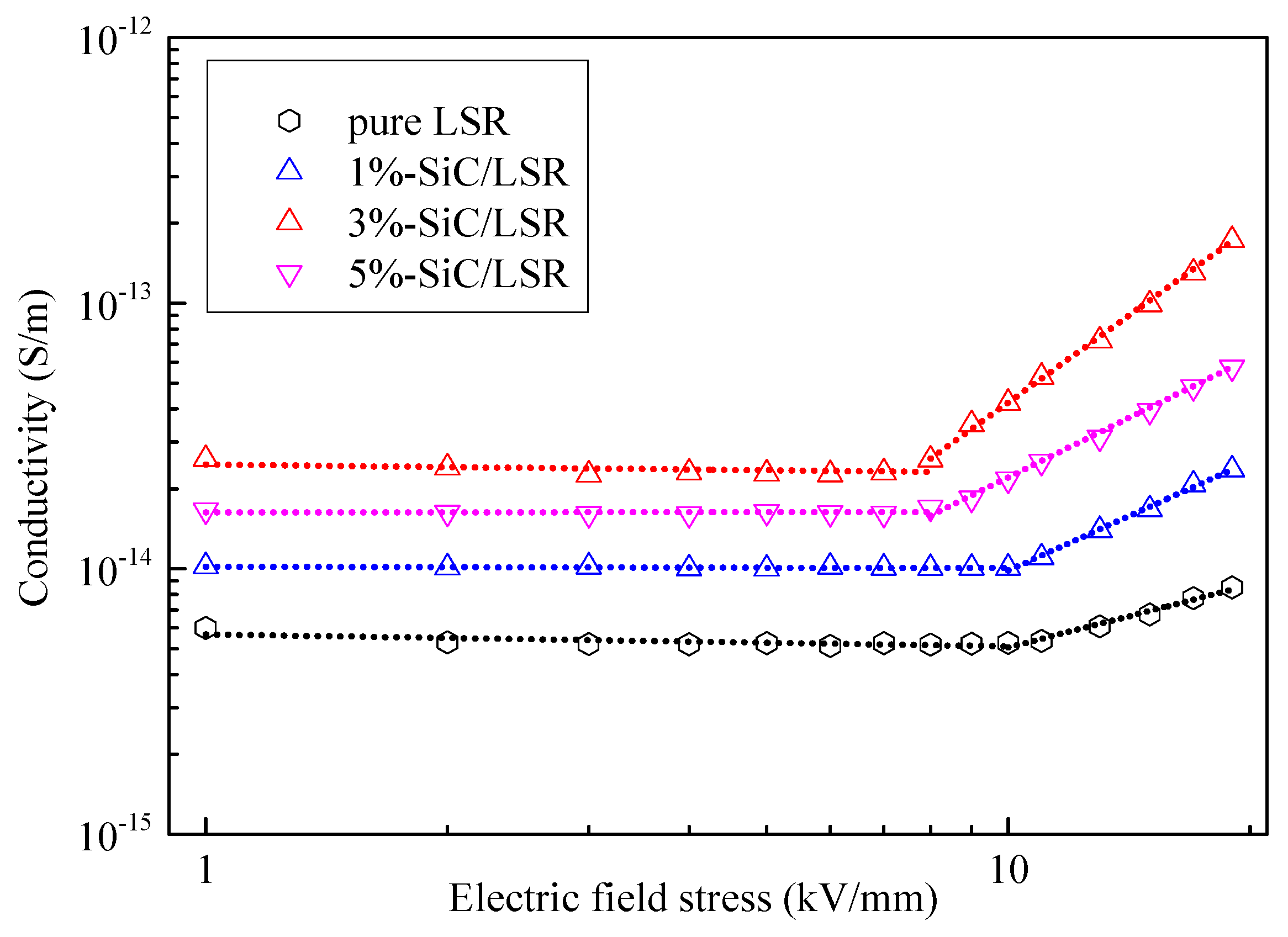
3.2. Conductivity
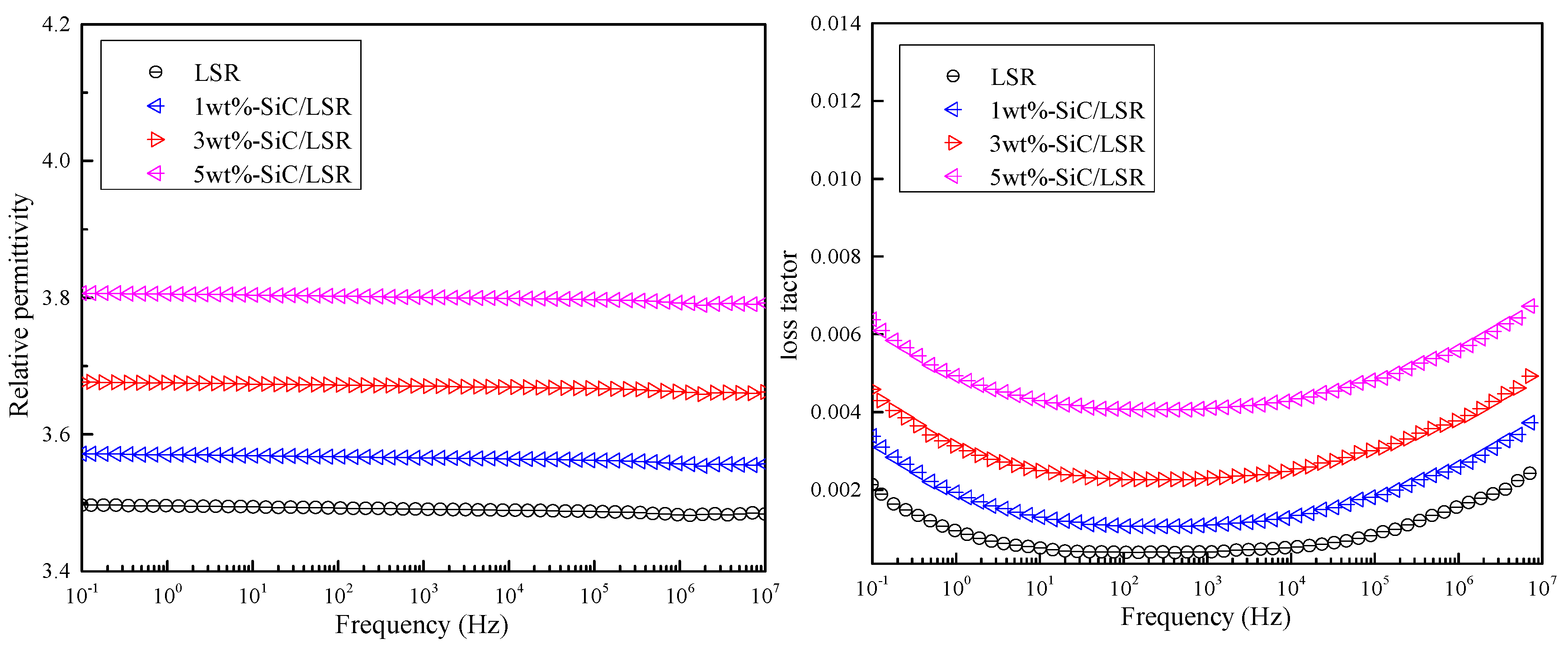
3.3. Relative Permittivity and Dielectric Loss Factor
3.4. DC Breakdown Strength
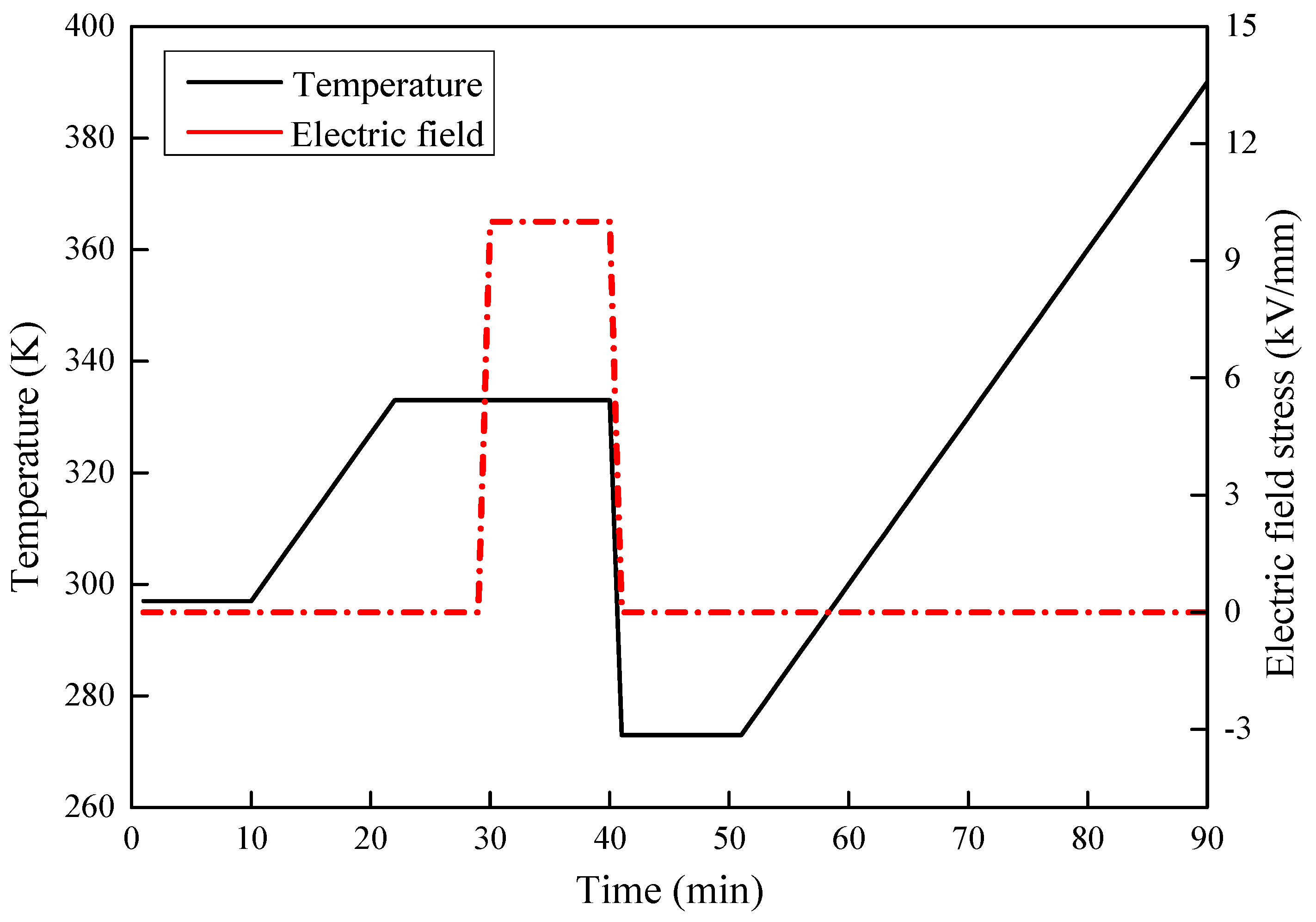
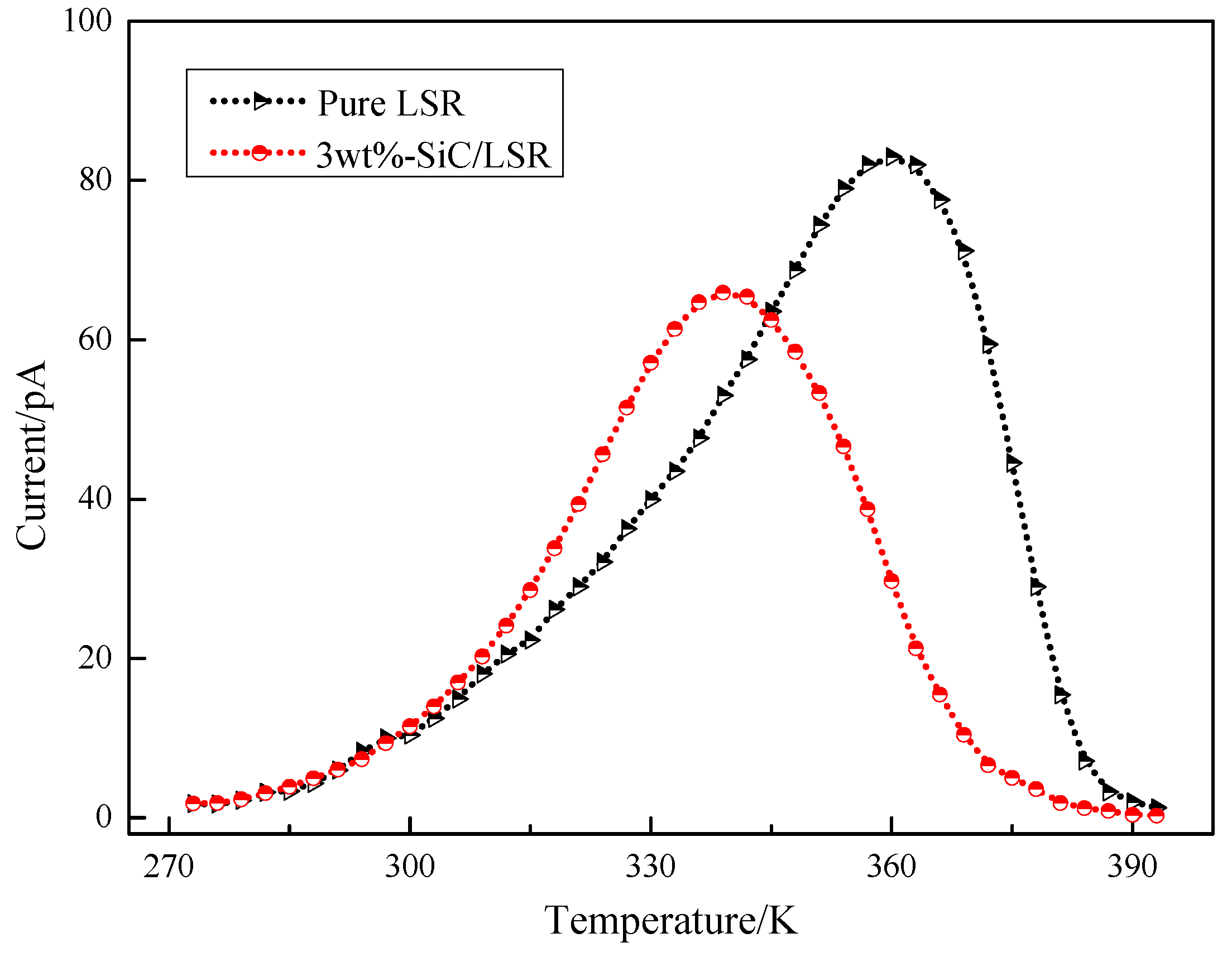
3.5. TSC
4. Conclusions
- (1)
- SiC nanoparticles doping decreases the breakdown strength of LSR, greatly increases its conductivity, and increases its relative permittivity and dielectric loss factor.
- (2)
- SiC/LSR nanocomposites have better nonlinear conductivity characteristics than pure LSR, as their temperature coefficient and nonlinear coefficients are greatly improved, which in turn makes the distribution of the electric field more uniform in HVDC cable accessories.
- (3)
- The introduction of SiC nanoparticles leads to the decrease in the trap level and trap charge of LSR, which affects the transport of carriers in the polymers. The TSC test verifies that the trap parameters have an important effect on the macroscopic dielectric properties of the polymer.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- He, J.L.; Peng, L.; Zhou, Y. Research progress of environment friendly HVDC power cable insulation materials. High Volt. Eng. 2017, 43, 337–343. [Google Scholar]
- Zhang, C.; Zha, J.W.; Wang, S.J.; Wu, Y.H.; Yan, H.D.; Li, W.K.; Chen, X.; Dang, Z.M. Development and outlook of insulating materials for high voltage direct current cables. Insul. Mater. 2016, 49, 1–9. [Google Scholar]
- Wen, J.L.; Wu, R.; Peng, C.; Wang, Y. Analysis of DC grid prospects in China. Proc. CSEE 2012, 32, 7–12. [Google Scholar]
- Chen, N.G.; Hao, M.; Xu, Z.; Vaughan, A.; Cao, J.; Wang, H. Review of high voltage direct current cables. CSEE J. Power Energy Syst. 2015, 1, 9–21. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.X.; Fan, N.Y.; Chen, H. Preparation and properties of Al2O3 nanosheets/epoxy composites. Acta Mater. Compos. Sin. 2014, 31, 1142–1147. [Google Scholar]
- Zhou, Y.X.; Zhao, J.K.; Liu, R.; Chen, Z.Z.; Zhang, Y.X. Key Technical Analysis and Prospect of High Voltage and Extra-high Voltage Power Cable. High Volt. Eng. 2014, 40, 2593–2612. [Google Scholar]
- Meyer, L.; Jayaram, S.; Chereny, E.A. Thermal conductivity of filled silicone rubber and its relationship to erosion resistance in the inclined plane test. IEEE. Trans. Dielectr. Electr. Insul. 2004, 11, 620–630. [Google Scholar] [CrossRef]
- Samuel, A.; Frank, S.; Konstantin, O. Improved silicone rubber for the use as housing material in composite insulators. IEEE. Trans. Dielectr. Electr. Insul. 2012, 11, 209–217. [Google Scholar]
- Yang, J.M.; Wang, X.; Han, B.Z.; Zhao, H.; Xu, M.Z. DC conductivity characteristic of LDPE nanocomposite and its effect on electric field distribution in HVDC cables. Proc. CSEE 2014, 9, 1454–1461. [Google Scholar]
- Wang, X.; Nelson, J.K.; Schadler, L.S.; Hillborg, H. Mechanism leading to nonlinear electrical response of a nano p-SiC/Silicone rubber composite. IEEE. Trans. Dielectr. Electr. Insul. 2010, 17, 1687–1696. [Google Scholar] [CrossRef]
- Yao, L.Z.; Wu, J.; Wang, Z.B.; Li, Y.; Lu, Z.X. Pattern analysis of future HVDC grid development. Proc. CSEE 2014, 34, 6007–6020. [Google Scholar]
- Zhou, Y.X.; Hou, F.; Nie, Q.; Liu, R.; Yang, L.; Zhao, J.; Chen, Z.; Xue, W.; Zhang, X. Temperature effects on electrical tree aging characteristics of silicone rubber. High Volt. Eng. 2012, 38, 2640–2646. [Google Scholar]
- Delphino, S.; Fabiani, D.; Montanari, G.C.; Laurent, C.; Teyssedre, G.; Morshuis, P.H.F.; Bodega, R.; Dissado, L.A. Polymeric HVDC cable design and space charge accumulation, part 2: Insulation interfaces. IEEE Eiectrical. Insul. Mag. 2008, 24, 14–24. [Google Scholar]
- Yin, Y.; Xiao, D.M.; Tu, D.M. An application of space charge invaliding the electric aging degree of insulating polymer. Proc. CSEE 2002, 22, 43–48. [Google Scholar]
- Cheng, X.; Cheng, S.Q.; Wang, X.; Tu, D.M. Effect of nano ZnO on space charge distribution in polyethylene during corona aging. Insul. Mater. 2008, 41, 44–48. [Google Scholar]
- Cheng, Y.J.; Guo, N.; Wang, R.S.; Zhang, X.H. Effect of nano-ZnO and nano-montmorillonte on dielectric properties of low density polyethylene. Acta Mater. Compos. Sin. 2015, 32, 94–100. [Google Scholar]
- Vutt, N.; Teyssedre, G.; Vissouvanadin, B.; Le Roy, S.; Laurent, C.; Mammeri, M.; Denizet, I. Electric field profile measurement and modeling in multi-dielectrics for HVDC application. In Proceedings of the 2013 IEEE International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; pp. 413–416. [Google Scholar]
- Murakami, Y.; Nemoto, M.; Okuzumi, S.; Masuda, S.; Nagao, M.; Hozumi, N.; Sekiguchi, Y.; Murata, Y. DC conduction and electrical breakdown of MgO/LDPE nanocomposite. IEEE. Trans. Dielectr. Electr. Insul. 2008, 15, 33–39. [Google Scholar] [CrossRef]
- Reddy, C.C.; Ramu, T.S. On the computation of electric field and temperature distribution in HVDC cable insulation. IEEE. Trans. Dielectr. Electr. Insul. 2006, 13, 1236–1244. [Google Scholar] [CrossRef]
- Dang, Z.M.; Wang, H.Y.; Wang, L. New inorganic/organic functional composites with high temperature and high dielectric constant. Acta Mater. Compos. Sin. 2005, 22, 9–15. [Google Scholar]
- Wu, J.D.; Yin, Y.; Lang, L.; Wang, Q.; Li, X.; Xiao, D. The influence of nano-filler concentration on space charge behavior in LDPE/Silica nanocomposites. Proc. CSEE 2012, 32, 177–183. [Google Scholar]
- Lv, L.; Wang, X.; He, H.Q.; Fu, H.J.; Tu, D.M. Formation of space charges at interface between ethylene propylene diene terpolymer and silicone rubber. Proc. CSEE 2007, 27, 106–109. [Google Scholar]
- Weida, D.; Steinmetz, T.; Clemens, M. Electro-Quasistatic High Voltage Field Simulations of Large Scale Insulator Structures Including 2-D Models for Nonlinear Field-Grading Material Layers. IEEE Trans. Magn. 2009, 45, 980–983. [Google Scholar] [CrossRef]
- Christen, T.; Donzel, L.; Greuter, F. Nonlinear Resistive Electric Field Grading Part 1: Theory and Simulation. IEEE Trans. Electr. Insul. Mag. 2010, 26, 47–59. [Google Scholar] [CrossRef]
- Pourrahimi, A.M.; Hoang, T.A.; Liu, D.M. Highly efficient interfaces nanocomposites based on polyethylene and ZnO nano/hierarchical particles: A novel approach toward ultralow electrical conductivity insulations. Adv. Mater. 2016, 28, 8651–8657. [Google Scholar] [CrossRef] [PubMed]
- Norikazu, F.; Yoshimichi, O. Comparison of nano-strucation effects in polypropylene among four typical dielectric properties. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 671–677. [Google Scholar]
- Donnelly, K.P.; Varlow, B.R. Non-linear dc and ac Conductivity in Electrically Insulating Composites. IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 610–614. [Google Scholar] [CrossRef]
- Tanaka, T.; Kozako, M.; Fuse, N.; Ohki, Y. Proposal of a multi-core model for polymer nanocomposite dielectrics. IEEE. Trans. Dielectr. Electr. Insul. 2005, 12, 669–681. [Google Scholar] [CrossRef]
- Yang, J.M.; Zhao, H.; Zheng, C.J.; Wang, X.; Yang, C.C. Effects of nanoparticles dispersion on the DC dielectric properties of SiO2/LDPE nanocomposite. Proc. CSEE 2015, 35, 5087–5094. [Google Scholar]
- Tu, Y.P.; He, J.; Wang, G.Q.; Liu, M.; Xu, G.L.; Ding, L.J. Measurement of thermally stimulated current in ZnO varistor. Proc. CSEE 2010, 30, 116–121. [Google Scholar]
- Wu, Y.H.; Zha, J.W.; Wang, S.J. Insulating electrical properties of low density polyethylene affected by multilayer mesoporous MgO. Acta Mater. Compos. Sin. 2016, 33, 503–509. [Google Scholar]
- Chen, Q.G.; Liu, H.Q.; Chi, M.H.; Wang, Y.; Wei, X. Experimental study on influence of trap parameters on dielectric characteristics of nano-modified insulation pressboard. Materials 2017, 10, 90. [Google Scholar] [CrossRef] [PubMed]

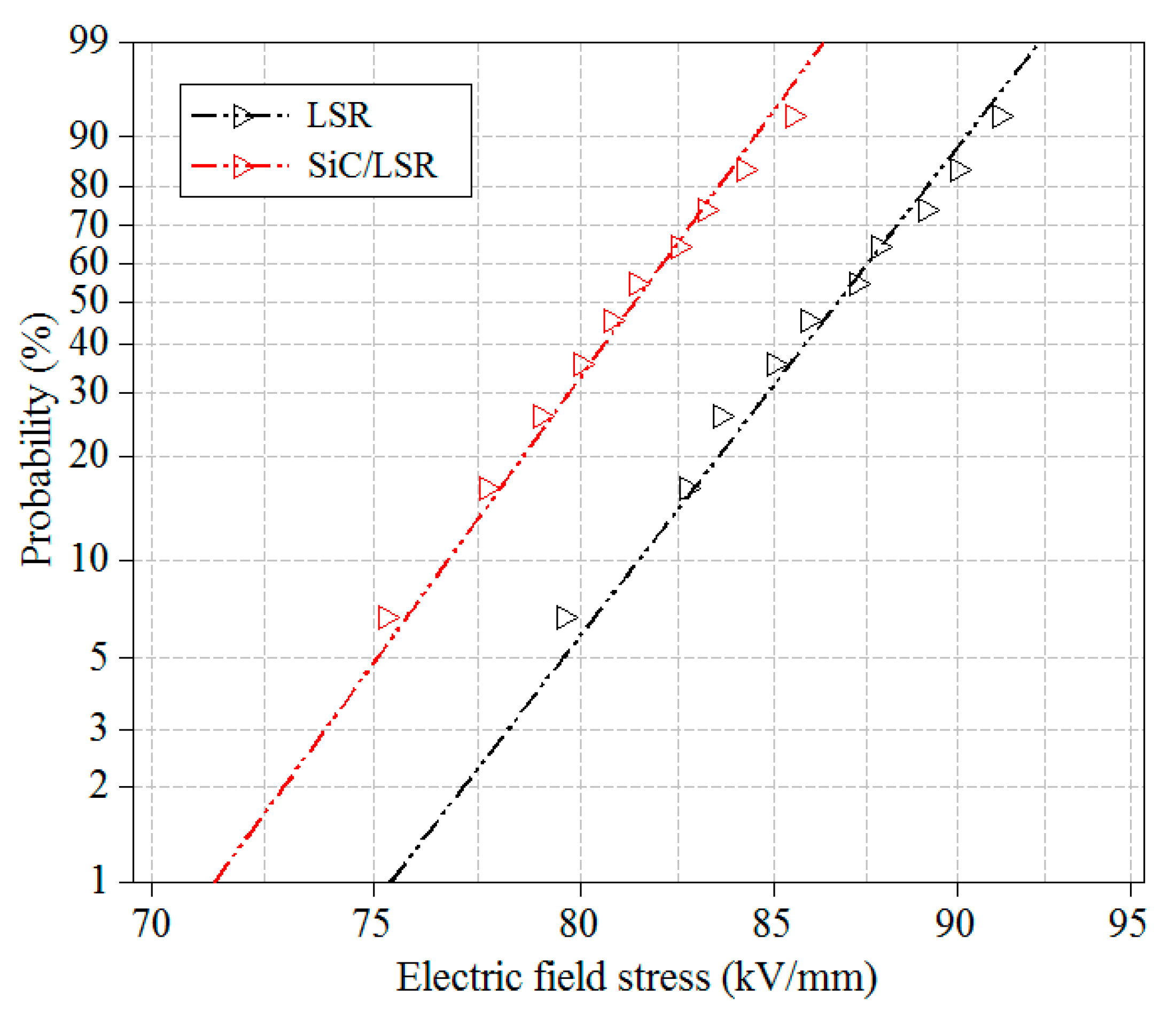
| Sample | Ec (kV/mm) | β |
|---|---|---|
| LSR | 12 | 0.32 |
| 1 wt % SiC/LSR | 10 | 0.58 |
| 3 wt % SiC/LSR | 7 | 1.63 |
| 5 wt % SiC/LSR | 8 | 1.21 |
| Sample | Peak Value Current (pA) | Peak Value Temperature (K) | Trap Charge Quantity (nC) | Trap Level (eV) |
|---|---|---|---|---|
| LSR | 82.9 | 360 | 80.78 | 0.614 |
| 3 wt % SiC/LSR | 65.9 | 339 | 59.80 | 0.583 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, N.; Chen, Q.; Wei, X. Preparation and Dielectric Properties of SiC/LSR Nanocomposites for Insulation of High Voltage Direct Current Cable Accessories. Materials 2018, 11, 403. https://doi.org/10.3390/ma11030403
Shang N, Chen Q, Wei X. Preparation and Dielectric Properties of SiC/LSR Nanocomposites for Insulation of High Voltage Direct Current Cable Accessories. Materials. 2018; 11(3):403. https://doi.org/10.3390/ma11030403
Chicago/Turabian StyleShang, Nanqiang, Qingguo Chen, and Xinzhe Wei. 2018. "Preparation and Dielectric Properties of SiC/LSR Nanocomposites for Insulation of High Voltage Direct Current Cable Accessories" Materials 11, no. 3: 403. https://doi.org/10.3390/ma11030403
APA StyleShang, N., Chen, Q., & Wei, X. (2018). Preparation and Dielectric Properties of SiC/LSR Nanocomposites for Insulation of High Voltage Direct Current Cable Accessories. Materials, 11(3), 403. https://doi.org/10.3390/ma11030403




