Critical Current Simulation and Measurement of Second Generation, High-Temperature Superconducting Coil under External Magnetic Field
Abstract
:1. Introduction
2. Experimental Setup
3. Simulation Model
4. Discussion
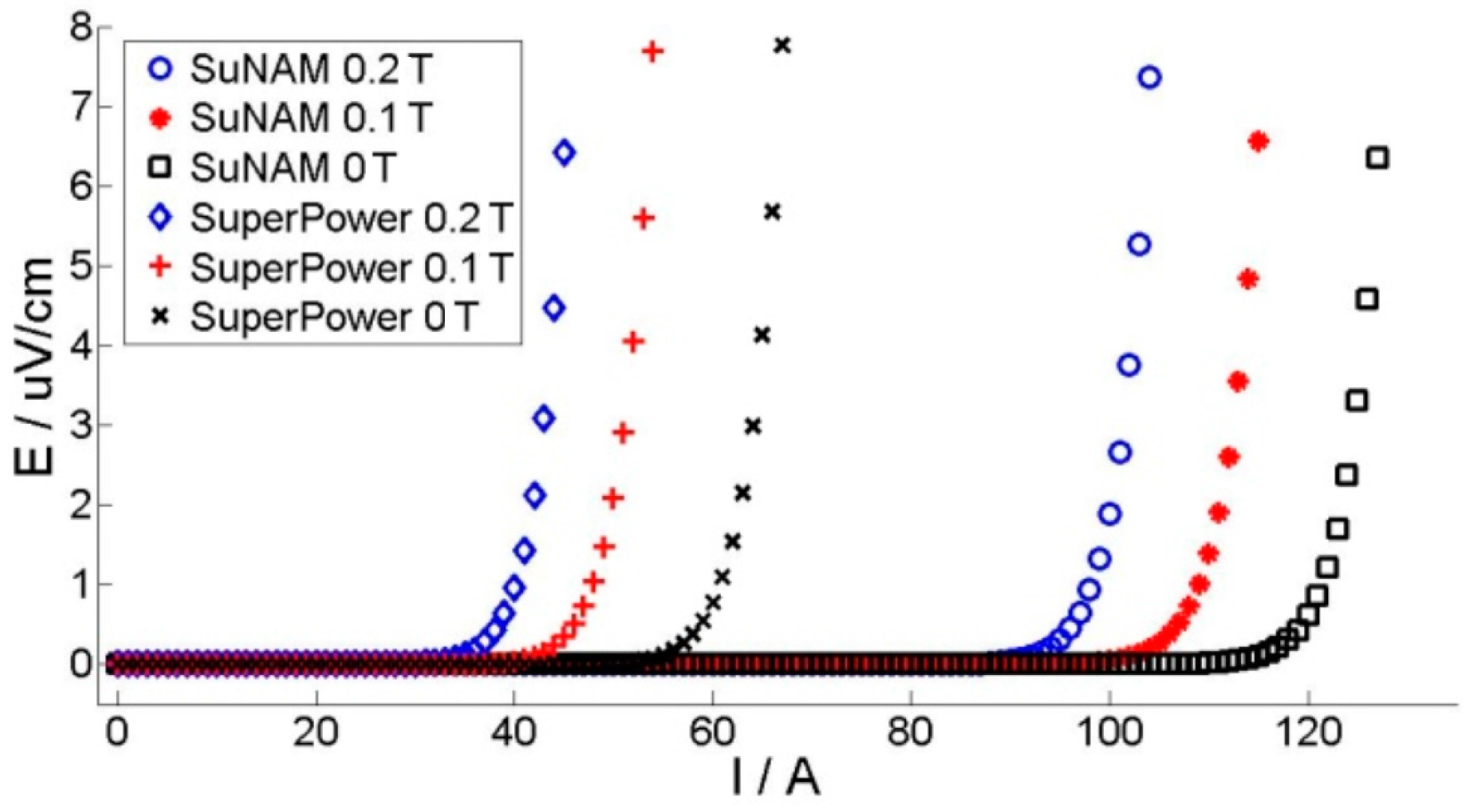
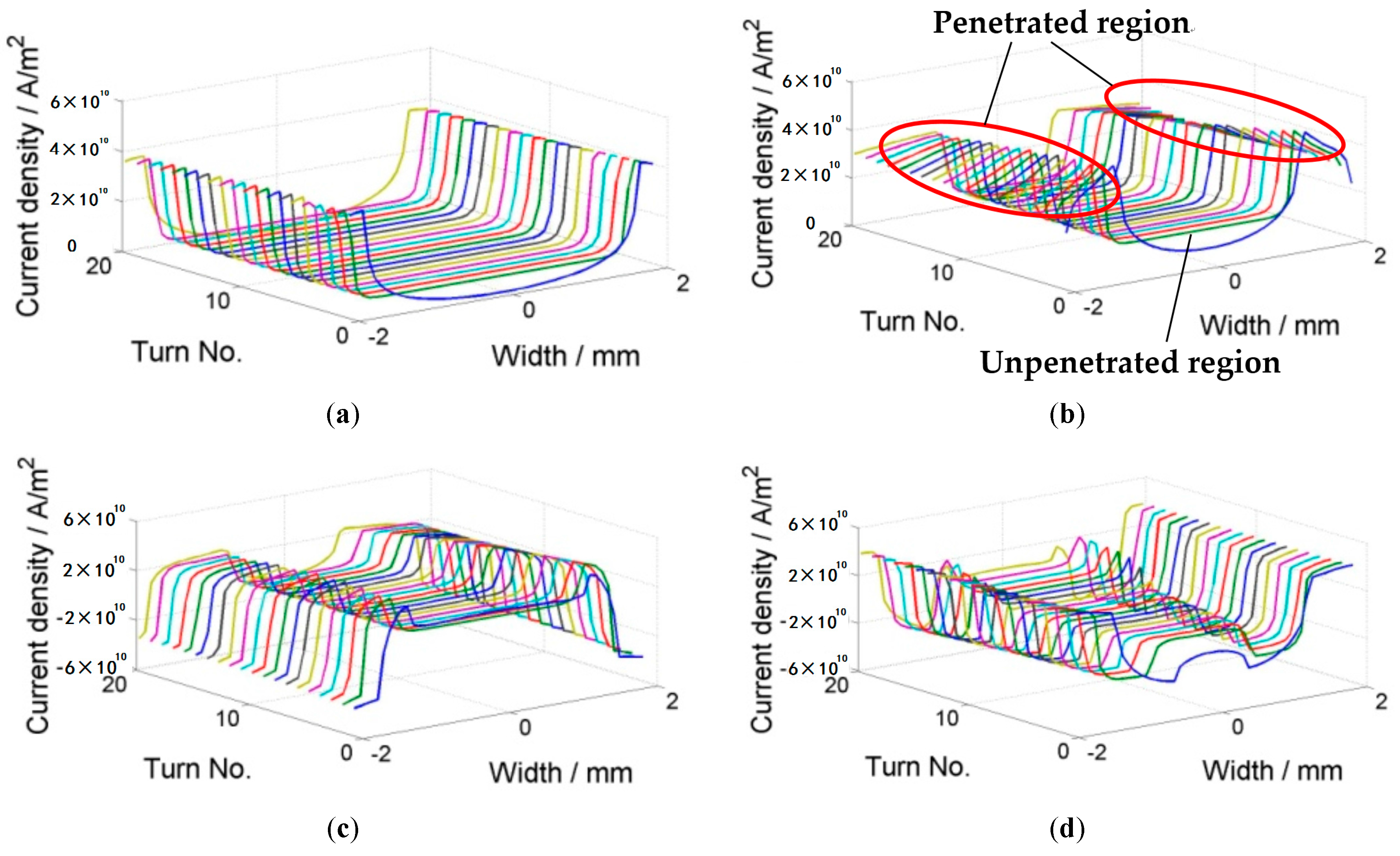
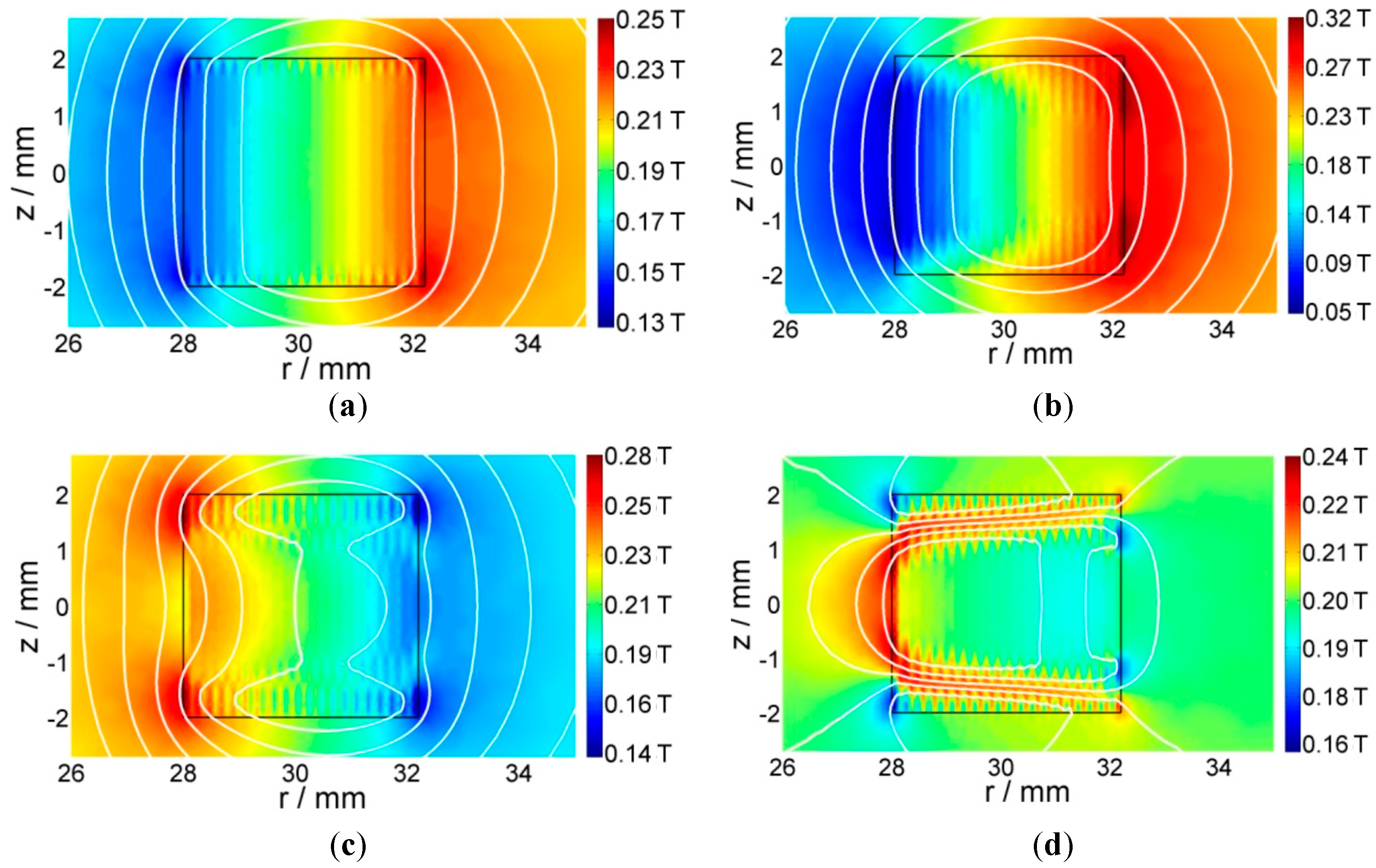
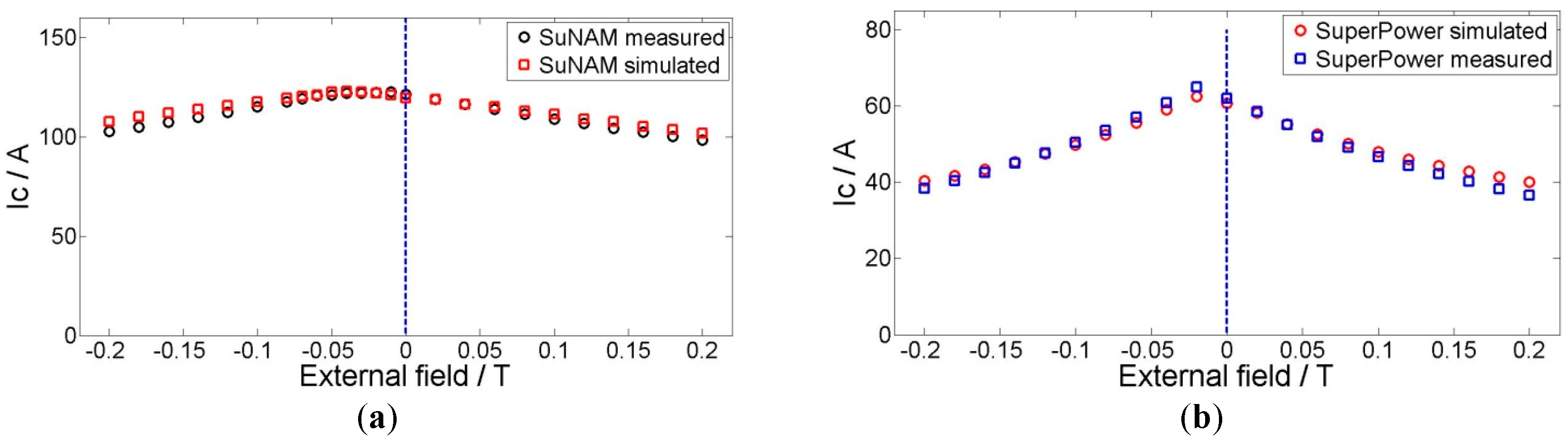
4.1. Model Validation
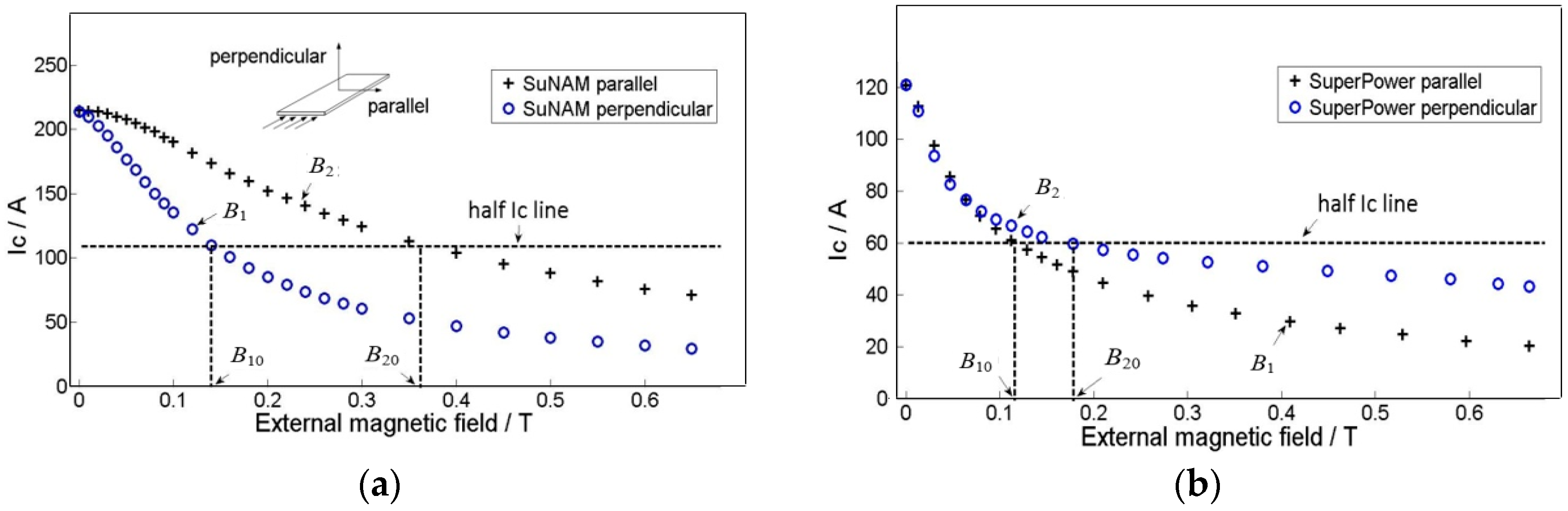
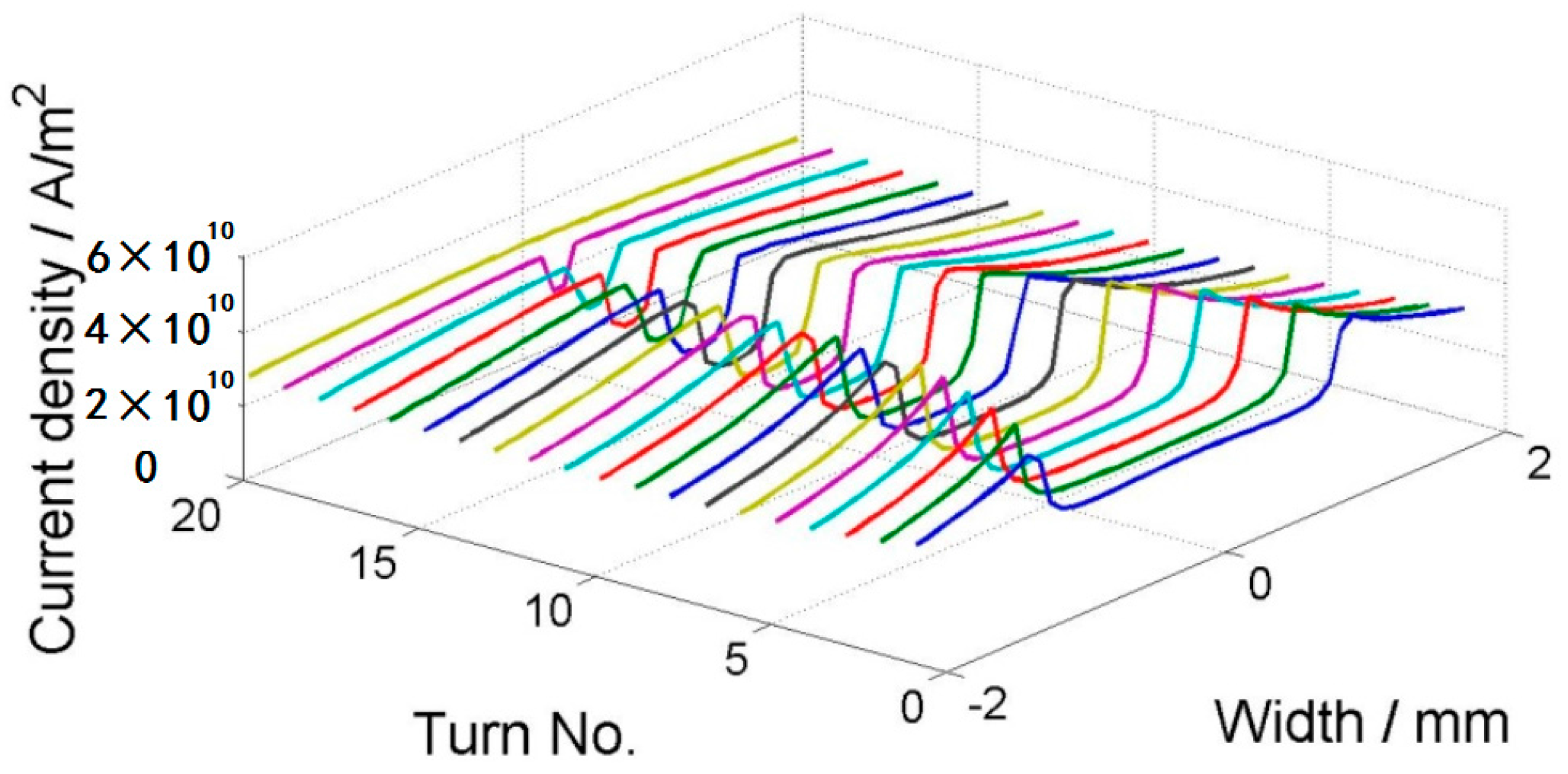
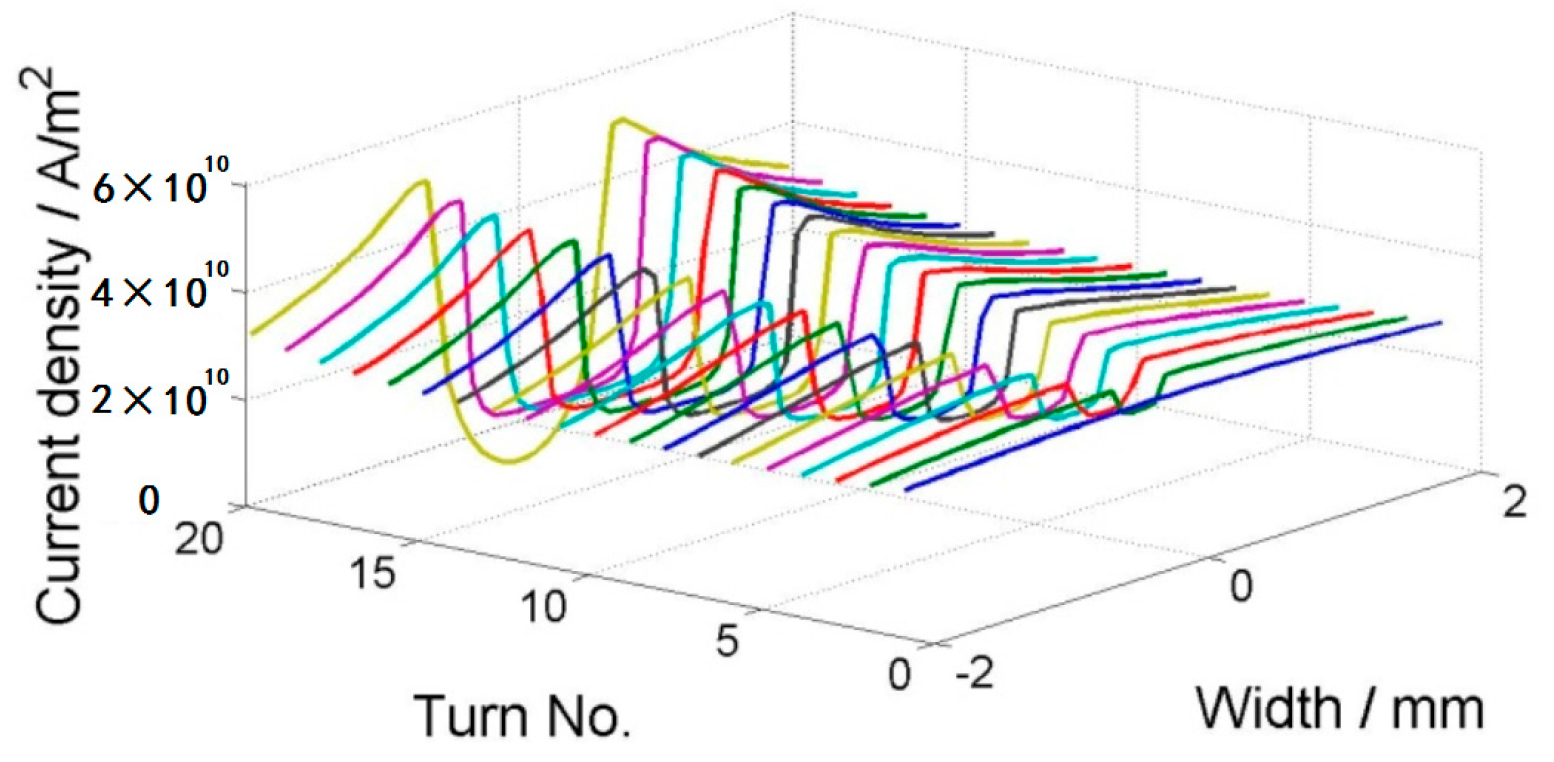
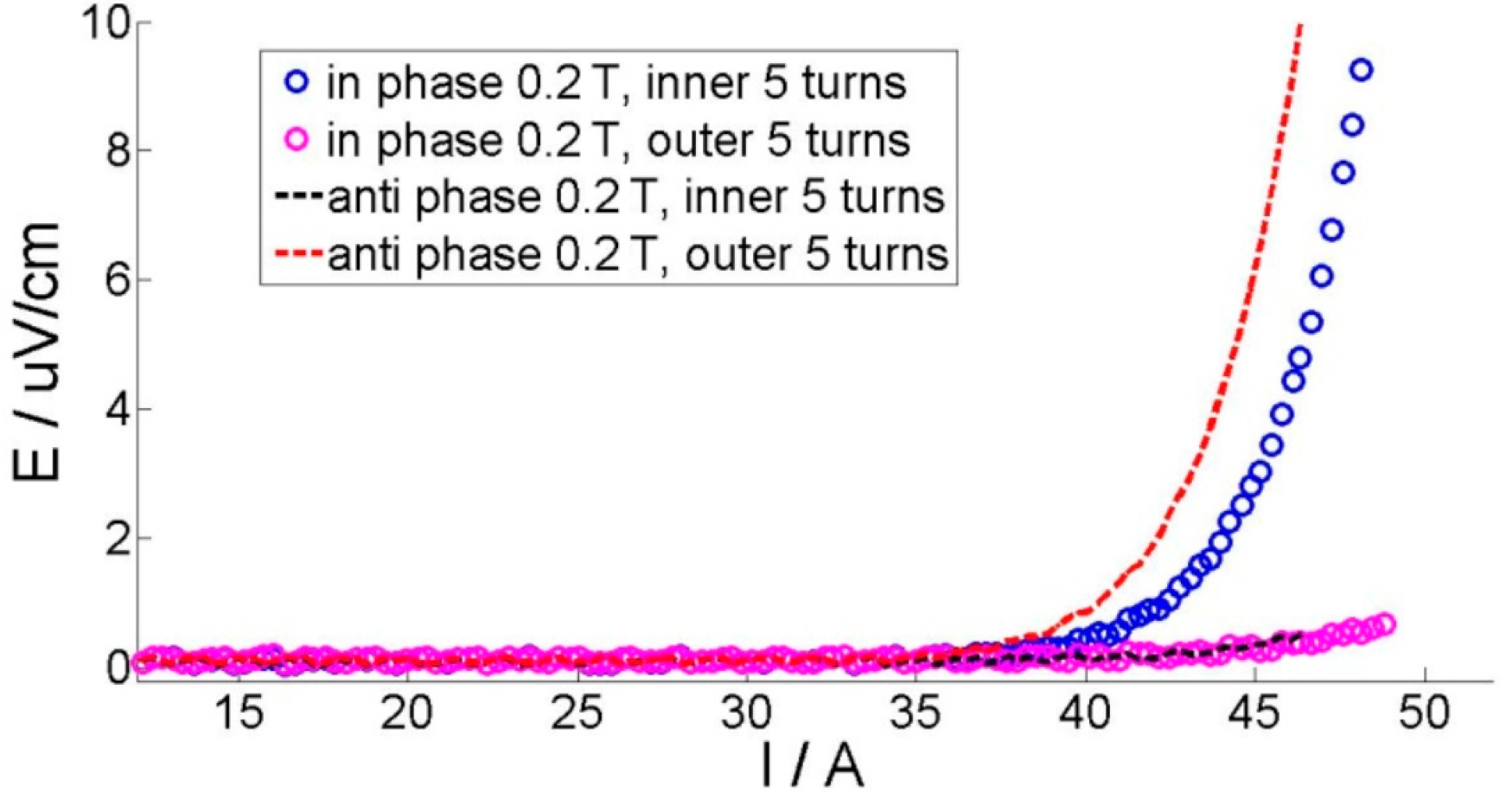
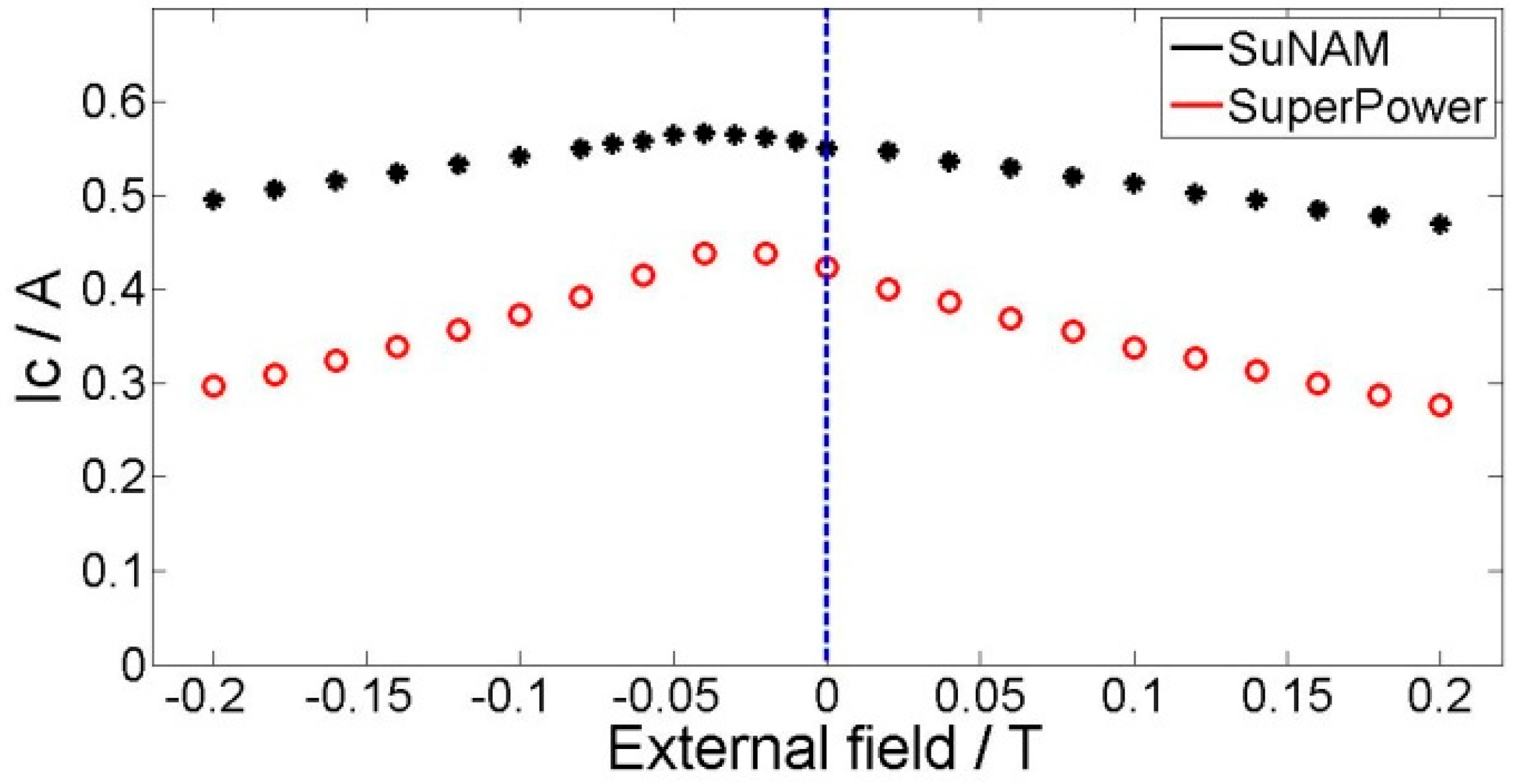
4.2. Comparison of Two Different Tapes
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Koyanagi, K.; Ono, M.; Hanai, S.; Watanabe, K.; Awaji, S.; Hamajima, T.; Kiyoshi, T.; Kumakura, H. Design of a 30 T superconducting magnet using a coated conductor insert. IEEE Trans. Appl. Supercond. 2009, 19, 1617–1620. [Google Scholar] [CrossRef]
- Awaji, S.; Watanabe, K.; Oguro, H.; Hanai, S.; Miyazaki, H.; Takahashi, M.; Ioka, S.; Sugimoto, M.; Tsubouchi, H.; Fujita, S.; et al. New 25 T cryogen-free superconducting magnet project at Tohoku University. IEEE Trans. Appl. Supercond. 2014, 24. [Google Scholar] [CrossRef]
- Senatore, C.; Alessandrini, M.; Lucarelli, A.; Tediosi, R.; Uglietti, D.; Iwasa, Y. Progresses and challenges in the development of high-field solenoidal magnets based on RE123 coated conductors. Supercond. Sci. Technol. 2014, 27, 103001. [Google Scholar] [CrossRef]
- Weijers, H.W.; Markiewicz, W.D.; Voran, A.J.; Gundlach, S.R.; Sheppard, W.R.; Jarvis, B.; Johnson, Z.L.; Noyes, P.D.; Lu, J.; Kandel, H.; et al. Progress in the development of a superconducting 32 T magnet with ReBCO high field coils. IEEE Trans. Appl. Supercond. 2014, 24. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, J.; Song, S.; Zhu, G.; Li, Y.; Hu, X.; Yan, L. High temperature superconducting YBCO insert for 25 T full superconducting magnet. IEEE Trans. Appl. Supercond. 2015, 25. [Google Scholar] [CrossRef]
- Gavrilin, A.V.; Jun, L.; Hongyu, B.; Hilton, D.K.; Markiewicz, W.D.; Weijers, H.W. Observations from the analyses of magnetic field and ac loss distributions in the NHMFL 32 T all-superconducting magnet HTS insert. IEEE Trans. Appl. Supercond. 2013, 23, 4300704. [Google Scholar] [CrossRef]
- Zhang, M.; Kvitkovic, J.; Kim, C.H.; Pamidi, S.V.; Combs, T.A. Study of 2G high temperature superconducting coils: Influence of anisotropic characteristics. J. Appl. Phys. 2013, 114, 631–870. [Google Scholar] [CrossRef]
- Wang, Y.; Song, H.; Xu, D.; Li, Z.F.; Jin, Z.; Hong, Z. An equivalent circuit grid model for no-insulation HTS pancake coils. Supercond. Sci. Technol. 2015, 28, 045017. [Google Scholar] [CrossRef]
- Zhang, M.; Kim, J.-H.; Pamidi, S.; Chudy, M.; Yuan, W.; Coombs, T. Study of second generation, high-temperature superconducting coils: Determination of critical current. J. Appl. Phys. 2012, 111, 083902. [Google Scholar] [CrossRef]
- Polak, M.; Barnes, P.; Levin, G. YBCO/Ag boundary resistivity in YBCO tapes with metallic substrates. Supercond. Sci. Technol. 2006, 19, 817. [Google Scholar] [CrossRef]
- Fukushima, H.; Ibi, A.; Takahashi, H.; Kuriki, R.; Miyata, S.; Yamada, Y.; Shiohara, Y.; Kato, T.; Hirayama, T. Properties of long GdBCO coated conductor by IBAD-PLD method—The first GdBCO coil test. IEEE Trans. Appl. Supercond. 2007, 17, 3367–3370. [Google Scholar] [CrossRef]
- Šouc, J.; Pardo, E.; Vojenčiak, M.; Gömöry, F. Theoretical and experimental study of AC loss in high temperature superconductor single pancake coils. Supercond. Sci. Technol. 2009, 22, 015006. [Google Scholar] [CrossRef]
- Chudy, M.; Chen, Y.; Zhang, M.; Coombs, T. Anisotropy of 2G HTS racetrack coils in external magnetic fields. Supercond. Sci. Technol. 2013, 26, 075012. [Google Scholar] [CrossRef]
- Hu, D.; Ainslie, M.; Rush, J.; Durrell, J.; Zou, J.; Raine, M.; Hampshire, D. DC characterization and 3D modelling of a triangular, epoxy-impregnated high temperature superconducting coil. Supercond. Sci. Technol. 2015, 28, 065011. [Google Scholar] [CrossRef]
- Hong, Z.; Campbell, A.; Coombs, T. Numerical solution of critical state in superconductivity by finite element software. Supercond. Sci. Technol. 2006, 19, 1246. [Google Scholar] [CrossRef]
- Clem, J.R.; Claassen, J.; Mawatari, Y. AC losses in a finite z stack using an anisotropic homogeneous-medium approximation. Supercond. Sci. Technol. 2007, 20, 1130. [Google Scholar] [CrossRef]
- Yuan, W.; Campbell, A.; Hong, Z.; Ainslie, M.; Coombs, T. Comparison of AC losses, magnetic field/current distributions and critical currents of superconducting circular pancake coils and infinitely long stacks using coated conductors. Supercond. Sci. Technol. 2010, 23, 085011. [Google Scholar] [CrossRef]
- Prigozhin, L.; Sokolovsky, V. Computing AC losses in stacks of high-temperature superconducting tapes. Supercond. Sci. Technol. 2011, 24, 075012. [Google Scholar] [CrossRef]
- Grilli, F.; Pardo, E.; Stenvall, A.; Nguyen, D.N.; Yuan, W.; Gomory, F. Computation of losses in HTS under the action of varying magnetic fields and currents. IEEE Trans. Appl. Supercond. 2013, 24, 78–110. [Google Scholar] [CrossRef]
- Yuan, W.; Campbell, A.; Coombs, T. A model for calculating the AC losses of second-generation high temperature superconductor pancake coils. Supercond. Sci. Technol. 2009, 22, 075028. [Google Scholar] [CrossRef]
- Pitel, J.; Kováč, P. On some consequences of an external magnetic field applied to HTS coils. Phys. C Supercond. 2011, 471, 1680–1688. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, Z.; Zhang, H.; Zhang, M.; Qiu, M.; Yuan, W. Electric measurement of the critical current, AC loss, and current distribution of a prototype HTS cable. IEEE Trans. Appl. Supercond. 2014, 24. [Google Scholar] [CrossRef]
- Pitel, J. Differences between two definitions of the critical current of HTS coils. Supercond. Sci. Technol. 2013, 26, 125002. [Google Scholar] [CrossRef]




| Tape Yype | HCN4045 | SCS4050 |
|---|---|---|
| Manufacturer | SuNAM | SuperPower |
| Tape Ic | 217 A | 120 A |
| Tape thickness | 0.20 mm | 0.20 mm |
| Inner diameter | 56 mm | |
| Total turns | 20 | |
| Tape width | 4 mm | |
| Insulation | Kapton tape | |
| Type of Tapes | SuNAM | SuperPower |
|---|---|---|
| B1 | Perpendicular | Parallel |
| B10 (T) | 0.140 | 0.115 |
| B2 | Parallel | Perpendicular |
| B20 (mT) | 0.360 | 0.180 |
| k | 0.140/0.360 | 0.115/0.180 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, D.; Liu, H.; Zhang, X.; Gong, T. Critical Current Simulation and Measurement of Second Generation, High-Temperature Superconducting Coil under External Magnetic Field. Materials 2018, 11, 339. https://doi.org/10.3390/ma11030339
Yu D, Liu H, Zhang X, Gong T. Critical Current Simulation and Measurement of Second Generation, High-Temperature Superconducting Coil under External Magnetic Field. Materials. 2018; 11(3):339. https://doi.org/10.3390/ma11030339
Chicago/Turabian StyleYu, Dongmin, Huanan Liu, Xinhe Zhang, and Taorong Gong. 2018. "Critical Current Simulation and Measurement of Second Generation, High-Temperature Superconducting Coil under External Magnetic Field" Materials 11, no. 3: 339. https://doi.org/10.3390/ma11030339
APA StyleYu, D., Liu, H., Zhang, X., & Gong, T. (2018). Critical Current Simulation and Measurement of Second Generation, High-Temperature Superconducting Coil under External Magnetic Field. Materials, 11(3), 339. https://doi.org/10.3390/ma11030339





