The Microstructure and Mechanical Properties of Refractory High-Entropy Alloys with High Plasticity
Abstract
:1. Introduction
2. Experimental Methods
3. Results and Discussion
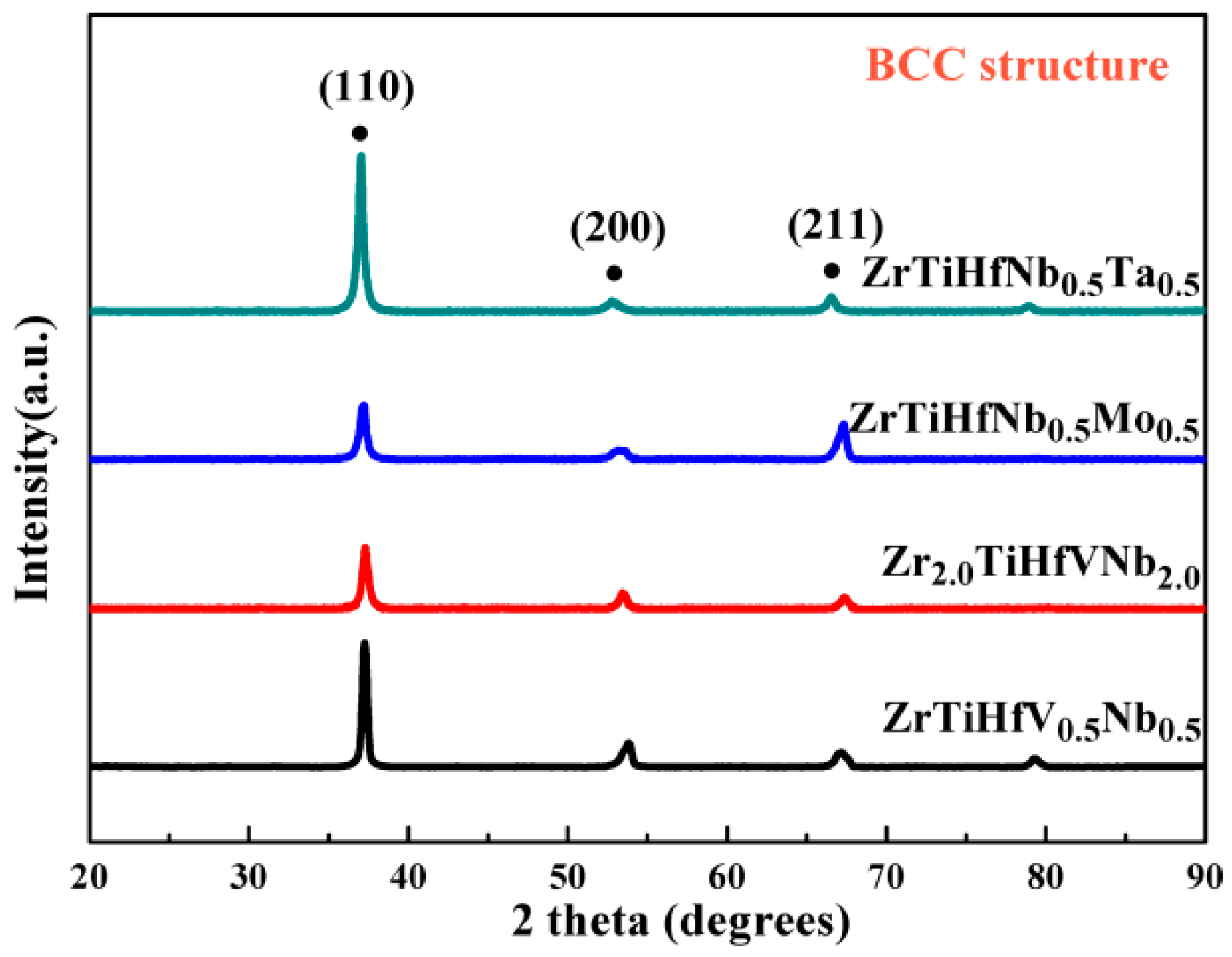
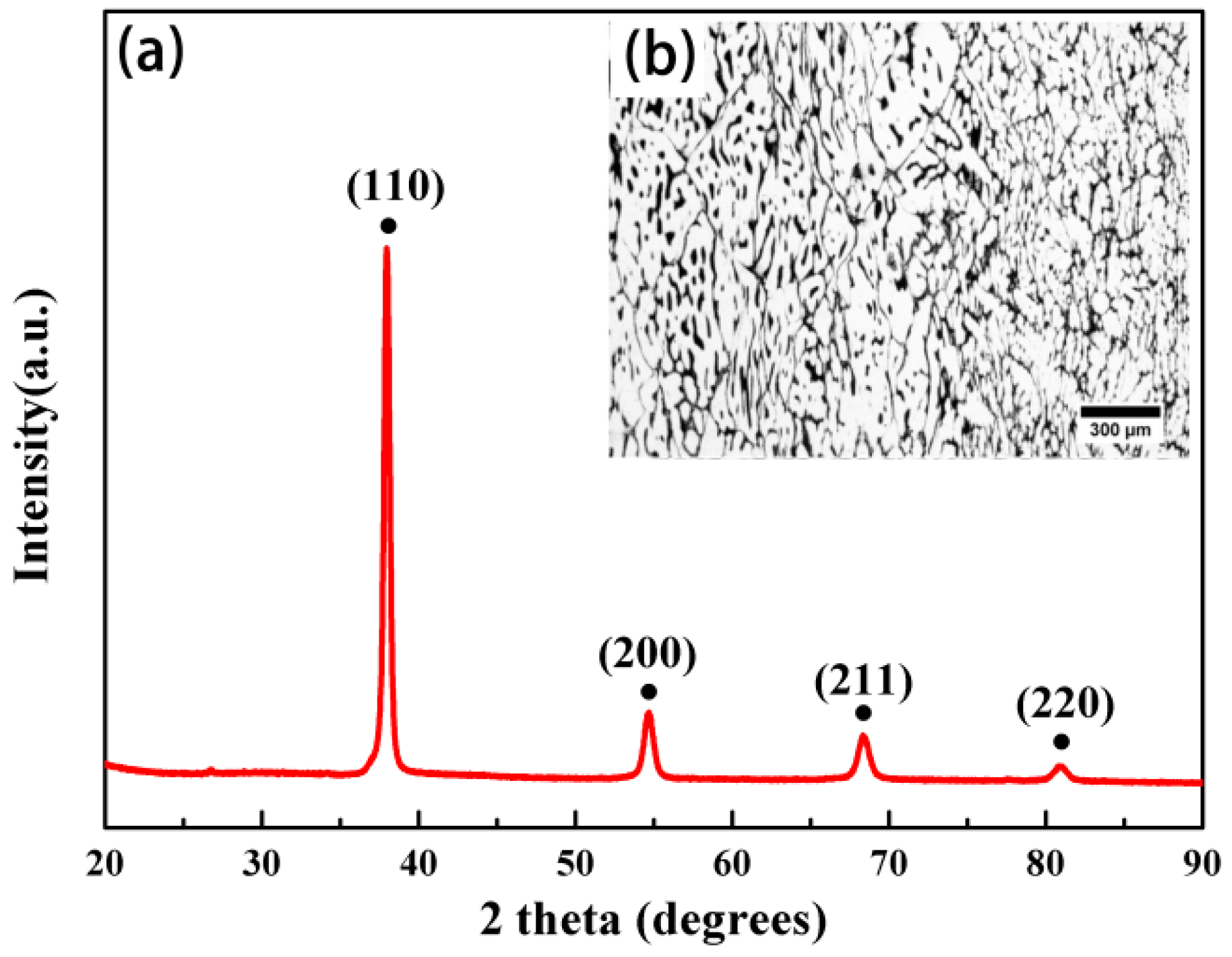
3.1. Crystal Structure and Microstructure Analysis
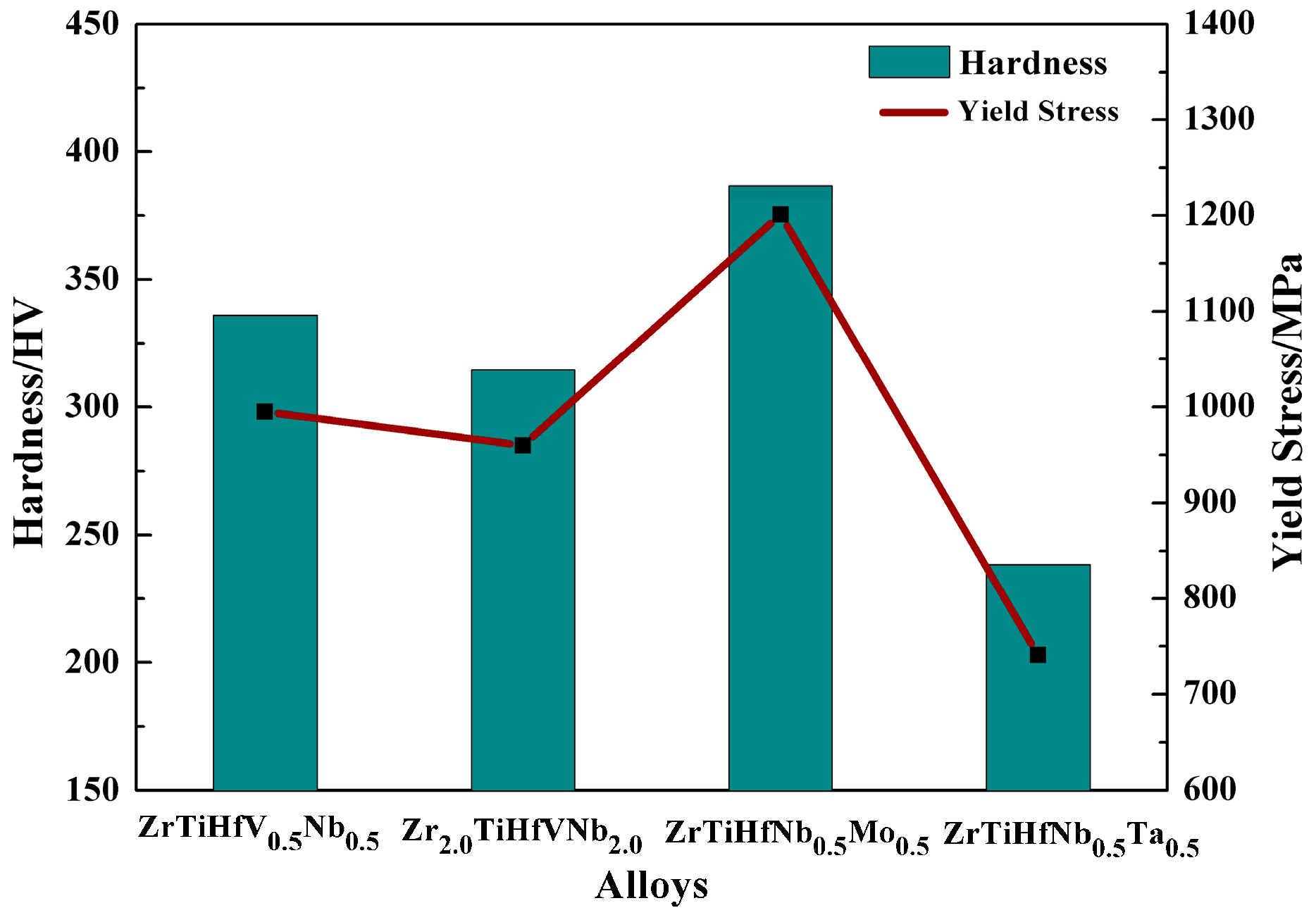
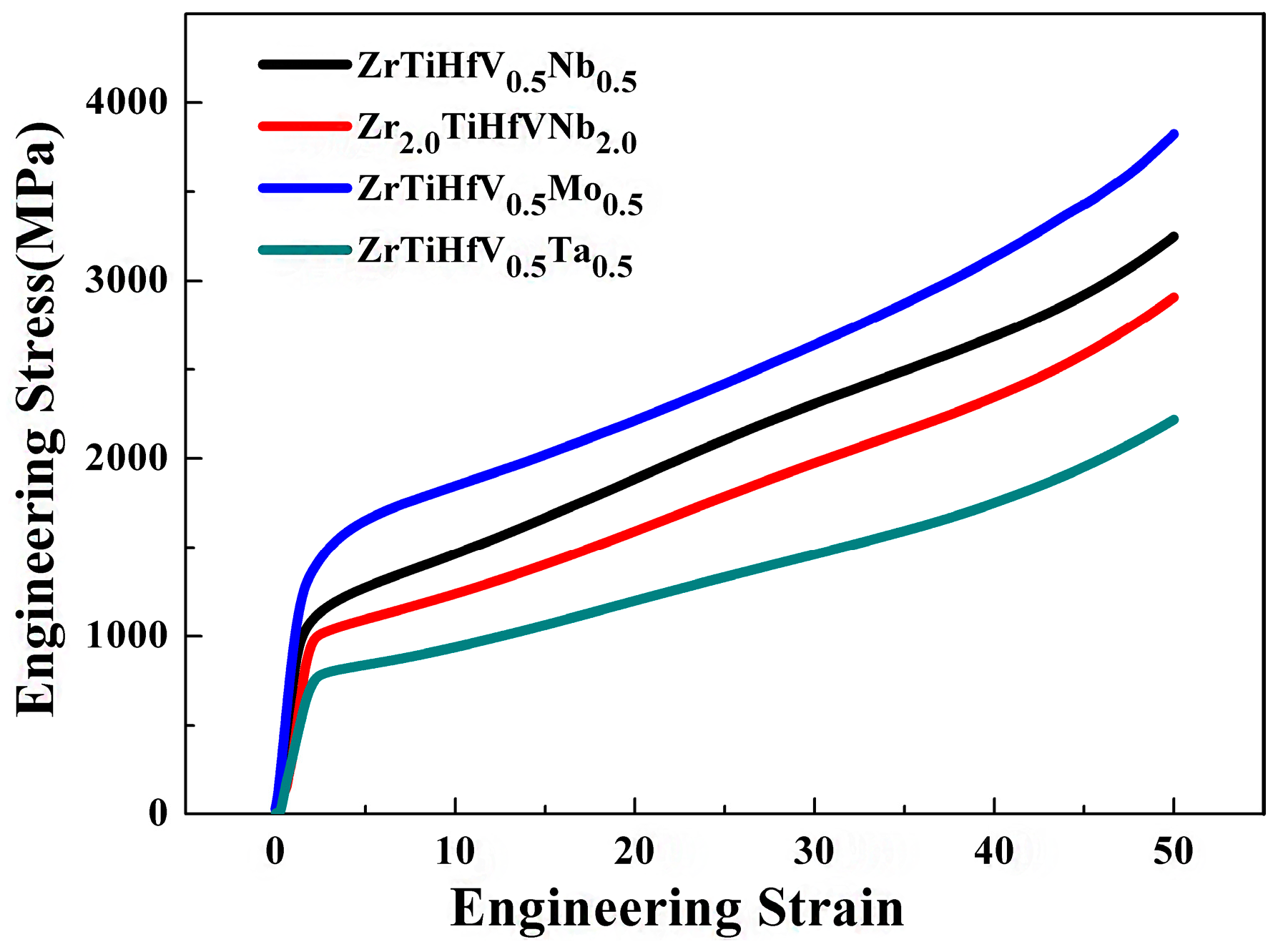
3.2. Static Compression Properties and Hardness Analysis
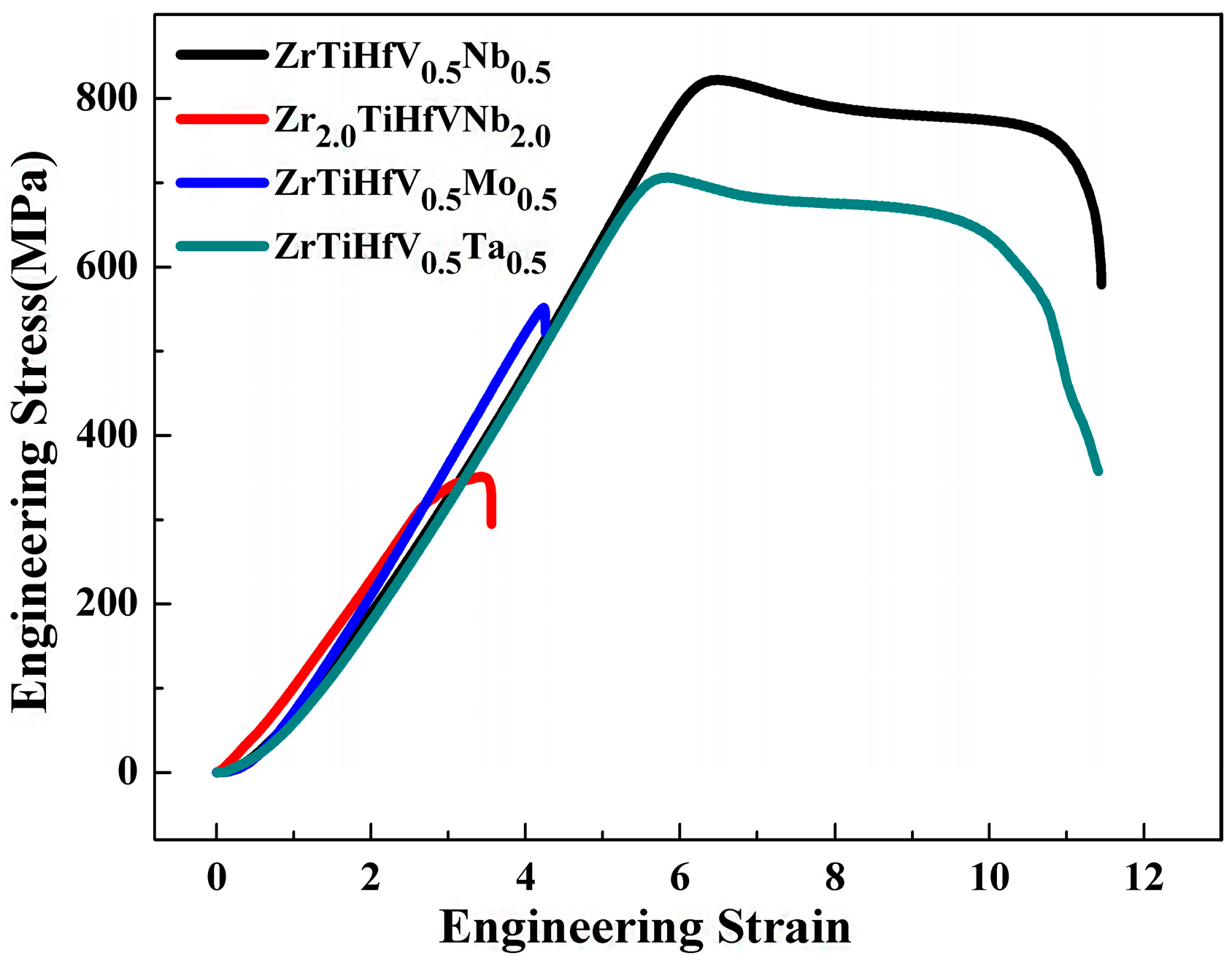
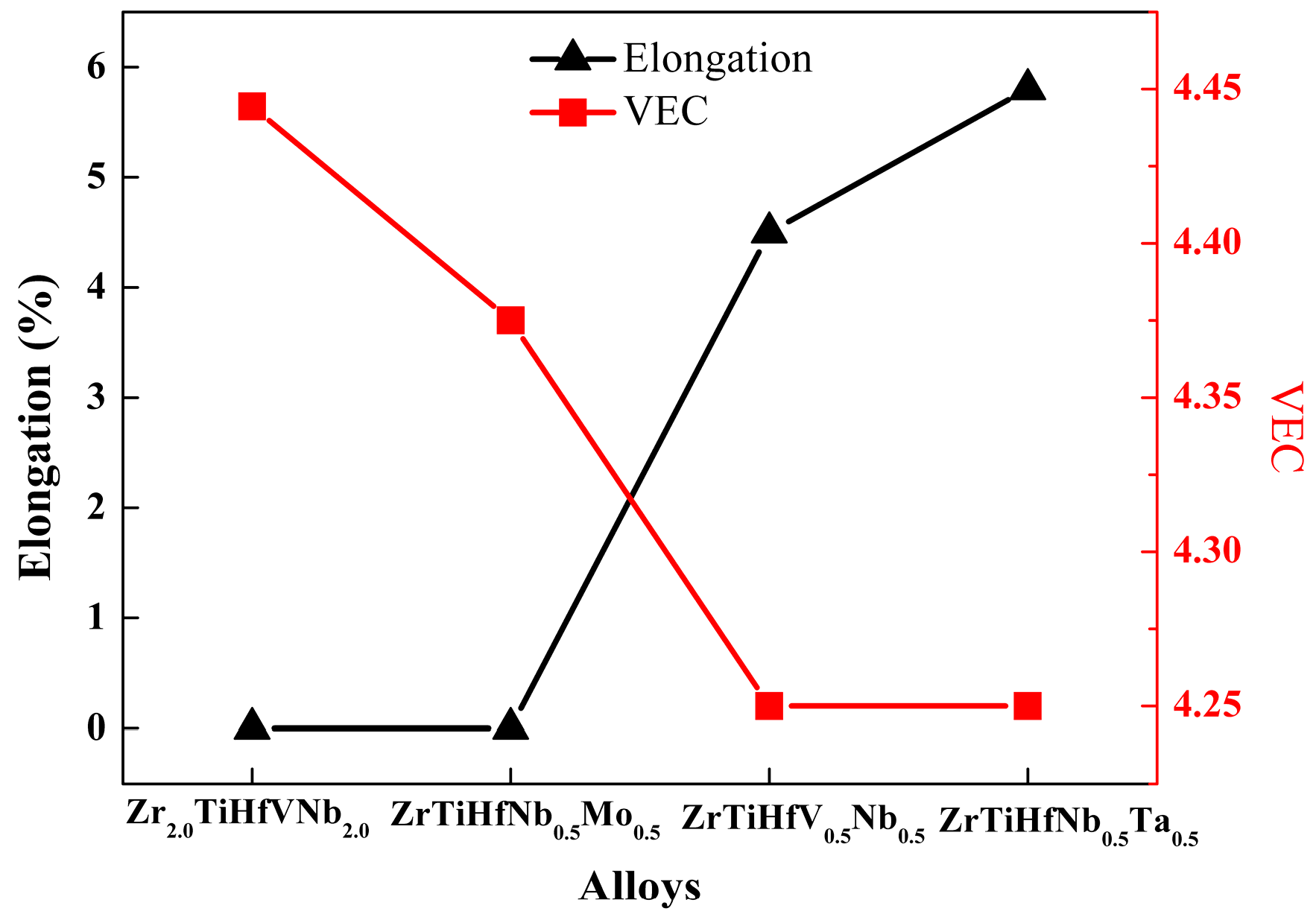
3.3. Tensile Properties Analysis
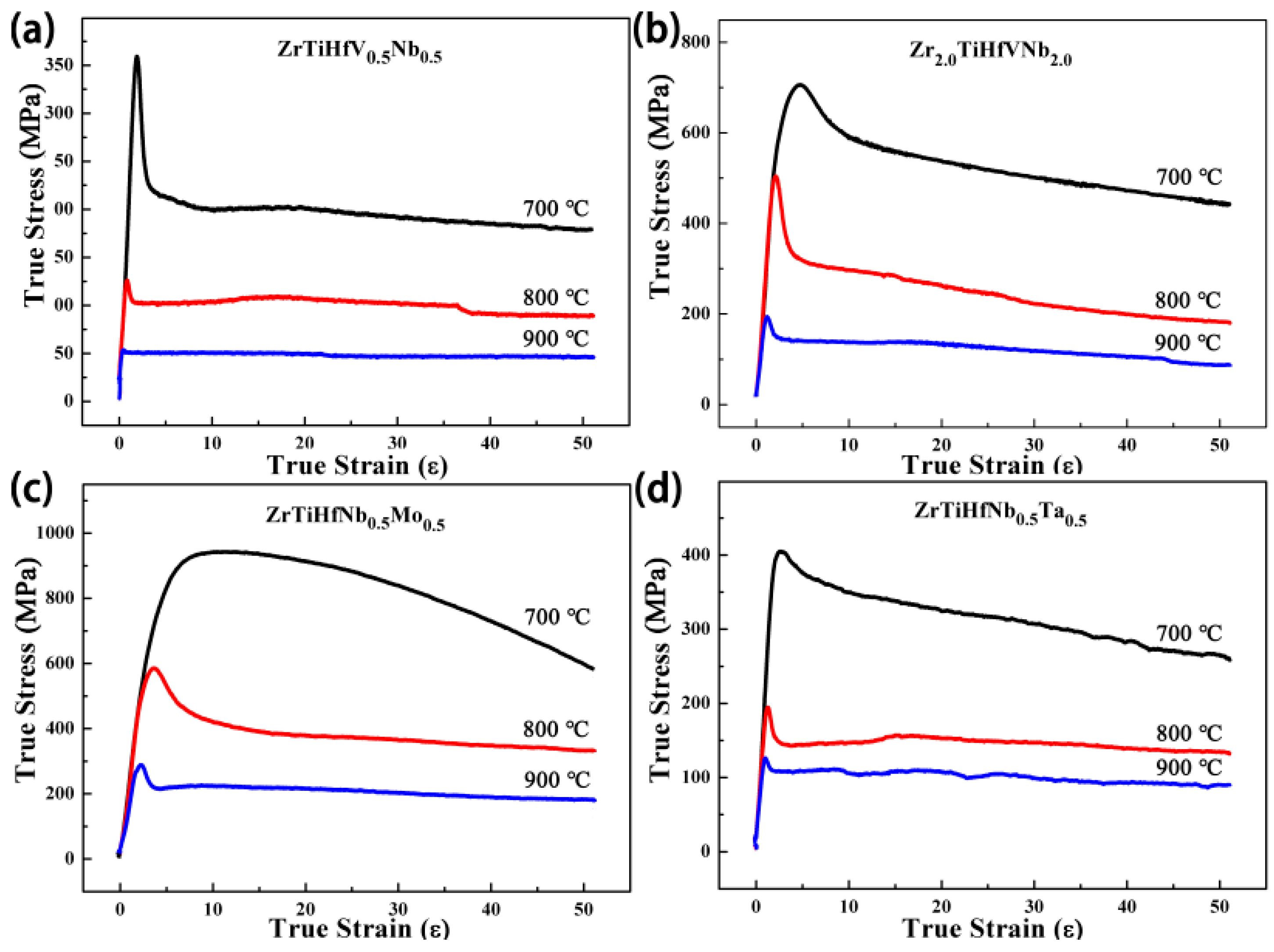
3.4. High-Temperature Compressive Properties
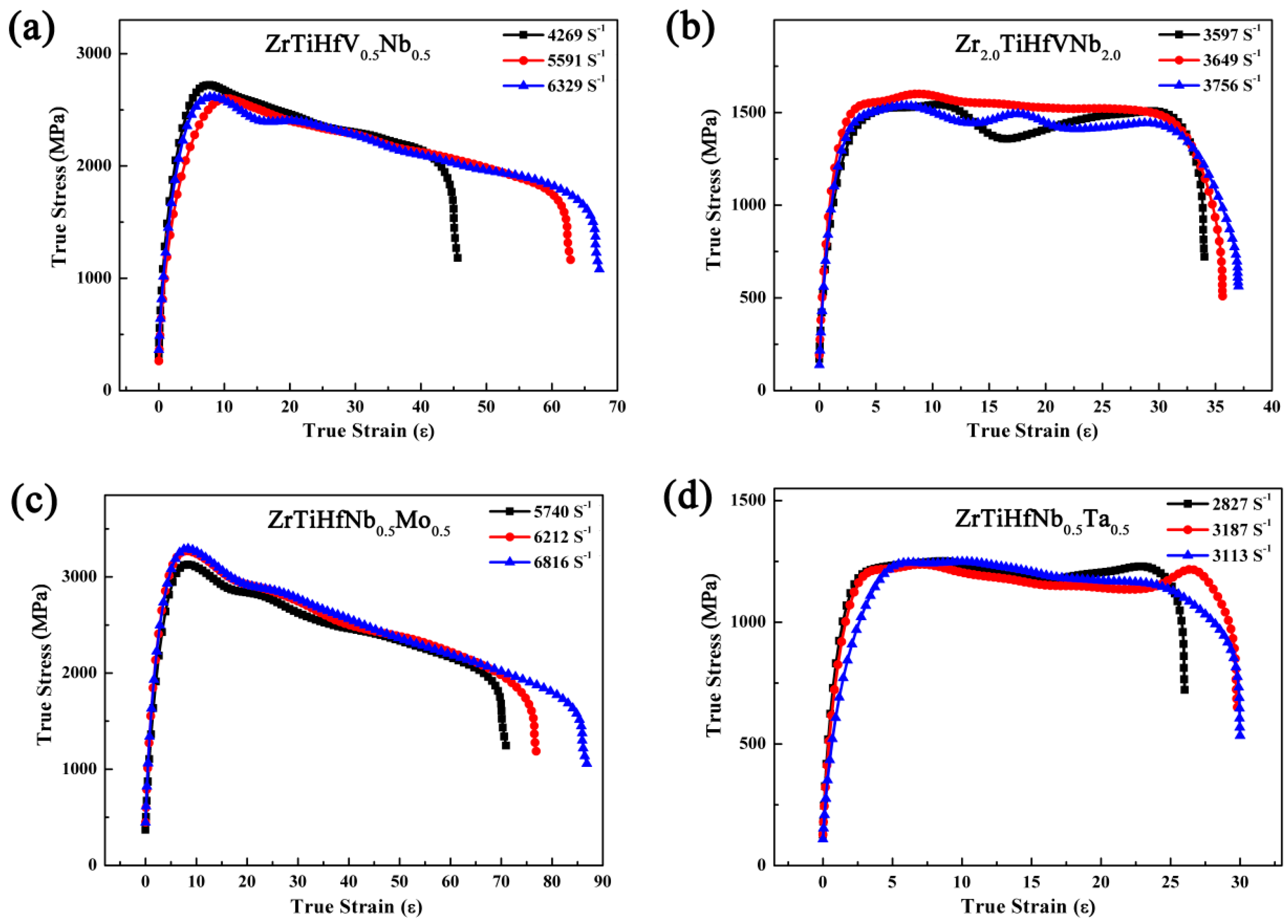
3.5. Dynamic Compressive Properties Analysis
4. Conclusions
- (1)
- The crystal structure of the RHEAs was identified as a BCC structure and the dendrites were found in the optical microscope.
- (2)
- The compressive strain of these alloys was higher than 50% and the compressive strength was relatively higher. The RHEAs with the minimum VEC exhibited the maximum tensile deformation.
- (3)
- The addition of Nb, Mo, and Ta contributed to a high-temperature strength.
- (4)
- It would be beneficial to explore new-type RHEAs with good plasticity by controlling the VEC. RHEAs that combine good plasticity and high strength would be convenient for processing and manufacturing.
Author Contributions
Conflicts of Interest
References
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Yeh, J.-W.; Chang, S.-Y.; Hong, Y.-D.; Chen, S.-K.; Lin, S.-J. Anomalous decrease in X-ray diffraction intensities of Cu–Ni–Al–Co–Cr–Fe–Si alloy systems with multi-principal elements. Mater. Chem. Phys. 2007, 103, 41–46. [Google Scholar] [CrossRef]
- Xiao, D.H.; Zhou, P.F.; Wu, W.Q.; Diao, H.Y.; Gao, M.C.; Song, M.; Liaw, P.K. Microstructure, mechanical and corrosion behaviors of AlCoCuFeNi-(Cr,Ti) high entropy alloys. Mater. Des. 2017, 116, 438–447. [Google Scholar] [CrossRef]
- Daoud, H.M.; Manzoni, A.M.; Volkl, R.; Wanderka, N.; Glatzel, U. Oxidation Behavior of Al8Co17Cr17Cu8Fe17Ni33, Al23Co15Cr23Cu8Fe15Ni15, and Al17Co17Cr17Cu17Fe17Ni17 Compositionally Complex Alloys (High-Entropy Alloys) at Elevated Temperatures in Air. Adv. Eng. Mater. 2015, 17, 1134–1141. [Google Scholar] [CrossRef]
- Gorr, B.; Azim, M.; Christ, H.J.; Mueller, T.; Schliephake, D.; Heilmaier, M. Phase equilibria, microstructure, and high temperature oxidation resistance of novel refractory high-entropy alloys. J. Alloys Compd. 2015, 624, 270–278. [Google Scholar] [CrossRef]
- Melnick, A.B.; Soolshenko, V.K. Thermodynamic design of high-entropy refractory alloys. J. Alloys Compd. 2017, 694, 223–227. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.B.; Scott, J.M.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar] [CrossRef]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Meisenkothen, F.; Miracle, D.B.; Woodward, C.F. Microstructure and elevated temperature properties of a refractory TaNbHfZrTi alloy. J. Mater. Sci. 2012, 47, 4062–4074. [Google Scholar] [CrossRef]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Miracle, D.B.; Woodward, C.F. Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J. Alloys Compd. 2011, 509, 6043–6048. [Google Scholar] [CrossRef]
- Juan, C.C.; Tseng, K.K.; Hsu, W.L.; Tsai, M.H.; Tsai, C.W.; Lin, C.M.; Chen, S.K.; Lin, S.J.; Yeh, J.W. Solution strengthening of ductile refractory HfMoxNbTaTiZr high-entropy alloys. Mater. Lett. 2016, 175, 284–287. [Google Scholar] [CrossRef]
- Yurchenko, N.Y.; Stepanov, N.D.; Zherebtsov, S.V.; Tikhonovsky, M.A.; Salishchev, G.A. Structure and mechanical properties of B2 ordered refractory AlNbTiVZr x (x = 0–1.5) high-entropy alloys. Mater. Sci. Eng. A 2017, 704, 82–90. [Google Scholar] [CrossRef]
- Senkov, O.N.; Semiatin, S.L. Microstructure and properties of a refractory high-entropy alloy after cold working. J. Alloys Compd. 2015, 649, 1110–1123. [Google Scholar] [CrossRef]
- Tsai, M.H.; Fan, A.C.; Wang, H.A. Effect of atomic size difference on the type of major intermetallic phase in arc-melted CoCrFeNiX high-entropy alloys. J. Alloys Compd. 2017, 695, 1479–1487. [Google Scholar] [CrossRef]
- Nagasako, N.; Jahnátek, M.; Asahi, R.; Hafner, J. Anomalies in the response of V, Nb, and Ta to tensile and shear loading: Ab initiodensity functional theory calculations. Phys. Rev. B 2010, 81, 094108. [Google Scholar] [CrossRef]
- Qi, L.; Chrzan, D.C. Tuning ideal tensile strengths and intrinsic ductility of bcc refractory alloys. Phys. Rev. Lett. 2014, 112, 115503. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, S.; Shafeie, S.; Hu, Q.; Ahlstrom, J.; Persson, C.; Vesely, J.; Zyka, J.; Klement, U.; Guo, S. Alloy design for intrinsically ductile refractory high-entropy alloys. J. Appl. Phys. 2016, 120, 164902. [Google Scholar] [CrossRef]
- King, D.J.M.; Middleburgh, S.C.; McGregor, A.G.; Cortie, M.B. Predicting the formation and stability of single phase high-entropy alloys. Acta Mater. 2016, 104, 172–179. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, X.; Liaw, P.K. Alloy Design and Properties Optimization of High-Entropy Alloys. JOM 2012, 64, 830–838. [Google Scholar] [CrossRef]
- Guo, N.N.; Wang, L.; Luo, L.S.; Li, X.Z.; Su, Y.Q.; Guo, J.J.; Fu, H.Z. Microstructure and mechanical properties of refractory MoNbHfZrTi high-entropy alloy. Mater. Des. 2015, 81, 87–94. [Google Scholar] [CrossRef]
- Fazakas, E.; Zadorozhnyy, V.; Varga, L.K.; Inoue, A.; Louzguine-Luzgin, D.V.; Tian, F.Y.; Vitos, L. Experimental and theoretical study of Ti20Zr20Hf20Nb20X20 (X = V or Cr) refractory high-entropy alloys. Int. J. Refract Met. Hard Mater. 2014, 47, 131–138. [Google Scholar] [CrossRef]
- Senkov, O.N.; Senkova, S.V.; Miracle, D.B.; Woodward, C. Mechanical properties of low-density, refractory multi-principal element alloys of the Cr-Nb-Ti-V-Zr system. Mater. Sci. Eng. A 2013, 565, 51–62. [Google Scholar] [CrossRef]




| Alloy | Delta/% | Hmix () | Smix | Tm (K) | |
|---|---|---|---|---|---|
| ZrTiHfV0.5Nb0.5 | 2.58 | 5.88 | −9.44 | 12.9671 | 2257 |
| Zr2.0TiHfVNb2.0 | 2.19 | 6.05 | −11.77 | 12.8860 | 2336 |
| ZrTiHfNb0.5Mo0.5 | 1.62 | 5.10 | −16.70 | 12.9671 | 2349 |
| ZrTiHfNb0.5Ta0.5 | 2.83 | 4.26 | −9.44 | 12.9671 | 2398 |
| Alloys | Region | Zr | Ti | Hf | V | Nb | Mo | Ta |
|---|---|---|---|---|---|---|---|---|
| ZrTiHfV0.5Nb0.5 | Dendrite | 24.31 | 24.34 | 25.91 | 12.03 | 13.42 | - | - |
| Interdendrite | 22.35 | 23.74 | 26.7 | 13.32 | 13.89 | - | - | |
| SR | 0.92 | 0.98 | 1.03 | 1.11 | 1.04 | - | - | |
| Zr2.0TiHfVNb2.0 | Dendrite | 27.57 | 13.58 | 14.65 | 13.4 | 30.8 | - | - |
| Interdendrite | 25.92 | 13.72 | 14.8 | 14.61 | 30.97 | - | - | |
| SR | 0.94 | 1.01 | 1.01 | 1.09 | 1.01 | - | - | |
| ZrTiHfNb0.5Mo0.5 | Dendrite | 22.99 | 21.85 | 25.58 | - | 18.99 | 10.59 | - |
| Interdendrite | 25.95 | 20.37 | 25.6 | - | 20.35 | 7.73 | - | |
| SR | 1.13 | 0.93 | 1 | - | 1.07 | 0.73 | - | |
| ZrTiHfNb0.5Ta0.5 | Dendrite | 23.56 | 21.36 | 23.33 | - | 17.5 | - | 10.78 |
| Interdendrite | 28.53 | 21.47 | 23.69 | - | 16.38 | - | 6.96 | |
| SR | 1.21 | 1.01 | 1.02 | - | 0.94 | - | 0.65 |
| Alloys | Density/g·cm−3 | Strain/% | Yield Stress/MPa | Specific Strength/MPa·cm3/g | Elevated Temperature Strength (800 °C) | Specific Strength/MPa·cm3/g (800 °C) | VEC |
|---|---|---|---|---|---|---|---|
| CrNbTiZr | 6.70 | 6% | 1260 | 188.06 | 300 | 44.78 [23] | 4.75 |
| HfMoNbTiZr | 8.69 | 9% | 1575 | 181.24 | 635 | 73.07 [21] | 4.60 |
| HfNbTiVZr | 8.06 | 30% | 1170 | 145.16 | 408 | 50.62 [22] | 4.40 |
| HfNbTaTiZr | 9.94 | >50% | 929 | 93.46 | 535 | 53.82 [9] | 4.40 |
| ZrTiHfV0.5Nb0.5 | 8.08 | >50% | 990 | 122.51 | 125 | 15.47 | 4.25 |
| Zr2.0TiHfVNb2.0 | 7.83 | >50% | 956 | 122.17 | 507 | 64.79 | 4.43 |
| ZrTiHfNb0.5Mo0.5 | 8.43 | >50% | 1195 | 141.77 | 595 | 70.59 | 4.38 |
| ZrTiHfNb0.5Ta0.5 | 9.14 | >50% | 738 | 80.79 | 193 | 21.13 | 4.25 |
| Alloys | Average Stress/MPa | Average Strain/% | Energy Absorption/(MJ·m−2) | ||
|---|---|---|---|---|---|
| 0.3 Atm | 0.4 Atm | 0.5 Atm | |||
| ZrTiHfV0.5Nb0.5 | 2642 | 50.03 | 4.21 | 4.08 | 5.71 |
| Zr2.0TiHfVNb2.0 | 1594 | 31.98 | 1.93 | 2.09 | 2.04 |
| ZrTiHfNb0.5Mo0.5 | 3337 | 70.1 | 7.02 | 7.78 | 8.46 |
| ZrTiHfNb0.5Ta0.5 | 1237 | 24.86 | 1.22 | 1.36 | 1.34 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Li, Y.; Cheng, X.; Wu, C.; Cheng, B.; Xu, Z. The Microstructure and Mechanical Properties of Refractory High-Entropy Alloys with High Plasticity. Materials 2018, 11, 208. https://doi.org/10.3390/ma11020208
Chen Y, Li Y, Cheng X, Wu C, Cheng B, Xu Z. The Microstructure and Mechanical Properties of Refractory High-Entropy Alloys with High Plasticity. Materials. 2018; 11(2):208. https://doi.org/10.3390/ma11020208
Chicago/Turabian StyleChen, Yiwen, Yunkai Li, Xingwang Cheng, Chao Wu, Bo Cheng, and Ziqi Xu. 2018. "The Microstructure and Mechanical Properties of Refractory High-Entropy Alloys with High Plasticity" Materials 11, no. 2: 208. https://doi.org/10.3390/ma11020208
APA StyleChen, Y., Li, Y., Cheng, X., Wu, C., Cheng, B., & Xu, Z. (2018). The Microstructure and Mechanical Properties of Refractory High-Entropy Alloys with High Plasticity. Materials, 11(2), 208. https://doi.org/10.3390/ma11020208




