Characterization of Different Cable Ferrite Materials to Reduce the Electromagnetic Noise in the 2–150 kHz Frequency Range
Abstract
:1. Introduction
2. Materials and Methods
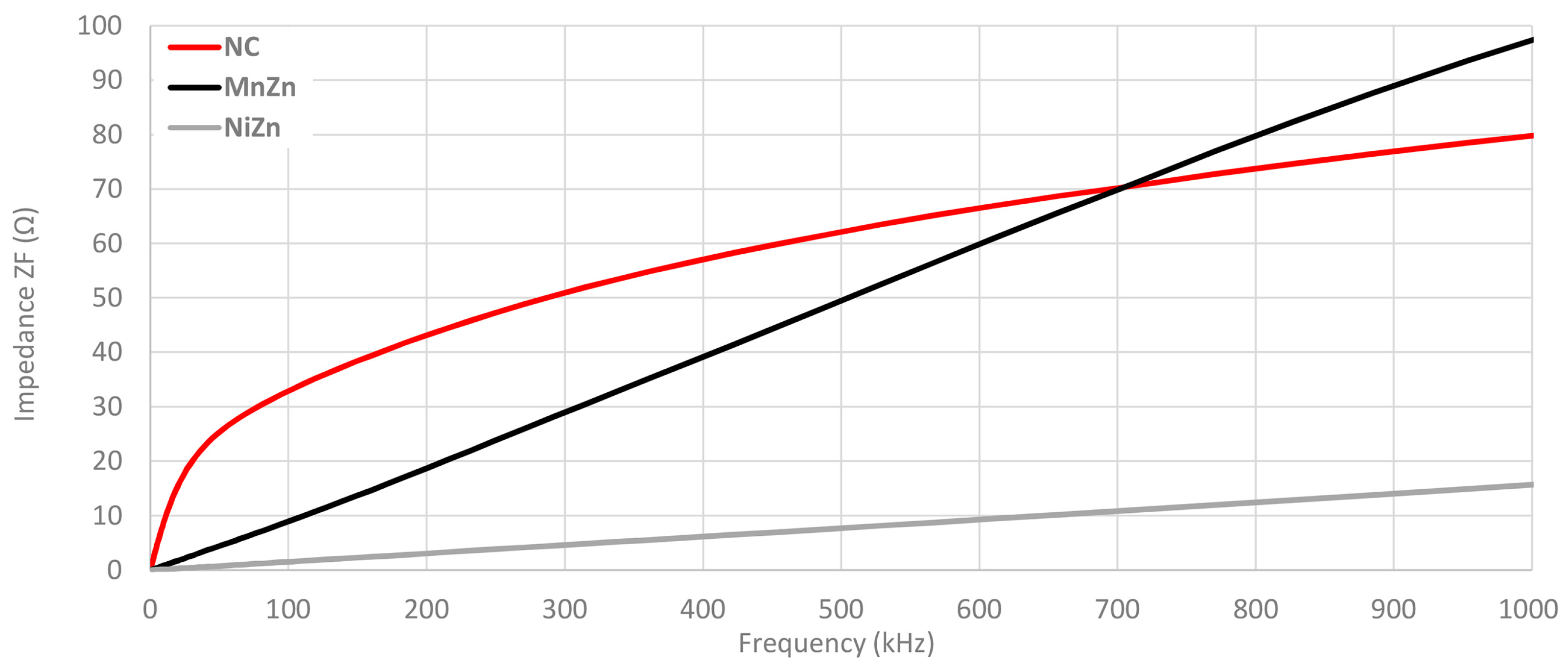
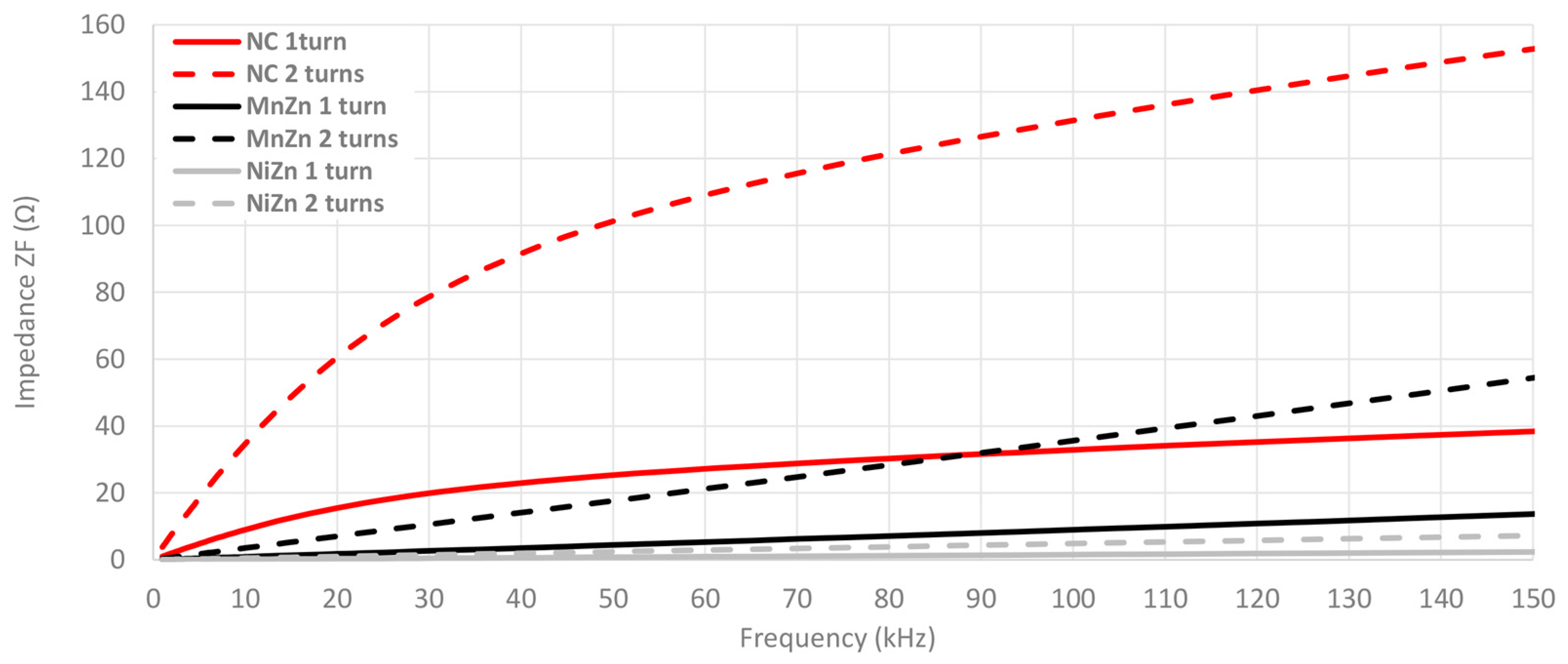
2.1. Cable Ferrites Characterization
2.2. Theoretical Insertion Loss Calculation Method
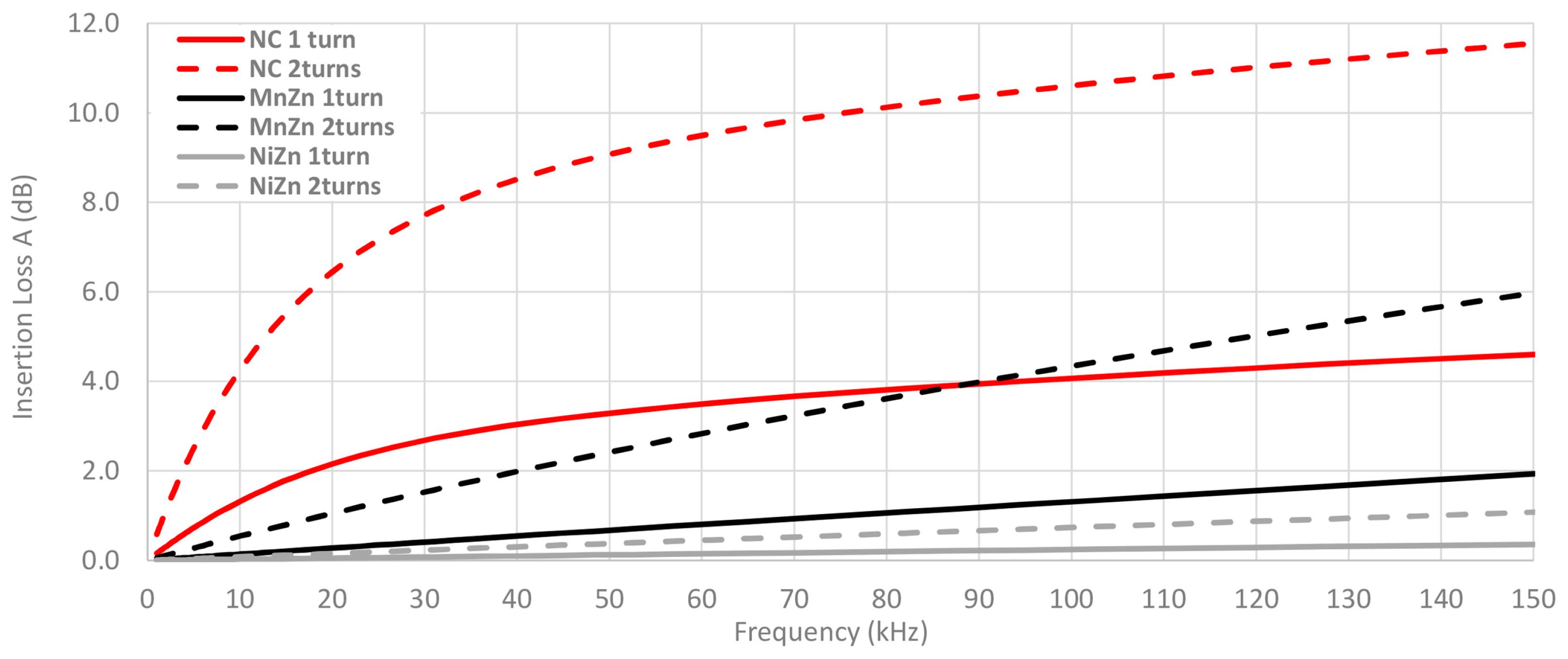
2.3. Insertion Loss Experimental Measurement Setup
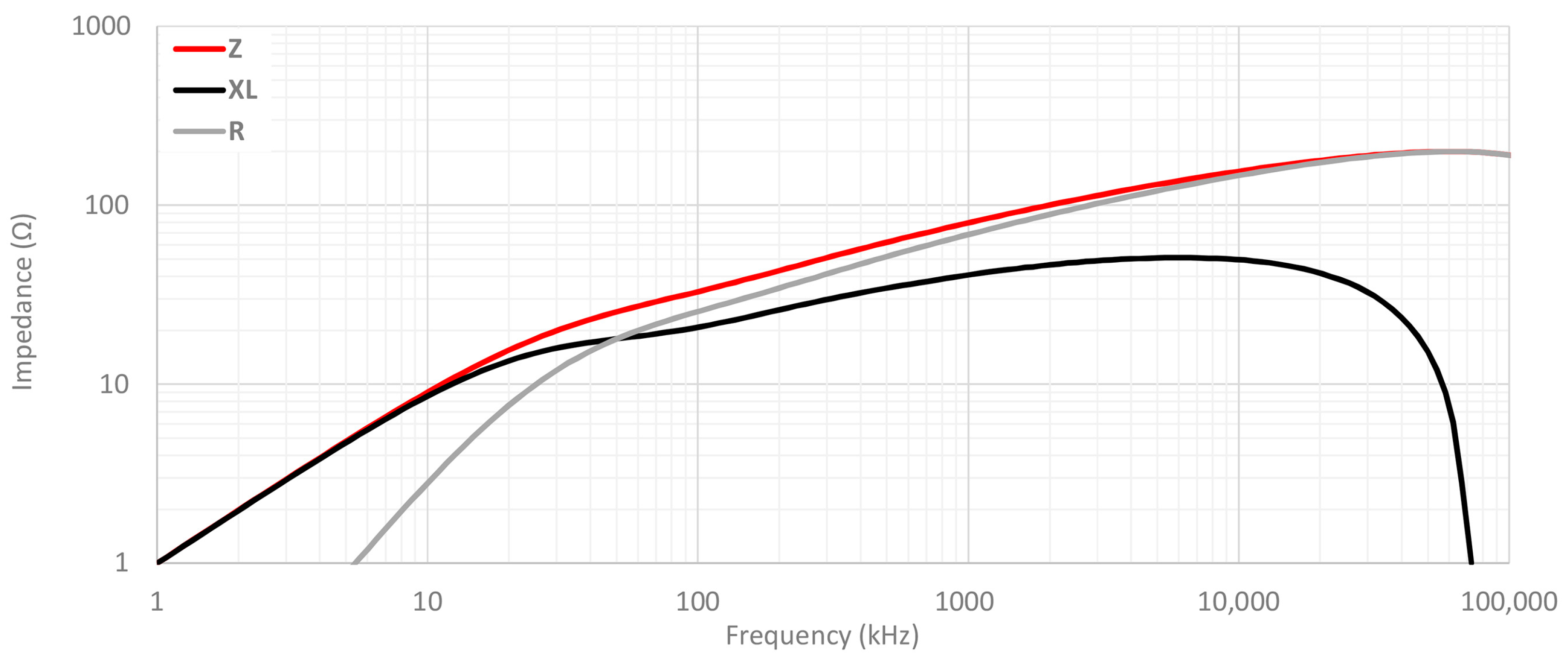
- A low frequency immunity test system based on the NSG-4060/1 Low Frequency Signal Generator (TESEQ, Luterbach, Switzerland) with 50 Ω of output impedance is employed to generate the reference signal that crosses the cable ferrite. Thus, this 50 Ω output resistance represents the ZA in the insertions loss block diagram. This sine wave generator and integrated power amplifier consists of a signal generator able to provide signals for the frequency range of 15 Hz to 150 kHz. The probe connected to this generator separates the signal and the ground terminals to place the cable ferrite only in the signal path. The main objective of this part of the setup is focused on characterizing the performance of cable ferrites in this range of frequencies through simulating the electromagnetic noise which can appear in a real system.
- The N9010A Spectrum Analyzer (Keysight, Santa Rosa, CA, USA) is used both for measuring the amplitude of the signal generated as a reference and the signal when the cable ferrite is placed around the cable. This equipment makes it possible to analyze the attenuation provided by each kind of cable ferrite in the range of 2–150 kHz. The measurement is carried out with a low frequency current probe which measures the signal before and after placing the cable ferrite.
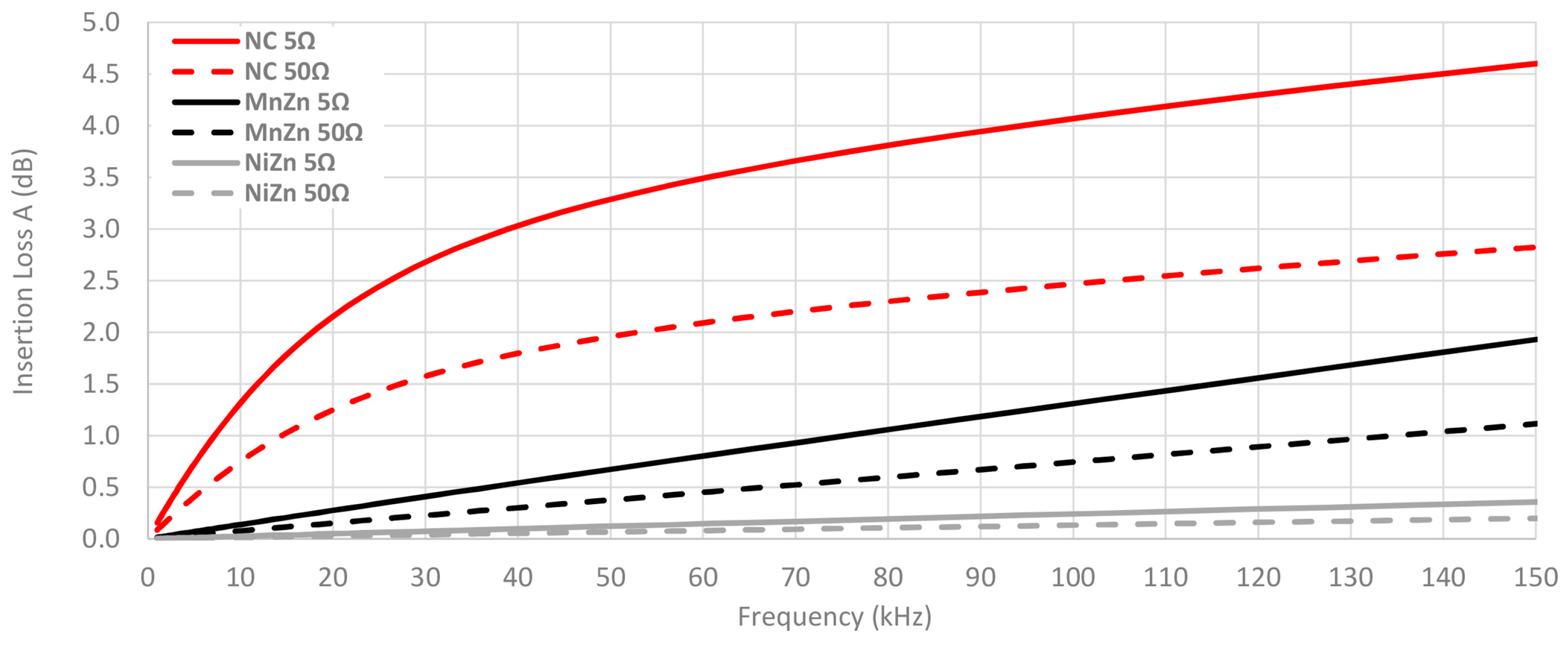
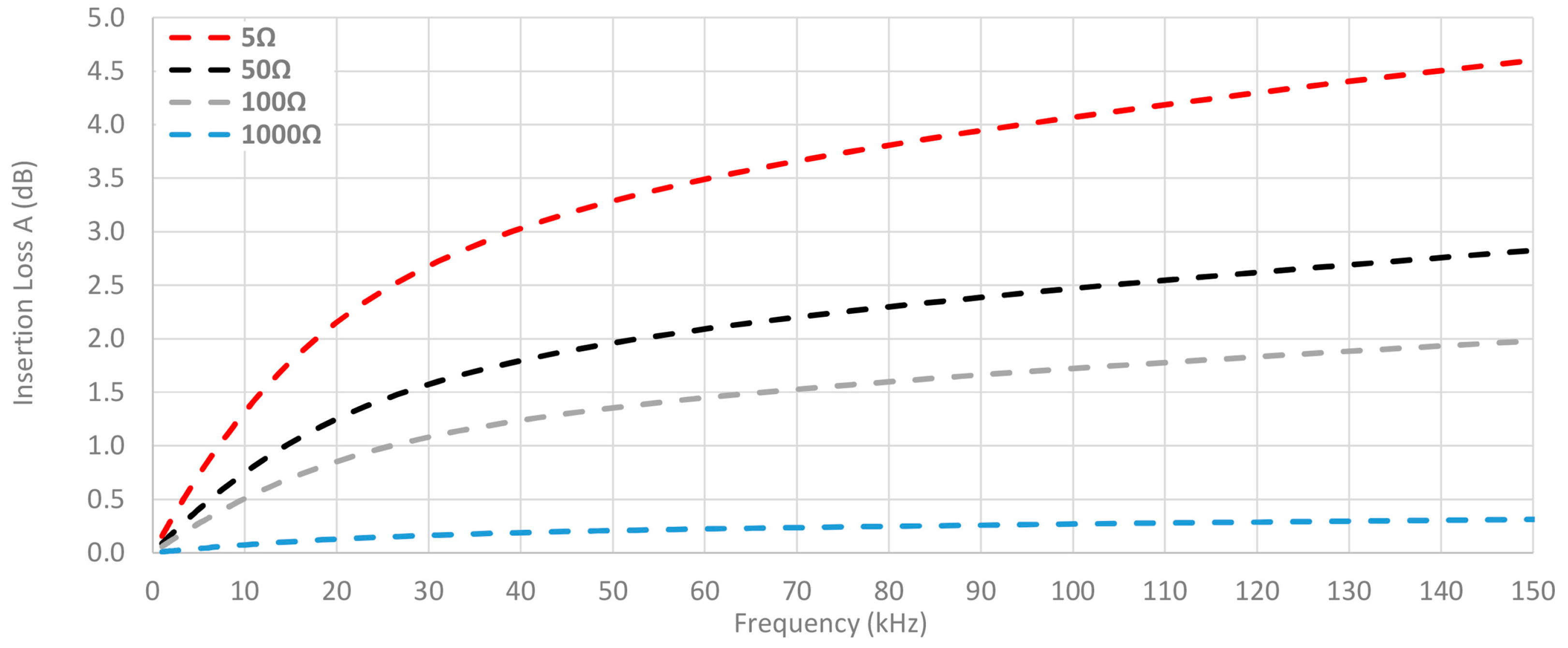
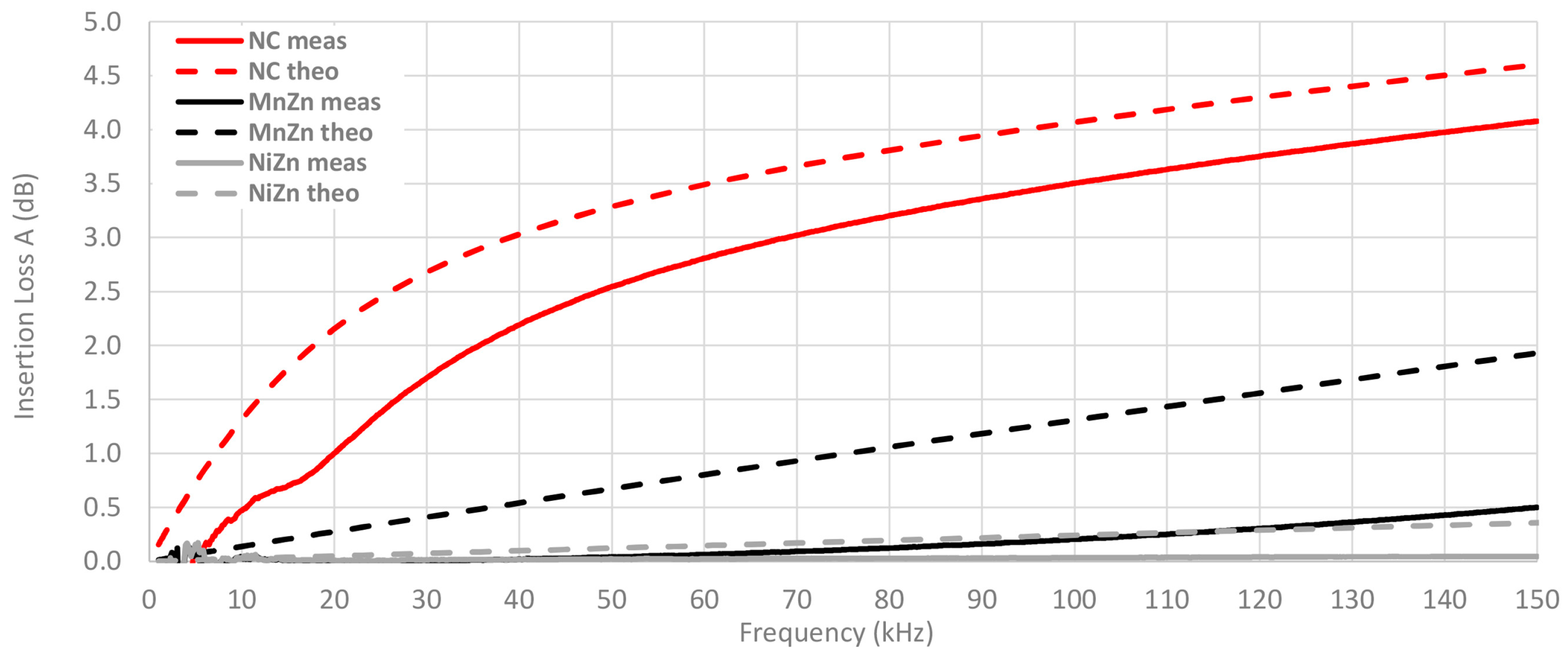
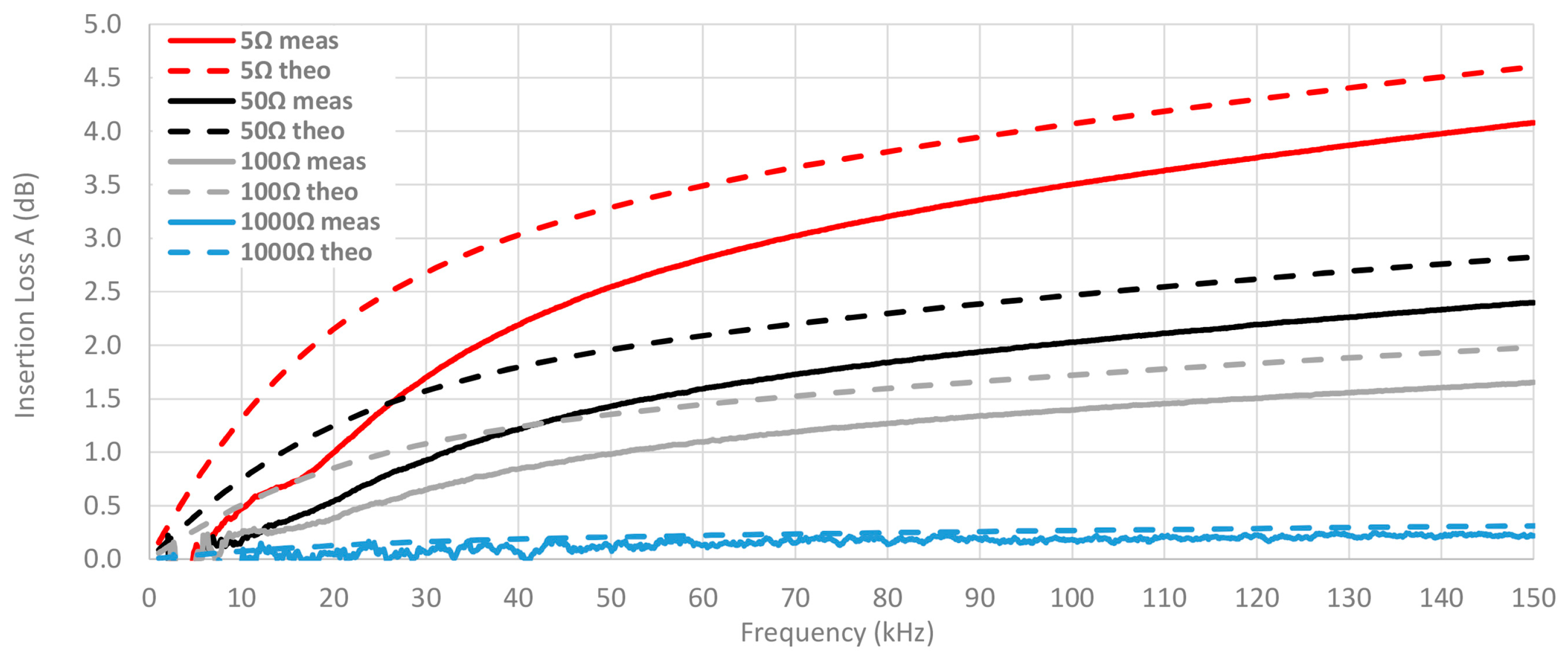
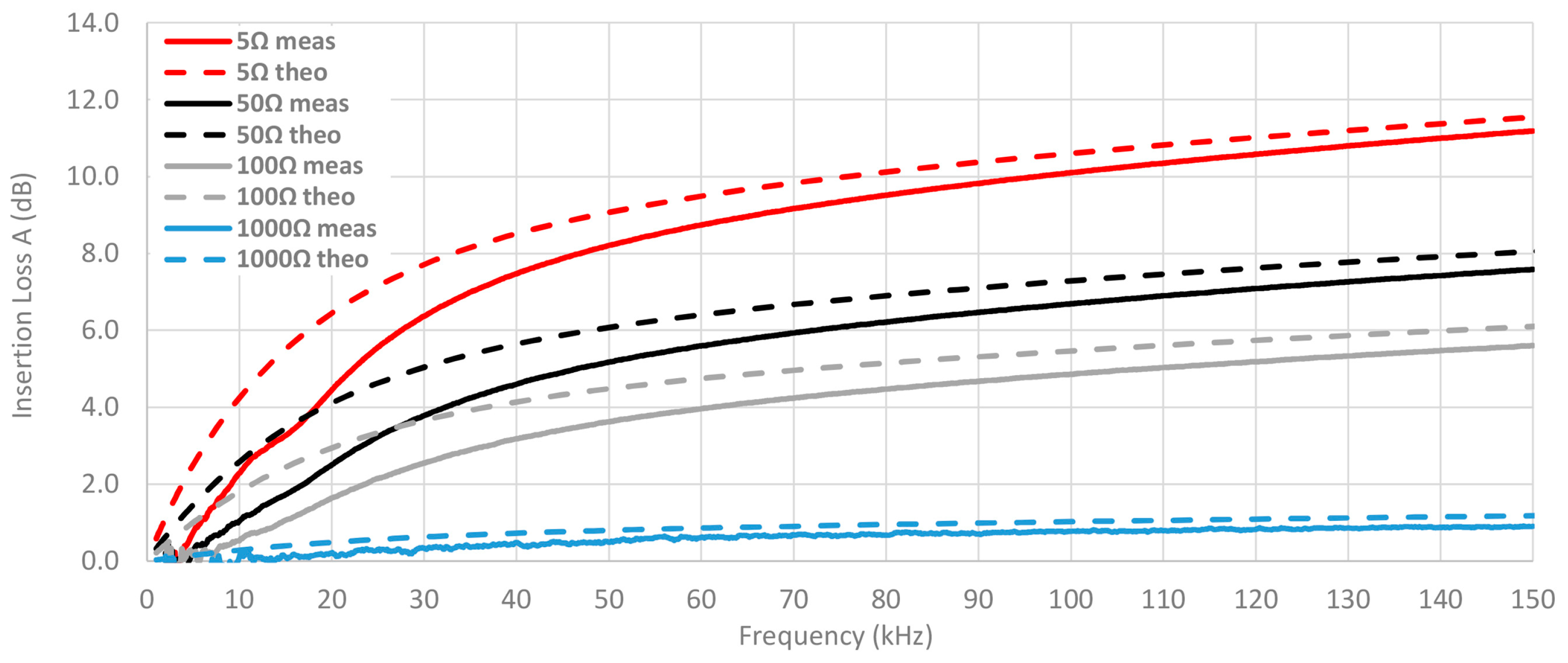
- Different resistance loads are employed to evaluate the performance and robustness of ferrites. In order to analyze the characteristics of cable ferrites with different values of load impedance, a PCB (Printed Circuit Board) which holds several values of impedance has been designed. This circuit is intended for switching among four different values of ZB 5 Ω, 50 Ω, 100 Ω and 1000 Ω. Since the performance of cable ferrites relies on the load impedance, this part of the setup allows us to study the behavior of each material composition in systems with different load values.
3. Results and Discussion
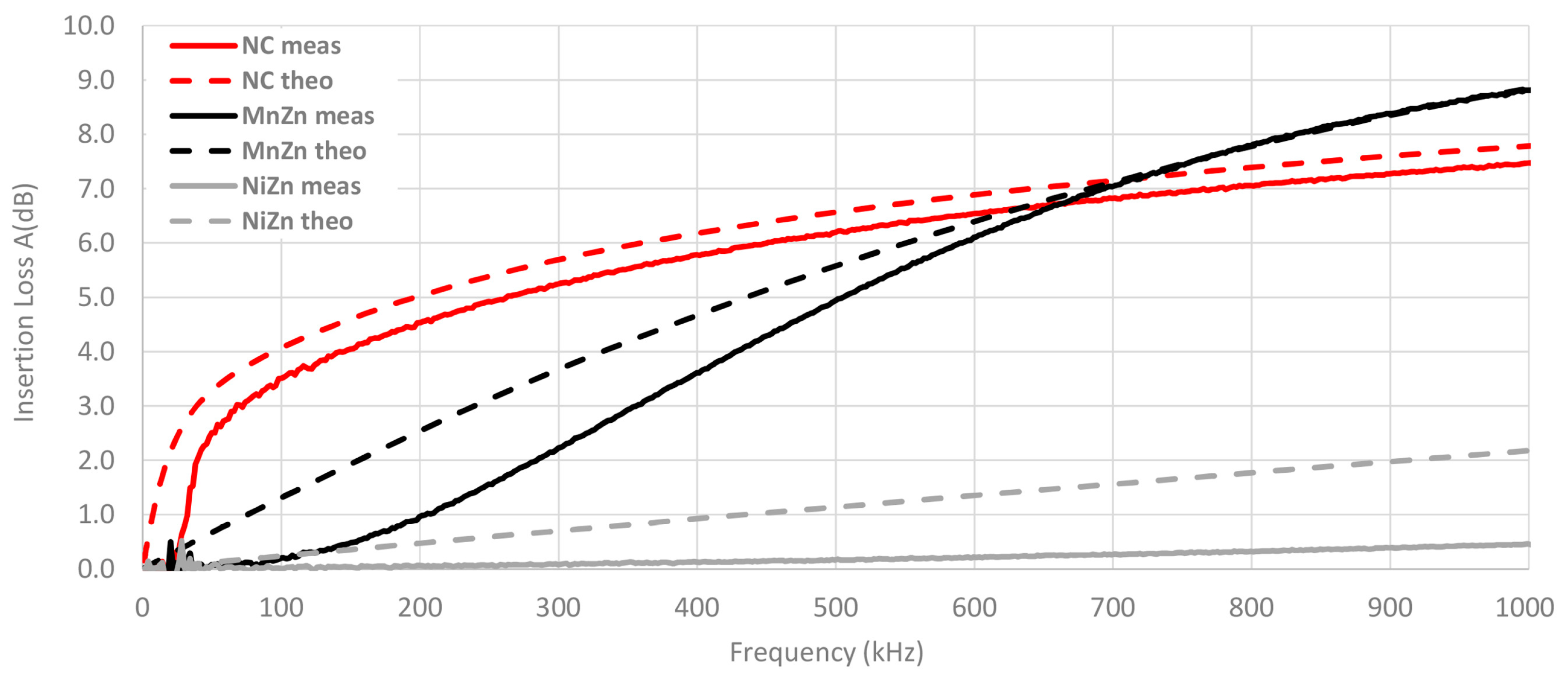
3.1. Theoretical Insertion Loss Results
3.2. Experimental Insertion Loss Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bollen, M.; Olofsson, M.; Larsson, A.; Rönnberg, S.; Lundmark, M. Standards for supraharmonics (2 to 150 kHz). IEEE Electromagn. Compat. Mag. 2014, 3, 114–119. [Google Scholar]
- Luszcz, J. High Frequency Harmonics Emission in Smart Grids. In Power Quality Issues; Zobaa, A., Ed.; InTech: Rijeka, Croatia, 2013; pp. 277–280. [Google Scholar]
- Schöttke, S.; Meyer, J.; Schegner, P.; Bachmann, S. Emission in the frequency range of 2 kHz to 150 kHz caused by electrical vehicle charging. In Proceedings of the International Symposium on Electromagnetic Compatibility, Gothenburg, Sweden, 1–4 September 2014; pp. 620–625. [Google Scholar]
- Rönnberg, S.; Bollen, M.; Larsson, A. Emission from small scale PV-installations on the low voltage grid. In Proceedings of the International Conference on Renewable Energies and Power Quality, Córdoba, Spain, 8–10 April 2014; pp. 617–621. [Google Scholar]
- Bartak, G.F.; Abart, A. EMI of emissions in the frequency range 2 kHz–150 kHz. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution, Stockholm, Sweden, 10–13 June 2013. [Google Scholar]
- Gil-de-Castro, A.; Rönnberg, S.K.; Bollen, M.H.; Moreno-Muñoz, A. Study on harmonic emission of domestic equipment combined with different types of lighting. Int. J. Electr. Power Energy Syst. 2014, 55, 116–127. [Google Scholar]
- Subhani, S.; Cuk, V.; Coben, J.F.G. A Literature Survey on Power Quality Disturbances in the Frequency Range of 2–150 kHz. In Proceedings of the International Conference on Renewable Energies and Power Quality, Málaga, Spain, 8–10 April 2017; pp. 405–410. [Google Scholar]
- Smolenski, R. Conducted Electromagnetic Interference (EMI) in Smart Grids. In Power Systems; Springer Science & Business Media: London, UK, 2012. [Google Scholar]
- Coenen, M.; van Roermund, A. Conducted mains test method in 2–150 kHz band. In Proceedings of the International Symposium on Electromagnetic Compatibility, Gothenburg, Sweden, 1–4 September 2014; pp. 601–604. [Google Scholar]
- Ott, H.W. Electromagnetic Compatibility Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 225–234. [Google Scholar]
- Brander, T.; Gerfer, A.; Rall, B.; Zenkner, H. Trilogy of Magnetics: Design Guide for EMI Filter Design, SMP & RF Circuits, 4th ed.; Swiridoff Verlag: Künzelsau, Germany, 2010. [Google Scholar]
- Lukovic, M.D.; Nikolic, M.V.; Blaz, N.V.; Zivanov, L.D.; Aleksic, O.S.; Lukic, L.S. Mn-Zn ferrite round cable EMI suppressor with deep grooves and a secondary short circuit for different frequency ranges. IEEE Electromagn. Compat. Mag. 2013, 49, 1172–1177. [Google Scholar]
- Tsutaoka, T. Frequency dispersion of complex permeability in Mn-Zn and Ni-Zn spinel ferrites and their composite materials. J. Appl. Phys. 2003, 93, 2789–2796. [Google Scholar]
- Herzer, G.; Vazquez, M.; Knobel, M.; Zhukov, A.; Reininger, T.; Davies, H.A.; Sanchez Ll, J.S. Round table discussion: Present and future applications of nanocrystalline magnetic materials. J. Magn. Magn. Mater. 2005, 294, 252–266. [Google Scholar]
- Thierry, W.; Thierry, S.; Benoît, V.; Dominique, G. Strong volume reduction of common mode choke for RFI filters with the help of nanocrystalline cores design and experiments. J. Magn. Magn. Mater. 2006, 304, 847–849. [Google Scholar]
- Herzer, G. Modern soft magnets: Amorphous and nanocrystalline materials. Acta Mater. 2013, 61, 718–734. [Google Scholar]
- Liu, Y.; Han, Y.; Liu, S.; Lin, F. Pulse Magnetic Properties Measurement and Characterization of Fe-Based Nanocrystalline Cores for High-Voltage Pulse Magnetics Applications. IEEE Trans. Power Electron. 2015, 30, 6883–6896. [Google Scholar]
- Davies, H.; Gibbs, M. Handbook of Magnetism and Advanced Materials; Kronmüller, K., Parkin, S., Eds.; John Wiley & Sons: London, UK, 2007; Volume 4. [Google Scholar]
- Boll, R.; Hilzinger, HR.; Warlimont, H. The Magnetic, Chemical and Structural Properties of Glassy Metallic Alloys; Hasegawa, R., Ed.; CRC Press: Boca Raton, FL, USA, 1983. [Google Scholar]
- Yoshizawa, Y.; Oguma, S.; Yamauchi, K. New Fe-based soft magnetic alloys composed of ultrafine grain structure. J. Appl. Phys. 1988, 64, 6044–6046. [Google Scholar]
- Kawano, K.; Hachiya, M.; Iijima, Y.; Sato, N.; Mizuno, Y. The grain size effect on the magnetic properties in NiZn ferrite and the quality factor of the inductor. J. Magn. Magn. Mater. 2009, 321, 2488–2493. [Google Scholar]
- Goldman, A. Modern Ferrite Technology, 2nd ed.; Springer Science & Business Media: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Suarez, A.; Victoria, J.; Alcarria, A.; Torres, J. Characterization of electromagnetic noise suppression sheet for aerospace applications. In Proceedings of the ESA Workshop on Aerospace EMC, Valencia, Spain, 23–25 May 2016; pp. 1–6. [Google Scholar]
- Sharma, A.; Rahman, N.; Obol, M.; Afsar, M. Precise characterization and design of composite absorbers for wideband microwave applications. In Proceedings of the European Microwave Conference, Paris, France, 28–30 September 2010; pp. 160–163. [Google Scholar]
- Jiles, D. Introduction to Magnetism and Magnetic Materials, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hu, P.; Yang, H.B.; Pan, D.A.; Wang, H.; Tian, J.J.; Zhang, S.; Wang, X.; Volinsky, A.A. Heat treatment effects on microstructure and magnetic properties of Mn-Zn ferrite powders. J. Magn. Magn. Mater. 2010, 322, 173–177. [Google Scholar]
- Beatrice, C.; Bottauscio, O.; Chiampi, M.; Fiorillo, F.; Manzin, A. Magnetic loss analysis in Mn-Zn ferrite cores. J. Magn. Magn. Mater. 2006, 304, e743–e745. [Google Scholar]
- Sun, G.L.; Li, J.B.; Sun, J.J.; Yang, X.Z. The influences of Zn2+ and some rare-earth ions on the magnetic properties of nickel-zinc ferrites. J. Magn. Magn. Mater. 2004, 281, 173–177. [Google Scholar]
- Costa, A.C.F.M.; Tortella, E.; Morelli, M.R.; Kiminami, R.H.G.A. Synthesis, microstructure and magnetic properties of Ni-Zn ferrites. J. Magn. Magn. Mater. 2003, 256, 174–182. [Google Scholar]
- Stergiou, C.A.; Zaspalis, V. Analysis of the complex permeability of NiCuZn ferrites up to 1 GHz with regard to Cu content and sintering temperature. Ceram. Int. 2014, 40, 357–366. [Google Scholar]
- Keysight E5061B-3L3/3L4/3L5 LF-RF Network Analyzer with Option 005 Impedance Analysis Function. Available online: http://literature.cdn.keysight.com/litweb/pdf/5990-7033EN.pdf (accessed on 22 November 2017).


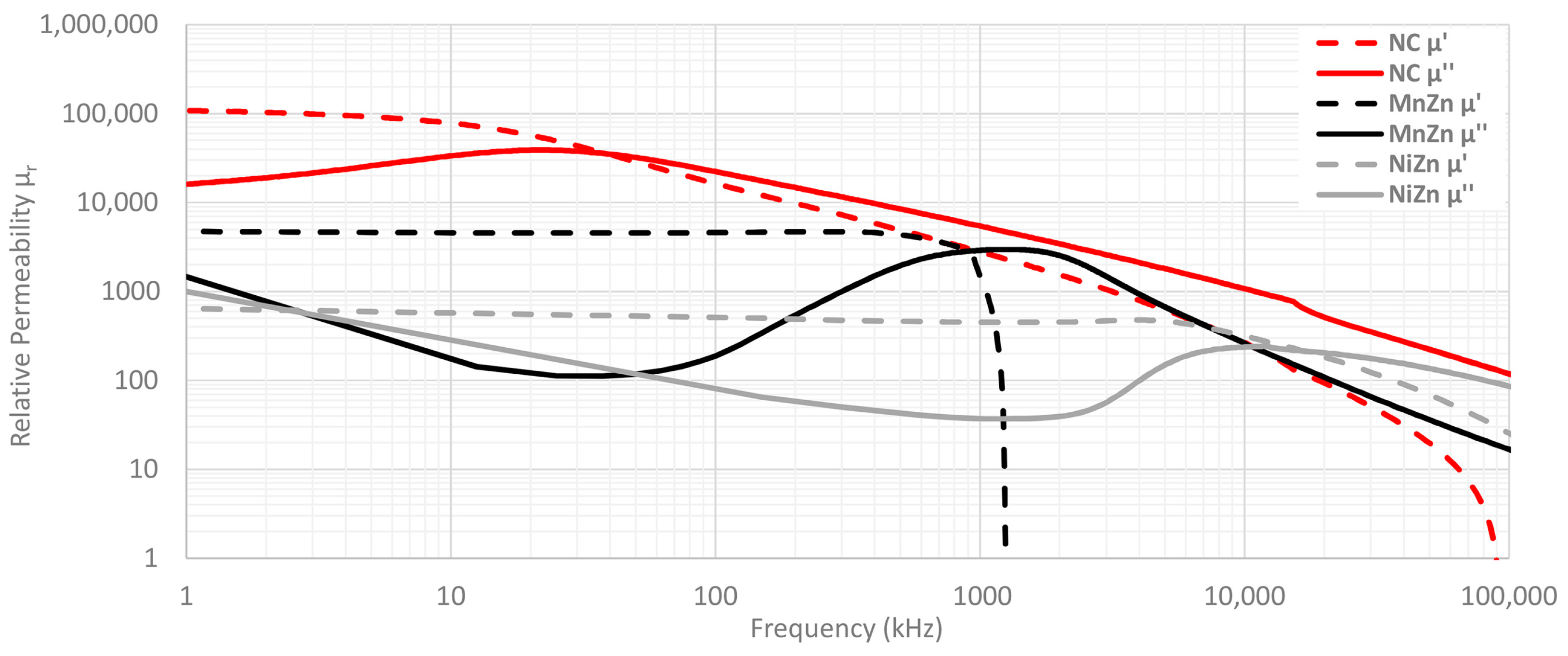
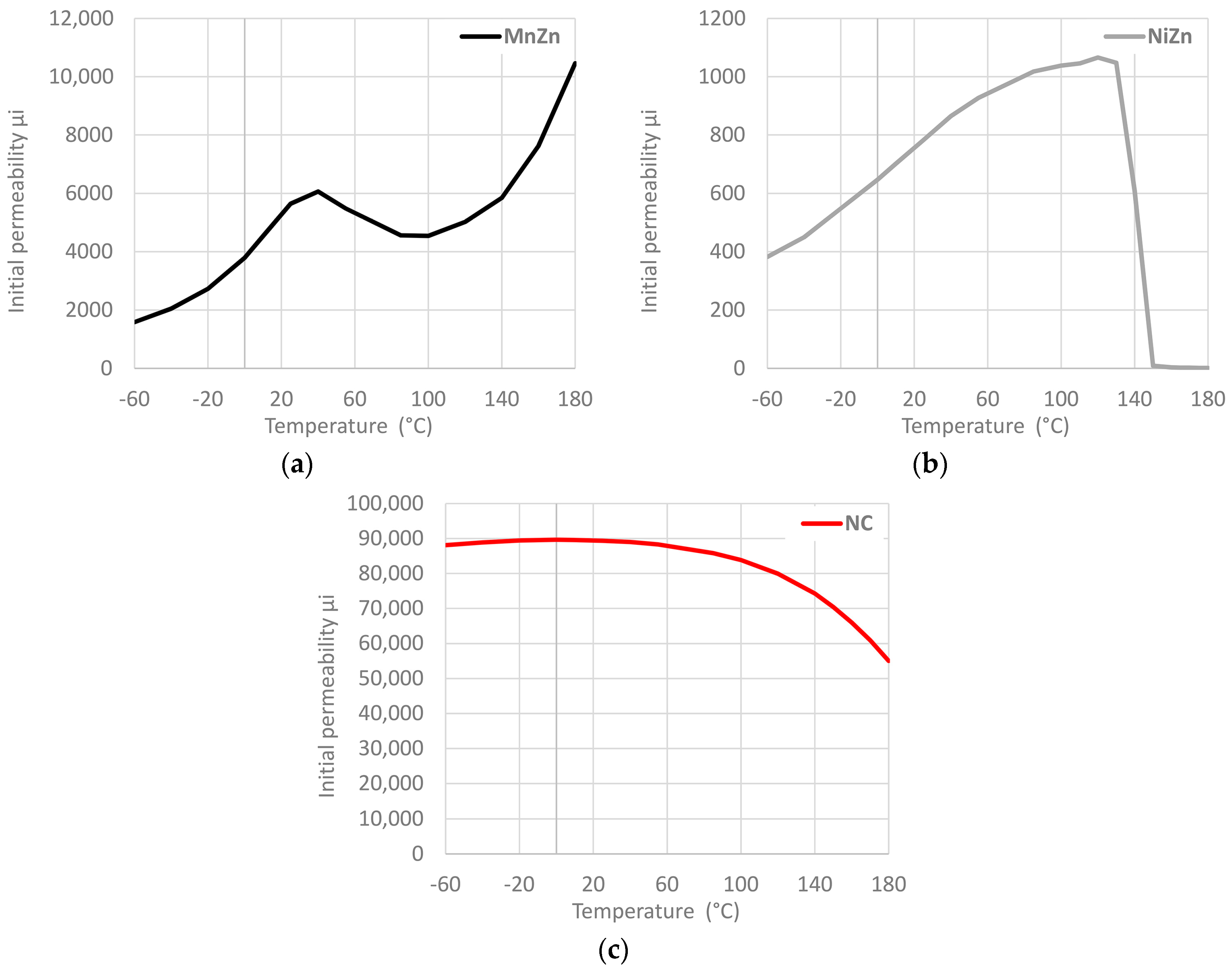

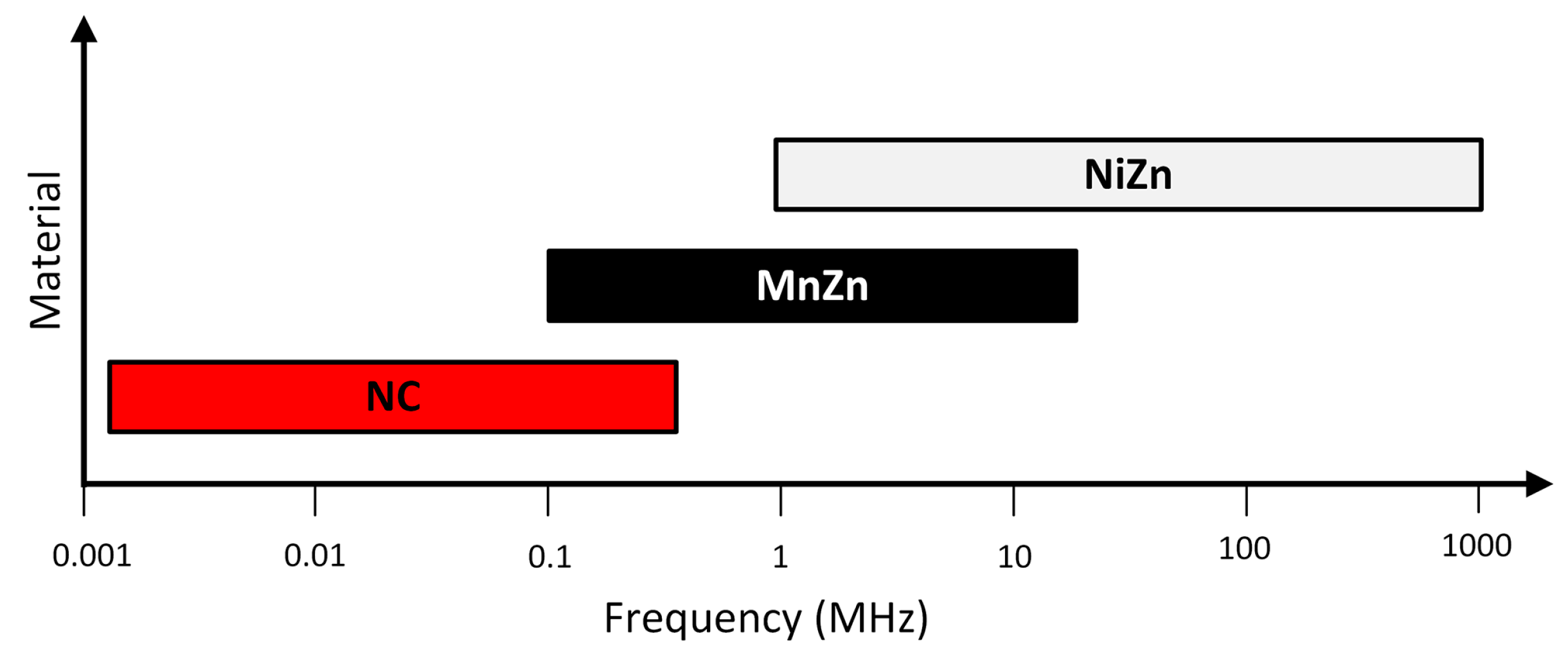





| Ferrite Part Number | Magnetic Material | External Diameter (mm) | Internal Diameter (mm) | Height (mm) |
|---|---|---|---|---|
| M-4304-02 | NC | 18.9 | 12.9 | 27.7 |
| 74277255 | MnZn | 18.6 | 10.2 | 28.5 |
| 74270055 | NiZn | 18.6 | 10.2 | 28.5 |
| Ferrite PN | Material | Initial Perm 1 | Curie Temp 2 | Sat. Flux Density 3 | Sat. Field Density 4 | Coercivity 5 | Resonance Frequency |
|---|---|---|---|---|---|---|---|
| M-4304-02 | NC | 89,400 | 150 °C | 717.8 mT | 222.4 A/m | 8.5 A/m | 33 kHz |
| 74277255 | MnZn | 5638 | >180 °C | 404.8 mT | 477.4 A/m | 9.2 A/m | 875 kHz |
| 74270055 | NiZn | 783 | 135 °C | 296.7 mT | 567.9 A/m | 30.9 A/m | 16.5 MHz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suarez, A.; Victoria, J.; Alcarria, A.; Torres, J.; Martinez, P.A.; Martos, J.; Soret, J.; Garcia-Olcina, R.; Muetsch, S. Characterization of Different Cable Ferrite Materials to Reduce the Electromagnetic Noise in the 2–150 kHz Frequency Range. Materials 2018, 11, 174. https://doi.org/10.3390/ma11020174
Suarez A, Victoria J, Alcarria A, Torres J, Martinez PA, Martos J, Soret J, Garcia-Olcina R, Muetsch S. Characterization of Different Cable Ferrite Materials to Reduce the Electromagnetic Noise in the 2–150 kHz Frequency Range. Materials. 2018; 11(2):174. https://doi.org/10.3390/ma11020174
Chicago/Turabian StyleSuarez, Adrian, Jorge Victoria, Antonio Alcarria, Jose Torres, Pedro A. Martinez, Julio Martos, Jesus Soret, Raimundo Garcia-Olcina, and Steffen Muetsch. 2018. "Characterization of Different Cable Ferrite Materials to Reduce the Electromagnetic Noise in the 2–150 kHz Frequency Range" Materials 11, no. 2: 174. https://doi.org/10.3390/ma11020174
APA StyleSuarez, A., Victoria, J., Alcarria, A., Torres, J., Martinez, P. A., Martos, J., Soret, J., Garcia-Olcina, R., & Muetsch, S. (2018). Characterization of Different Cable Ferrite Materials to Reduce the Electromagnetic Noise in the 2–150 kHz Frequency Range. Materials, 11(2), 174. https://doi.org/10.3390/ma11020174






