Use of the Wilshire Equations to Correlate and Extrapolate Creep Data of Inconel 617 and Nimonic 105
Abstract
1. Introduction
2. Wilshire and Larson–Miller Parameter Equations
2.1. Wilshire Equation
2.2. Larson–Miller Parameter Equation
3. Methods
3.1. Data
3.1.1. Inconel 617
3.1.2. Nimonic 105
3.2. Wilshire Equation
3.3. Larson–Miller Parameter Equation
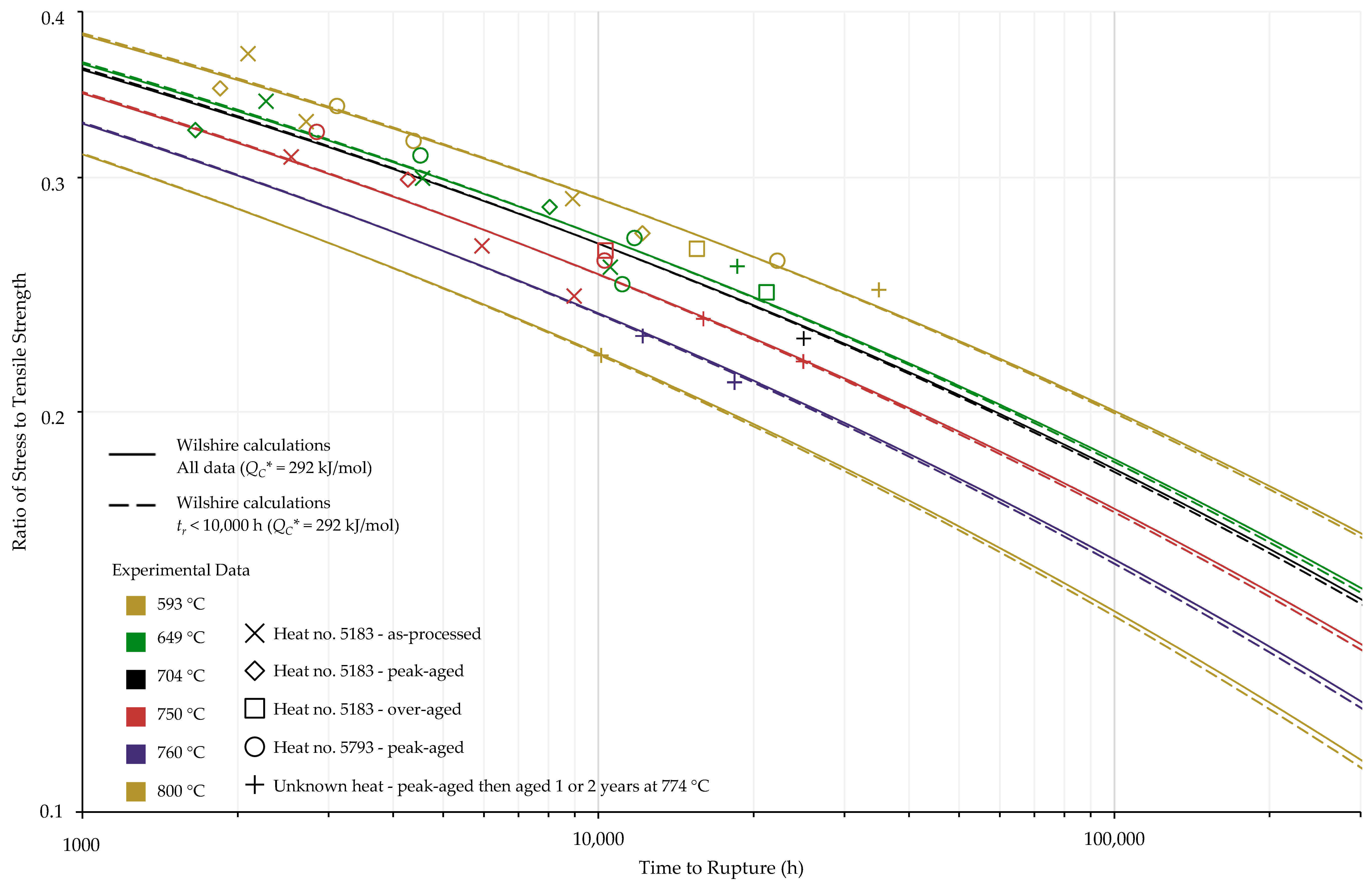
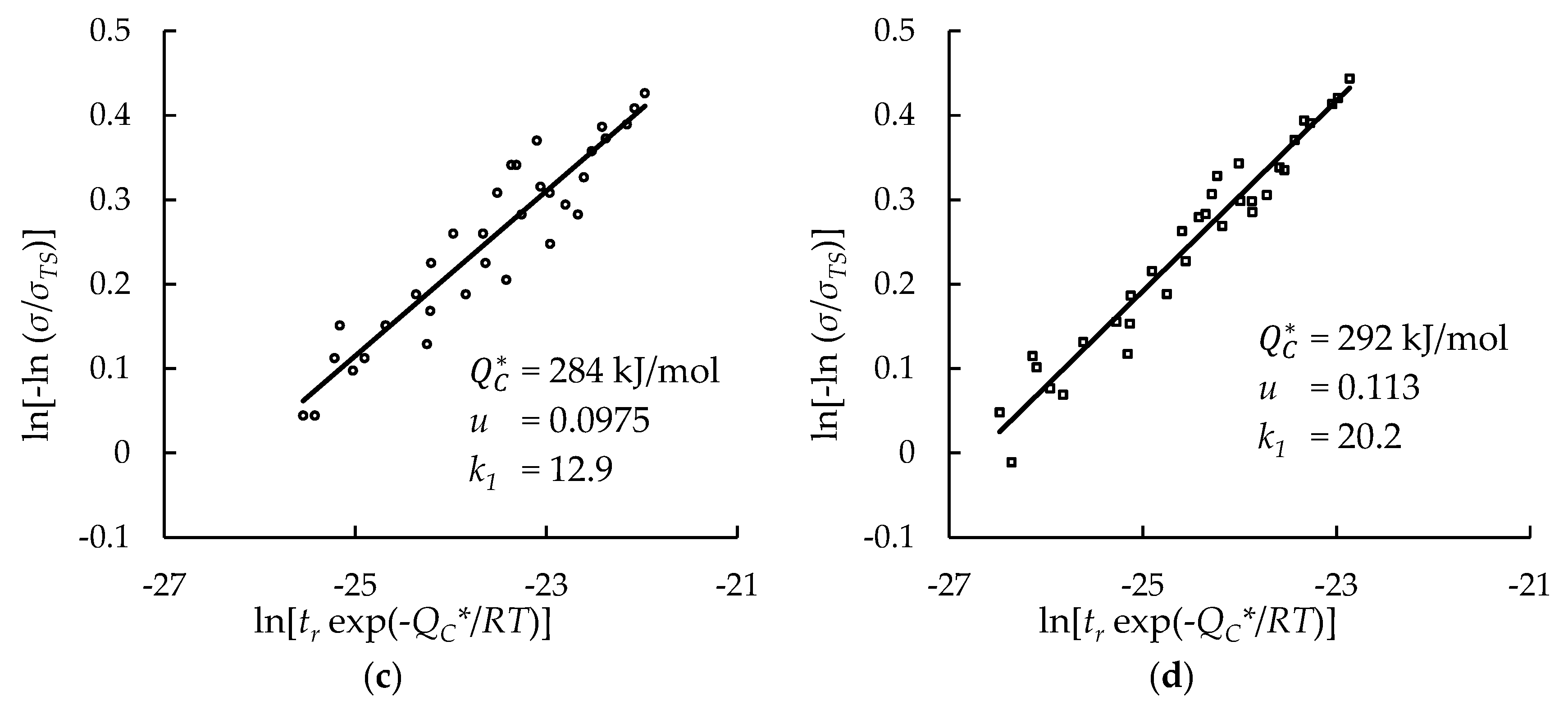
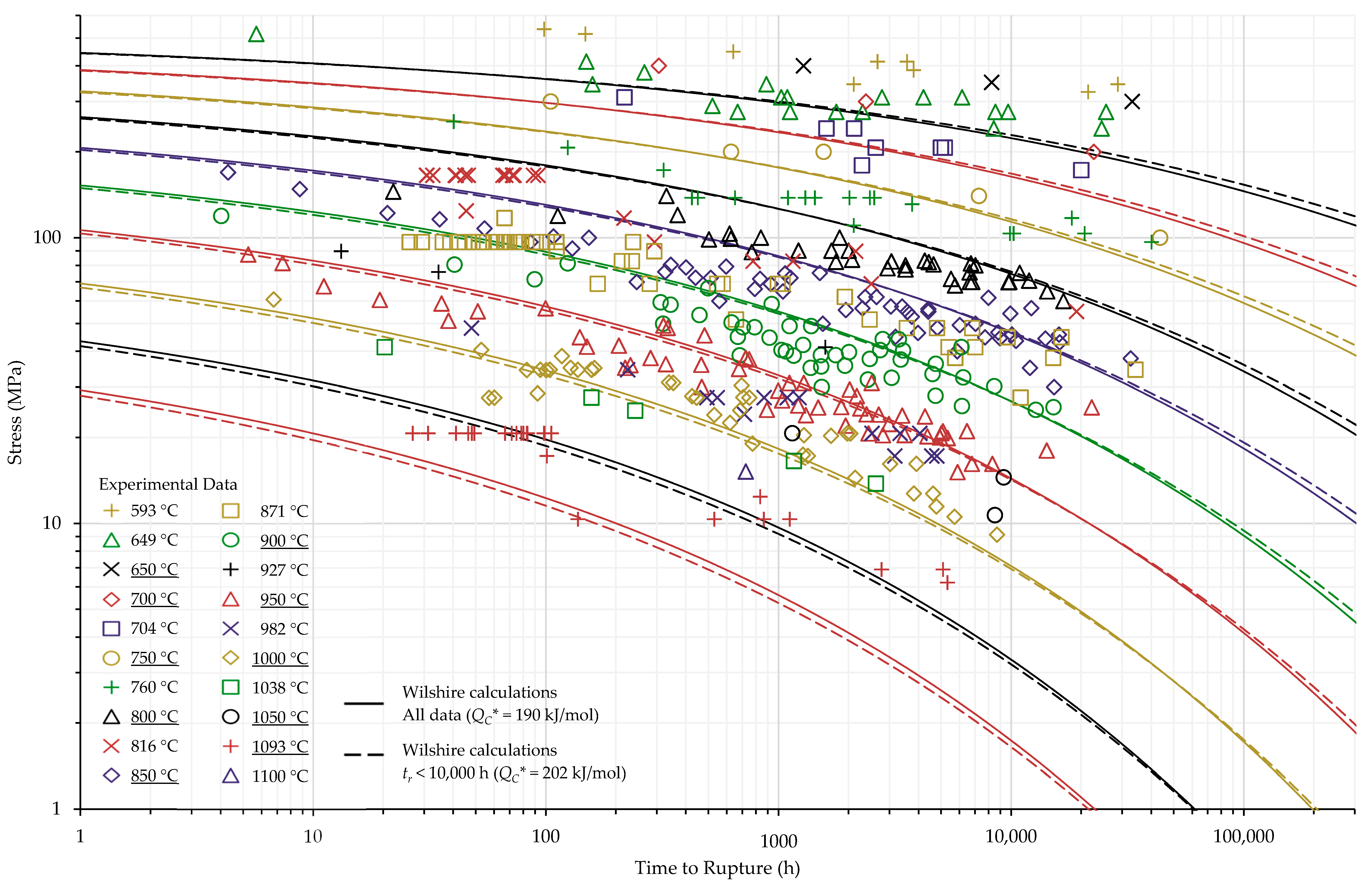
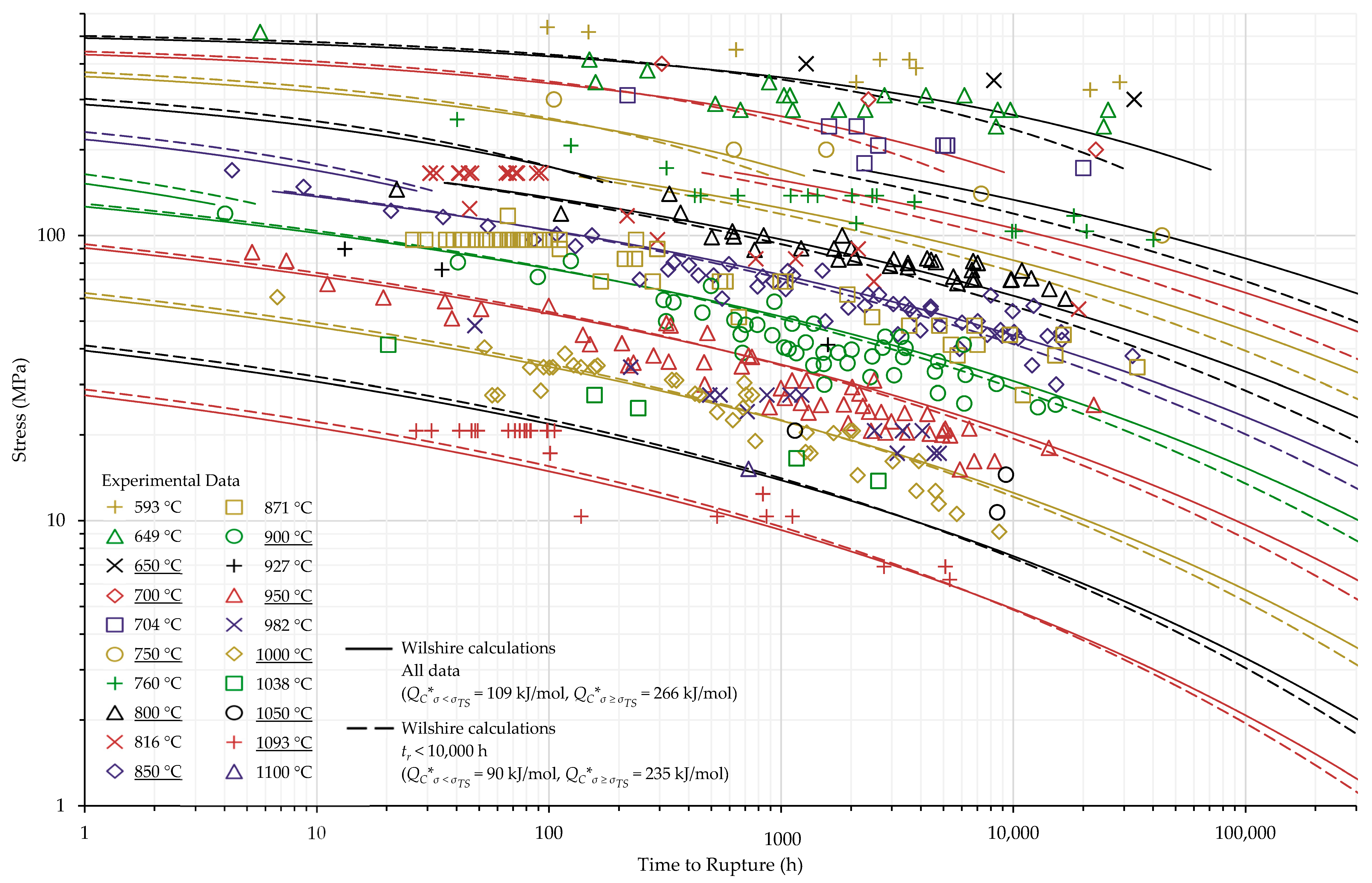
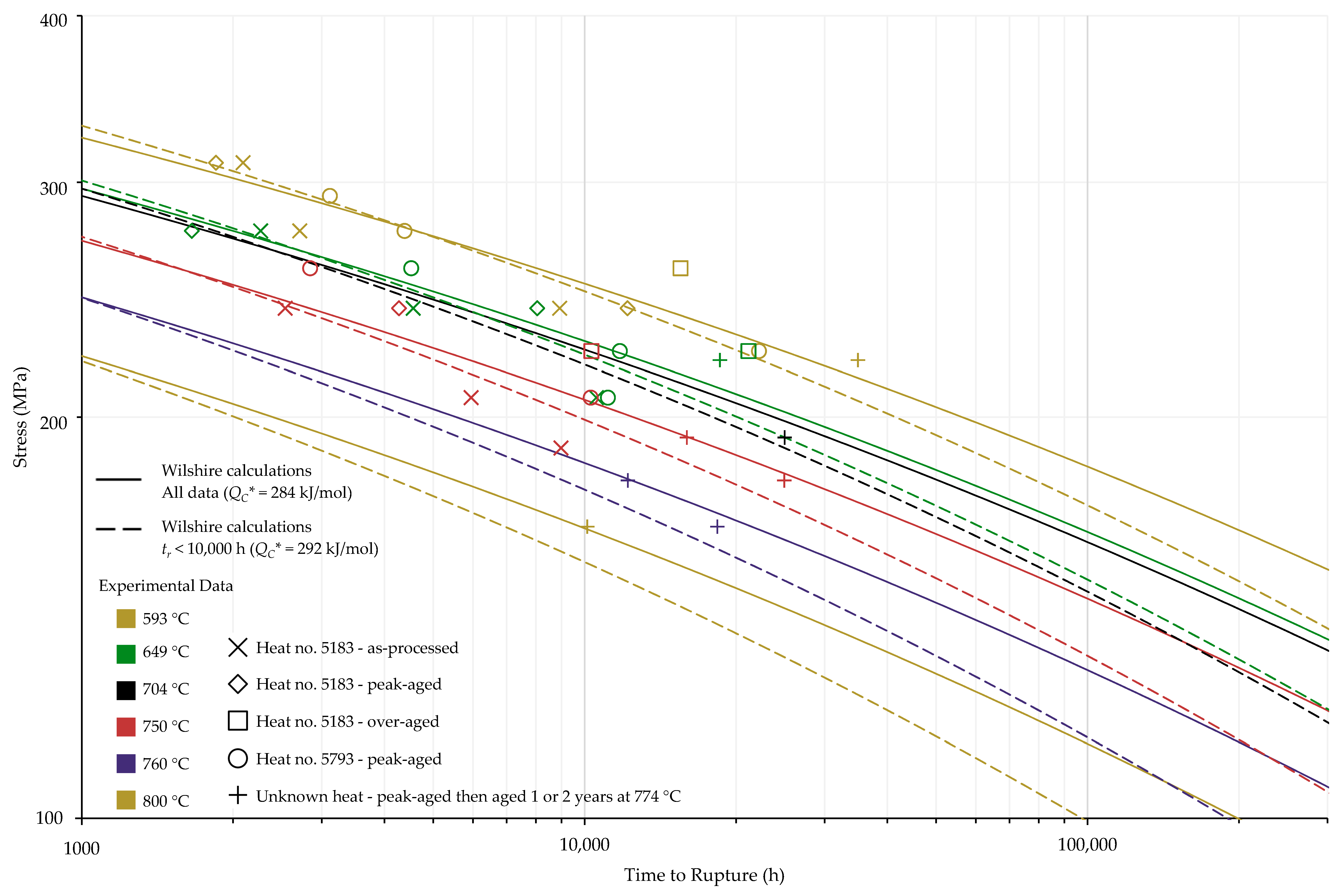
4. Results and Discussion
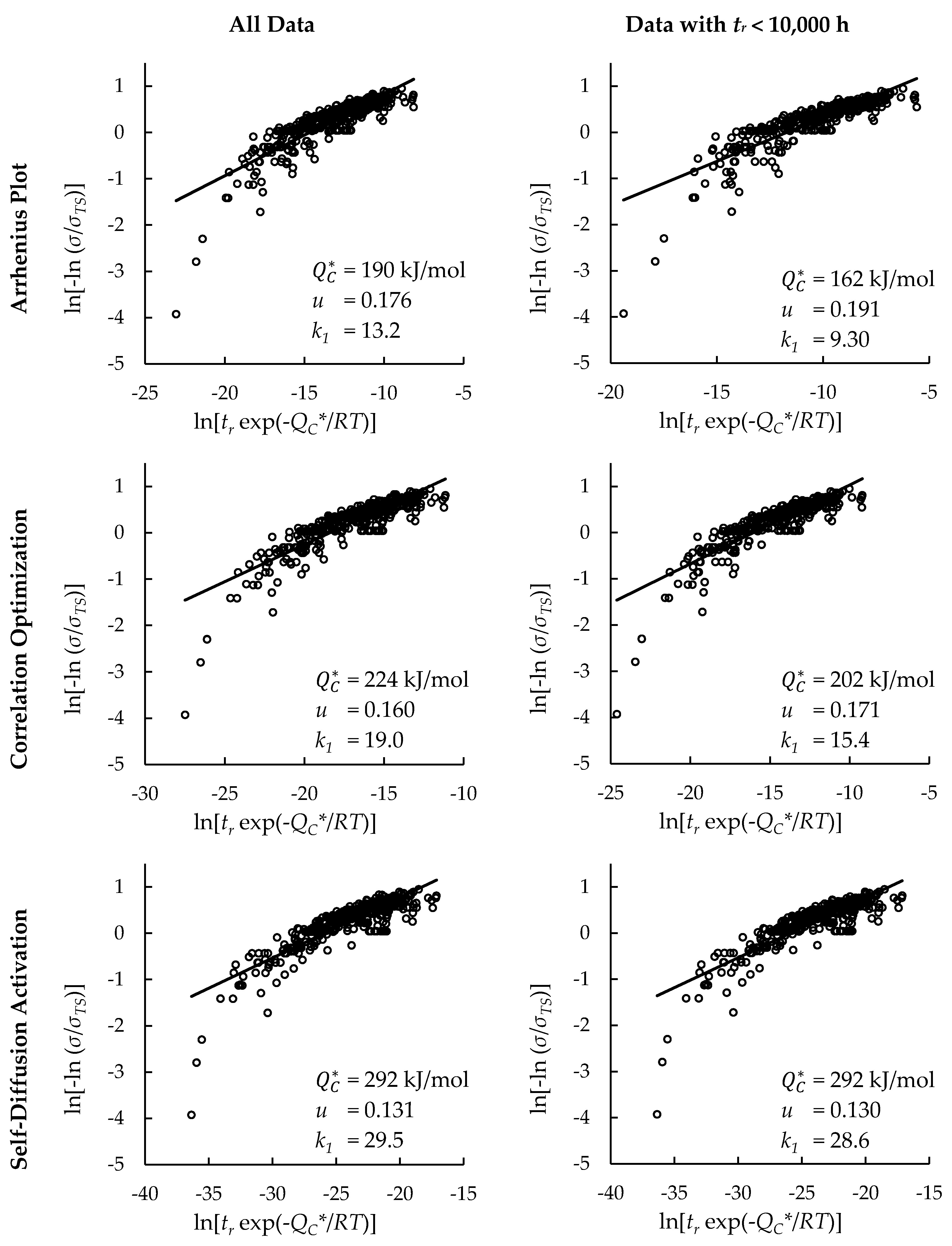
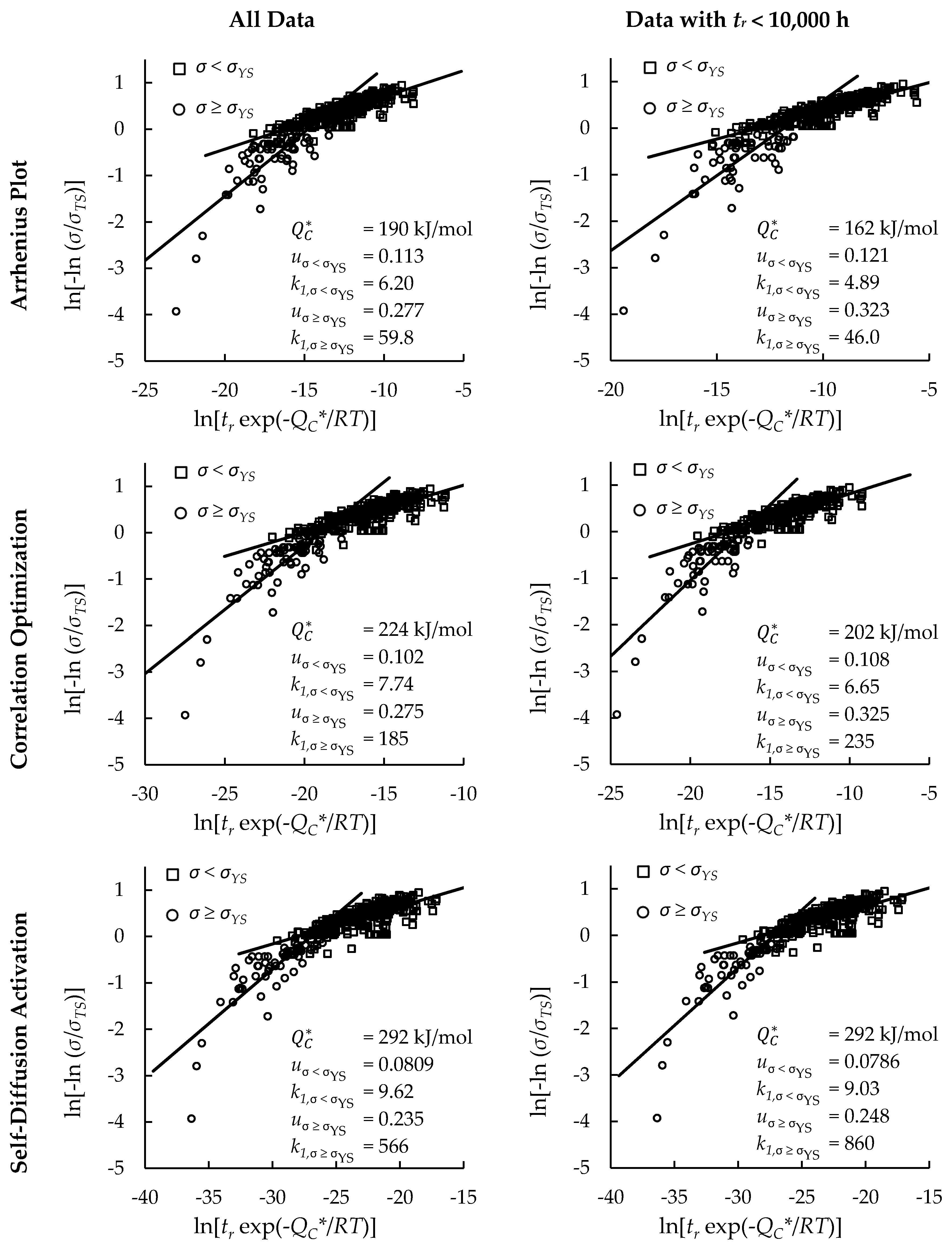
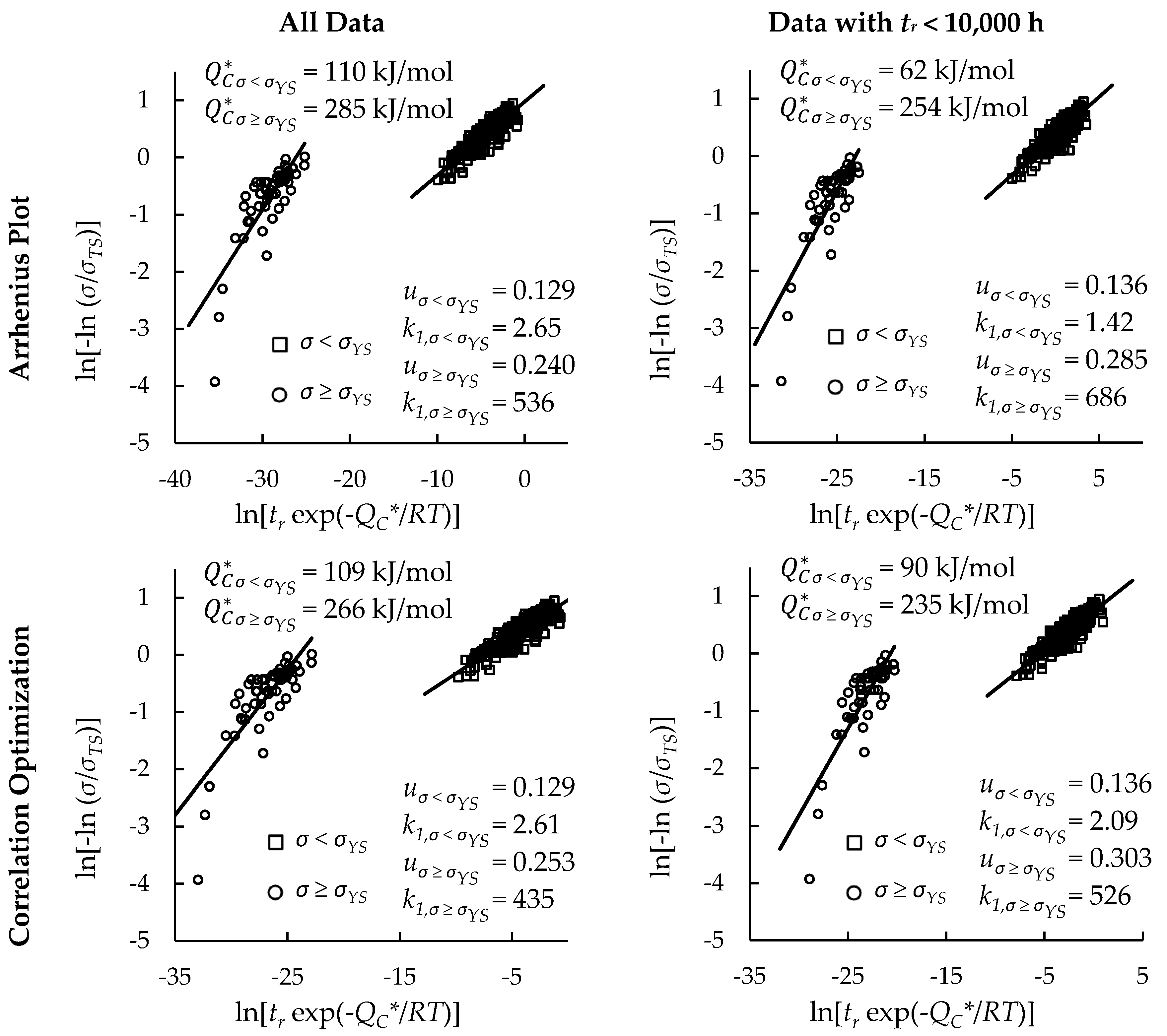
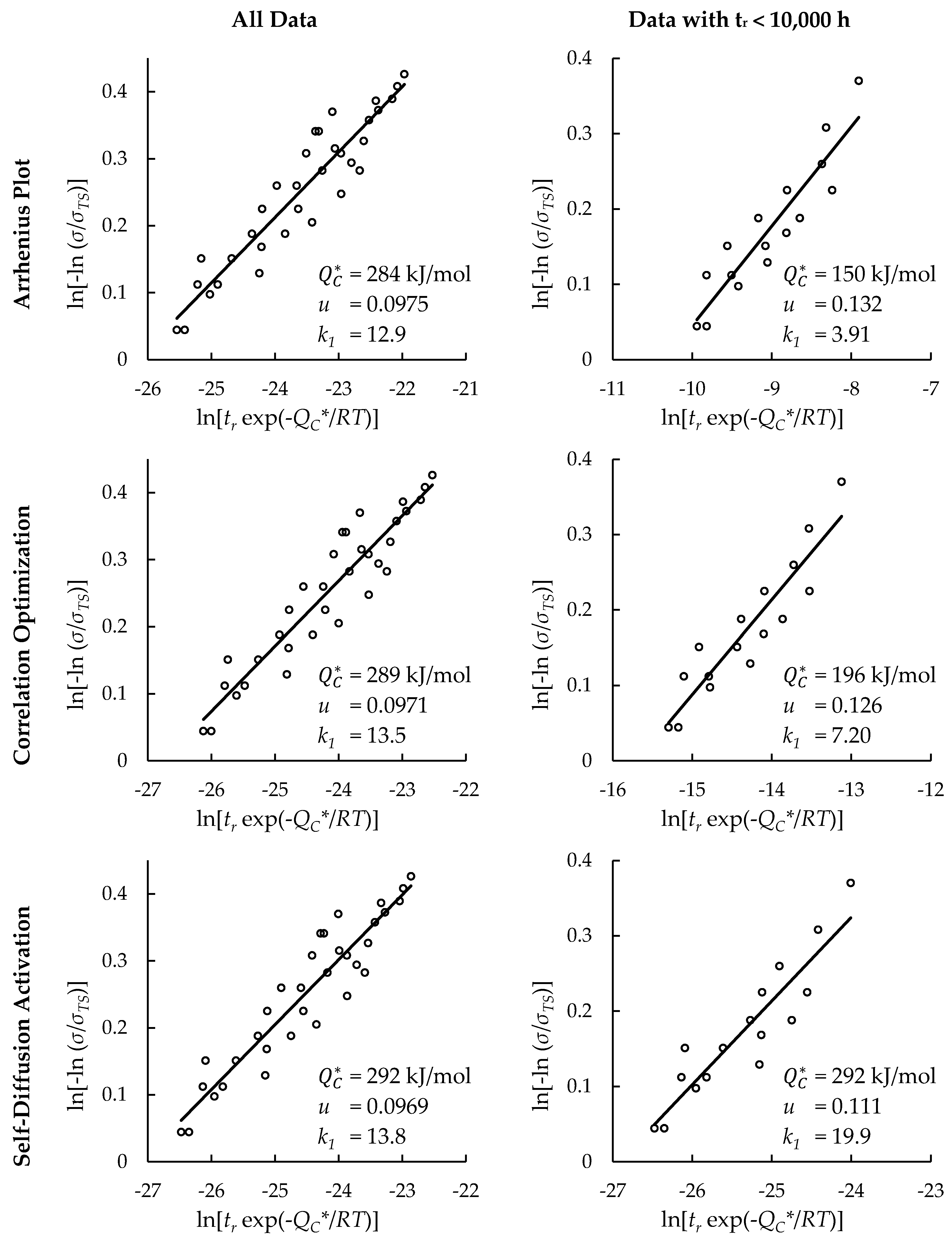
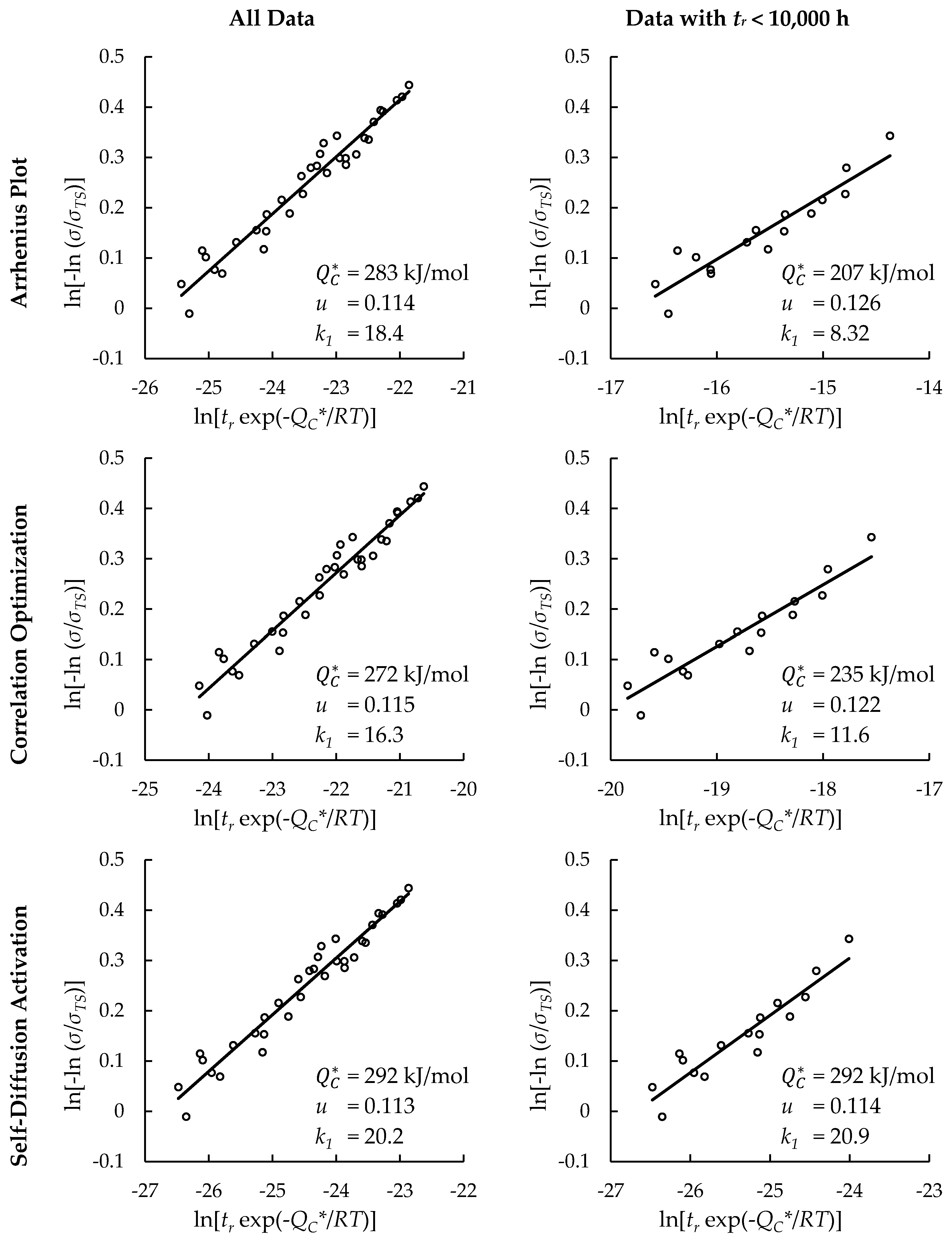
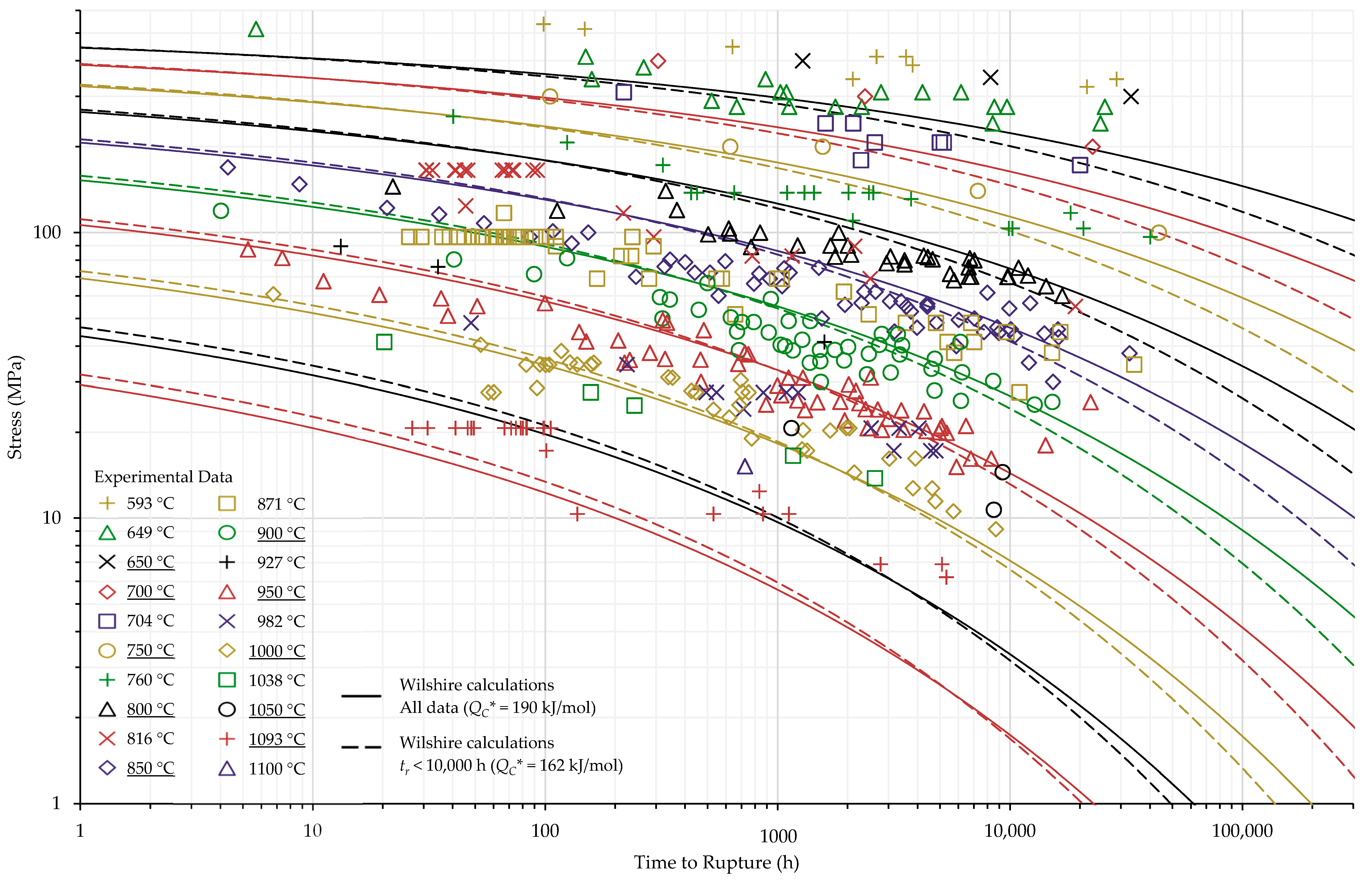
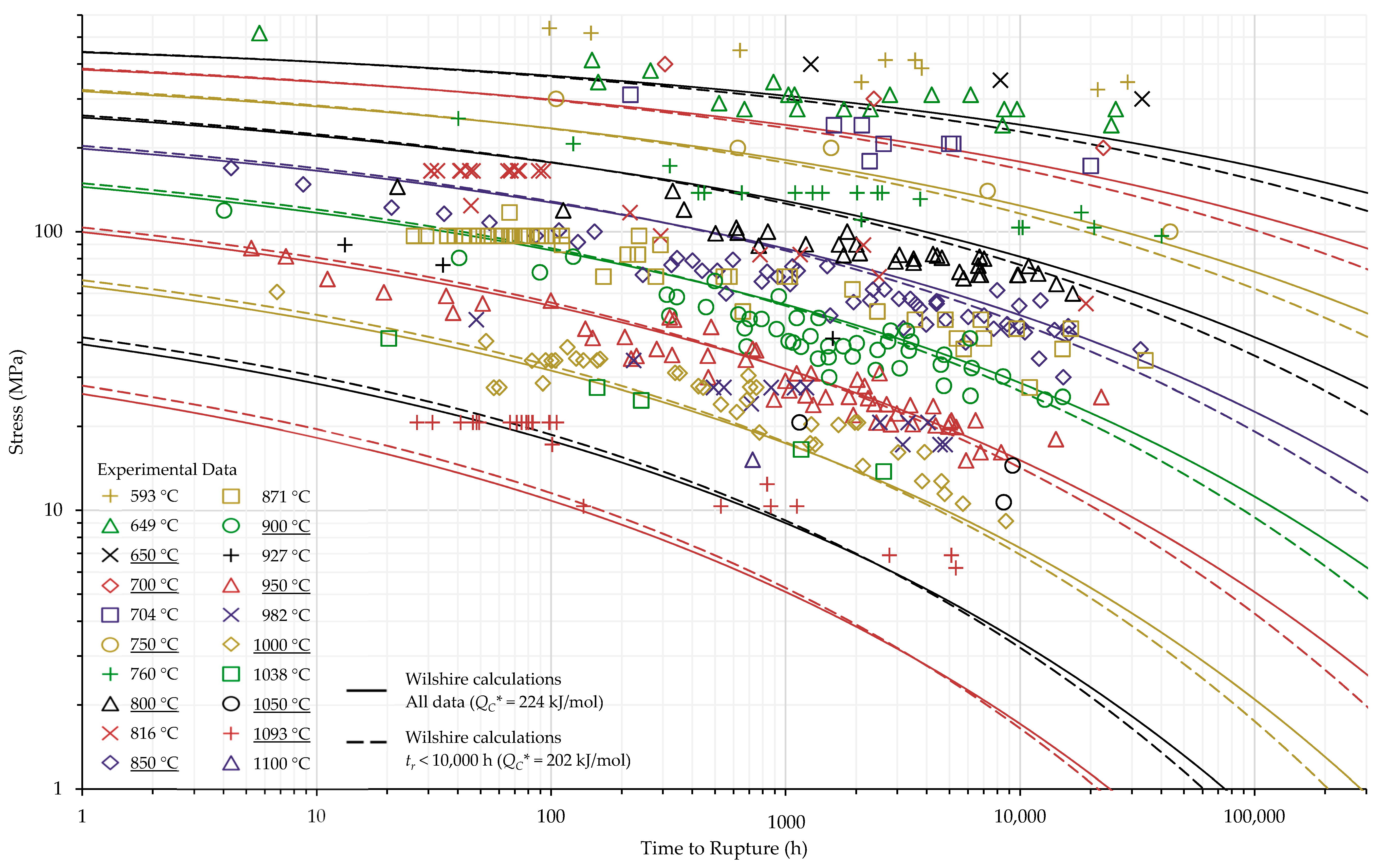
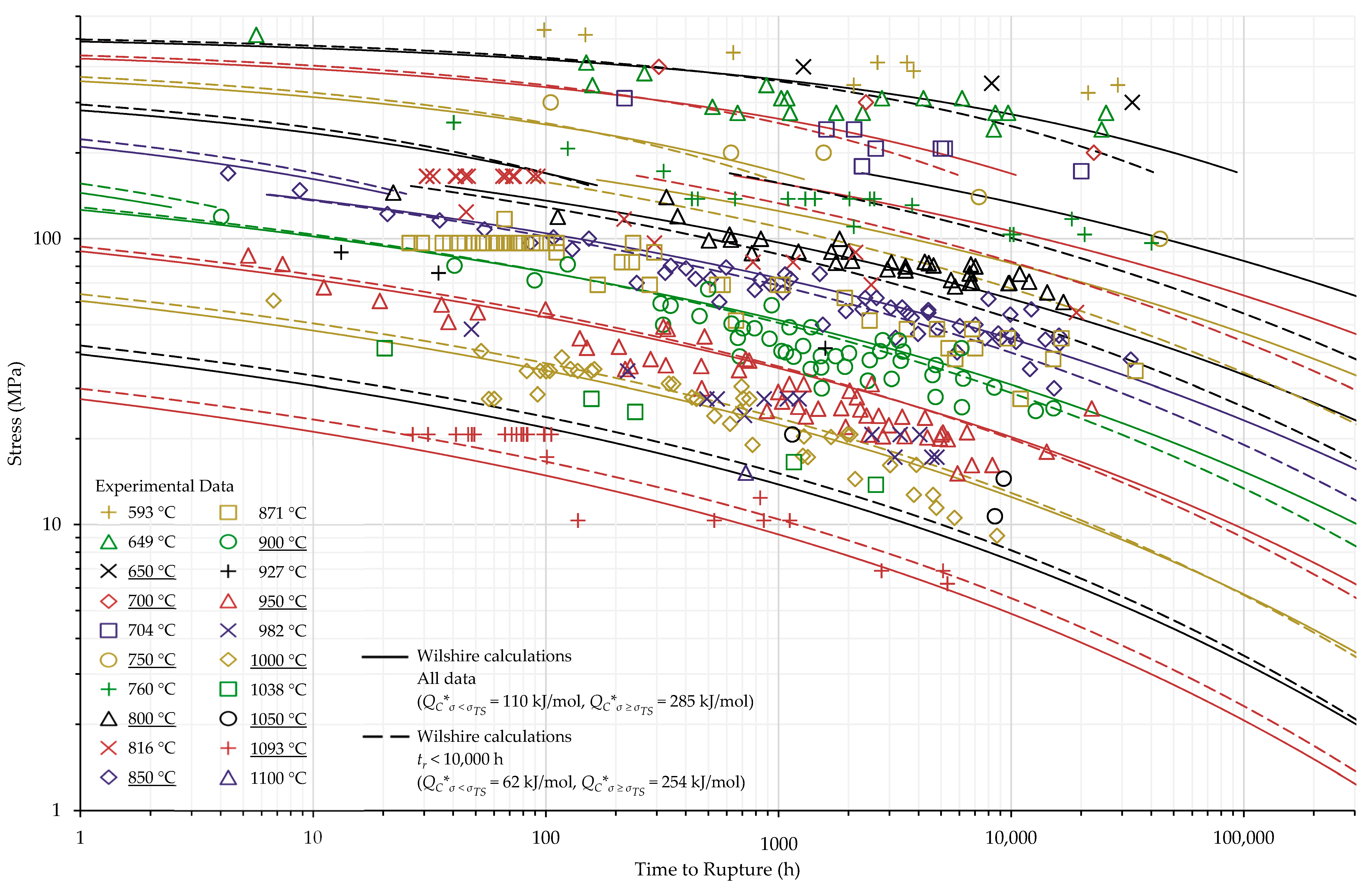
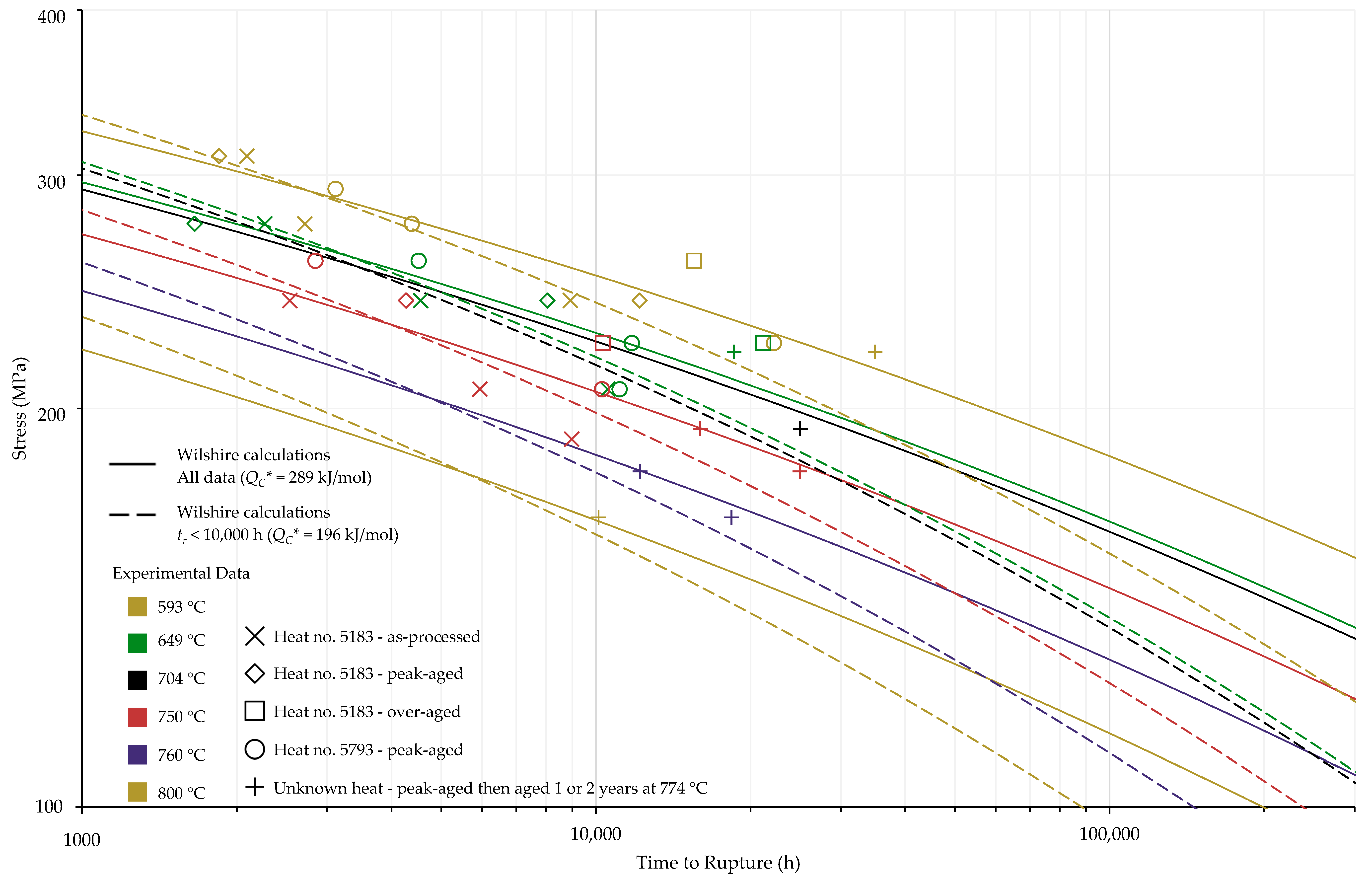
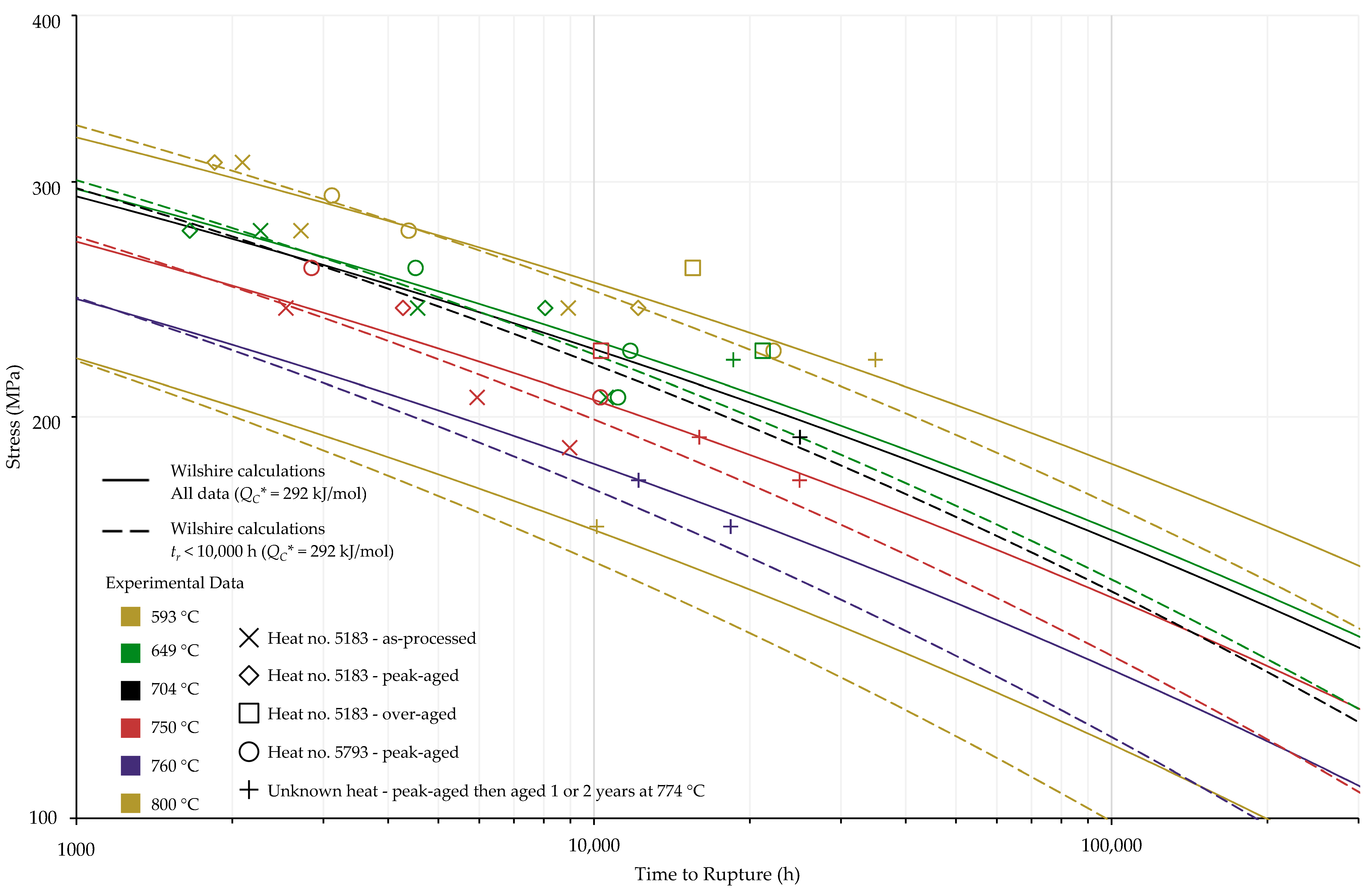
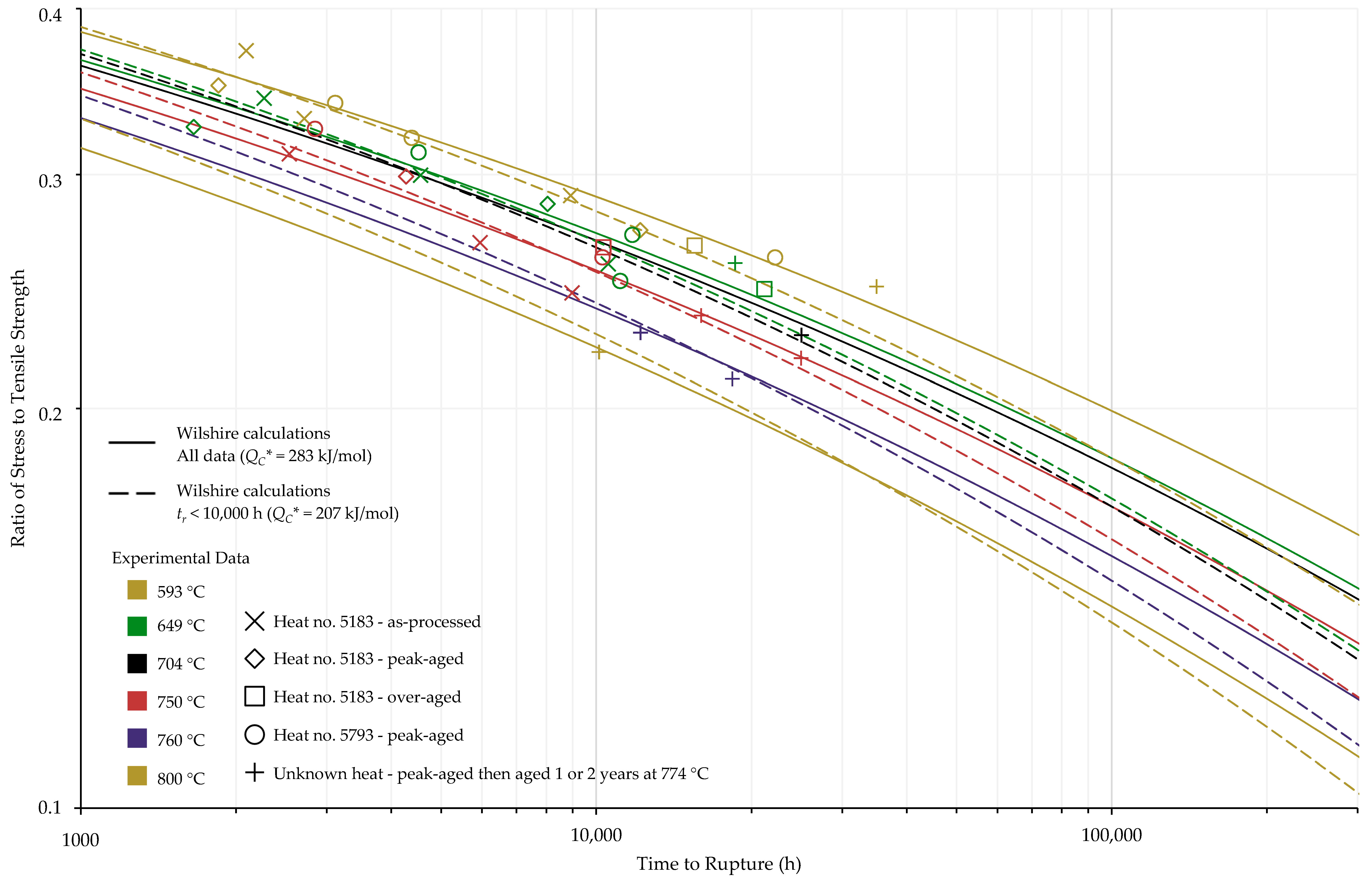
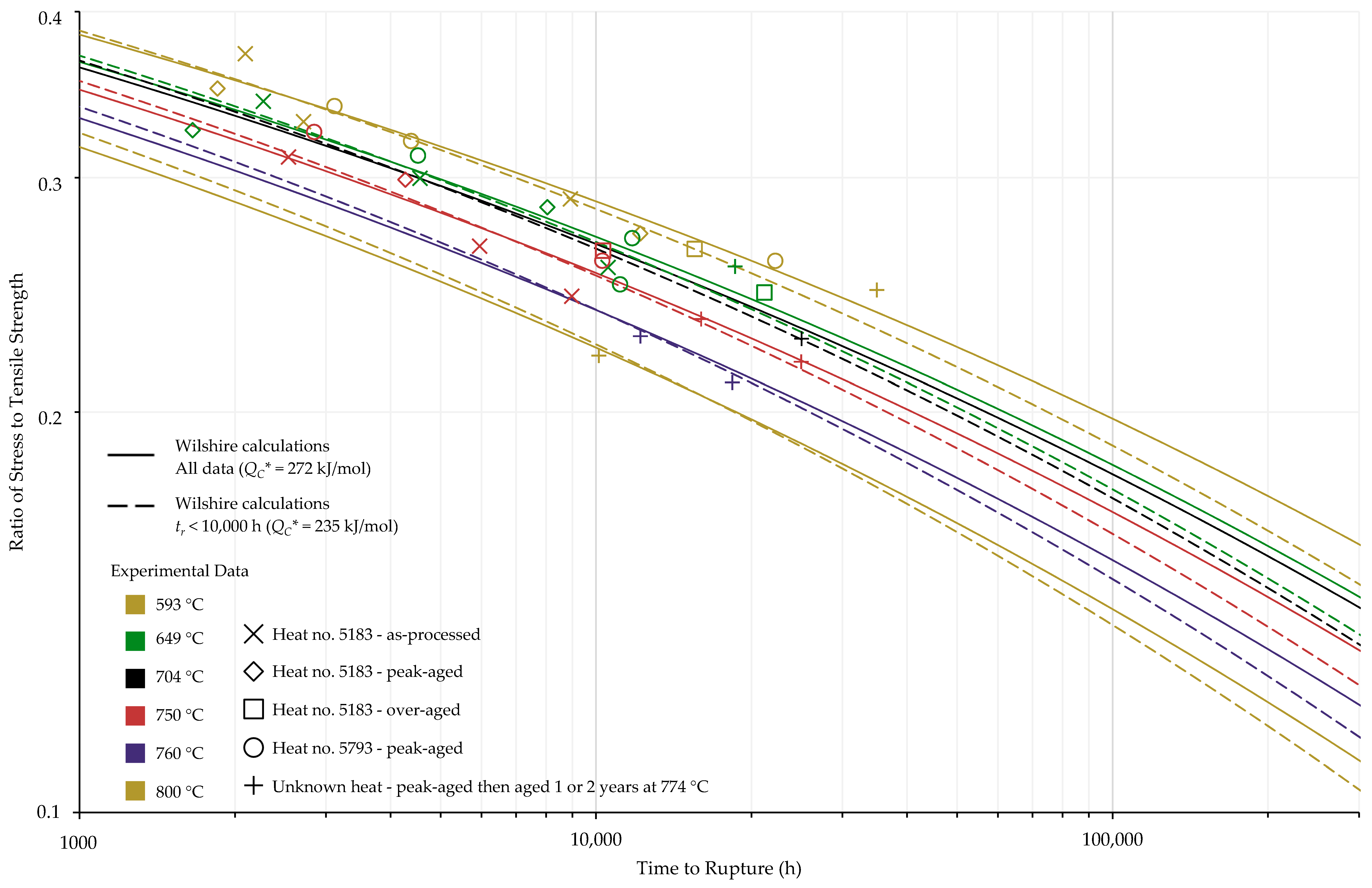
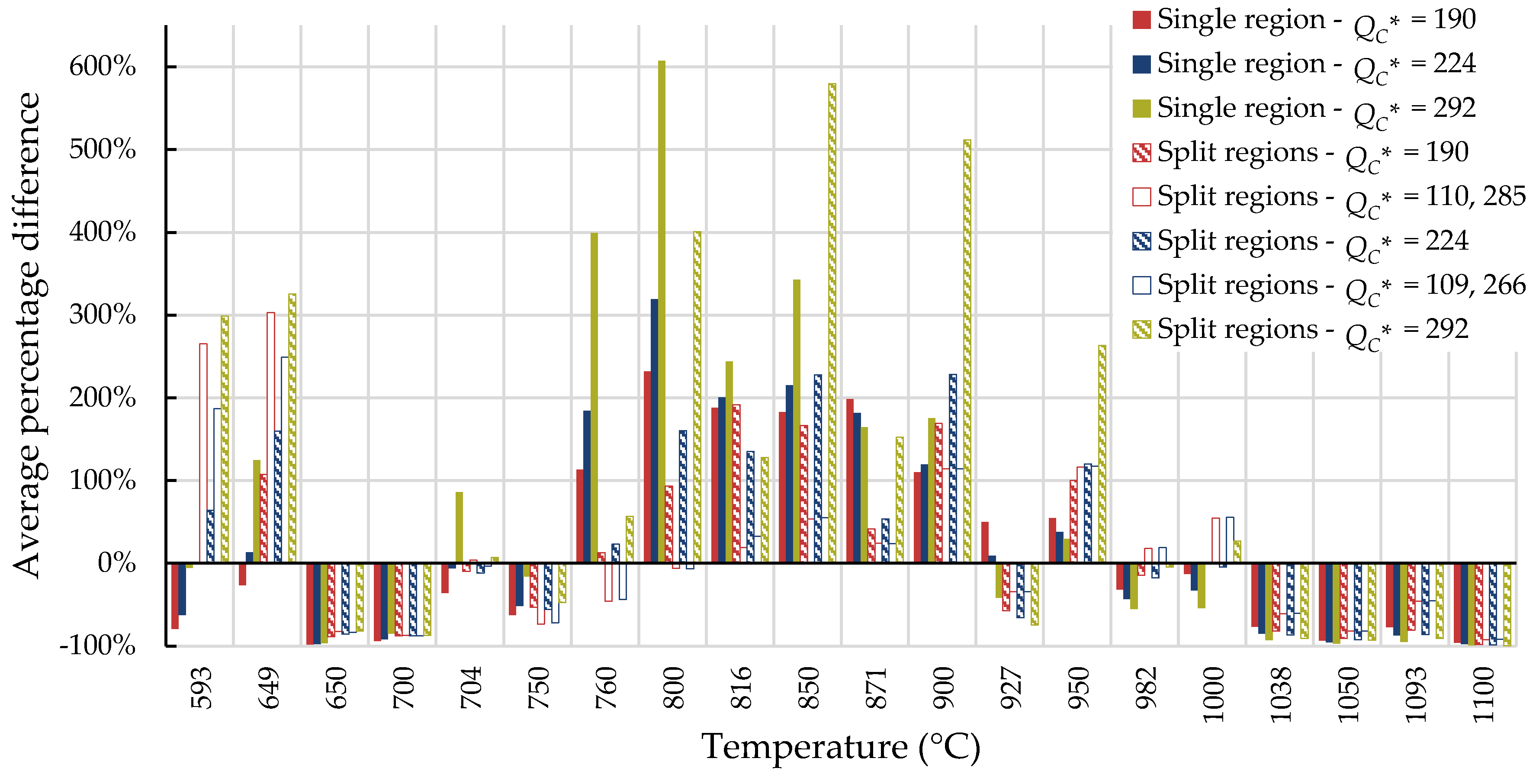
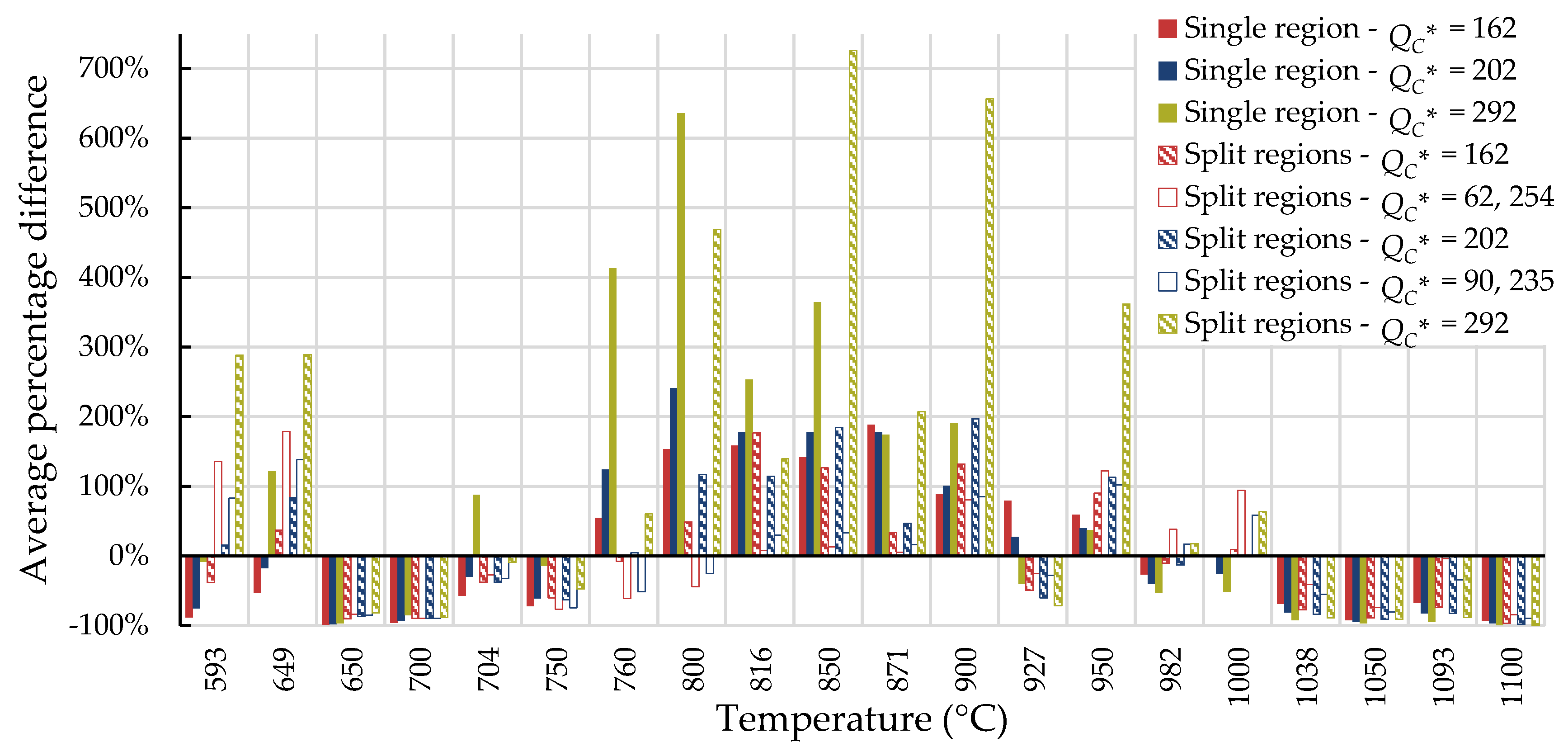
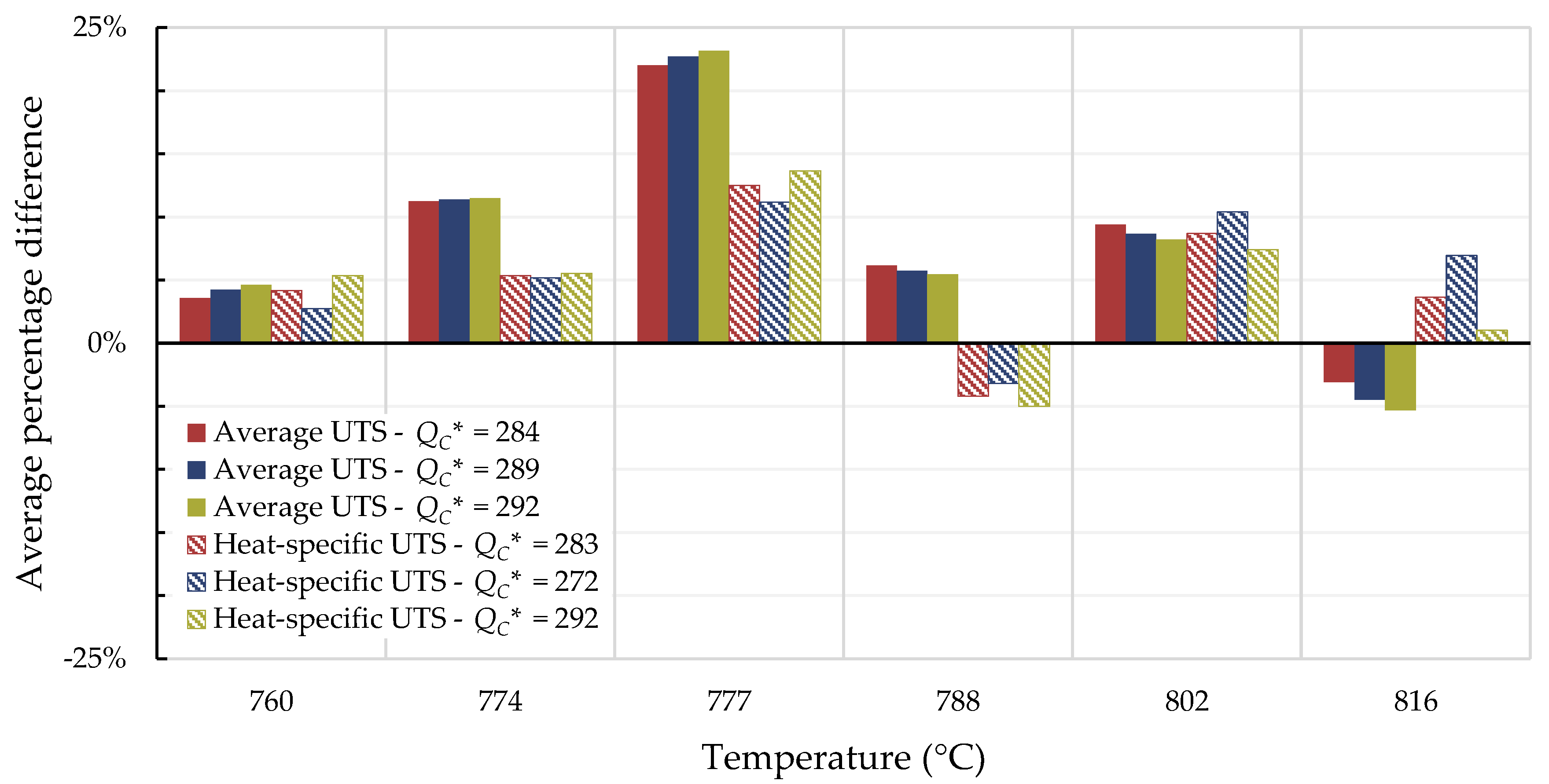
4.1. Investigation of Multiple Methods to Determine , Region-Splitting, the Use of Heat- and Processing-Specific Tensile Strength Values, and the Use of Short-Term Creep Rupture Data to Extrapolate Creep Life
4.2. Comparison of Calculations of the Wilshire and Larson-Miller Parameter Equations
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Disclaimer
Appendix A


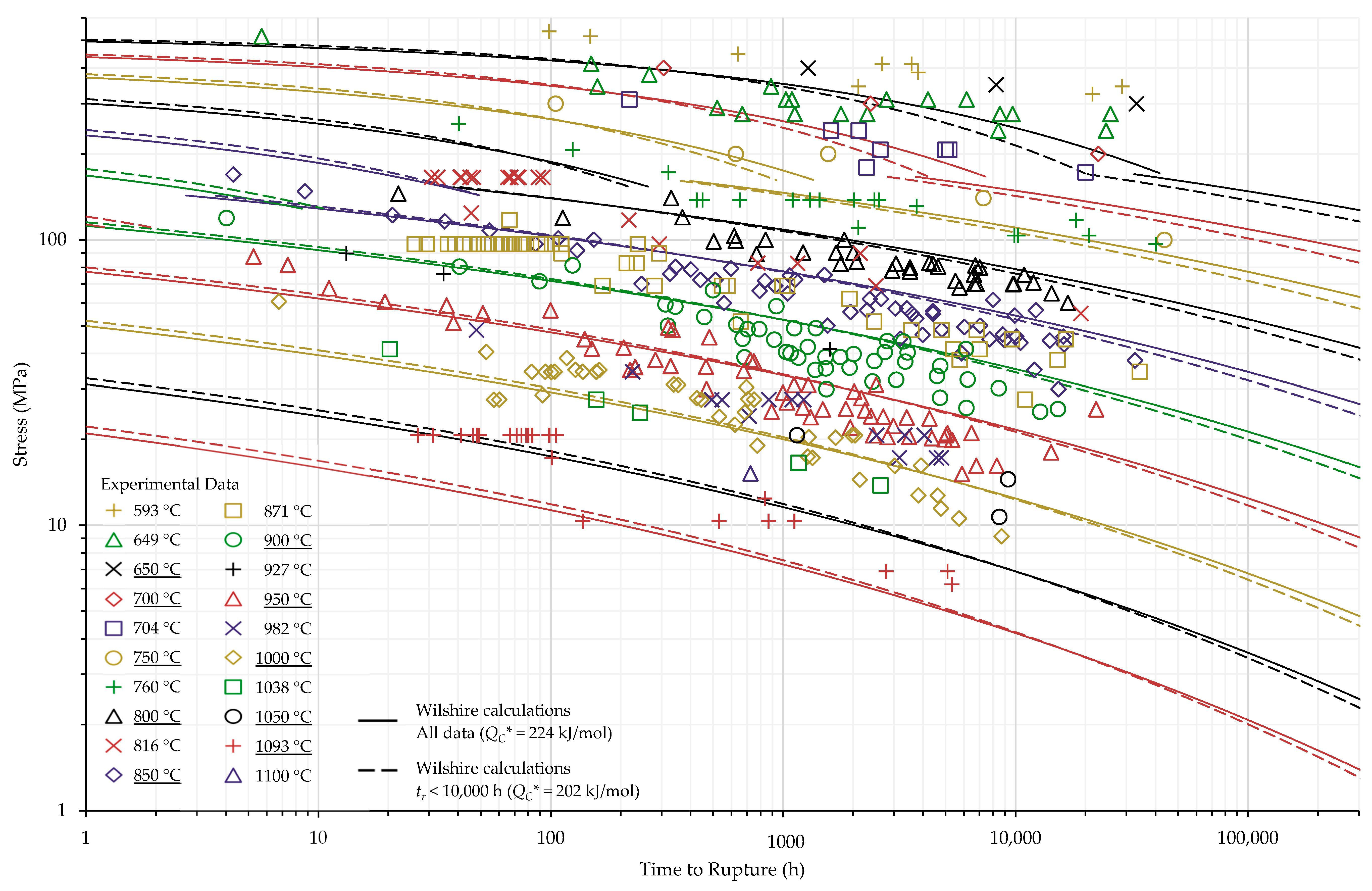
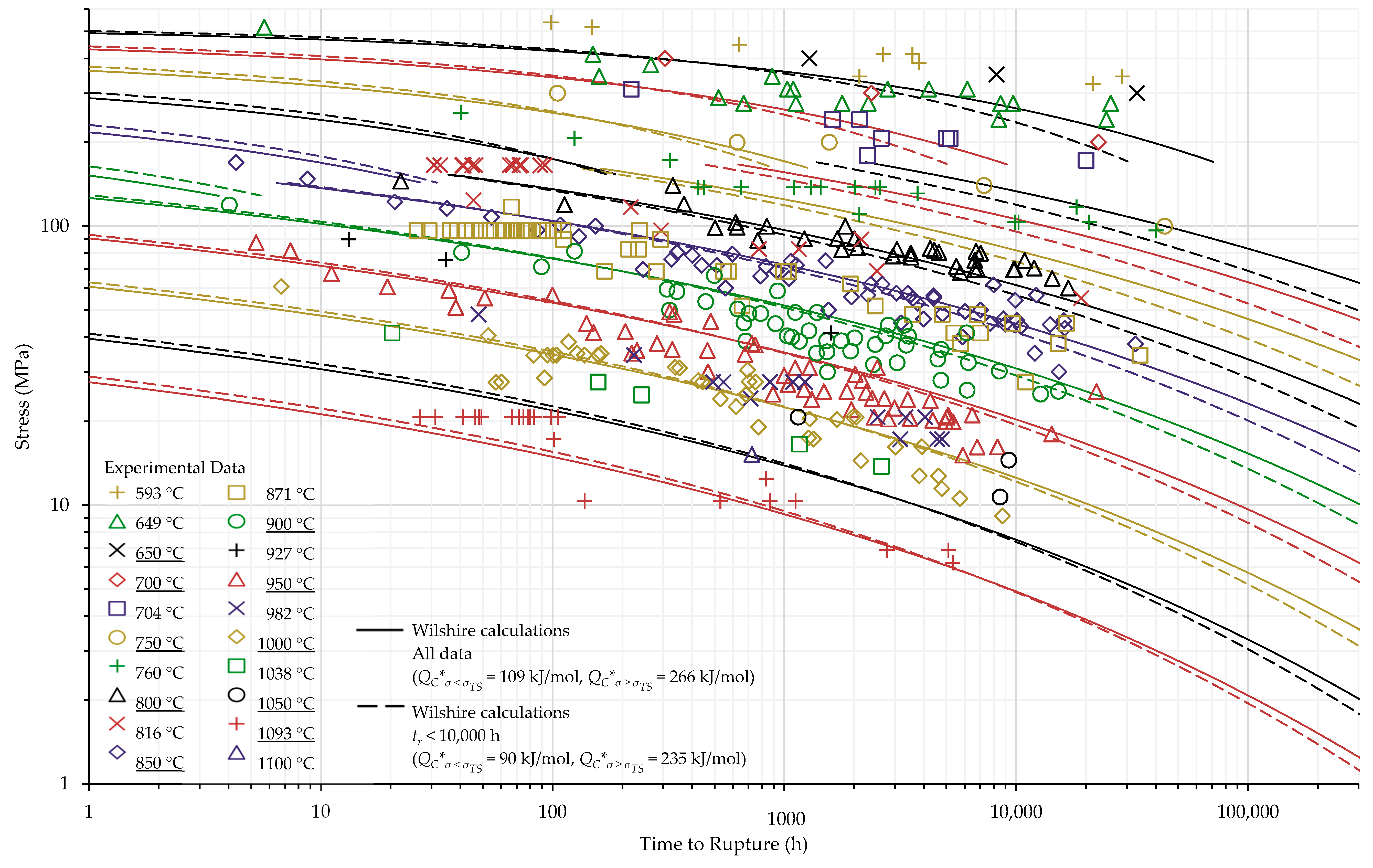
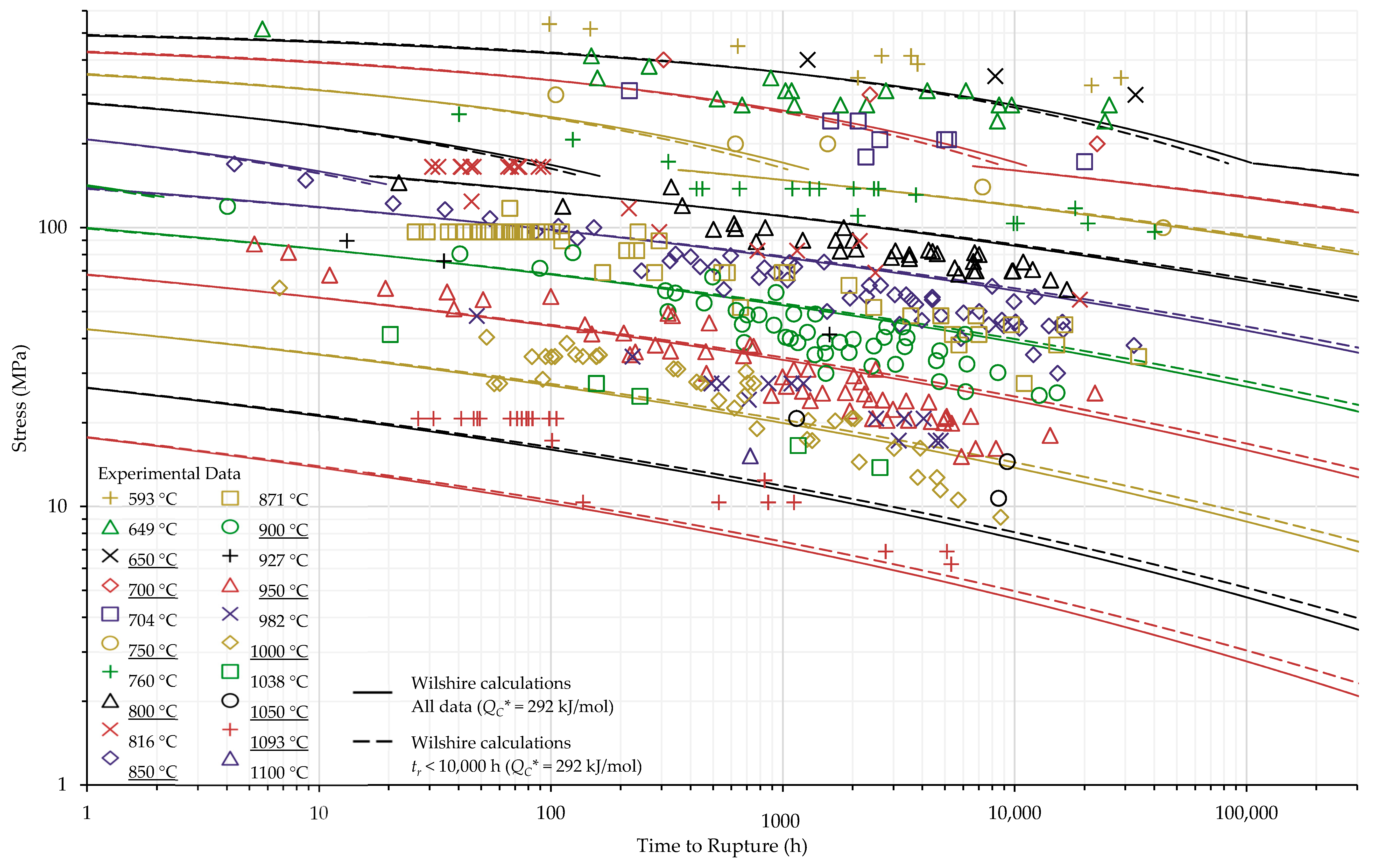
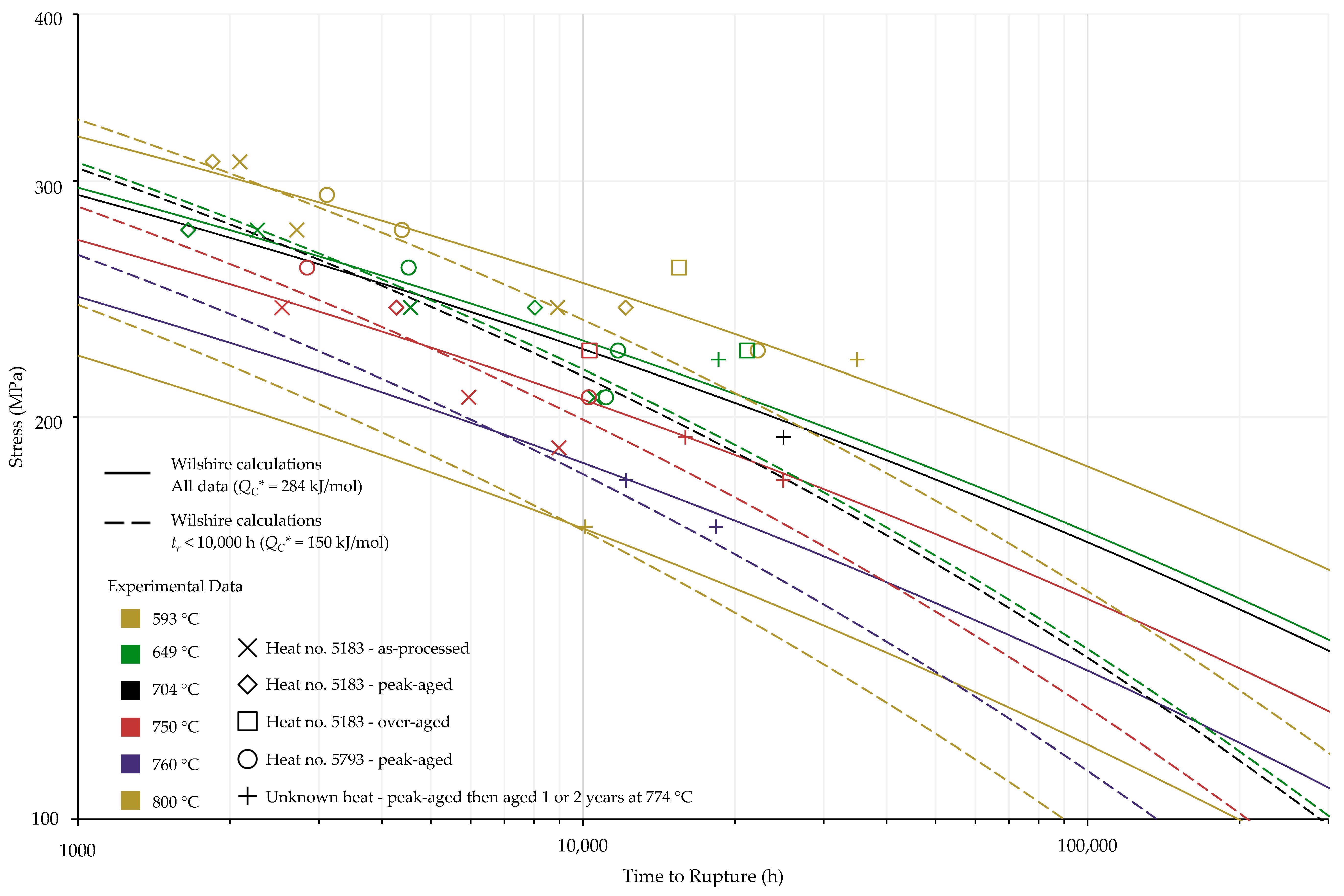
| Temperature | Heat No. | Processing Condition | Tensile Strength (MPa) | Yield Strength (MPa) |
|---|---|---|---|---|
| 760 °C | 5183 | AP | 834 | 737 |
| PA | 886 | 724 | ||
| OA | 975 | 722 | ||
| 5793 | PA | 863 | 719 | |
| Unknown | PA 1 | 893 | 687 | |
| 816 °C | 5183 | AP | 718 | 680 |
| PA | 728 | 625 | ||
| OA | 720 | 605 | ||
| 5793 | PA | 729 | 672 | |
| Unknown | PA 1 | 751 | 610 |
| Heat No. [3,4,21] | Processing Condition [3,4,21] | Temperature (°C) [3,4,21] | Applied Stress (MPa) [3,4,21] | Heat- and Processing-Specific TS (MPa) [3,4,21] | Experimental Time to Rupture (h) [3,4,21] | Calculated Time to Rupture (h) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 | Case 8 | Case 9 | Case 10 | Case 11 | Case 12 | LMP Equation | ||||||
| 5183 | AP | 760 | 310 | 834 | 2092 | 1545 | 1545 | 1545 | 1771 | 1773 | 1768 | 1281 | 1324 | 1340 | 1401 | 1400 | 1378 | 1729 |
| 5183 | AP | 760 | 276 | 834 | 2713 | 4617 | 4638 | 4651 | 4572 | 4514 | 4620 | 3170 | 3350 | 3637 | 5054 | 5263 | 5717 | 4950 |
| 5183 | AP | 760 | 241 | 834 | 8914 | 14,068 | 14,201 | 14,281 | 12,011 | 11,688 | 12,284 | 7934 | 8571 | 9998 | 11,949 | 12,795 | 14,843 | 13,395 |
| 5183 | AP | 774 | 276 | 805 | 2268 | 1999 | 1989 | 1984 | 2091 | 2110 | 2075 | 1933 | 1891 | 1734 | 2699 | 2665 | 2589 | 2640 |
| 5183 | AP | 774 | 241 | 805 | 4560 | 6351 | 6352 | 6352 | 5695 | 5663 | 5722 | 4979 | 4982 | 4920 | 6590 | 6697 | 6966 | 7052 |
| 5183 | AP | 774 | 207 | 805 | 10,546 | 20,879 | 20,988 | 21,055 | 15,976 | 15,643 | 16,261 | 13,132 | 13,448 | 14,326 | 16,520 | 17,296 | 19,301 | 18,524 |
| 5183 | AP | 788 | 241 | 776 | 2537 | 2834 | 2809 | 2793 | 2677 | 2720 | 2643 | 3094 | 2871 | 2407 | 3600 | 3475 | 3244 | 3775 |
| 5183 | AP | 788 | 207 | 776 | 5946 | 9720 | 9683 | 9662 | 7791 | 7790 | 7795 | 8398 | 7982 | 7234 | 9324 | 9281 | 9319 | 9792 |
| 5183 | AP | 788 | 190 | 776 | 8969 | 18,348 | 18,329 | 18,319 | 13,513 | 13,401 | 13,614 | 14,032 | 13,503 | 12,739 | 15,230 | 15,403 | 16,056 | 16,106 |
| 5183 | OA | 760 | 259 | 975 | 15,515 | 8032 | 8088 | 8122 | 7388 | 7242 | 7511 | 13,681 | 14,974 | 18,228 | 7751 | 8184 | 9185 | 8187 |
| 5183 | OA | 774 | 224 | 911 | 21,173 | 11,450 | 11,481 | 11,499 | 9492 | 9366 | 9598 | 16,940 | 17,454 | 18,968 | 10,388 | 10,714 | 11,539 | 11,405 |
| 5183 | OA | 788 | 224 | 847 | 10,317 | 5221 | 5188 | 5168 | 4546 | 4582 | 4518 | 8812 | 8386 | 7628 | 5770 | 5655 | 5473 | 6067 |
| 5183 | PA | 760 | 310 | 886 | 1849 | 1545 | 1545 | 1545 | 1771 | 1773 | 1768 | 2060 | 2155 | 2262 | 2170 | 2199 | 2239 | 1729 |
| 5183 | PA | 760 | 241 | 886 | 12,170 | 14,068 | 14,201 | 14,281 | 12,011 | 11,688 | 12,284 | 11,618 | 12,665 | 15,222 | 11,949 | 12,795 | 14,843 | 13,395 |
| 5183 | PA | 774 | 276 | 847 | 1655 | 1999 | 1989 | 1984 | 2091 | 2110 | 2075 | 2793 | 2757 | 2602 | 2699 | 2665 | 2589 | 2640 |
| 5183 | PA | 774 | 241 | 847 | 8045 | 6351 | 6352 | 6352 | 5695 | 5663 | 5722 | 6913 | 6972 | 7064 | 6590 | 6697 | 6966 | 7052 |
| 5183 | PA | 788 | 241 | 807 | 4274 | 2834 | 2809 | 2793 | 2677 | 2720 | 2643 | 4036 | 3770 | 3226 | 3600 | 3475 | 3244 | 3775 |
| 5793 | PA | 760 | 293 | 863 | 3114 | 2667 | 2673 | 2676 | 2842 | 2825 | 2854 | 2592 | 2726 | 2914 | 3308 | 3398 | 3574 | 2949 |
| 5793 | PA | 760 | 276 | 863 | 4382 | 4617 | 4638 | 4651 | 4572 | 4514 | 4620 | 4025 | 4278 | 4733 | 5054 | 5263 | 5717 | 4950 |
| 5793 | PA | 760 | 224 | 863 | 22,216 | 24,872 | 25,168 | 25,348 | 19,682 | 19,012 | 20,255 | 15,491 | 17,004 | 20,902 | 18,554 | 20,151 | 24,177 | 21,804 |
| 5793 | PA | 774 | 259 | 829 | 4519 | 3553 | 3544 | 3539 | 3442 | 3448 | 3436 | 3808 | 3785 | 3661 | 4207 | 4215 | 4236 | 4338 |
| 5793 | PA | 774 | 207 | 829 | 11,123 | 20,879 | 20,988 | 21,055 | 15,976 | 15,643 | 16,261 | 15,615 | 16,057 | 17,339 | 16,520 | 17,296 | 19,301 | 18,524 |
| 5793 | PA | 774 | 224 | 829 | 11,746 | 11,450 | 11,481 | 11,499 | 9492 | 9366 | 9598 | 9679 | 9840 | 10,235 | 10,388 | 10,714 | 11,539 | 11,405 |
| 5793 | PA | 788 | 259 | 796 | 2845 | 1550 | 1532 | 1521 | 1587 | 1625 | 1556 | 2278 | 2099 | 1717 | 2259 | 2148 | 1935 | 2337 |
| 5793 | PA | 788 | 207 | 796 | 10,277 | 9720 | 9683 | 9662 | 7791 | 7790 | 7795 | 9791 | 9341 | 8568 | 9324 | 9281 | 9319 | 9792 |
| Unknown | PA | 760 | 221 | 893 | 34,955 | 27,912 | 28,258 | 28,469 | 21,750 | 20,979 | 22,412 | 20,816 | 23,013 | 28,949 | 20,282 | 22,092 | 26,686 | 24,039 |
| Unknown | PA | 774 | 221 | 857 | 18,583 | 12,899 | 12,940 | 12,965 | 10,524 | 10,369 | 10,656 | 13,013 | 13,323 | 14,184 | 11,389 | 11,782 | 12,779 | 12,557 |
| Unknown | PA | 777 | 193 | 850 | 24,994 | 30,499 | 30,675 | 30,782 | 21,942 | 21,427 | 22,385 | 25,303 | 25,984 | 28,402 | 22,219 | 23,336 | 26,306 | 24,288 |
| Unknown | PA | 788 | 193 | 822 | 15,975 | 16,137 | 16,112 | 16,098 | 12,090 | 12,009 | 12,163 | 17,522 | 16,951 | 16,272 | 13,793 | 13,904 | 14,384 | 14,544 |
| Unknown | PA | 788 | 179 | 822 | 24,951 | 27,089 | 27,108 | 27,121 | 18,942 | 18,690 | 19,164 | 26,190 | 25,582 | 25,340 | 20,577 | 21,013 | 22,414 | 22,110 |
| Unknown | PA | 802 | 179 | 786 | 12,187 | 12,400 | 12,298 | 12,239 | 9116 | 9185 | 9066 | 16,570 | 15,044 | 12,708 | 11,459 | 11,129 | 10,687 | 11,758 |
| Unknown | PA | 802 | 165 | 786 | 18,363 | 21,500 | 21,374 | 21,301 | 14,689 | 14,694 | 14,696 | 25,338 | 23,241 | 20,295 | 17,527 | 17,259 | 17,120 | 18,490 |
| Unknown | PA | 816 | 165 | 751 | 10,122 | 9811 | 9669 | 9585 | 7061 | 7210 | 6945 | 16,035 | 13,692 | 10,228 | 9733 | 9122 | 8157 | 9935 |
References
- Purgert, R.; Shingledecker, J.; Pschirer, J.; Ganta, R.; Weitzel, P.; Sarver, J.; Vitalis, B.; Gagliano, M.; Stanko, G.; Tortorelli, P. Boiler Materials for Ultra Supercritical Coal Power Plants; Report No. DOE-EIO-EPRI-01NT41175; US Department of Energy: Washington, DC, USA, 2016. [CrossRef]
- Tortorelli, P.F.; Wang, H.; Unocic, K.A.; Santella, M.L.; Shingledecker, J.P.; Cedro III, V. Long-Term Creep-Rupture Behavior of Inconel® 740 and Haynes® 282. In Proceedings of the ASME 2014 Symposium on Elevated Temperature Application of Materials for Fossil, Nuclear, and Petrochemical Industries, Seattle, WA, USA, 25–27 March 2014. [Google Scholar] [CrossRef]
- Viswanathan, R.; Hawk, J.; Schwant, R.; Saha, D.; Totemeier, T.; Goodstine, S.; McNally, M.; Allen, D.B.; Purgert, R. Steam Turbine Materials for Ultrasupercritical Coal Power Plants; US Department of Energy: Washington, DC, USA, 2009. [CrossRef]
- Purgert, R.; Shingledecker, J.; Saha, D.; Thangirala, M.; Booras, G.; Powers, J.; Riley, C.; Hendrix, H. Materials for Advanced Ultrasupercritical Steam Turbines; US Department of Energy: Washington, DC, USA, 2015. [CrossRef]
- Wilshire, B.; Battenbough, A.J. Creep and creep fracture of polycrystalline copper. Mater. Sci. Eng. A 2007, 443, 156–166. [Google Scholar] [CrossRef]
- Wilshire, B.; Scharning, P.J. A new methodology for analysis of creep and creep fracture data for 9–12% chromium steels. Int. Mater. Rev. 2008, 53, 91–104. [Google Scholar] [CrossRef]
- Arrhenius, S.A. Über die Dissociationswärme und den Einfluß der Temperatur auf den Dissociationsgrad der Elektrolyte. Z. Phys. Chem. 1889, 4, 96–116. [Google Scholar] [CrossRef]
- Norton, F.H. The Creep of Steels at High Temperatures; McGraw-Hill: New York, NY, USA, 1929. [Google Scholar]
- Monkman, F.C.; Grant, N.J. An empirical relationship between rupture life and minimum creep rate in creep-rupture tests. Proc. Am. Soc. Test Mater. 1956, 56, 593–620. [Google Scholar]
- Bonora, N.; Esposito, L. Mechanism based creep model incorporating damage. J. Eng. Mater. Technol. 2010, 132, 021013. [Google Scholar] [CrossRef]
- Esposito, L.; Bonora, N.; De Vita, G. Creep modelling of 316H stainless steel over a wide range of stress. Proc. Struct. Int. 2016, 2, 927–933. [Google Scholar] [CrossRef]
- Abdallah, Z.; Gray, V.; Whittaker, M.; Perkins, K. A critical analysis of the conventionally employed creep lifing methods. Materials 2014, 5, 3371–3398. [Google Scholar] [CrossRef]
- Bolton, J. Reliable analysis and extrapolation of creep rupture data. Int. J. Pres. Ves. Pip. 2017, 157, 1–19. [Google Scholar] [CrossRef]
- Larson, F.R.; Miller, J. A Time-Temperature Relationship for Rupture and Creep Stresses. Trans. ASME 1952, 74, 765–771. [Google Scholar]
- Dagra Data Digitizer. Available online: http://www.datadigitization.com/ (accessed on 2 May 2018).
- Lillo, T. High Temperature Alloy 617 Properties for Engineering Design: Program Overview & Approach to ASME Code Qualification. In Proceedings of the Technical Meeting on High-Temperature Qualification of High Temperature Gas Cooled Reactor Materials, Vienna, Austria, 10–13 June 2014. [Google Scholar]
- Schubert, F.; Bruch, U.; Cook, R.; Diehl, H.; Ennis, P.J.; Jakobeit, W.; Penkalla, H.J.; Heesen, E.T.; Ullrich, G. Creep rupture behavior of candidate materials for nuclear process heat applications. Nucl. Technol. 1984, 66, 227–240. [Google Scholar] [CrossRef]
- Kim, W.G.; Park, J.Y.; Ekaputra, I.M.W.; Kim, S.J.; Kim, M.H.; Kim, Y.W. Creep deformation and rupture behavior of Alloy 617. Eng. Fail. Anal. 2015, 58, 441–451. [Google Scholar] [CrossRef]
- Kim, W.G.; Ekaputra, I.M.W.; Park, J.Y.; Kim, M.H.; Kim, Y.W. Investigation of creep rupture properties in air and He environments of alloy 617 at 800 °C. Nucl. Eng. Des. 2016, 306, 177–185. [Google Scholar] [CrossRef]
- Ren, W.; Swindeman, R.W. Assessment of Existing Alloy 617 Data for Gen IV Materials Handbook; Report No. ORNL/TM-2005/510; US Department of Energy: Washington, DC, USA, 2015. [CrossRef]
- Saha, D.; (General Electric Company, Power & Water Division, Schenectady, NY, USA). Personal communication, 2012.
- Cedro, V., III; Garcia, C.; Render, M. Use of the Wilshire Equations to Correlate and Extrapolate Creep Data of HR6W and Sanicro 25. Materials 2018, 11, 1585. [Google Scholar] [CrossRef] [PubMed]
- Wilshire, B.; Scharning, P.J.; Hurst, R. New methodology for long term creep data generation for power plant components. Energy Mater. 2007, 2, 84–88. [Google Scholar] [CrossRef]
- Wilshire, B.; Scharning, P.J. Theoretical and practical approaches to creep of Waspaloy. Mater. Sci. Technol. 2009, 25, 242–248. [Google Scholar] [CrossRef]
- Wilshire, B.; Scharning, P.J. Prediction of long term creep data for forged 1Cr–1Mo–0.25V steel. Mater. Sci. Technol. 2008, 24, 1–9. [Google Scholar] [CrossRef]
- Wilshire, B.; Scharning, P.J. Long-term creep life prediction for a high chromium steel. Scr. Mater. 2007, 56, 701–704. [Google Scholar] [CrossRef]
- Wilshire, B.; Scharning, P.J. Extrapolation of creep life data for 1Cr–0.5 Mo steel. Int. J. Pres. Ves. Pip. 2008, 85, 739–743. [Google Scholar] [CrossRef]
- Wilshire, B.; Scharning, P.J. Creep and creep fracture of commercial aluminum alloys. J. Mater. Sci. 2008, 43, 3992–4000. [Google Scholar] [CrossRef]
- Wilshire, B.; Scharning, P.J.; Hurst, R. A new approach to creep data assessment. Mater. Sci. Eng. A 2009, 510, 3–6. [Google Scholar] [CrossRef]
- Wilshire, B.; Whittaker, M.T. The role of grain boundaries in creep strain accumulation. Acta Mater. 2009, 57, 4115–4124. [Google Scholar] [CrossRef]
- Wilshire, B.; Scharning, P.J. Creep ductilities of 9–12% chromium steels. Scr. Mater. 2007, 56, 1023–1026. [Google Scholar] [CrossRef]
- Whittaker, M.T.; Harrison, W.J. Evolution of Wilshire equations for creep life prediction. Mater. High Temp. 2014, 31, 233–238. [Google Scholar] [CrossRef]
- Whittaker, M.T.; Evans, M.; Wilshire, B. Long-term creep data prediction for type 316H stainless steel. Mater. Sci. Eng. A 2012, 552, 145–150. [Google Scholar] [CrossRef]
- Whittaker, M.T.; Harrison, W.J.; Lancaster, R.J.; Williams, S. An analysis of modern creep lifing methodologies in the titanium alloy Ti6-4. Mater. Sci. Eng. A 2013, 577, 114–119. [Google Scholar] [CrossRef]
- Jeffs, S.P.; Lancaster, R.J.; Garcia, T.E. Creep lifing methodologies applied to a single crystal superalloy by use of small scale test techniques. Mater. Sci. Eng. A 2015, 636, 529–535. [Google Scholar] [CrossRef]
- Whittaker, M.T.; Wilshire, B. Long term creep life prediction for Grade 22 (2.25Cr–1Mo) steels. Mater. Sci. Technol. 2011, 27, 642–647. [Google Scholar] [CrossRef]
- Gray, V.; Whittaker, M. The changing constants of creep: A letter on region splitting in creep lifing. Mater. Sci. Eng. A 2015, 632, 96–102. [Google Scholar] [CrossRef]
- Whittaker, M.; Wilshire, B. Creep and creep fracture of 2.25 Cr–1.6 W steels (Grade 23). Mater. Sci. Eng. A 2010, 527, 4932–4938. [Google Scholar] [CrossRef]
- Whittaker, M.; Wilshire, B. Advanced procedures for long-term creep data prediction for 2.25 chromium steels. Metall. Mater. Trans. A 2013, 44, 136–153. [Google Scholar] [CrossRef]
- Whittaker, M.; Harrison, W.; Deen, C.; Rae, C.; Williams, S. Creep deformation by dislocation movement in Waspaloy. Materials 2017, 10, 61. [Google Scholar] [CrossRef] [PubMed]
- Evans, M. A Re-Evaluation of the Causes of Deformation in 1Cr-1Mo-0.25 V Steel for Turbine Rotors and Shafts Based on iso-Thermal Plots of the Wilshire Equation and the Modelling of Batch to Batch Variation. Materials 2017, 10, 575. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.W.; Cheng, H.H.; Shen, M.H.; Pan, J.P. Determination of C Parameter of Larson-miller Equation for 15CrMo steel. Adv. Mater. Res. 2013, 791, 374–377. [Google Scholar] [CrossRef]
- MacEwan, J.R.; MacEwan, J.U.; Yaffe, L. Self-diffusion in polycrystalline Nickel. Can. J. Chem. 1959, 37, 1623–1628. [Google Scholar] [CrossRef]
- Whittaker, M.; Wilshire, B.; Brear, J. Creep fracture of the centrifugally-cast superaustenitic steels, HK40 and HP40. Mater. Sci. Eng. A 2013, 580, 391–396. [Google Scholar] [CrossRef]
- Fujio, A.; Tabuchi, M.; Hayakawa, M. Influence of Data Scattering on Estimation of 100,000 hrs Creep Rupture Strength of Alloy 617 at 700 °C by Larson–Miller Method. J. Press. Vessel Technol. 2017, 139, 011403. [Google Scholar] [CrossRef]
- Woo-Gon, K.; Yin, S.N.; Kim, Y.W.; Ryu, W.S. Creep behaviour and long-term creep life extrapolation of alloy 617 for a very high temperature gas-cooled reactor. Trans. Indian Inst. Met. 2010, 63, 145–150. [Google Scholar] [CrossRef]
- ECCC Data Sheets 2017. Available online: http://eccc.c-s-m.it/layout_html_standard/en/eccc_european_creep_collaborative_committee/eccc_data_sheets_2017.html (accessed on 21 August 2018).
- Bullough, C.; Krein, R.; Lombardi, P.; Spindler, M.; Poggio, E. Development of an ECCC Interim Creep Rupture Datasheet for Alloy 617B using a Strength Averaging and Blending Approach. In Proceedings of the 4th International ECCC Creep & Fracture Conference, Düsseldorf, Germany, 10–14 September 2017. [Google Scholar]
- Evans, M. A Statistical Test for Identifying the Number of Creep Regimes When Using the Wilshire Equations for Creep Property Predictions. Metall. Mater. Trans. A 2016, 47, 6593–6607. [Google Scholar] [CrossRef]
- Evans, M. Incorporating specific batch characteristics such as chemistry, heat treatment, hardness and grain size into the Wilshire equations for safe life prediction in high temperature applications: An application to 12Cr stainless steel bars for turbine blades. Appl. Math. Model. 2016, 40, 10342–10359. [Google Scholar] [CrossRef]
- Evans, M. Formalisation of Wilshire–Scharning methodology to creep life prediction with application to 1Cr–1Mo–0·25V rotor steel. Mater. Sci. Technol. 2010, 26, 309–317. [Google Scholar] [CrossRef]
- Evans, M. Obtaining confidence limits for safe creep life in the presence of multi batch hierarchical databases: An application to 18Cr–12Ni–Mo steel. Appl. Math. Model. 2011, 35, 2838–2854. [Google Scholar] [CrossRef]
- Evans, M. The importance of creep strain in linking together the Wilshire equations for minimum creep rates and times to various strains (including the rupture strain): An illustration using 1CrMoV rotor steel. J. Mater. Sci. 2014, 49, 329–339. [Google Scholar] [CrossRef]
- Evans, M. Constraints Imposed by the Wilshire Methodology on Creep Rupture Data and Procedures for Testing the Validity of Such Constraints: Illustration Using 1Cr-1Mo-0.25 V Steel. Metall. Mater. Trans. A 2015, 46, 937–947. [Google Scholar] [CrossRef]



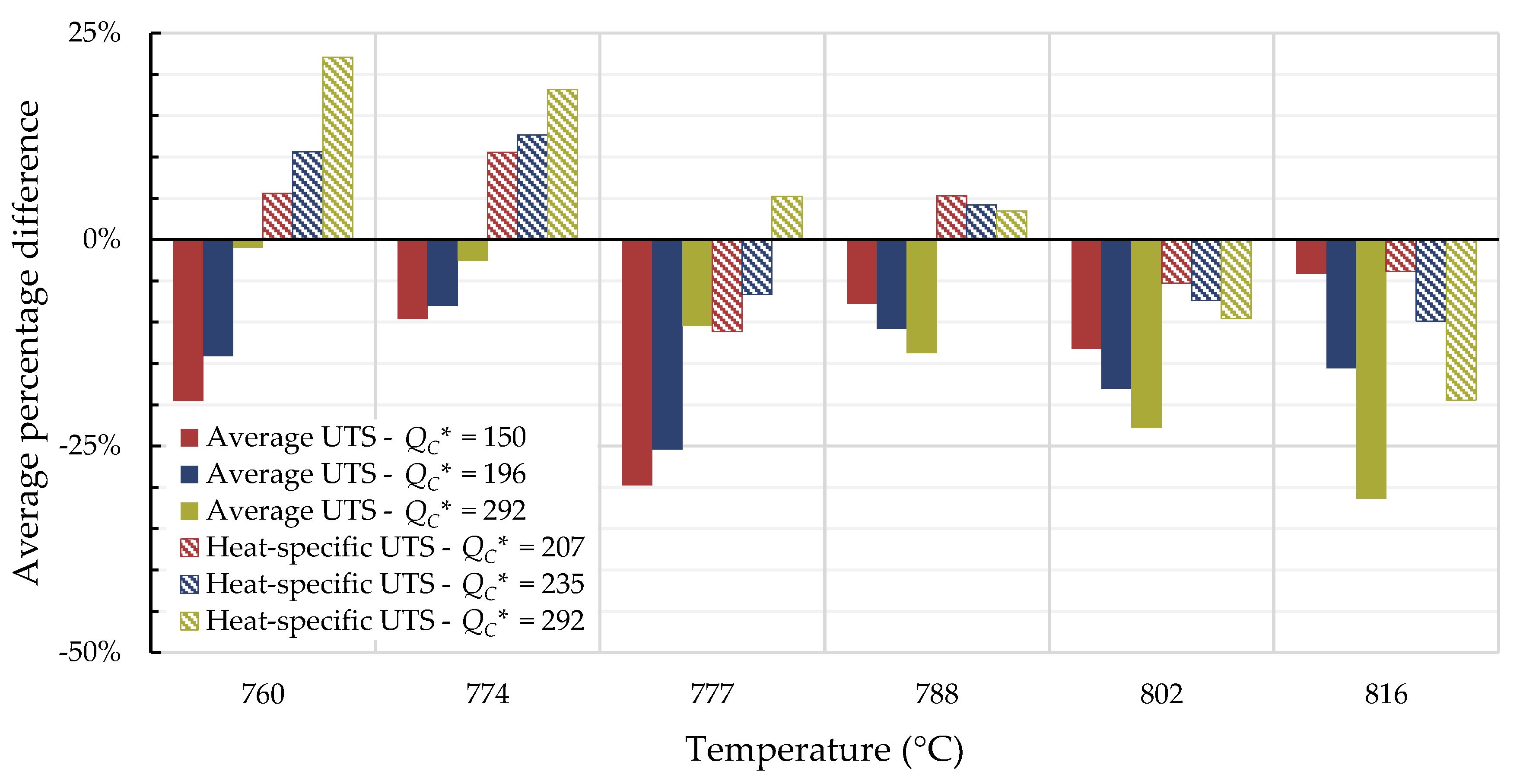

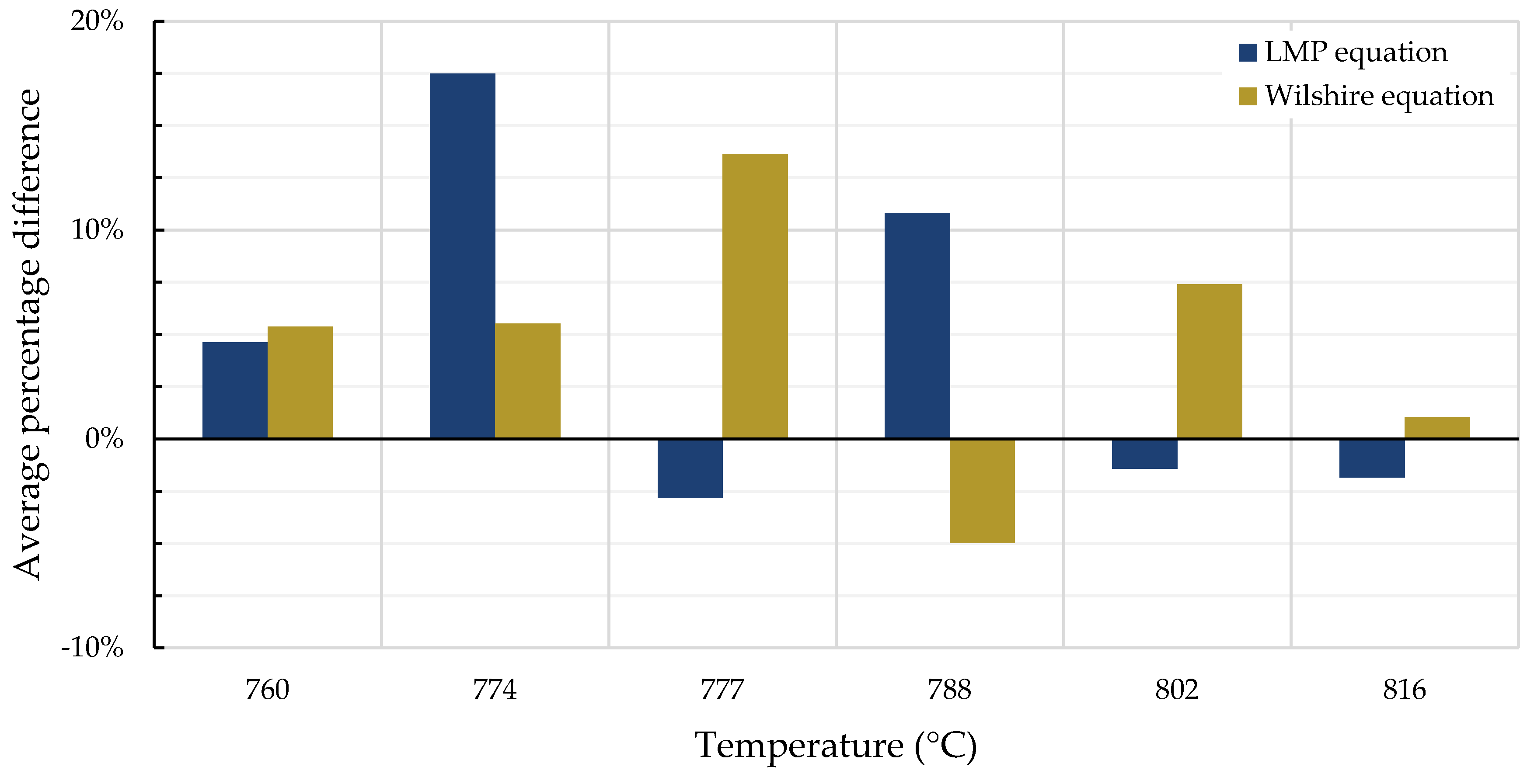
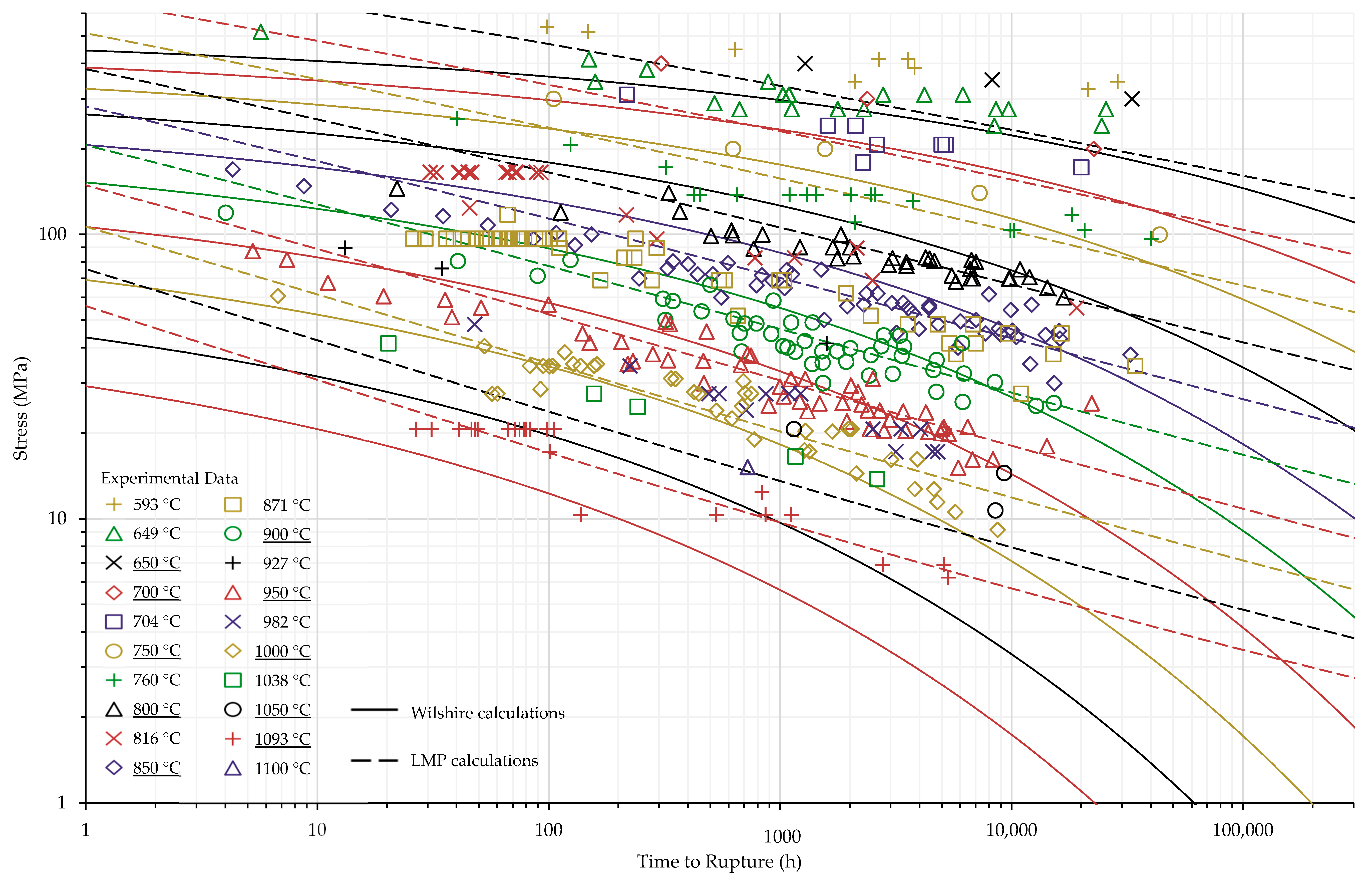

| Data Set | Stress Region | Average | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |||
| All Data | All σ | 190 | 63 | 122 | 118 | 193 | 252 | 362 | 173 | 28 | 401 |
| σ < σYS | 110 | 72 | 152 | 108 | −12 a | −154 a | – | – | – | – | |
| σ ≥ σYS | 285 | – | – | – | 530 | 318 | 274 | 161 | 28 | 401 | |
| tr < 10,000 h | All σ | 162 | 50 | 60 | 106 | 157 | 227 | 307 | 151 | 26 | 376 |
| σ < σYS | 62 | 45 | 68 | 73 | −6 a | −132 a | – | – | – | – | |
| σ ≥ σYS | 254 | – | – | – | 413 | 285 | 278 | 148 | 26 | 376 | |
| Data Set | Tensile Strength | Average | ||
|---|---|---|---|---|
| 0.2 | 0.3 | |||
| All Data | Average | 284 | 372 | 196 |
| Heat- and processing-specific | 283 | 311 | 255 | |
| tr < 10,000 h | Average | 150 | – | 150 |
| Heat- and processing-specific | 207 | – | 207 | |
| Data Set | Tensile Strength | |
|---|---|---|
| All Data | All σ | 224 |
| σ < σYS | 109 | |
| σ ≥ σYS | 266 | |
| tr < 10,000 h | All σ | 202 |
| σ < σYS | 90 | |
| σ ≥ σYS | 235 |
| Data Set | Tensile Strength | |
|---|---|---|
| All Data | Average | 289 |
| Heat- and processing-specific | 272 | |
| tr < 10,000 h | Average | 196 |
| Heat- and processing-specific | 235 |
| Data Set | Split Regions? | Determination Method | R2 All σ | R2 σ < σYS | R2 σ ≥ σYS | MSE | |||
|---|---|---|---|---|---|---|---|---|---|
| All Data | No | Arrhenius Plot | 190 | — | — | 0.742 | — | — | |
| Correlation Optimization | 224 | — | — | 0.750 | — | — | |||
| Self-Diffusion Activation | 292 | — | — | 0.732 | — | — | |||
| Yes | Arrhenius Plot | 190 | — | — | — | 0.722 | 0.594 | ||
| — | 110 | 285 | — | 0.794 | 0.677 | ||||
| Correlation Optimization | 224 | — | — | — | 0.665 | 0.657 | |||
| — | 109 | 266 | — | 0.794 | 0.680 | ||||
| Self-Diffusion Activation | 292 | — | — | — | 0.542 | 0.674 | |||
| tr < 10,000 h | No | Arrhenius Plot | 162 | — | — | 0.724 | — | — | |
| Correlation Optimization | 202 | — | — | 0.741 | — | — | |||
| Self-Diffusion Activation | 292 | — | — | 0.720 | — | — | |||
| Yes | Arrhenius Plot | 162 | — | — | — | 0.757 | 0.568 | ||
| — | 62 | 254 | — | 0.795 | 0.701 | ||||
| Correlation Optimization | 202 | — | — | — | 0.691 | 0.671 | |||
| — | 90 | 235 | — | 0.811 | 0.700 | ||||
| Self-Diffusion Activation | 292 | — | — | — | 0.530 | 0.682 |
| Data Set | Tensile Strength | Determination Method | All σ | R2 All σ | MSE |
|---|---|---|---|---|---|
| All Data | Average | Arrhenius Plot | 284 | 0.880 | |
| Correlation Optimization | 289 | 0.880 | |||
| Self-Diffusion Activation | 292 | 0.880 | |||
| Heat- and processing-specific | Arrhenius Plot | 283 | 0.950 | ||
| Correlation Optimization | 272 | 0.950 | |||
| Self-Diffusion Activation | 292 | 0.949 | |||
| tr < 10,000 h | Average | Arrhenius Plot | 150 | 0.849 | |
| Correlation Optimization | 196 | 0.854 | |||
| Self-Diffusion Activation | 292 | 0.838 | |||
| Heat- and processing-specific | Arrhenius Plot | 207 | 0.879 | ||
| Correlation Optimization | 235 | 0.880 | |||
| Self-Diffusion Activation | 292 | 0.875 |
| Data Set | Split Regions? | 650 (°C) | 700 (°C) | 750 (°C) | 760 (°C) | 800 (°C) | 850 (°C) | 900 (°C) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All Data | No | Arrhenius Plot | 190 | — | — | 146 | 95.8 | 59.0 | 53.2 | 34.0 | 18.3 | 9.07 |
| Correlation Optimization | 224 | — | — | 171 | 115 | 71.8 | 64.8 | 41.8 | 22.6 | 11.2 | ||
| Self-Diffusion Activation | 292 | — | — | 210 | 146 | 94.5 | 86.0 | 57.1 | 32.0 | 16.4 | ||
| Yes | Arrhenius Plot | 190 | — | — | 131 | 96.1 | 67.9 | 63.1 | 46.3 | 30.3 | 18.8 | |
| — | 110 | 285 | 83.6 | 63.3 | 46.6 | 43.8 | 33.4 | 23.2 | 15.3 | |||
| Correlation Optimization | 224 | — | — | 148 | 109 | 77.2 | 71.8 | 52.7 | 34.4 | 21.3 | ||
| — | 109 | 266 | 83.0 | 62.9 | 46.4 | 43.6 | 33.3 | 23.1 | 15.3 | |||
| Self-Diffusion Activation | 292 | — | — | 173 | 128 | 92.5 | 86.3 | 64.2 | 42.7 | 26.8 | ||
| tr < 10,000 h | No | Arrhenius Plot | 162 | — | — | 118 | 76.2 | 46.2 | 41.5 | 26.3 | 14.0 | 6.93 |
| Correlation Optimization | 202 | — | — | 153 | 101 | 62.4 | 56.2 | 35.9 | 19.2 | 9.44 | ||
| Self-Diffusion Activation | 292 | — | — | 210 | 146 | 95.4 | 86.9 | 58.0 | 32.7 | 16.9 | ||
| Yes | Arrhenius Plot | 162 | — | — | 114 | 83.9 | 59.5 | 55.3 | 40.7 | 26.9 | 16.8 | |
| — | 62 | 254 | 54.7 | 43.6 | 34.0 | 32.2 | 25.8 | 19.0 | 13.4 | |||
| Correlation Optimization | 202 | — | — | 137 | 101 | 71.8 | 66.7 | 49.0 | 32.2 | 20.0 | ||
| — | 90 | 235 | 69.1 | 52.8 | 39.4 | 37.0 | 28.6 | 20.1 | 13.5 | |||
| Self-Diffusion Activation | 292 | — | — | N/A 1 | 129 | 93.9 | 87.8 | 65.7 | 44.1 | 28.0 | ||
| ECCC Inconel 617 Data Sheet (Year: 2005) | 179 | 112 | 68 | 62 | 41 | 24 | 14.9 | |||||
| ECCC Interim Inconel 617B Data Sheet (Year: 2014) | 222 | 129 | 70.6 | 62.7 | 39.9 | — | — | |||||
| Data Set | Tensile Strength | Heat and Processing Condition | 760 (°C) | 774 (°C) | 777 (°C) | 788 (°C) | 802 (°C) | 816 (°C) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| All Data | Average | Arrhenius Plot | 284 | — | 183 | 164 | 161 | 146 | 129 | 114 |
| Correlation Optimization | 289 | — | 184 | 164 | 161 | 146 | 129 | 114 | ||
| Self-Diffusion Activation | 292 | — | 184 | 164 | 161 | 146 | 129 | 113 | ||
| Heat- and processing-specific | Arrhenius Plot | 283 | 5183 AP | 166 | 148 | 144 | 131 | 116 | 102 | |
| 5183 PA | 176 | 155 | 151 | 136 | 119 | 103 | ||||
| 5183 OA | 194 | 167 | 162 | 143 | 121 | 102 | ||||
| 5793 PA | 172 | 152 | 148 | 134 | 118 | 103 | ||||
| Unknown PA 1 | 178 | 157 | 153 | 139 | 122 | 106 | ||||
| Correlation Optimization | 272 | 5183 AP | 165 | 147 | 143 | 130 | 115 | 102 | ||
| 5183 PA | 175 | 154 | 150 | 136 | 119 | 103 | ||||
| 5183 OA | 193 | 166 | 161 | 142 | 121 | 102 | ||||
| 5793 PA | 170 | 151 | 148 | 134 | 118 | 104 | ||||
| Unknown PA 1 | 176 | 156 | 153 | 138 | 122 | 107 | ||||
| Self-Diffusion Activation | 292 | 5183 AP | 167 | 148 | 145 | 131 | 116 | 102 | ||
| 5183 PA | 177 | 156 | 152 | 136 | 119 | 103 | ||||
| 5183 OA | 195 | 168 | 163 | 143 | 121 | 102 | ||||
| 5793 PA | 173 | 153 | 149 | 134 | 118 | 103 | ||||
| Unknown PA 1 | 179 | 158 | 154 | 139 | 122 | 106 | ||||
| tr < 10,000 h | Average | Arrhenius Plot | 150 | — | 148 | 134 | 132 | 121 | 109 | 97 |
| Correlation Optimization | 196 | — | 155 | 139 | 136 | 124 | 110 | 97 | ||
| Self-diffusion Activation | 292 | — | 172 | 151 | 148 | 132 | 115 | 99 | ||
| Heat- and processing-specific | Arrhenius Plot | 207 | 5183 AP | 153 | 138 | 135 | 124 | 111 | 99 | |
| 5183 PA | 162 | 145 | 141 | 129 | 114 | 100 | ||||
| 5183 OA | 179 | 156 | 151 | 135 | 116 | 99 | ||||
| 5793 PA | 158 | 142 | 139 | 127 | 113 | 101 | ||||
| Unknown PA 1 | 164 | 147 | 143 | 131 | 117 | 103 | ||||
| Correlation Optimization | 235 | 5183 AP | 157 | 141 | 138 | 126 | 112 | 99 | ||
| 5183 PA | 167 | 148 | 144 | 131 | 115 | 101 | ||||
| 5183 OA | 184 | 159 | 155 | 137 | 117 | 99 | ||||
| 5793 PA | 163 | 145 | 142 | 129 | 114 | 101 | ||||
| Unknown PA 1 | 168 | 150 | 146 | 133 | 118 | 104 | ||||
| Self-Diffusion Activation | 292 | 5183 AP | 166 | 147 | 144 | 130 | 115 | 101 | ||
| 5183 PA | 177 | 155 | 151 | 136 | 118 | 102 | ||||
| 5183 OA | 194 | 167 | 162 | 142 | 120 | 101 | ||||
| 5793 PA | 172 | 152 | 148 | 134 | 117 | 102 | ||||
| Unknown PA 1 | 178 | 157 | 153 | 138 | 121 | 105 |
| Alloy | C | R2 | ||||
|---|---|---|---|---|---|---|
| Inconel 617 | 32,630 | −8114 | 1749 | −357.2 | 16.02 | 0.837 |
| Nimonic 105 | 354,200 | −426,900 | 185,600 | −27,280 | 16.88 | 0.842 |
| Alloy | Equation | R2 | MSE |
|---|---|---|---|
| Inconel 617 | LMP Equation | 0.837 | |
| Wilshire Equation 1 | 0.742 | ||
| Nimonic 105 | LMP Equation | 0.842 | |
| Wilshire Equation 2 | 0.949 |
| Alloy | Calculation Method | Percentage Difference | Experimental Values of Longest Test Duration | ||
|---|---|---|---|---|---|
| Temperature (°C) | Stress (MPa) | Time to Rupture (h) | |||
| Inconel 617 | LMP Equation | −73.8% | 750 | 100 | 43,706 |
| Wilshire Equation 1 | −61.0% | ||||
| Nimonic 105 | LMP Equation | −31.2% | 760 | 221 | 34,955 |
| Wilshire Equation 2 | −17.2% | ||||
| Calculation Method | 650 °C | 700 °C | 750 °C | 800 °C | 850 °C | 900 °C | 950 °C | 1000 °C |
|---|---|---|---|---|---|---|---|---|
| LMP Equation | 161 | 104 | 66.0 | 41.7 | 26.4 | 16.8 | 10.8 | 7.13 |
| Wilshire Equation 1 | 145 | 95.8 | 59.0 | 34.0 | 18.3 | 9.07 | 4.14 | 1.72 |
| ECCC (Year: 2005) | 179 | 112 | 68 | 41 | 24 | 14.9 | — | — |
| Calculation Method | Heat and Processing Condition | 700 °C | 750 °C | 800 °C | 850 °C |
|---|---|---|---|---|---|
| LMP Equation | — | 273 | 189 | 129 | 99.7 |
| Wilshire Equation1 | 5183 AP | 270 | 182 | 117 | 72.5 |
| 5183 PA | 297 | 194 | 121 | 70.8 | |
| 5183 OA | 351 | 217 | 124 | 63.1 | |
| 5793 PA | 282 | 188 | 120 | 72.7 | |
| Unknown PA 2 | 294 | 195 | 124 | 74.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cedro III, V.; Garcia, C.; Render, M. Use of the Wilshire Equations to Correlate and Extrapolate Creep Data of Inconel 617 and Nimonic 105. Materials 2018, 11, 2534. https://doi.org/10.3390/ma11122534
Cedro III V, Garcia C, Render M. Use of the Wilshire Equations to Correlate and Extrapolate Creep Data of Inconel 617 and Nimonic 105. Materials. 2018; 11(12):2534. https://doi.org/10.3390/ma11122534
Chicago/Turabian StyleCedro III, Vito, Christian Garcia, and Mark Render. 2018. "Use of the Wilshire Equations to Correlate and Extrapolate Creep Data of Inconel 617 and Nimonic 105" Materials 11, no. 12: 2534. https://doi.org/10.3390/ma11122534
APA StyleCedro III, V., Garcia, C., & Render, M. (2018). Use of the Wilshire Equations to Correlate and Extrapolate Creep Data of Inconel 617 and Nimonic 105. Materials, 11(12), 2534. https://doi.org/10.3390/ma11122534





