Why Should the “Alternative” Method of Estimating Local Interfacial Shear Strength in a Pull-Out Test Be Preferred to Other Methods?
Abstract
1. Introduction
- briefly present the model and main equations used to calculate the local interfacial strength parameters from a recorded force–displacement curve;
- show how different methods for τd determination can be developed using different sets of characteristic points;
- estimate the accuracy and “general quality” of all these methods by applying them to determine the local IFSS and the interfacial frictional stress, τf, from theoretical and experimental (for various fiber–matrix pairs) force–displacement curves;
- discuss the problems encountered in estimating τd and τf from force–displacement curves for different systems and under different conditions, and recommend the most reliable method if possible.
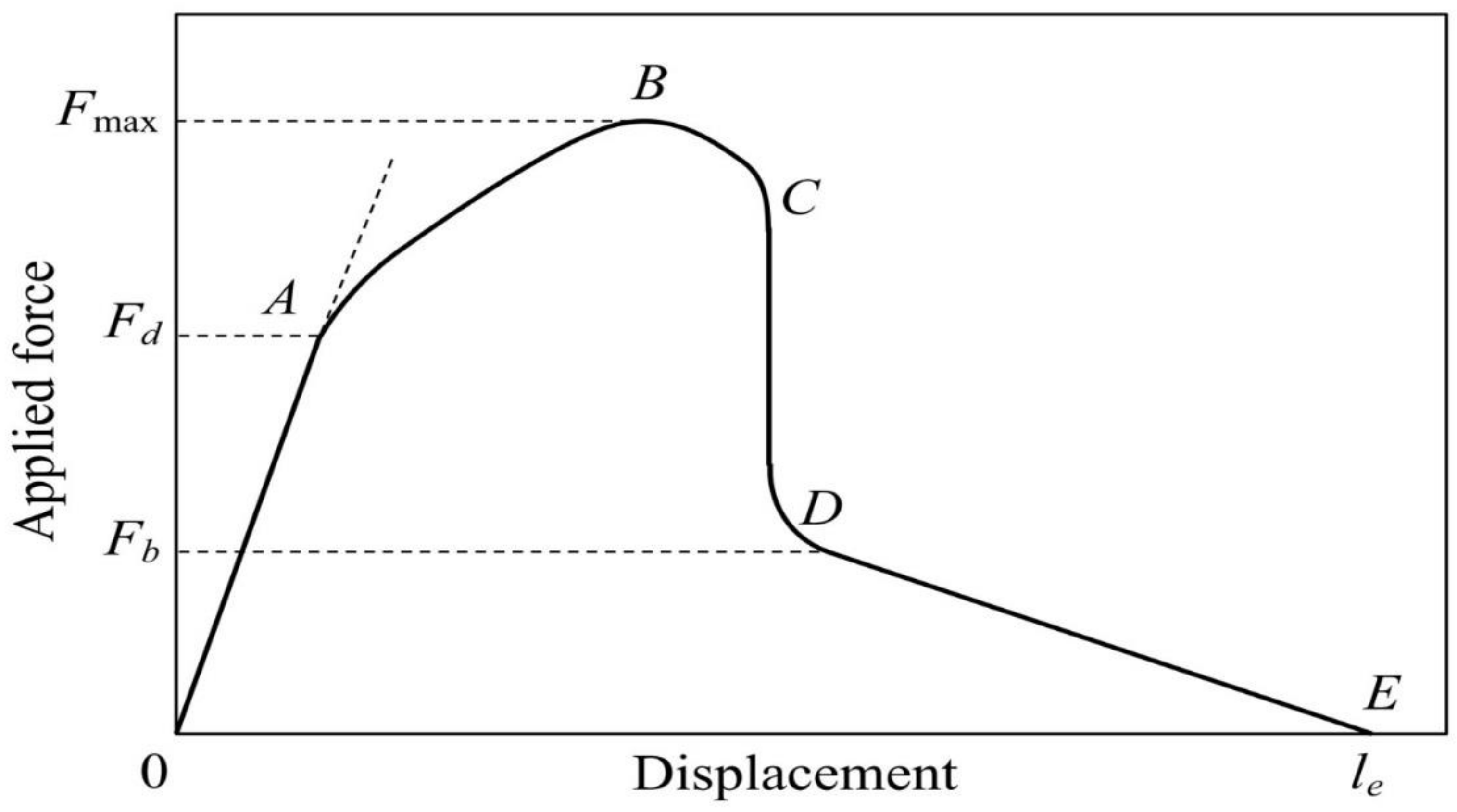
2. The Model
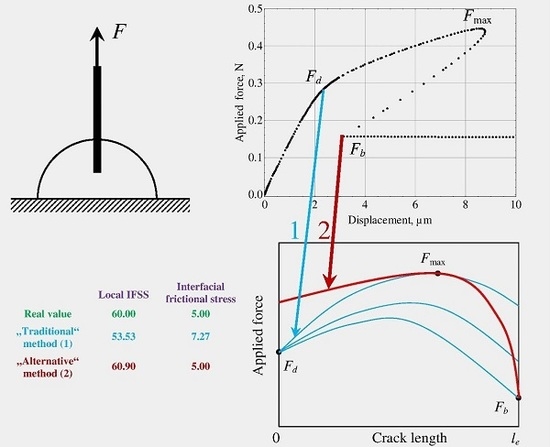
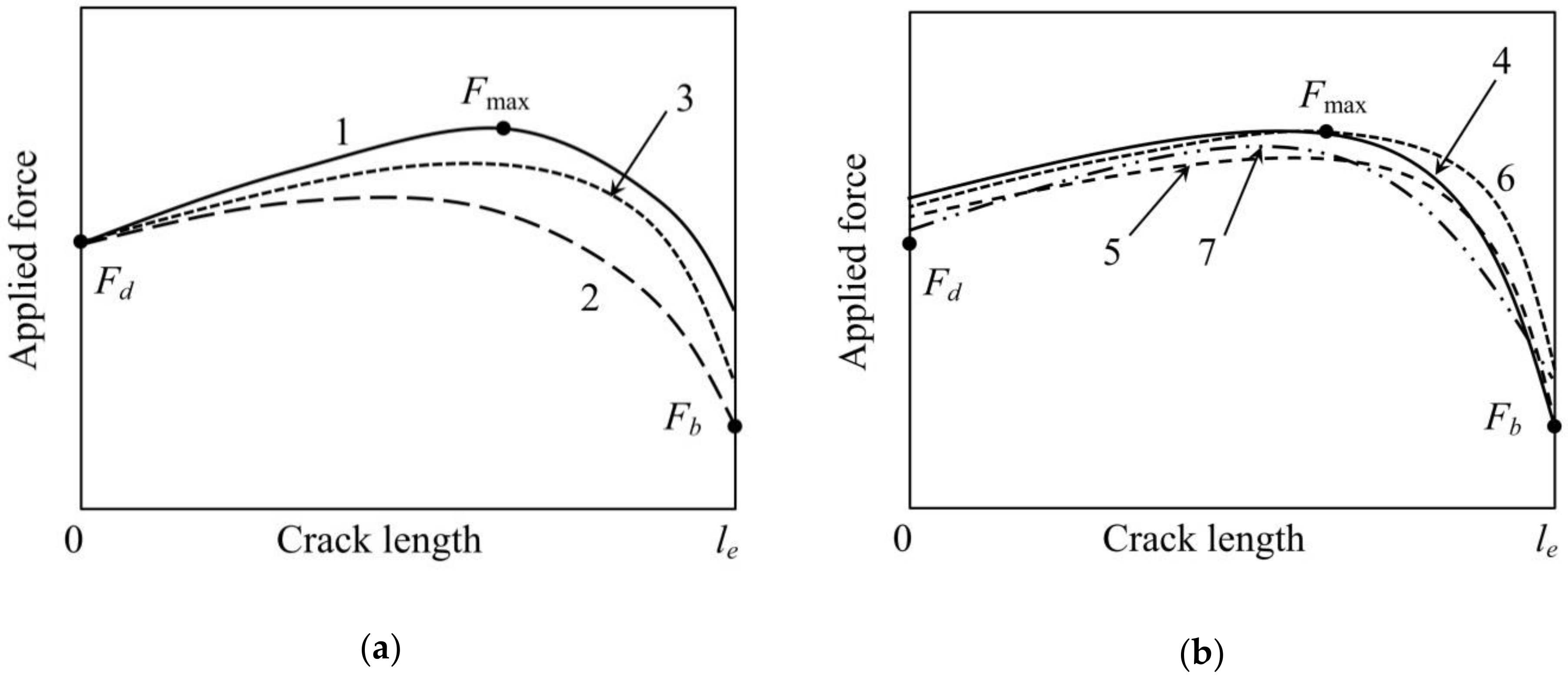
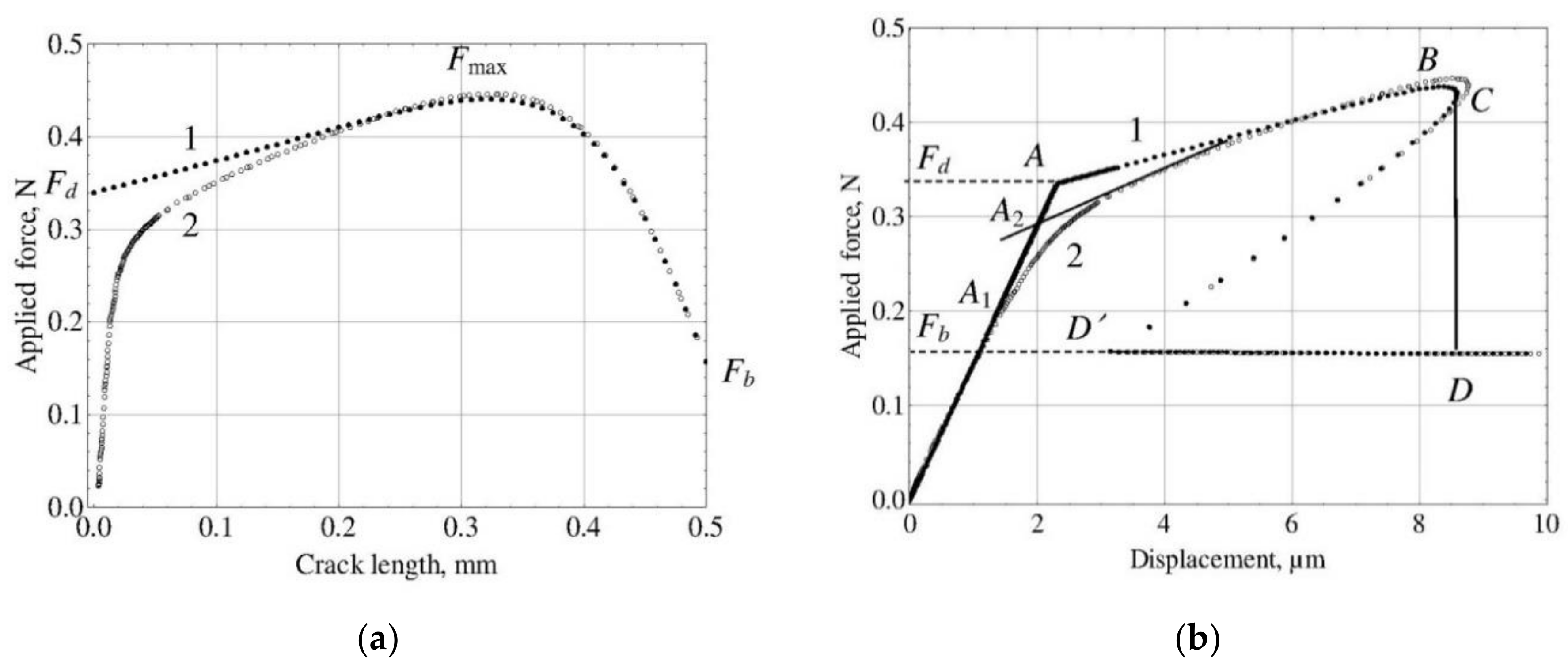
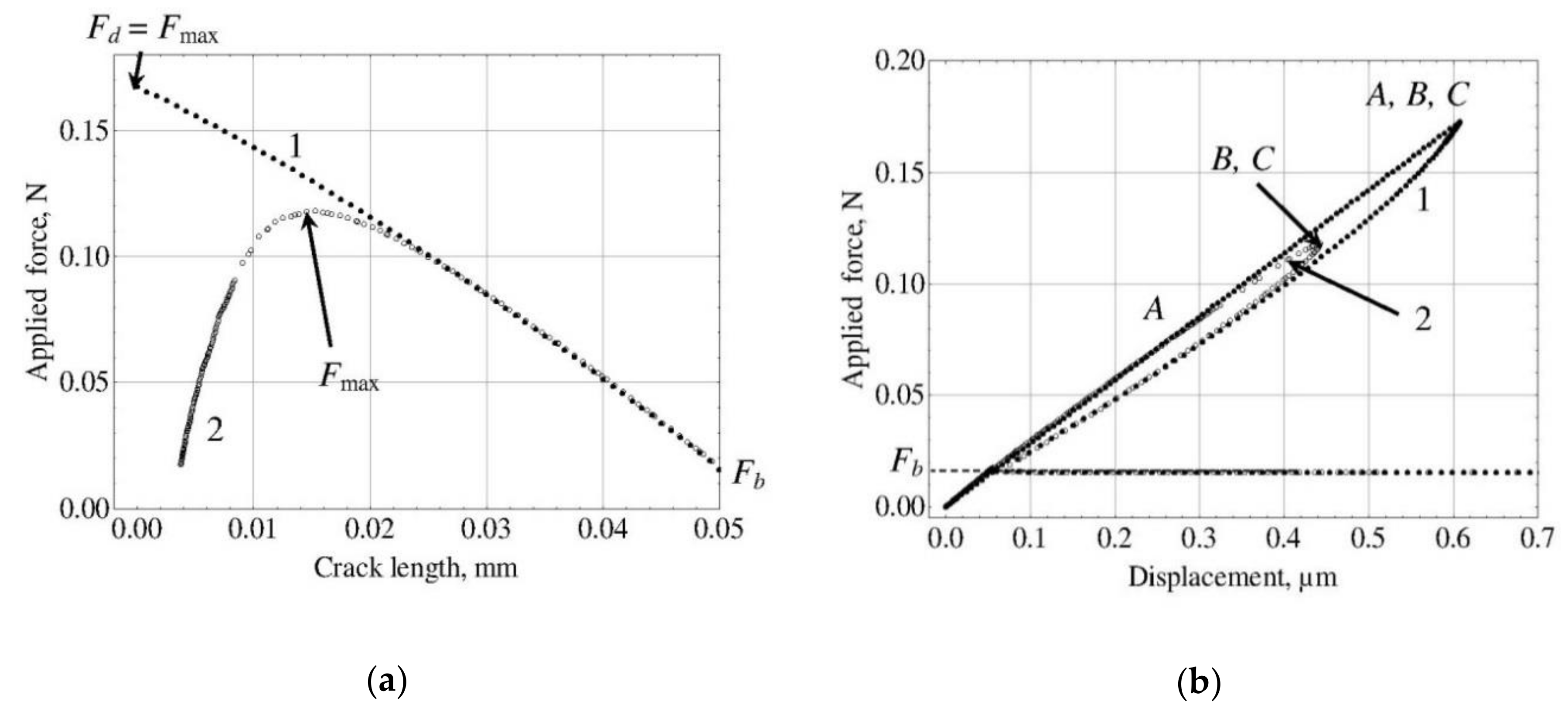
3. Methods for Determination of Interfacial Strength Parameters
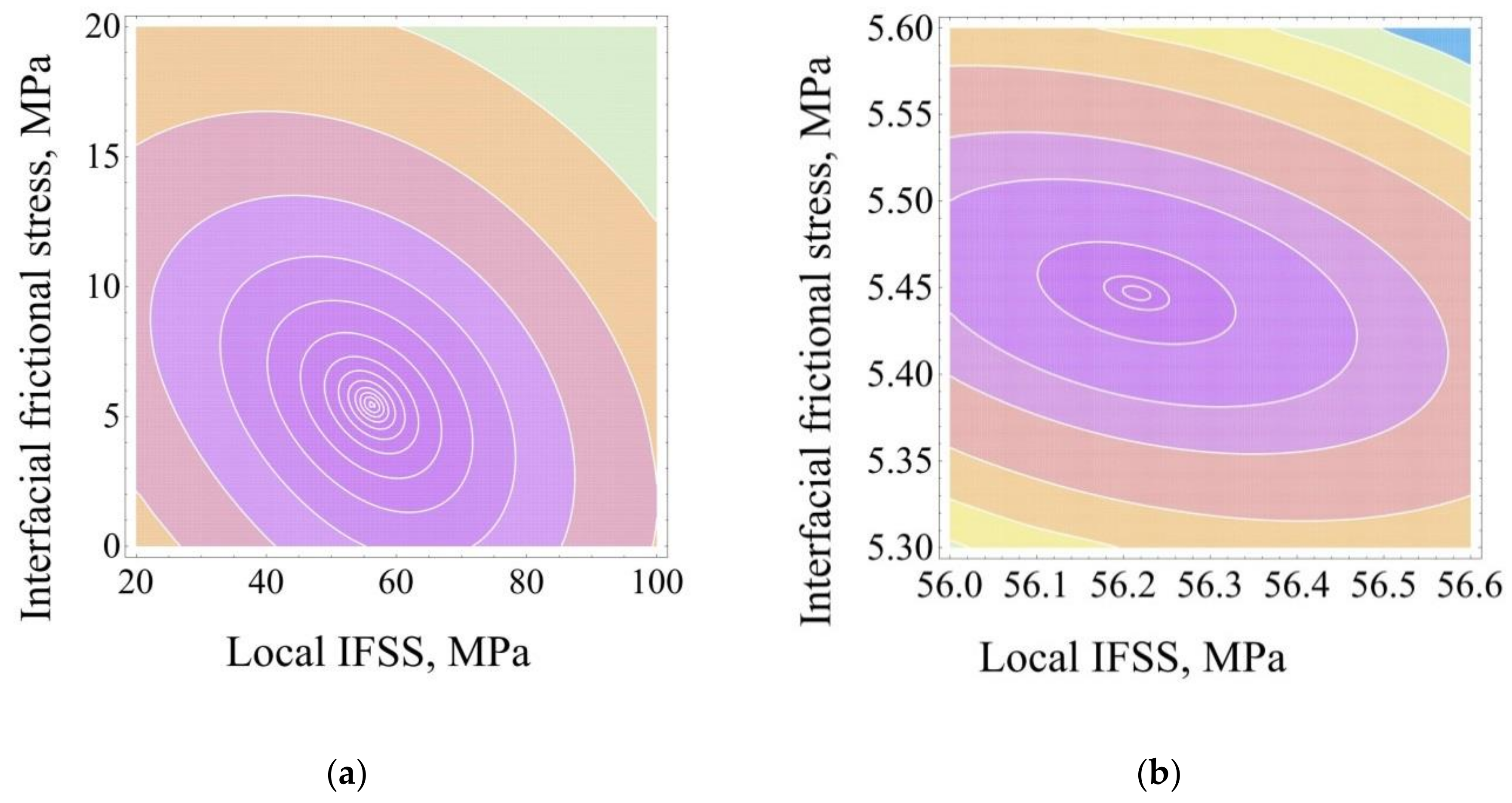
4. Evaluation of Interfacial Strength Parameters from Theoretical Force–Displacement Curves: Comparison of the Methods
- Non-cylindrical shape of the matrix droplet. The interfacial crack starts at the top of the droplet, where the fiber content is extremely high (well above its mean value, Vf), and then propagates into the regions with continuously decreasing Vf.
- Non-ideal elasticity, especially of the matrix, which distorts the theoretical curve and can affect positions of the characteristic points.
- Too short embedded length; in such specimens, most of the crack may be located in the meniscus region which is essentially non-cylindrical.
- Imperfect interface: large interfacial defects can result in additional “kinks” and decrease the measured debond force.
- Possible movement of the opposite (fixed) fiber end within the glue or in the clamps.
- Non-linear frictional force which indicates substantial effect of transverse (normal) interfacial stresses.
5. Evaluation of Interfacial Strength Parameters from Theoretical Force–Displacement Curves: Comparison of the Methods
5.1. Experimental
5.1.1. Materials and Specimen Preparation
- (1)
- melting for 100 s at 45 °C, then fiber embedding, 1 h at 85 °C and curing for 6 h at 80 °C;
- (2)
- 290 °C/10 s (embedding), then 15 min cooling down to 23 °C;
- (3)
- the same procedure as in (1);
- (4)
- 255 °C/2 min (embedding), then cooling down to 23 °C;
- (5)
- 24 h at 23 °C and RH = 50%, then 1 week at 23 °C and RH = 90%.
5.1.2. Pull-Out Testing
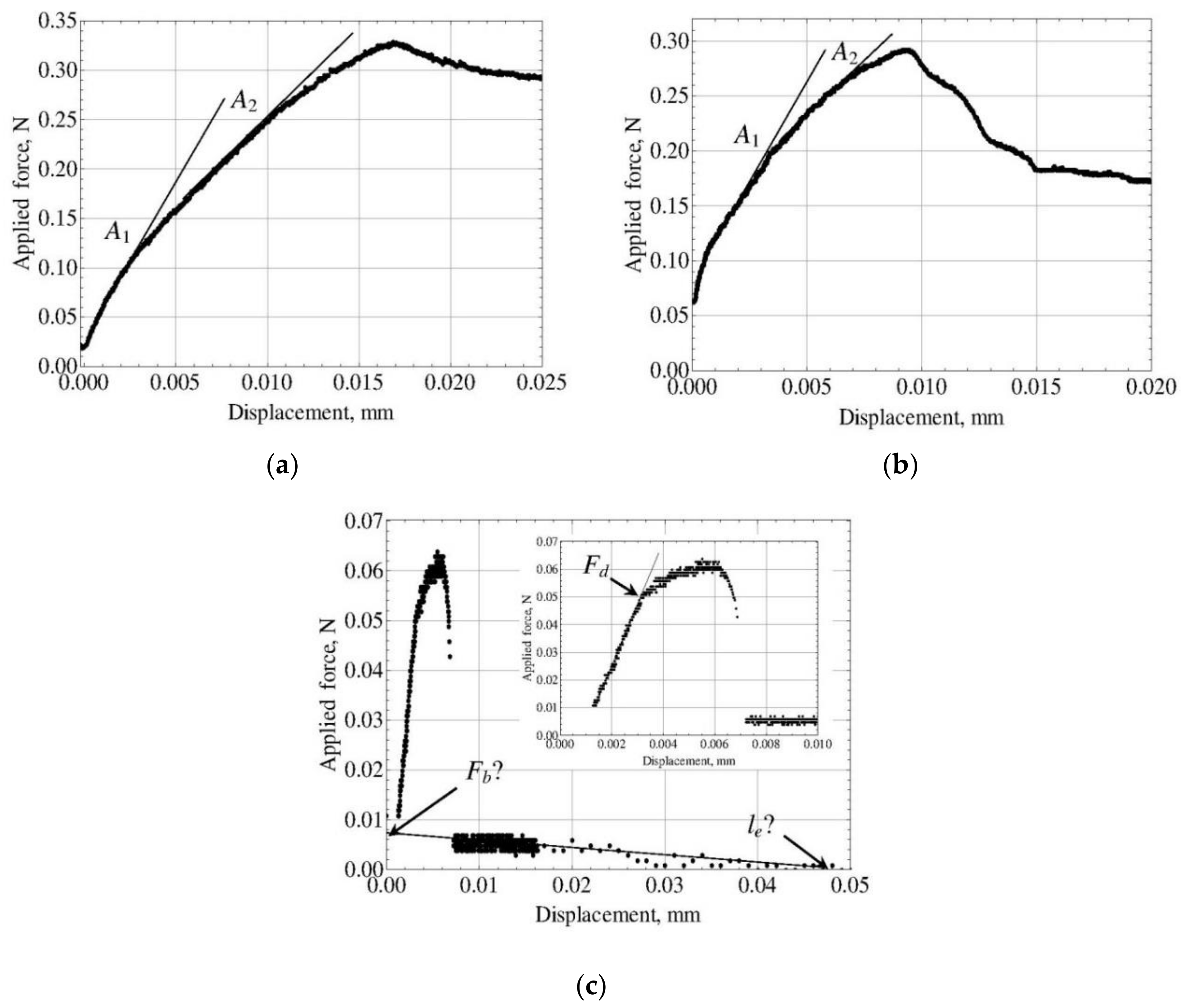
5.2. Evaluation Results and Comparison of the Methods
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shiriajeva, G.V.; Andreevskaya, G.D. Method of determination of the adhesion of resins to the surface of glass fibers. Plast. Massy (Polym. Compd. USSR) 1962, 4, 42–43. [Google Scholar]
- Favre, J.P.; Perrin, J. Carbon fibre adhesion to organic matrices. J. Mater. Sci. 1972, 7, 1113–1118. [Google Scholar] [CrossRef]
- Penn, L.S.; Bowler, E.R. A new approach to surface energy characterization for adhesive performance prediction. Surf. Interface Anal. 1981, 3, 161–164. [Google Scholar] [CrossRef]
- Désarmot, G.; Favre, J.P. Advances in pull-out testing and data analysis. Compos. Sci. Technol. 1991, 42, 151–187. [Google Scholar] [CrossRef]
- Gorbatkina, Y.A. Adhesive Strength of Fiber-Polymer Systems; Ellis Horwood: New York, NY, USA, 1992; ISBN 0-13-005455-0. [Google Scholar]
- Miller, B.; Muri, P.; Rebenfeld, L. A microbond method for determination of the shear strength of a fiber–resin interface. Compos. Sci. Technol. 1987, 28, 17–32. [Google Scholar] [CrossRef]
- Herrera-Franco, P.J.; Drzal, L.T. Comparison of methods for the measurement of fibre/matrix adhesion in composites. Composites 1992, 23, 2–27. [Google Scholar] [CrossRef]
- Sirisha, K.; Rambabu, T.; Shankar, Y.R.; Ravikumar, P. Validity of bond strength tests: A critical review: Part I. J. Conserv. Dent. 2014, 17, 305–311. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.-C.; Mai, Y.-W.; Cotterell, B. Fracture of fiber-reinforced materials. ZAMP 1988, 39, 550–572. [Google Scholar] [CrossRef]
- Liu, C.H.; Nairn, J.A. Analytical fracture mechanics of the microbond test including the effects of friction and thermal stresses. Int. J. Adhes. Adhes. 1999, 19, 59–70. [Google Scholar] [CrossRef]
- Kerans, R.J.; Parthasarathy, T.A. Theoretical analysis of the fiber pullout and pushout tests. J. Am. Ceram. Soc. 1991, 74, 1585–1596. [Google Scholar] [CrossRef]
- Nairn, J.A. Analytical fracture mechanics analysis of the pull-out test including the effects of friction and thermal stresses. Adv. Compos. Lett. 2000, 9, 373–383. [Google Scholar]
- Marotzke, C.; Qiao, L. Interfacial crack propagation arising in single-fiber pull-out tests. Compos. Sci. Technol. 1997, 57, 887–897. [Google Scholar] [CrossRef]
- Piggott, M.R.; Xiong, Y.J. Visualisation of debonding of fully and partially embedded glass fibres in epoxy resins. Compos. Sci. Technol. 1994, 52, 535–540. [Google Scholar] [CrossRef]
- Shioya, M.; Mikami, E.; Kikutani, T. Analysis of single-fiber pull-out from composites by using stress birefringence. Compos. Interfaces 1997, 4, 429–446. [Google Scholar] [CrossRef]
- Andrews, M.C.; Young, R.J.; Mahy, J. Interfacial failure mechanisms in aramid/epoxy model composites. Compos. Interfaces 1994, 2, 433–456. [Google Scholar] [CrossRef]
- Bannister, D.J.; Andrews, M.C.; Cervenka, A.; Young, R.J. Analysis of the single-fibre pull-out test using Raman spectroscopy. Part II: Micromechanics of deformation for an aramid/epoxy system. Compos. Sci. Technol. 1995, 53, 411–421. [Google Scholar] [CrossRef]
- Zhandarov, S.; Pisanova, E.; Schneider, K. Fiber-stretching test: A new technique for characterizing the fiber–matrix interface using direct observation of crack initiation and propagation. J. Adhes. Sci. Technol. 2000, 14, 381–398. [Google Scholar] [CrossRef]
- Pisanova, E.; Zhandarov, S.; Mäder, E.; Ahmad, I.; Young, R.J. Three techniques of interfacial bond strength estimation from direct observation of crack initiation and propagation in polymer–fibre systems. Compos. Part A 2001, 32, 435–443. [Google Scholar] [CrossRef]
- Leung, C.K.Y.; Li, V.C. New strength-based model for the debonding of discontinuous fibers in an elastic matrix. J. Mater. Sci. 1991, 26, 5996–6010. [Google Scholar] [CrossRef]
- Favre, J.P.; Désarmot, G.; Sudre, O.; Vassel, A. Were McGarry or Shiriajeva right to measure glass–fiber adhesion? Compos. Interfaces 1997, 4, 313–326. [Google Scholar] [CrossRef]
- Kanda, T.; Li, V.C. Interface property and apparent strength of high-strength hydrophilic fiber in cement matrix. J. Mater. Civ. Eng. 1998, 10, 5–13. [Google Scholar] [CrossRef]
- Zhandarov, S.; Pisanova, E.; Mäder, E. Is there any contradiction between the stress and energy failure criteria in micromechanical tests? Part II Crack propagation: Effect of friction on force–displacement curves. Compos. Interfaces 2000, 7, 149–175. [Google Scholar] [CrossRef]
- Zhandarov, S.; Mäder, E. Peak force as function of the embedded length in the pull-out and microbond tests: Effect of specimen geometry. J. Adhes. Sci. Technol. 2005, 19, 817–855. [Google Scholar] [CrossRef]
- Stang, H.; Shah, S.P. Failure of fiber reinforced composites by pull-out fracture. J. Mater. Sci. 1986, 21, 953–958. [Google Scholar] [CrossRef]
- Leung, C.K.Y. Fracture-based two-way debonding model for discontinuous fibers in an elastic matrix. J. Eng. Mech. 1992, 118, 2298–2318. [Google Scholar] [CrossRef]
- Scheer, R.J.; Nairn, J.A. A comparison of several fracture mechanics methods for measuring interfacial toughness with microbond tests. J. Adhes. 1995, 53, 45–68. [Google Scholar] [CrossRef]
- Hampe, A.; Marotzke, C. The energy release rate of the fiber/polymer matrix interface: Measurement and theoretical analysis. J. Reinf. Plast. Compos. 1997, 16, 341–352. [Google Scholar] [CrossRef]
- Mäder, E.; Grundke, K.; Jacobasch, H.-J.; Wachinger, G. Surface, interphase and composite property relations in fibre-reinforced composites. Composites 1994, 25, 739–744. [Google Scholar] [CrossRef]
- Hampe, A.; Kalinka, G.; Meretz, S.; Schulz, E. An advanced equipment for single-fibre pull-out designed to monitor the fracture process. Compos. Part A 1995, 26, 40–46. [Google Scholar] [CrossRef]
- Textechno, H. Stein GmbH & Co. KG, Moenchengladbach, Fibre-Matrix Adhesion Tester FIMATEST. Available online: http://www.textechno.com/product/fimatest/ (accessed on 24 October 2018).
- Yang, L.; Thomason, J.L. Development and application of micromechanical techniques for characterising interfacial shear strength in fibre-thermoplastic composites. Polym. Test. 2012, 31, 895–903. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Z.; Wang, X.; Zhang, G.; Long, S.; Yang, J. Interfacial shear strength of carbon fiber reinforced polyphenylene sulfide measured by the microbond test. Polym. Test. 2013, 32, 724–730. [Google Scholar] [CrossRef]
- Zhandarov, S.; Mäder, E.; Scheffler, C.; Kalinka, G.; Poitzsch, C.; Fliescher, S. Investigation of interfacial strength parameters in polymer matrix composites: Compatibility and reproducibility. Adv. Ind. Eng. Polym. Res. 2018, 1, 82–92. [Google Scholar] [CrossRef]
- Zhandarov, S.F.; Mäder, E.; Yurkevich, O.R. Indirect estimation of fiber/polymer bond strength and interfacial friction from maximum load values recorded in the microbond and pull-out tests. Part I: Local bond strength. J. Adhes. Sci. Technol. 2002, 16, 1171–1200. [Google Scholar] [CrossRef]
- Zhandarov, S.F.; Mäder, E. Characterization of fiber/matrix interface strength: Applicability of different tests, approaches and parameters. Compos. Sci. Technol. 2005, 65, 149–160. [Google Scholar] [CrossRef]
- Jäger, J.; Sause, M.G.R.; Burkert, F.; Moosburger-Will, J.; Greisel, M.; Horn, S. Influence of plastic deformation on single-fiber push-out tests of carbon fiber reinforced epoxy resin. Compos. Part A 2015, 71, 157–167. [Google Scholar] [CrossRef]
- Zhandarov, S.; Mäder, E. An alternative method of determining the local interfacial shear strength from force–displacement curves in the pull-out and microbond tests. Int. J. Adhes. Adhes. 2014, 55, 37–42. [Google Scholar] [CrossRef]
- Zhandarov, S.; Mäder, E. Determining the interfacial toughness from force–displacement curves in the pull-out and microbond tests using the alternative method. Int. J. Adhes. Adhes. 2016, 65, 11–18. [Google Scholar] [CrossRef]
- Mäder, E.; Liu, J.; Hiller, J.; Lu, W.; Li, Q.; Zhandarov, S.; Chou, T.-W. Coating of carbon nanotube fibers: Variation of tensile properties, failure behavior, and adhesion strength. Front. Mater. 2015, 2, 53. [Google Scholar] [CrossRef][Green Version]
- Scheffler, C.; Zhandarov, S.; Mäder, E. Alkali resistant glass fiber reinforced concrete: Pull-out investigation of interphase behavior under quasi-static and high rate loading. Cem. Concr. Compos. 2017, 84, 19–27. [Google Scholar] [CrossRef]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Thermomechanically induced interfacial stresses in fibrous composites. Fibre Sci. Technol. 1977, 10, 195–209. [Google Scholar] [CrossRef]
- Andrews, M.C.; Bannister, D.J.; Young, R.J. Review: The interfacial properties of aramid/epoxy model composites. J. Mater. Sci. 1996, 31, 3893–3913. [Google Scholar] [CrossRef]
- Wolfram Language & System Documentation Center. Available online: https://reference.wolfram.com/language/ (accessed on 25 October 2018).
- Zhandarov, S.; Pisanova, E.; Lauke, B. Is there any contradiction between the stress and energy failure criteria in micromechanical tests? Part I. Crack initiation: Stress-controlled or energy-controlled? Compos. Interfaces 1998, 5, 387–404. [Google Scholar] [CrossRef]
- Zhandarov, S.; Pisanova, E.; Mäder, E.; Nairn, J.A. Investigation of load transfer between the fiber and the matrix in pull-out tests with fibers having different diameters. J. Adhes. Sci. Technol. 2001, 15, 205–222. [Google Scholar] [CrossRef]
- Goettler, R.W.; Faber, K.T. Interfacial shear stresses in fiber-reinforced glasses. Compos. Sci. Technol. 1989, 37, 129–147. [Google Scholar] [CrossRef]
- Pitkethly, M.J.; Doble, J.B. Characterizing the fibre/matrix interface of carbon fibre-reinforced composites using a single fibre pull-out test. Composites 1990, 21, 389–395. [Google Scholar] [CrossRef]
- Park, S.-J.; Seo, M.-K.; Kim, H.-J.; Lee, D.-R. Studies on PAN-based carbon fibers irradiated by Ar+ ion beams. J. Colloid Interface Sci. 2003, 261, 393–398. [Google Scholar] [CrossRef]
- Eichhorn, S.J.; Bennett, J.A.; Shyng, Y.T.; Young, R.J.; Davies, R.J. Analysis of interfacial micromechanics in microdroplet model composites using synchrotron microfocus X-ray diffraction. Compos. Sci. Technol. 2006, 66, 2197–2205. [Google Scholar] [CrossRef]
- Li, Y.; Hu, C.; Yu, Y. Interfacial studies of sisal fiber reinforced high density polyethylene (HDPE) composites. Compos. Part A 2008, 39, 570–578. [Google Scholar] [CrossRef]
- Chen, X.; Yao, L.; Xue, J.; Zhao, D.; Lan, Y.; Qian, X.; Wang, C.X.; Qiu, Y. Plasma penetration depth and mechanical properties of atmospheric plasma-treated 3D aramid woven composites. Appl. Surf. Sci. 2008, 255, 2864–2868. [Google Scholar] [CrossRef]
- Vautard, F.; Fioux, P.; Vidal, L.; Schultz, J.; Nardin, M.; Defoort, B. Influence of an oxidation of the carbon fiber surface on the adhesion strength in carbon fiber-acrylate composites cured by electron beam. Int. J. Adhes. Adhes. 2012, 34, 93–106. [Google Scholar] [CrossRef]
- Maeder, E.; Moerschel, U.; Effing, M. Quality assessment of composites. JEC Compos. Mag. 2016, 102, 49–51. [Google Scholar]
- Zhandarov, S.; Mäder, E. Analysis of a pull-out test with real specimen geometry. Part I: Matrix droplet in the shape of a spherical segment. J. Adhes. Sci. Technol. 2013, 27, 430–465. [Google Scholar] [CrossRef]
- Zhandarov, S.; Mäder, E. Analysis of a pull-out test with real specimen geometry. Part II: The effect of meniscus. J. Adhes. Sci. Technol. 2014, 28, 65–84. [Google Scholar] [CrossRef]
- Scheffler, C.; Zhandarov, S.; Jenschke, W.; Mäder, E. Poly (vinyl alcohol) fiber reinforced concrete: Investigation of strain rate dependent interphase behavior with single fiber pullout test under quasi-static and high rate loading. J. Adhes. Sci. Technol. 2013, 27, 385–402. [Google Scholar] [CrossRef]
- Palmer, A.C.; Rice, J.R. The growth of slip surfaces in the progressive failure of over-consolidated clay. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1973, 332, 527–548. [Google Scholar] [CrossRef]
- Wang, Y.; Li, V.C.; Backer, S. Modeling of fiber pull-out from a cement matrix. Int. J. Cem. Compos. Lightweight Concr. 1988, 10, 143–149. [Google Scholar] [CrossRef]
- Shao, Y.; Li, Z.; Shah, S.P. Matrix cracking and interface debonding in fiber-reinforced cement-matrix composites. J. Adv. Cem. Based Mater. 1993, 1, 55–66. [Google Scholar] [CrossRef]
| Property | GF a | CF1 b | CF2 c | PVA d | Epoxy e | PP f | PA 6,6 g | Concrete h |
|---|---|---|---|---|---|---|---|---|
| Fiber diameter, df (µm) | 10–25 | 6–8 | 3–6 | 25–49 | - | - | - | - |
| Radius of the matrix droplet, Rm (mm) | - | - | - | - | 1.25 | 1.25 | 1.25 | 1.3 |
| Axial tensile modulus, EA or Em (GPa) | 75 | 240 | 205 | 35 | 2.9 | 1.4 | 3.2 | 28 |
| Axial Poisson ratio, νA | 0.17 | 0.2 | 0.2 | 0.2 | 0.35 | 0.35 | 0.3 | n/a |
| Axial CTE, αA or αm (10−6 K−1) | 5 | −0.1 | −0.9 | n/a i | 76 | 150 i | 81 | n/a |
| Stress-free temperature, Tref (°C) | - | - | - | - | 80 | 23 i | 65 | 23 i |
| Embedded length, le (µm) | 100–900 | 80–200 | 30–120 | 300–2000 | - | - | - | - |
| Method | Fd, N | Fmax, N | Fb, N | τd, MPa | τf, MPa | s × 103, N2 | Rank |
|---|---|---|---|---|---|---|---|
| 1 (Fd, Fmax) | 0.2939 | 0.4466 | 0.2284 | 53.53 | 7.27 | 5.11 | 7 |
| 2 (Fd, Fb) | 0.2939 | 0.3982 | 0.1569 | 53.53 | 5.00 | 2.34 | 5 |
| 3 (Fd, best{Fmax, Fb}) | 0.2939 | 0.4132 | 0.1794 | 53.53 | 5.71 | 1.62 | 3 |
| 4 (Fb, Fmax) | 0.3472 | 0.4466 | 0.1569 | 60.90 | 5.00 | 2.84 | 6 |
| 5 (Fb, best{Fd, Fmax}) | 0.3180 | 0.4200 | 0.1569 | 56.87 | 5.00 | 1.29 | 2 |
| 6 (Fmax, best{Fd, Fb}) | 0.3288 | 0.4466 | 0.1827 | 58.35 | 5.81 | 1.88 | 4 |
| 7 (best { Fd, Fmax, Fb}) | 0.3133 | 0.4250 | 0.1712 | 56.21 | 5.45 | 1.04 | 1 |
| Equivalent cylinder | 0.3401 | 0.4412 | 0.1569 | 60 | 5 | - | - |
| 30° meniscus | 0.2939 | 0.4466 | 0.1569 | 60 | 5 | - | - |
| Method | Fd, N | Fmax, N | Fb, N | τd, MPa | τf, MPa | s × 103, N2 | Rank |
|---|---|---|---|---|---|---|---|
| 1 (Fd, Fmax) | 0.05681 | 0.1181 | 0.07463 | 23.76 | 23.76 | 3.47 | 3 |
| 2 (Fd, Fb) | 0.05681 | 0.05681 | 0.01572 | 23.76 | 5.00 | 3.76 | 4–7 |
| 3 (Fd, best{Fmax, Fb}) | 0.05681 | 0.05681 | 0.01572 | 23.76 | 5.00 | 3.76 | 4–7 |
| 4 (Fb, Fmax) | 0.1181 | 0.1181 | 0.01572 | 45.01 | 5.00 | 3.76 | 4–7 |
| 5 (Fb, best{Fd, Fmax}) | 0.08746 | 0.08746 | 0.01572 | 34.38 | 5.00 | 1.88 | 1–2 |
| 6 (Fmax, best{Fd, Fb}) | 0.1181 | 0.1181 | 0.01571 | 45.01 | 5.00 | 3.76 | 3 |
| 7 (best { Fd, Fmax, Fb}) | 0.08745 | 0.08745 | 0.01571 | 34.38 | 5.00 | 1.88 | 1–2 |
| Equivalent cylinder | 0.1730 | 0.1730 | 0.01572 | 60 | 5 | - | - |
| 30° meniscus | 0.05681 | 0.1181 | 0.01572 | 60 | 5 | - | - |
| Method | Fd, N | Fmax, N | Fb, N | τd, MPa | τf, MPa | s × 103, N2 | Rank |
|---|---|---|---|---|---|---|---|
| 1 (Fd, Fmax) | 0.1259 | 0.3296 | 0.3038 | 15.22 | 8.73 | 0.292 | 6 |
| 0.2659 | 0.3296 | 0.1356 | 32.14 | 3.90 | 22.82 | 7 | |
| 2 (Fd, Fb) | 0.1259 | 0.3158 | 0.2867 | 15.22 | 8.24 | 0.191 | 5 |
| 0.2659 | 0.4272 | 0.2867 | 32.14 | 8.24 | 9.53 | 5 | |
| 3 (Fd, best{Fmax, Fb}) | 0.1259 | 0.3212 | 0.2935 | 15.22 | 8.44 | 0.116 | 2 |
| 0.2659 | 0.3968 | 0.2419 | 32.14 | 6.95 | 6.53 | 3 | |
| 4 (Fb, Fmax) | 0.1455 | 0.3296 | 0.2867 | 17.59 | 8.24 | 0.384 | 7 |
| 0.1455 | 0.3296 | 0.2867 | 17.59 | 8.24 | 14.50 | 6 | |
| 5 (Fb, best{Fd, Fmax}) | 0.1324 | 0.3203 | 0.2867 | 16.01 | 8.24 | 0.130 | 3 |
| 0.2183 | 0.2869 | 0.2867 | 26.39 | 8.24 | 5.55 | 2 | |
| 6 (Fmax, best{Fd, Fb}) | 0.1344 | 0.3296 | 0.2966 | 16.25 | 8.53 | 0.172 | 4 |
| 0.1977 | 0.3296 | 0.2304 | 23.89 | 6.62 | 7.83 | 4 | |
| 7 (best { Fd, Fmax, Fb}) | 0.1305 | 0.3230 | 0.2918 | 15.77 | 8.39 | 0.091 | 1 |
| 0.2282 | 0.3736 | 0.2560 | 27.59 | 7.36 | 4.30 | 1 | |
| Experimental values | 0.1259 | 0.3296 | 0.2867 | - | - | - | - |
| 0.2659 |
| Method | Fd, N | Fmax, N | Fb, N | τd, MPa | τf, MPa | s × 103, N2 | Rank |
|---|---|---|---|---|---|---|---|
| 1 (Fd, Fmax) | 0.2000 | 0.2924 | 0.1006 | 36.10 | 0.44 | 2.85 | 7 |
| 0.2812 | 0.2924 | 0.0126 | 50.76 | 0.054 | 19.99 | 7 | |
| 2 (Fd, Fb) | 0.2000 | 0.3422 | 0.1540 | 36.10 | 0.67 | 2.48 | 5 |
| 0.2812 | 0.4228 | 0.1540 | 50.76 | 0.67 | 16.99 | 5 | |
| 3 (Fd, best{Fmax, Fb}) | 0.2000 | 0.3190 | 0.1292 | 36.10 | 0.56 | 1.32 | 3 |
| 0.2812 | 0.3625 | 0.0891 | 50.76 | 0.39 | 9.13 | 3 | |
| 4 (Fb, Fmax) | 0.1497 | 0.2924 | 0.1540 | 27.02 | 0.67 | 2.53 | 6 |
| 0.1497 | 0.2924 | 0.1540 | 27.02 | 0.67 | 17.30 | 6 | |
| 5 (Fb, best{Fd, Fmax}) | 0.1751 | 0.3175 | 0.1540 | 31.61 | 0.67 | 1.25 | 2 |
| 0.2161 | 0.3581 | 0.1540 | 39.00 | 0.67 | 8.56 | 2 | |
| 6 (Fmax, best{Fd, Fb}) | 0.1734 | 0.2924 | 0.1289 | 31.30 | 0.56 | 1.34 | 4 |
| 0.2112 | 0.2924 | 0.0886 | 38.13 | 0.39 | 9.17 | 4 | |
| 7 (best {Fd, Fmax, Fb}) | 0.1825 | 0.3100 | 0.1381 | 32.95 | 0.60 | 0.87 | 1 |
| 0.2363 | 0.3376 | 0.1104 | 42.65 | 0.48 | 5.96 | 1 | |
| Experimental values | 0.2000 | 0.2924 | 0.1540 | - | - | - | - |
| 0.2812 |
| Method | Fd, N | Fmax, N | Fb, N | τd, MPa | τf, MPa | s × 103, N2 | Rank |
|---|---|---|---|---|---|---|---|
| 1 (Fd, Fmax) | 0.05197 | 0.06386 | 0.06181 | 89.25 | 75.92 | 2.935 | 7 |
| 2 (Fd, Fb) | 0.05197 | 0.51973 | 0.00764 | 89.25 | 9.38 | 0.141 | 3–6 |
| 3 (Fd, best{Fmax, Fb}) | 0.05197 | 0.05197 | 0.00764 | 89.25 | 9.38 | 0.141 | 3–6 |
| 4 (Fb, Fmax) | 0.06386 | 0.06386 | 0.00764 | 107.47 | 9.38 | 0.141 | 3–6 |
| 5 (Fb, best{Fd, Fmax}) | 0.05792 | 0.05792 | 0.00764 | 98.36 | 9.38 | 0.071 | 1–2 |
| 6 (Fmax, best{Fd, Fb}) | 0.06386 | 0.06386 | 0.00766 | 107.47 | 9.41 | 0.141 | 3–6 |
| 7 (best { Fd, Fmax, Fb}) | 0.05792 | 0.05792 | 0.00764 | 98.36 | 9.38 | 0.071 | 1–2 |
| Experimental values | 0.05197 | 0.06386 | 0.00764 | - | - | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhandarov, S.; Mäder, E.; Gohs, U. Why Should the “Alternative” Method of Estimating Local Interfacial Shear Strength in a Pull-Out Test Be Preferred to Other Methods? Materials 2018, 11, 2406. https://doi.org/10.3390/ma11122406
Zhandarov S, Mäder E, Gohs U. Why Should the “Alternative” Method of Estimating Local Interfacial Shear Strength in a Pull-Out Test Be Preferred to Other Methods? Materials. 2018; 11(12):2406. https://doi.org/10.3390/ma11122406
Chicago/Turabian StyleZhandarov, Serge, Edith Mäder, and Uwe Gohs. 2018. "Why Should the “Alternative” Method of Estimating Local Interfacial Shear Strength in a Pull-Out Test Be Preferred to Other Methods?" Materials 11, no. 12: 2406. https://doi.org/10.3390/ma11122406
APA StyleZhandarov, S., Mäder, E., & Gohs, U. (2018). Why Should the “Alternative” Method of Estimating Local Interfacial Shear Strength in a Pull-Out Test Be Preferred to Other Methods? Materials, 11(12), 2406. https://doi.org/10.3390/ma11122406