Development of Laser-Based Powder Bed Fusion Process Parameters and Scanning Strategy for New Metal Alloy Grades: A Holistic Method Formulation
Abstract
1. Introduction
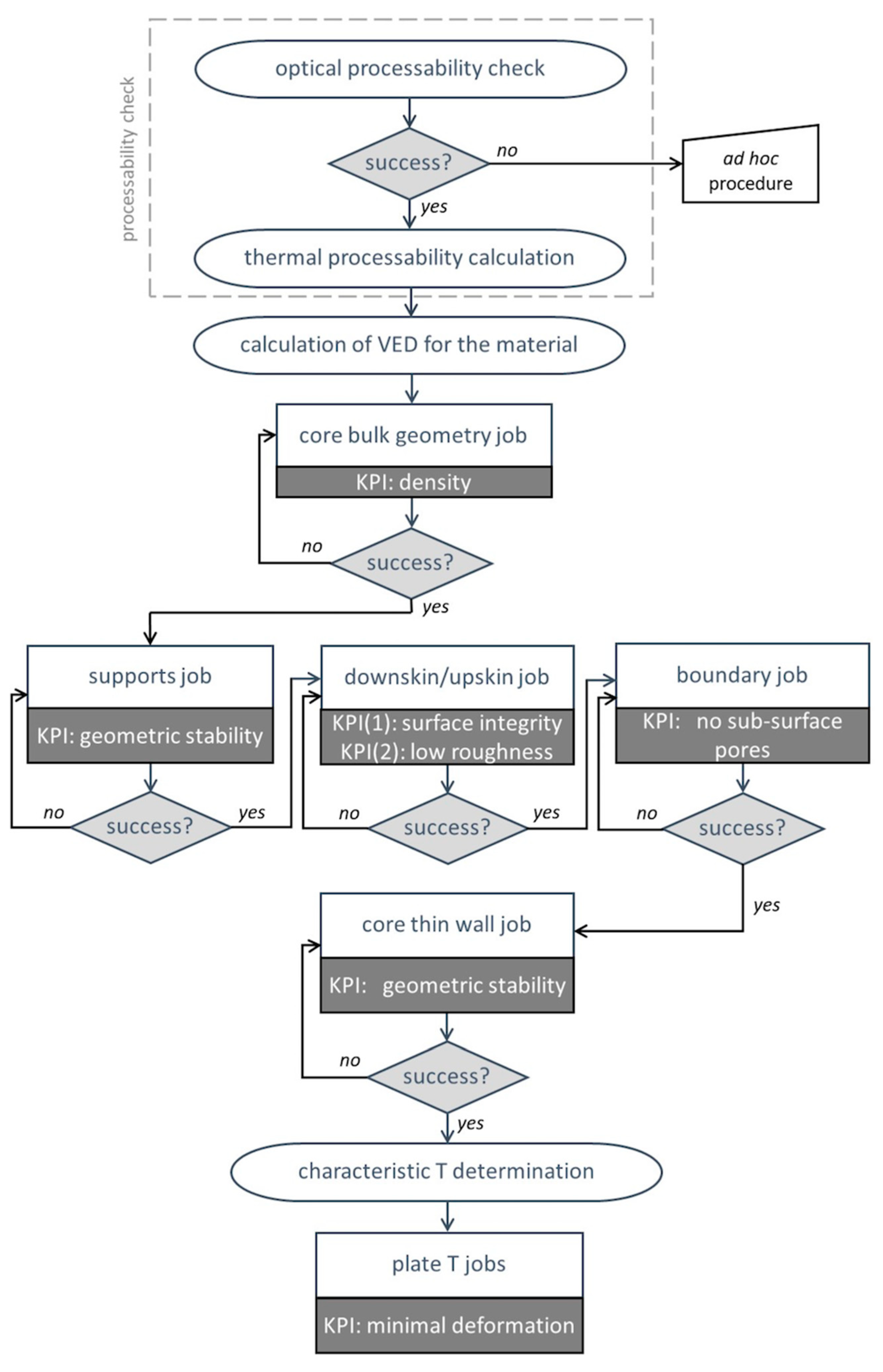
2. Method
2.1. General Outline
2.2. Processability Check
2.3. Core Bulk Parameters
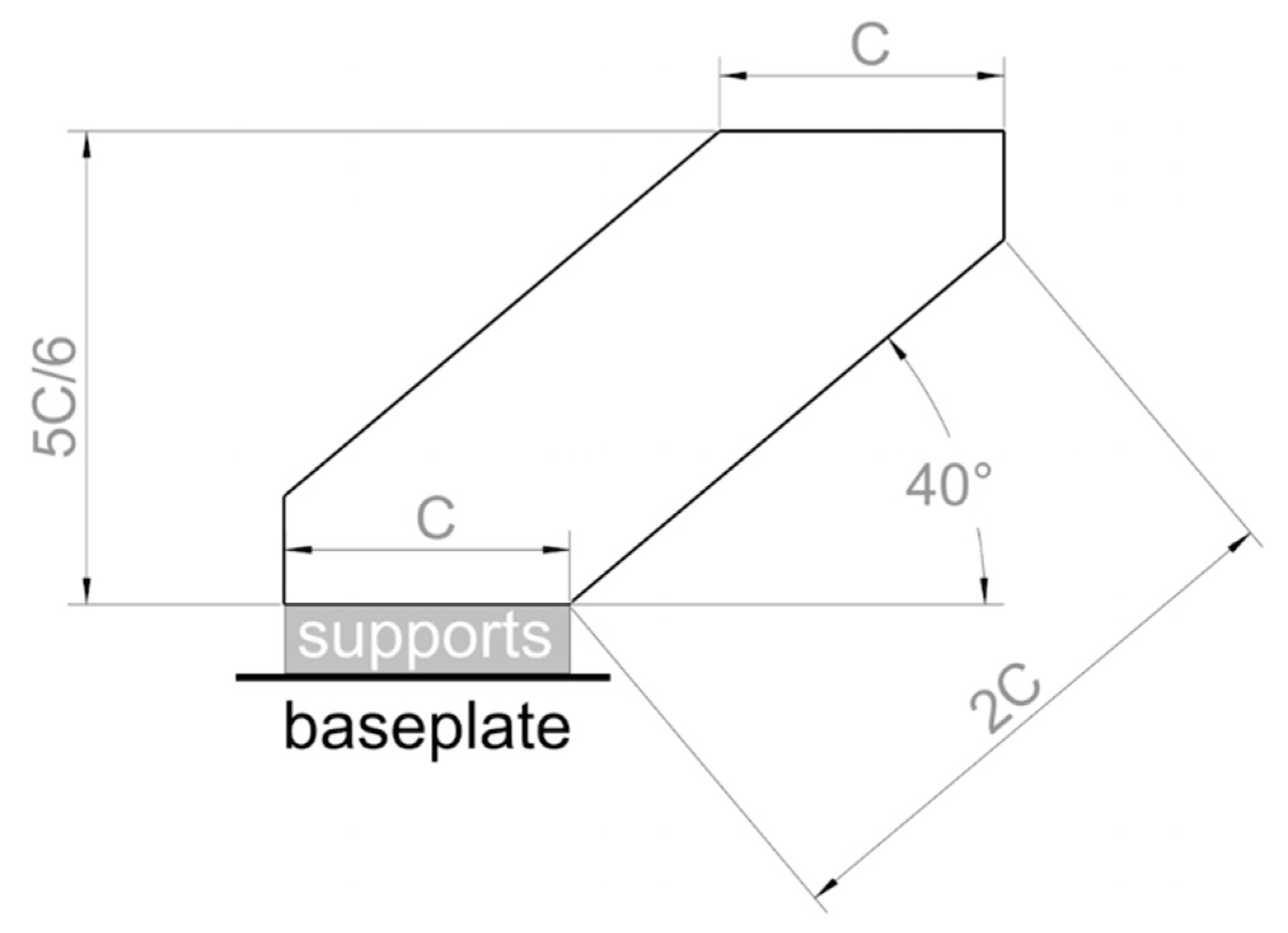
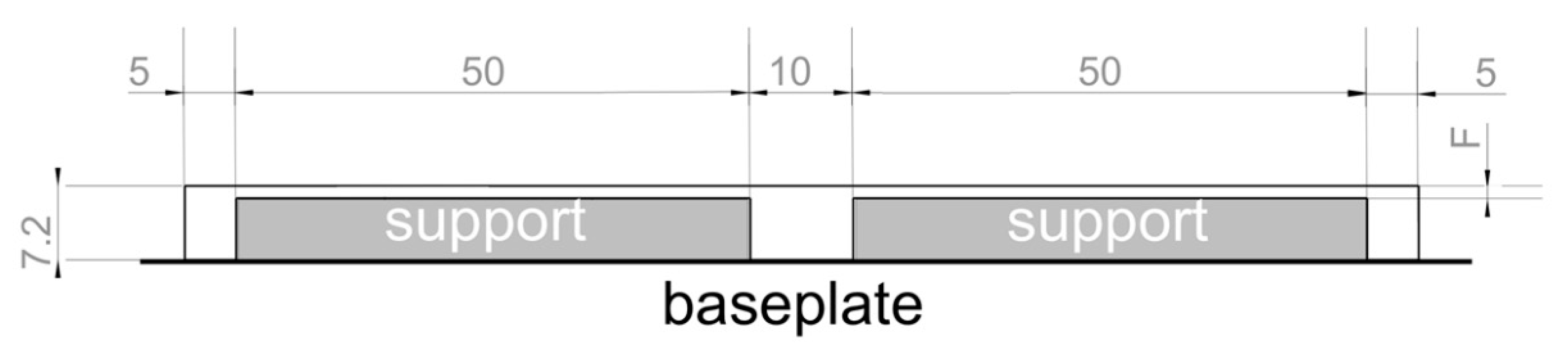
2.4. Support Parameters
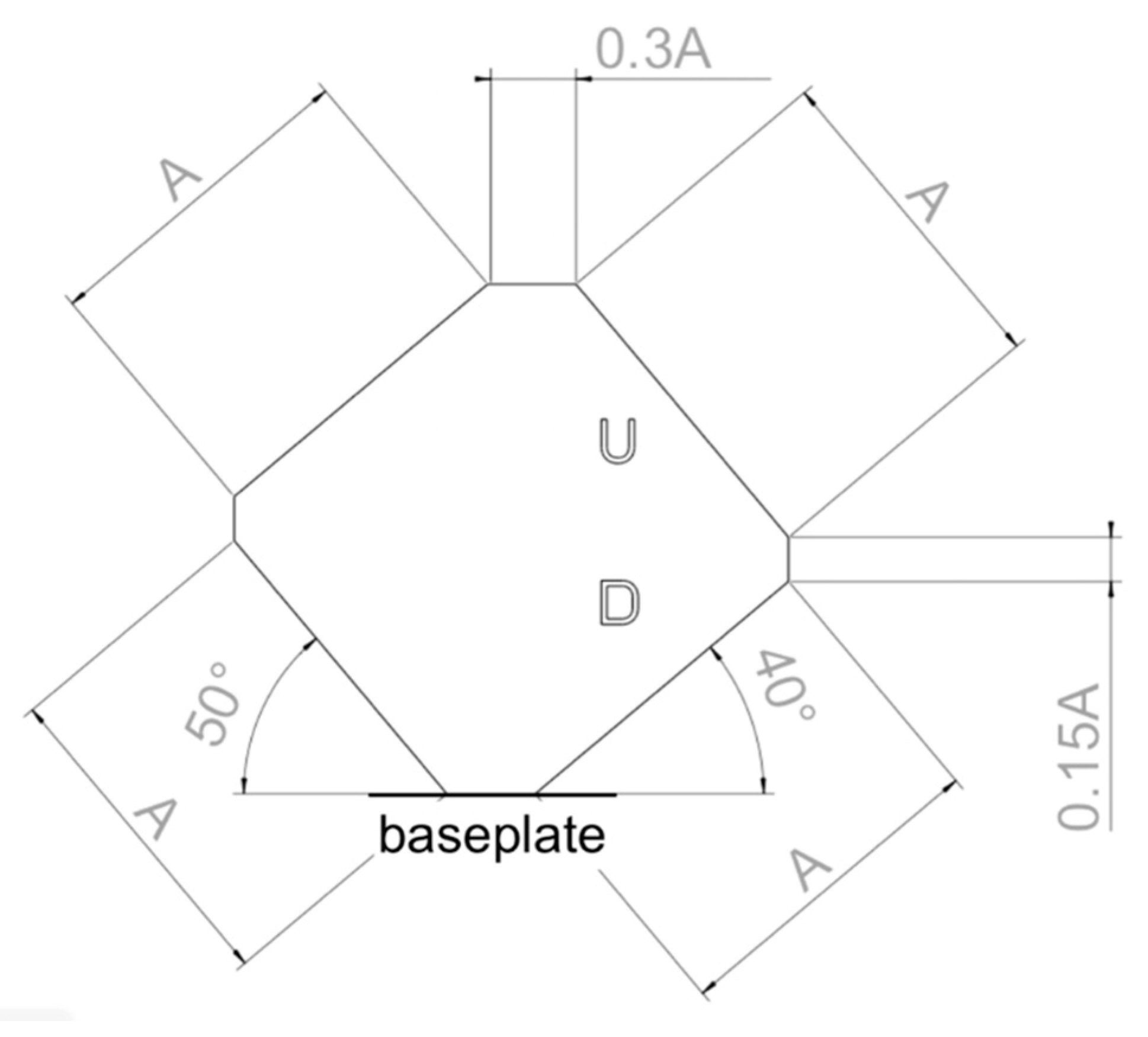
2.5. Downskin and Upskin Parameters
2.6. Boundary Parameters
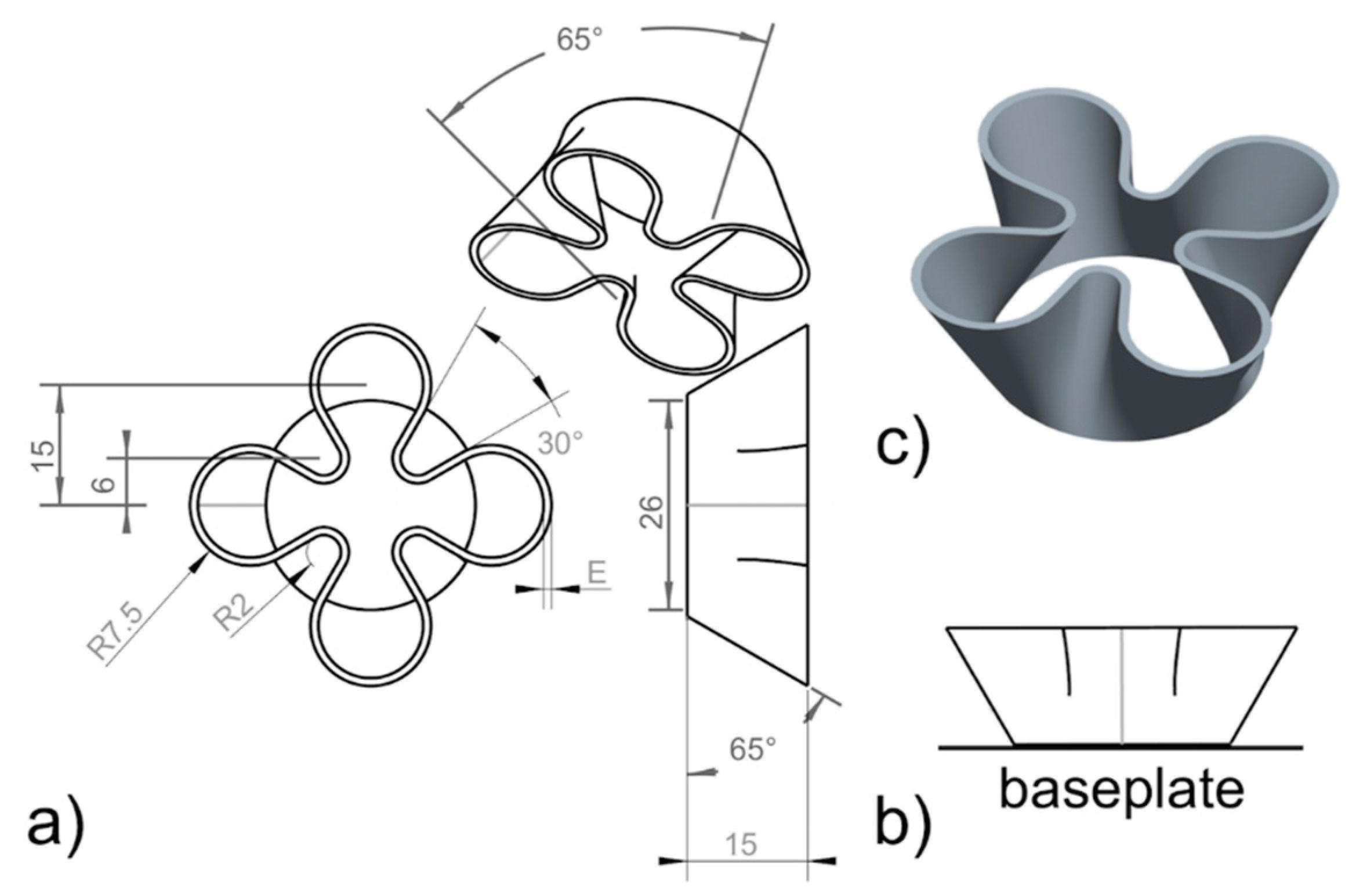
2.7. Thin Wall Parameters
2.8. Plate Temperature
3. Application Hints and Final Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Petrovic, V.; Vicente Haro Gonzalez, J.; Jorda Ferrando, O.; Delgado Gordillo, J.; Ramon Blasco Puchades, J.; Portolès Griñan, L. Additive layered manufacturing: Sectors of industrial application shown through case studies. Int. J. Prod. Res. 2011, 49, 1061–1079. [Google Scholar] [CrossRef]
- Linxi, Z.; Quanzhan, Y.; Guirong, Z.; Fangxin, Z.; Gang, S.; Bo, Y. Additive manufacturing technologies of porous metal implants. China Foundry 2014, 11, 322–331. [Google Scholar]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies. In Rapid Prototyping to Direct Digital Manufacturing; Springer Science + Business Media; LLC: New York, NY, USA, 2010; ISBN 978-1-4419-1119-3. [Google Scholar]
- Atzeni, E.; Iuliano, L.; Marchiandi, G.; Minetola, P.; Salmi, A.; Bassoli, E.; Denti, L.; Gatto, A. Additive manufacturing as a cost-effective way to produce metal parts. High Value Manufacturing: Advanced Research in Virtual and Rapid Prototyping. In Proceedings of the 6th International Conference on Advanced Research in Virtual and Rapid Prototyping, Leiria, Portugal, 1–5 October 2013; pp. 3–8, ISBN 9781138001374. [Google Scholar]
- Bassoli, E.; Sewell, N.; Denti, L.; Gatto, A. Investigation into the failure of Inconel exhaust collector produced by laser consolidation. Eng. Fail. Anal. 2013, 35, 397–404. [Google Scholar] [CrossRef]
- Girardin, E.; Barucca, G.; Mengucci, P.; Fiori, F.; Bassoli, E.; Gatto, A.; Iuliano, L.; Rutkowski, B. Biomedical Co-Cr-Mo components produced by Direct Metal Laser Sintering. Mater. Today Proc. 2016, 3, 889–897. [Google Scholar] [CrossRef]
- Grasso, M.; Colosimo, B.M. Process defects and in situ monitoring methods in metal powder bed fusion: A review. Meas. Sci. Technol. 2017, 28, 044005. [Google Scholar] [CrossRef]
- Mani, M.; Lane, B.; Donmez, A.; Feng, S.; Moylan, S.; Fesperman, R. Measurement Science Needs for Real-Time Control of Additive Manufacturing Powder Bed Fusion Processes, NISTIR 8036. Available online: http://dx.doi.org/10.6028/NIST.IR.8036 (accessed on 18 October 2018). [CrossRef]
- Baturynska, I.; Semeniuta, O.; Martinsen, K. Optimization of process parameters for powder bed fusion additive manufacturing by combination of machine learning and finite element method: A conceptual framework. Procedia CIRP 2018, 67, 227–232. [Google Scholar] [CrossRef]
- Vlasea, M.L.; Lane, B.M.; Lopez, F.F.; Mekhontsev, S.; Donmez, M.A. Development of powder bed fusion additive manufacturing test bed for enhanced real time process control. In Proceedings of the International Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2015; pp. 527–539. [Google Scholar]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; Van Humbeeck, J.; Kruth, J.-P. A study of the microstructural evolution during selective laser melting of Ti-6Al-4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Gong, H.; Rafi, K.; Gu, H.; Janaki Ram, G.D.; Starr, T.; Stucker, B. Influence of defects on mechanical properties of Ti–6Al–4 V components produced by selective laser melting and electron beam melting. Mater. Des. 2015, 86, 545–554. [Google Scholar] [CrossRef]
- Tang, M.; Pistorius, P.C. Oxides, porosity and fatigue performance of AlSi10Mg parts produced by selective laser melting. Int. J. Fatigue 2017, 94, 192–201. [Google Scholar] [CrossRef]
- Mumtaz, K.A.; Erasenthiran, P.; Hopkinson, N. High density selective laser melting of Waspaloy®. J. Mater. Process. Technol. 2008, 195, 77–87. [Google Scholar] [CrossRef]
- Yap, C.Y.; Tan, H.K.; Du, Z.; Chua, C.K.; Dong, Z. Selective laser melting of nickel powder. Rapid Prototyp. J. 2017, 23, 750–757. [Google Scholar] [CrossRef]
- Casalino, G.; Campanelli, S.L.; Contuzzi, N.; Ludovico, A.D. Experimental investigation and statistical optimisation of the selective laser melting process of a maraging steel. Opt. Laser Technol. 2015, 65, 51–158. [Google Scholar] [CrossRef]
- Morgan, D.; Agba, E.; Hill, C. Support structure development and initial results for metal powder bed fusion additive manufacturing. Procedia Manuf. 2017, 10, 819–830. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Gusarov, A.; Yadroitsava, I.; Smurov, I. Single track formation in selective laser melting of metal powders. J. Mater. Process. Technol. 2010, 210, 1624–1631. [Google Scholar] [CrossRef]
- Ciurana, J.; Hernandez, L.; Delgado, J. Energy density analysis on single tracks formed by selective laser melting with CoCrMo powder material. Int. J. Adv. Manuf. Technol. 2013, 68, 1103–1110. [Google Scholar] [CrossRef]
- Song, B.; Dong, S.; Zhang, B.; Liao, H.; Coddet, C. Effects of processing parameters on microstructure and mechanical property of selective laser melted Ti6Al4V. Mater. Des. 2012, 35, 120–125. [Google Scholar] [CrossRef]
- Wang, Y.M.; Kamath, C.; Voisin, T.; Li, Z. A processing diagram for high-density Ti-6Al-4V by selective laser melting. Rapid Prototyping J. 2017, in press. [Google Scholar] [CrossRef]
- Wei, K.; Wang, Z.; Zeng, X. Preliminary investigation on selective laser melting of Ti-5Al-2.5Sn-Ti alloy: From single tracks to bulk 3D components. J. Mater. Process. Technol. 2017, 244, 73–85. [Google Scholar] [CrossRef]
- Kempen, K.; Thijs, L.; Van Humbeeck, J.; Kruth, J.P. Processing AlSi10Mg by selective laser melting: Parameter optimisation and material characterisation. Mater. Sci. Technol. 2014, 31, 917–923. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Maskery, I.; Tuck, C.; Ashcroft, I.; Everitt, N.M. On the formation of AlSi10Mg single tracks and layers in selective laser melting: Microstructure and nano-mechanical properties. J. Mater. Process. Technol. 2016, 230, 88–98. [Google Scholar] [CrossRef]
- Nie, X.; Zhang, H.; Zhu, H.; Hu, Z.; Ke, L.; Zeng, X. Analysis of processing parameters and characteristics of selective laser melted high strength Al-Cu-Mg alloys: From single tracks to cubic samples. J. Mater. Process. Technol. 2018, 256, 69–77. [Google Scholar] [CrossRef]
- Cheng, B.; Shrestha, S.; Chou, K. Stress and deformation evaluations of scanning strategy effect in selective laser melting. Addit. Manuf. 2016, 12, 240–251. [Google Scholar] [CrossRef]
- Jhabvala, J.; Boillat, E.; Antignac, T.; Glardon, R. On the effect of scanning strategies in the selective laser melting process. Virtual Phys. Prototyp. 2010, 5, 99–109. [Google Scholar] [CrossRef]
- AlMangour, B.; Grzesiak, D.; Yang, J.-M. Scanning strategies for texture and anisotropy tailoring during selective laser melting of TiC/316L stainless steel nanocomposites. J. Alloy Compd. 2017, 728, 424–435. [Google Scholar] [CrossRef]
- ISO/ASTM 52910:2018(E). Additive Manufacturing—Design—Requirements, Guidelines and Recommendations; International Organization for Standardization ISO: Geneva, Switzerland, 2018. [Google Scholar]
- ASTM F3303-18. Standard for Additive Manufacturing—Process Characteristics and Performance: Practice for Metal Powder Bed Fusion Process to Meet Critical Applications; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- Frazier, W.E.; Polakovics, D.; Koegel, W. Qualifying of metallic materials and structures for aerospace applications. JOM J. Miner. Metals Mater. Soc. 2001, 53, 16–18. [Google Scholar] [CrossRef]
- Brice, C.A. Unintended consequences: How qualification constraints innovation. In 1st World Congress on Integrated Computational Materials Engineering, TMS (The Minerals, Metals & Materials Society), 2011; Allison, J., Collins, P., Spanos, G., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 241–246. ISBN 9780470943199. [Google Scholar]
- Portolés, L.; Jordá, O.; Jordá, L.; Uriondo, A.; Esperon-Migueza, M.; Perinpanayagam, S. A qualification procedure to manufacture and repair aerospace parts with electron beam melting. J. Manuf. Syst. 2016, 41, 65–75. [Google Scholar] [CrossRef]
- Boley, C.D.; Khairallah, S.A.; Rubenchik, A.M. Calculation of laser absorption by metal powders in additive manufacturing. Appl. Optics 2015, 54, 2477–2482. [Google Scholar] [CrossRef] [PubMed]
- Aboulkhair, N.T.; Everitt, N.M.; Ashcroft, I.; Tuck, C. Reducing porosity in AlSi10Mg parts processed by selective laser melting. Addit. Manuf. 2014, 1–4, 77–86. [Google Scholar] [CrossRef]
- Naeem, M. Laser processing of reflective materials. Laser Tech. J. 2013, 10, 18–20. [Google Scholar] [CrossRef]
- Zavala-Arredondo, M.; Boone, N.; Willmott, J.; Childs, D.T.D.; Ivanov, P.; Groom, K.M.; Mumtaz, K. Laser diode area melting for high speed additive manufacturing of metallic components. Mater. Des. 2017, 117, 305–315. [Google Scholar] [CrossRef]
- ASM Handbook Volume 2: Properties and Selection: Nonferrous Alloys and Special-Purpose Materials; American Society for Metals; ASM International; The Materials Information Company: Almere, The Netherlands, 1990; ISBN 978-0-87170-378-1.
- ASM Handbook Volume 1: Properties and Selection: Irons, Steels, and High-Performance Alloys; American Society for Metals; ASM International; The Materials Information Company: Almere, The Netherlands, 1990; ISBN 978-0-87170-377-4.
- Carter, L.N.; Wang, X.; Read, N.; Khan, R.; Aristizabal, M.; Essa, K.; Attallah, M.M. Process optimisation of selective laser melting using energy density model for nickel based superalloys. Mater. Sci. Technol. 2016, 32, 657–661. [Google Scholar] [CrossRef]
- Cheng, B.; Chou, K. Melt pool evolution study in selective laser melting. In Proceedings of the International Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2015; pp. 1182–1194. [Google Scholar]
- Gürtler, F.-J.; Karg, M.; Leitz, K.-H.; Schmidt, M. Simulation of laser beam melting of steel powders using the three-dimensional volume of fluid method. Phys. Proc. 2013, 41, 881–886. [Google Scholar] [CrossRef]
- Li, L.; Lough, C.; Replogle, A.; Bristow, D.; Landers, R.; Kinzel, E. Thermal modeling of 304L stainless steel selective laser melting. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Advanced Manufacturing, Tampa, FL, USA, 3–9 November 2017; pp. 1068–1081, ISBN 978-0-7918-5835-6. [Google Scholar]
- Thompson, S.M.; Bian, L.; Shamsaei, N.; Yadollahi, A. An overview of Direct Laser Deposition for additive manufacturing; Part I: Transport phenomena, modeling and diagnostics. Addit. Manuf. 2015, 8, 36–62. [Google Scholar] [CrossRef]
- Galba, M.J.; Reischle, M. Additive manufacturing of metals using powder-based technology. In Chapter 4: Additive Manufacturing; Bandyopadhyay, A., Bose, S., Eds.; CRC Press: Boca Raton, FL, USA, 2016; ISBN 9781482223606. [Google Scholar]
- Jopek, H.; Strek, T. Optimization of the effective thermal conductivity of a composite. In Convection and Conduction Heat Transfer; Ahsan, A., Ed.; InTech: Manila, Philippines, 2011; ISBN 978-953-307-582-2. [Google Scholar]
- Bauereiß, A.; Scharowsky, T.; Körner, C. Defect generation and propagation mechanism during additive manufacturing by selective beam melting. J. Mater. Process. Technol. 2014, 214, 2522–2528. [Google Scholar] [CrossRef]
- Yang, K.V.; Rometsch, P.; Jarvis, T.; Rao, J.; Cao, S.; Davies, C.; Wu, X. Porosity formation mechanisms and fatigue response in Al-Si-Mg alloys made by selective laser melting. Mater. Sci. Eng. A 2018, 712, 166–174. [Google Scholar] [CrossRef]
- AlMangour, B.; Grzesiak, D.; Borkar, T.; Yang, J.-M. Densification behavior, microstructural evolution, and mechanical properties of TiC/316L stainless steel nanocomposites fabricated by selective laser melting. Mater. Des. 2018, 138, 119–128. [Google Scholar] [CrossRef]
- Kim, F.H.; Moylan, S.P.; Garboczi, E.J.; Slotwinski, J.A. Investigation of pore structure in cobalt chrome additively manufactured parts using X-ray computed tomography and three-dimensional image analysis. Addit. Manuf. 2017, 17, 23–38. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Corfield, M.R.; Tuck, C.; Clare, A.T.; Leach, R.K.; Wildman, R.D.; Ashcroft, I.A.; Hague, R.J.M. Quantification and characterisation of porosity in selectively laser melted Al–Si10–Mg using X-ray computed tomography. Mater. Charact. 2016, 111, 193–204. [Google Scholar] [CrossRef]
- Criales, L.E.; Arısoy, Y.M.; Özel, T. Sensitivity analysis of material and process parameters in finite element modeling of selective laser melting of Inconel 625. Int. J. Adv. Manuf. Technol. 2016, 86, 2653–2666. [Google Scholar] [CrossRef]
- Liu, L.; Hirose, A.; Kobayashi, K.F. A numerical approach for predicting laser surface annealing process of Inconel 718. Acta Mater. 2002, 50, 1331–1347. [Google Scholar] [CrossRef]


| Metal of Interest | Target of Optimization | Reference |
|---|---|---|
| Waspaloy | 3D parts | [14] |
| Nickel | 3D parts | [15] |
| Maraging steel | 3D parts | [16] |
| 17-4 PH | Support structures | [17] |
| 304 L and 904 L | Single tracks | [18] |
| CoCrMo | Single tracks | [19] |
| Ti-6Al-4V | Single tracks | [20] |
| Ti-6Al-4V | 3D parts | [21] |
| Ti-5Al-2.5Sn | From single tracks to 3D parts | [22] |
| AlSi10Mg | Single tracks | [23] |
| AlSi10Mg | From single tracks to single layers | [24] |
| Al-Cu-Mg alloy | From single tracks to 3D parts | [25] |
| Material | k | α | ΔT = Tm − T0 | TP = k/(α ×ΔT) |
|---|---|---|---|---|
| (W·m−1·K−1) | (K−1) | (K) | (W m−1 K−1) | |
| AlSi10 [38] | 113 | 22 × 10−6 | 570 | ≈9000 |
| Ti-6Al-4V [38] | 6.7 | 9.2 × 10−6 | 1635 | ≈445 |
| Inconel 625 [39] | 9.8 | 15 × 10−6 | 1330 | ≈490 |
| AISI316 [39] | 16.2 | 16.2 × 10−6 | 1380 | ≈725 |
| Hastelloy X [39] | 9.1 | 16 × 10−6 | 1335 | ≈430 |
| Cu [38] | 391 | 17.7 × 10−6 | 1060 | ≈21,000 |
| Material Properties | ||||||
|---|---|---|---|---|---|---|
| Rbulk | 0.70 (70%) | |||||
| k (W·m−1·K−1) | 9.8 | |||||
| α (K−1) | 15 × 10−6 | |||||
| Tm (K) | 1623 | |||||
| c (J·kg−1·K−1) | 410 | |||||
| lf (J·kg−1) | 227 × 103 | |||||
| ρ (kg·mm−3) | 8.44 × 10−6 | |||||
| Technical Specifications | ||||||
| Laser spot diameter (μm) | 55 | |||||
| Processability check | ||||||
| Optical processability check | Rbulk < 0.95 | verified | ||||
| Thermal processability check | TP = 490 (W·m−1·K−1) | verified | ||||
| Calculation of the VED | ||||||
| Calculation of q (J·mm−3) | 6.58 | |||||
| Estimate of ƞ | 0.10 (10%) | |||||
| VED (J·mm−3) | 64 | |||||
| Calculation of the SED | ||||||
| SED (J·mm−2) | 3.5 | |||||
| Parameter Optimization | ||||||
| VEDmin | VEDmedium | VEDmax | SEDmin | SEDmedium | SEDmax | |
| (J·mm−3) | (J·mm−3) | (J·mm−3) | (J·mm−2) | (J·mm−2) | (J·mm−2) | |
| CORE BULK DOE | 49 | 64 | 83 | |||
| SUPPORTS DOE | 2.9 | 3.5 | 4.2 | |||
| DOWNSKIN DOE | 27 | 32 | 38 | |||
| UPSKIN DOE | 42 | 51 | 61 | |||
| BOUNDARY DOE | SEDmedium −80% | t.b.d. based on CORE BULK DOE | SEDmedium +80% | |||
| THIN WALL DOE | ||||||
| Core parameters | VEDmedium −15% | t.b.d. based on CORE BULK DOE | VEDmedium +15% | |||
| Boundary parameters | SEDmedium −15% | t.b.d. based on BOUNDARY DOE | SEDmedium +15% | |||
| PLATE TEMPERATURE Jobs | ||||||
| Calculation of Thigh | ||||||
| Calculation of temperatures to be tested | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassoli, E.; Sola, A.; Celesti, M.; Calcagnile, S.; Cavallini, C. Development of Laser-Based Powder Bed Fusion Process Parameters and Scanning Strategy for New Metal Alloy Grades: A Holistic Method Formulation. Materials 2018, 11, 2356. https://doi.org/10.3390/ma11122356
Bassoli E, Sola A, Celesti M, Calcagnile S, Cavallini C. Development of Laser-Based Powder Bed Fusion Process Parameters and Scanning Strategy for New Metal Alloy Grades: A Holistic Method Formulation. Materials. 2018; 11(12):2356. https://doi.org/10.3390/ma11122356
Chicago/Turabian StyleBassoli, Elena, Antonella Sola, Mattia Celesti, Sandro Calcagnile, and Carlo Cavallini. 2018. "Development of Laser-Based Powder Bed Fusion Process Parameters and Scanning Strategy for New Metal Alloy Grades: A Holistic Method Formulation" Materials 11, no. 12: 2356. https://doi.org/10.3390/ma11122356
APA StyleBassoli, E., Sola, A., Celesti, M., Calcagnile, S., & Cavallini, C. (2018). Development of Laser-Based Powder Bed Fusion Process Parameters and Scanning Strategy for New Metal Alloy Grades: A Holistic Method Formulation. Materials, 11(12), 2356. https://doi.org/10.3390/ma11122356







