Effective Elastic Behavior of Irregular Closed-Cell Foams
Abstract
:1. Introduction
2. Modeling of Irregular Closed-Cell Structure
2.1. Material and Its Properties
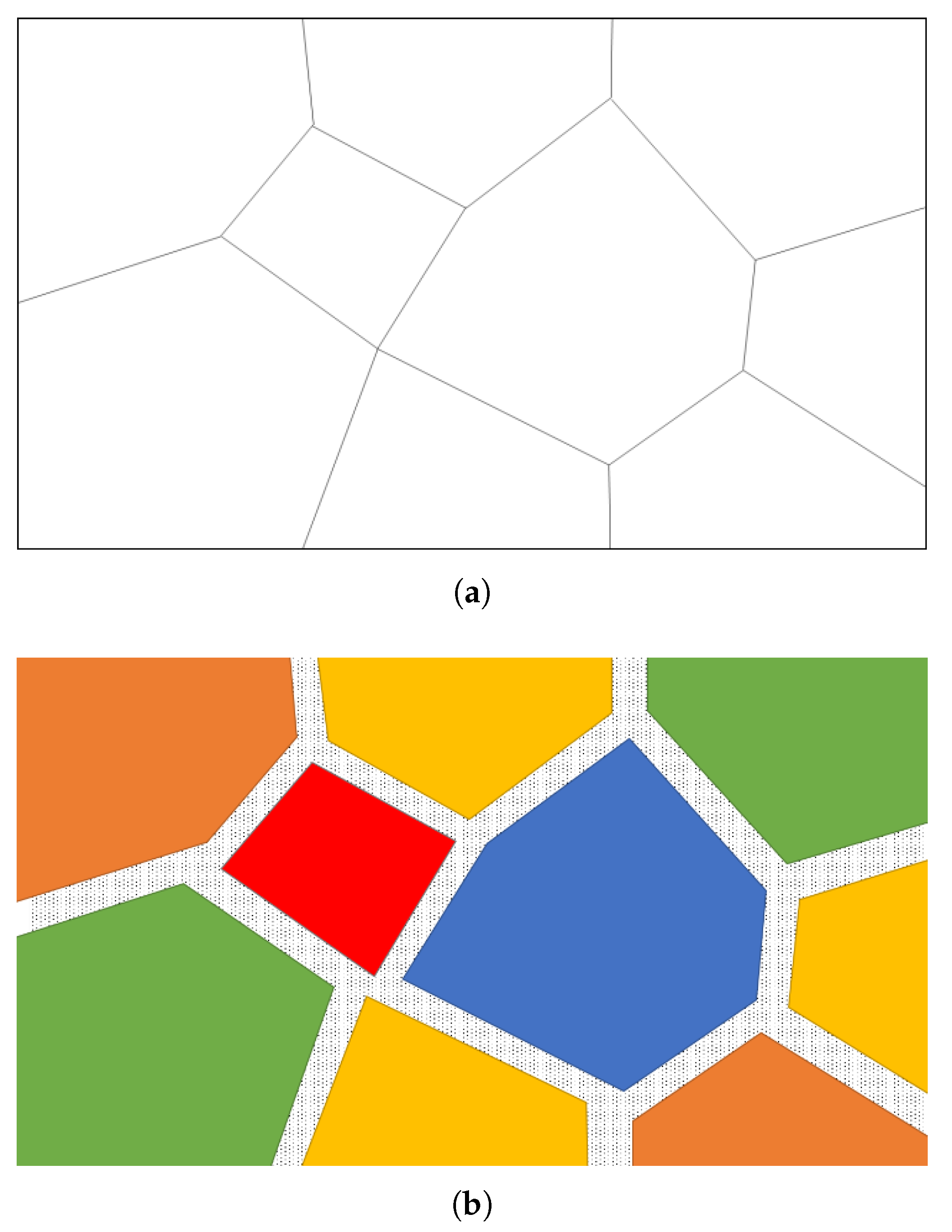
2.2. Morphological Description
- The relative density (in this paper, the superscript notations and stand for homogenized property and bulk property, respectively), which was introduced in the previous section;
- The coefficient of variation , which represents the dispersion of cell size distribution;
- The anisotropy of the structure.
2.2.1. Dispersion of Cell Size Distribution
2.2.2. Anisotropy
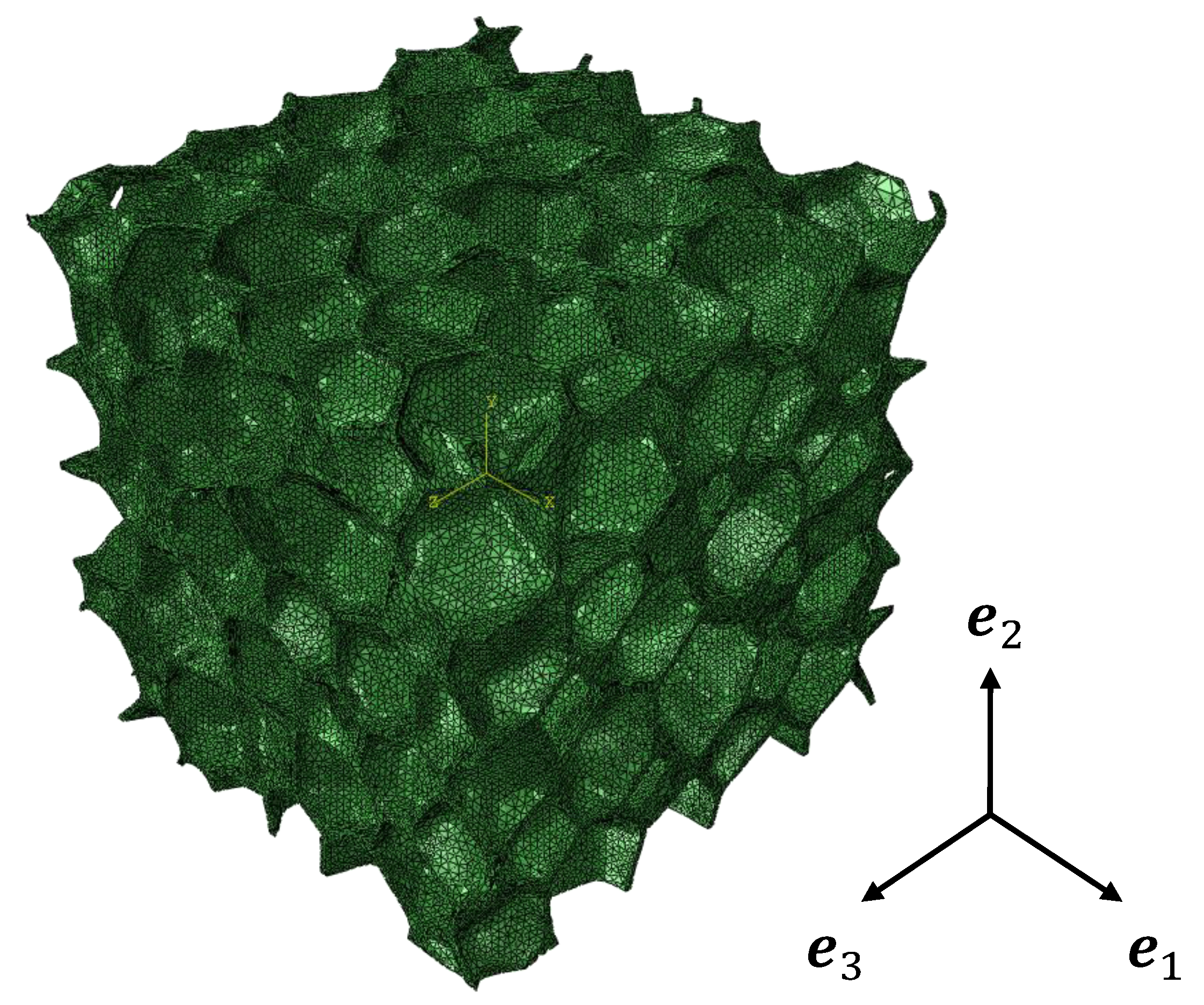
2.3. Generation of Numerical Models
3. Computational Homogenization
3.1. RVE Periodic Equilibrium State
3.2. Finite Element Implementation
- is the matrix representation of the Voigt bound of the elastic stiffness matrix of the studied RVE. In the case of a bulk-porous foam, it corresponds to .
- The pseudo-force matrix is obtained with the finite element assembly by computingwhere the matrix relates the fluctuation strain and displacement in the finite element discretization with .
- is the FEM rigidity matrix that is inverted under the periodicity condition.
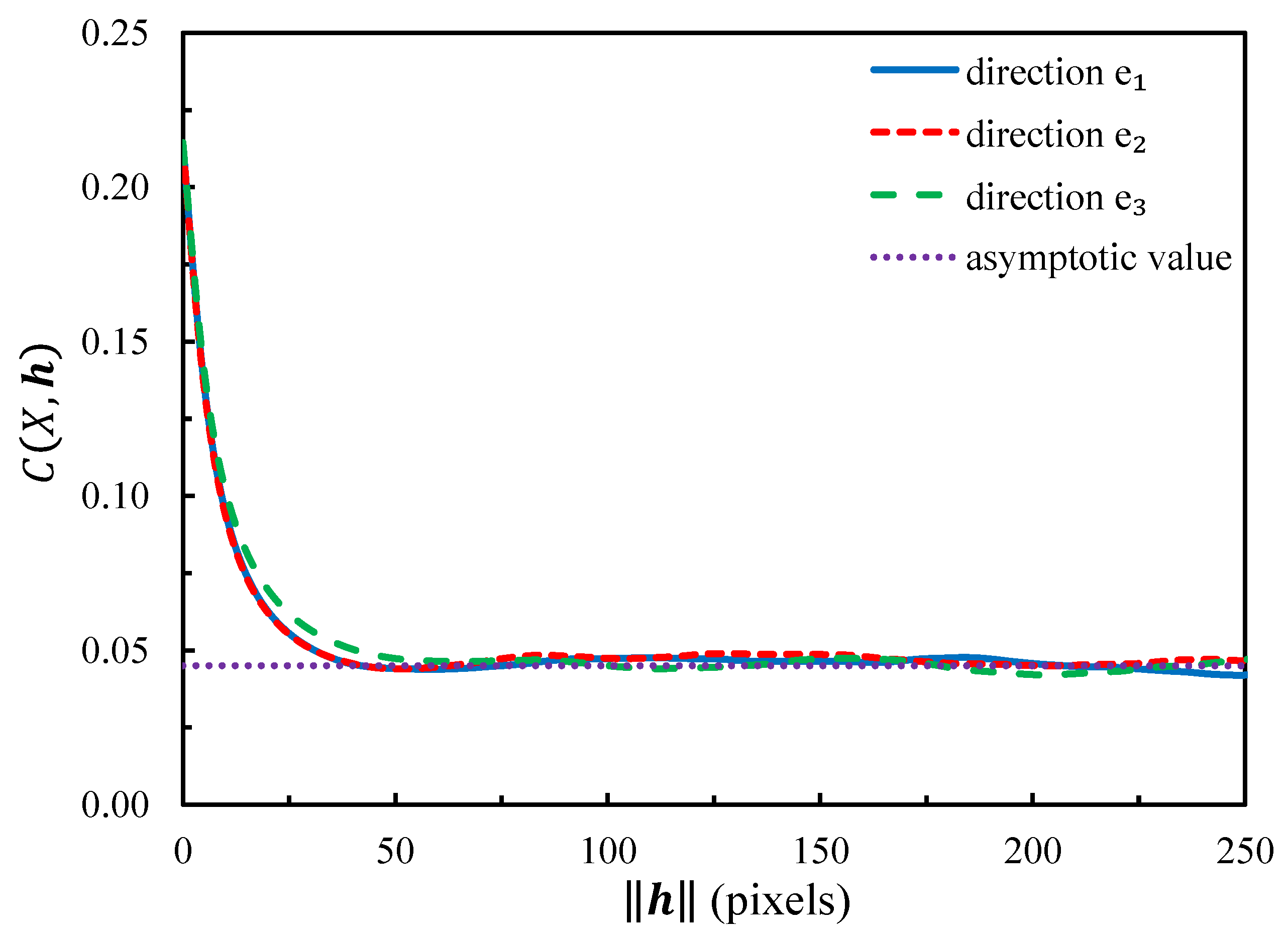
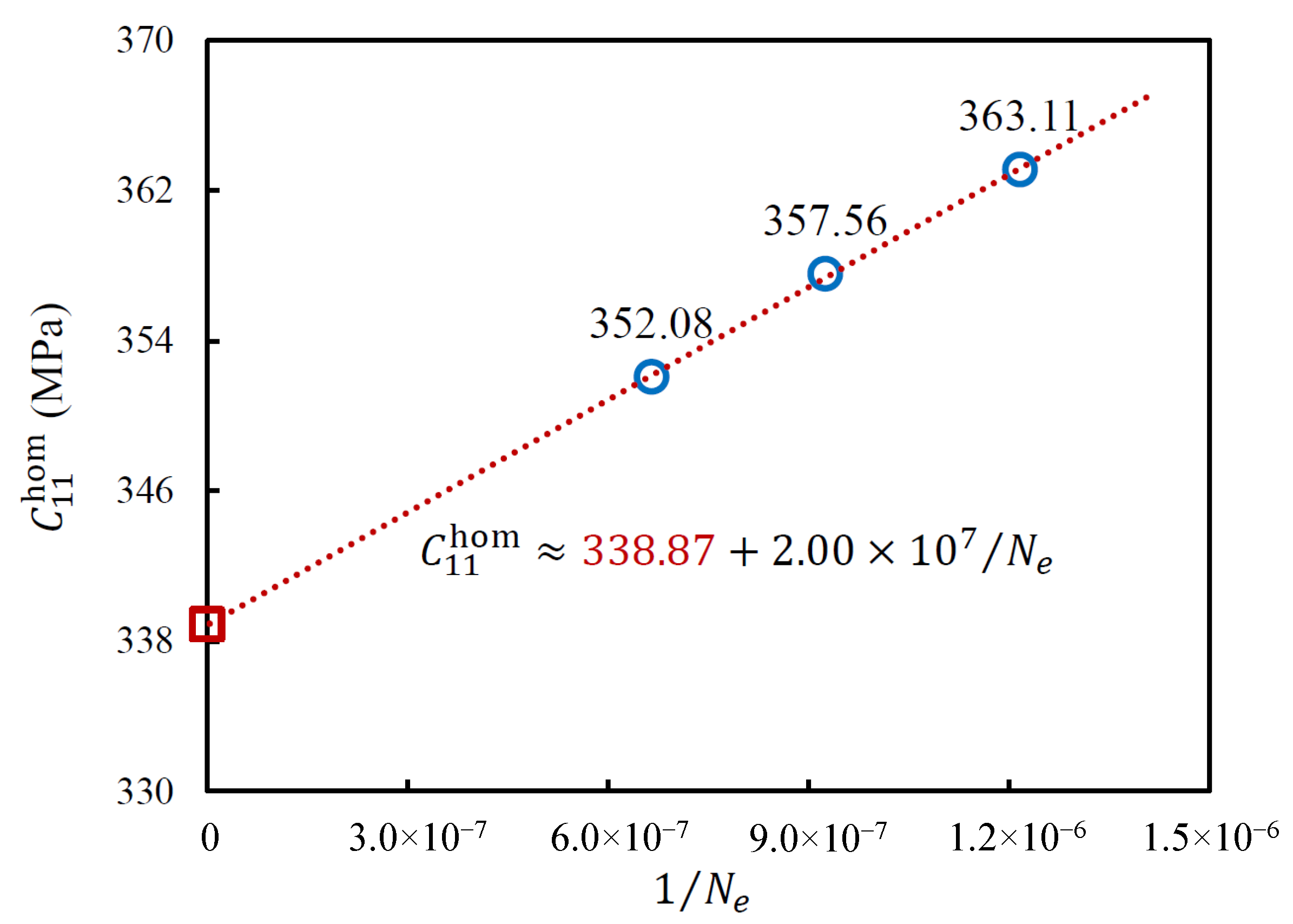
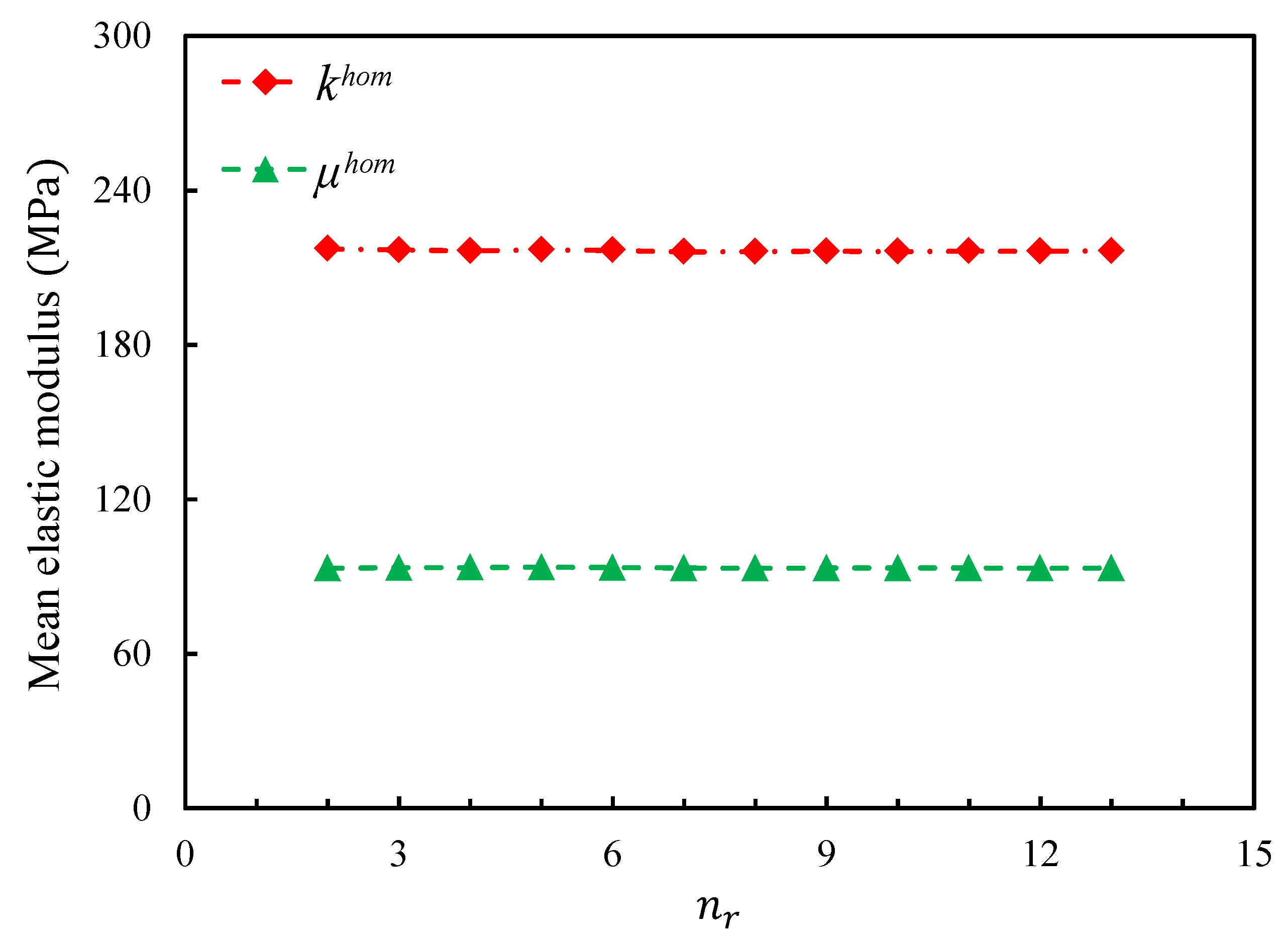
3.3. Mesh Sensitivity
4. Results and Discussion
4.1. Influence of RVE Parameters
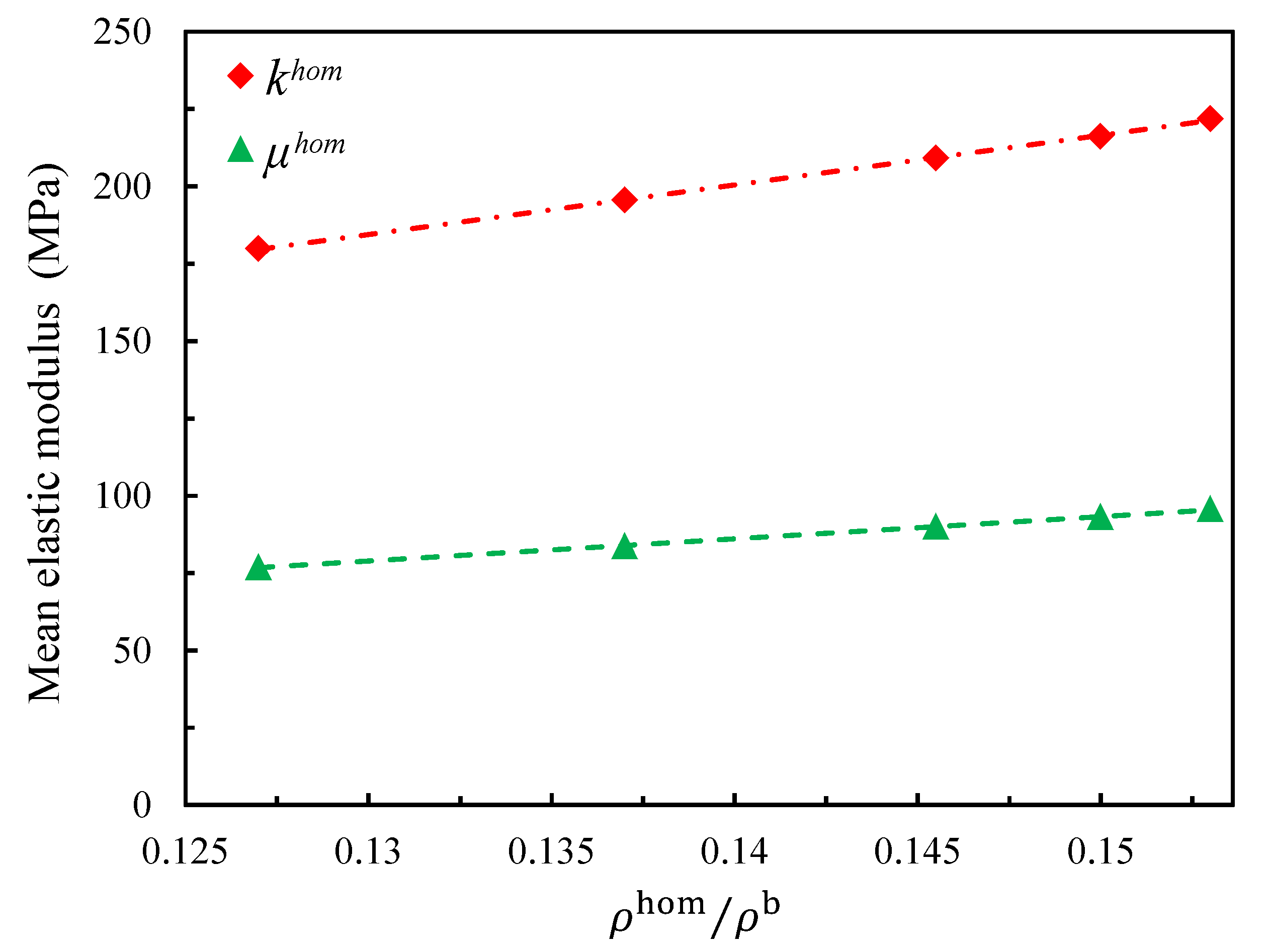
4.2. Influence of the Relative Density
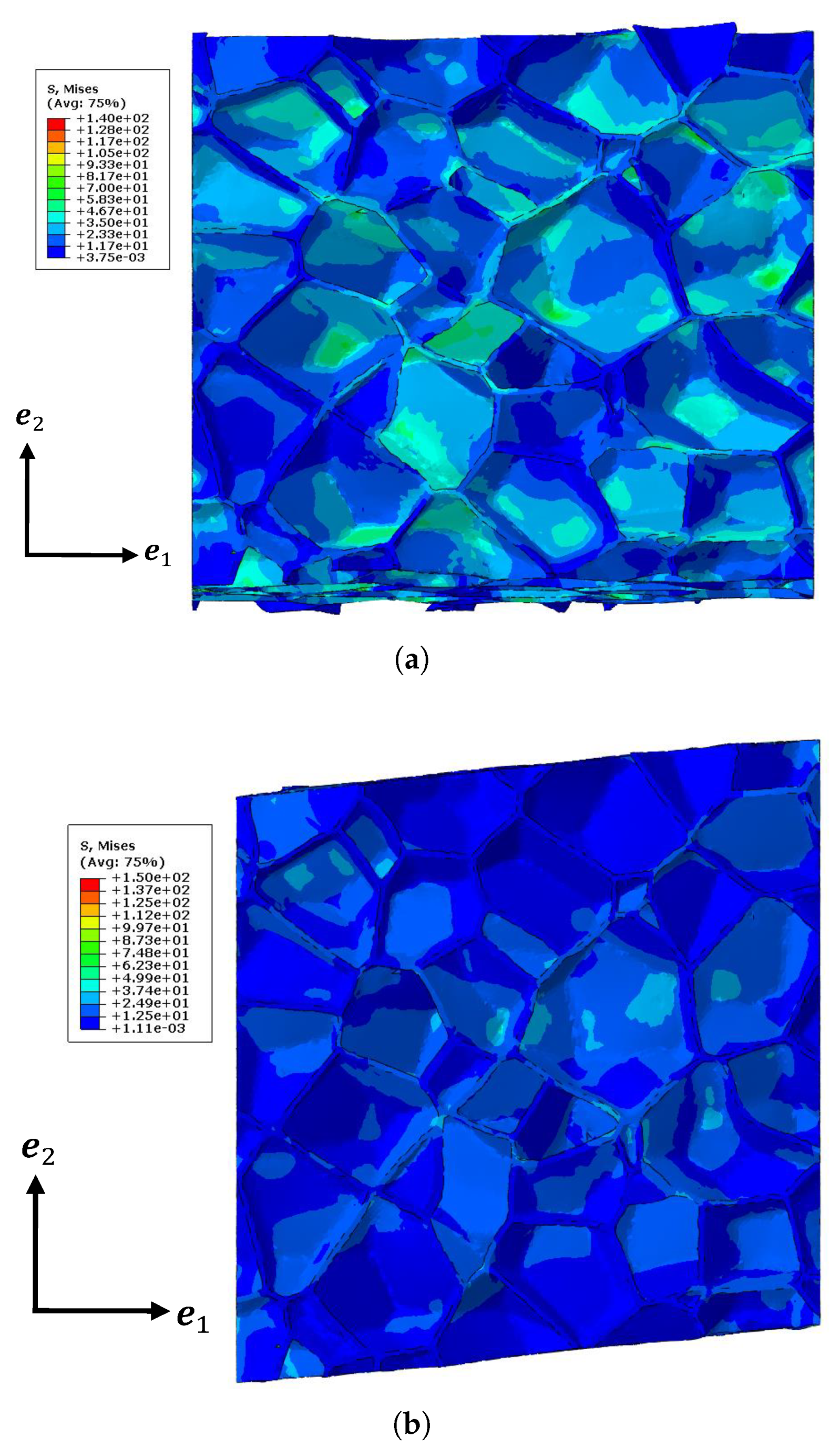
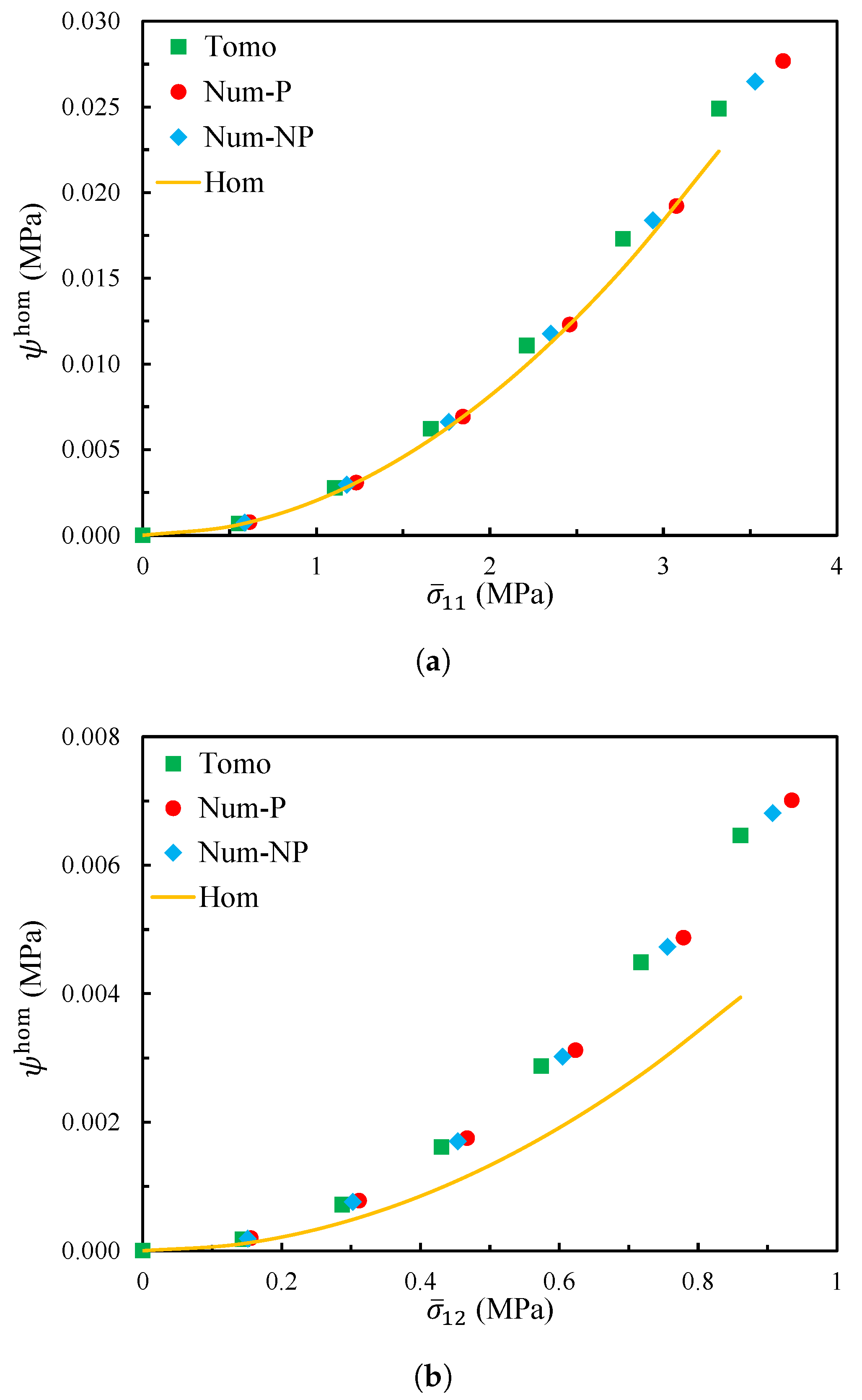
4.3. Comparison with the Tomography Model
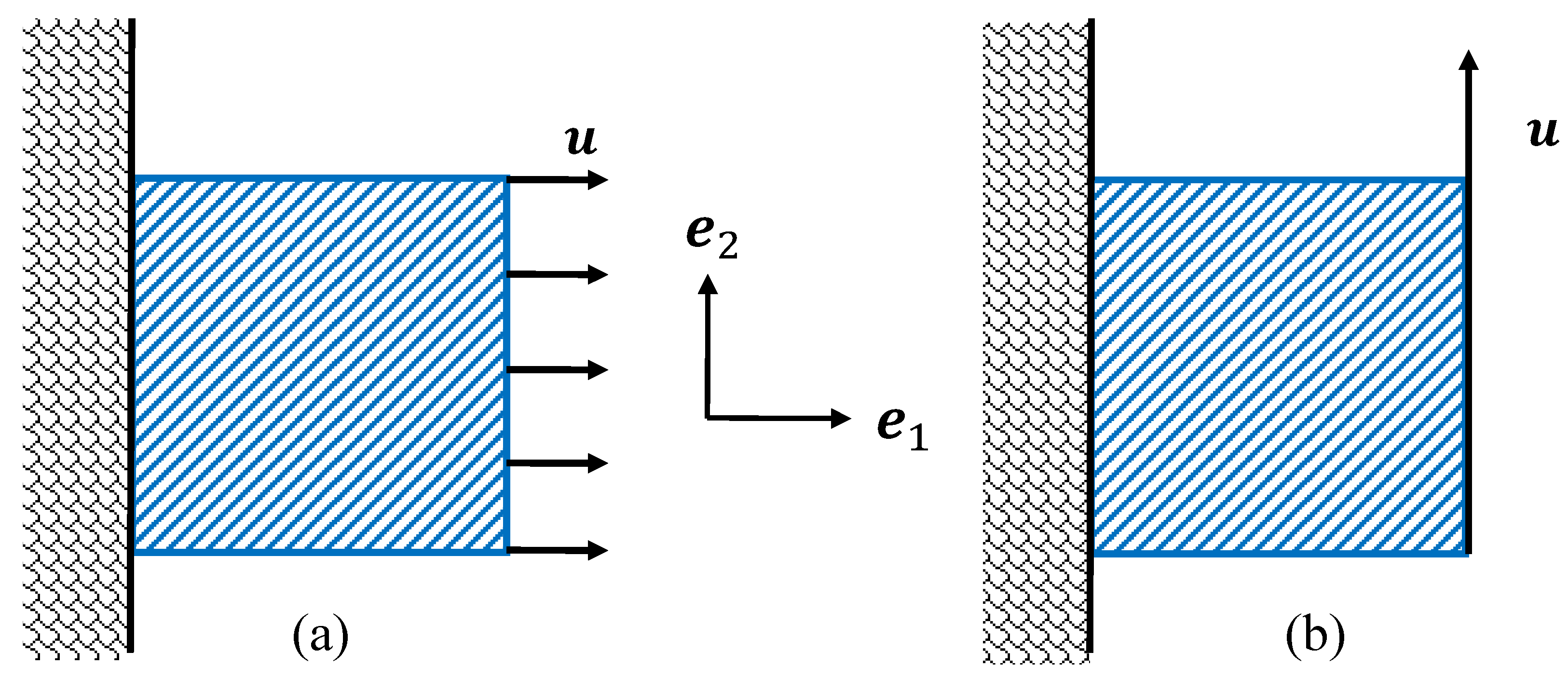
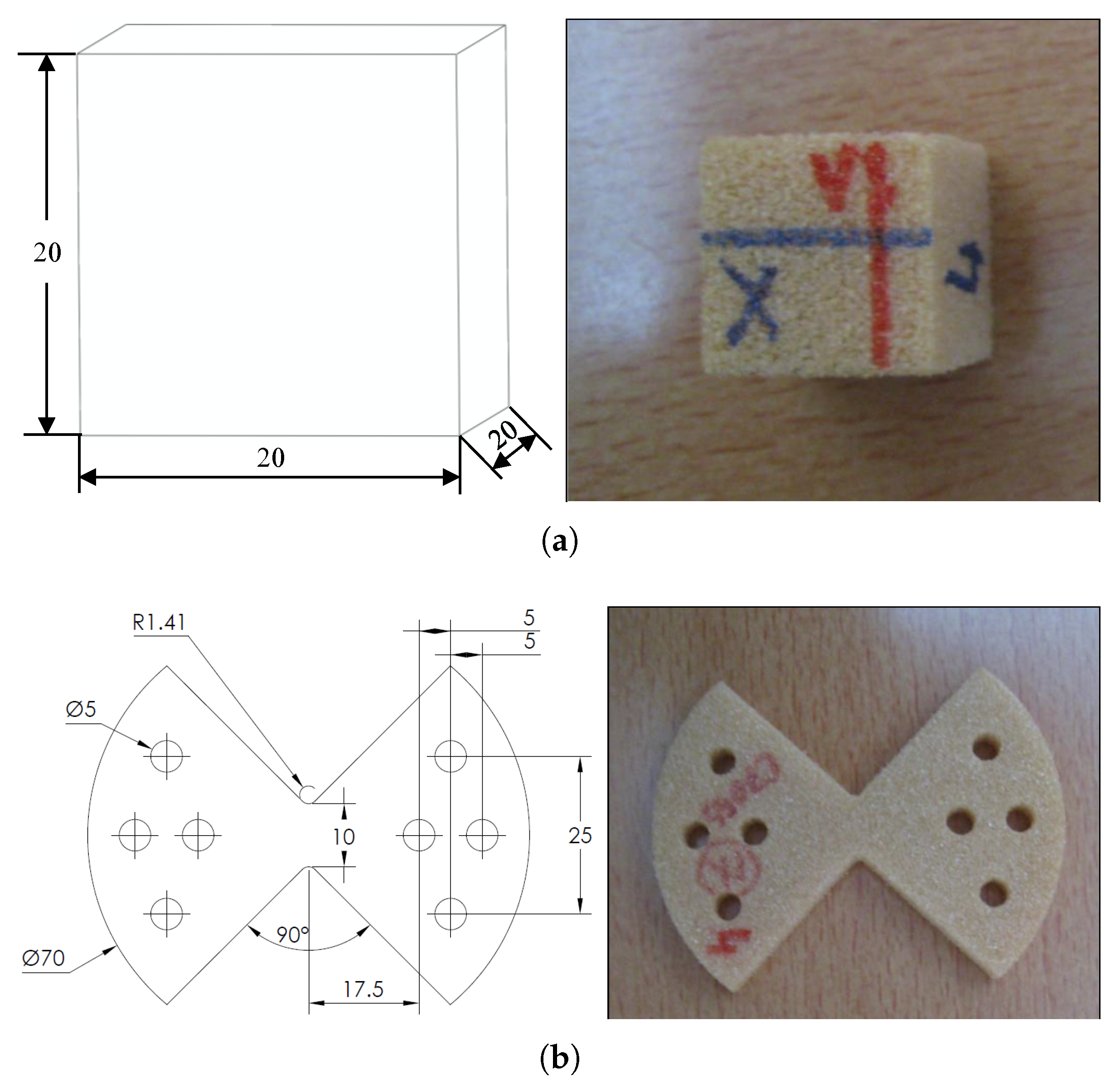
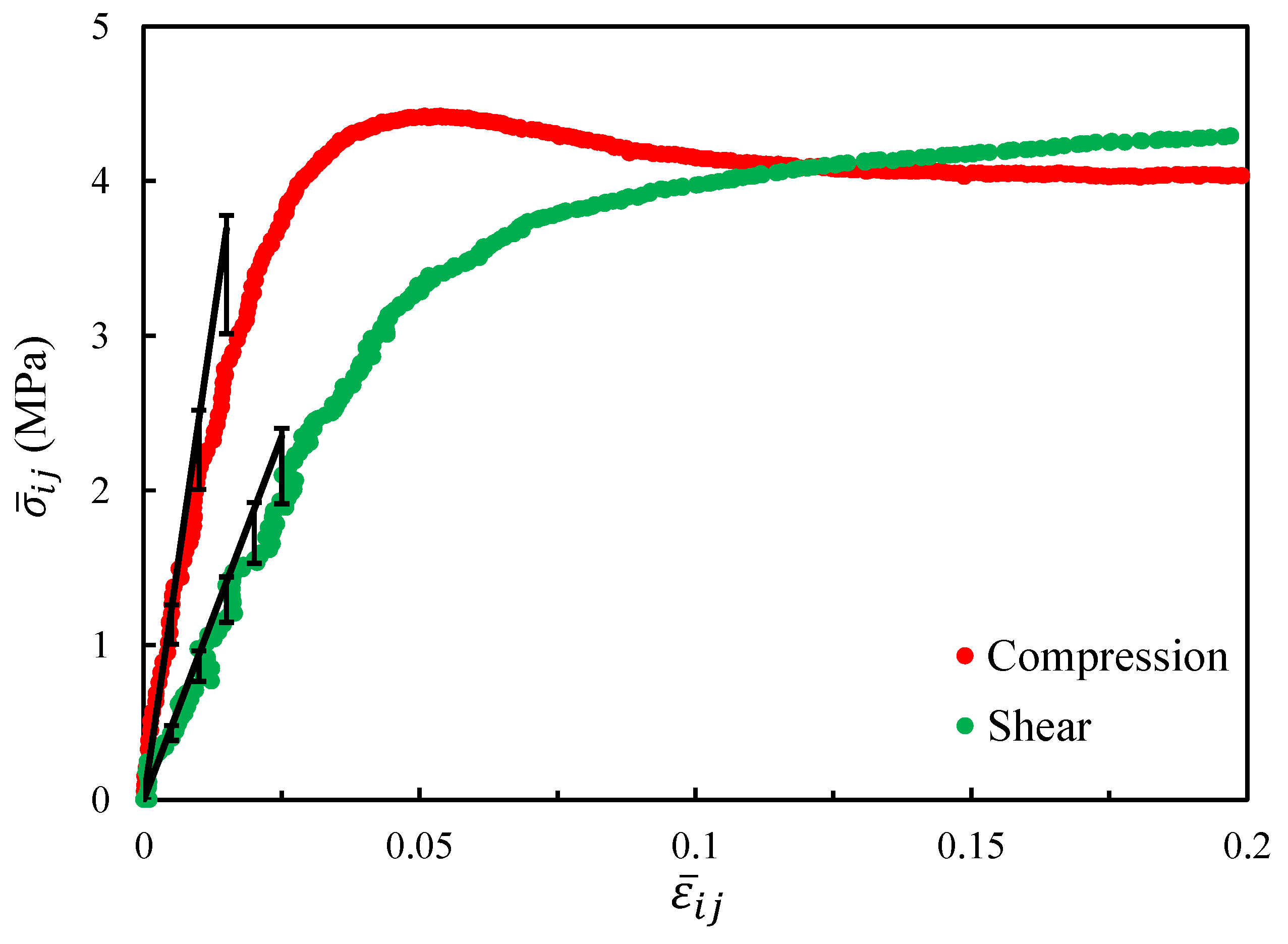
4.4. Comparison with Experimental Results
5. Conclusions
- By analysing the tomography slices, the dispersion of cell size distribution and the anisotropy of the real irregular closed-cell foam were obtained. Using the approach based on Voronoi diagram, realistic irregular closed-cell foam structures were numerically generated with the morphological parameters.
- The Hill’s lemma computational homogenization approach was used to predict the effective elastic behavior of the closed-cell foam models. The closed-cell foam models required only a small number of realizations to reach convergence. The influence of the relative density on the effective elastic moduli was studied. The approximately linear evolution was found in the small range. The energy density was investigated to compare the homogenized model with the tomography reconstruction model (without the periodic boundary condition). Two numerically generated models were also tested under the kinematic boundary conditions (similarly to the tomography model). One was generated with geometrically periodic boundaries and the other one was generated with geometrically non-periodic boundaries. Both of them had the same size and statistical morphology description as the tomography model. The results of these three models were very similar, while a deviation was observed with the homogenized model. This suggests that the numerically generated models did not bias the real tomography model. Furthermore, it suggests that the tomography sample was not large enough to obtain the correct results. The homogenized results were compared with the experimental results, and a satisfying agreement was achieved. Future investigations should be continued for larger samples to highlight the influence of size samples.
Author Contributions
Funding
Conflicts of Interest
References
- Kishimoto, S.; Wang, Q.; Tanaka, Y.; Kagawa, Y. Compressive mechanical properties of closed-cell aluminum foam-polymer composites. Compos. Part B Eng. 2014, 64, 43–49. [Google Scholar] [CrossRef]
- Chen, Y.; Das, R.; Battley, M. Effects of cell size and cell wall thickness variations on the strength of closed-cell foams. Int. J. Eng. Sci. 2017, 120, 220–240. [Google Scholar] [CrossRef]
- Su, B.Y.; Huang, C.M.; Sheng, H.; Jang, W.Y. The effect of cell-size dispersity on the mechanical properties of closed-cell aluminum foam. Mater. Charact. 2018, 135, 203–213. [Google Scholar] [CrossRef]
- Marvi-Mashhadi, M.; Lopes, C.; LLorca, J. Effect of anisotropy on the mechanical properties of polyurethane foams: An experimental and numerical study. Mech. Mater. 2018, 124, 143–154. [Google Scholar] [CrossRef]
- Shi, X.; Liu, S.; Nie, H.; Lu, G.; Li, Y. Study of cell irregularity effects on the compression of closed-cell foams. Int. J. Mech. Sci. 2018, 135, 215–225. [Google Scholar] [CrossRef]
- Placido, E.; Arduini-Schuster, M.; Kuhn, J. Thermal properties predictive model for insulating foams. Infrared Phys. Technol. 2005, 46, 219–231. [Google Scholar] [CrossRef]
- Coquard, R.; Rousseau, B.; Echegut, P.; Baillis, D.; Gomart, H.; Iacona, E. Investigations of the radiative properties of Al-NiP foams using tomographic images and stereoscopic micrographs. Int. J. Heat Mass Transf. 2012, 55, 1606–1619. [Google Scholar] [CrossRef]
- Coquard, R.; Loretz, M.; Baillis, D. Conductive Heat Transfer in Metallic/Ceramic Open-Cell Foams. Adv. Eng. Mater. 2008, 10, 323–337. [Google Scholar] [CrossRef]
- Coquard, R.; Baillis, D.; Randrianalisoa, J. Homogeneous phase and multi-phase approaches for modeling radiative transfer in foams. Int. J. Therm. Sci. 2011, 50, 1648–1663. [Google Scholar] [CrossRef]
- Baillis, D.; Coquard, R.; Cunsolo, S. Effective conductivity of Voronoi’s closed- and open-cell foams: Analytical laws and numerical results. J. Mater. Sci. 2017, 52, 11146–11167. [Google Scholar] [CrossRef]
- Roberts, A.; Garboczi, E. Elastic moduli of model random three-dimensional closed-cell cellular solids. Acta Mater. 2001, 49, 189–197. [Google Scholar] [CrossRef] [Green Version]
- Beckmann, C.; Hohe, J. Assessment of material uncertainties in solid foams based on local homogenization procedures. Int. J. Solids Struct. 2012, 49, 2807–2822. [Google Scholar] [CrossRef]
- Chen, Y.; Das, R.; Battley, M. Effects of cell size and cell wall thickness variations on the stiffness of closed-cell foams. Int. J. Solids Struct. 2015, 52, 150–164. [Google Scholar] [CrossRef]
- Mirzaali, M.; Libonati, F.; Vena, P.; Mussi, V.; Vergani, L.; Strano, M. Investigation of the Effect of Internal Pores Distribution on the Elastic Properties of Closed-Cell Aluminum Foam: A Comparison with Cancellous Bone. Procedia Struct. Integr. 2016, 2, 1285–1294. [Google Scholar] [CrossRef]
- Köll, J.; Hallström, S. Elastic properties of equilibrium foams. Acta Mater. 2016, 113, 11–18. [Google Scholar] [CrossRef]
- Pabst, W.; Uhlířová, T.; Gregorová, E.; Wiegmann, A. Young’s modulus and thermal conductivity of closed-cell, open-cell and inverse ceramic foams–model-based predictions, cross-property predictions and numerical calculations. J. Eur. Ceram. Soc. 2018, 38, 2570–2578. [Google Scholar] [CrossRef]
- Babin, P.; Valle, G.D.; Dendievel, R.; Lourdin, D.; Salvo, L. X-ray tomography study of the cellular structure of extruded starches and its relations with expansion phenomenon and foam mechanical properties. Carbohydr. Polym. 2007, 68, 329–340. [Google Scholar] [CrossRef]
- Badiche, X.; Forest, S.; Guibert, T.; Bienvenu, Y.; Bartout, J.D.; Ienny, P.; Croset, M.; Bernet, H. Mechanical properties and non-homogeneous deformation of open-cell nickel foams: Application of the mechanics of cellular solids and of porous materials. Mater. Sci. Eng. A 2000, 289, 276–288. [Google Scholar] [CrossRef]
- Maire, E.; Fazekas, A.; Salvo, L.; Dendievel, R.; Youssef, S.; Cloetens, P.; Letang, J.M. X-ray tomography applied to the characterization of cellular materials. Related finite element modeling problems. Compos. Sci. Technol. 2003, 63, 2431–2443. [Google Scholar] [CrossRef]
- Jang, W.Y.; Kyriakides, S. On the crushing of aluminum open-cell foams: Part I. Experiments. Int. J. Solids Struct. 2009, 46, 617–634. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Blal, N.; Cunsolo, S.; Baillis, D. Effective elastic properties of periodic irregular open-cell foams. Int. J. Solids Struct. 2018, 143, 155–166. [Google Scholar] [CrossRef]
- Rycroft, C.H. VORO++: A three-dimensional Voronoi cell library in C++. Chaos Interdisciplin. J. Nonlinear Sci. 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barbier, C.; Michaud, P.; Baillis, D.; Randrianalisoa, J.; Combescure, A. New laws for the tension/compression properties of Voronoi closed-cell polymer foams in relation to their microstructure. Eur. J. Mech. A/Solids 2014, 45, 110–122. [Google Scholar] [CrossRef]
- Ye, W.; Barbier, C.; Zhu, W.; Combescure, A.; Baillis, D. Macroscopic multiaxial yield and failure surfaces for light closed-cell foams. Int. J. Solids Struct. 2015, 69–70, 60–70. [Google Scholar] [CrossRef]
- Zhu, W.; Blal, N.; Cunsolo, S.; Baillis, D. Micromechanical modeling of effective elastic properties of open-cell foam. Int. J. Solids Struct. 2017, 115–116, 61–72. [Google Scholar] [CrossRef]
- Fish, J.; Belsky, V. Multi-grid method for periodic heterogeneous media Part 2: Multiscale modeling and quality control in multidimensional case. Comput. Methods Appl. Mech. Eng. 1995, 126, 17–38. [Google Scholar] [CrossRef]
- Moulinec, H.; Suquet, P. A numerical method for computing the overall response of nonlinear composites with complex microstructure. Comput. Methods Appl. Mech. Eng. 1998, 157, 69–94. [Google Scholar] [CrossRef]
- Feyel, F.; Chaboche, J.L. FE2 multiscale approach for modelling the elastoviscoplastic behaviour of long fibre SiC/Ti composite materials. Comput. Methods Appl. Mech. Eng. 2000, 183, 309–330. [Google Scholar] [CrossRef]
- Fritzen, F.; Forest, S.; Böhlke, T.; Kondo, D.; Kanit, T. Computational homogenization of elasto-plastic porous metals. Int. J. Plast. 2012, 29, 102–119. [Google Scholar] [CrossRef]
- Geers, M.; Yvonnet, J. Multiscale Modeling of Microstructure-Property Relations. MRS Bull. 2016, 41, 610–616. [Google Scholar] [CrossRef]
- Martínez-Ayuso, G.; Friswell, M.I.; Adhikari, S.; Khodaparast, H.H.; Berger, H. Homogenization of porous piezoelectric materials. Int. J. Solids Struct. 2017, 113, 218–229. [Google Scholar] [CrossRef]
- Brach, S.; Dormieux, L.; Kondo, D.; Vairo, G. Strength properties of nanoporous materials: A 3-layered based non-linear homogenization approach with interface effects. Int. J. Eng. Sci. 2017, 115, 28–42. [Google Scholar] [CrossRef]
- Rastkar, S.; Zahedi, M.; Korolev, I.; Agarwal, A. A meshfree approach for homogenization of mechanical properties of heterogeneous materials. Eng. Anal. Bound. Elem. 2017, 75, 79–88. [Google Scholar] [CrossRef]
- Yu, W.; Tang, T. Variational asymptotic method for unit cell homogenization of periodically heterogeneous materials. Int. J. Solids Struct. 2007, 44, 3738–3755. [Google Scholar] [CrossRef]
- Cunsolo, S.; Coquard, R.; Baillis, D.; Chiu, W.K.; Bianco, N. Radiative properties of irregular open cell solid foams. Int. J. Therm. Sci. 2017, 117, 77–89. [Google Scholar] [CrossRef]
- Ashby, M.F. Materials Selection in Mechanical Design, 3th ed.; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Brun, E.; Vicente, J.; Topin, F.; Occelli, R. IMorph: A 3D morphological tool to fully analyse all kind of cellular materials. In Cellular Metals for Structural and Functional Applications; CELLMET: Dresden, Germany,, 2008. [Google Scholar]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Wojtacki, K.; Daridon, L.; Monerie, Y. Computing the elastic properties of sandstone submitted to progressive dissolution. Int. J. Rock Mech. Min. Sci. 2017, 95, 16–25. [Google Scholar] [CrossRef] [Green Version]
- Dillard, T.; N’guyen, F.; Maire, E.; Salvo, L.; Forest, S.; Bienvenu, Y.; Bartout, J.D.; Croset, M.; Dendievel, R.; Cloetens, P. 3D quantitative image analysis of open-cell nickel foams under tension and compression loading using X-ray microtomography. Philos. Mag. 2005, 85, 2147–2175. [Google Scholar] [CrossRef]
- Abaqus 6.11. Abaqus Analysis User’s Manual; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2011. [Google Scholar]
- Brakke, K.A. The Surface Evolver. Exp. Math. 1992, 1, 141–165. [Google Scholar] [CrossRef]
- MATLAB. MATLAB Primer; The MathWorks Inc.: Natick, MA, USA, 2016. [Google Scholar]
- Pelissou, C.; Baccou, J.; Monerie, Y.; Perales, F. Determination of the size of the representative volume element for random quasi-brittle composites. Int. J. Solids Struct. 2009, 46, 2842–2855. [Google Scholar] [CrossRef] [Green Version]
- Moussaddy, H.; Therriault, D.; Lévesque, M. Assessment of existing and introduction of a new and robust efficient definition of the representative volume element. Int. J. Solids Struct. 2013, 50, 3817–3828. [Google Scholar] [CrossRef]
- Suquet, P.M. Elements of Homogenization for Inelastic Solid Mechanics. In Homogenization Techniques for Composite Media: Lectures Delivered at the CISM International Center for Mechanical Sciences Udine, Italy, 1–5 July 1985; Sanchez-Palencia, E., Zaoui, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 193–278. [Google Scholar]
- Yu, W.; Tang, T. A variational asymptotic micromechanics model for predicting thermoelastic properties of heterogeneous materials. Int. J. Solids Struct. 2007, 44, 7510–7525. [Google Scholar] [CrossRef]
- ANSYS. ICEM CFD User’s Manual; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Roberts, A.P.; Garboczi, E.J. Elastic Properties of Model Porous Ceramics. J. Am. Ceram Soc. 2000, 83, 3041–3048. [Google Scholar] [CrossRef] [Green Version]
- Gatt, J.M.; Monerie, Y.; Laux, D.; Baron, D. Elastic behavior of porous ceramics: Application to nuclear fuel materials. J. Nucl. Mater. 2005, 336, 145–155. [Google Scholar] [CrossRef]
- Arcan, M.; Hashin, Z.; Voloshin, A. A method to produce uniform plane-stress states with applications to fiber-reinforced materials. Exp. Mech. 1978, 18, 141–146. [Google Scholar] [CrossRef]
- Hung, S.C.; Liechti, K.M. An evaluation of the arcan specimen for determining the shear moduli of fiber-reinforced composites. Exp. Mech. 1997, 37, 460–468. [Google Scholar] [CrossRef]
- Cognard, J.; Sohier, L.; Davies, P. A modified Arcan test to analyze the behavior of composites and their assemblies under out-of-plane loadings. Compos. Part A Appl. Sci. Manuf. 2011, 42, 111–121. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Mguil-Touchal, S.; Morestin, F.; Brunei, M. Various experimental applications of digital image correlation method. In Proceedings of the International Conference on Computational Methods and Experimental Measurements, Rhodes, Greece, 21–23 May 1997; pp. 45–58. [Google Scholar]




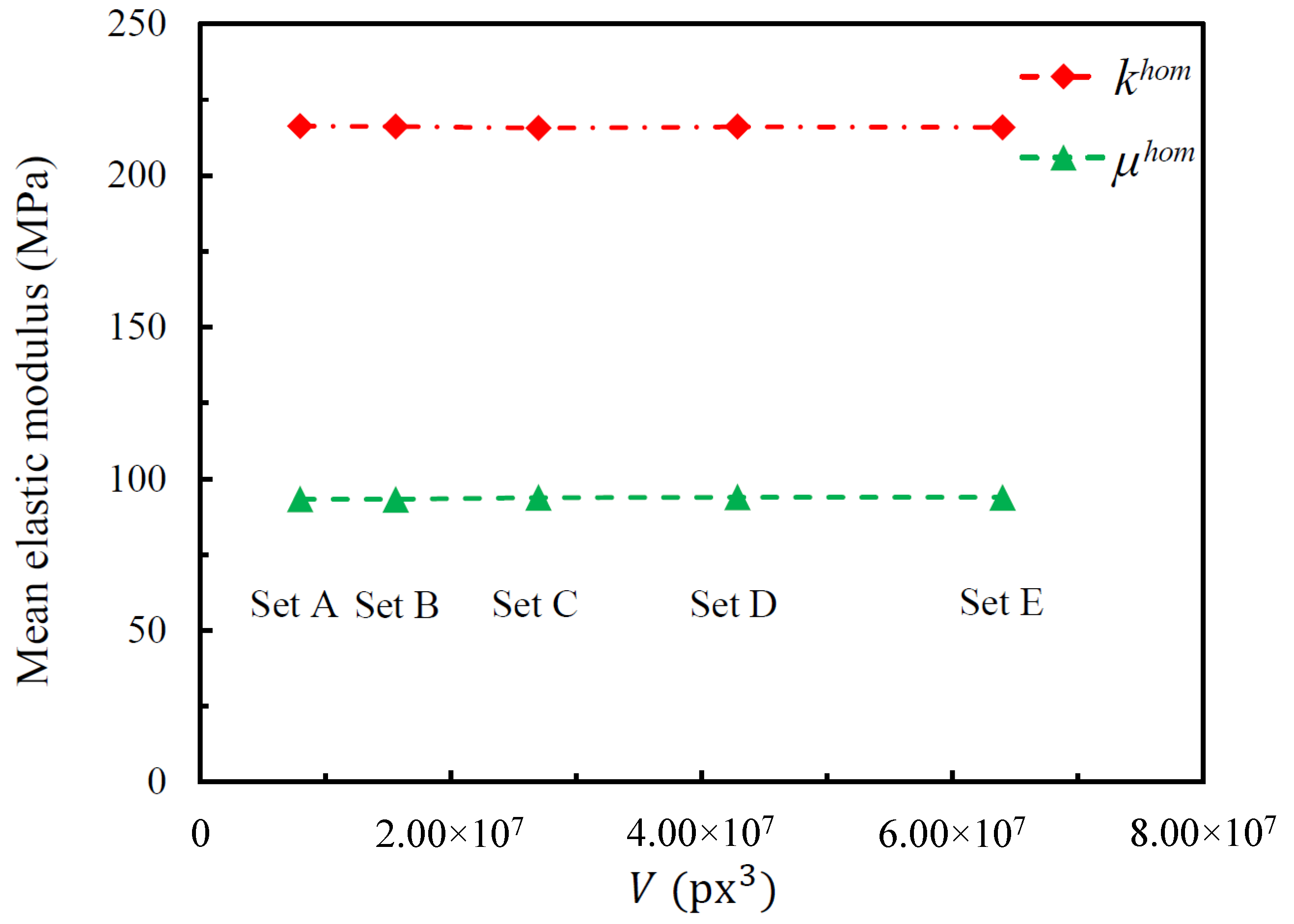

| Domain Dimensions (px) | Number of Cells | |
|---|---|---|
| Set A | 30 | |
| Set B | 58 | |
| Set C | 100 | |
| Set D | 159 | |
| Set E | 238 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Blal, N.; Cunsolo, S.; Baillis, D.; Michaud, P.-M. Effective Elastic Behavior of Irregular Closed-Cell Foams. Materials 2018, 11, 2100. https://doi.org/10.3390/ma11112100
Zhu W, Blal N, Cunsolo S, Baillis D, Michaud P-M. Effective Elastic Behavior of Irregular Closed-Cell Foams. Materials. 2018; 11(11):2100. https://doi.org/10.3390/ma11112100
Chicago/Turabian StyleZhu, Wenqi, Nawfal Blal, Salvatore Cunsolo, Dominique Baillis, and Paul-Marie Michaud. 2018. "Effective Elastic Behavior of Irregular Closed-Cell Foams" Materials 11, no. 11: 2100. https://doi.org/10.3390/ma11112100
APA StyleZhu, W., Blal, N., Cunsolo, S., Baillis, D., & Michaud, P.-M. (2018). Effective Elastic Behavior of Irregular Closed-Cell Foams. Materials, 11(11), 2100. https://doi.org/10.3390/ma11112100







