Mechanical Metamaterials Foams with Tunable Negative Poisson’s Ratio for Enhanced Energy Absorption and Damage Resistance
Abstract
1. Introduction
2. Geometrical Models of the CCF
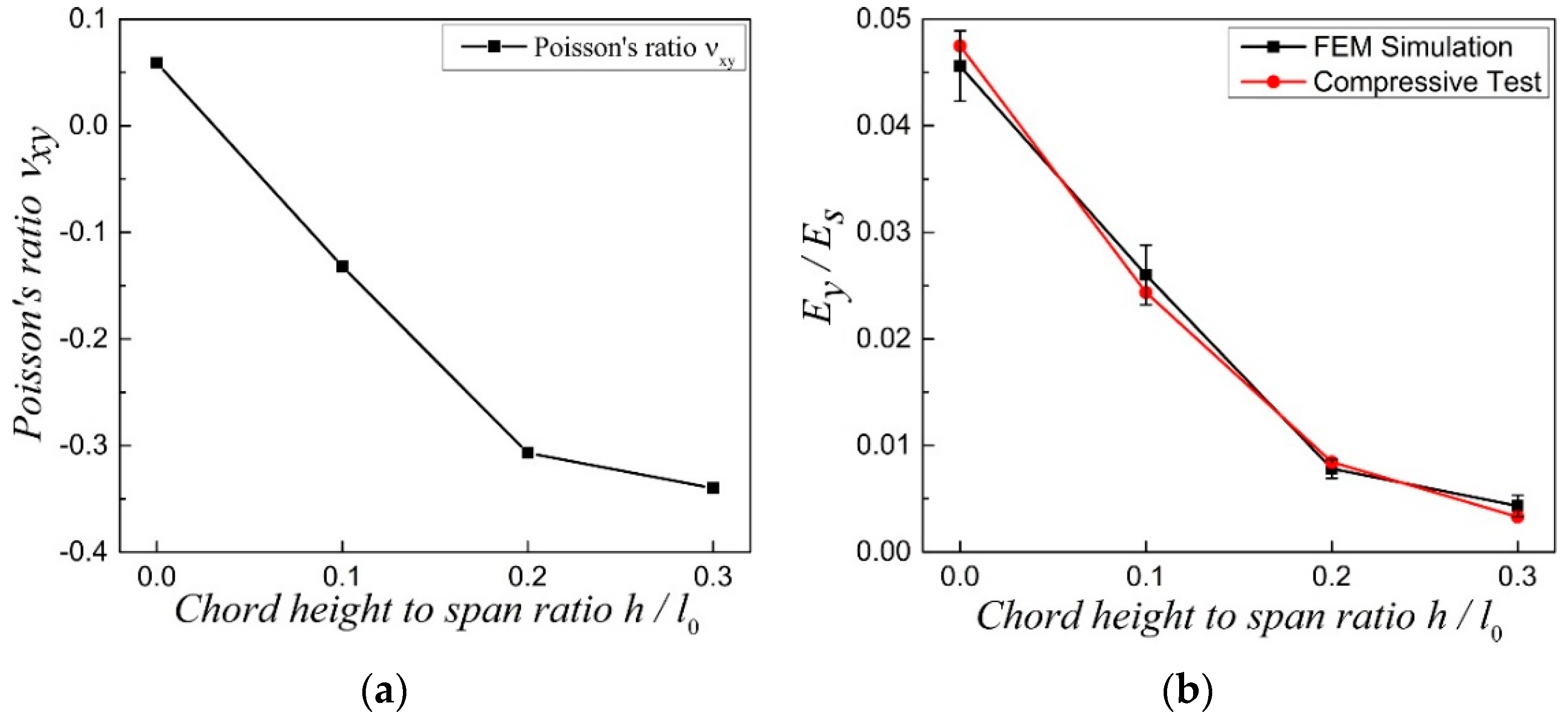
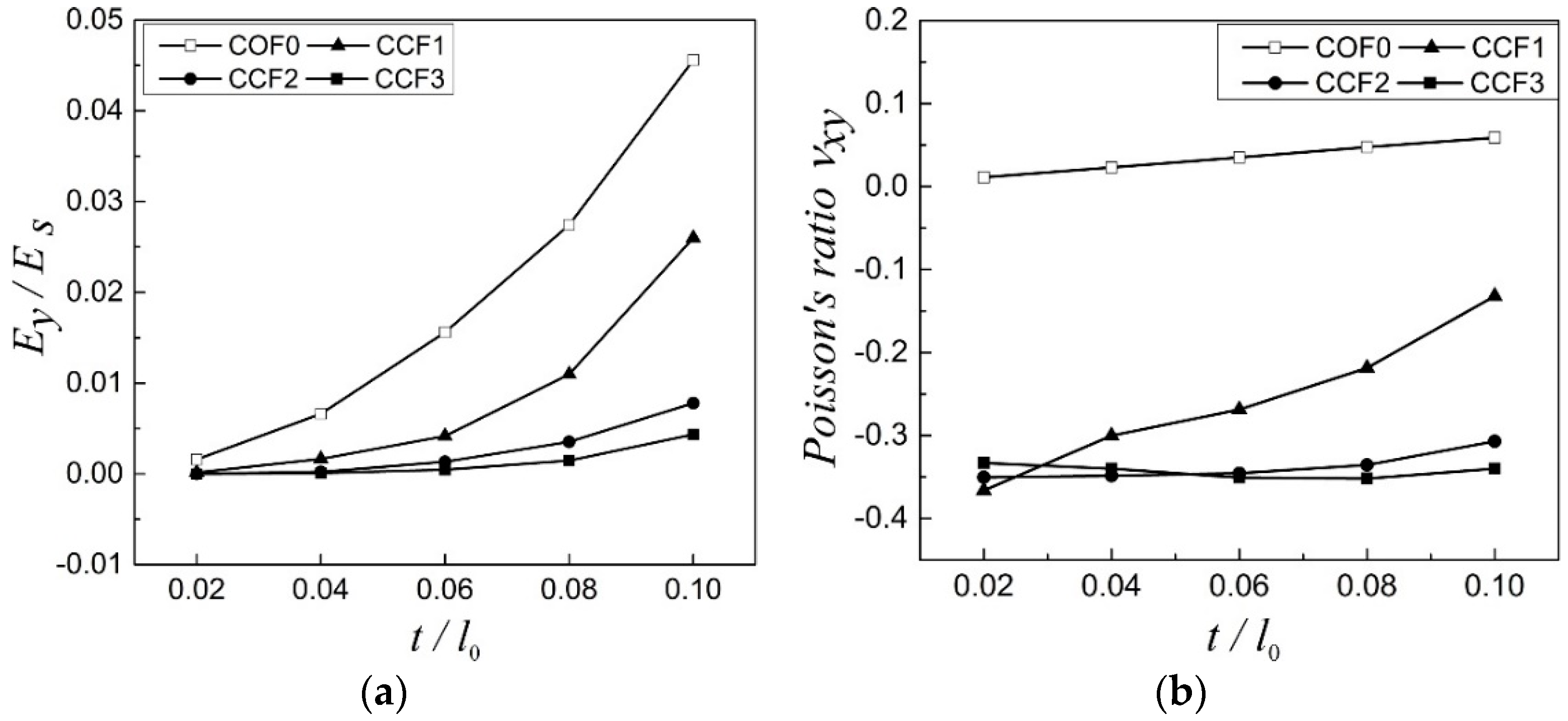
3. Effect of Geometrical Morphology on Elastic Moduli of the NPR CCF
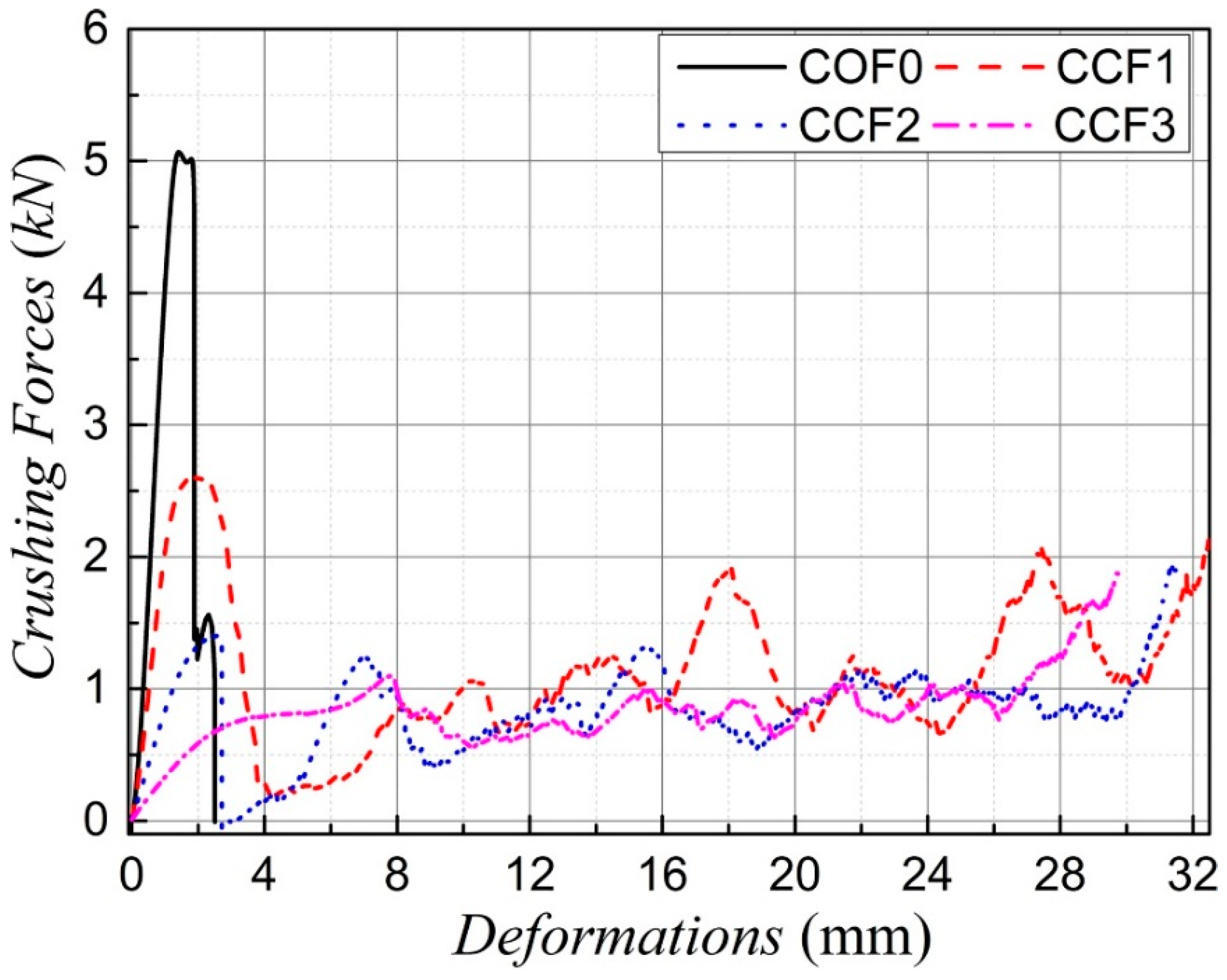
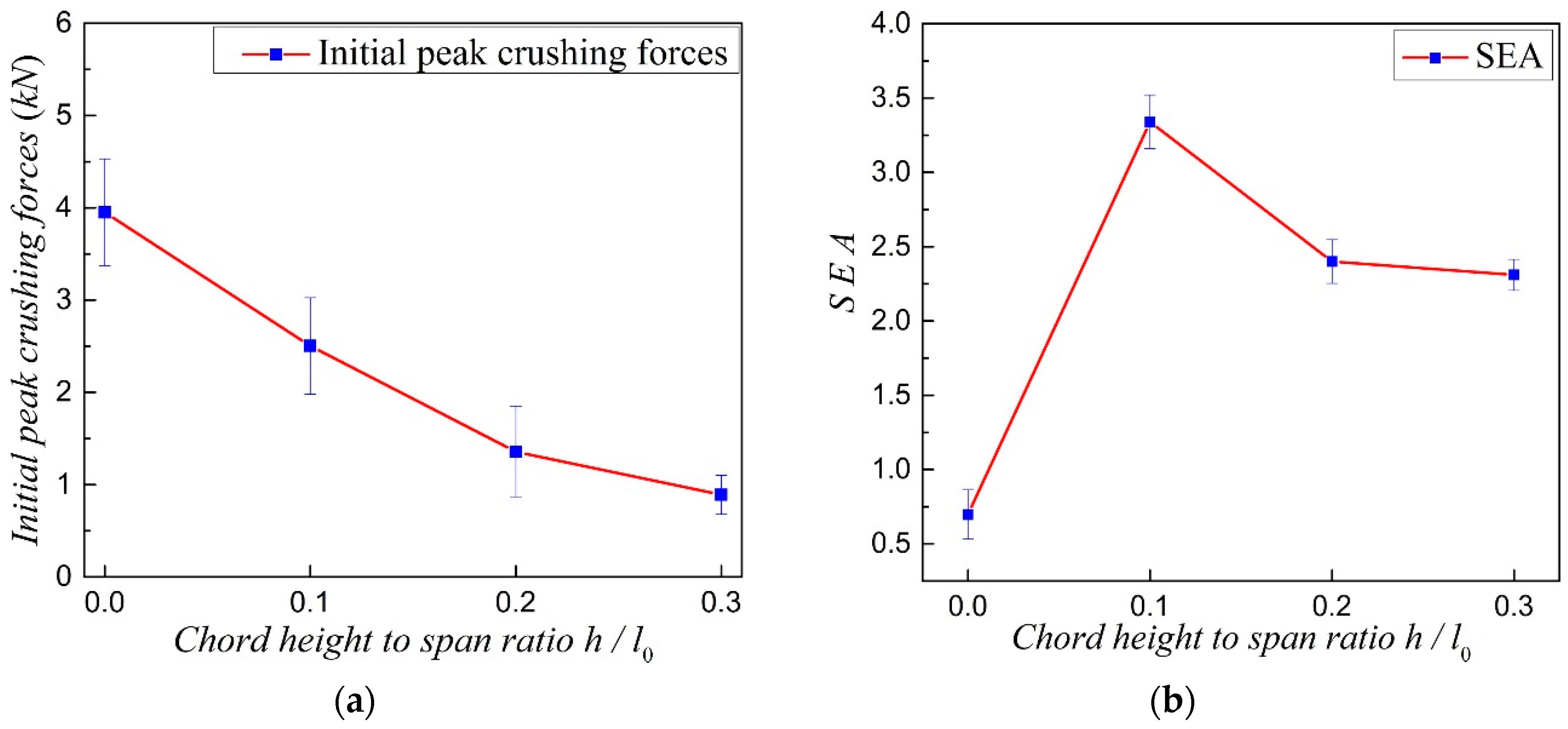
4. Effect of Geometrical Morphology on Energy Absorption Properties the NPR CCF
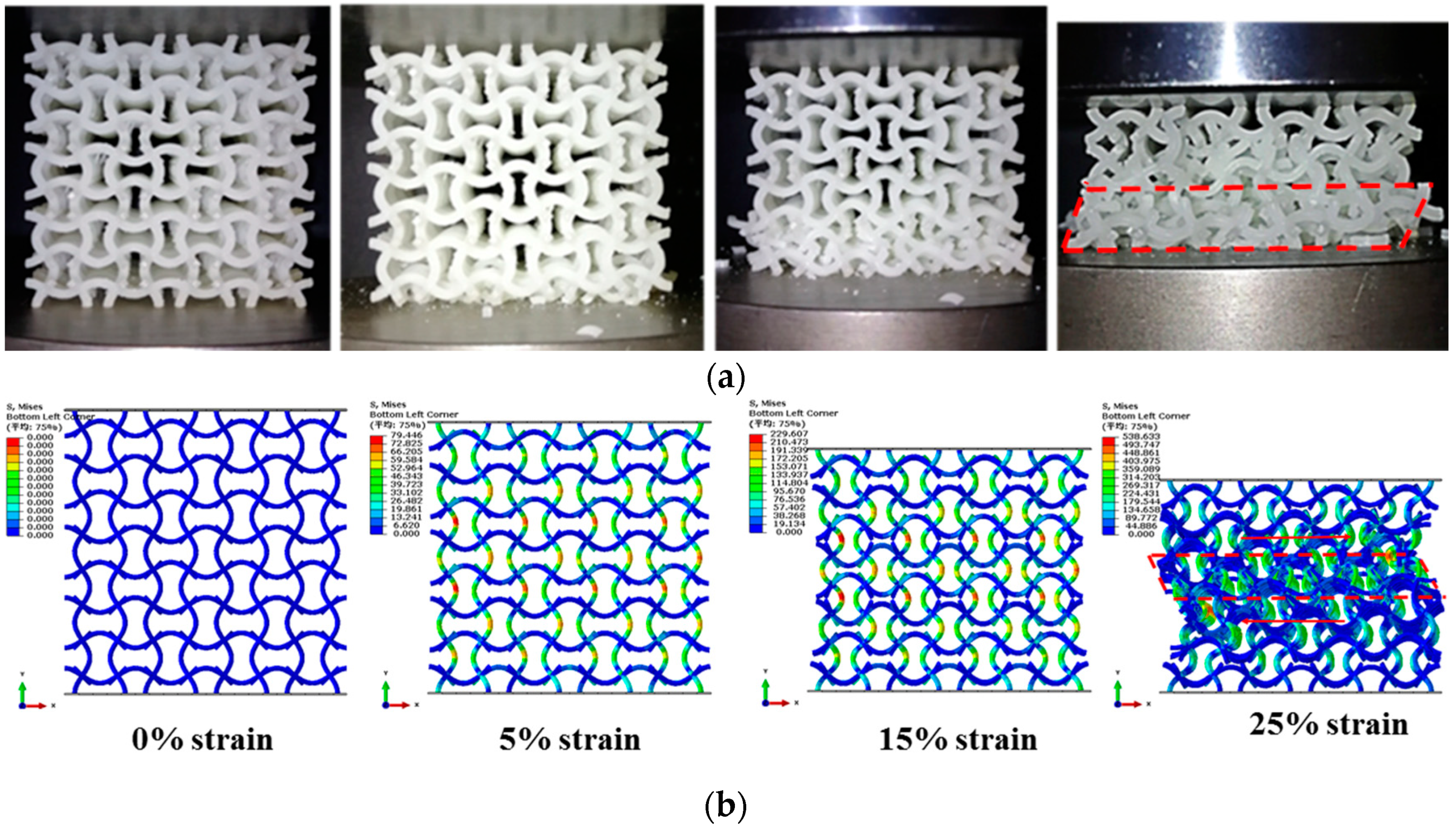
5. Effect of Geometrical Morphology on Collapse Modes of the NPR CCF under Quasi-Static Uniaxial Compressions
6. Effect of Geometrical Morphology on Damage Properties of the NPR CCF
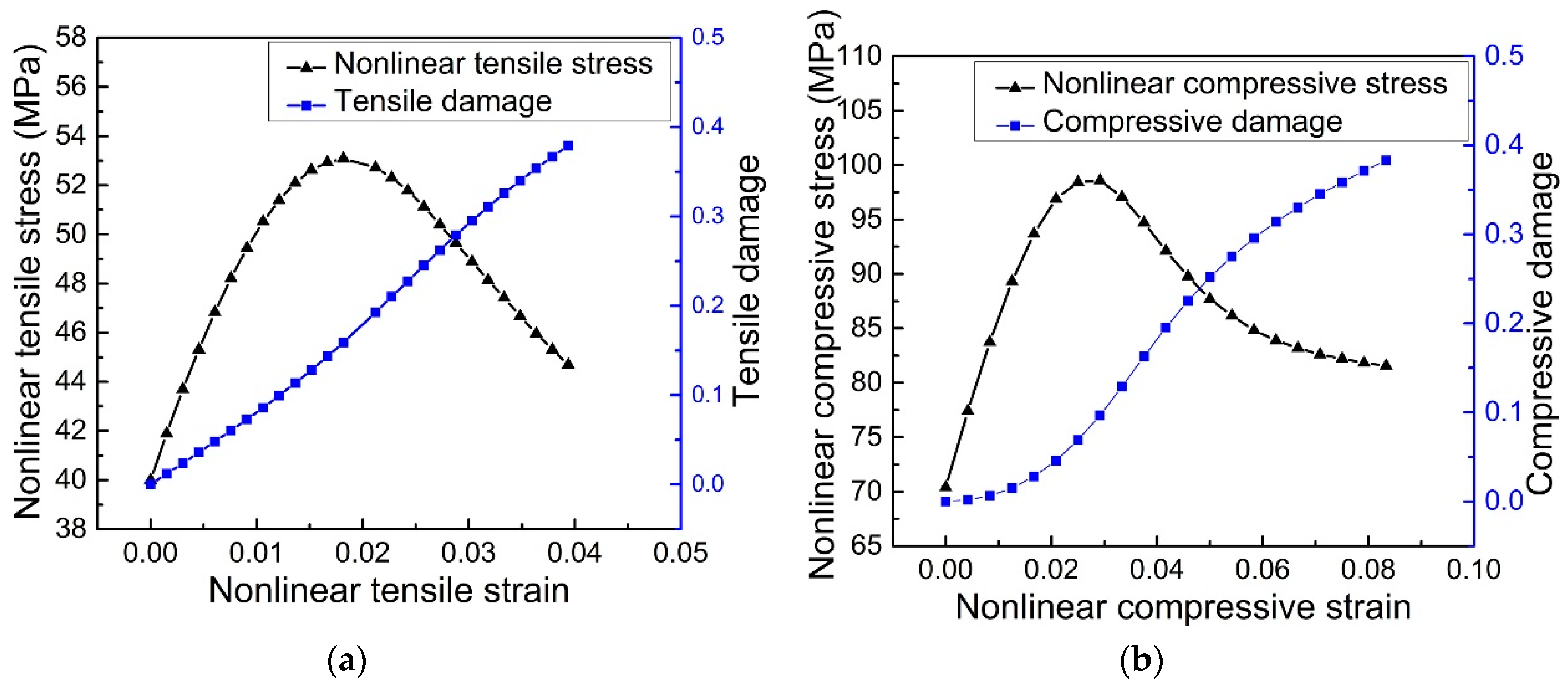
6.1. Plastic-Damage Constitute Model for the 3D-Printed VeroWhite Plus Materials
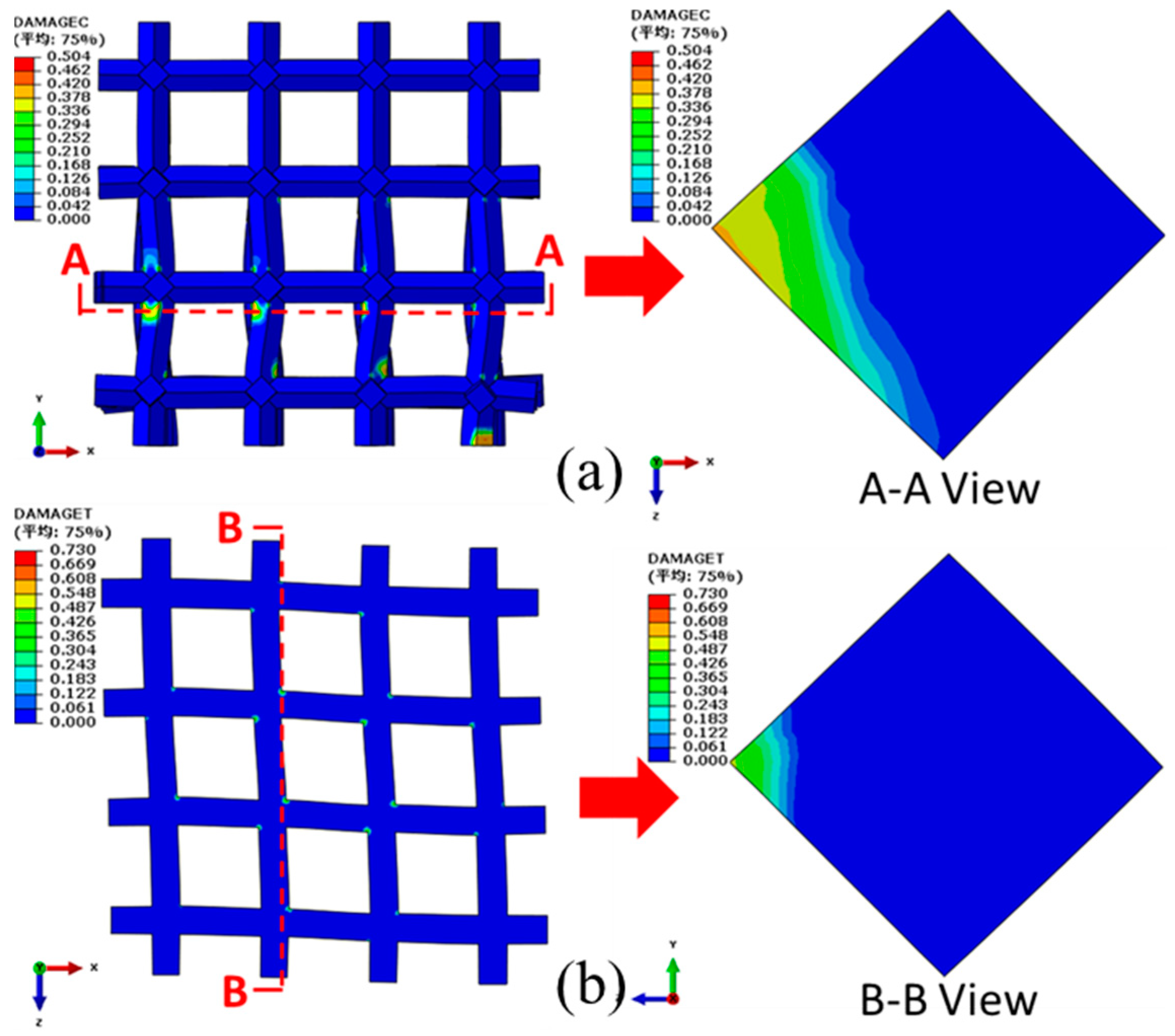
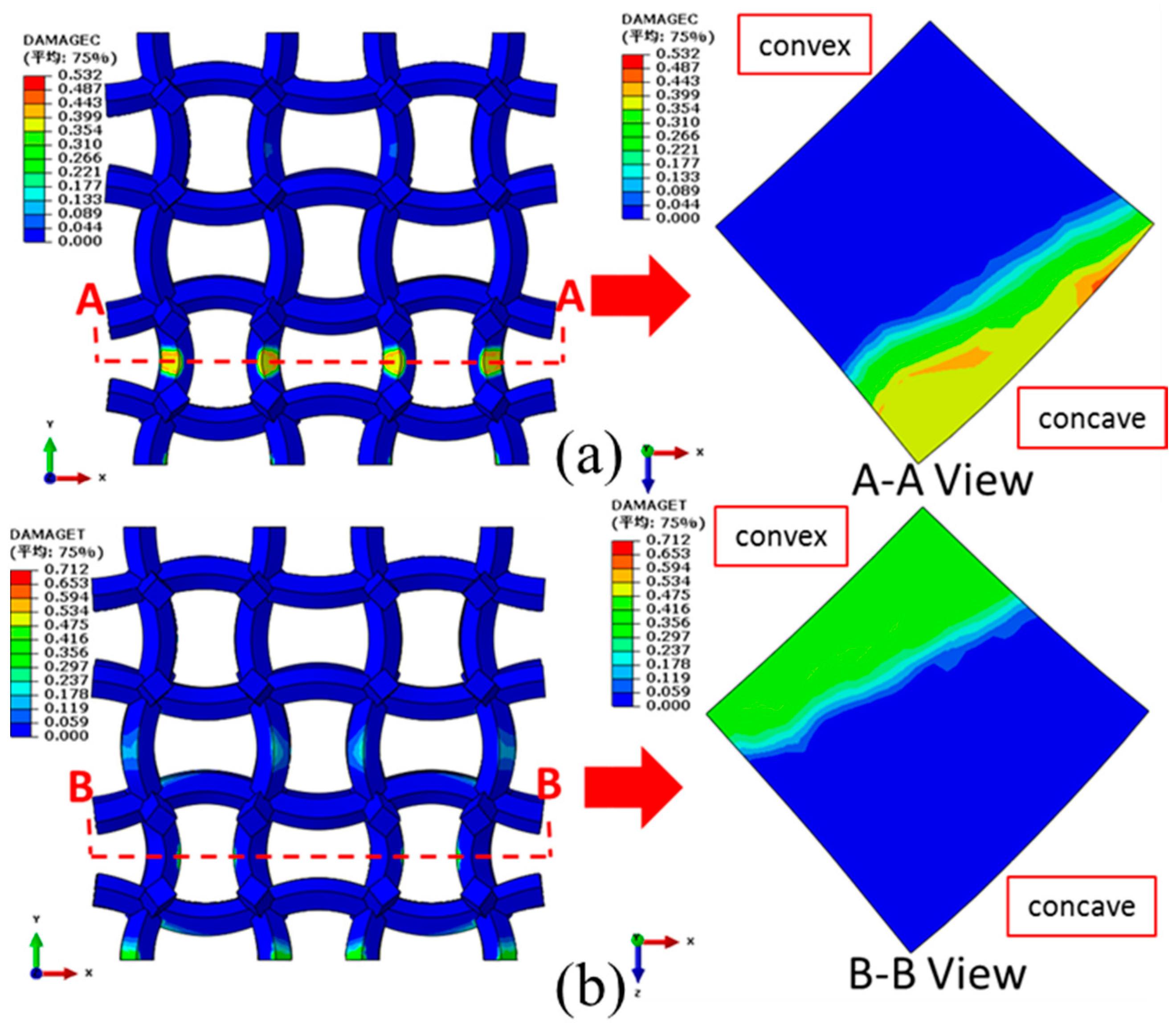
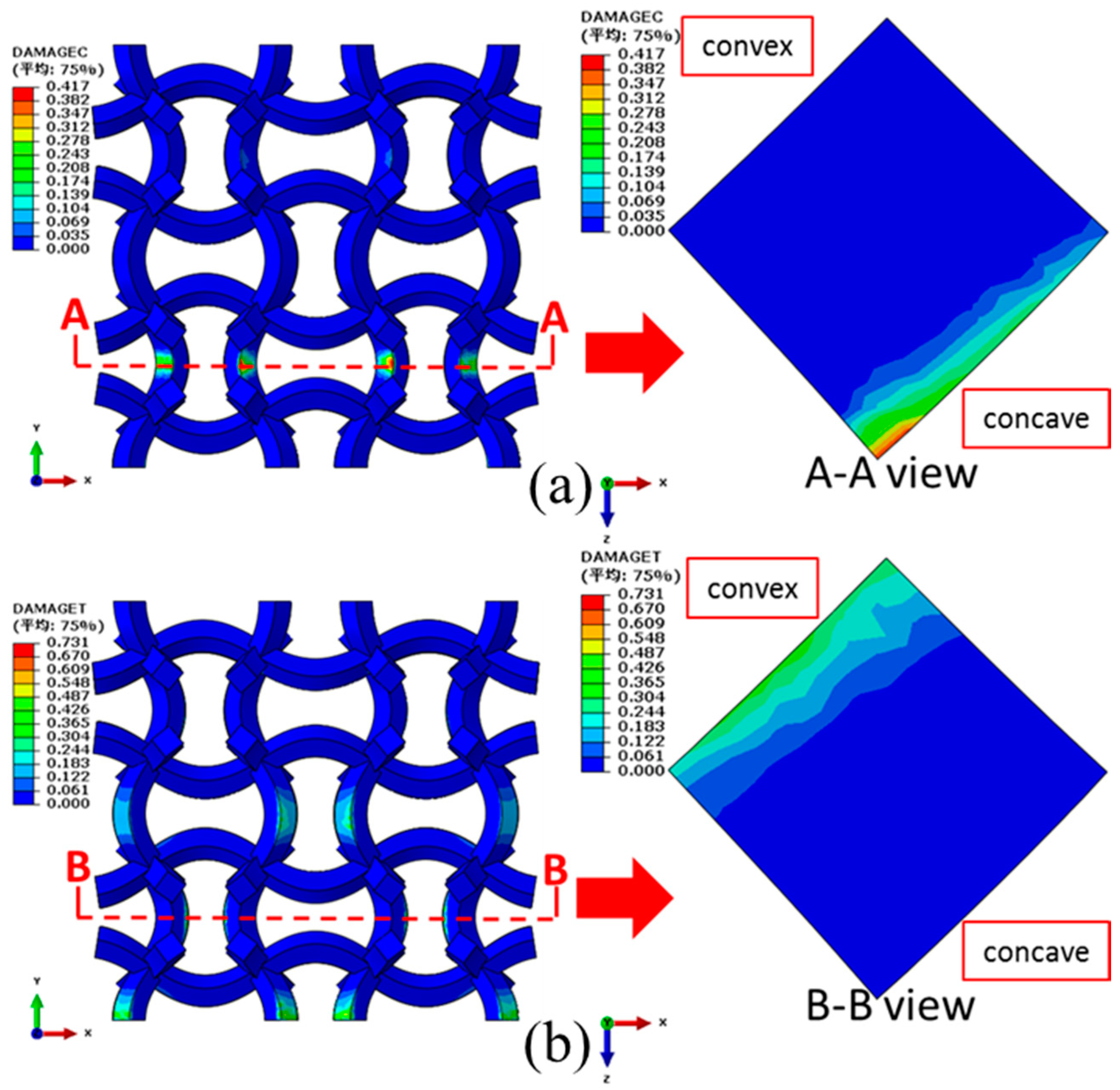
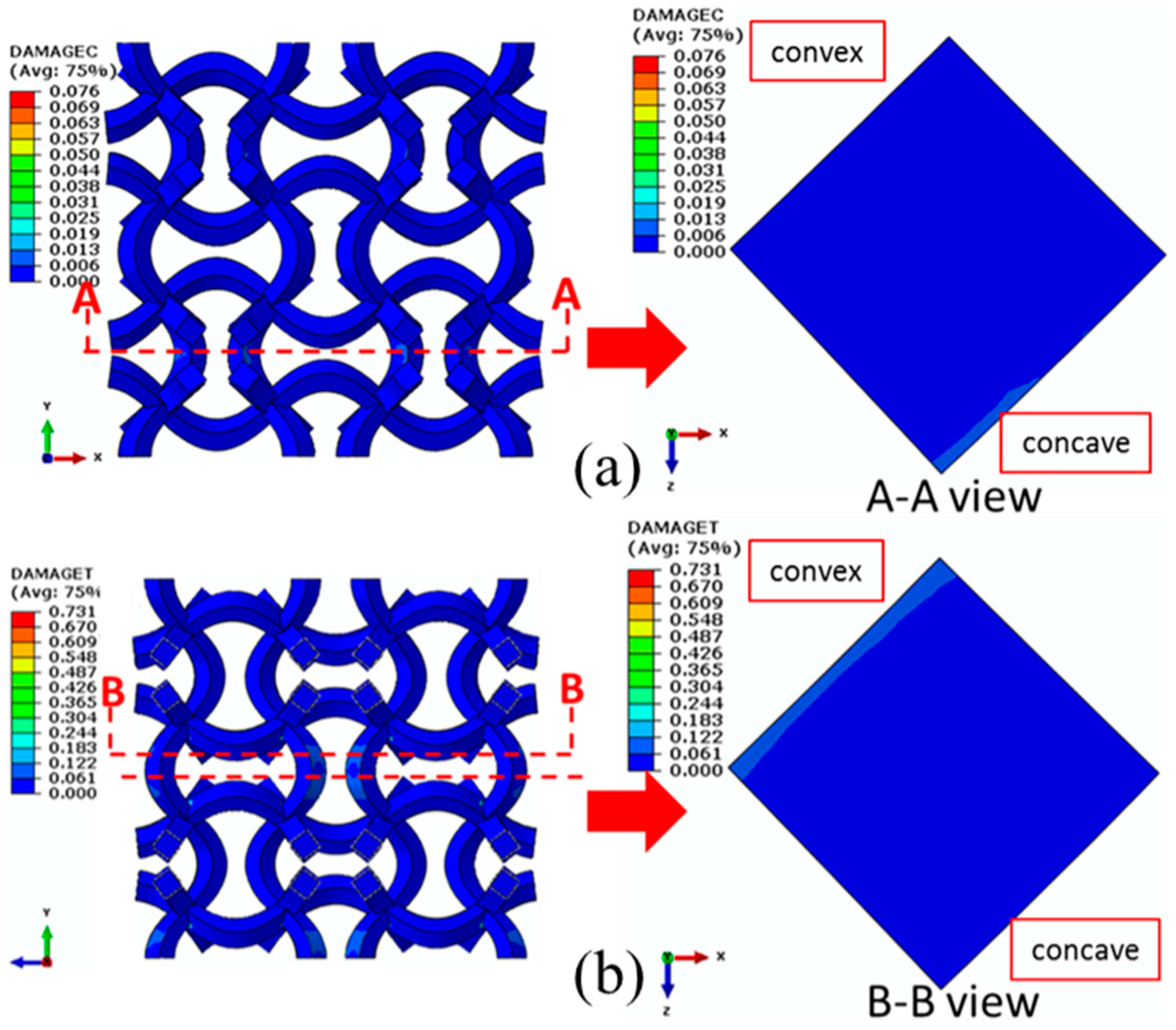
6.2. Damage Properties of the NPR CCF
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, Y.; Pugno, N.M. In plane stiffness of multifunctional hierarchical honeycombs with negative Poisson’s ratio sub-structures. Compos. Struct. 2013, 106, 681–689. [Google Scholar] [CrossRef]
- Lee, J.H.; Singer, J.P.; Thomas, E.L. Micro-/nanostructured mechanical metamaterials. Adv. Mater. 2012, 24, 4782–4810. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.L.; Zhou, J.; Liang, H.Y.; Jiang, Z.Y.; Wu, L.L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Mizzi, L.; Mahdi, E.M.; Titov, K. Mechanical metamaterials with star-shaped pores exhibiting negative and zero Poisson’s ratio. Mater. Des. 2018, 146, 28–37. [Google Scholar] [CrossRef]
- Hewage, T.A.M.; Alderson, K.L.; Alderson, A. Double-negative mechanical metamaterials displaying simultaneous negative stiffness and negative Poisson’s ratio properties. Adv. Mater. 2016, 28, 10323–10332. [Google Scholar] [CrossRef] [PubMed]
- Berger, J.B.; Wadley, H.N.; Mcmeeking, R.M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Hu, H. A review on auxetic structures and polymeric materials. Sci. Res. Essays 2010, 5, 1052–1063. [Google Scholar]
- Lakes, R.S.; Elms, K. Indentability of conventional and negative Poisson’s ratio foams. J. Compos. Mater. 1992, 27, 1193–1202. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef] [PubMed]
- Duncan, O.; Shepherd, T.; Moroney, C. Review of auxetic materials for sports applications: Expanding options in comfort and protection. Appl. Sci. 2018, 8, 941. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.M.; Li, W.; Xie, B.H.; Yang, M.B. Review on auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.B.; Lakes, R.S. Fracture toughness of re-entrant foam materials with a negative Poisson’s ratio: Experiment and analysis. Int. J. Facture 1996, 80, 73–83. [Google Scholar] [CrossRef]
- Lowe, A.; Lakes, R.S. Negative Poisson’s ratio foam as seat cushion material. Cell. Polym. 2000, 19, 157–167. [Google Scholar]
- Wang, Y.C.; Lakes, R. Analytical parametric analysis of the contact problem of human buttocks and negative Poisson’s ratio foam cushions. Int. J. Solids Struct. 2002, 39, 4825–4838. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J. Auxetic foams: Modelling negative Poisson’s ratios. Acta Mater. 1994, 42, 1289–1294. [Google Scholar] [CrossRef]
- Scarpa, F.; Ciffo, L.G.; Yates, J.R. Dynamic properties of high structural integrity auxetic open cell foam. Smart Mater. Stuct. 2003, 13, 49. [Google Scholar] [CrossRef]
- Bezazi, A.; Scarpa, F. Mechanical behaviour of conventional and negative Poisson’s ratio thermoplastic polyurethane foams under compressive cyclic loading. Int. J. Fatigue 2007, 29, 922–930. [Google Scholar] [CrossRef]
- Bezazi, A.; Scarpa, F. Tensile fatigue of conventional and negative Poisson’s ratio open cell PU foams. Int. J. Fatigue 2009, 31, 488–494. [Google Scholar] [CrossRef]
- Bianchi, M.; Scarpa, F. Vibration transmissibility and damping behaviour for auxetic and conventional foams under linear and nonlinear regimes. Smart Mater. Stuct. 2013, 22, 084010. [Google Scholar] [CrossRef]
- Shen, J.; Zhou, S.; Huang, X. Simple cubic three-dimensional auxetic metamaterials. Phys. Status Solidi (b) 2014, 251, 1515–1522. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, X.; Wang, W. Compressive property of Al-based auxetic lattice structures fabricated by 3-D printing combined with investment casting. Mat. Sci. Eng. A 2018, 722, 255–262. [Google Scholar] [CrossRef]
- Wang, X.T.; Li, X.W.; Ma, L. Interlocking assembled 3D auxetic cellular structures. Mater. Des. 2016, 99, 467–476. [Google Scholar] [CrossRef]
- Ai, L.; Gao, X.L. Three-dimensional metamaterials with a negative Poisson’s ratio and a non-positive coefficient of thermal expansion. Int. J. Mech. Sci. 2018, 135, 101–113. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gambarotta, L. Homogenization of periodic hexa-and tetrachiral cellular solids. Compos. Struct. 2014, 116, 461–476. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gambarotta, L. Simplified modelling of chiral lattice materials with local resonators. Int. J. Solids Struct. 2016, 83, 126–141. [Google Scholar] [CrossRef]
- Lepidi, M.; Bacigalupo, A. Asymptotic approximation of the band structure for tetrachiral metamaterials. Procedia Eng. 2017, 199, 1460–1465. [Google Scholar] [CrossRef]
- Lepidi, M.; Bacigalupo, A. Multi-parametric sensitivity analysis of the band structure for tetrachiral acoustic metamaterials. Int. J. Solids Struct. 2018, 136–137, 186–202. [Google Scholar] [CrossRef]
- Vadalà, F.; Bacigalupo, A.; Lepidi, M.; Gambarotta, L. Bloch wave filtering in tetrachiral materials via mechanical tuning. Compos. Struct. 2018, 201, 340–351. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Bellis, M.L.D. Auxetic anti-tetrachiral materials: Equivalent elastic properties and frequency band-gaps. Compos. Struct. 2015, 131, 530–544. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Lepidi, M. High-frequency parametric approximation of the Floquet-Bloch spectrum for anti-tetrachiral materials. Int. J. Solids Struct. 2016, 97–98, 575–592. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Lepidi, M.; Gnecco, G.; Gambarotta, L. Optimal design of low-frequency band gaps in anti-tetrachiral lattice meta-materials. Compos. Part B Eng. 2017, 115, 341–359. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gambarotta, L. Damped bloch waves in Lattices metamaterials with inertial resonators. Procedia Eng. 2017, 199, 1441–1446. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gambarotta, L. Wave propagation in non-centrosymmetric beam-lattices with lumped masses: Discrete and micropolar modeling. Int. J. Solids Struct. 2017, 118–119, 128–145. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gambarotta, L. Generalized micropolar continualization of 1D beam lattices. Comput. Phys. 2018, arXiv:1808.07125. [Google Scholar]
- Bacigalupo, A.; Gambarotta, L. Dispersive wave propagation in two-dimensional rigid periodic blocky materials with elastic interfaces. J. Mech. Phys. Solids 2017, 102, 165–186. [Google Scholar] [CrossRef]
- Dolla, W.J.S. Rotational Expansion Auxetic Structures. U.S. Patent US8652602, 18 February 2014. [Google Scholar]
- Körner, C.; Lieboldribeiro, Y. A systematic approach to identify cellular auxetic materials. Smart Mater. Stuct. 2015, 24, 025013. [Google Scholar] [CrossRef]
- Dolla, W.J.S.; Fricke, B.A.; Becker, B.R. Auxetic drug-eluting stent design. In Proceedings of the ASME 2006 Frontiers in Biomedical Devices Conference, Irvine, CA, USA, 8–9 June 2006. [Google Scholar]
- Dolla, W.J.S.; Fricke, B.A.; Becker, B.R. Structural and drug diffusion models of conventional and auxetic drug-eluting stents. J. Med. Devices 2006, 1, 47–55. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Wojciechowski, K.W. The influence of large deformations on mechanical properties of sinusoidal ligament structures. Smart Mater. Struct. 2016, 25, 054002. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Idczak, E.; Krzysztof, W. Computational modelling of structures with non-intuitive behaviour. Materials 2017, 10, 1386. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.Y.; Li, Y.N. 3D printed auxetic mechanical metamaterial with chiral cells and re-entrant cores. Sci. Rep. 2018, 8, 2397. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 2014; pp. 487–488. [Google Scholar]
- Du, Y.H.; Pugno, N.; Gong, B.M. Mechanical properties of the hierarchical honeycombs with stochastic Voronoi sub-structures. Epl-Europhys Lett. 2015, 111, 56007. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.L.; Sun, Y.T.; Ding, Q.; Li, Y.J.; Ren, F.G.; Guo, C.X.; Gong, B.M. Negative Poisson’s ratio convex-concave honeycomb columns with high-performance crashworthiness. Mater. Des. under review.
- Costas, M.; Morin, D.; Langseth, M. Axial crushing of aluminum extrusions filled with PET foam and GFRP. An experimental investigation. Thin-Walled Struct. 2016, 99, 45–57. [Google Scholar] [CrossRef]
- Sun, G.; Sun, G.; Hou, S. Crashworthiness design for functionally graded foam-filled thin-walled structures. Mater. Sci. Eng. A 2010, 527, 1911–1919. [Google Scholar] [CrossRef]
- Yin, H.; Wen, G.; Hou, S. Multiobjective crashworthiness optimization of functionally lateral graded foam-filled tubes. Mater. Des. 2013, 44, 414–428. [Google Scholar] [CrossRef]
- Wu, S.; Zheng, G.; Sun, G. On design of multi-cell thin-wall structures for crashworthiness. Int. J. Impact Eng. 2016, 88, 102–117. [Google Scholar] [CrossRef]
- Saenz, L.P. Discussion of equation for the stress-strain curve of concrete by Desai and Krishnan. ACI J. 1964, 61, 1229–1235. [Google Scholar]
- Pan, H.; Abu Alrub, R. A finite deformation coupled plastic-damage model for simulating fracture of metal foams. In Proceedings of the Society of Engineering Science 51st Annual Technical Meeting, West Lafayette, IN, USA, 1–3 October 2014. [Google Scholar]
- Diebels, S.; Ebinger, T.; Steeb, H. An anisotropic damage model of foams on the basis of a micromechanical description. J. Mater. Sci. 2005, 40, 5919–5924. [Google Scholar] [CrossRef]
- Shan, Y.; Nian, G.; Xu, Q. Strength analysis of syntactic foams using a three-dimensional continuum damage finite element model. Int. J. Appl. Mech. 2015, 82, 021004. [Google Scholar] [CrossRef]
- Qiao, L.; Zencker, U.; Kasparek, E.M. Simulation of damping concrete under severe loads using a crushable foam model with damage mechanisms. In Proceedings of the Twelfth International Conference on Computational Structures Technology, Naples, Italy, 2–5 September 2014. [Google Scholar]
- Cicekli, U.; Voyiadjis, G.Z.; Al-Rub, R.K.A. A plasticity and anisotropic damage model for plain concrete. Int. J. Plast. 2007, 23, 1874–1900. [Google Scholar] [CrossRef]
- Kim, S.M.; Al-Rub, R.K.A. Meso-scale computational modeling of the plastic-damage response of cementitious composites. Cem. Concr. Res. 2011, 41, 339–358. [Google Scholar] [CrossRef]
- Souissi, S.; Miled, K.; Hamdi, E. Numerical modeling of rocks damage during indentation process with reference to hard rock drilling. Int. J. Geomech. 2017, 17, 04017002. [Google Scholar] [CrossRef]
- Li, W.G.; Luo, Z.; Sun, Z.; Hu, Y.; Duan, W.H. Numerical modelling of plastic-damage response and crack propagation in RAC under uniaxial loading. Mag. Concr. Res. 2017, 70, 459–472. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Tensile Properties of Plastics; ASTM D638; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, S.; Gong, B.; Ding, Q.; Sun, Y.; Ren, F.; Liu, X.; Yan, Q.; Yang, H.; Wang, X.; Song, B. Mechanical Metamaterials Foams with Tunable Negative Poisson’s Ratio for Enhanced Energy Absorption and Damage Resistance. Materials 2018, 11, 1869. https://doi.org/10.3390/ma11101869
Cui S, Gong B, Ding Q, Sun Y, Ren F, Liu X, Yan Q, Yang H, Wang X, Song B. Mechanical Metamaterials Foams with Tunable Negative Poisson’s Ratio for Enhanced Energy Absorption and Damage Resistance. Materials. 2018; 11(10):1869. https://doi.org/10.3390/ma11101869
Chicago/Turabian StyleCui, Shaohua, Baoming Gong, Qian Ding, Yongtao Sun, Fuguang Ren, Xiuguo Liu, Qun Yan, Hai Yang, Xin Wang, and Bowen Song. 2018. "Mechanical Metamaterials Foams with Tunable Negative Poisson’s Ratio for Enhanced Energy Absorption and Damage Resistance" Materials 11, no. 10: 1869. https://doi.org/10.3390/ma11101869
APA StyleCui, S., Gong, B., Ding, Q., Sun, Y., Ren, F., Liu, X., Yan, Q., Yang, H., Wang, X., & Song, B. (2018). Mechanical Metamaterials Foams with Tunable Negative Poisson’s Ratio for Enhanced Energy Absorption and Damage Resistance. Materials, 11(10), 1869. https://doi.org/10.3390/ma11101869



