Research on the Crack Risk of Early-Age Concrete under the Temperature Stress Test Machine
Abstract
1. Introduction
2. The Temperature Stress Test
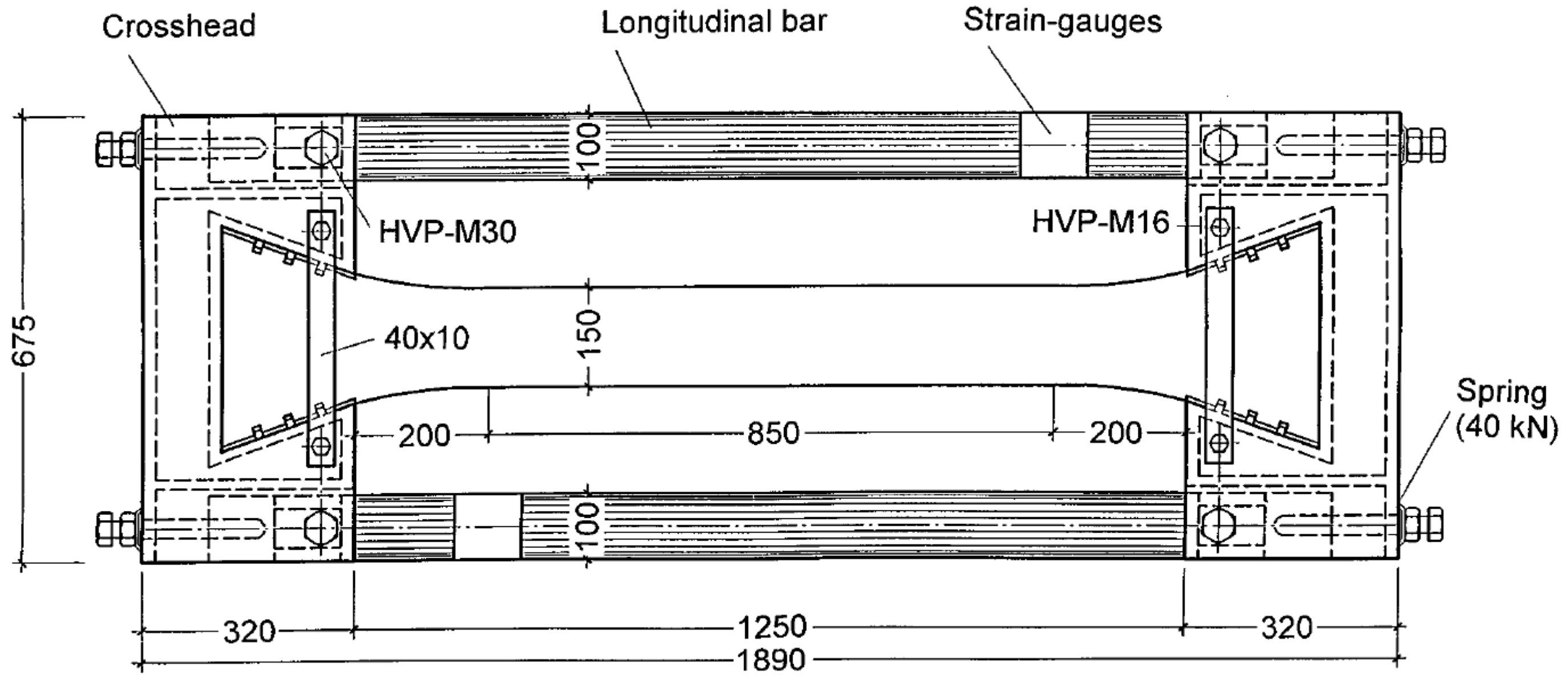
2.1. Test Method
2.2. Concrete Mixture Proportions
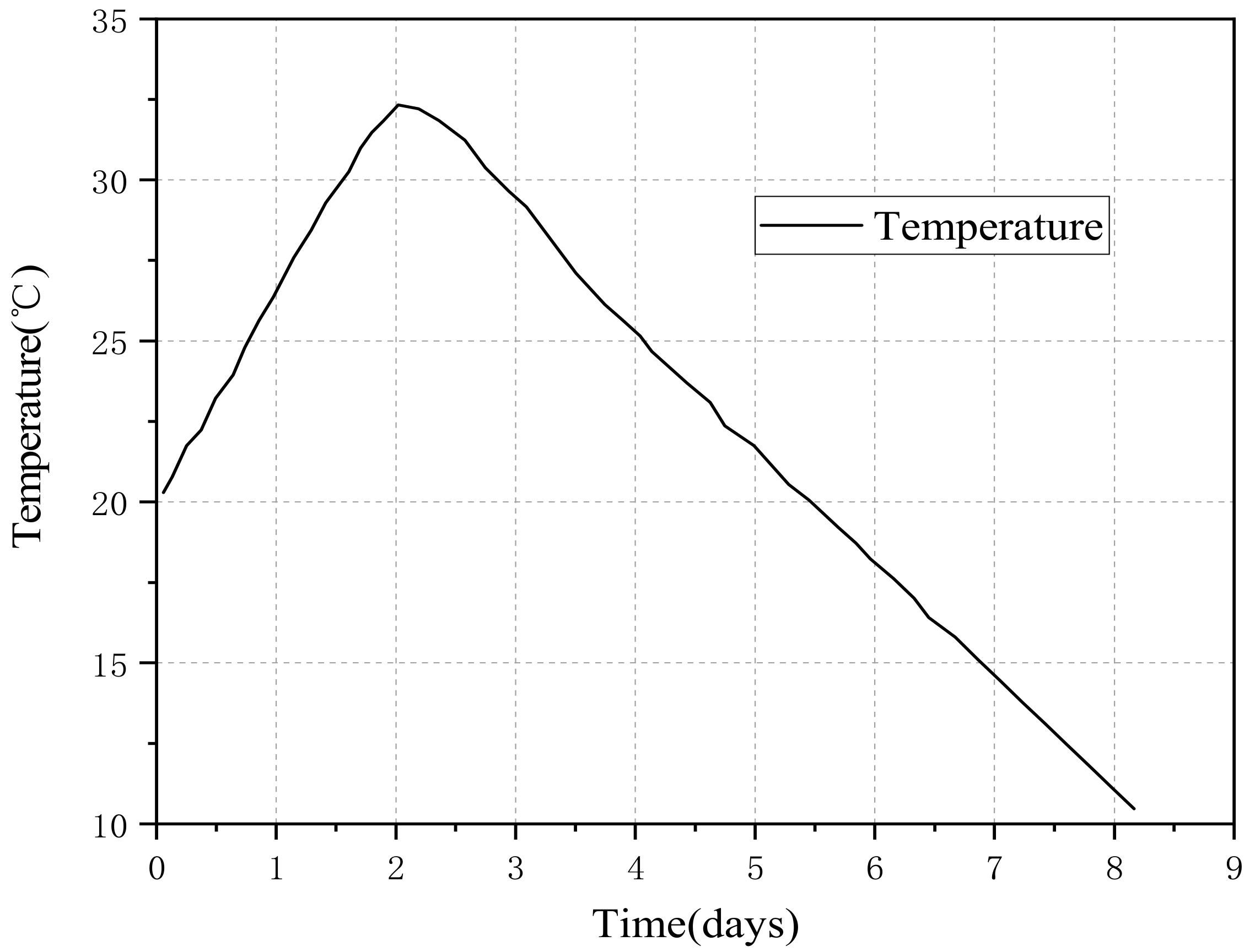
2.3. Temperature History and Free Deformation
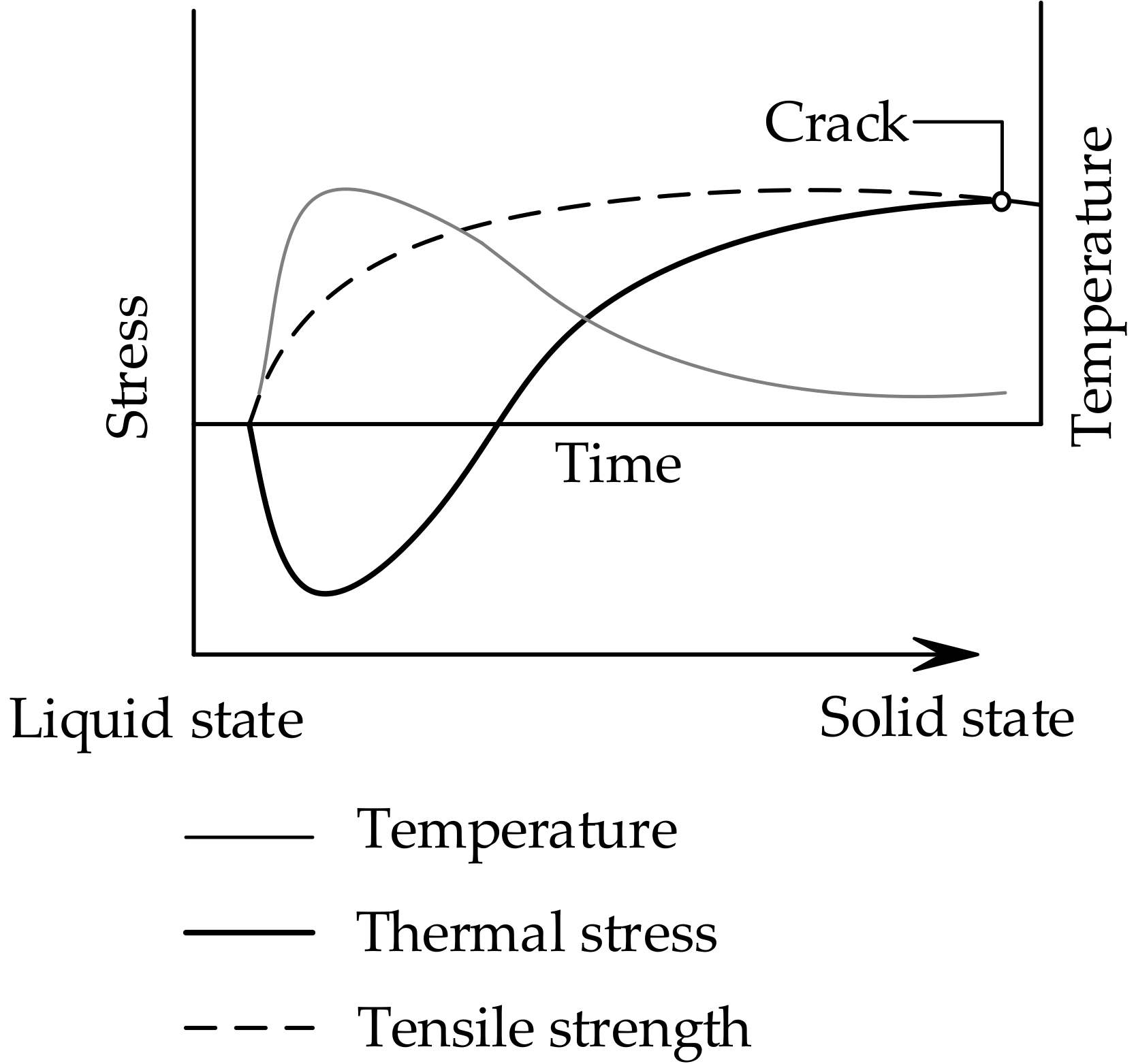
2.4. Restrained Deformation and Stress Evolution of Concrete Specimen
3. Results and Discussions
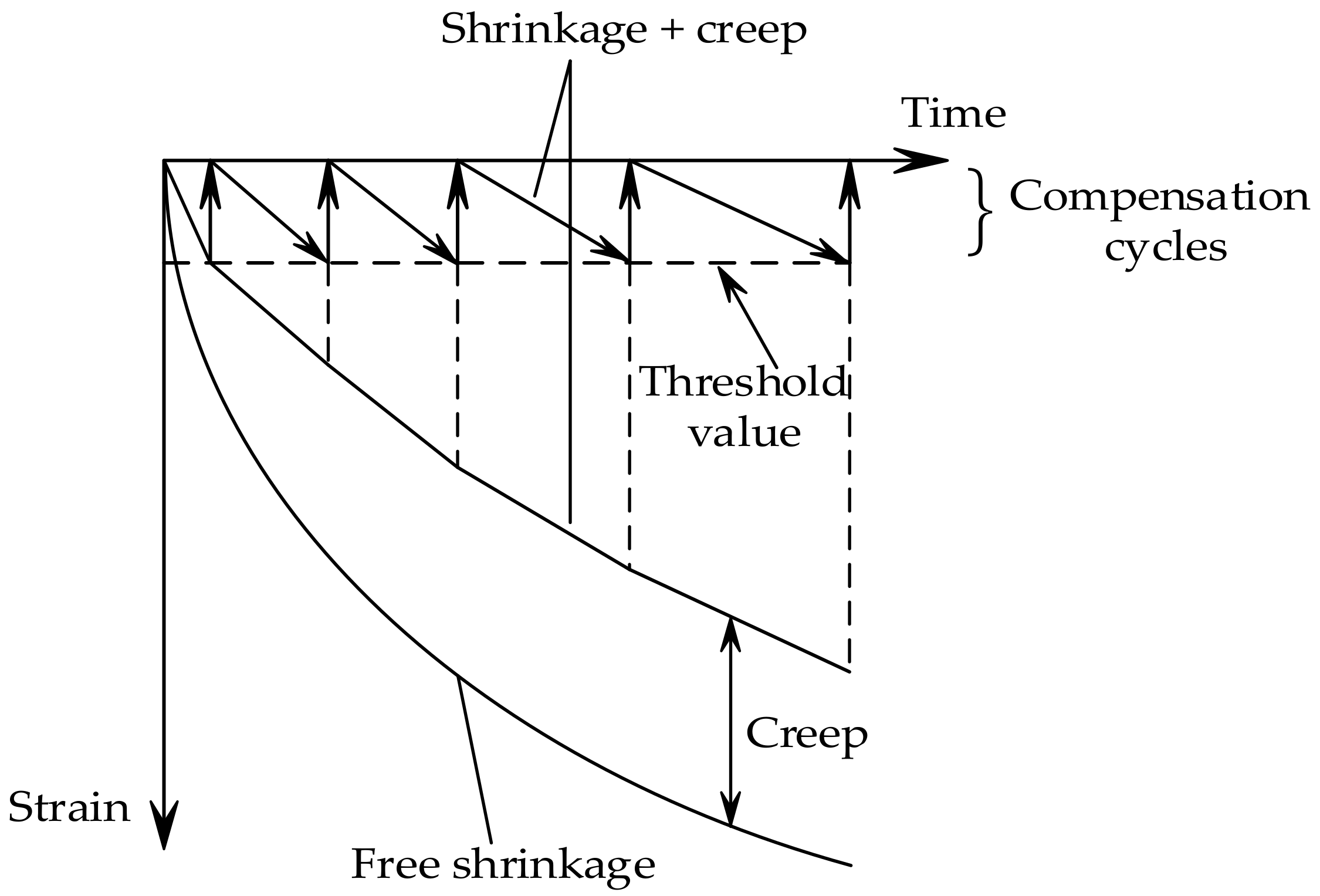
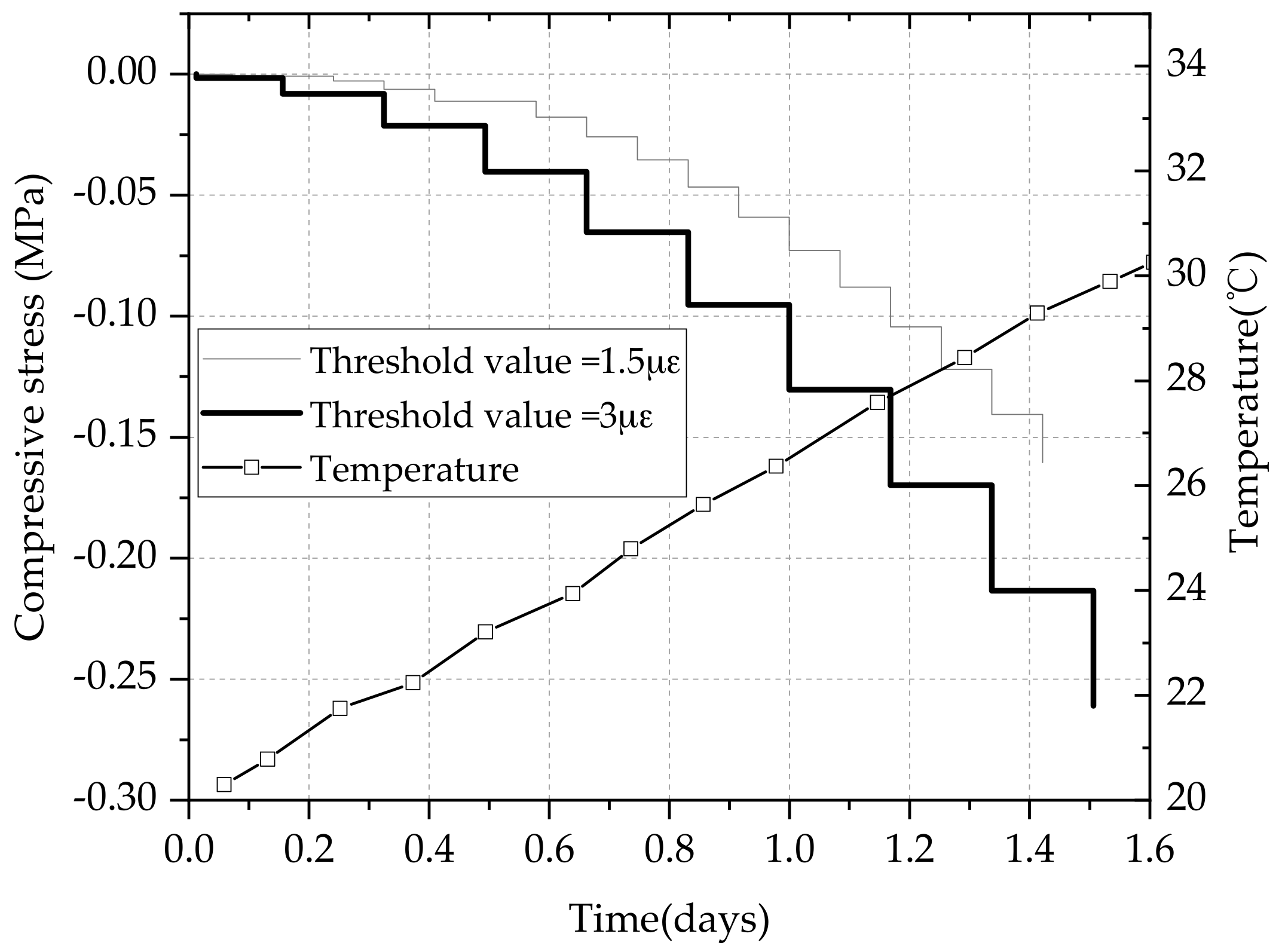
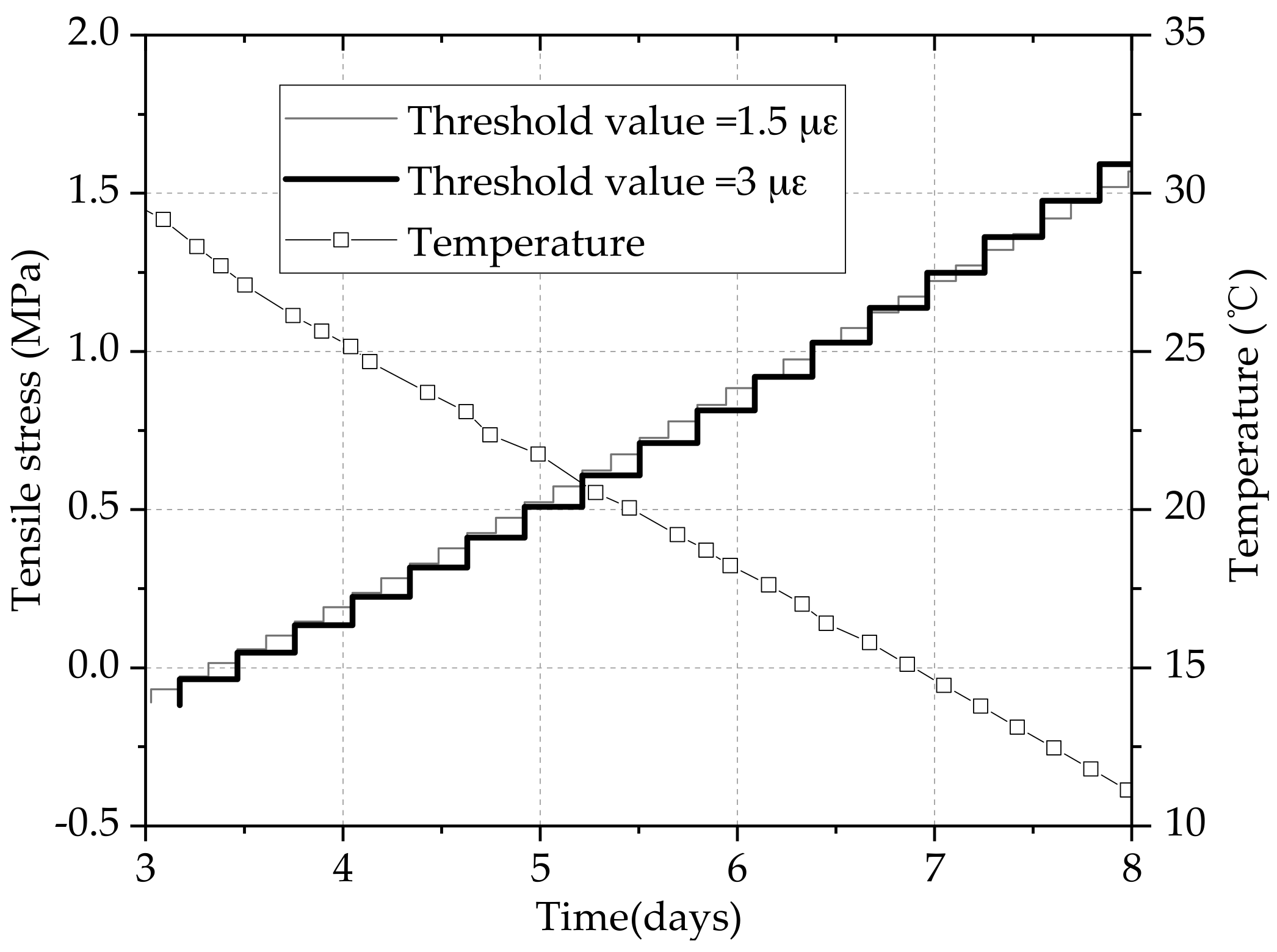
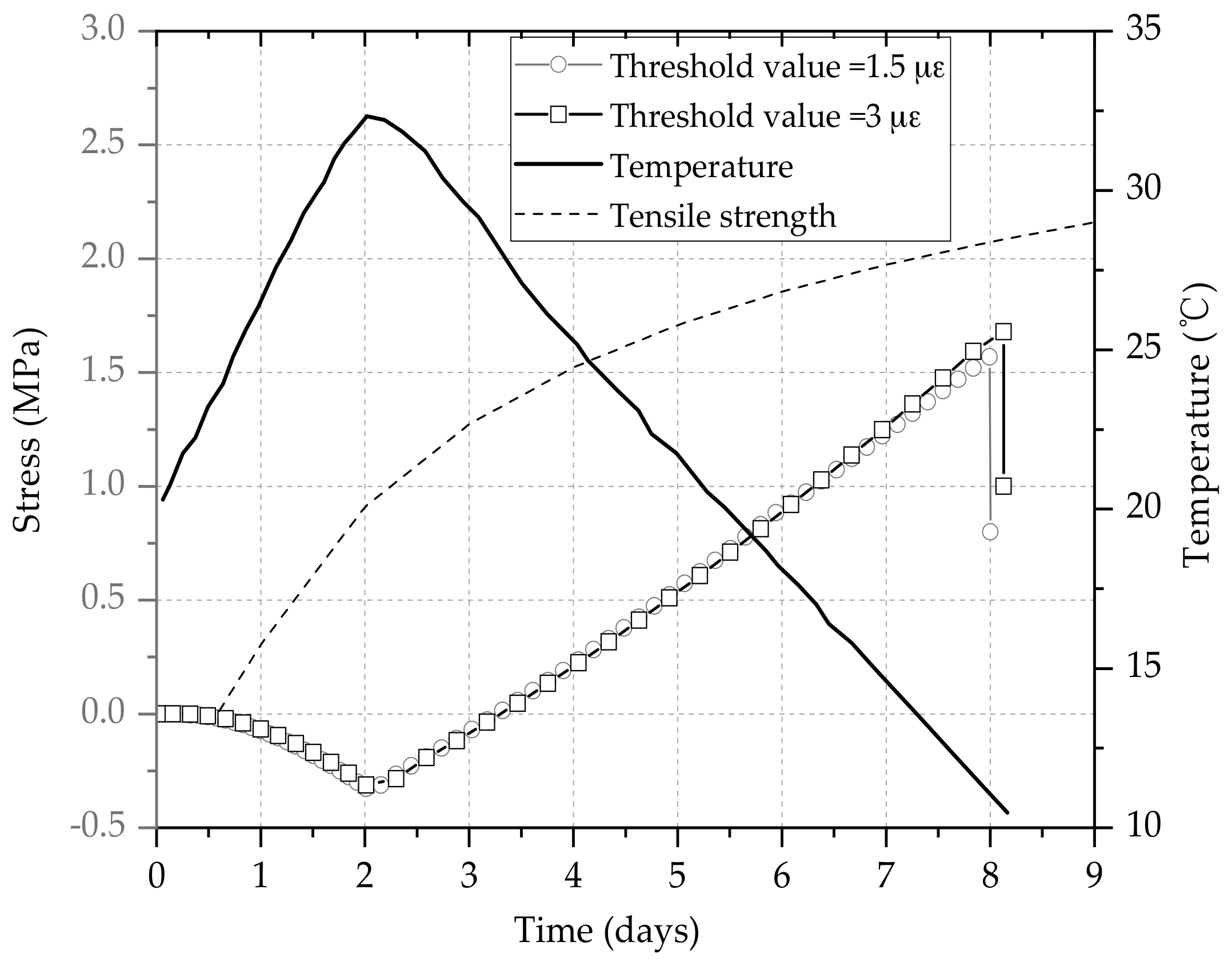
3.1. Thermal Stress Development under Different Threshold Values
3.2. Evaluation of Crack Risk Coefficient
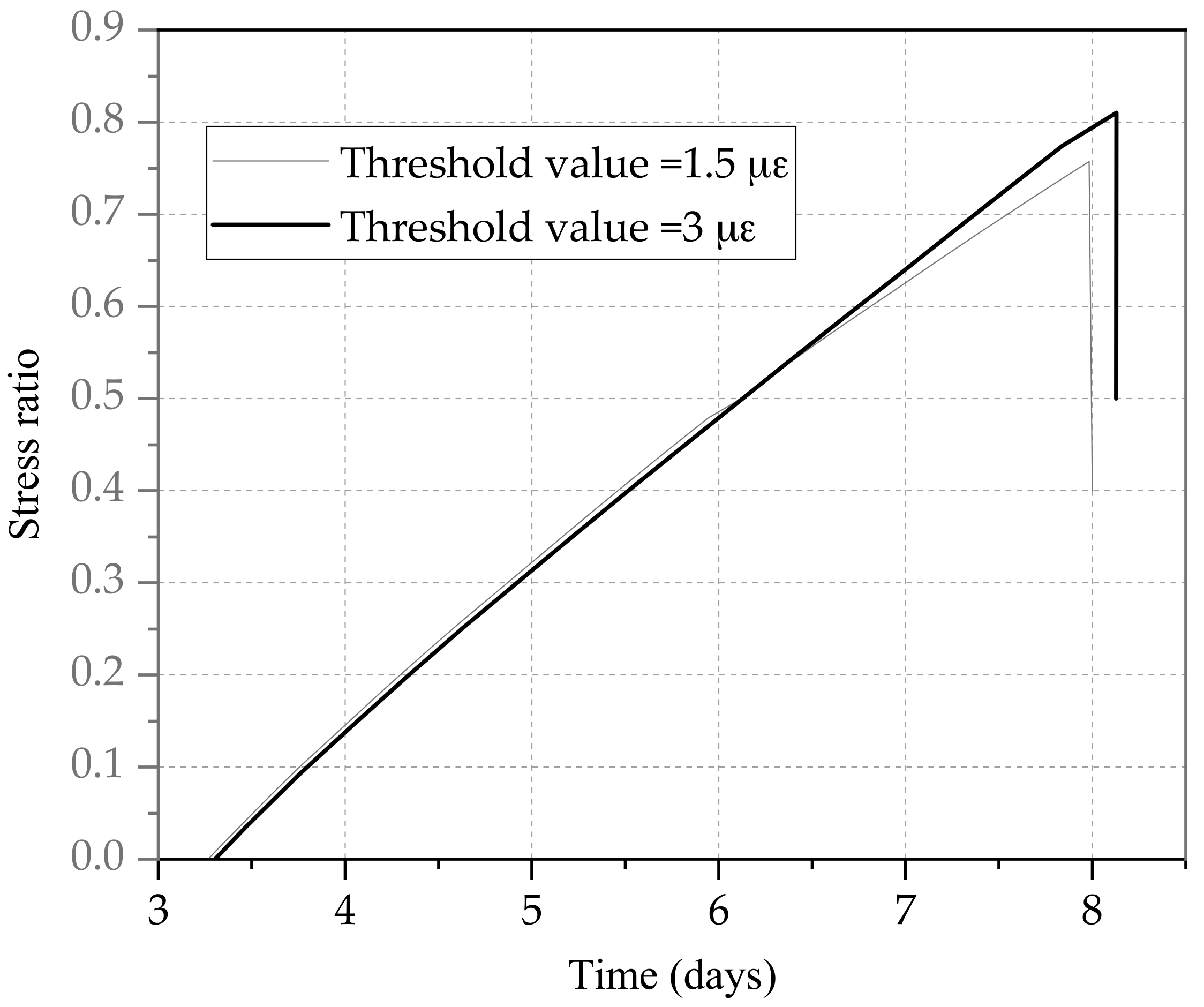
3.3. Effect of Threshold Value on the Whole Stress History
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Samouh, H.; Rozière, E.; Wisniewski, V.; Loukili, A. Consequences of longer sealed curing on drying shrinkage, cracking and carbonation of concrete. Cem. Concr. Res. 2017, 95, 117–131. [Google Scholar] [CrossRef]
- Klemczak, B.; Batog, M.; Pilch, M.; Żmij, A. Analysis of cracking risk in early age mass concrete with different aggregate types. Procedia Eng. 2017, 193, 234–241. [Google Scholar] [CrossRef]
- Li, Q.; Liang, G.; Hu, Y.; Zuo, Z. Numerical analysis on temperature rise of a concrete arch dam after sealing based on measured data. Math. Probl. Eng. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Larson, M. Thermal Crack Estimation in Early Age Concrete: Models and Methods for Practical Application. Ph.D. Thesis, Lulea University of Technology, Luleå, Sweden, 2003. [Google Scholar]
- Mangold, M. Prevention of Thermal Cracking in Concrete at Early Ages. In Methods for Experimental Determination of Thermal Stresses and Crack Sensitivity in the Laboratory; Springenschmid, R., Ed.; RILEM Report 15; CRC Press: London, UK, 1998; pp. 26–39. [Google Scholar]
- Springenschmid, R.; Breitenbucher, R.; Mangold, M. Thermal Cracking in Concrete at Early Ages. In Development of the Cracking Frame and the Temperature-Stress Testing Machine; Springenschmid, R., Ed.; RILEM Proceedings 25; CRC Press: London, UK; pp. 137–144.
- Springenschmid, R.; Gierlinger, E.; Kiernozycki, W. Thermal stresses in mass concrete: A new method and the influence of different cements. In Proceedings of the 15th Congress of the International Commission on Large Dams, Quinzieme Congres des Grands Barrages, Lausanne, Switzerland, 24–28 June 1985; Quinzieme Congres des Grands Barrages: Lausanne, Switzerland, 1985; pp. 57–72. [Google Scholar]
- Zhu, H.; Li, Q.; Hu, Y. Self-developed testing system for determining the temperature behavior of concrete. Materials 2017, 10, 419. [Google Scholar] [CrossRef] [PubMed]
- Rilem TC 119-TCE. Recommendations of TC 119-TCE: Avoidance of thermal cracking in concrete at early ages. Mater. Struct. 1997, 30, 451–464. [Google Scholar]
- Breitenbücher, R. Investigation of thermal cracking with the cracking-frame. Mater. Struct. 1990, 23, 172–177. [Google Scholar] [CrossRef]
- Samouh, H.; Rozière, E.; Loukili, A. The differential drying shrinkage effect on the concrete surface damage: Experimental and numerical study. Cem. Concr. Res. 2017, 102, 212–224. [Google Scholar] [CrossRef]
- Wang, X.F.; Huang, Y.J.; Wu, G.Y.; Fang, C.; Li, D.W.; Han, N.X.; Xing, F. Effect of nano-sio2 on strength, shrinkage and cracking sensitivity of lightweight aggregate concrete. Constr. Build. Mater. 2018, 175, 115–125. [Google Scholar] [CrossRef]
- Chen, B.; Cai, Y.B.; Ding, J.T.; Jian, Y. Crack resistance evaluating of HSC based on thermal stress testing. Adv. Mater. Res. 2011, 168–170, 716–720. [Google Scholar] [CrossRef]
- Kovler, K.; Bentur, A. Cracking sensitivity of normal and high strength concretes. ACI Mater. J. 2009, 106, 537–542. [Google Scholar]
- Lenormand, T.; Rozière, E.; Loukili, A.; Staquet, S. Incorporation of treated municipal solid waste incineration electrostatic precipitator fly ash as partial replacement of portland cement: Effect on early age behaviour and mechanical properties. Constr. Build. Mater. 2015, 96, 256–269. [Google Scholar] [CrossRef]
- Riding, K.A.; Poole, J.L.; Schindler, A.K.; Juenger, M.C.G.; Folliard, K.J. Quantification of effects of fly ash type on concrete early-age cracking. ACI Mater. J. 2008, 105, 149–155. [Google Scholar]
- Altoubat, S.A. Early Age Stresses and Creep-Shrinkage Interaction of Restrained Concrete; University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2000. [Google Scholar]
- Kovler, K. Testing system for determining the mechanical behaviour of early age concrete under restrained and free uniaxial shrinkage. Mater. Struct. 1994, 27, 324–330. [Google Scholar] [CrossRef]
- Delsaute, B.; Boulay, C.; Staquet, S. Creep testing of concrete since setting time by means of permanent and repeated minute-long loadings. Cem. Concr. Compos. 2016, 73, 75–88. [Google Scholar] [CrossRef]
- Feng, W.; Liu, F.; Yang, F.; Li, L.; Jing, L. Experimental study on dynamic split tensile properties of rubber concrete. Constr. Build. Mater. 2018, 165, 675–687. [Google Scholar] [CrossRef]
- Liu, L.; Gao, S.; Xin, J.; Huang, D. Effect of low-stress fatigue on the off-crack-plane fracture energy in engineered cementitious composites. Adv. Civ. Eng. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Chen, B.; Sun, W.; Ding, J. Concrete crack resistance research based on temperature stress test—A short review. J. Chin. Ceram. Soc. 2013, 41, 1124–1133. [Google Scholar]
- Darquennes, A.; Staquet, S.; Delplancke-Ogletree, M.P.; Espion, B. Effect of autogenous deformation on the cracking risk of slag cement concretes. Cem. Concr. Compos. 2011, 33, 368–379. [Google Scholar] [CrossRef]
- Switek-Rey, A.; Denarié, E.; Brühwiler, E. Early age creep and relaxation of UHPFRC under low to high tensile stresses. Cem. Concr. Res. 2016, 83, 57–69. [Google Scholar] [CrossRef]
- Altoubat, S.A.; Lange, D.A. Creep, shrinkage, and cracking of restrained concrete at early age. ACI Mater. J. 2001, 98, 323–331. [Google Scholar]
- Darquennes, A.; Staquet, S.; Espion, B. Behaviour of slag cement concrete under restraint conditions. Eur. J. Environ. Civ. Eng. 2011, 15, 787–798. [Google Scholar] [CrossRef]
- Hedlund, H. Hardening Concrete–Measurements and Evaluation of Non-Elastic Deformation and Associated Restraint Stresses. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2000. [Google Scholar]
- Igarashi, S.I.; Bentur, A.; Kovler, K. Autogenous shrinkage and induced restraining stresses in high-strength concretes. Cem. Concr. Res. 2000, 30, 1701–1707. [Google Scholar] [CrossRef]
- Zhang, T.; Qin, W. Studies on cracking sensitivity and restraint stress of concrete at early ages. Concrete 2014, 5, 44–48. [Google Scholar]
- Knoppik-Wróbel, A.; Klemczak, B. Degree of restraint concept in analysis of early-age stresses in concrete walls. Eng. Struct. 2015, 102, 369–386. [Google Scholar] [CrossRef]
- Zhang, T.; Qin, W. Tensile creep due to restraining stresses in high-strength concrete at early ages. Cem. Concr. Res. 2006, 36, 584–591. [Google Scholar]
- Rys, D.; Judycki, J.; Pszczola, M.; Jaczewski, M.; Mejlun, L. Comparison of low-temperature cracks intensity on pavements with high modulus asphalt concrete and conventional asphalt concrete bases. Constr. Build. Mater. 2017, 147, 478–487. [Google Scholar] [CrossRef]
- Cortas, R.; Rozière, E.; Staquet, S.; Hamami, A.; Loukili, A.; Delplancke-Ogletree, M.P. Effect of the water saturation of aggregates on the shrinkage induced cracking risk of concrete at early age. Cem. Concr. Compos. 2014, 50, 1–9. [Google Scholar] [CrossRef]
- Khan, I.; Castel, A.; Gilbert, R.I. Tensile creep and early-age concrete cracking due to restrained shrinkage. Constr. Build. Mater. 2017, 149, 705–715. [Google Scholar] [CrossRef]
- Bloom, R.; Bentur, A. Restrained Shrinkage of High Strength Concrete. In Proceedings of the Symposium on Utilization of High Strength Concrete, Lillehammer, Norway, 20–23 June 1993; pp. 1007–1014. [Google Scholar]
- Zhu, H.; Li, Q.; Hu, Y.; Ma, R. Double feedback control method for determining early-age restrained creep of concrete using a temperature stress testing machine. Materials 2018, 11, 1079. [Google Scholar] [CrossRef] [PubMed]
- Kolver, K.; Igarashi, S.; Bentur, A. Tensile creep behavior of high strength concretes at early ages. Mater. Struct. 1999, 32, 383–387. [Google Scholar] [CrossRef]
- GB/T50081. Test Standards and Methods for Mechanical Properties of Normal Concrete; China Architecture and Building Press: Beijing, China, 2002.
- Xin, J. Study on Thermal Stress of Early-Age Reinforced Concrete. Ph.D. Thesis, Beihang University, Beijing, China, 2017. [Google Scholar]
- Zhu, B. Stress–strain relation and analysis of viscoelastic stress of mass concrete. In Thermal Stresses and Temperature Control of Mass Concrete; Tsinghua University Press: Beijing, China, 2014; pp. 105–119. [Google Scholar]
- Wang, L.; Li, X.; Xu, S.; Wang, H.; Zhang, Z. Micro-crack damage in strip of fracture process zone. Int. J. Solids Struct. 2018, 147, 29–39. [Google Scholar]
- Wang, C.; Xiao, J. Evaluation of the stress-strain behavior of confined recycled aggregate concrete under monotonic dynamic loadings. Cem. Concr. Compos. 2018, 87, 149–163. [Google Scholar] [CrossRef]
- Ren, X.; Liu, K.; Li, J.; Gao, X. Compressive behavior of stirrup-confined concrete under dynamic loading. Constr. Build. Mater. 2017, 154, 10–22. [Google Scholar] [CrossRef]
- Moazam, A.M.; Hasani, N.; Yazdani, M. Incremental dynamic analysis of small to medium spans plain concrete arch bridges. Eng. Fail. Anal. 2018, 91, 12–27. [Google Scholar] [CrossRef]
- Hattel, J.H.; Thorborg, J. A numerical model for predicting the thermomechanical conditions during hydration of early-age concrete. Appl. Math. Model. 2003, 27, 1–26. [Google Scholar] [CrossRef]
- Zhang, T. Studies on Influencing Factors of Cracking Sensitivity of Concrete at Early Ages. Ph.D. Thesis, Tsinghua University, Beijing, China, 2006. [Google Scholar]




| Cement | Water | FA | Coarse | Fine | Superplasticizer | Air Entraining Agent |
|---|---|---|---|---|---|---|
| 216 | 166 | 116 | 844 | 1118 | 1.992 | 0.053 |
| Source | Threshold (με) | W/C | W/B | Age (h) | Stress (MPa) | Direct Tensile Strength (MPa) | Stress/Strength (η2) |
|---|---|---|---|---|---|---|---|
| Hedlund [27] | 0.2 | 0.3 | 0.27 | 128.3 | 3.8 | 4.58 | 0.83 |
| 0.2 | 0.3 | 0.27 | 83.6 | 3.41 | 4.1 | 0.83 | |
| 0.2 | 0.3 | 0.27 | 75.8 | 2.36 | 3.1 | 0.76 | |
| 0.2 | 0.34 | 0.31 | 110.5 | 3.12 | 3.95 | 0.79 | |
| 0.2 | 0.34 | 0.31 | 118.5 | 3.58 | 4.42 | 0.81 | |
| 0.2 | 0.34 | 0.31 | 139.4 | 4.03 | 4.58 | 0.88 | |
| 0.2 | 0.42 | 0.4 | 97.74 | 2.32 | 2.68 | 0.865 | |
| 0.2 | 0.42 | 0.4 | 192.6 | 2.79 | 3.42 | 0.816 | |
| 0.2 | 0.42 | 0.4 | 215.8 | 2.17 | 2.66 | 0.816 | |
| 0.2 | 0.42 | 0.4 | 72.2 | 2.39 | 3.32 | 0.72 | |
| 0.2 | 0.42 | 0.4 | 102.4 | 3.05 | 3.63 | 0.84 | |
| 0.2 | 0.42 | 0.4 | 122.9 | 2.10 | 2.53 | 0.83 | |
| 0.2 | 0.42 | 0.42 | 94.42 | 2.57 | 2.74 | 0.94 | |
| 0.2 | 0.43 | 0.43 | 136.2 | 2.38 | 2.87 | 0.83 | |
| Zhang [29] | 2 | 0.41 | 0.35 | - | 2.76 | 3.42 | 0.81 |
| 2 | 0.5 | 0.35 | - | 2.38 | 2.91 | 0.82 | |
| 2 | 0.35 | 0.35 | - | 2.28 | 3.04 | 0.75 | |
| 2 | 0.3 | 0.3 | - | 3.26 | 4.26 | 0.76 | |
| 2 | 0.29 | 0.29 | - | 2.54 | 3.77 | 0.67 | |
| 2 | 0.32 | 0.29 | - | 2.5 | 3.45 | 0.72 | |
| 2 | 0.3 | 0.27 | - | 3.32 | 4.29 | 0.77 | |
| 2 | 0.38 | 0.35 | - | 2.68 | 3.84 | 0.7 | |
| Igarashi [28] | 5 | 0.25 | 0.25 | 100.4 | 2.98 | 4.44 | 0.672 |
| 5 | 0.28 | 0.25 | 100.7 | 3.1 | 5.74 | 0.54 | |
| 5 | 0.33 | 0.33 | 144.0 | 2.87 | 4.35 | 0.66 | |
| 5 | 0.37 | 0.33 | 142.0 | 1.4 | 4.83 | 0.29* | |
| Darquennes [26] | 6.7 | 0.44 | 0.44 | 79.2 | 3 | 4.0 | 0.75 |
| 6.7 | 0.44 | 0.44 | 110.4 | 3 | 4.0 | 0.75 | |
| Altoubat [25] | 10 | 0.32 | 0.4 | 69.5 | 1.76 | 2.325 | 0.757 |
| 10 | 0.4 | 0.35 | 144.7 | 2.13 | 2.649 | 0.804 | |
| 10 | 0.5 | 0.35 | 159.5 | 1.78 | 2.214 | 0.805 |
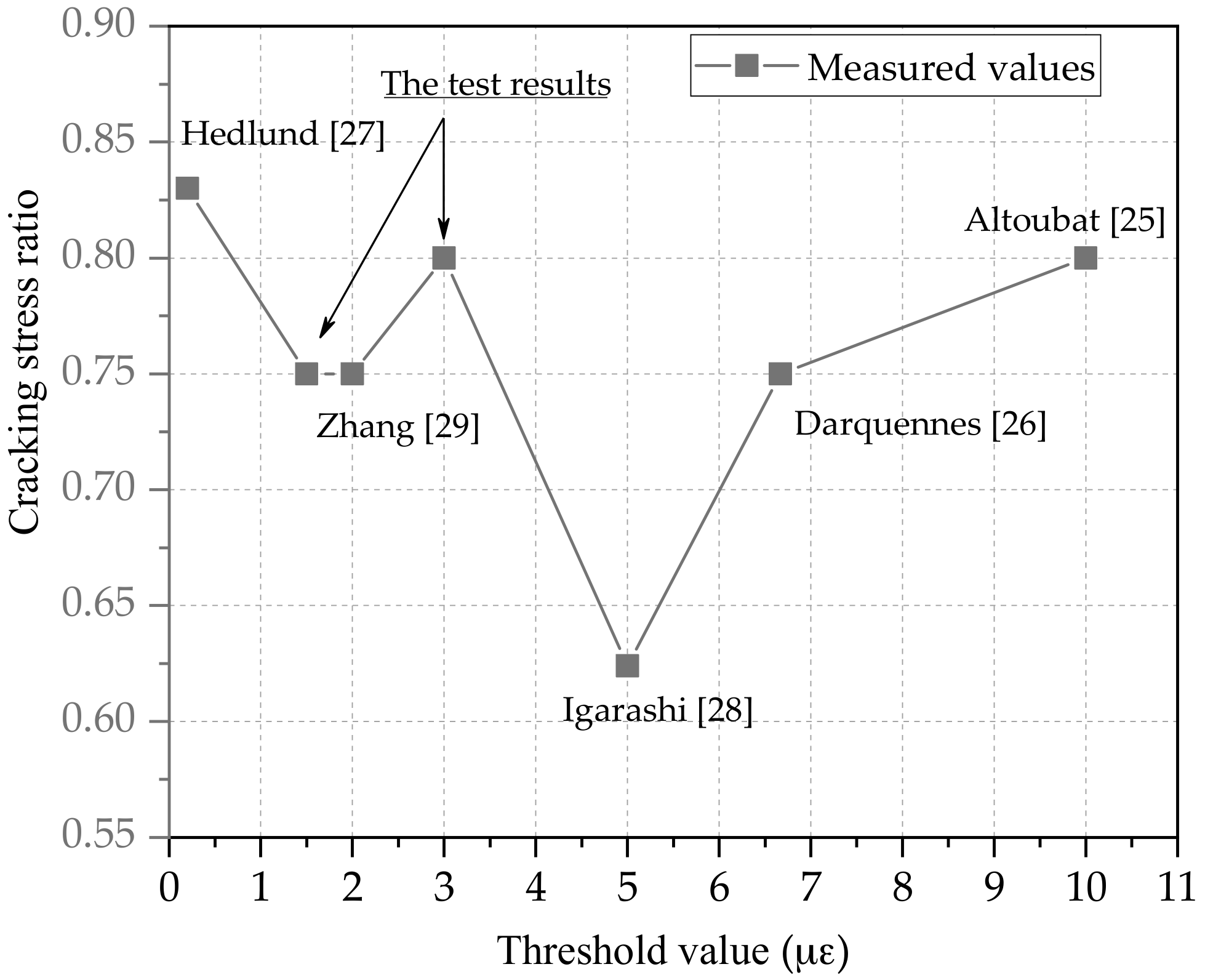
| Design Parameters | Hedlund [27] | Zhang [29] | Igarashi [28] | Darquennes [26] | Altoubat [25] |
|---|---|---|---|---|---|
| Threshold value (με) | 0.2 | 2 | 5 | 6.67 | 10 |
| Section size (mm × mm) | 150 × 150 | 100 × 100 | 40 × 40 | 100 × 100 | 76.2 × 76.2 |
| Specimen length (mm) | 1000 | 1000 | 1000 | 1000 | 1000 |
| Measured distance (mm) | 1000 | 1000 | 1000 | 750 | 1000 |
| Average of stress ratio () | 0.83 | 0.75 | 0.624 | 0.75 | 0.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Ouyang, J.; Li, F.; Xin, J.; Huang, D.; Gao, S. Research on the Crack Risk of Early-Age Concrete under the Temperature Stress Test Machine. Materials 2018, 11, 1822. https://doi.org/10.3390/ma11101822
Liu L, Ouyang J, Li F, Xin J, Huang D, Gao S. Research on the Crack Risk of Early-Age Concrete under the Temperature Stress Test Machine. Materials. 2018; 11(10):1822. https://doi.org/10.3390/ma11101822
Chicago/Turabian StyleLiu, Longlong, Jianshu Ouyang, Feilong Li, Jianda Xin, Dahai Huang, and Shuling Gao. 2018. "Research on the Crack Risk of Early-Age Concrete under the Temperature Stress Test Machine" Materials 11, no. 10: 1822. https://doi.org/10.3390/ma11101822
APA StyleLiu, L., Ouyang, J., Li, F., Xin, J., Huang, D., & Gao, S. (2018). Research on the Crack Risk of Early-Age Concrete under the Temperature Stress Test Machine. Materials, 11(10), 1822. https://doi.org/10.3390/ma11101822





