FEM Modeling of the Relationship between the High-Temperature Hardness and High-Temperature, Quasi-Static Compression Experiment
Abstract
1. Introduction
2. Experiments
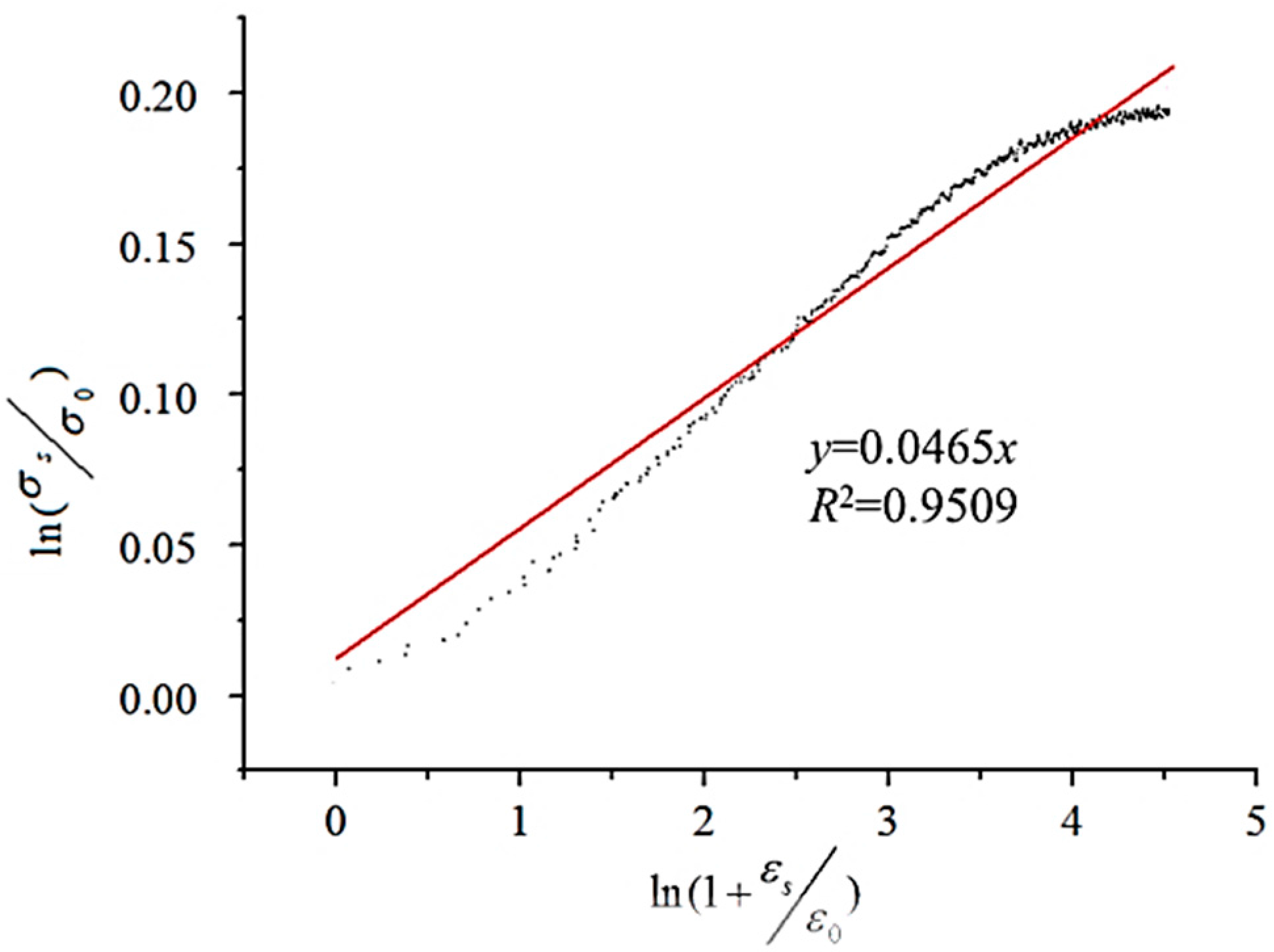
2.1. High-Temperature, Quasi-Static Compression Experiments
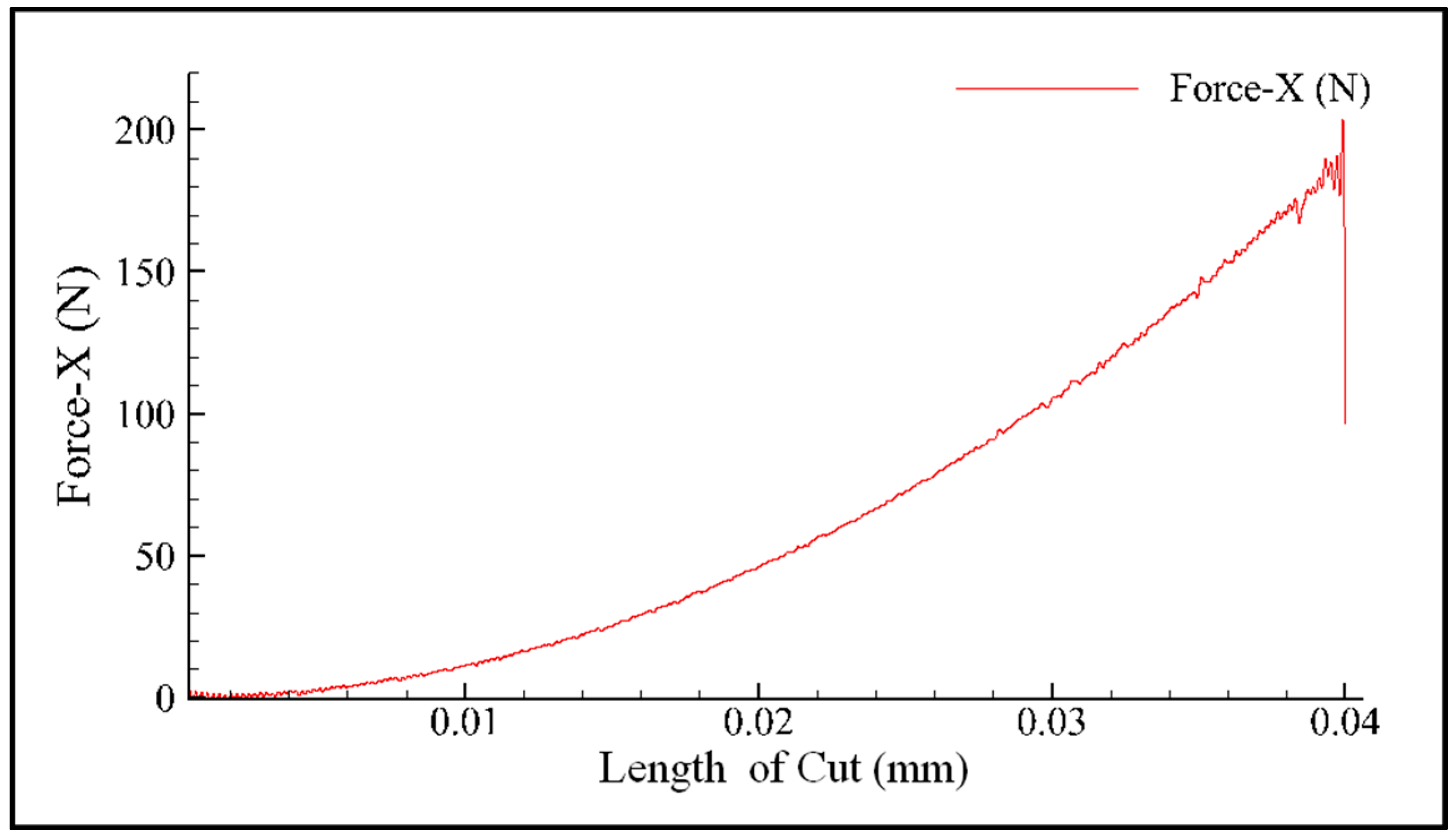
2.2. High-Temperature Hardness Experiments
3. The Development of the FE Simulation Model
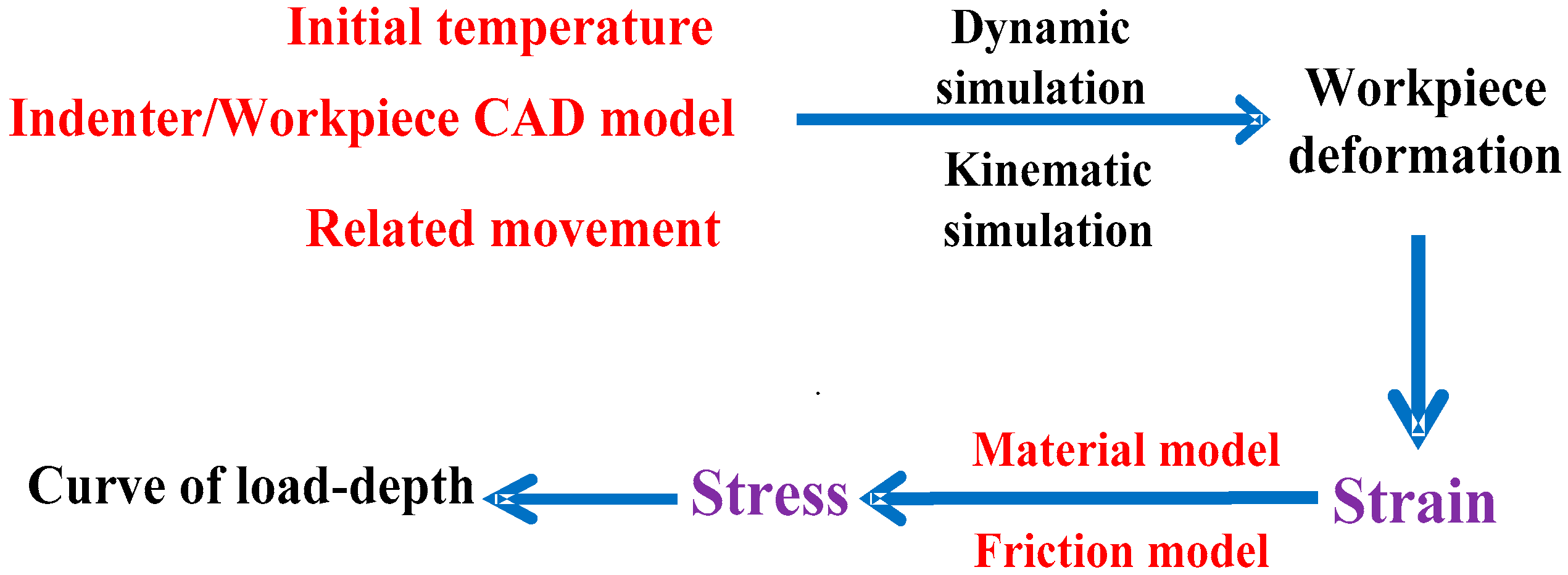
3.1. The Procedure of FE Simulation
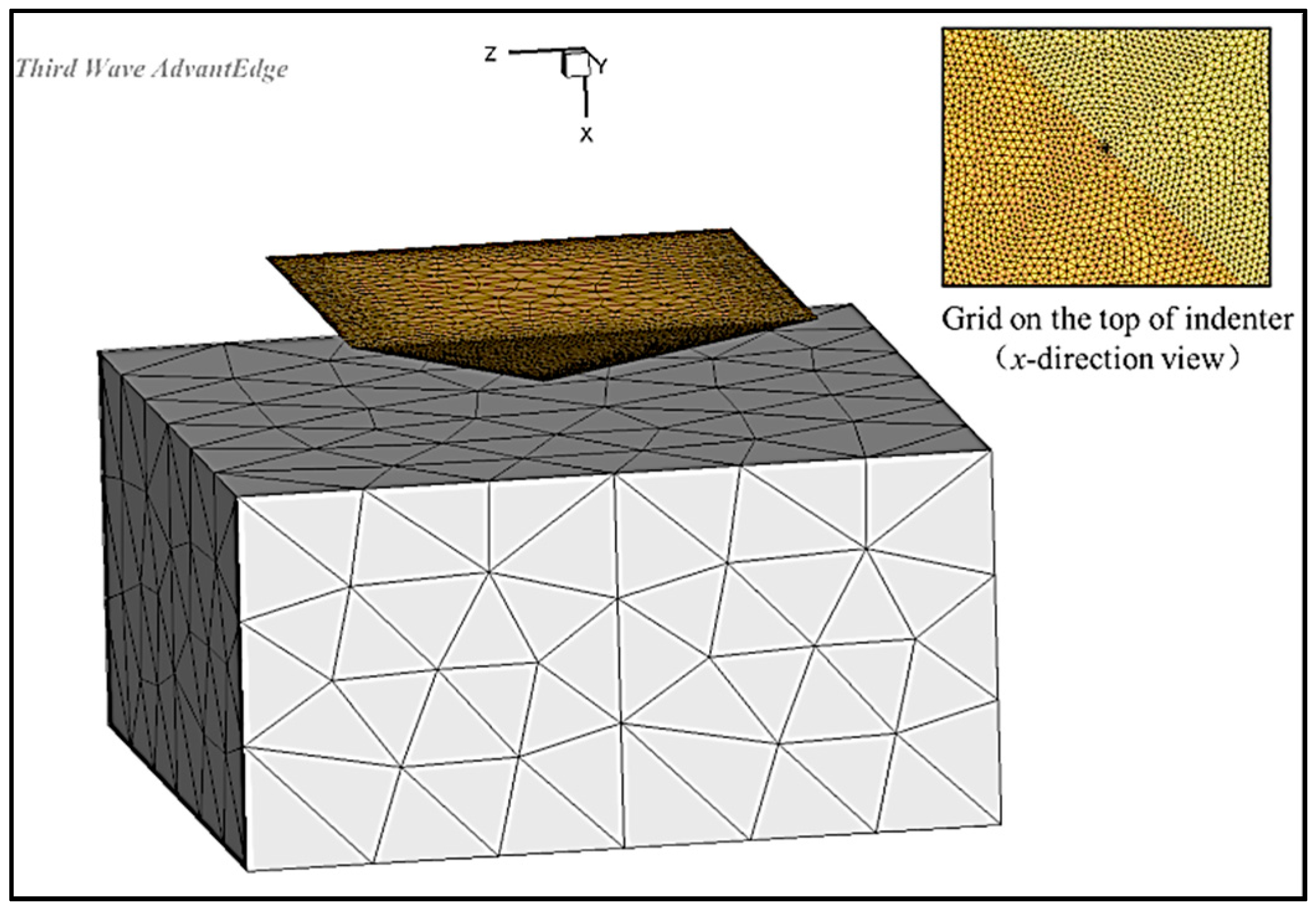
3.2. The Geometrical Model
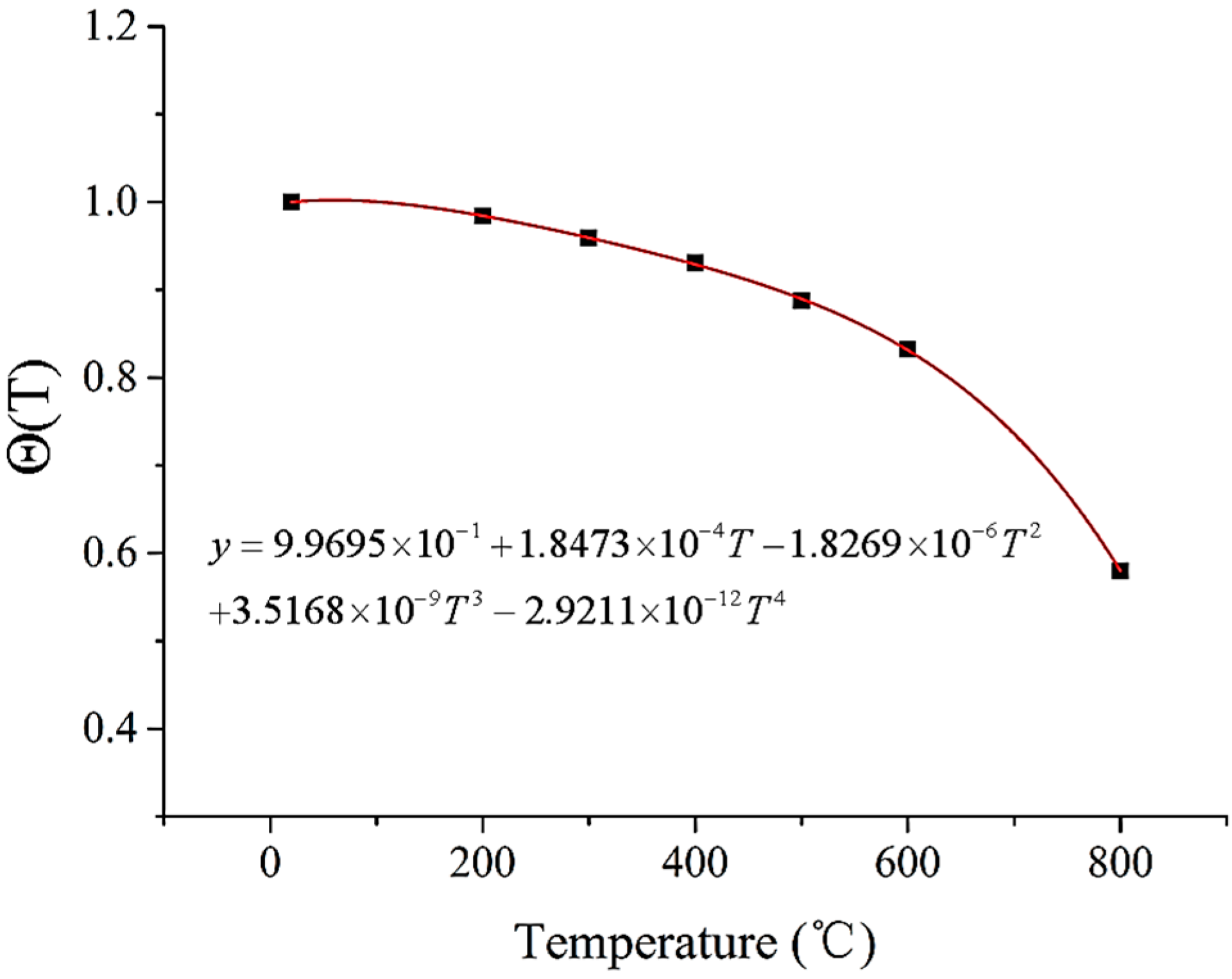
3.3. The Material Model
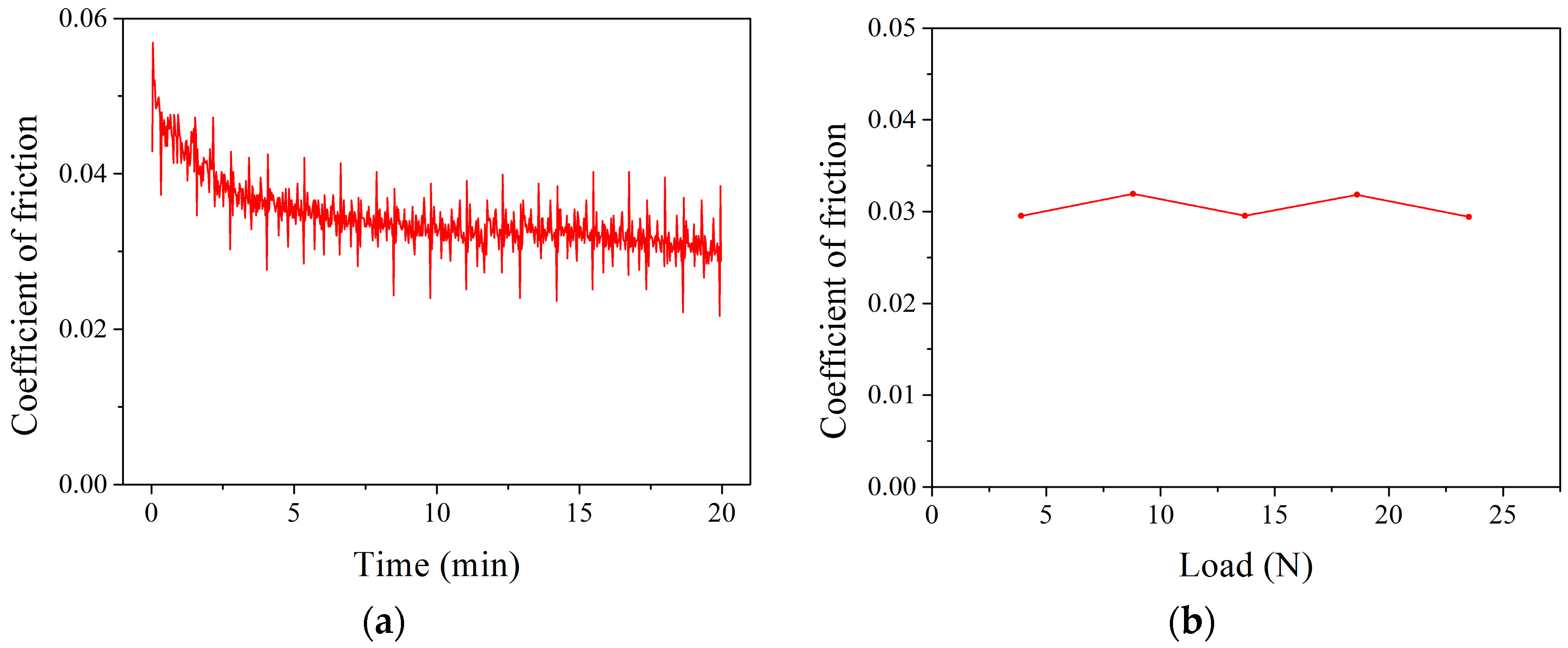
3.4. The Friction Model
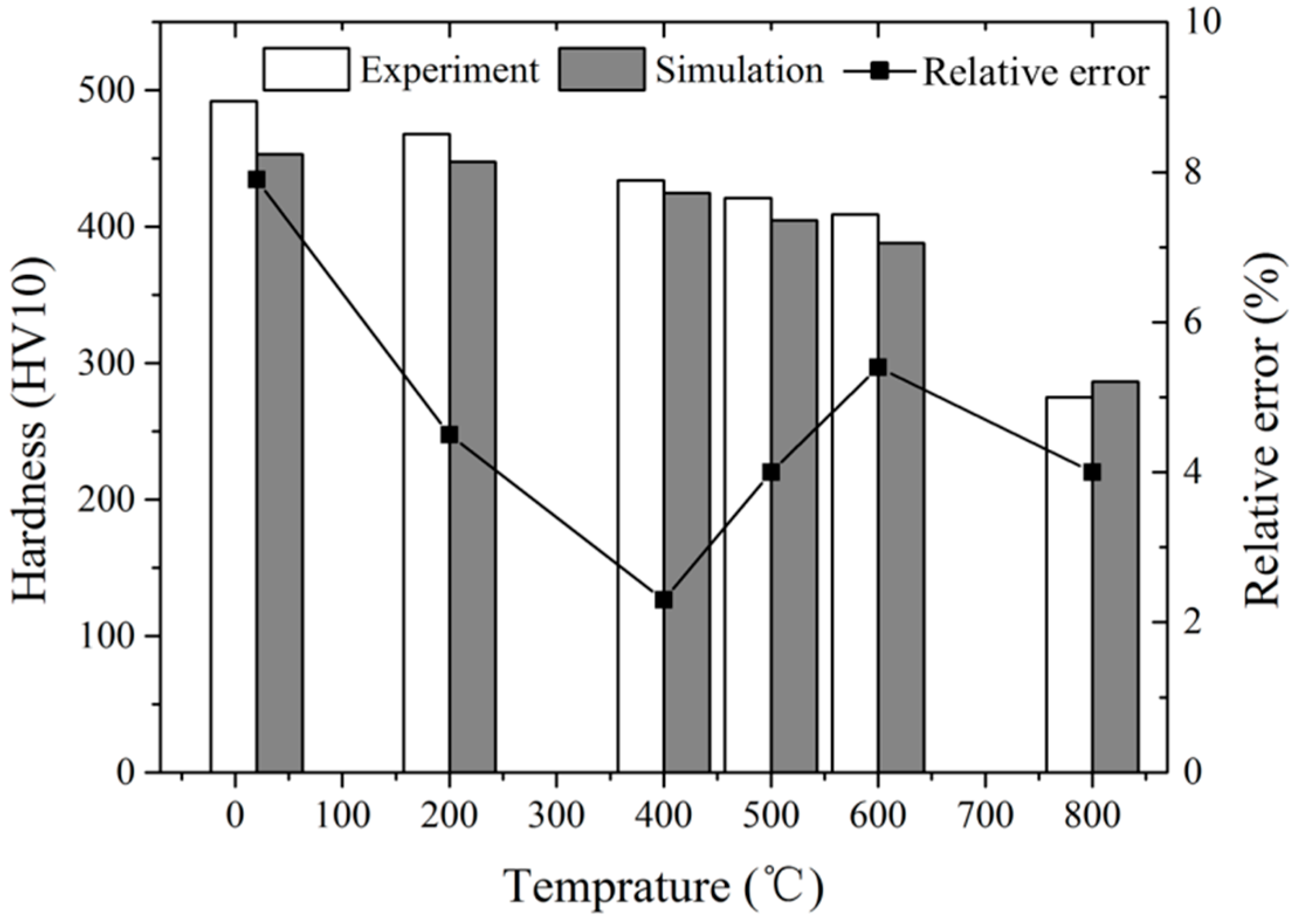
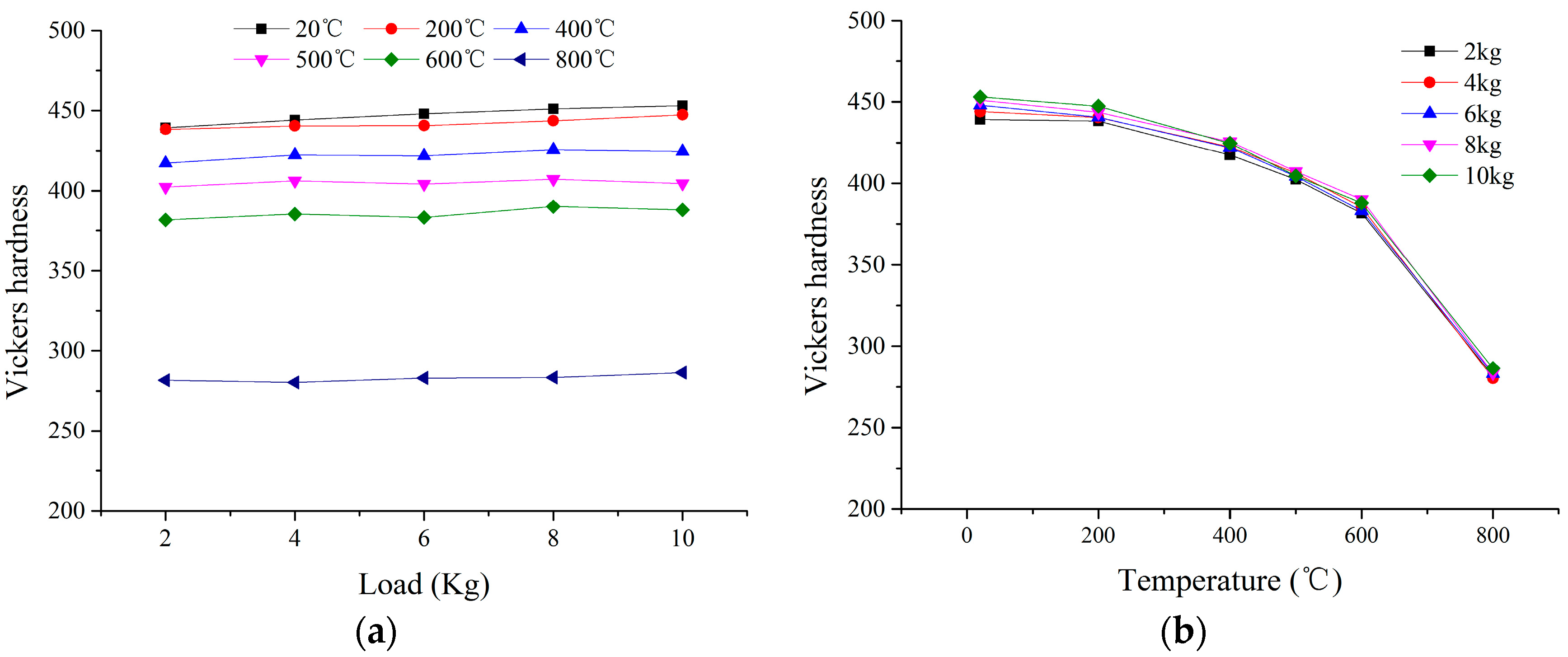
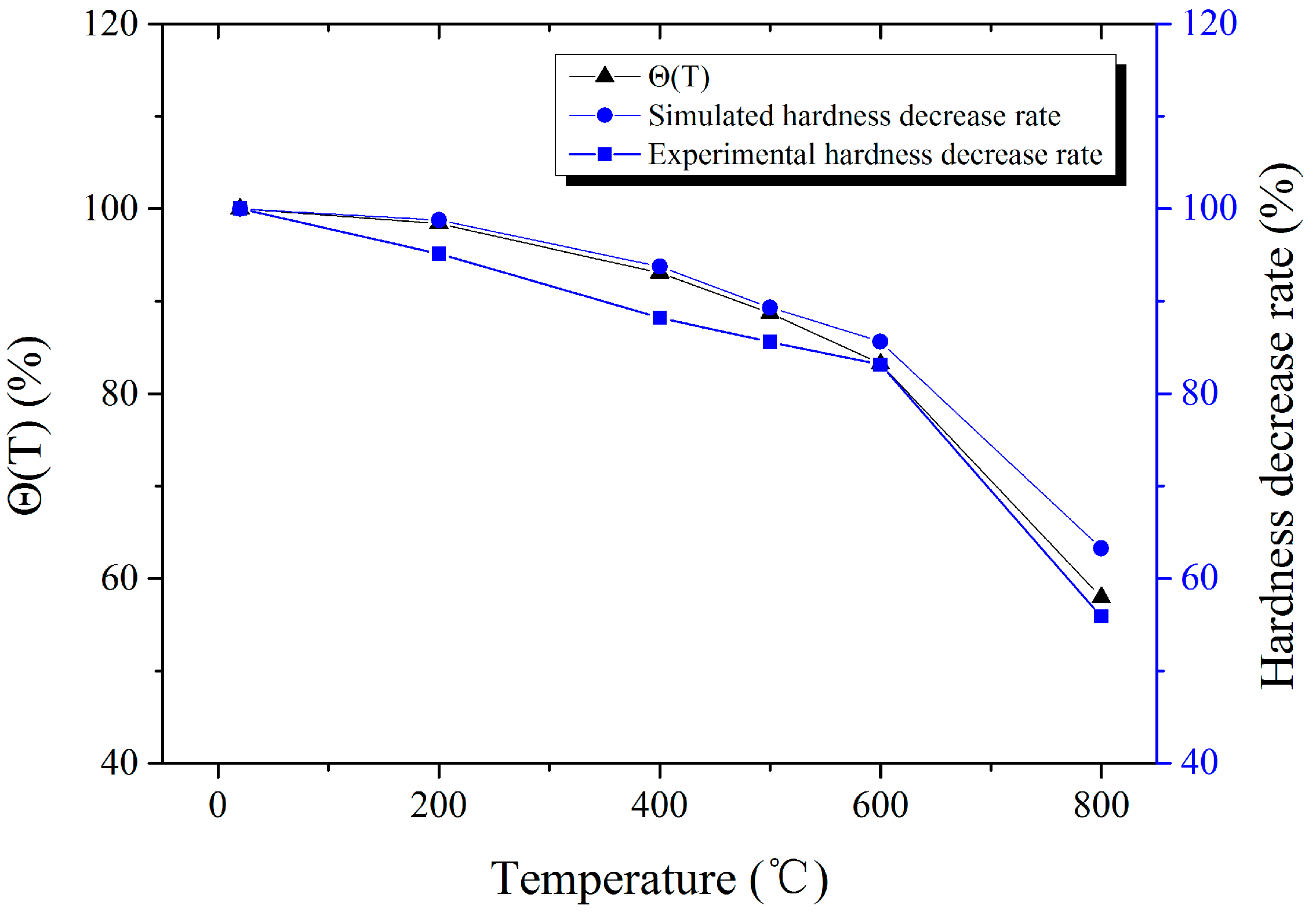
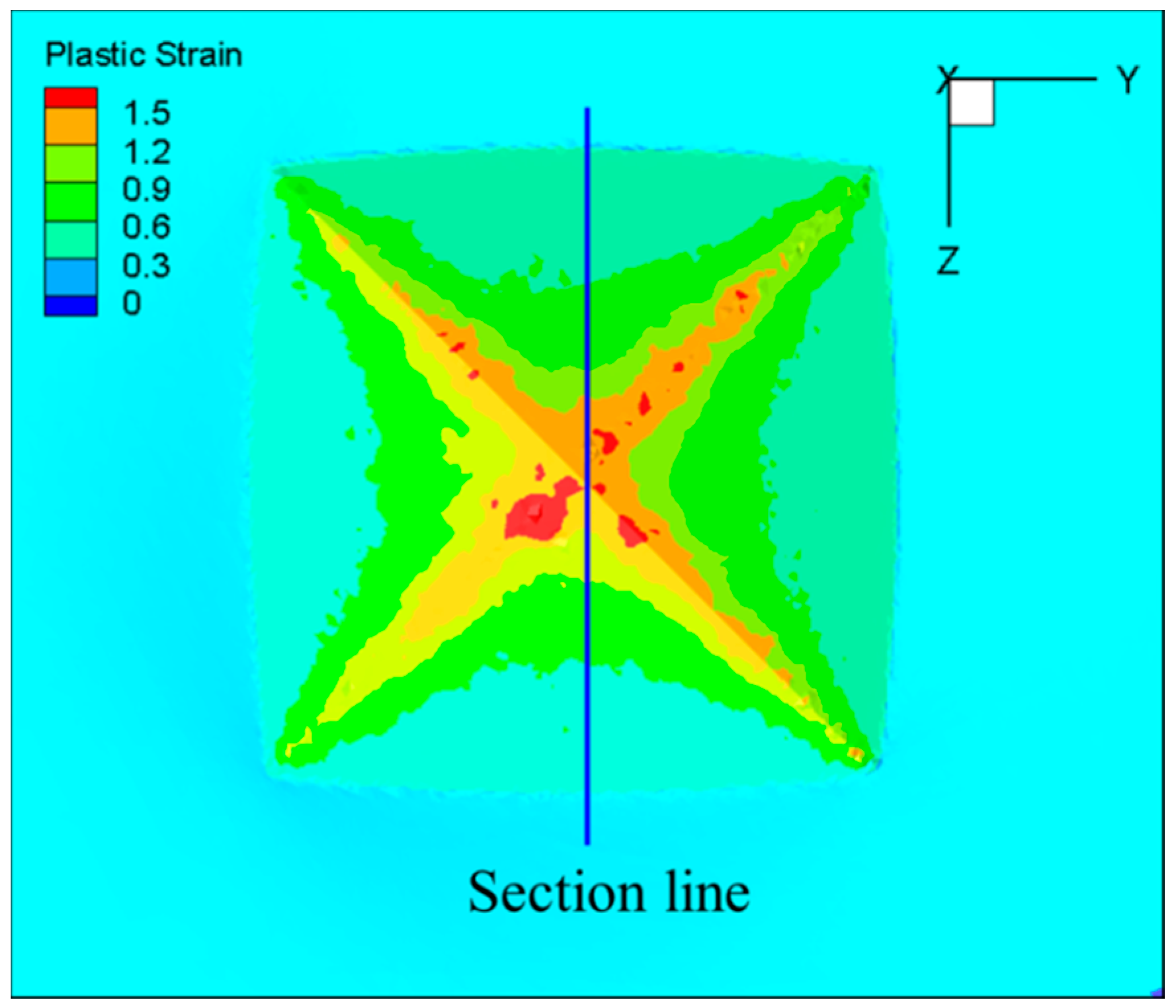
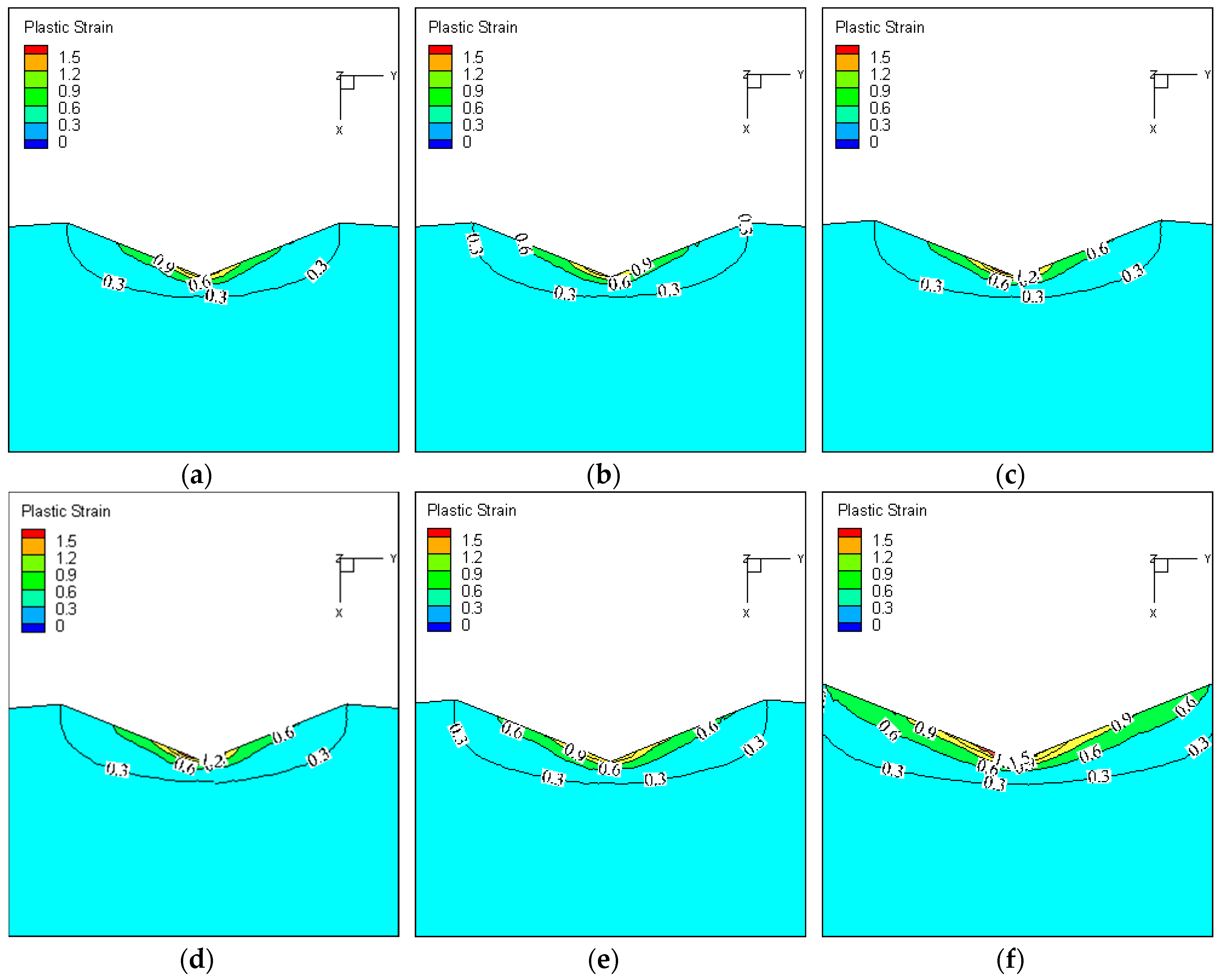
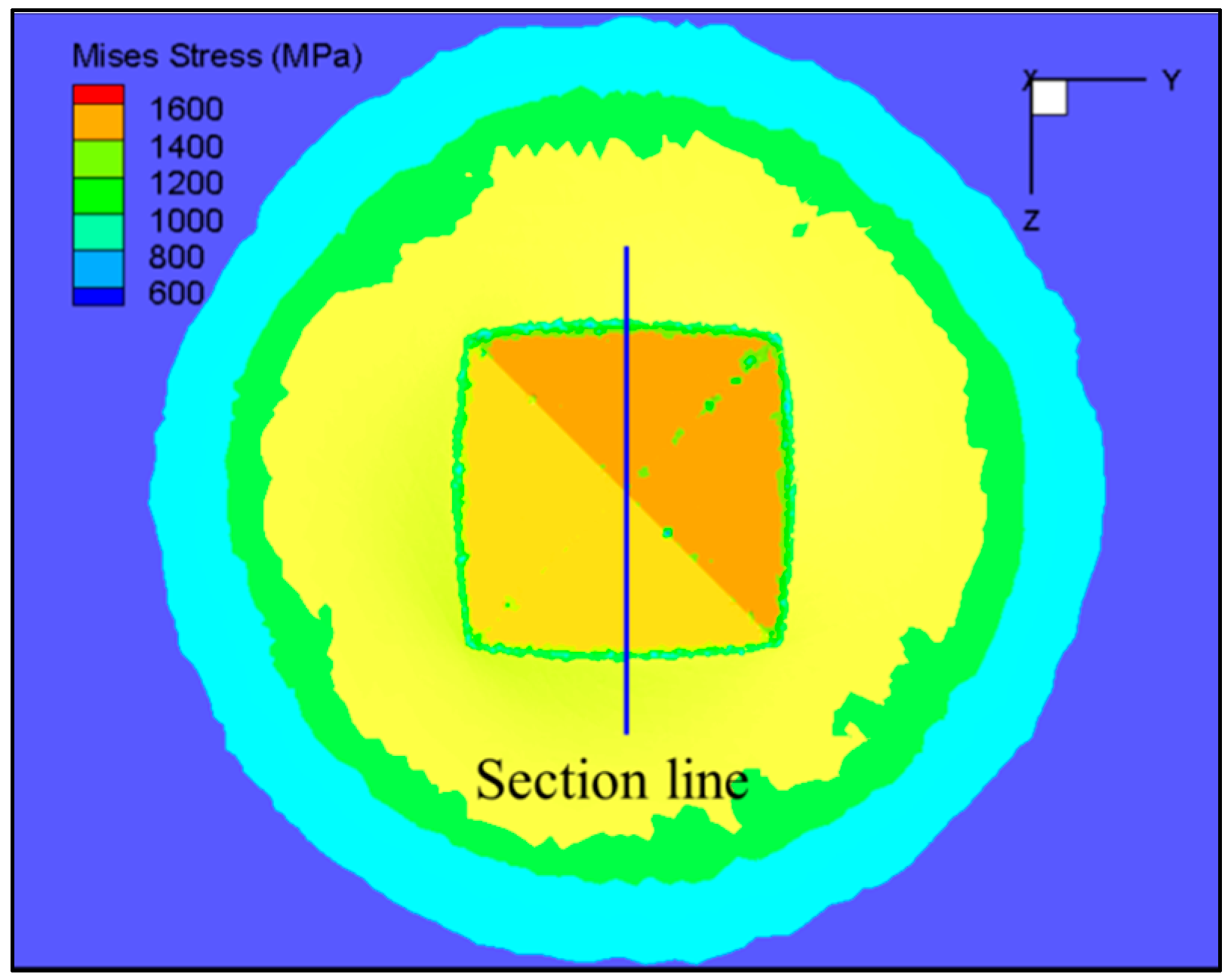
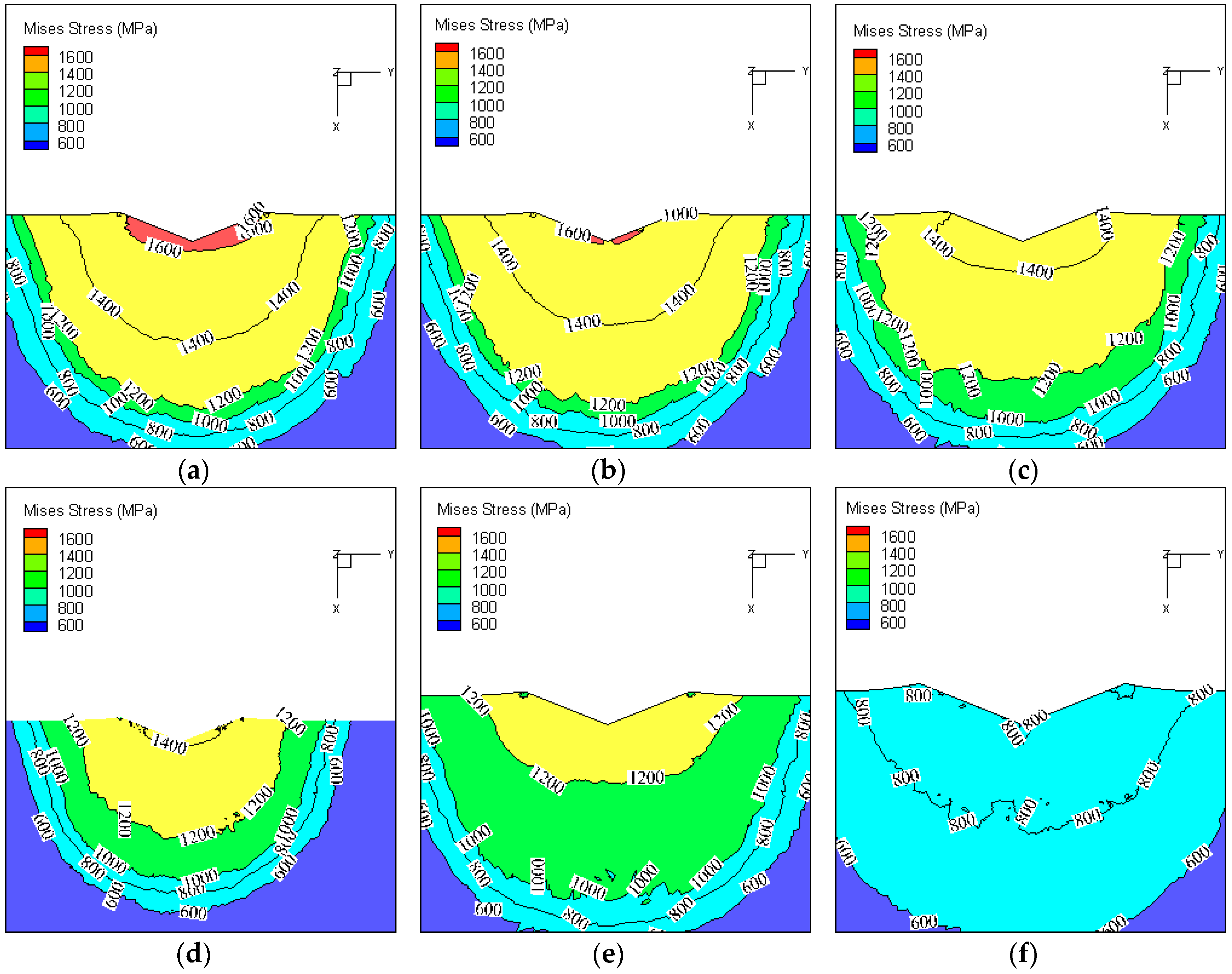
4. Results and Discussion
5. Conclusions
- An FEM model of the relationship between high-temperature hardness and high-temperature, quasi-static compression experiment was developed.
- The simulated and experimental results of high temperature hardness were compared, which verified the accuracy of the high-temperature indentation FE simulation.
- The high-temperature hardness basically does not change with the change of load when the pile-up is ignored, and the hardness decrease rate and thermal softening are consistent.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Park, C.; Lee, J.; Kang, S.; Kim, Y.; Woo, K.; Jeon, S.; Kwon, D. Evaluation of high-temperature Vickers hardness using instrumented indentation system. Mater. Sci. Eng. A 2016, 650, 15–19. [Google Scholar] [CrossRef]
- Yonenaga, I.; Hoshi, T.; Usui, A. High-temperature hardness of bulk single-crystal gallium nitride—In comparison with other wide-gap materials. J. Phys. Condens. Matter 2000, 12, 10319. [Google Scholar] [CrossRef]
- Manakari, V.; Parande, G.; Doddamani, M.; Gupta, M. Enhancing the ignition, hardness and compressive response of magnesium by reinforcing with hollow glass microballoons. Materials 2017, 10, 997. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Y.; Zhang, X.; Hu, J.; Guo, Q.; Du, Y. Evolution of the microstructure and hardness of the Ti–Si alloys during high temperature heat-treatment. J. Alloys Compd. 2009, 479, 246–251. [Google Scholar] [CrossRef]
- Yonenaga, I. Thermo-mechanical stability of wide-bandgapsemiconductors: High temperature hardness of SiC, AlN, GaN, ZnO and ZnSe. Phys. B 2001, 308–310, 1150–1152. [Google Scholar] [CrossRef]
- Dascăl, A.A. Experimental studies to assess stainless steel high temperature hardness. Rev. Fac. Ing. Univ. Antioq. 2006, 38, 119–127. [Google Scholar]
- Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. Hardness of materials at high temperature and high pressure. Philos. Mag. 2009, 89, 2117–2127. [Google Scholar] [CrossRef]
- Torres, H.; Varga, M.; Ripoll, M.R. High temperature hardness of steels and iron-based alloys. Mater. Sci. Eng. A 2016, 671, 170–181. [Google Scholar] [CrossRef]
- Liu, R.; Wu, X.J.; Kapoor, S.; Yao, M.X.; Collier, R. Effects of temperature on the hardness and wear resistance of High-Tungsten stellite alloys. Metall. Mater. Trans. A 2015, 46, 587–599. [Google Scholar] [CrossRef]
- Angella, G.; Barbieri, G.; Donnini, R.; Montanari, R.; Richetta, M. Electron beam welding of IN792 DS: Effects of pass speed and PWHT on microstructure and hardness. Materials 2017, 10, 1033. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Malzbender, J.; Gross, S.M. The effect of room temperature and high temperature exposure on the elastic modulus, hardness and fracture toughness of glass ceramic sealants for solid oxide fuel cells. J. Eur. Ceram. Soc. 2011, 31, 541–548. [Google Scholar] [CrossRef]
- Chen, P.; Yang, F.; Lee, S. Effect of gamma irradiation on high temperature hardness of low-density polyethylene. Philos. Mag. 2015, 95, 3486–3496. [Google Scholar] [CrossRef]
- Otani, S.; Korsukova, M.M.; Aizawa, T. High-temperature hardness of ReB2 single crystals. J. Alloys Compd. 2009, 477, L28–L29. [Google Scholar] [CrossRef]
- Feng, K.; Chen, Y.; Deng, P.; Li, Y.; Zhao, H.; Lu, F.; Li, R.; Huang, J.; Li, Z. Improved high-temperature hardness and wear resistance of Inconel 625 coatings fabricated by laser cladding. J. Mater. Process. Technol. 2017, 243, 82–91. [Google Scholar] [CrossRef]
- Yun, E.; Lee, K.; Lee, S. Improvement of high-temperature hardness of (TiC, TiB)/Ti–6Al–4V surface composites fabricated by high-energy electron-beam irradiation. Surf. Coat. Technol. 2004, 184, 74–83. [Google Scholar] [CrossRef]
- Mahmudi, R.; Alibabaie, S. Elevated-temperature shear strength and hardness of Zn–3Cu–xAl ultra-high-temperature lead-free solders. Mater. Sci. Eng. A 2013, 559, 421–426. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, T.; Feng, Y. Theoretical analysis of the relationships between hardness, elastic modulus, and the work of indentation for work-hardening materials. J. Mater. Res. 2010, 25, 2072–2077. [Google Scholar] [CrossRef]
- Canuto, C.; Tabacco, A.; Urban, K. Relationships between hardness, elastic modulus, and the work of indentation. Appl. Phys. Lett. 1998, 73, 614–616. [Google Scholar]
- Yang, R.; Zhang, T.; Jiang, P.; Bai, Y. Experimental verification and theoretical analysis of the relationships between hardness, elastic modulus, and the work of indentation. Appl. Phys. Lett. 2008, 92, 1564. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, W.; Zhou, Y. Investigation of the relationship between elastic modulus and hardness based on depth-sensing indentation measurements. Acta Mater. 2004, 52, 5397–5404. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Oxford University Press: Oxford, UK, 1951. [Google Scholar]
- Wang, W. Reverse Engineering: Technology of Reinvention; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Suwanprateeb, J. Calcium carbonate filled polyethylene: Correlation of hardness and yield stress. Compos. Part A Appl. Sci. Manuf. 2000, 31, 353–359. [Google Scholar] [CrossRef]
- Victor, P.; Catalin, P.A.; Mihai, V.I.; Ionelia, V.; Elena-Manuela, S.; Doru, P. Finite element method for simulating the Vickers hardness test. Appl. Mech. Mater. 2014, 555, 419–424. [Google Scholar]
- Bouzakis, K.D.; Michailidis, N.; Skordaris, G. Hardness determination by means of a FEM-supported simulation of nanoindentation and applications in thin hard coatings. Surf. Coat. Technol. 2005, 200, 867–871. [Google Scholar] [CrossRef]
- Skliarov, V.; Zalohin, M.; Dovzhenko, J. Application of the FEM for modeling and prediction of the relationship between the hardness and stress of the deformed body. In Proceedings of the 2017 SPIE Smart Structures and Materials and Nondestructive Evaluation and Health Monitoring, Portland, OR, USA, 25–29 March 2017. [Google Scholar]
- Choi, Y.; Park, J.H.; Kim, B.M.; Choi, J.C.; Min, B.H. Estimation of Relation between Effective Strain and Hardness by Rigid-Plastic FEM. Met. Mater. Int. 2000, 6, 111–116. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principles, 2nd ed.; Oxford Uiversity Press: Oxford, UK, 2005. [Google Scholar]
- Hamada, S.; Nakanishi, M.; Moriyama, T.; Noguchi, H. Re-Examination of correlation between hardness and tensile properties by numerical analysis. Exp. Mech. 2017, 57, 773–781. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, F.; Yan, L.; Xu, X. Research on the stress and material flow with single particle—Simulations and experiments. J. Mater. Eng. Perform. 2017, 26, 2689–2697. [Google Scholar] [CrossRef]
- Shi, H.; Atkinson, M. A friction effect in low-load hardness testing of copper and aluminium. J. Mater. Sci. 1990, 25, 2111–2114. [Google Scholar] [CrossRef]
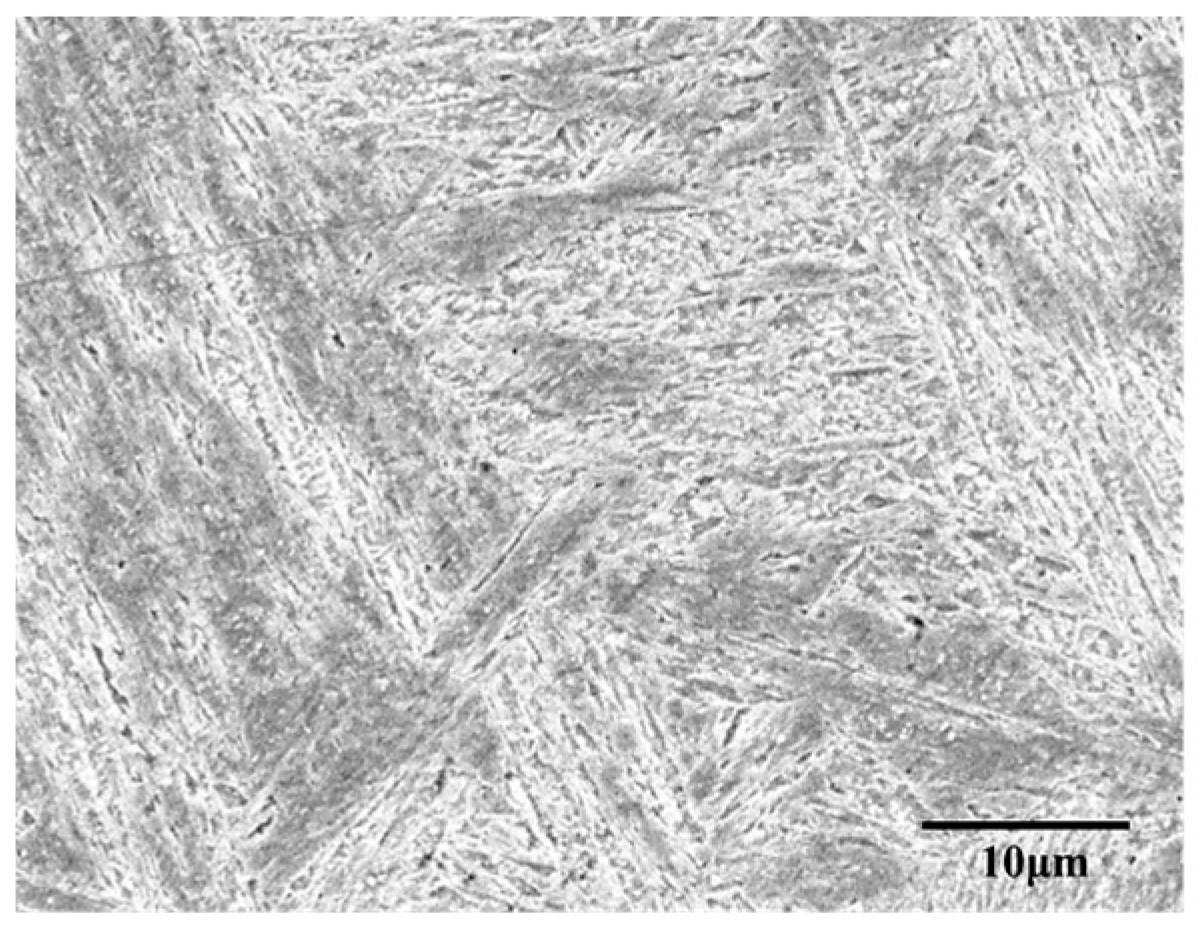
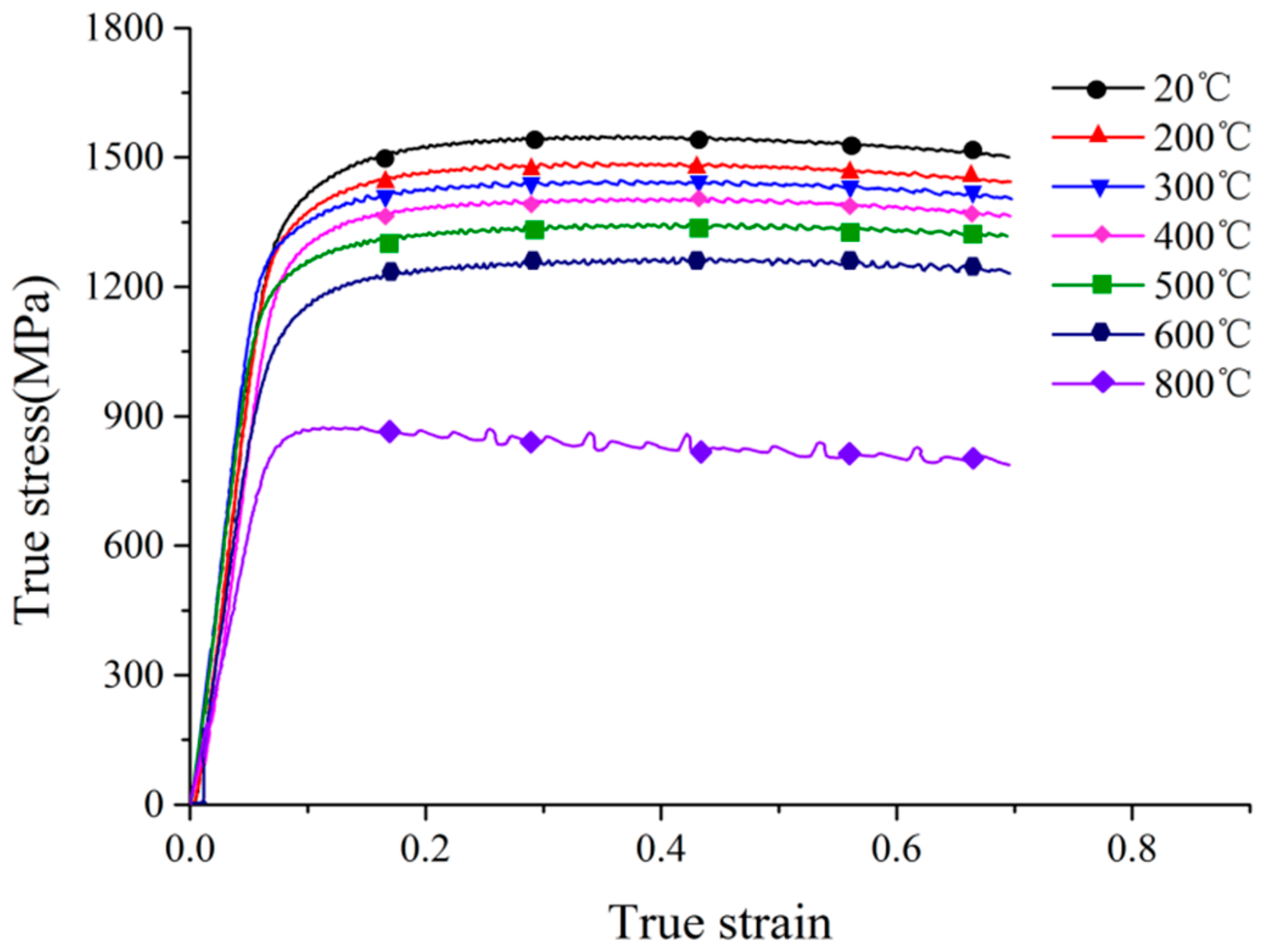



| Composition | C | Si | Mn | P | S | Ni | Cr | Mo | V | N | Nb | Fe |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Content | 0.17 | <0.07 | <0.30 | <0.01 | <0.01 | 3.5 | 11.50 | 3.00 | 0.28 | 0.07 | 0.12 | Balance |
| Items | Parameters |
|---|---|
| Sample size (mm) | Diameter: 5, Height: 5 (cylindrical specimen) |
| Compression speed (mm/min) | 0.3 |
| Insulation time (min) | 15 |
| Test temperature (°C) | 20, 200, 300, 400, 500, 600, 800 |
| Items | Parameters |
|---|---|
| Test load (kg) | 10 |
| The time to keep the temperature (min) | 15 |
| The time to keep the load (s) | 30 |
| Test temperature (°C) | 20, 200, 400, 500, 600, 800 |
| Items | Parameters |
|---|---|
| Reciprocating stroke (mm) | 6 |
| Reciprocating speed (mm/s) | 0.5 |
| Load (N) | 4.9, 9.8, 14.7,19.6, 24.5 |
| Items | Parameters |
|---|---|
| Pressing depth (μm) | 40 |
| Pressing speed (mm/s) | 0.3 |
| Initial temperature | 20, 200, 400, 500, 600, 800 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Jiang, F.; Yan, L.; Xu, X. FEM Modeling of the Relationship between the High-Temperature Hardness and High-Temperature, Quasi-Static Compression Experiment. Materials 2018, 11, 34. https://doi.org/10.3390/ma11010034
Zhang T, Jiang F, Yan L, Xu X. FEM Modeling of the Relationship between the High-Temperature Hardness and High-Temperature, Quasi-Static Compression Experiment. Materials. 2018; 11(1):34. https://doi.org/10.3390/ma11010034
Chicago/Turabian StyleZhang, Tao, Feng Jiang, Lan Yan, and Xipeng Xu. 2018. "FEM Modeling of the Relationship between the High-Temperature Hardness and High-Temperature, Quasi-Static Compression Experiment" Materials 11, no. 1: 34. https://doi.org/10.3390/ma11010034
APA StyleZhang, T., Jiang, F., Yan, L., & Xu, X. (2018). FEM Modeling of the Relationship between the High-Temperature Hardness and High-Temperature, Quasi-Static Compression Experiment. Materials, 11(1), 34. https://doi.org/10.3390/ma11010034





