Glass Polarization Induced Drift of a Closed-Loop Micro-Accelerometer
Abstract
:1. Introduction
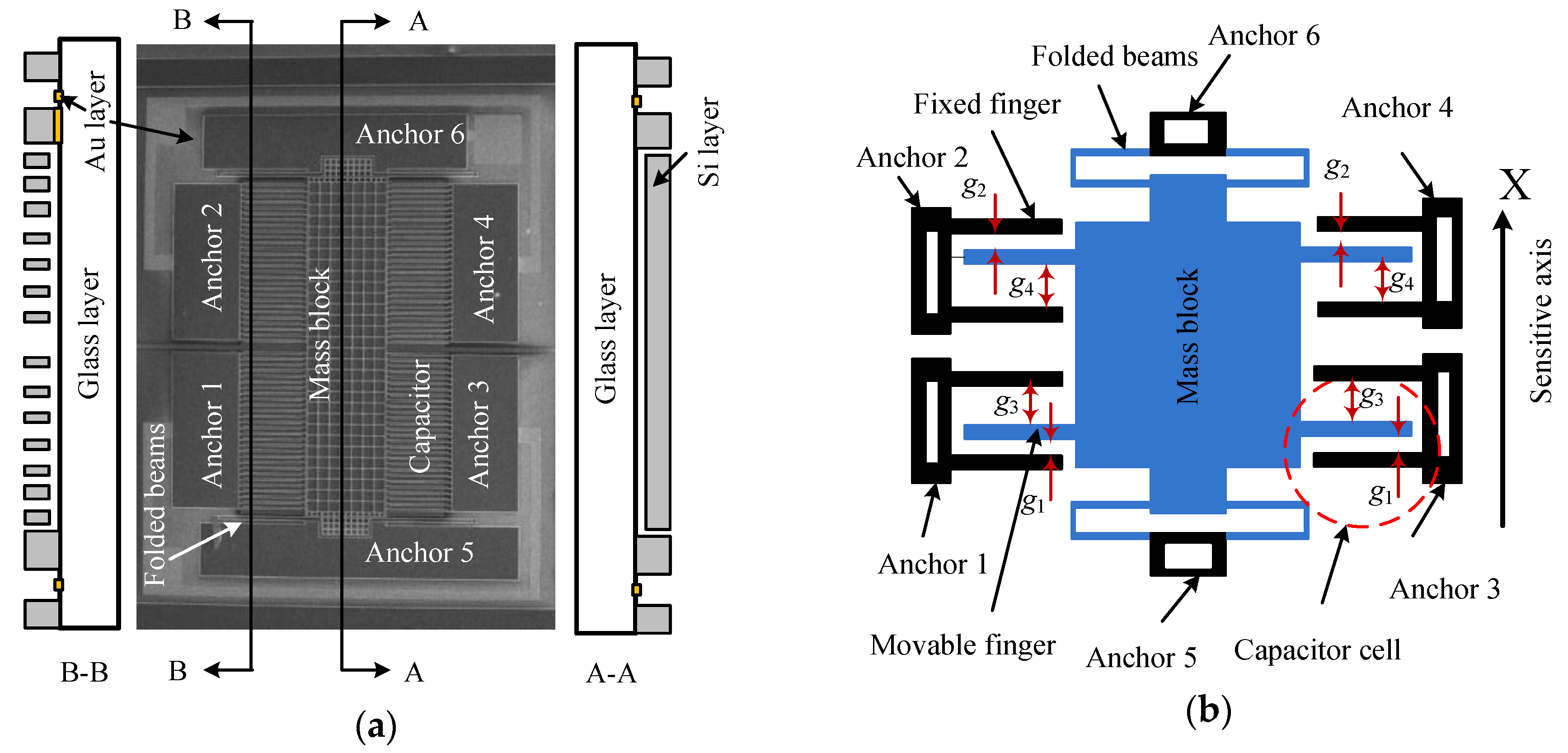
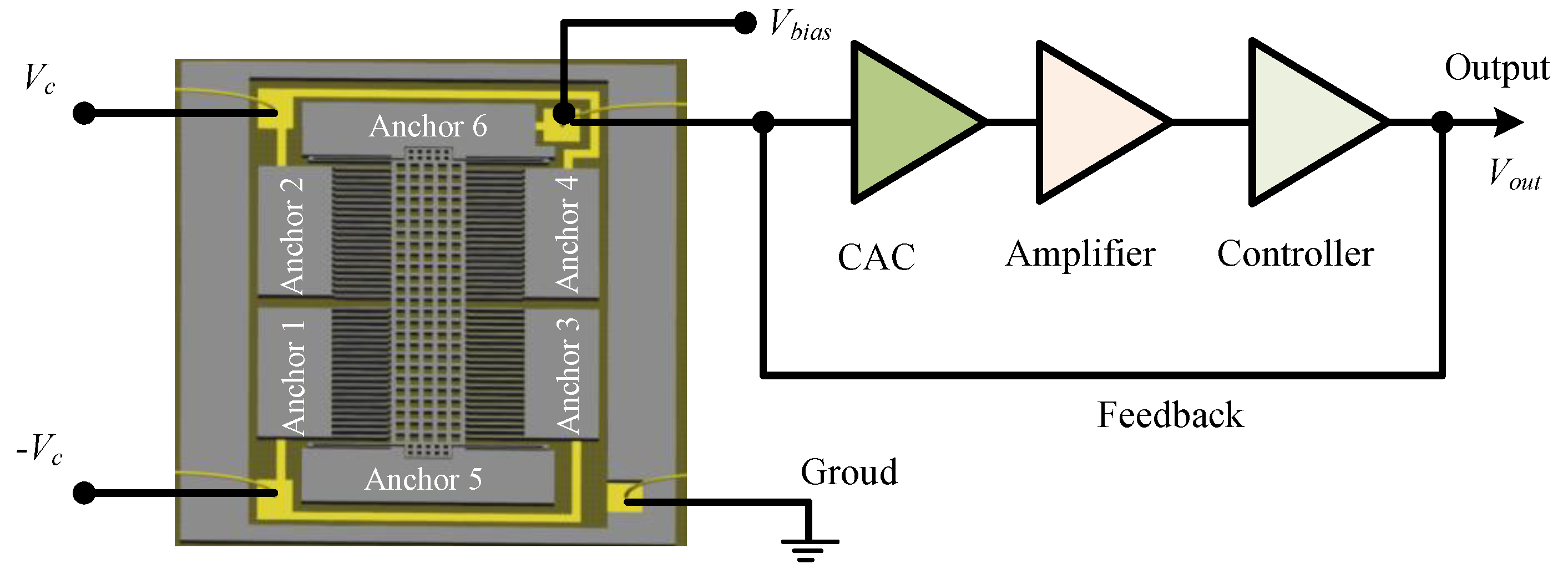
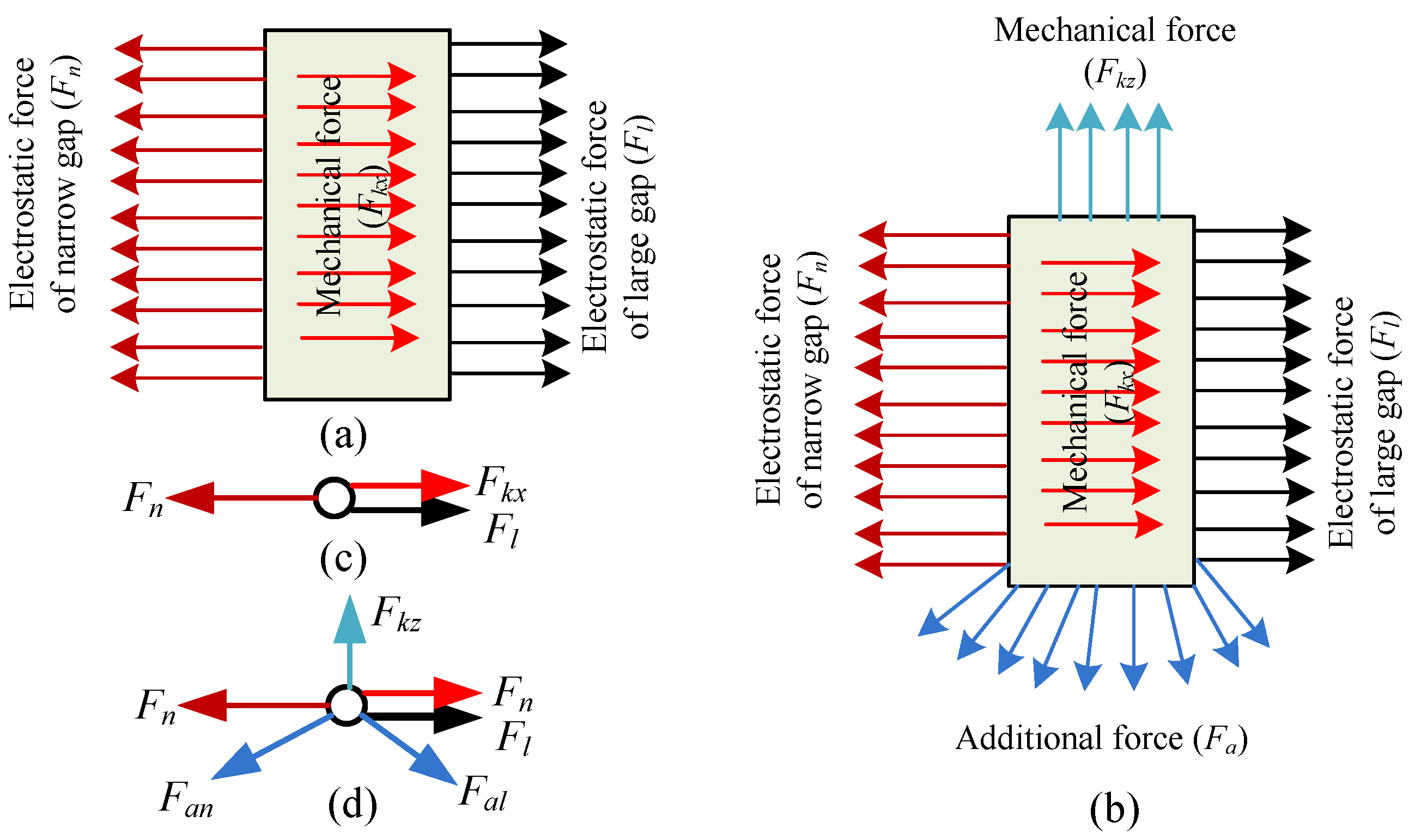
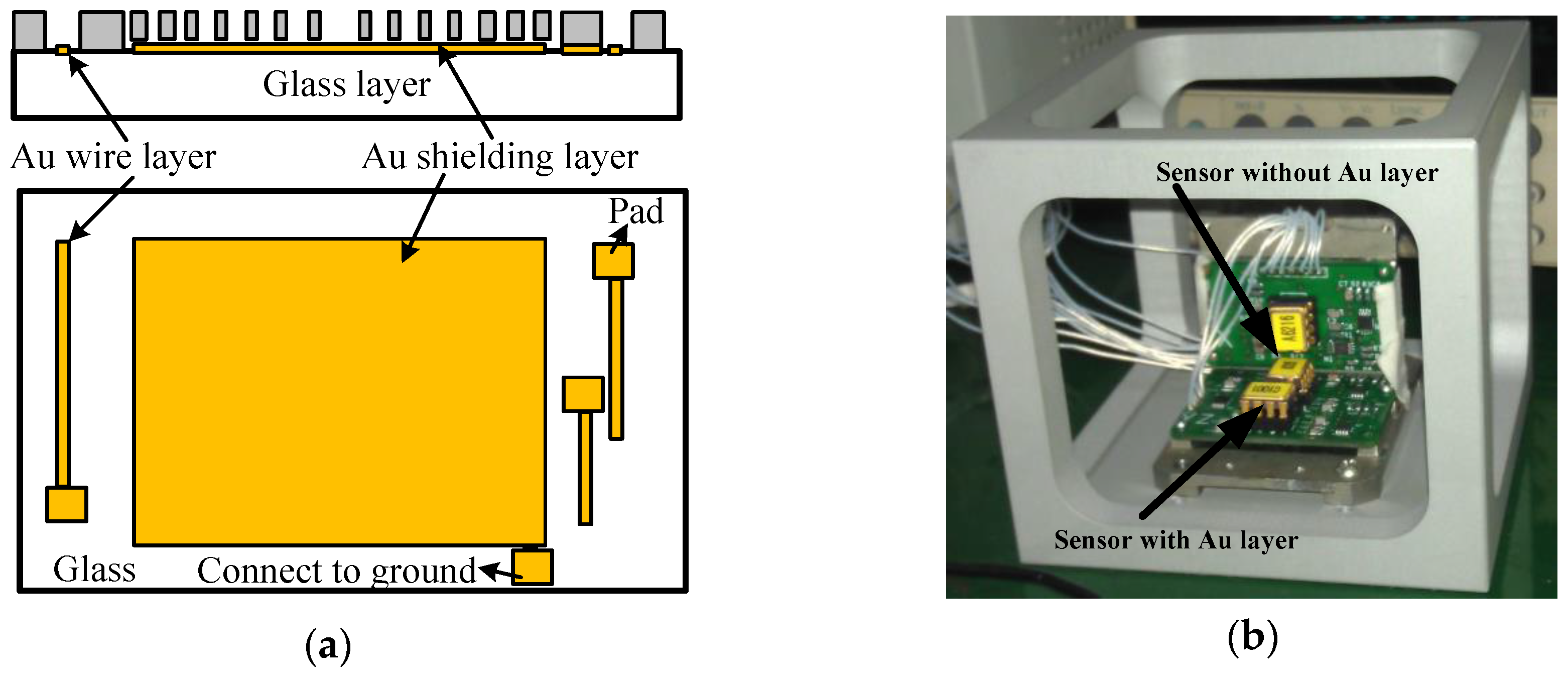
2. Materials and Structure
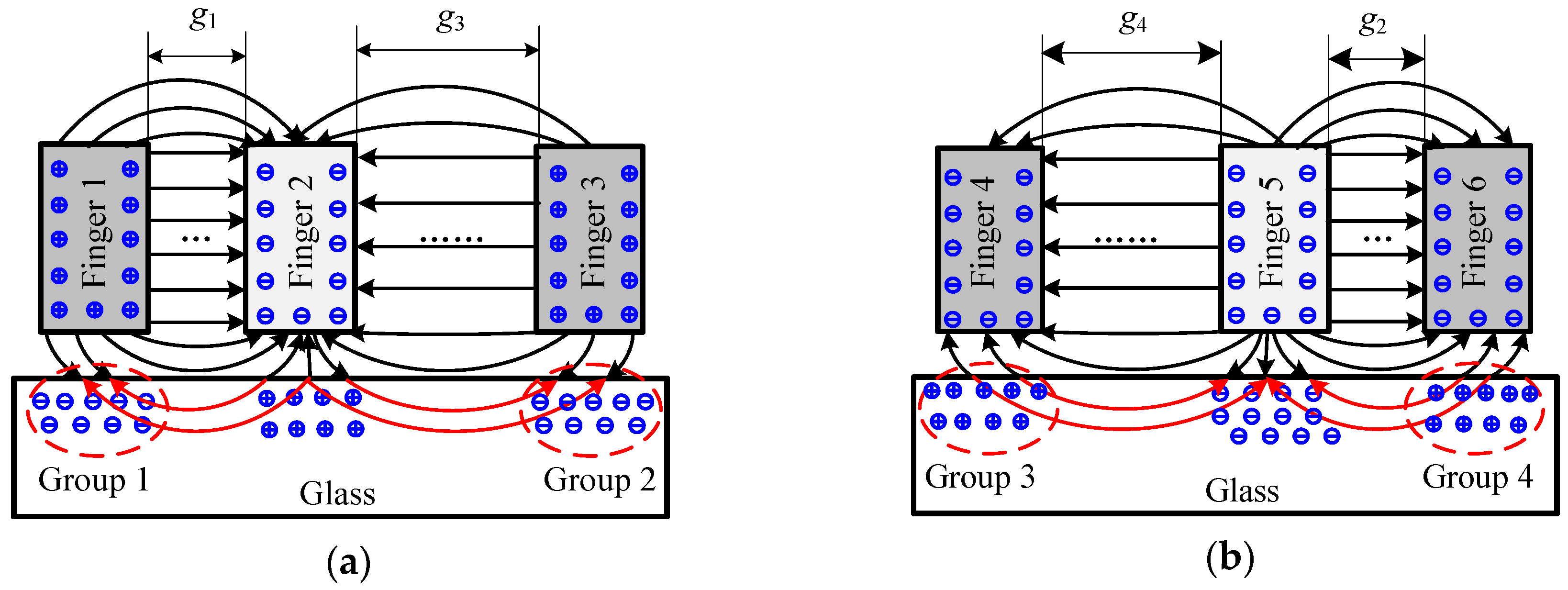
3. Polarization Process
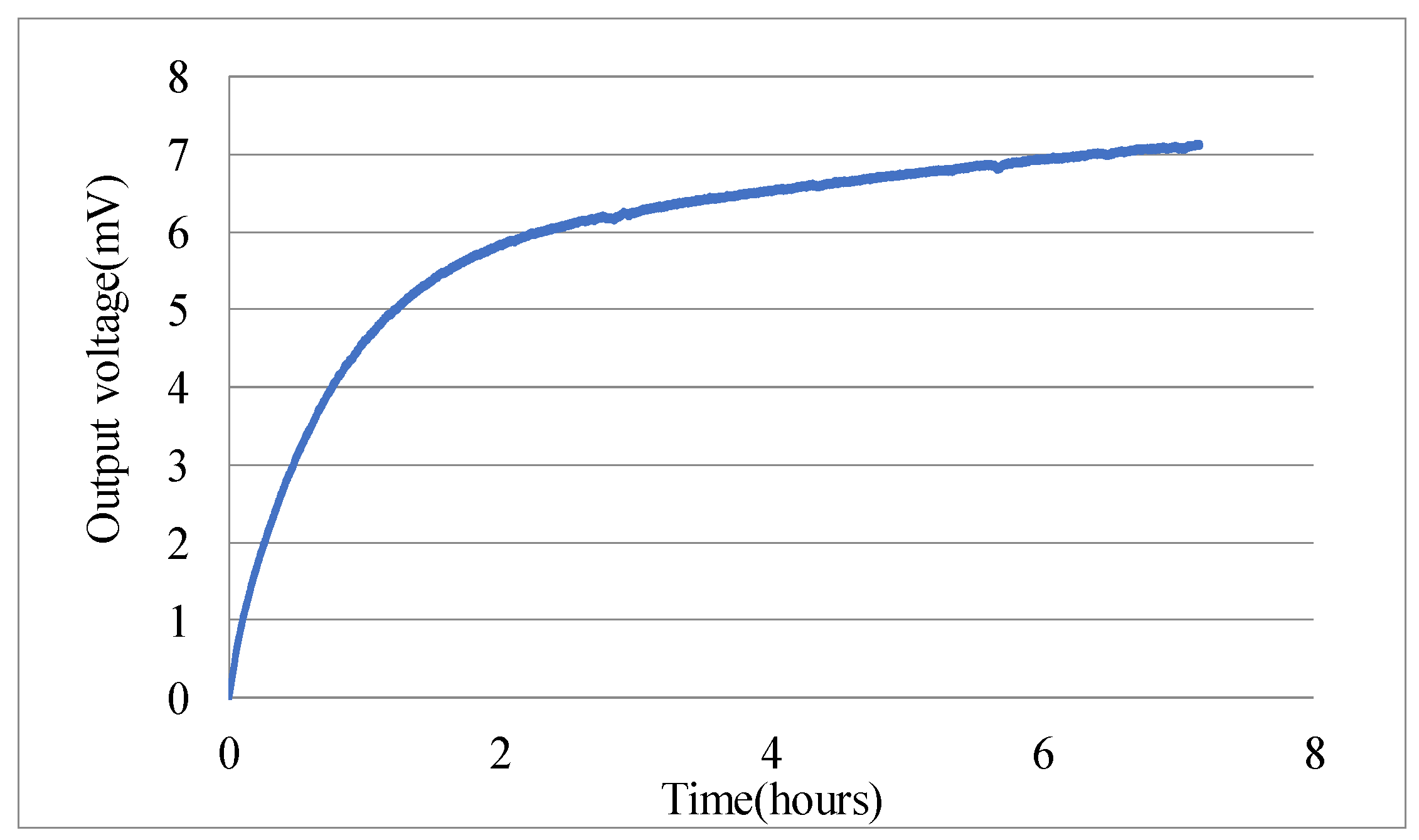
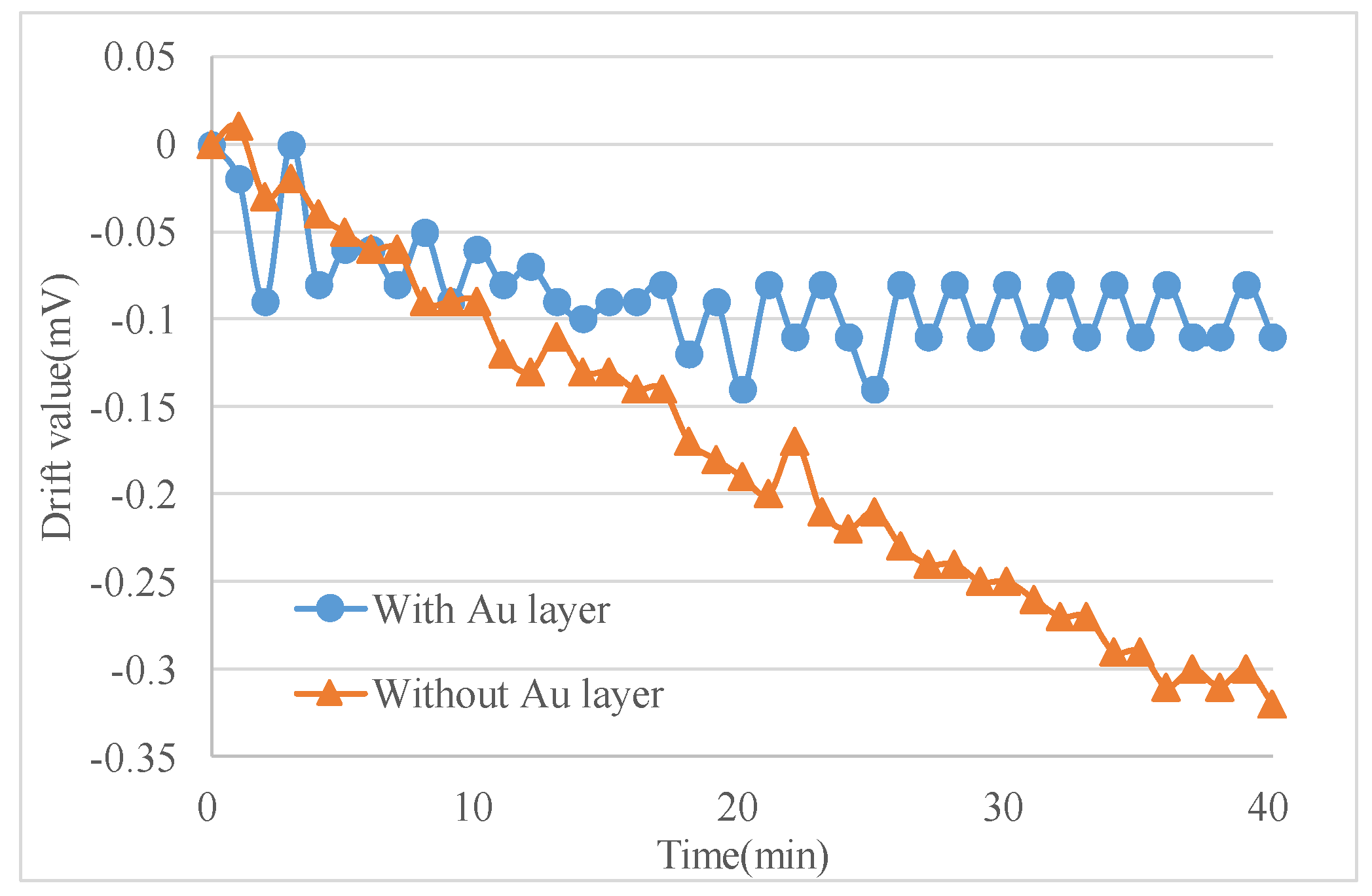
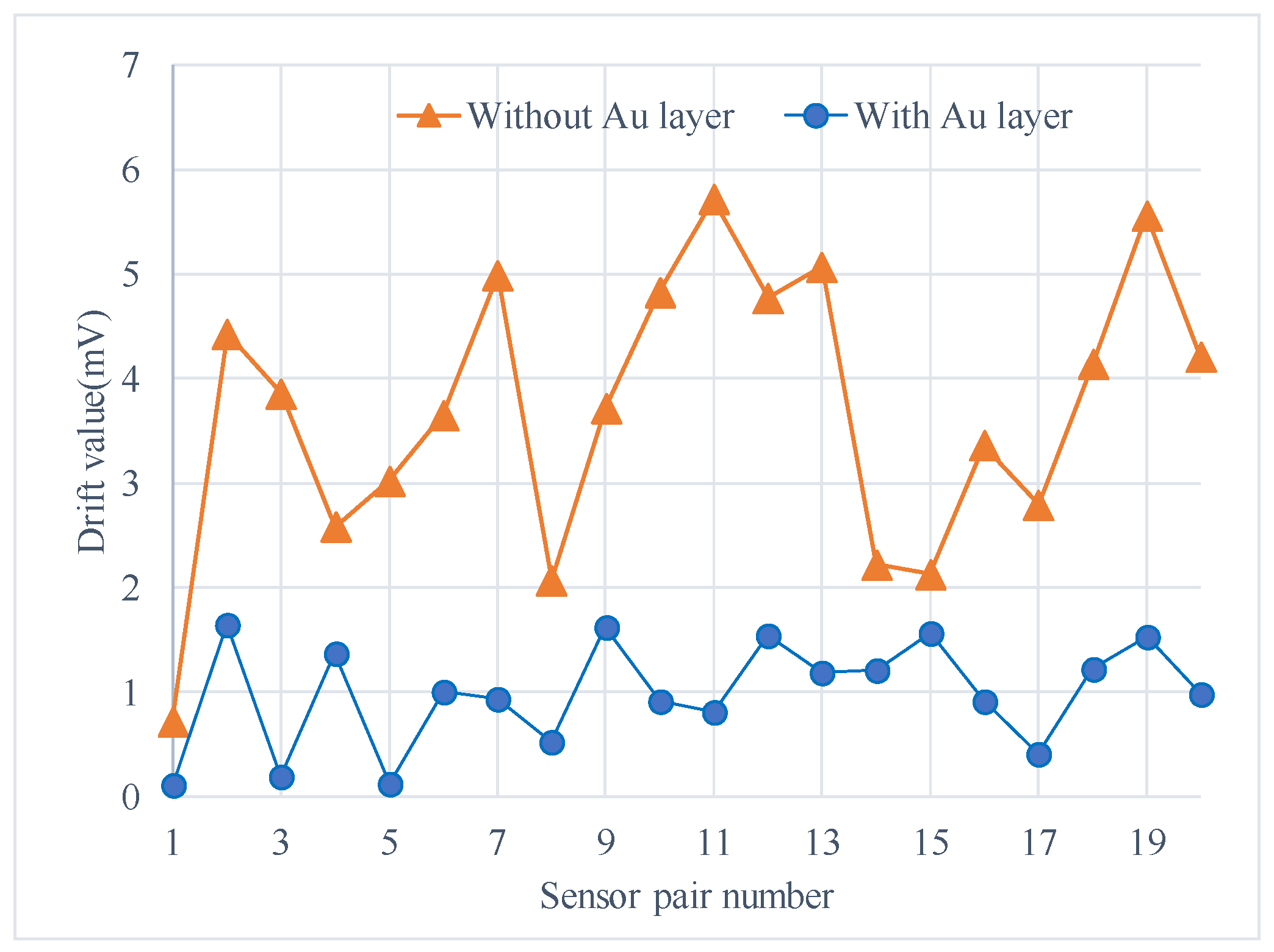
4. Experiment and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, W.; He, J.; He, X.; Yu, J.; Peng, B. Dielectric charging induced drift in micro device reliability-a review. Microelectron. Reliab. 2016, 66, 1–9. [Google Scholar] [CrossRef]
- Prikhodko, I.P.; Trusov, A.A.; Shkel, A.M. Compensation of drifts in high-Q MEMS gyroscopes using temperature self-sensing. Sens. Actuators A Phys. 2012, 201, 517–524. [Google Scholar] [CrossRef]
- Dai, G.; Li, M.; He, X.; Du, L.; Shao, B.; Su, W. Thermal drift analysis using a multiphysics model of bulk silicon MEMS capacitive accelerometer. Sens. Actuators A Phys. 2011, 172, 369–378. [Google Scholar] [CrossRef]
- Tatar, E.; Mukherjee, T.; Fedder, G.K. Stress Effects and Compensation of Bias Drift in a MEMS Vibratory-Rate Gyroscope. J. Microelectromech. Syst. 2017, 26, 569–579. [Google Scholar] [CrossRef]
- Michalas, L.; Koutsoureli, M.; Papandreou, E.; Giacomozzi, F.; Papaioannou, G. Dielectric charging effects in floating electrode MEMS capacitive switches. Microelectron. Reliab. 2015, 55, 1891–1895. [Google Scholar] [CrossRef]
- Gorreta, S.; Pons-Nin, J.; Blokhina, E.; Dominguez, M. A second-order delta-sigma control of dielectric charge for contactless capacitive MEMS. J. Microelectromech. Syst. 2015, 24, 259–261. [Google Scholar] [CrossRef]
- Koutsoureli, M.; Michalas, L.; Papandreou, E.; Papaioannou, G. Induced charging phenomena on SiNx dielectric films used in RF MEMS capacitive switches. Microelectron. Reliab. 2015, 55, 1911–1915. [Google Scholar] [CrossRef]
- Dauderstädt, U.; Dürr, P.; Sinning, S.; Wullinger, I.; Wagner, M. Charging effects in micromirror spatial light modulators. J. Micro Nanolithogr. MEMS MOEMS 2008, 7, 021011. [Google Scholar] [CrossRef]
- Bahl, G.; Melamud, R.; Kim, B.; Chandorkar, S.A.; Salvia, J.C.; Hopcroft, M.A.; Elata, D.; Hennessy, R.G.; Candler, R.N.; Howe, R.T.; et al. Model and Observations of Dielectric Charge in Thermally Oxidized Silicon Resonators. J. Microelectromech. Syst. 2010, 19, 162–174. [Google Scholar] [CrossRef]
- Spengen, W.M.V. Capacitive RF MEMS switch dielectric charging and reliability: A critical review with recommendations. J. Micromech. Microeng. 2012, 22, 074001. [Google Scholar] [CrossRef]
- Gorreta, S.; Pons-Nin, J.; Blokhina, E.; Feely, O.; Dominguez-Pumar, M. Delta-sigma control of dielectric charge for contactless capacitive MEMS. J. Microelectromech. Syst. 2014, 23, 829–841. [Google Scholar] [CrossRef]
- Qu, H.; Yu, H.; Zhou, W.; Peng, B.; He, X. Effects of dielectric charging on the output voltage of capacitive accelerometer. J. Micromech. Microeng. 2016, 26, 115001. [Google Scholar] [CrossRef]
- Sutton, P.M. Space Charge and Electrode Polarization in Glass, I. J. Am. Ceram. Soc. 1964, 47, 188–194. [Google Scholar] [CrossRef]
- Snow, E.H.; Deal, B.E. Polarization phenomena and other properties of phosphosilicate glass films on silicon. J. Electrochem. Soc. 1966, 113, 263–269. [Google Scholar] [CrossRef]
- Eldridge, J.M.; Laibowitz, R.B.; Balk, P. Polarization of thin phosphosilicate glass films in MGOS structures. J. Appl. Phys. 1969, 40, 1922–1930. [Google Scholar] [CrossRef]
- Korkinova, T.N.; Andreichin, R.E. Chalcogenide glass polarization and the type of contacts. J Non-Cryst. Solids 1996, 194, 256–259. [Google Scholar] [CrossRef]
- Doremus, R.H. Mechanism of electrical polarization of silica glass. Appl. Phys. Lett. 2005, 87, 232904. [Google Scholar] [CrossRef]
- Petrov, M.I.; Lepen’kin, Y.A.; Lipovskii, A.A. Polarization of glass containing fast and slow ions. J. Appl. Phys. 2012, 112, 043101. [Google Scholar] [CrossRef]
- Kamenskii, A.N.; Lipovskaia, M.Y. A diffractometric method of studying the polarization process of glasses. J. Opt. Technol. 2016, 83, 283–285. [Google Scholar] [CrossRef]
- Czarnecki, P.; Rottenberg, X.; Soussan, P.; Ekkels, P.; Muller, P.; Nolmans, P.; De Raedt, W.; Tilmans, H.A.C.; Puers, R.; Marchand, L.; et al. Effect of substrate charging on the reliability of capacitive RF MEMS switches. Sens. Actuators A Phys. 2009, 154, 261–268. [Google Scholar] [CrossRef]
- Haarahiltunen, A.; Varpula, A.; Leinvuo, J.; Siren, E.; Rytkönen, V.-P.; Savi, H. Glass polarization induced drift in microelectromechanical capacitor. J. Appl. Phys. 2012, 111, 103523. [Google Scholar] [CrossRef]
- Chesbro, D.L. Design, Fabrication, and Characterization of Electrostatically-Actuated Silicon Micro-Mirrors. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, April 2010. [Google Scholar]
- Zhou, W.; Peng, P.; Yu, H.; Peng, B.; He, X. Material Viscoelasticity-Induced Drift of Micro-Accelerometers. Materials 2017, 10, 1077. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Li, B.; Peng, B.; Su, W.; He, X. Prediction of Gap Asymmetry in Differential Micro-accelerometers. Sensors 2012, 12, 6857–6868. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Yu, H.; Peng, B.; Shen, H.; He, X.; Su, W. Modeling the Microstructure Curvature of Boron-Doped Silicon in Bulk Micromachined Accelerometer. Materials 2013, 6, 244–254. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.B. A theoretical response of the electrostatic parallel plate to constant and low-frequency accelerations. Smart Mater. Struct. 2009, 18, 115004. [Google Scholar] [CrossRef]
- Laboriante, I.; Farrokhzad, N.; Fisch, M.; Shavezipur, M.; Carraro, C.; Maboudian, R.; Bai, Q.; Liu, M.; Hoen, S. Charging and discharging behavior in dielectric-coated MEMS electrodes probed by Kelvin probe force microscopy. J. Micromech. Microeng. 2012, 22, 065031. [Google Scholar] [CrossRef]
- Zaghloul, U.; Papaioannou, G.J.; Coccetti, F.; Pons, P.; Plana, R. A systematic reliability investigation of the dielectric charging process in electrostatically actuated MEMS based on Kelvin probe force microscopy. J. Micromech. Microeng. 2010, 20, 064016. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; He, J.; Yu, H.; Peng, B.; He, X. Glass Polarization Induced Drift of a Closed-Loop Micro-Accelerometer. Materials 2018, 11, 163. https://doi.org/10.3390/ma11010163
Zhou W, He J, Yu H, Peng B, He X. Glass Polarization Induced Drift of a Closed-Loop Micro-Accelerometer. Materials. 2018; 11(1):163. https://doi.org/10.3390/ma11010163
Chicago/Turabian StyleZhou, Wu, Jiangbo He, Huijun Yu, Bei Peng, and Xiaoping He. 2018. "Glass Polarization Induced Drift of a Closed-Loop Micro-Accelerometer" Materials 11, no. 1: 163. https://doi.org/10.3390/ma11010163
APA StyleZhou, W., He, J., Yu, H., Peng, B., & He, X. (2018). Glass Polarization Induced Drift of a Closed-Loop Micro-Accelerometer. Materials, 11(1), 163. https://doi.org/10.3390/ma11010163




