Comparisons of Different Models on Dynamic Recrystallization of Plate during Asymmetrical Shear Rolling
Abstract
:1. Introduction
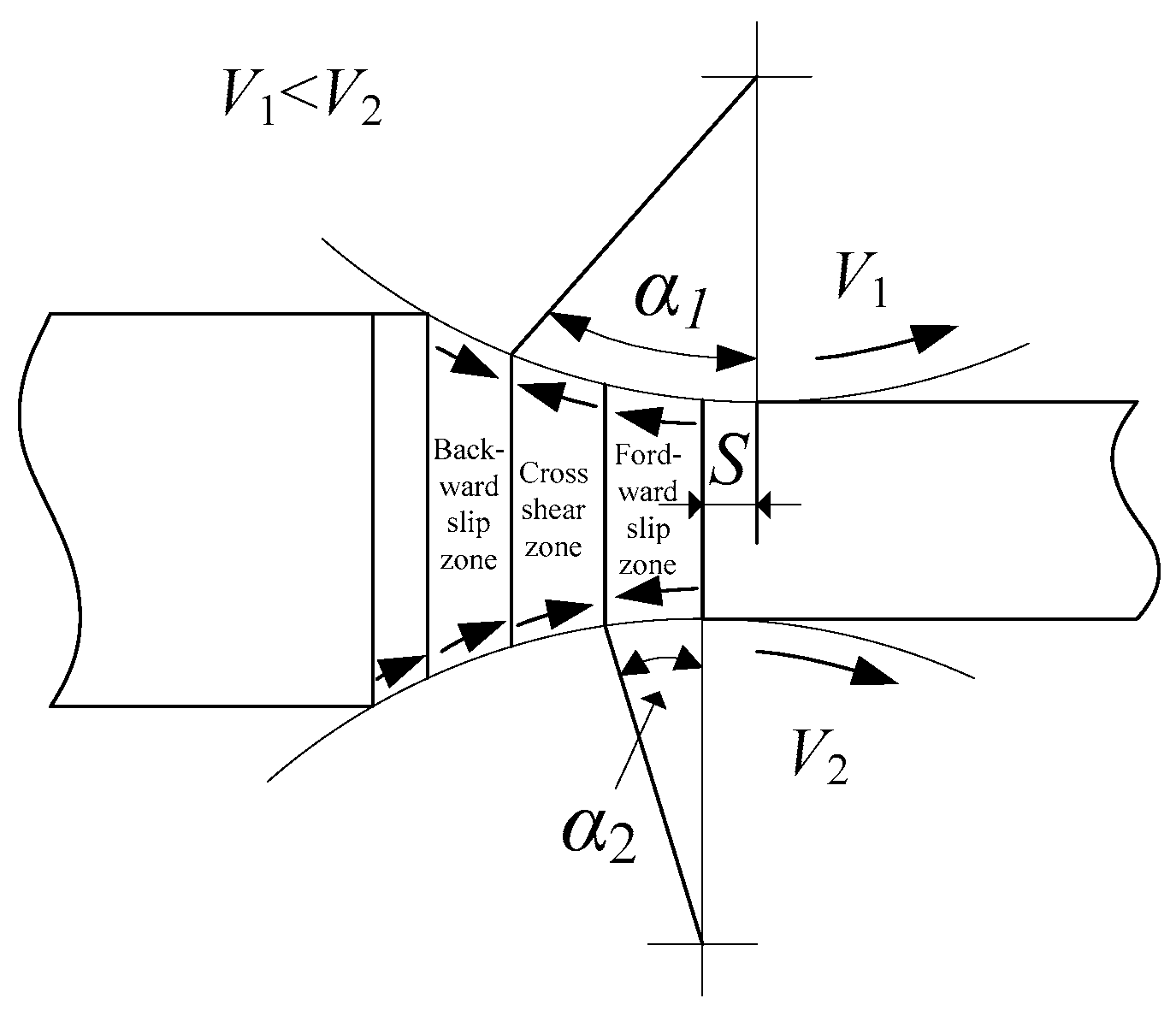
2. Asymmetrical Shear Rolling
3. Models Establishment
3.1. Microstructure Evolution Model
3.2. Cellular Automata Model
4. Results and Discussion
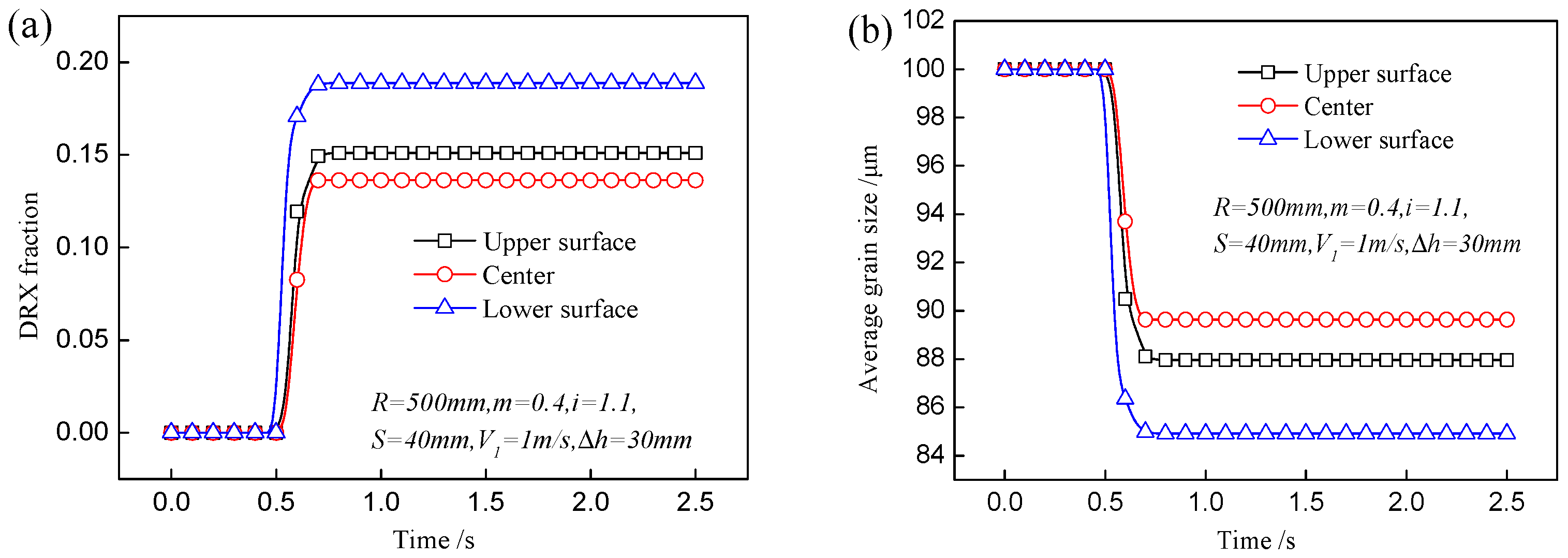
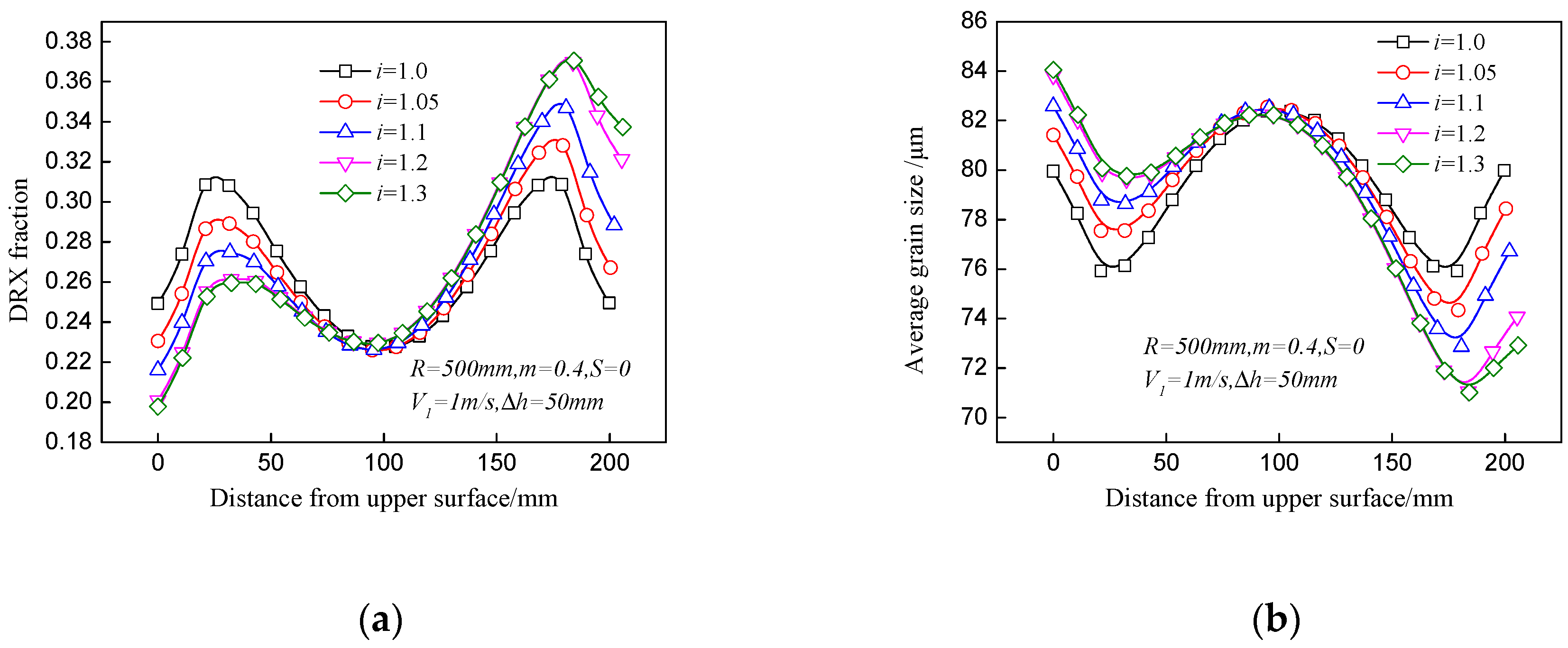
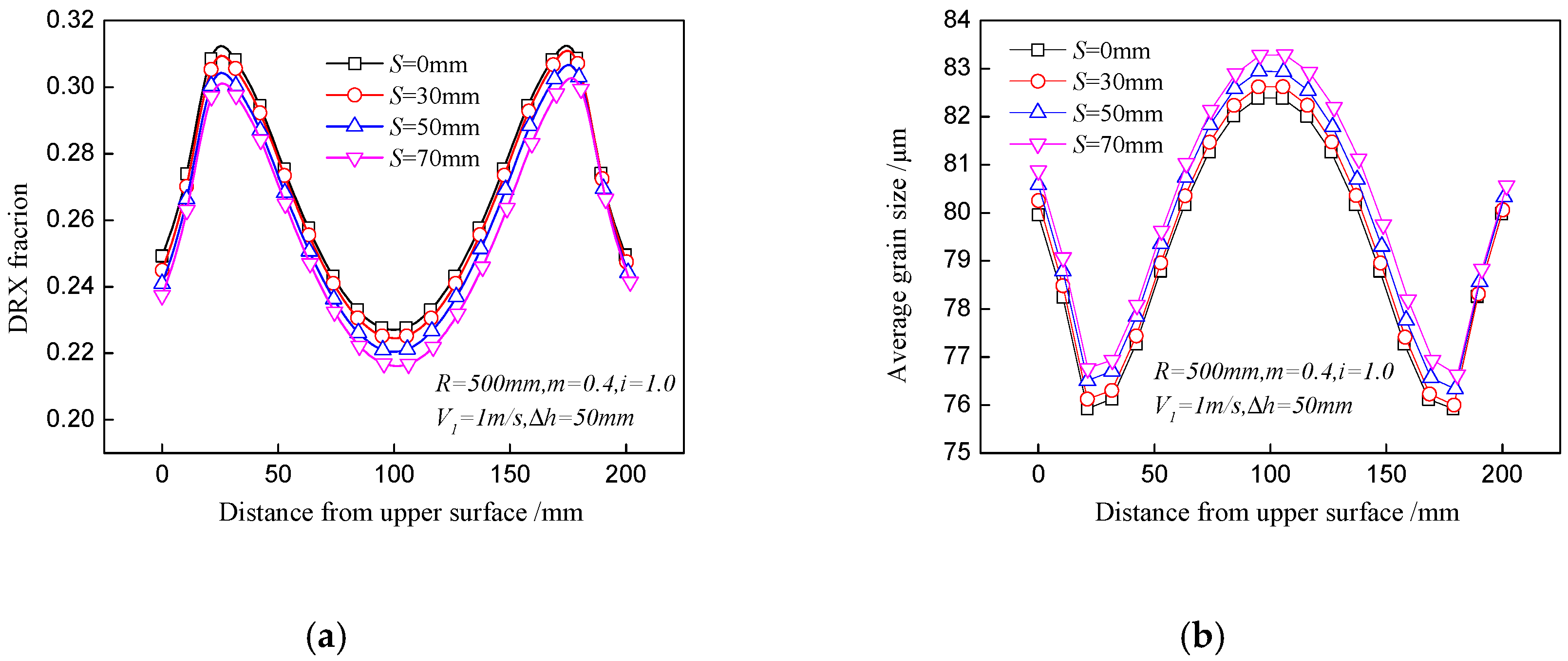
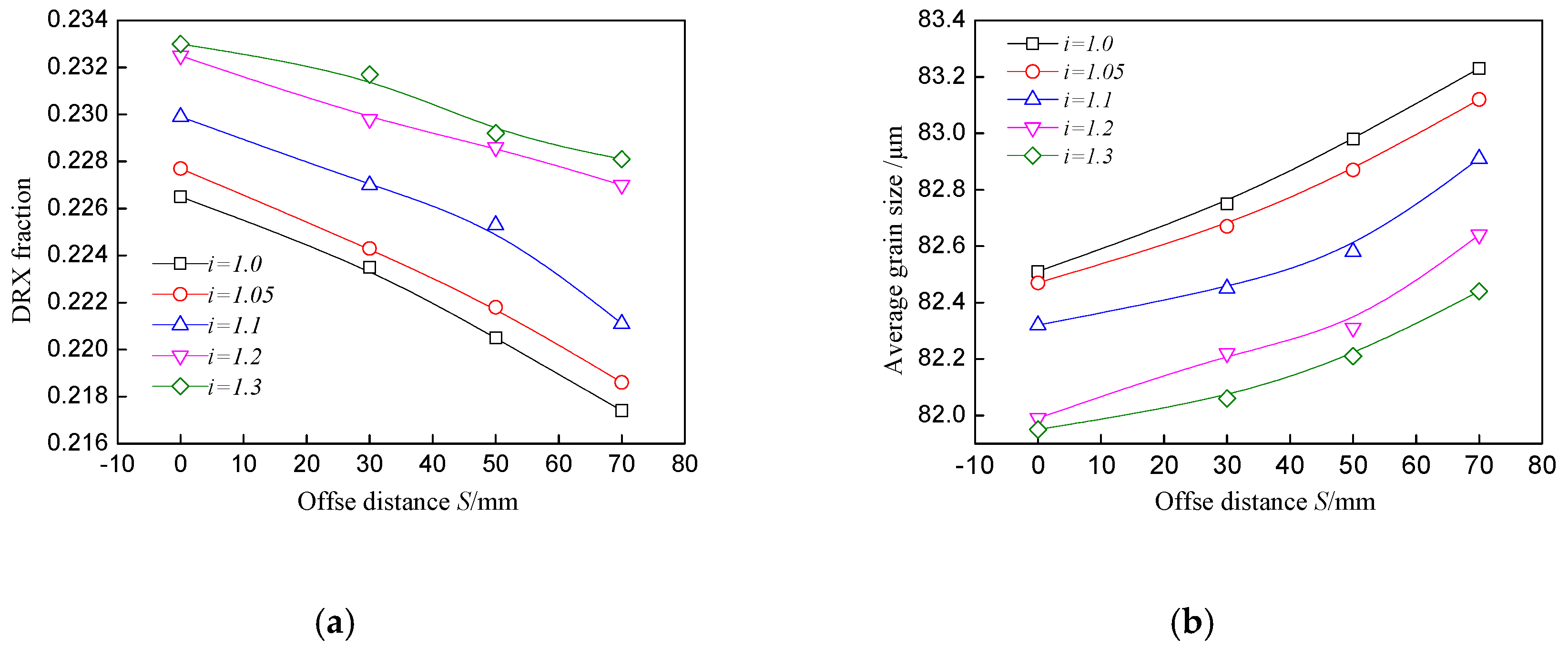
4.1. DRX Fraction and Grain Size
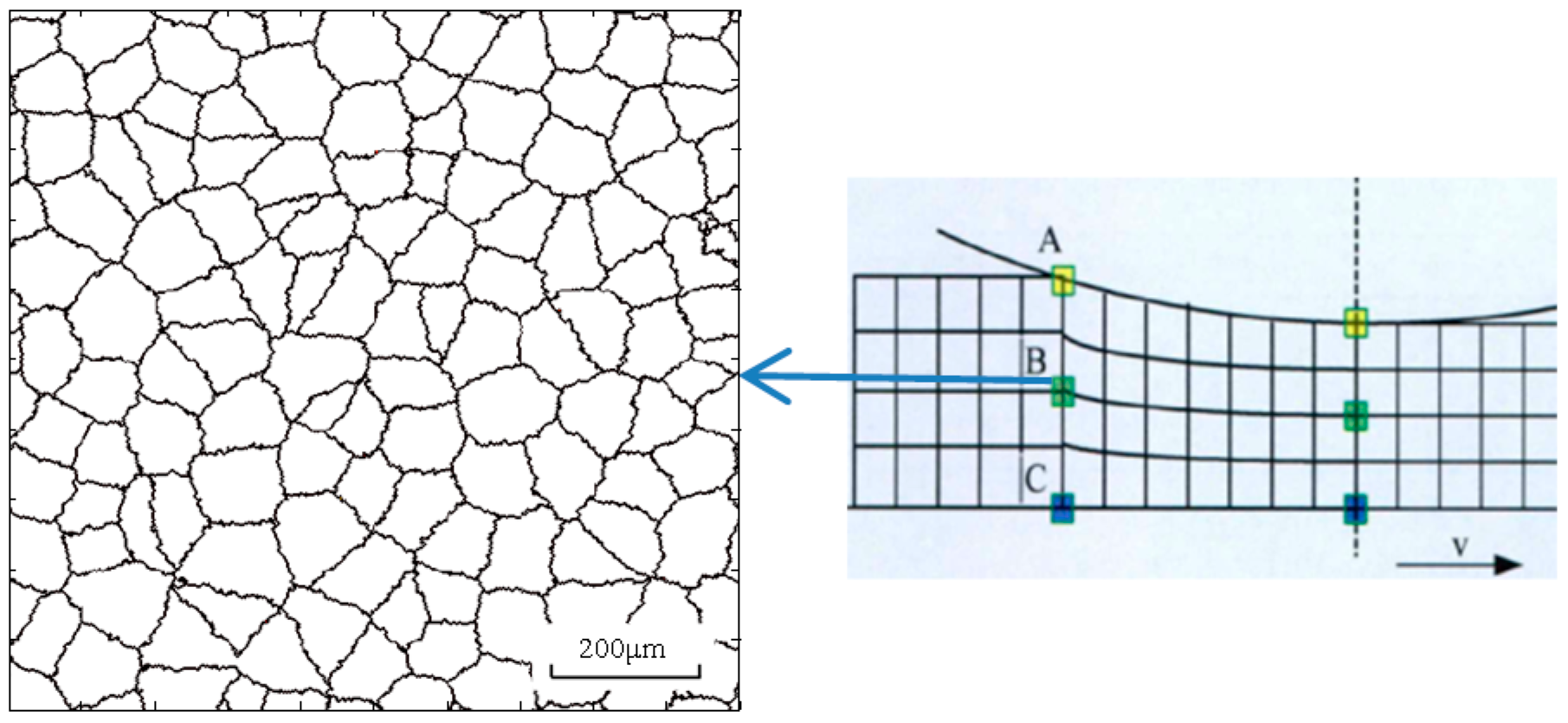
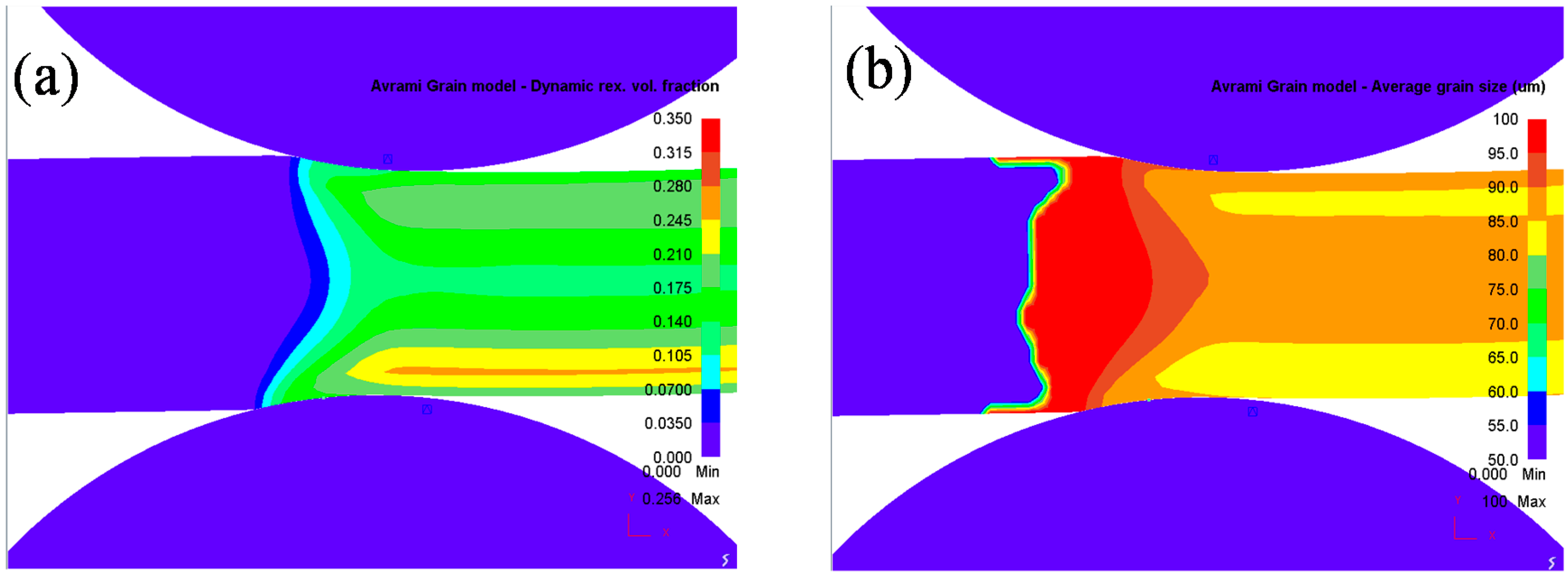
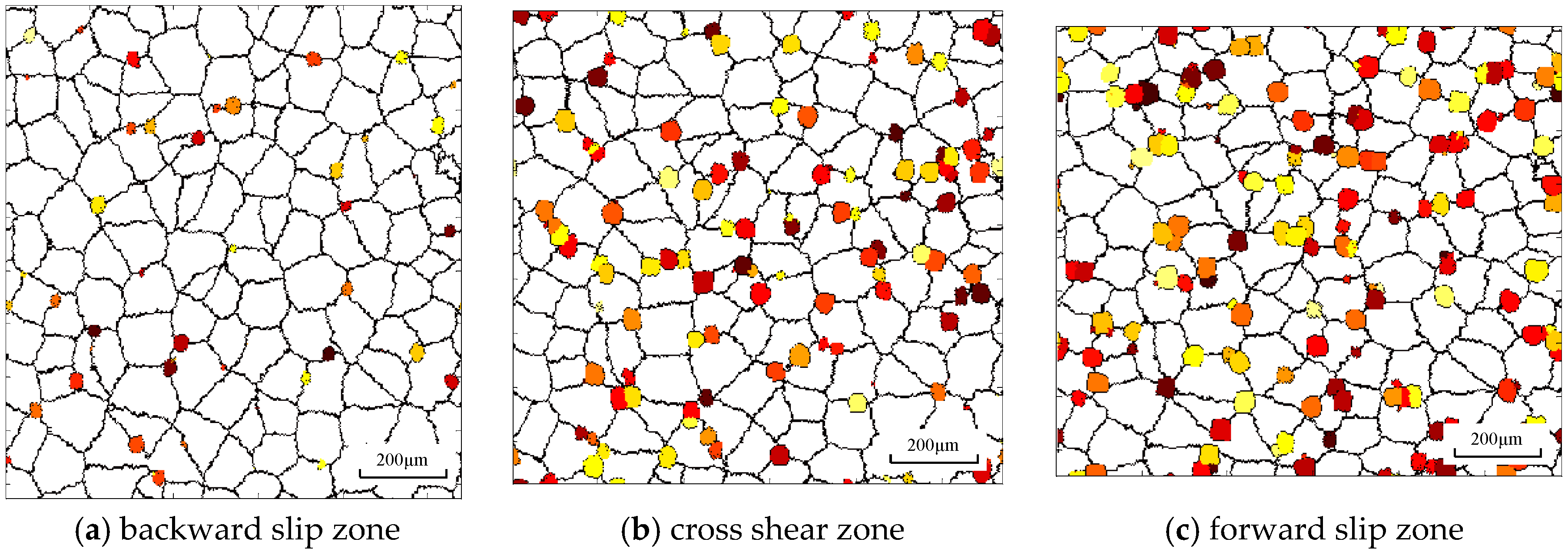
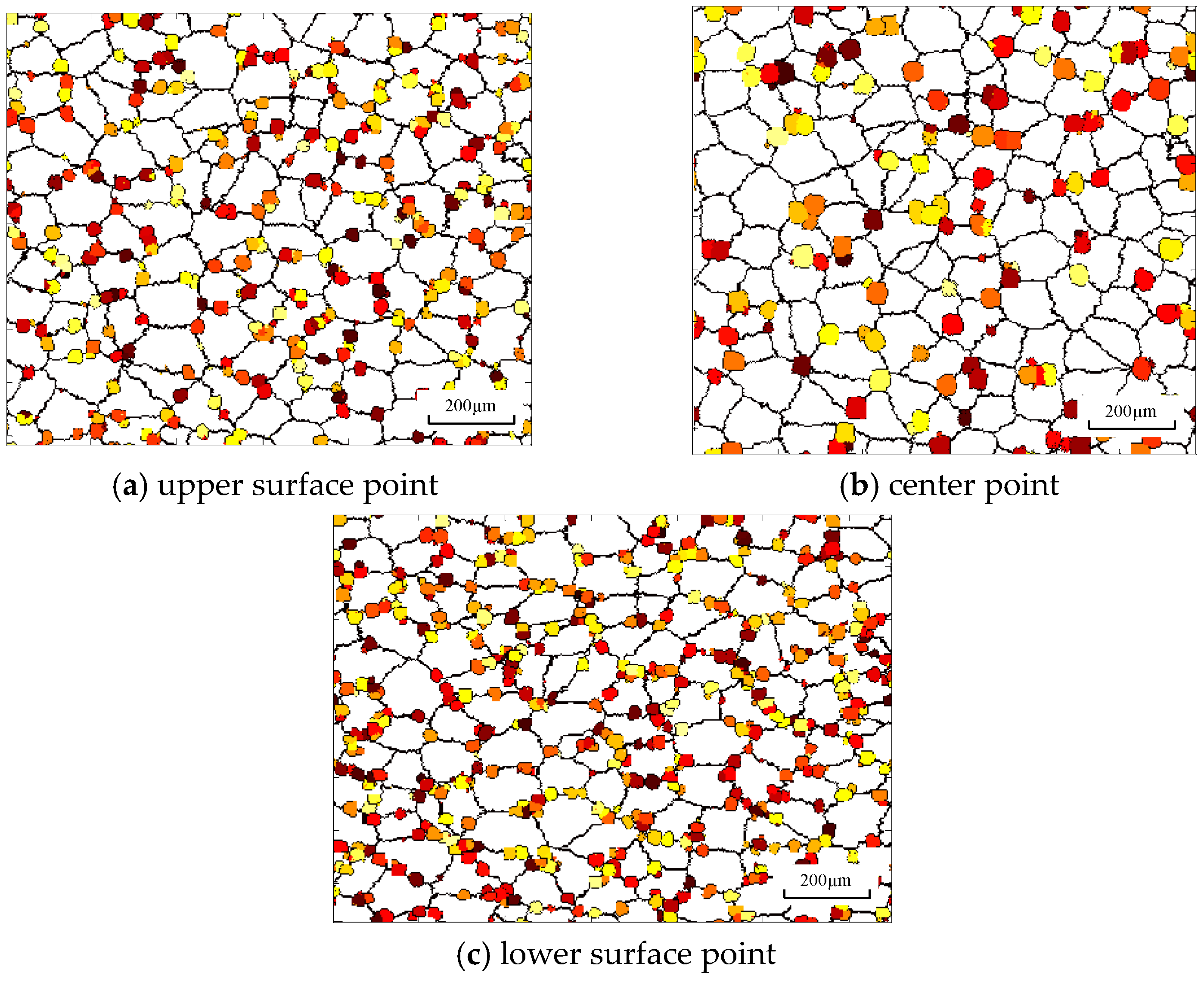
4.2. Microstructure Visualization
5. Experiments
6. Conclusions
- (1)
- Microstructure evolution models and CA models are established to study the DRX behavior of the plate in asymmetrical shear rolling. The effects of the speed ratio and offset distance on the DRX fraction as well as grain size during asymmetrical shear rolling are analyzed.
- (2)
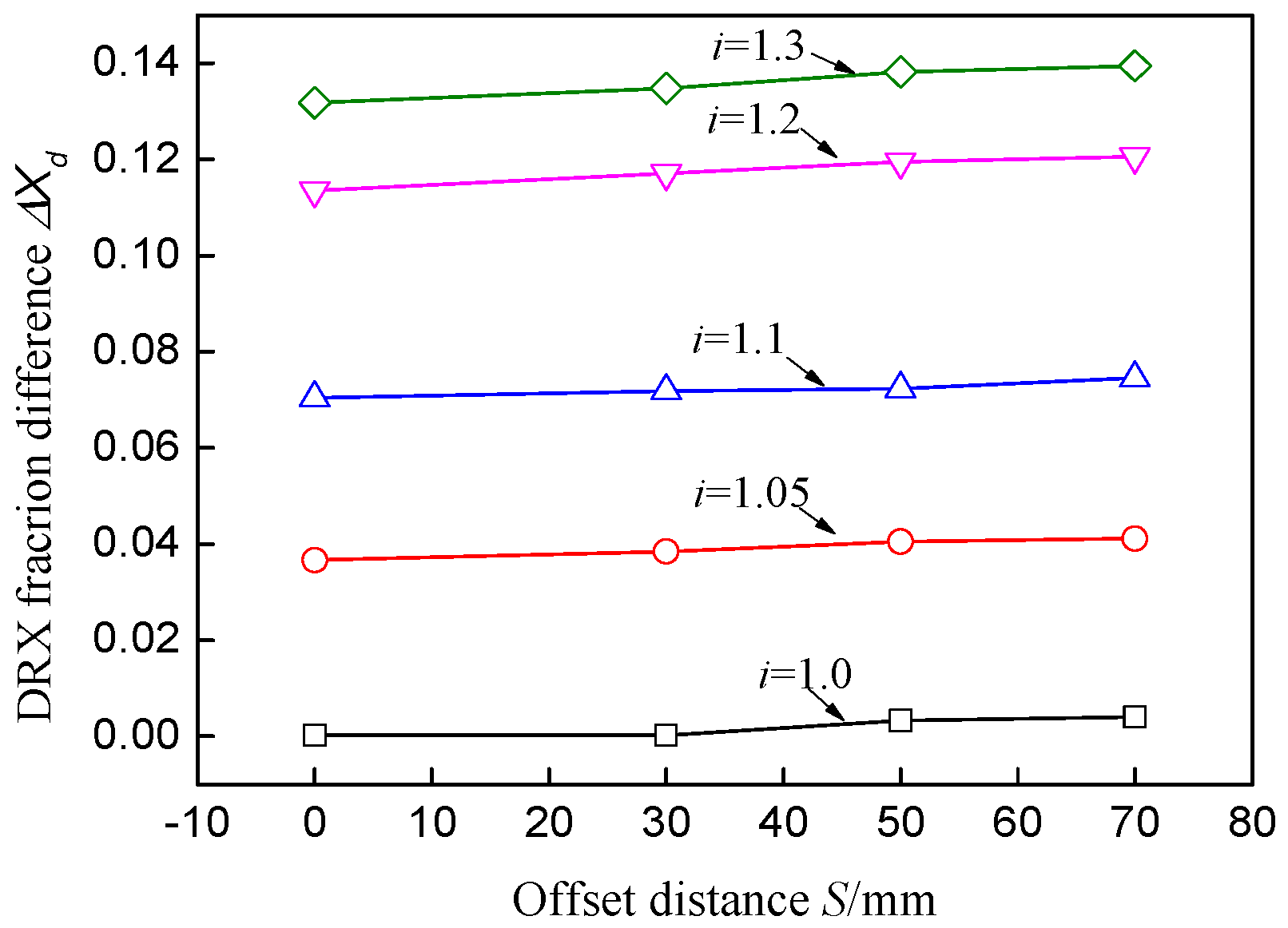
- The distributions of the DRX fraction and average grain size are asymmetrical in asymmetrical shear rolling and the lower part of the plate has a larger DRX fraction and finer grain than the upper part. The DRX fraction difference between the upper and lower surfaces increases with ascending speed ratio, but the variation of the offset distance has little effect on this difference.
- (3)
- More sufficient DRX and finer grain can be obtained with ascending speed ratio, while the increase of the offset distance will slightly decrease the DRX fraction and increase the average grain size.
- (4)
- A proper speed ratio should be selected to ensure sufficient DRX on the basis of small bending behavior of the plate, and the existence of the offset distance is mainly used to decrease the bending behavior of the plate during asymmetrical shear rolling.
- (5)
- CA models have a higher accuracy than FEM models because they take comprehensive consideration of DRX nuclei, grain growth, and grain morphology.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heinz, A.; Haszler, A.; Keidel, C. Recent development in aluminium alloys for aerospace applications. Mater. Sci. Eng. A-Struct. 2000, 280, 102–107. [Google Scholar] [CrossRef]
- Fu, Y.; Xie, S.; Xiong, B.; Huang, G.; Cheng, L. Effect of rolling parameters on plate curvature during snake rolling. J. Wuhan Univ. Technol. 2012, 27, 247–251. [Google Scholar] [CrossRef]
- Shi, C.; Lai, J.; Chen, X.G. Microstructural evolution and dynamic softening mechanisms of Al-Zn-Mg-Cu Alloy during hot compressive deformation. Materials 2014, 7, 244–264. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhai, S.C. Dynamic recrystallization kinetics of 690 alloy during hot compression of double-cone samples. J. Mater. Eng. Perform. 2017, 26, 1–11. [Google Scholar] [CrossRef]
- Zhou, P.; Ma, Q. Dynamic recrystallization behavior and constitutive modeling of as-cast 30Cr2Ni4MoV steel based on flow curves. Met. Mater. Int. 2017, 23, 359–368. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, B.; Qi, L. Modeling of the dynamic recrystallization behavior of Csf/AZ91D magnesium matrix composites during hot compression process. J. Alloys Compd. 2017, 708, 328–336. [Google Scholar] [CrossRef]
- Yin, X.Q.; Park, C.H.; Li, Y.F. Mechanism of continuous dynamic recrystallization in a 50Ti-47Ni-3Fe shape memory alloy during hot compressive deformation. J. Alloys Compd. 2017, 693, 426–431. [Google Scholar] [CrossRef]
- Maire, L.; Scholtes, B.; Moussa, C. Modeling of dynamic and post-dynamic recrystallization by coupling a full field approach to phenomenological laws. Mater. Des. 2017, 133, 498–519. [Google Scholar] [CrossRef]
- Aashranth, B.; Davinci, M.A.; Samantaray, D. A new critical point on the stress-strain curve: Delineation of dynamic recrystallization from grain growth. Mater. Des. 2017, 116, 495–503. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S. Numerical simulation and experimental verification of microstructure evolution in a three-dimensional hot upsetting process. J. Mater. Process. Technol. 2009, 209, 4578–4583. [Google Scholar] [CrossRef]
- Wen, D.X.; Lin, Y.C.; Zhou, Y. A new dynamic recrystallization kinetics model for a Nb containing Ni-Fe-Cr-base superalloy considering influences of initial δ phase. Vacuum 2017, 141, 316–327. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, B.; Li, L. Dynamic recrystallization of AZ31 magnesium alloy simulated by Laasraoui-Jonas dislocation equation coupled cellular automata method. Trans. Nonferr. Met. Soc. 2013, 23, 898–904. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z.; Liu, J. Mesoscale simulation of the high-temperature austenitizing and dynamic recrystallization by coupling a cellular automaton with a topology deformation technique. Mater. Sci. Eng. A-Struct. 2010, 527, 5539–5549. [Google Scholar] [CrossRef]
- Wąs, J.; Sirakoulis, G.C. Cellular automata applications for research and industry. J. Comput. Sci. 2015, 11, 223–225. [Google Scholar] [CrossRef]
- Sitko, M.; Pietrzyk, M.; Madej, L. Time and length scale issues in numerical modelling of dynamic recrystallization based on the multi space cellular automata method. J. Comput. Sci. 2016, 16, 98–113. [Google Scholar] [CrossRef]
- Lee, H.W.; Im, Y.T. Numerical modeling of dynamic recrystallization during non-isothermal hot compression by cellular automata and finite element analysis. Int. J. Mech. Sci. 2010, 52, 1277–1289. [Google Scholar]
- Salehi, M.; Serajzadeh, S. Simulation of static recrystallization in non-isothermal annealing using a coupled cellular automata and finite element model. Comput. Mater. Sci. 2012, 53, 145–152. [Google Scholar] [CrossRef]
- Zheng, C.; Xiao, N.; Li, D. Microstructure prediction of the austenite recrystallization during multi-pass steel strip hot rolling: A cellular automaton modeling. Comput. Mater. Sci. 2008, 44, 507–514. [Google Scholar] [CrossRef]
- Li, S.; Qin, N.; Liu, J. Microstructure, texture and mechanical properties of AA1060 aluminum plate processed by snake rolling. Mater. Des. 2016, 90, 1010–1017. [Google Scholar] [CrossRef]
- Jiang, J.; Ding, Y.; Zuo, F.; Shan, A. Mechanical properties and microstructures of ultrafine-grained pure aluminum by asymmetric rolling. Scr. Mater. 2009, 60, 905–908. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, Y.X.; Gong, H. Analysis of strain variation in cross shear zone of plate during snake hot rolling. J. Cent. South Univ. 2017, 24, 296–302. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Liu, J.; Li, X.; Zhang, X. Finite element analysis of bending behavior and strain heterogeneity in snake rolling of AA7050 plates using a hyperbolic sine-type constitutive law. J. Mater. Process. Technol. 2017, 240, 274–283. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, Y.X.; Gong, H. Bending analysis and control of rolled plate during snake hot rolling. J. Cent. South Univ. 2015, 22, 2463–2469. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, Y.; Gong, H.; Shi, W.; Jiang, S. Flow stress behavior and constitutive model of 7055 aluminium alloy during hot plastic deformation. MECHANIKA 2016, 22, 359–365. [Google Scholar] [CrossRef]
- Kang, Y.H.; Liu, Y.L.; He, Y. Temperature simulation of single pass hot rolling process of aluminum alloy. Mater. Mech. Eng. 2010, 34, 92–96. [Google Scholar]
- Sellars, C.M.; Whiteman, J.A. Recrystallization and grain growth in hot rolling. Met. Sci. 1979, 13, 187–194. [Google Scholar] [CrossRef]
- Senuma, T.; Yada, H.; Yoshimura, H. Deformation resistance and recrystallization of commercially pure titanium in the high strain rate hot deformation. Adv. Mater. Res. 1986, 626, 430–435. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, Y.; Li, H.; Wen, D.; Chen, X.; Chen, M. Study of dynamic recrystallization in a Ni-based superalloy by experiments and cellular automaton model. Mater. Sci. Eng. A-Struct. 2015, 626, 432–440. [Google Scholar] [CrossRef]
- Ding, R.; Guo, Z.X. Coupled quantitative simulation of microstructural evolution and plastic flow during dynamic recrystallization. Acta Mater. 2001, 49, 3163–3175. [Google Scholar] [CrossRef]
- Ding, R.; Guo, Z.X. Microstructural modelling of dynamic recrystallisation using an extended cellular automaton approach. Comput. Mater. Sci. 2002, 23, 209–218. [Google Scholar] [CrossRef]
- Afshari, E.; Serajzadeh, S. Simulation of static recrystallization after cold side-pressing of low carbon steels using cellular automata. J. Mater. Eng. Perform. 2012, 21, 1553–1561. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Work roll radius, R/mm | 500 |
| Shear friction coefficient, m | 0.4 |
| Velocity of lower roll, V2/(m/s) | 1~1.3 |
| Velocity of upper roll, V1/(m/s) | 1 |
| Pass reduction, Δh/mm | 30, 50 |
| Speed ratio, i = V2/V1 | 1.00~1.3 |
| Offset distance, S/mm | 0~70 |
| Average Grain Size | Upper Point | Center Point | Lower Point |
|---|---|---|---|
| Experimental value/μm | 36.4 | 39.1 | 33.1 |
| CA results/μm | 38.5 | 40.7 | 35.8 |
| Error (CA) | 5.8% | 4.1% | 8.2% |
| FEM results/μm | 40.2 | 44.8 | 36.4 |
| Error (FEM) | 10.4% | 14.6% | 10% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Li, L.; Lu, S.-H.; Gong, H.; Wu, Y.-X. Comparisons of Different Models on Dynamic Recrystallization of Plate during Asymmetrical Shear Rolling. Materials 2018, 11, 151. https://doi.org/10.3390/ma11010151
Zhang T, Li L, Lu S-H, Gong H, Wu Y-X. Comparisons of Different Models on Dynamic Recrystallization of Plate during Asymmetrical Shear Rolling. Materials. 2018; 11(1):151. https://doi.org/10.3390/ma11010151
Chicago/Turabian StyleZhang, Tao, Lei Li, Shi-Hong Lu, Hai Gong, and Yun-Xin Wu. 2018. "Comparisons of Different Models on Dynamic Recrystallization of Plate during Asymmetrical Shear Rolling" Materials 11, no. 1: 151. https://doi.org/10.3390/ma11010151
APA StyleZhang, T., Li, L., Lu, S.-H., Gong, H., & Wu, Y.-X. (2018). Comparisons of Different Models on Dynamic Recrystallization of Plate during Asymmetrical Shear Rolling. Materials, 11(1), 151. https://doi.org/10.3390/ma11010151






