Spin Absorption Effect at Ferromagnet/Ge Schottky-Tunnel Contacts
Abstract
1. Introduction
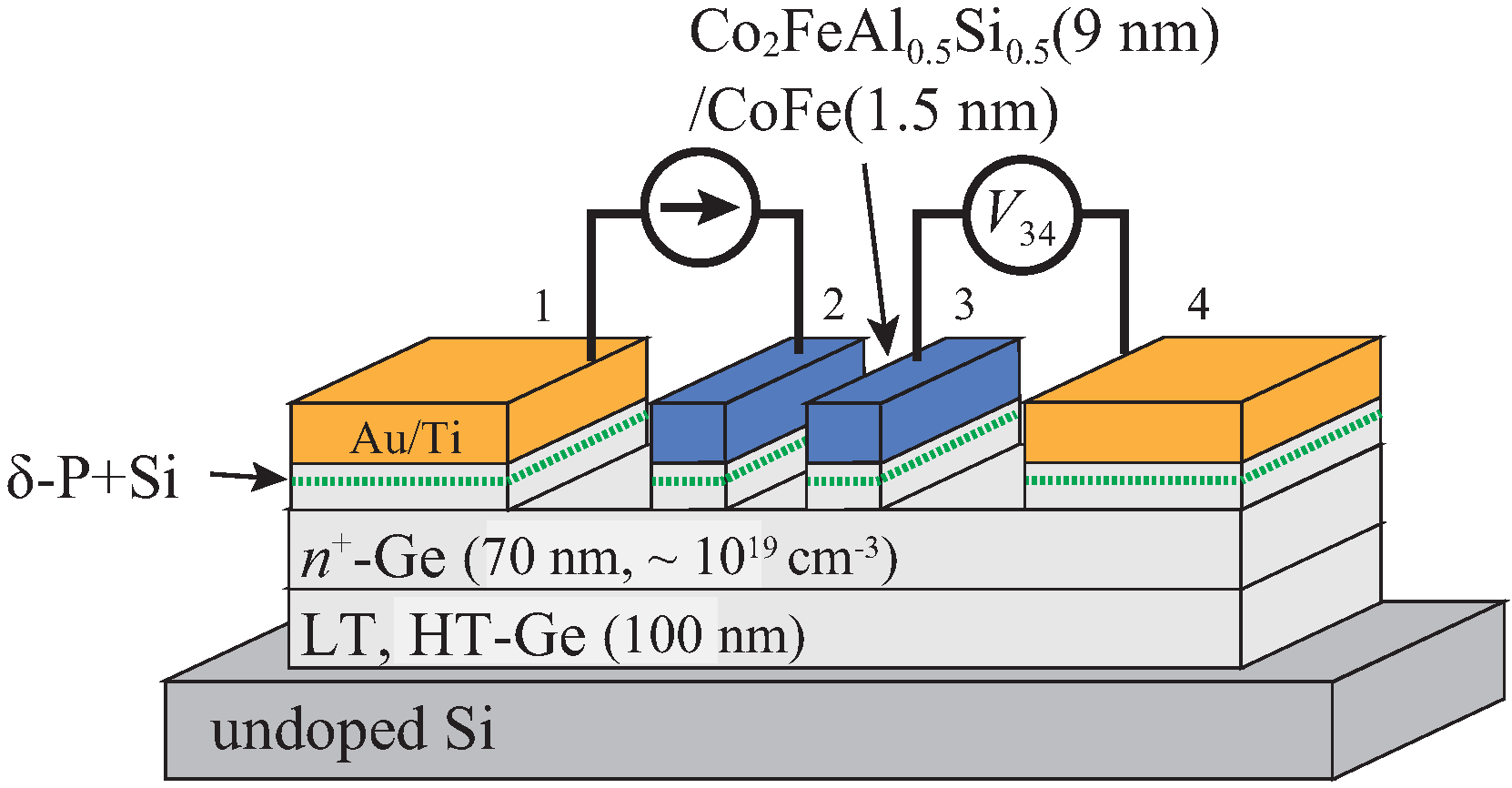
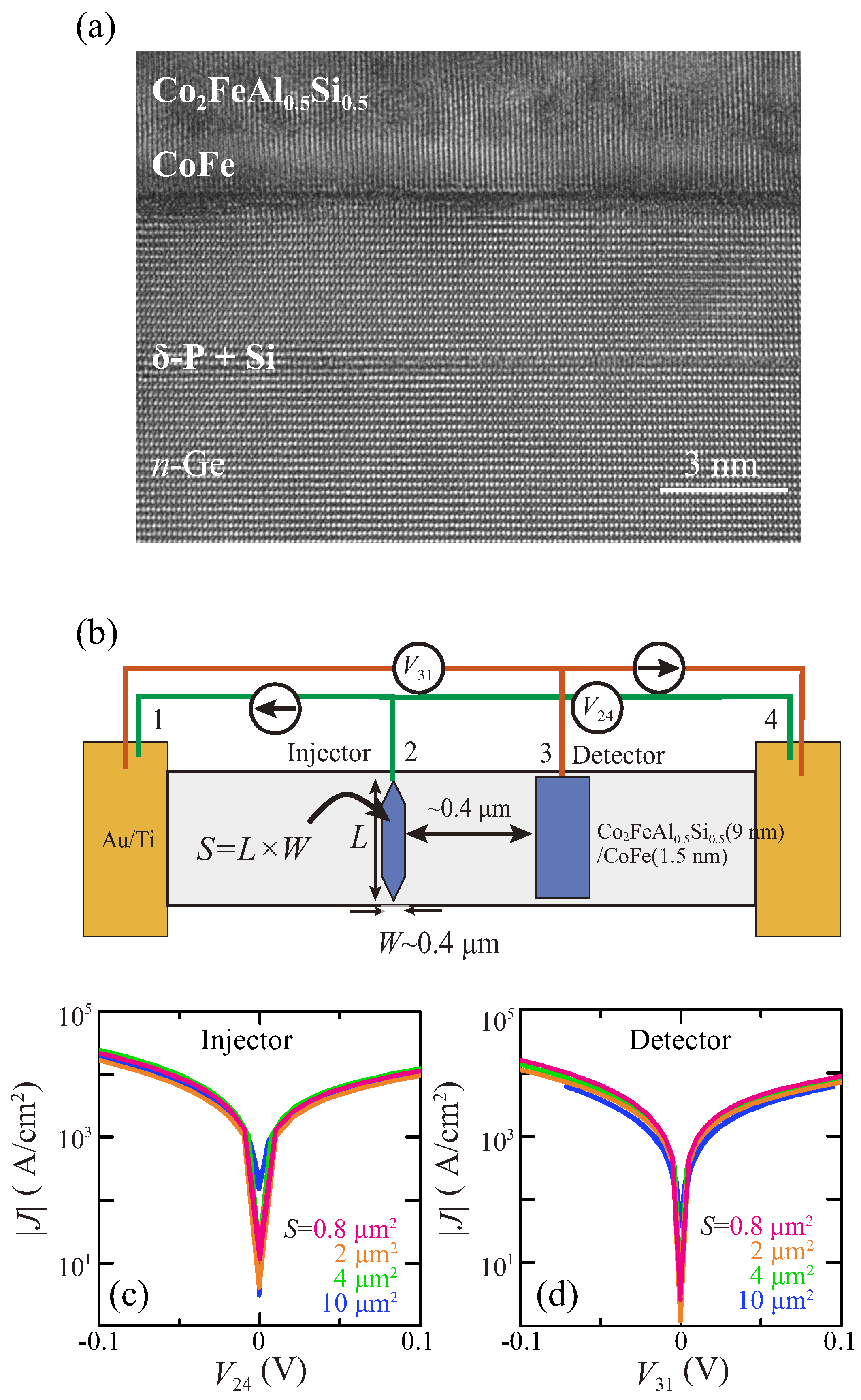
2. Samples and Fabrication Procedures
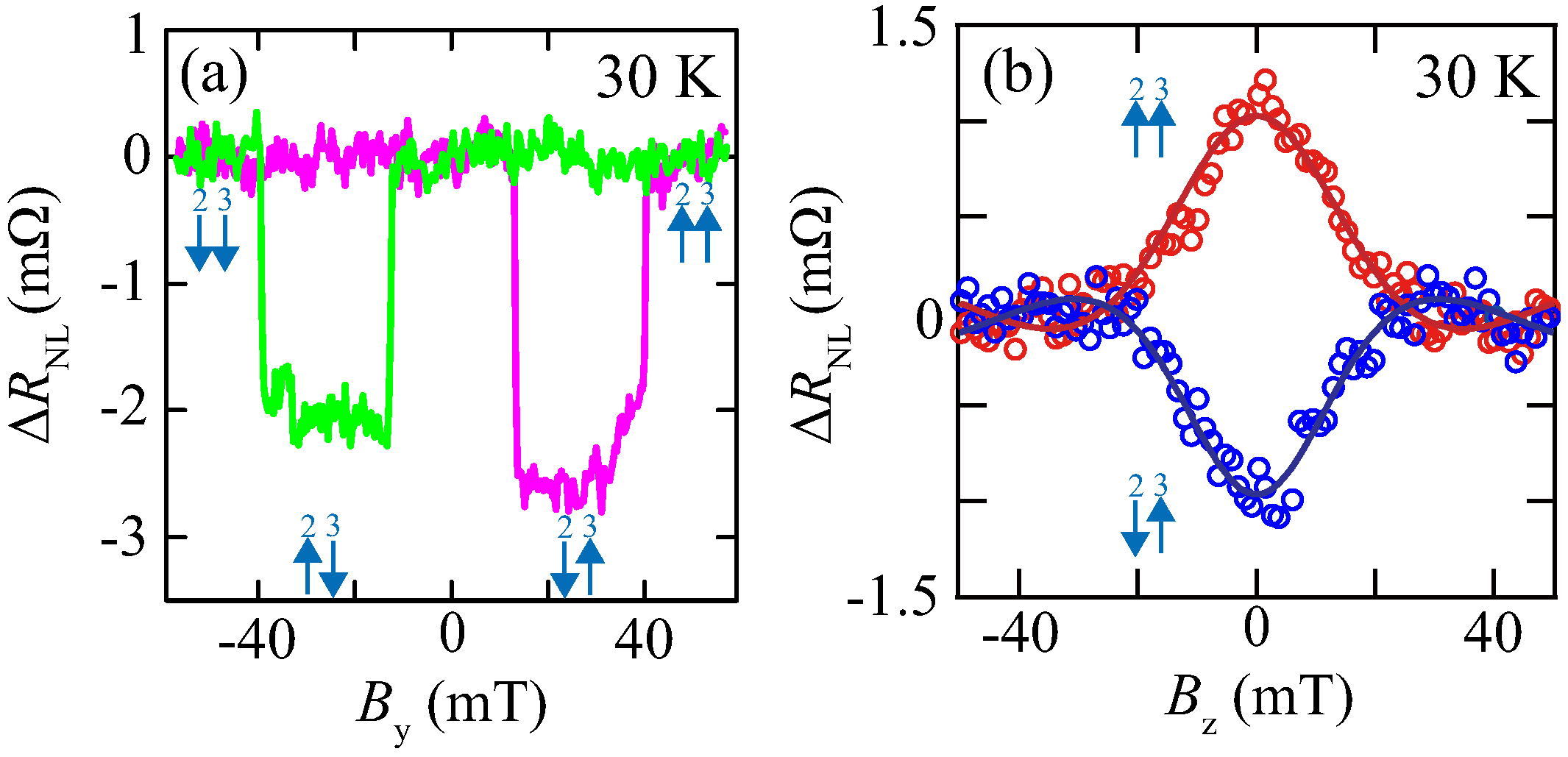
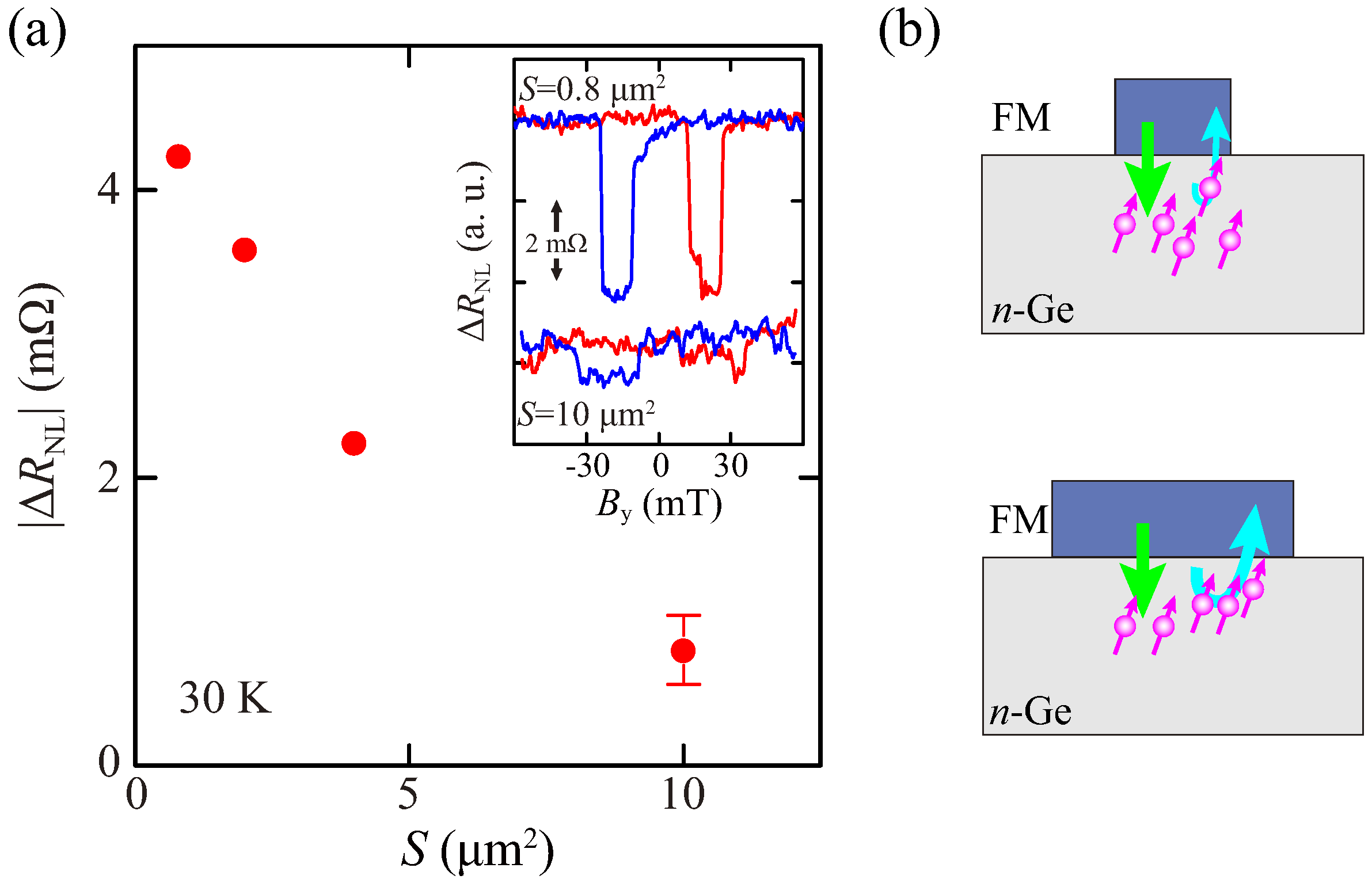
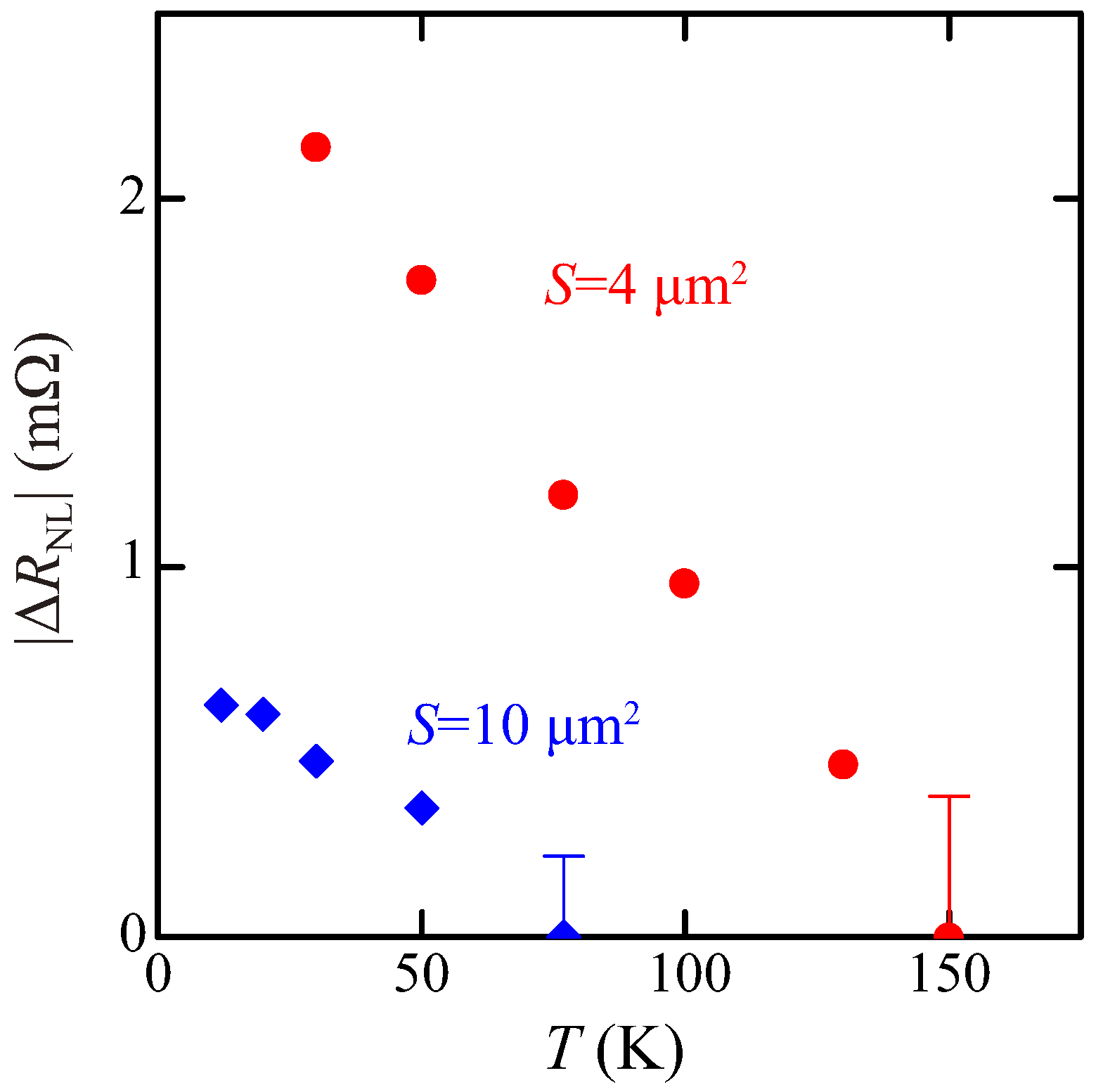
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Žutić, I.; Fabian, J.; Sarma, S.D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323. [Google Scholar] [CrossRef]
- Yuasa, S.; Djayaprawira, D.D. Giant tunnel magnetoresistance in magnetic tunnel junctions with a crystalline MgO(0 0 1) barrier. J. Phys. D Appl. Phys. 2007, 40, R337. [Google Scholar] [CrossRef]
- Tanaka, M.; Sugahara, S. MOS-Based Spin Devices for Reconfigurable Logic. IEEE Trans. Electron. Dev. 2007, 54, 961–976. [Google Scholar] [CrossRef]
- Taniyama, T.; Wada, E.; Itoh, M.; Yamaguchi, M. Electrical and optical spin injection in ferromagnet/ semiconductor heterostructures. NPG Asia Mater. 2011, 3, 65–73. [Google Scholar] [CrossRef]
- Hirohata, A.; Takanashi, K. Future perspectives for spintronic devices. J. Phys. D Appl. Phys. 2014, 47, 193001. [Google Scholar] [CrossRef]
- Lou, X.; Adelmann, C.; Crooker, S.A.; Garlid, E.S.; Zhang, J.; Reddy, K.S.M.; Flexner, S.D.; Palmstrøm, C.J.; Crowell, P.A. Electrical detection of spin transport in lateral ferromagnet-semiconductor devices. Nat. Phys. 2007, 3, 197–202. [Google Scholar] [CrossRef]
- Salis, G.; Fuhrer, A.; Schlittler, R.R.; Gross, L.; Alvarado, S.F. Temperature dependence of the nonlocal voltage in an Fe/GaAs electrical spin-injection device. Phys. Rev. B 2010, 81, 205323. [Google Scholar] [CrossRef]
- Song, C.; Sperl, M.; Utz, M.; Ciorga, M.; Woltersdorf, G.; Schuh, D.; Bougeard, D.; Back, C.H.; Weiss, D. Proximity Induced Enhancement of the Curie Temperature in Hybrid Spin Injection Devices. Phys. Rev. Lett. 2011, 107, 056601. [Google Scholar] [CrossRef] [PubMed]
- Bruski, P.; Manzke, Y.; Farshchi, R.; Brandt, O.; Herfort, J.; Remsteiner, M. All-electrical spin injection and detection in the Co2FeSi/GaAs hybrid system in the local and non-local configuration. Appl. Phys. Lett. 2013, 103, 052406. [Google Scholar] [CrossRef]
- Appelbaum, I.; Huang, B.; Monsma, D.J. Electronic measurement and control of spin transport in silicon. Nature 2007, 447, 295–298. [Google Scholar] [CrossRef] [PubMed]
- Van’t Erve, O.M.J.; Hanbicki, A.T.; Holub, M.; Awo-Affouda, C.; Li, C.H.; Thompson, P.E.; Jonker, B.T. Electrical injection and detection of spin-polarized carriers in silicon in a lateral transport geometry. Appl. Phys. Lett. 2007, 91, 212109. [Google Scholar] [CrossRef]
- Dash, S.P.; Sharma, S.; Patel, R.S.; Jong, M.P.; Jansen, R. Electrical creation of spin polarization in silicon at room temperature. Nature 2009, 462, 491–494. [Google Scholar] [CrossRef] [PubMed]
- Ando, Y.; Hamaya, K.; Kasahara, K.; Kishi, Y.; Ueda, K.; Sawano, K.; Sadoh, T.; Miyao, M. Electrical injection and detection of spin-polarized electrons in silicon through an Fe3Si/Si Schottky tunnel barrier. Appl. Phys. Lett. 2009, 94, 182105. [Google Scholar] [CrossRef]
- Ando, Y.; Maeda, Y.; Kasahara, K.; Yamada, S.; Masaki, K.; Hoshi, Y.; Sawano, K.; Izunome, K.; Sakai, A.; Miyao, M.; et al. Electric-field control of spin accumulation signals in silicon at room temperature. Appl. Phys. Lett. 2011, 99, 132511. [Google Scholar] [CrossRef]
- Sasaki, T.; Oikawa, T.; Suzuki, T.; Shiraishi, M.; Suzuki, Y.; Tagami, K. Electrical Spin Injection into Silicon Using MgO Tunnel Barrier. Appl. Phys. Exp. 2009, 2, 053003. [Google Scholar] [CrossRef]
- Suzuki, T.; Sasaki, T.; Oikawa, T.; Shiraishi, M.; Suzuki, Y.; Noguchi, K. Room-Temperature Electron Spin Transport in a Highly Doped Si Channel. Appl. Phys. Exp. 2011, 4, 023003. [Google Scholar] [CrossRef]
- Saito, Y.; Tanamoto, T.; Ishikawa, M.; Sugiyama, H.; Inokuchi, T.; Hamaya, K.; Tezuka, N. Local magnetoresistance through Si and its bias voltage dependence in ferromagnet/MgO/silicon-on-insulator lateral spin valves. J. Appl. Phys. 2014, 115, 17C514. [Google Scholar] [CrossRef]
- Ishikawa, M.; Oka, T.; Fujita, Y.; Sugiyama, H.; Saito, Y.; Hamaya, K. Spin relaxation through lateral spin transport in heavily doped n-type silicon. Phys. Rev. B 2017, 95, 115302. [Google Scholar] [CrossRef]
- Zhou, Y.; Han, W.; Chang, L.-T.; Xiu, F.; Wang, M.; Oehme, M.; Fischer, I.A.; Schulze, J.; Kawakami, R.K.; Wang, K.L. Electrical spin injection and transport in germanium. Phys. Rev. B 2011, 84, 125323. [Google Scholar] [CrossRef]
- Saito, H.; Watanabe, S.; Mineno, Y.; Sharma, S.; Jansen, R.; Yuasa, S.; Ando, K. Electrical creation of spin accumulation in p-type germanium. Sol. State Commun. 2011, 151, 1159–1161. [Google Scholar] [CrossRef]
- Jeon, K.-R.; Min, B.-C.; Jo, Y.-H.; Lee, H.-S.; Shin, I.-J.; Park, C.-Y.; Park, S.-Y.; Shin, S.-C. Electrical spin injection and accumulation in CoFe/MgO/Ge contacts at room temperature. Phys. Rev. B 2011, 84, 165315. [Google Scholar] [CrossRef]
- Kasahara, K.; Baba, Y.; Yamane, K.; Ando, Y.; Yamada, S.; Hoshi, Y.; Sawano, K.; Miyao, M.; Hamaya, K. Spin accumulation created electrically in an n-type germanium channel using Schottky tunnel contacts. J. Appl. Phys. 2012, 111, 07C503. [Google Scholar] [CrossRef]
- Jain, A.; Rojas-Sanchez, J.-C.; Cubukcu, M.; Peiro, J.; Le Breton, J.C.; Prestat, E.; Vergnaud, C.; Louahadj, L.; Portemont, C.; Ducruet, C.; et al. Crossover from Spin Accumulation into Interface States to Spin Injection in the Germanium Conduction Band. Phys. Rev. Lett. 2012, 109, 106603. [Google Scholar] [CrossRef] [PubMed]
- Kawano, M.; Santo, K.; Ikawa, M.; Yamada, S.; Kanashima, T.; Hamaya, K. Spin transport in p-Ge through a vertically stacked Ge/Fe3Si junction. Appl. Phys. Lett. 2016, 109, 022406. [Google Scholar] [CrossRef]
- Fujita, Y.; Yamada, M.; Tsukahara, M.; Oka, T.; Yamada, S.; Kanashima, T.; Sawano, K.; Hamaya, K. Spin Transport and Relaxation up to 250 K in Heavily Doped n-Type Ge Detected Using Co2FeAl0.5Si0.5 Electrodes. Phys. Rev. Appl. 2017, 8, 014007. [Google Scholar] [CrossRef]
- Yamada, M.; Tsukahara, M.; Fujita, Y.; Naito, T.; Yamada, S.; Sawano, K.; Hamaya, K. Room-temperature spin transport in n-Ge probed by four-terminal nonlocal measurements. Appl. Phys. Express 2017, 10, 093001. [Google Scholar] [CrossRef]
- Dushenko, S.; Koike, M.; Ando, Y.; Shinjo, T.; Myronov, M.; Shiraishi, M. Experimental Demonstration of Room-Temperature Spin Transport in n-Type Germanium Epilayers. Phys. Rev. Lett. 2015, 114, 196602. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, G.; Ferrand, D.; Molemkamp, L.W.; Filip, A.T.; Van Wees, B.J. Fundamental obstacle for electrical spin injection from a ferromagnetic metal into a diffusive semiconductor. Phys. Rev. B 2000, 62, R4790. [Google Scholar] [CrossRef]
- Rashba, E.I. Theory of electrical spin injection: Tunnel contacts as a solution of the conductivity mismatch problem. Phys. Rev. B 2000, 62, R16267. [Google Scholar] [CrossRef]
- Takahashi, S.; Maekawa, S. Spin injection and detection in magnetic nanostructures. Phys. Rev. B 2003, 67, 052409. [Google Scholar] [CrossRef]
- Fert, A.; Jaffrès, H. Conditions for efficient spin injection from a ferromagnetic metal into a semiconductor. Phys. Rev. B 2001, 64, 184420. [Google Scholar] [CrossRef]
- Kimura, T.; Otani, Y.; Hamrle, J. Enhancement of spin accumulation in a nonmagnetic layer by reducing junction size. Phys. Rev. B 2006, 73, 132405. [Google Scholar] [CrossRef]
- Yang, T.; Kimura, T.; Otani, Y. Giant spin-accumulation signal and pure spin-current-induced reversible magnetization switching. Nat. Phys. 2008, 4, 851–854. [Google Scholar] [CrossRef]
- Nomura, T.; Ohnishi, K.; Kimura, T. Geometrical dependence of spin current absorption into a ferromagnetic nanodot. J. Appl. Phys. 2016, 120, 142121. [Google Scholar] [CrossRef]
- Ishikawa, M.; Sugiyama, H.; Inokuchi, T.; Hamaya, K.; Saito, Y. Effect of the interface resistance of CoFe/MgO contacts on spin accumulation in silicon. Appl. Phys. Lett. 2012, 100, 252404. [Google Scholar] [CrossRef]
- Johnson, M.; Silsbee, R.H. Interfacial Charge-Spin Coupling: Injection and Detection of Spin Magnetization in Metals. Phys. Rev. Lett. 1985, 55, 1790–1793. [Google Scholar] [CrossRef] [PubMed]
- Jedema, F.J.; Heersche, H.B.; Filip, A.T.; Baselmans, J.J.A.; van Wees, B.J. Electrical detection of spin precession in a metallic mesoscopic spin valve. Nature 2002, 416, 713–716. [Google Scholar] [CrossRef] [PubMed]
- Kimura, T.; Otani, Y. Spin transport in lateral ferromagnetic/nonmagnetic hybrid structures. J. Phys. Condens. Matter 2007, 19, 165216. [Google Scholar] [CrossRef]
- Fujita, Y.; Yamada, M.; Yamada, S.; Kanashima, T.; Sawano, K.; Hamaya, K. Temperature-independent spin relaxation in heavily doped n-type germanium. Phys. Rev. B 2016, 94, 245302. [Google Scholar] [CrossRef]
- Yamada, M.; Fujita, Y.; Tsukahara, M.; Yamada, S.; Sawano, K.; Hamaya, K. Large impact of impurity concentration on spin transport in degenerate n-Ge. Phys. Rev. B 2017, 95, 161304(R). [Google Scholar] [CrossRef]
- Cesari, S.D.; Vitiello, E.; Giorgioni, A.; Pezzoli, F. Progress towards Spin-Based Light Emission in Group IV Semiconductors. Electronics 2017, 6, 19. [Google Scholar] [CrossRef]
- Sawano, K.; Hoshi, Y.; Kubo, S.; Arimoto, K.; Yamanaka, J.; Nakagawa, K.; Hamaya, K.; Miyao, M.; Shiraki, Y. Structural and electrical properties of Ge(111) films grown on Si(111) substrates and application to Ge(111)-on-Insulator. Thin Solid Films 2016, 613, 24–28. [Google Scholar] [CrossRef]
- Yamada, M.; Sawano, K.; Uematsu, M.; Itoh, K.M. Suppression of surface segregation of the phosphorous δ-doping layer by insertion of an ultra-thin silicon layer for ultra-shallow Ohmic contacts on n-type germanium. Appl. Phys. Lett. 2015, 107, 132101. [Google Scholar] [CrossRef]
- Yamada, M.; Fujita, Y.; Yamada, S.; Kanashima, T.; Sawano, K.; Hamaya, K. Control of electrical properties in Heusler-alloy/Ge Schottky tunnel contacts by using phosphorous δ-doping with Si-layer insertion. Mater. Sci. Semicond. Process. 2017, 70, 83–85. [Google Scholar] [CrossRef]
- Shan, R.; Sukegawa, H.; Wang, W.H.; Kodzuka, M.; Furubayashi, T.; Ohkubo, T.; Mitani, S.; Inomata, K.; Hono, K. Demonstration of Half-Metallicity in Fermi-Level-Tuned Heusler Alloy Co2FeAl0.5Si0.5 at Room Temperature. Phys. Rev. Lett. 2009, 102, 246601. [Google Scholar] [CrossRef] [PubMed]
- Hamaya, K.; Itoh, H.; Nakatsuka, O.; Ueda, K.; Yamamoto, K.; Itakura, M.; Taniyama, T.; Ono, T.; Miyao, M. Ferromagnetism and Electronic Structures of Nonstoichiometric Heusler-Alloy Fe3−xMnxSi Epilayers Grown on Ge(111). Phys. Rev. Lett. 2009, 102, 137204. [Google Scholar] [CrossRef] [PubMed]
- Yamada, S.; Sagar, J.; Honda, S.; Lari, L.; Takemoto, G.; Itoh, H.; Hirohata, A.; Mibu, K.; Miyao, M.; Hamaya, K. Room-temperature structural ordering of a Heusler compound Fe3Si. Phys. Rev. B 2012, 86, 174406. [Google Scholar] [CrossRef]
- Ikawa, M.; Kawano, M.; Sakai, S.; Yamada, S.; Kanashima, T.; Hamaya, K. Influence of the Ge diffusion on the magnetic and structural properties in Fe3Si and CoFe epilayers grown on Ge. J. Cryst. Growth 2017, 468, 676–679. [Google Scholar] [CrossRef]
- Fert, A.; George, J.-M.; Jaffrès, H.; Mattana, R. Semiconductors Between Spin-Polarized Sources and Drains. IEEE Trans. Electron. Dev. 2007, 54, 921–932. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, M.; Fujita, Y.; Yamada, S.; Sawano, K.; Hamaya, K. Spin Absorption Effect at Ferromagnet/Ge Schottky-Tunnel Contacts. Materials 2018, 11, 150. https://doi.org/10.3390/ma11010150
Yamada M, Fujita Y, Yamada S, Sawano K, Hamaya K. Spin Absorption Effect at Ferromagnet/Ge Schottky-Tunnel Contacts. Materials. 2018; 11(1):150. https://doi.org/10.3390/ma11010150
Chicago/Turabian StyleYamada, Michihiro, Yuichi Fujita, Shinya Yamada, Kentarou Sawano, and Kohei Hamaya. 2018. "Spin Absorption Effect at Ferromagnet/Ge Schottky-Tunnel Contacts" Materials 11, no. 1: 150. https://doi.org/10.3390/ma11010150
APA StyleYamada, M., Fujita, Y., Yamada, S., Sawano, K., & Hamaya, K. (2018). Spin Absorption Effect at Ferromagnet/Ge Schottky-Tunnel Contacts. Materials, 11(1), 150. https://doi.org/10.3390/ma11010150




