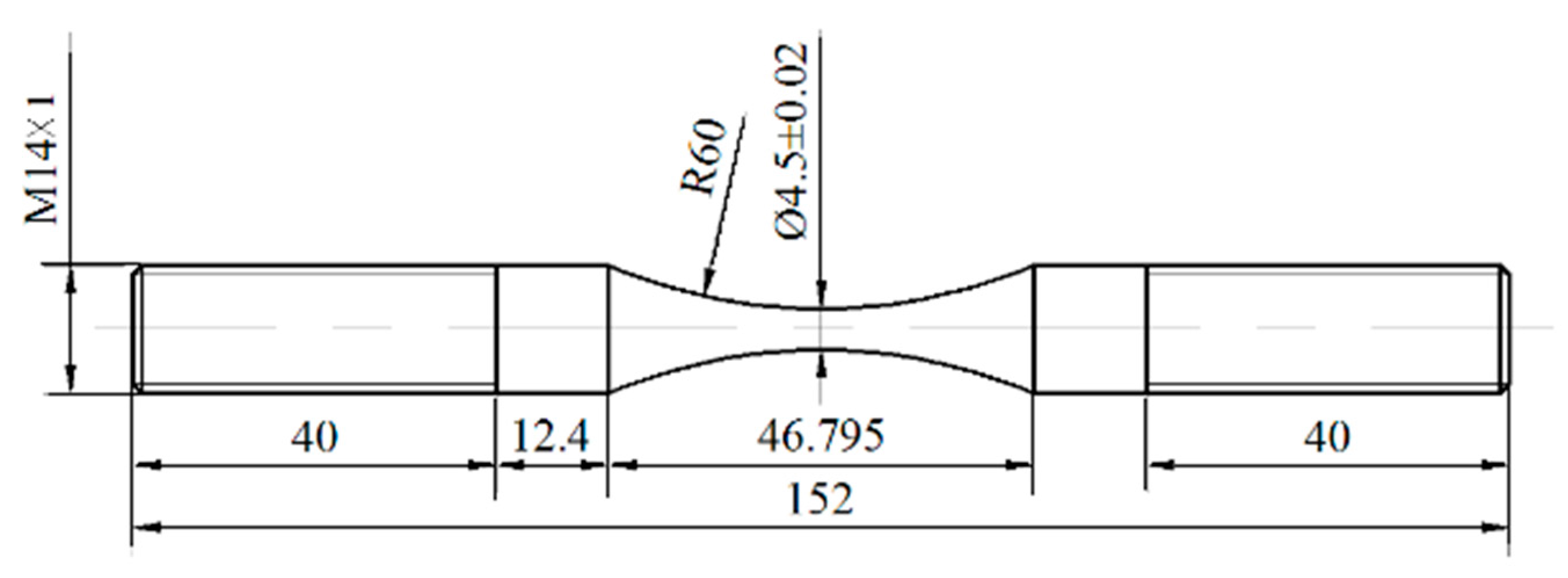
3.1. S-N Characteristics
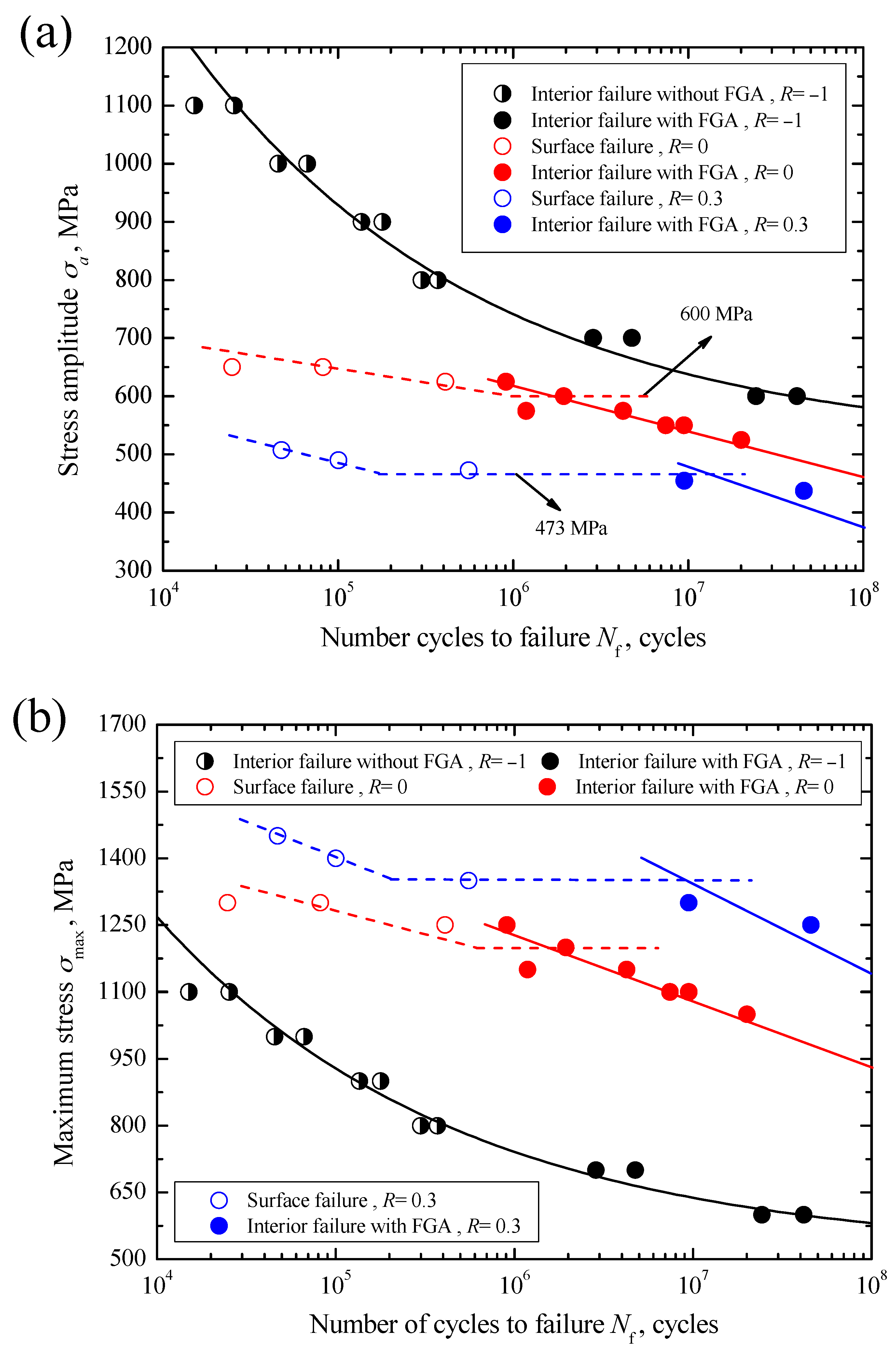
The data of applied stress amplitude
σa versus fatigue life
Nf for carburized Cr-Ni steel under axial loading with stress ratios of −1, 0 and 0.3 in the life region of 10
4–10
8 cycles are shown in
Figure 4a. Under
R = 0 and 0.3, by means of SEM observation of the crack initiation sites, fatigue failures of specimens can be divided into two modes: surface failure and interior failure. The surface failure mainly occurs at a relatively high stress region with a short life below 5 × 10
5 cycles, whereas the interior failure mainly occurs at a relatively low stress region with a long life beyond about 10
6 cycles. This result is very similar to the conventional results of some high strength steels in the long-life regime [
3,
6,
7,
9]. Approximately, duplex
S-N characteristics are presented. Thus, herein two
S-N curves are plotted to represent the
S-N characteristics of carburized Cr-Ni steel associated with surface and interior failures under
R = 0 or 0.3, indicated by dashed and solid lines in
Figure 4a, respectively. Moreover, for surface failure under
R = 0 or 0.3, a critical stress corresponding to around 10
6 cycles can be roughly determined, as indicated by the horizontal part of the dashed line in
Figure 4a, and below which surface failure cannot occur. It can be defined as the surface fatigue limit,
σw-s. Corresponding to
R = 0 and 0.3, the values of
σw-s are evaluated to be 600 MPa and 473 MPa, respectively. Conversely, for interior failure, the carburized Cr-Ni steel shows continuously descending
S-N characteristics under these two stress ratios. Herein the stress amplitude at 10
8 cycles is approximately defined as the interior fatigue limit,
σw-i, the values of
σw-i are evaluated to be about 455 MPa under
R = 0 and 370 MPa under
R = 0.3 by using fitted lines, respectively.
Differing from the fatigue failures under
R = 0 and 0.3, fatigue failure under
R = −1 only corresponds to the interior failure whether in the short or long life region. Especially at a stress amplitude of 1100 MPa, i.e., at the maximum stress of 1100 MPa, even if the applied maximum stress nearly approaches yield strength, interior failure still occurs. In consideration of the appearance of FGA or not, the interior failure can be further subdivided into interior failure without FGA and interior failure with FGA. The former mainly occurs in the short life region of below 5 × 10
5 cycles, whereas the latter mainly occurs in the long life region of more than 10
6 cycles. Actually, under
R = 0 and 0.3 the relevant interior failures only correspond to interior failure with FGA. Overall, the carburized Cr-Ni steel represents the constantly decreasing
S-N characteristics under
R = −1. Thus, a single
S-N curve is plotted to represent its
S-N characteristics under
R = −1, as indicated by a solid black line in
Figure 4a. The value of
σw-i under
R = −1 is evaluated to be about 580 MPa by using the fitted line. From
Figure 4a, it can be seen that the applied stress amplitudes are scattered in the ranges of 600–1100 MPa under
R = −1, 550–650 MPa under
R = 0 and about 438–508 MPa under
R = 0.3, respectively. Obviously, the allowable applied range of stress amplitude tends to decrease with increasing stress ratio. This is mainly attributed to the effect of the allowable applied maximum stress that should be less than the yield strength of the material. At a given stress amplitude, also it can be seen from
Figure 4a that the fatigue life tends to decrease with the increasing stress ratio regardless of the failure mode.
On the other hand, the data of maximum stress
σmax versus
Nf and the relevant
S-N curves associated with the surface failure or interior failure under these three stress ratios are shown in
Figure 4b. It can be seen from this figure that at a certain maximum stress level, the fatigue life tends to increase with increasing stress ratio regardless of failure mode. Also, the separation among
S-N curves with the same failure mode is distinct. Especially, the
S-N curve with the interior failure under
R = 0.3 is shifted to the long-life regime beyond 10
7 cycles. Combined with the results in
Figure 4a, therefore, it can be concluded that the fatigue life or strength of material in the long-life regime is not only determined by the stress amplitude, but also determined by the maximum stress.
In addition, with increasing stress ratio from −1 to 0.3, the failure probability for interior failure decreases and that for surface failure increases. That is, the life ranges for the interior failure are about 104–108 cycles under R = −1, about 106–108 cycles under R = 0 and about 107–108 cycles under R = 0.3, respectively. The reason is that, besides the effects of the maximum stress and stress amplitude, the failure mode of carburized Cr-Ni steel under axial loading is also affected by the carburized layer with higher hardness and compressive residual stress. It is well known that the compressive residual stress can restrain crack initiation. Under the condition of tension-tension, the allowably applied maximum tensile stress tends to increase with increasing stress ratio, and it can overcome the influence of the compressive residual stress as well as promote crack initiation from the surface. However, under the condition of tension-compression, due to the smaller tensile stress and the existence of compressive stress, the crack is more easily initiated from the interior region. Also, the high hardness can restrain crack initiation from the surface under axial stress.
3.2. Constant Life Diagram
The Goodman equation was used to represent the effect of stress ratio
R or mean stress
σm on the fatigue strength of carburized Cr-Ni steel under axial loading, given by [
26]
where
σ−1 is the fatigue strength at a given fatigue life under
R = −1. Based on the basic relation among
σm,
R and
σa, Equation (1) can be rewritten as:
Based on Equation (2) and the evaluated values of
σw-i under stress ratios from the
S-N diagram in
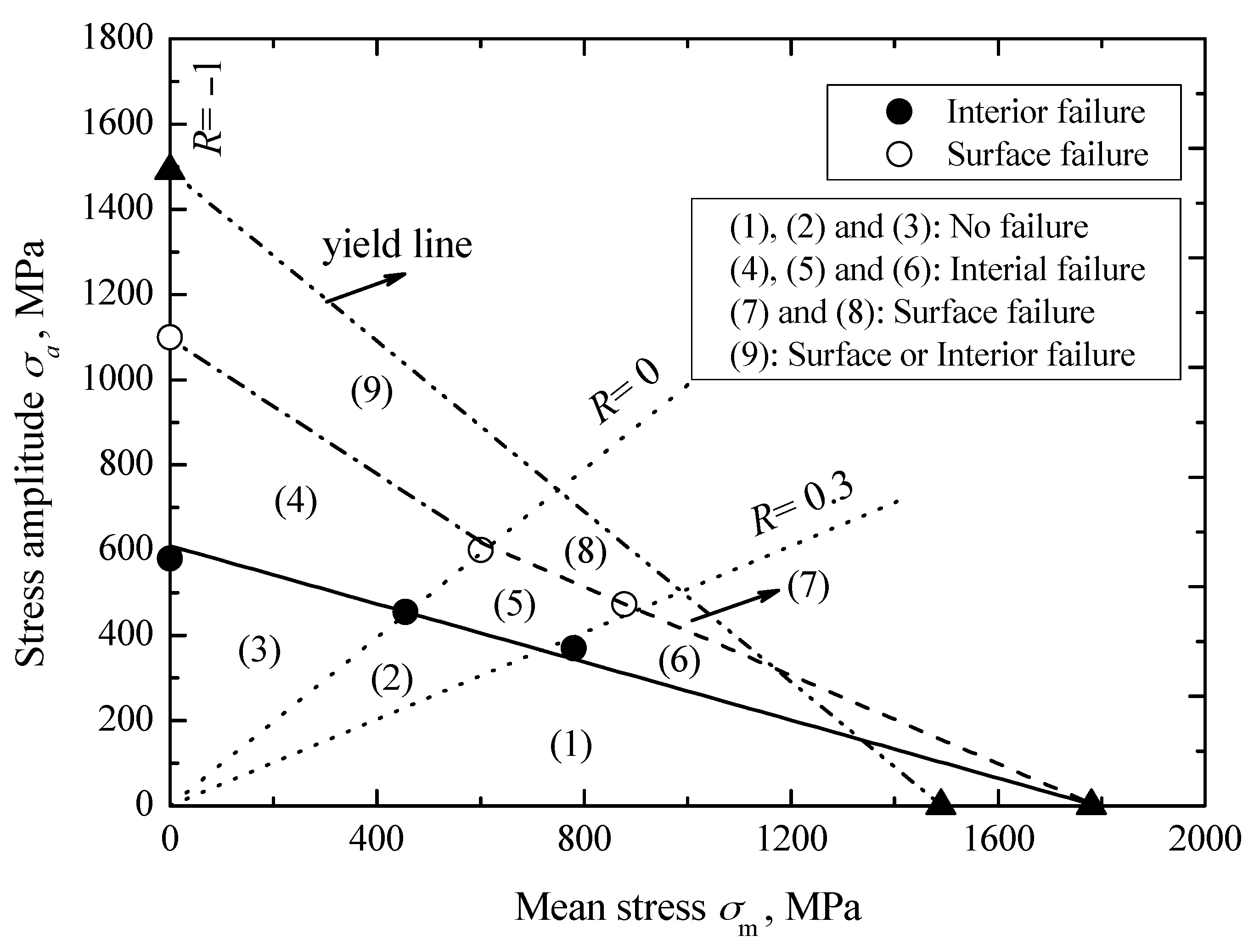
Figure 4a, the relationship between interior fatigue strength and mean stress can be established by using the least square method, as indicated by a solid line in
Figure 5. This line corresponds to the constant life line with interior failure at
N = 10
8 cycles, and is given by:
where the values of
σb and
σ−1 at
N = 10
8 cycles are 1780 MPa and 610 MPa, respectively. Similarly, combined with the evaluated values of
σw-s from the
S-N diagram, the relationship between surface fatigue strength and mean stress is established, as indicated by a dash line in
Figure 5. However since there is no surface failure data under
R = −1, so the stress amplitude
σa at 1100 MPa is herein assumed to be the transformation stress from surface failure to interior failure under
R = −1, i.e., the surface failure limit at
N = 10
6 cycles. Thus, the relationship between surface fatigue strength and mean stress, corresponding to the stress ratio from −1 to 0, can be established, as indicated by a dash-dot line in
Figure 5. The relevant constant life lines for the surface failure at
N = 10
6 cycles, can be given by:
Obviously, it can be seen from
Figure 5 that fatigue strength has a decreasing tendency with increasing mean stress, and the decreasing rate for the surface fatigue strength is faster than that for the interior fatigue strength. Moreover, at a certain mean stress, with the decreasing of the stress ratio from 0.3 to −1, fatigue strength tends to increase regardless of failure mode.
Furthermore, the yield criterion can be expressed as [
26]
where
is the cyclic yield strength, but it can be replaced by
σy as an approximation [
26]. A thick dash-dot-dot line in
Figure 5 indicates the relevant yield line. Therefore, combined with the established constant life lines for surface and interior failures, as well as the constant stress ratio lines for
R = 0 and 0.3 indicated by dot lines in
Figure 5, the total zone under this yield line can be divided into nine small zones. If the applied stress amplitude and mean stress fall in the zones of 1, 2, and 3, the fatigue failure and yield phenomenon do not occur within the 10
8 cycles. If they fall in the zones of 4, 5, and 6, the interior failure is the predominant failure mode and surface failure almost does not occur. If they fall in zones 7 and 8, surface failure is predominant and interior failure almost does not occur. If they fall in zone 9, both the surface failure and the interior failure all can occur. However, it should be noted that with the decrease of tensile mean stress, the probability for interior failure tends to increase.
3.3. Crack Initiation Mechanism
As mentioned above, fatigue failures of specimens consist of surface failure, interior failure without FGA and interior failure with FGA. For interior failure, fatigue cracks all originate from interior non-metallic inclusions. The deformation inconsistency between the inclusion and the ambient matrix contributes to the crack initiation.
Figure 6a–h present the typical fracture surfaces with interior failure under different stress ratios. The fisheyes can be observed on the fracture surfaces, and the inclusions are nearly located at the center of the fisheyes, as shown in
Figure 6a,c,e,g.
Because of the inhibiting effect of the carburized layer, the inclusions which cause crack initiation are mainly confined to the core matrix region under R = −1. In other words, even if there is a larger inclusion in the carburizing layer, it will not induce fatigue failure. However, with the increasing stress ratio from −1 to 0.3, the occurrence probability of interior inclusion-induced crack initiation in the carburizing layer tends to increase. This is attributed to the increasing tensile stress under higher stress ratio, which will overcome the effect of the carburized layer with compressive residual stress. Moreover, it can be found that the sizes of fisheyes within the carburized layer are smaller than those in the core region due to the relatively slow crack growth rate in the carburized layer. Detailed analysis about crack sizes will be given in the following section.
FGA cannot be observed around the inclusion in the short life region of below 5 × 10
5 cycles, as shown in
Figure 5b. Otherwise, in the long life region of about more than 10
6 cycles, it can be found under each stress ratio, as shown in
Figure 6d,f,h. It is confirmed that the formation of FGA is largely related to the number of loading cycles. Maybe, at least fatigue life with about 10
6 cycles is a necessary condition for FGA formation.
Furthermore, from
Figure 6d,f,h, it can be seen that with increasing stress ratio, the FGA morphology becomes vague and the FGA size approximately tends to decrease. Especially under
R = 0.3, the FGA is hard to distinguish. This reveals that increasing stress ratio, i.e., decreasing of compressive stress and stress amplitude, may restrain FGA formation. In general, the fracture surface without FGA can be divided into three areas: (i) inclusion; (ii) fisheye; (iii) momentary fracture area (MFA), as shown in
Figure 6a. The fracture surface with FGA can be divided into four areas: (i) inclusion; (ii) FGA; (iii) fisheye, and (iv) MFA, as shown in
Figure 6c or e.
For the surface induced failure, the typical fracture surfaces under different stress ratios are shown in
Figure 6i–l. Fatigue cracks mainly originate from surface inclusions shown in
Figure 6j,l or surface machining defects shown in
Figure 6k. Herein, the surface inclusion and machining defect are all defined as surface defect (SD). Therefore, the entire fracture surface with surface failure can be roughly divided into four areas: (i) SD; (ii) surface smooth area (SSA); (iii) surface rough area; (iv) MFA, as shown in
Figure 6i.
3.4. Discussion Based on Fractography
Based on fractography, several parameters were defined to discuss the crack geometrical characteristics. For interior failure, the parameter
dinc was defined to indicate the depth of interior inclusion from the center to the nearest edge of the fracture surface. Parameters
rinc,
rFGA, and
rfisheye were defined to denote the radius of inclusion, FGA, and fisheye, respectively. For surface failure, the shapes of SD and SSA were also approximately considered to be circular. Thus,
rSD and
rSSA were defined to denote the radius of SD and SSA, respectively. The relationships between
dinc and
Nf under stress ratios of −1, 0 and 0.3 are shown in
Figure 7.
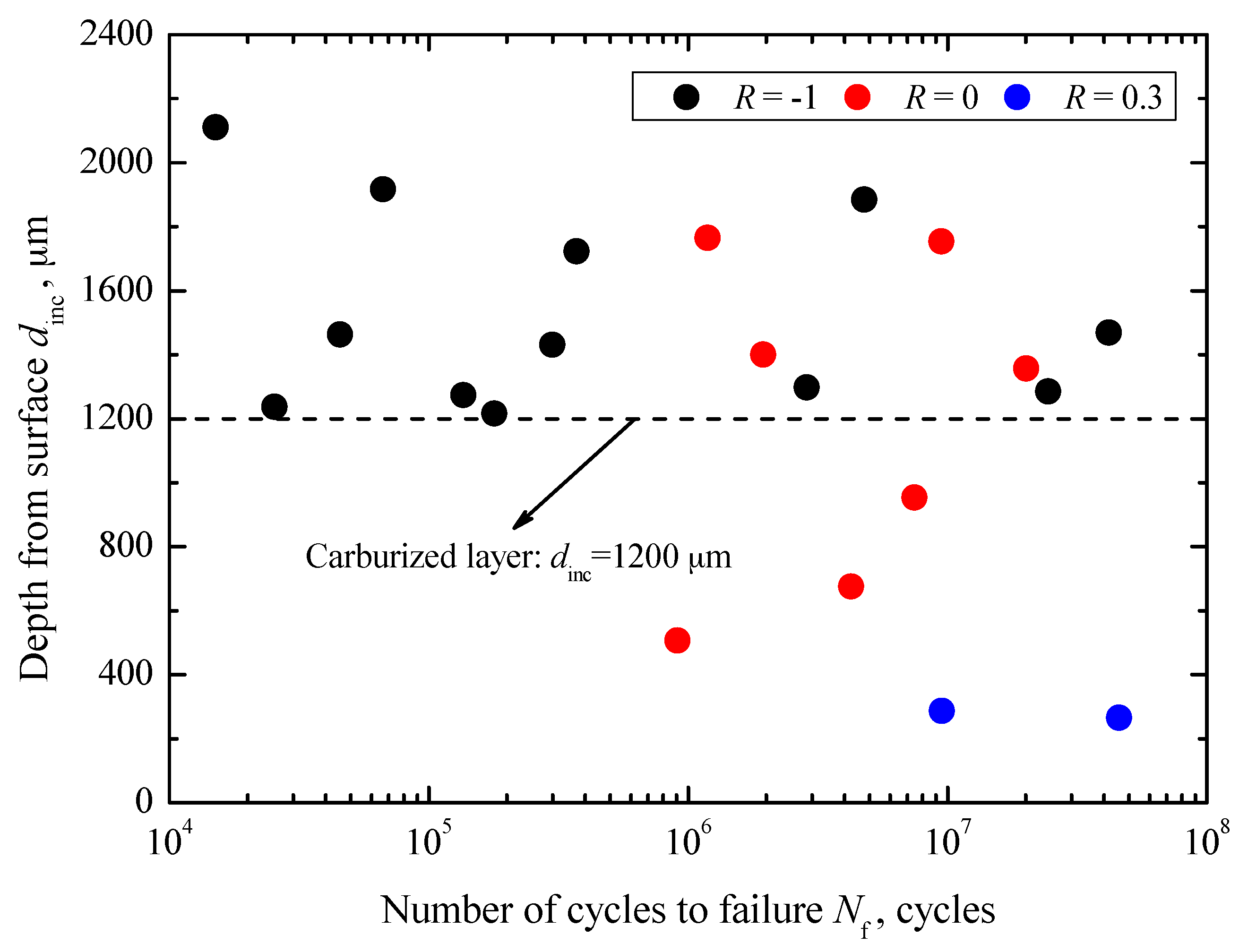
In general, the values of
dinc under these three stress ratios are independent of fatigue life. The values of
dinc under
R = −1 are scattered in the range of 1216–2110 μm, which are obviously larger than the depth of the carburized layer. Under
R = 0, the values of
dinc are scattered in the range of 506–1765 μm, some of which are less than the depth of carburized layer. Under
R = 0.3, the values of
dinc are only scattered in the range of 265–285 μm, all less than the depth of carburized layer. Even only two data points under the stress ratio of 0.3 are obtained, but it can be found that the failure probability relating to the inclusions contained in the carburized layer is larger at a higher stress ratio. This is consistent with the results of fracture surface observation. The reason is that at positive stress ratio, only tension is applied and it will easily overcome the compressive residual stress in the carburized layer and promote crack initiation from the carburized layer. In other words, under higher stress ratio, the effect of the damage zone becomes larger. The relationships between
rinc,
rFGA and
rfisheye, and
Nf under stress ratios of −1, 0 and 0.3 are shown in
Figure 8.
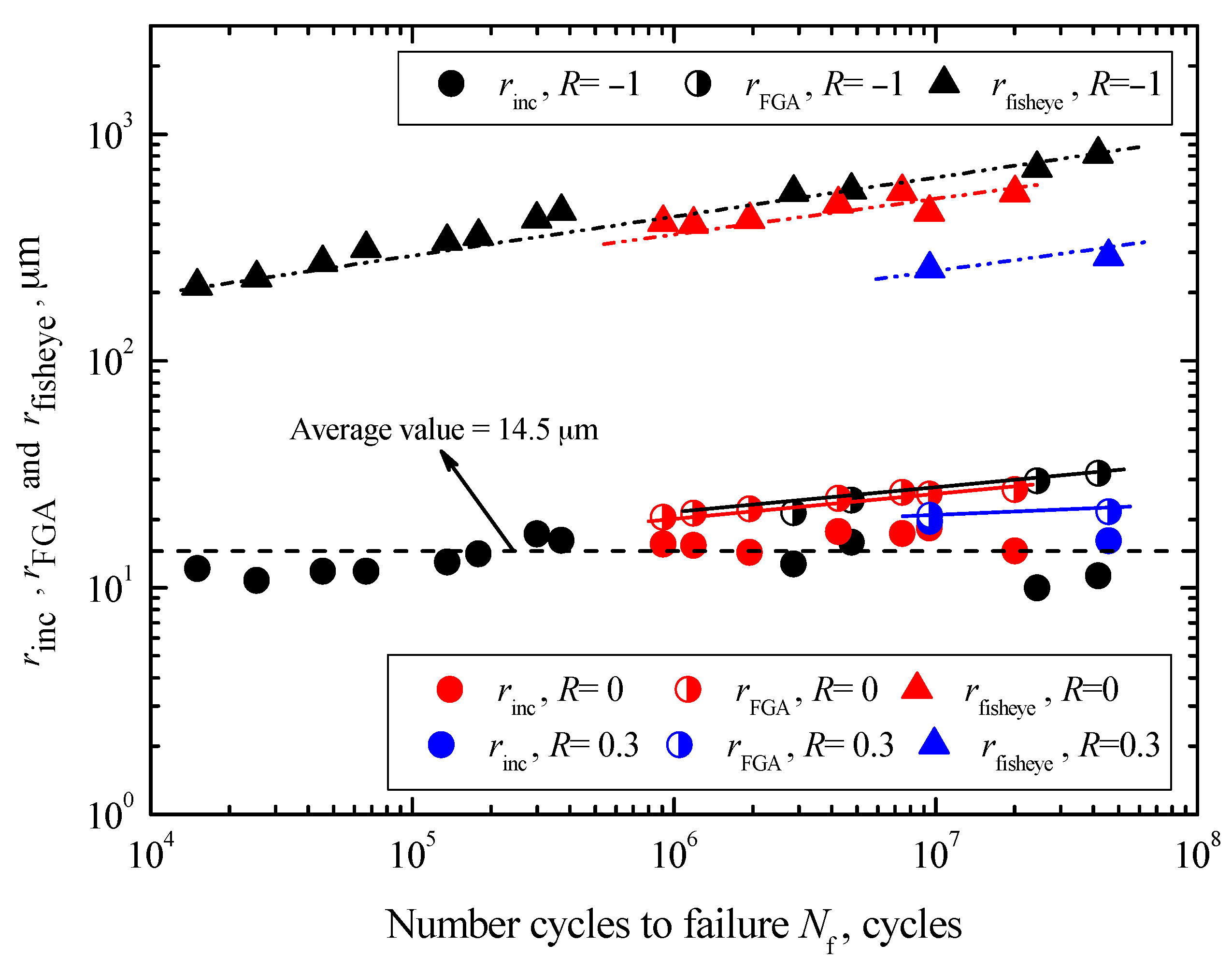
First, the values of
rinc are scattered over the range between 9.9 μm and 19.6 μm, regardless of both fatigue life and stress ratio. The average value is about 14.5 μm, as denoted by a dashed black line in
Figure 8. Conversely, this means that the sizes of inclusion mainly rely on the melting technique of steel. Secondly, under each stress ratio, the values of
rFGA all tend to increase with increasing
Nf, denoted by solid lines with different colors in
Figure 8. Corresponding to a certain fatigue life, the values of
rFGA under
R = −1 are slightly larger than those under
R = 0, but this phenomenon is not so distinct in the log-log coordinate. However, obviously the values of
rFGA are the smallest under
R = 0.3. Therefore, it can be concluded that the sizes of FGA tend to decrease with increasing stress ratio at a certain fatigue life. This confirms that at a given fatigue life, the higher stress ratio associated with larger
σmax and lower
σa will promote crack growth and restrain FGA formation at the crack initiation stage. Furthermore, by defining
ρFGA as the ratio of
rFGA to
rinc, the numerical relationships between
ρFGA and
σa under different stress ratios can be described as
and
where
f1(
R) and
f2(
R) are the functions of
R. Based on Equation (6), the FGA size at a given stress state can be estimated if the inclusion size is known. The sizes of the fisheye also tend to increase with increasing
Nf at each stress ratio, and the variation trends are indicated by doubly chained lines with different colors. The values of
rfisheye under
R = 0 are lower than those under
R = −1, while those under
R = 0.3 are lowest at a certain fatigue life. Just like FGA, the sizes of fisheye tend to decrease with increasing stress ratio at a certain fatigue life.
On the other hand, the relationships between
rSD and
rSSA, and
Nf under these three stress ratios are shown in
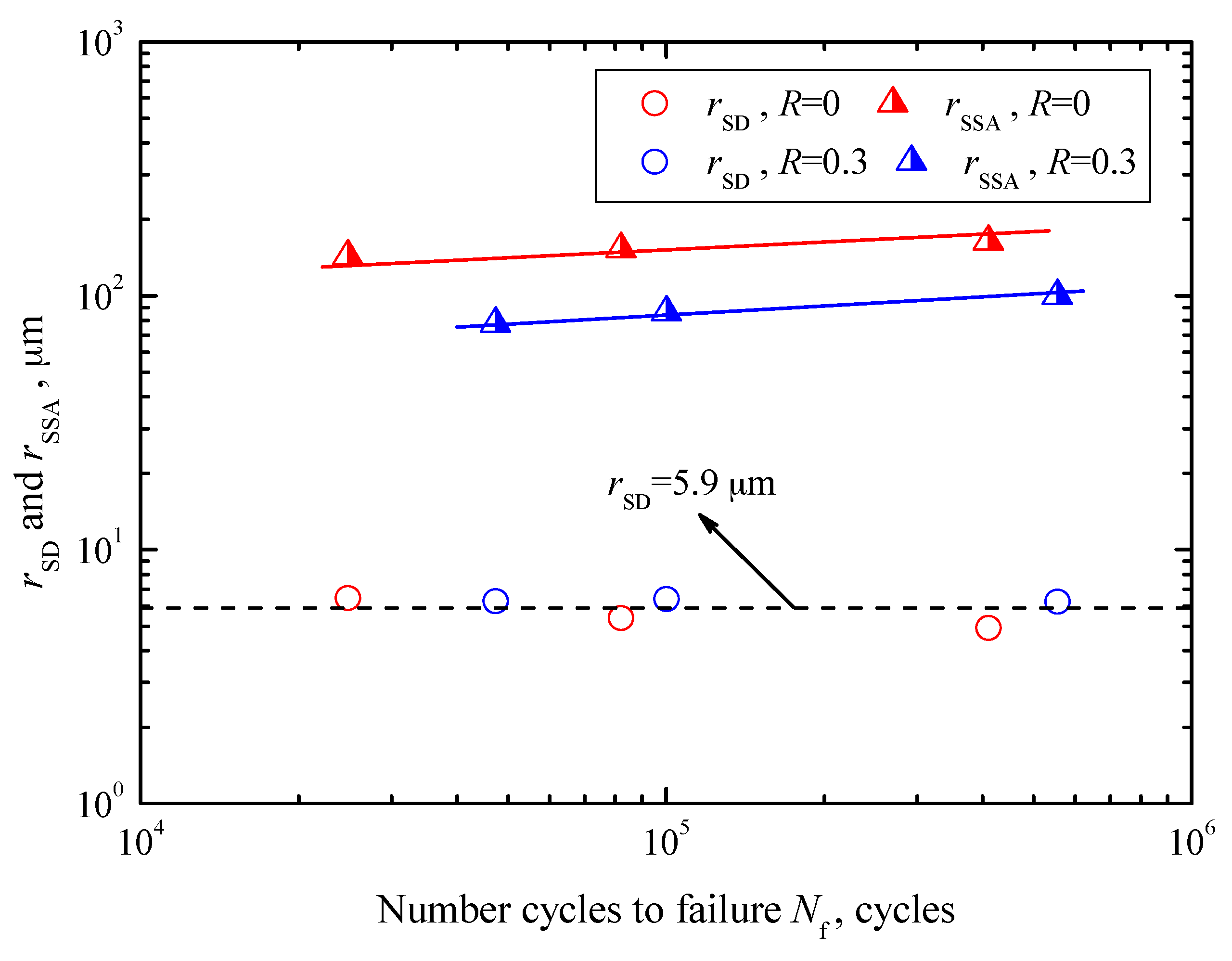
Figure 9. The values of
rSD are scattered throughout 4.9–6.5 μm with an average value of 5.9 μm, independent of fatigue life and stress ratio, as denoted by a dashed line in
Figure 9. Apparently, surface defects are mainly dependent on the machining process. Moreover, the values of
rSSA tend to increase with increasing fatigue life at each stress ratio, indicated by solid lines with different colors in
Figure 9. The values of
rSSA under
R = 0 are scattered in the range of 143.3–163.4 μm, while those under
R = 0.3 are scatted in the range of 77.7–99.9 μm. By contrast, the sizes of SSA under
R = 0 are obviously larger at a certain fatigue life.
3.5. Evaluation of Stress Intensity Factor
For interior failure, the inclusion, FGA, and fisheye all are approximately equivalent to interior circular cracks [
27]. Thus, their stress intensity factor (SIF) ranges, Δ
Kinc, Δ
KFGA, and Δ
Kfisheye, are determined by [
28]:
where ∆
σ is the stress range. Similarly, for surface failure, the SIF ranges for the SD and SSA, Δ
KSD and Δ
KSSA, are given by [
28]:
where parameter
E(
k) is between 1 and
π/2.
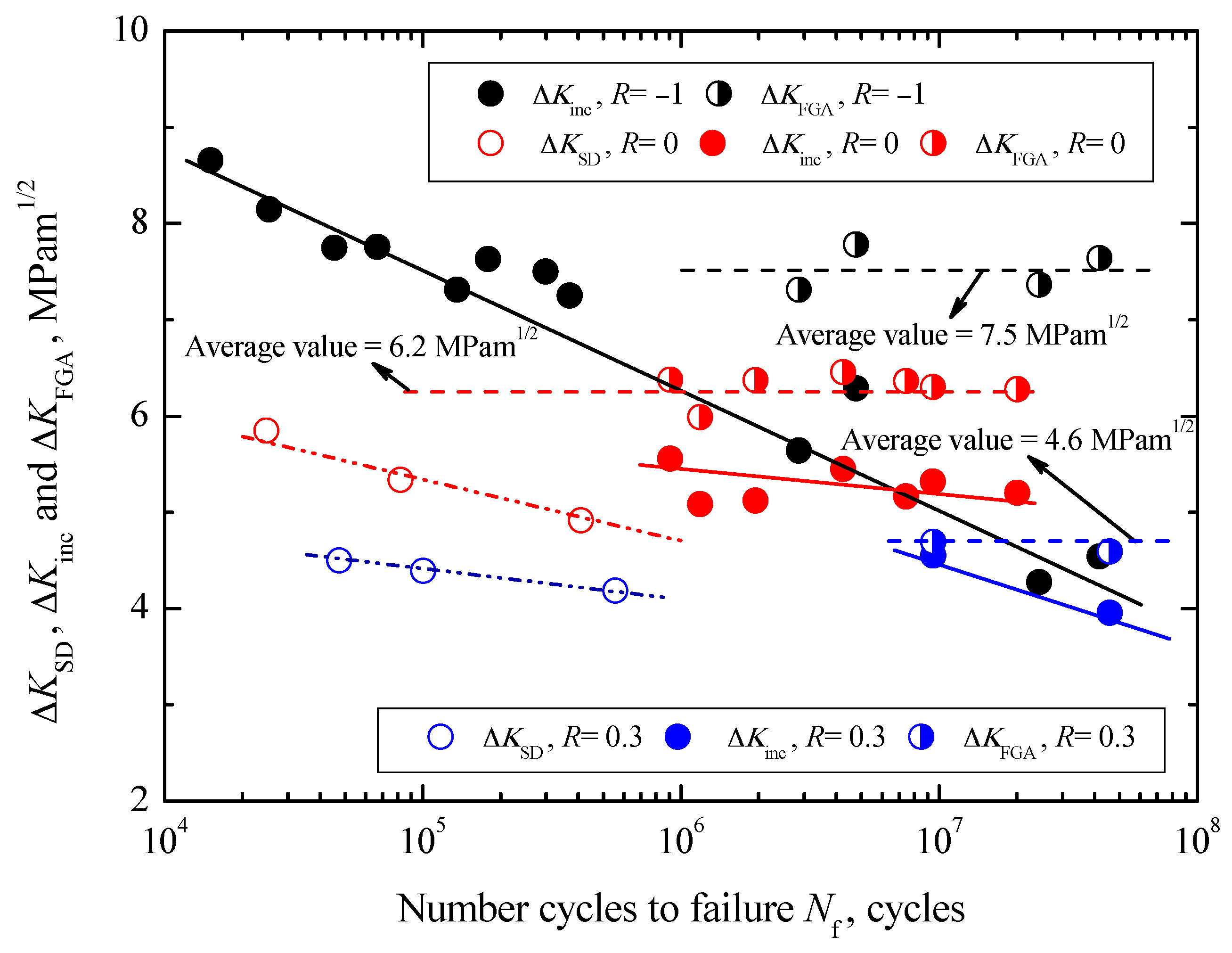
The relationships between Δ
Kinc and Δ
KFGA, and
Nf under three stress ratios are shown in
Figure 10. First, the values of Δ
Kinc are in the range of 4.3–8.6 MPa∙m
1/2 under
R = −1, 5.1–5.6 MPa∙m
1/2 under
R = 0 and 3.9–4.5 MPa∙m
1/2 under
R = 0.3, respectively. They all tend to decrease with increasing
Nf, i.e., decreasing of ∆
σ, under each stress ratio, denoted by some solid lines in
Figure 10. Moreover, at a given fatigue life the values of Δ
Kinc tend to decrease with increasing stress ratio. Secondly, the values of Δ
KFGA are in the ranges of 7.3–7.8 MPa∙m
1/2 under
R = −1, 5.9–6.5 MPa∙m
1/2 under
R = 0 and 4.5–4.7 MPa∙m
1/2 under
R = 0.3, respectively. Approximately, they keep constant under each stress ratio, and the mean values are 7.5 MPa∙m
1/2 under
R = −1, 6.2 MPa∙m
1/2 under
R = 0 and 4.6 MPa∙m
1/2 under
R = 0.3, respectively. Compared with the change tendency of Δ
Kinc, the values of Δ
KFGA are regardless of fatigue life, but also tend to decrease with increasing stress ratio, denoted by dashed lines in
Figure 10. Under
R = −1, the values of Δ
KFGA are larger than the values of Δ
Kinc at a certain fatigue life when the FGA can be observed in the vicinity of inclusion. However, the values of Δ
Kinc corresponding to the nonexistence of FGA are approximately not less than the mean value of Δ
KFGA at about 7.5 MPa∙m
1/2. Therefore, it can be assumed that the upper limit value of Δ
Kinc corresponding to the formation FGA is about 7.5 MPa∙m
1/2. In other words, FGA will not be formed if Δ
Kinc is larger than 7.5 MPa∙m
1/2. Similarly, the upper limit values of Δ
Kinc corresponding to the formation FGA are evaluated to be about 6.2 MPa∙m
1/2 under
R = 0 and 4.6 MPa∙m
1/2 under
R = 0.3, respectively.
Compared with the other experimental results [
3,
7], the evaluated values of Δ
KFGA under
R = −1 in this study are larger. The reason is that in these studies, the stress amplitude
σa is used for the calculation of Δ
K rather than the stress range. Based on the FGA formation mechanism and fracture surface morphology, Δ
KFGA at different stress ratios can be defined as the threshold values controlling stable growth of interior macroscopic crack at different stress ratios, and the fatigue behavior within the FGA is mainly governed by crack initiation.
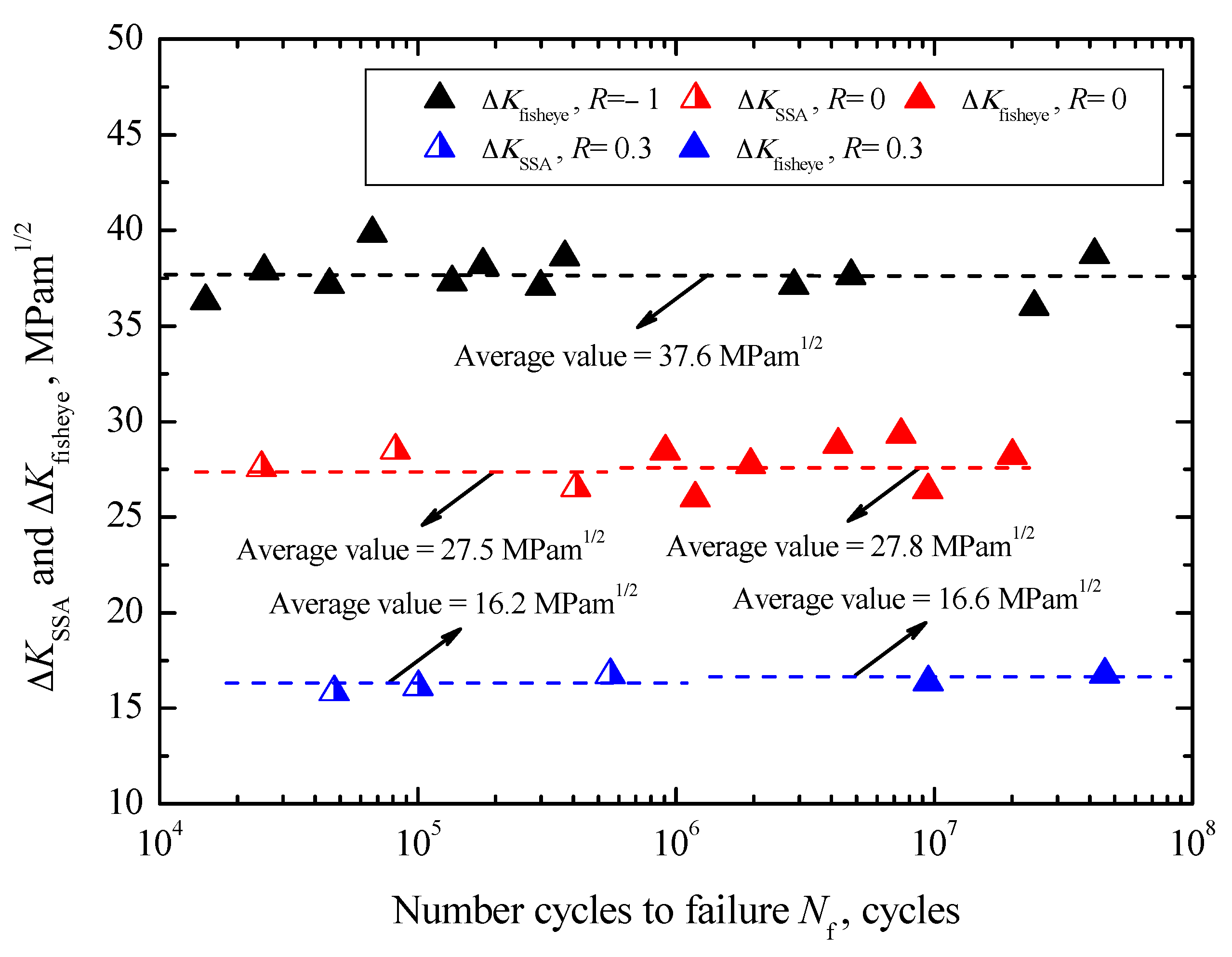
The values of Δ
Kfisheye are in the ranges of 35.9–39.8 MPa∙m
1/2 under
R = −1, 25.9–29.3 MPa∙m
1/2 under
R = 0, and 16.3–16.7 MPa∙m
1/2 under
R = 0.3, respectively. Approximately, they also keep constant under each stress ratio, and the corresponding mean values are 37.6 MPa∙m
1/2 under
R = −1, 27.8 MPa∙m
1/2 under
R = 0 and 16.6 MPa∙m
1/2 under
R = 0.3, respectively. Just like Δ
KFGA, the values of Δ
Kfisheye are also regardless of fatigue life and tend to decrease with increasing stress ratio, denoted by dashed lines in
Figure 11. Previous studies [
3,
7,
9] had confirmed that the formation of fisheye means the beginning of the interior crack growth in an unstable manner, and ∆
Kfisheye can be regarded as the threshold value referring to the condition in which a crack extends in an unstable manner without an increase in load.
On the other hand, the relationships between Δ
KSD and
Nf under two stress ratios are also shown in
Figure 10. The values of Δ
KSD are in the ranges of 4.9–5.8 MPa∙m
1/2 under
R = 0 and 4.2–4.5 MPa∙m
1/2 under
R = 0.3, respectively. By contrast, it can be found that under the same stress ratio, the values of Δ
KSD are slightly higher than those of Δ
Kinc, and the partial values are similar to the values of Δ
KFGA. Moreover, just like Δ
Kinc, they tend to decrease with increasing
Nf under each stress ratio, and to decrease with increasing stress ratio. From the viewpoint of crack growth, approximately the minimum value of Δ
KSD can be defined as the threshold value controlling surface crack growth under a given ratio, about 4.9 MPa∙m
1/2 under
R = 0 and 4.2 MPa∙m
1/2 under
R = 0.3. Correspondingly, that is the reason why the
S-N curves of carburized Cr-Ni steel have the traditional asymptote shape under stress ratios of 0 and 0.3.
The relationship between Δ
KSSA and
Nf is also shown in
Figure 11. The values of Δ
KSSA are in the range of 26.5–28.5 MPa∙m
1/2 with an average value of 27.5 MPa∙m
1/2 under
R = 0, while those are in the range of 15.8–16.7 MPa∙m
1/2 with an average value of 16.2 MPa∙m
1/2 under
R = 0.3, denoted by dashed lines in
Figure 11. Apparently, the values of Δ
KSSA tend to decrease with increasing stress ratio, regardless of fatigue life. Moreover, it should be noted that the values of Δ
KSSA are very similar to the values of Δ
Kfisheye at each stress ratio. Therefore, herein Δ
KSSA can be approximately regarded as the threshold value controlling the unstable growth of surface crack.
Therefore, it can be concluded that fatigue processes for the interior failure without FGA and surface failure in a short life regime less than 5 × 105 cycles are mainly dominated by crack growth from inclusion to fisheye or from SD to SSA. Conversely, the fatigue process for interior failure with FGA in the long life regime larger than 106 cycles is largely governed by crack initiation within FGA.
3.7. Fatigue Life Prediction
For interior failure with FGA, by using Equation (17), the crack initiation life curves corresponding to different
c-values under
R = −1 can be established, as denoted by some dashed lines in
Figure 12. Apparently, it can be seen that the crack initiation life has an increasing tendency with increasing crack size at a certain stress. Moreover, for a given crack size, the required number of cycles at the lower stress level is larger than that at the higher stress level, and almost approaches the total fatigue life. It should be noted that the established crack initiation life curve corresponding to the FGA size, indicated by a solid line in
Figure 12, is consistent with the experimental data. This further reveals that the long life is mainly consumed in the crack initiation stage inside the FGA. Based on the results under
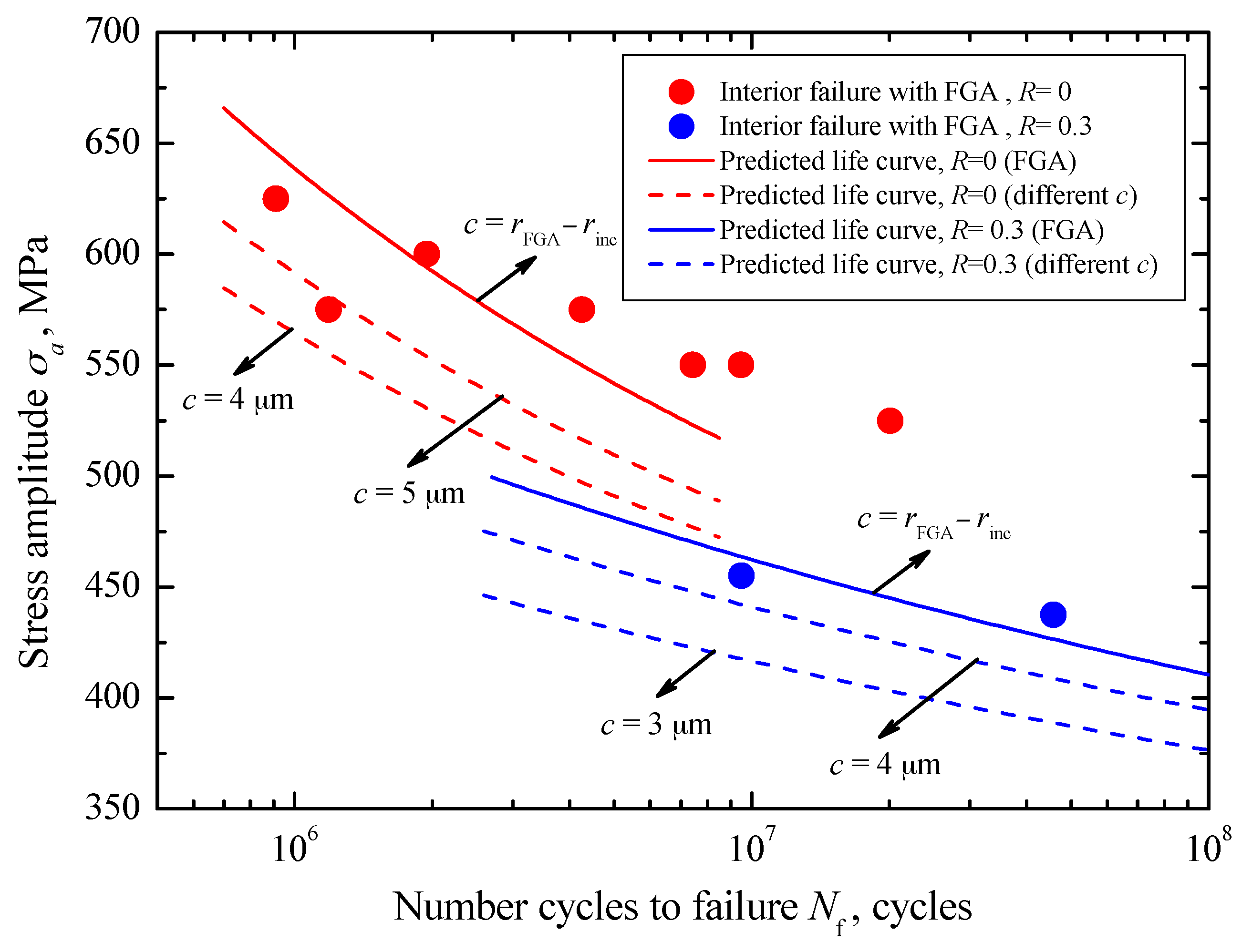
R = −1 and Equation (20), the predicted crack initiation life curves corresponding to FGA sizes under
R = 0 and
R = 0.3 can be plotted by two solid lines as in
Figure 13, respectively. Basically, the predicted curves well reflect the change trend of test data under these two stress ratios. Moreover, under each stress ratio, some crack initiation life curves corresponding to the small crack sizes less than the FGA size are plotted by the dashed lines in
Figure 13. Similar results can be seen in
Figure 12.
For interior failure without FGA, combined with the sizes of inclusion and the relevant
S-N data for
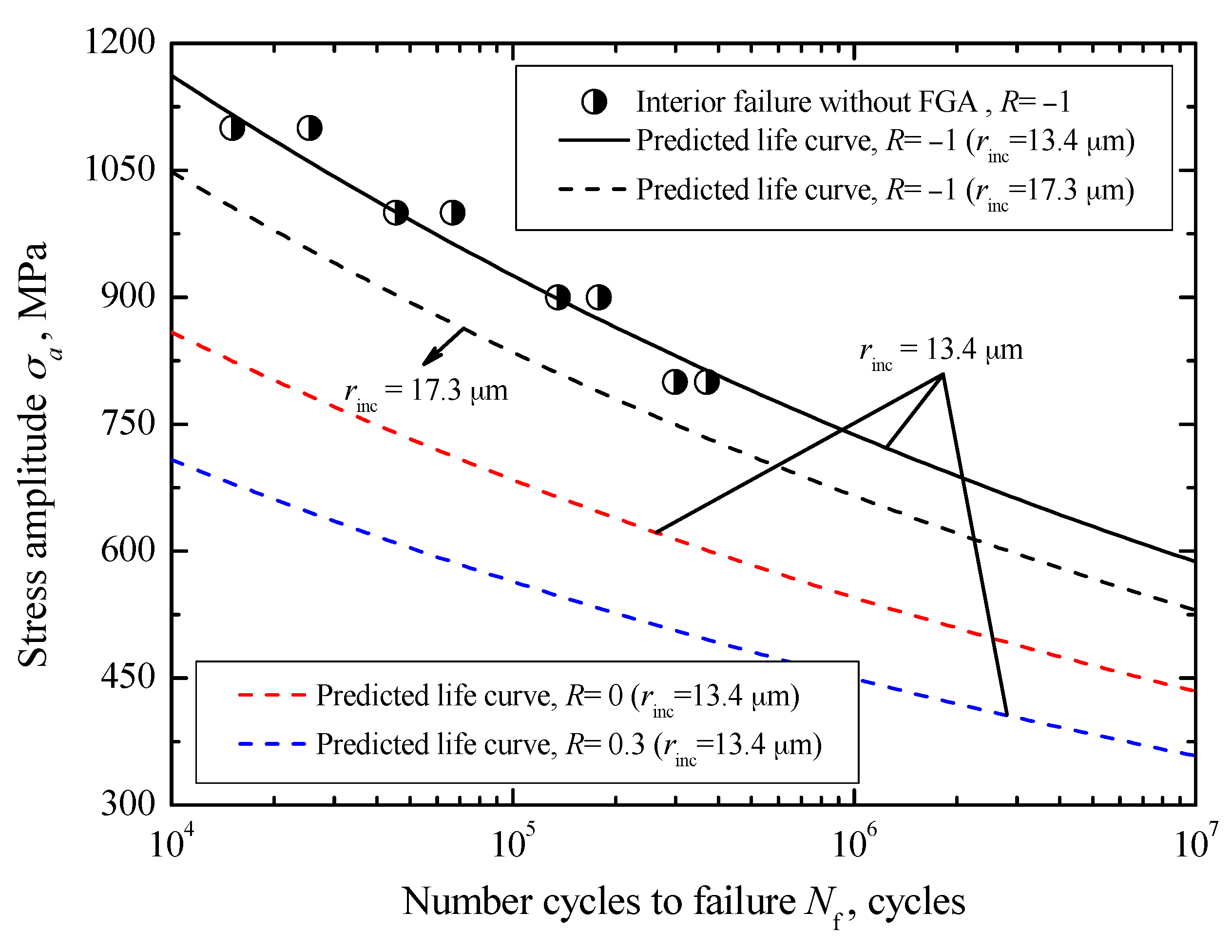
R = −1, the values of
Cint and
mint in Equation (24) were evaluated to be 3.75 × 10
−25 and 15.73 respectively. Corresponding to the mean value and the maximum value of
rinc, about 13.4 μm and 17.3 μm, the predicted crack growth life curves for
R = −1 are indicated by a solid line and a dashed line in
Figure 14, respectively. It can be found that the predicted curves all exhibit a continuously descending trend, which is consistent with the variation trend of the experimental data. Especially, the predicted curve associated with the maximum inclusion size indicates well the lower boundary of the data. Based on this, and by using Equation (25), the crack growth curves associated with the mean inclusion size under stress ratios of 0 and 0.3 is plotted by a red dashed line and a blue dashed line in
Figure 14, respectively.
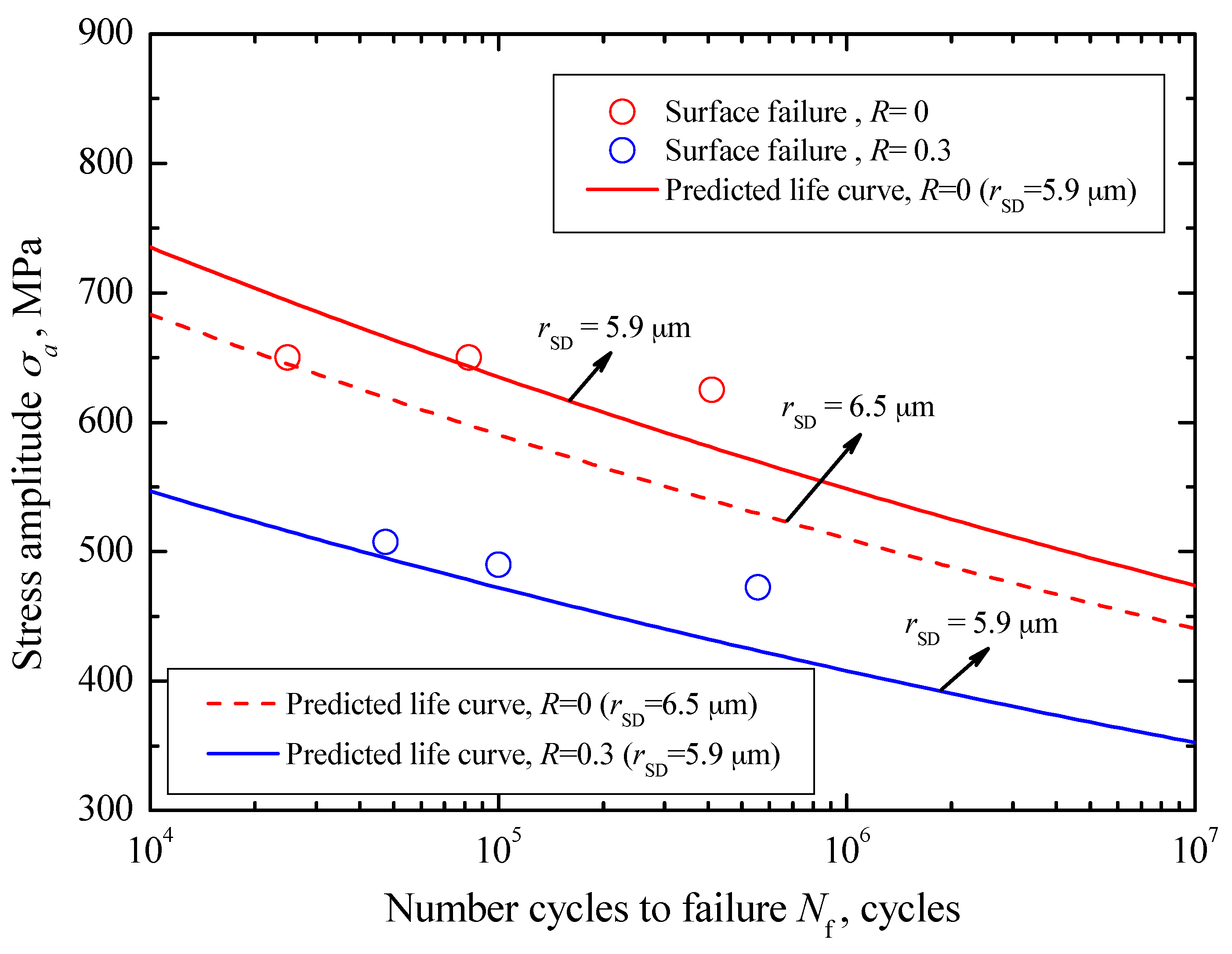
For surface failure, combined with the sizes of SD and the relevant
S-N data for
R = 0, the values of
Csur and
msur in Equation (26) were evaluated to be 3.75 × 10
−23 and 12.28, respectively. Corresponding to the mean value and the maximum value of
rSD, about 5.9 μm and 6.5 μm, the predicted crack growth life curves for
R = 0 are indicated by a solid line and a dashed line in
Figure 15, respectively. Similarly, based on the evaluated results for
R = 0, the crack growth life curve corresponding to the mean value of
rSD for
R = 0.3 is plotted by a dotted line in
Figure 15. They all reflect well the variation trend of the experimental data.
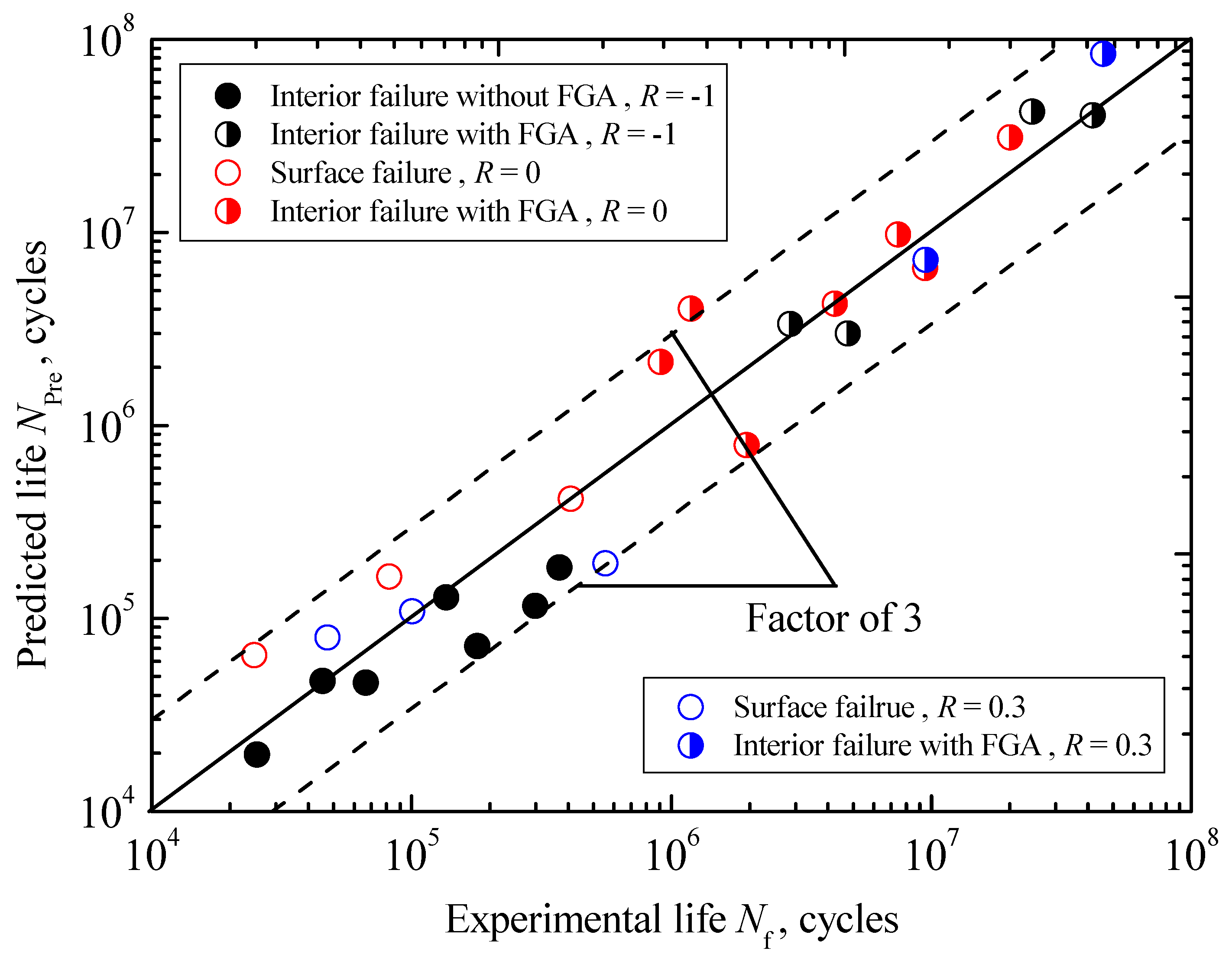
In addition, the comparison between predicted and experimental fatigue lives under three stress ratios is shown in
Figure 16. It can be seen that the agreement is fairly good within a factor of three. Thus, it can be concluded that the proposed life prediction approaches, corresponding to the interior inclusion-FGA-fisheye induced failure governed by the interior crack initiation in the long-life regime, the interior inclusion-fisheye induced failure governed by the interior crack growth in the short life regime and the surface SD-SSA induced failure governed by the surface crack growth in the short life regime, are acceptable in engineering design.