1. Introduction
Friction stir welding (FSW) was invented at The Welding Institute (TWI) and has been successfully employed to weld aluminum alloys, particularly 2XXX or 7XXX series aluminum alloys, which are especially difficult to weld by using fusion welding techniques [
1]. FSW is an attractive welding technique due to its low cost, having reduced weight by joining light-weight metals with metallurgical properties, and a reduced need for human skill [
2]. In addition, its energy efficiency and environmental friendliness makes FSW a “green” process [
3]. By using this welding technique, it has been reported that it is possible to reduce the consumption of energy by 99% and installation cost by 40% in comparison with resistance spot welding [
4]. On the other hand, FSW is a solid-state, hot-shear joining process in which a non-consumable rotational tool is used to produce frictional heat at the welding location without material melting [
5].
Researchers and practitioners are welding many different combinations of dissimilar alloys and materials due to their requirements in varied service conditions [
6,
7]. AA6XXX and AA7XXX Al alloys are two series of the most widely used structural materials in the automotive, rail transportation, and aerospace industries [
8]. Alloy 6061 Al is the most used of the 6XXX series aluminum alloys and possesses superior weldability as compared to other heat treatable alloys and is the most popular aluminum alloy extrusion [
9]. The medium strength (Al-Mg-Si) aluminum alloys such as AA6061 are extremely suited for applications in marine structures, pipelines, and storage tanks [
7]. One of the strongest aluminum alloys used in today’s manufacturing industry is AA7075 (Al-Zn-Mg-Cu). AA7075 has high strength compared to its weight, combined with its natural ageing characteristics, which makes it attractive for aerospace structural applications [
10].
It is well know that for any joining method, the main challenge for many manufacturers is to select the welding process parameters that will create a high quality welded joint [
6,
7]. It is clear that much progress has been made in FSW of dissimilar materials, but it has to be understood that study on this topic is far from enough and is still in the feasibility stages [
8]. Also, what is often not considered or achieved are optimized welding process parameter combinations for FSW dissimilar aluminum alloys [
11]. Since FSW involves complex interactions between many parameters that contribute in the process, the development of proper physical models for FSW which can anticipate the process’s main characteristics is a crucial concern. Thus, researchers attract development of the models based on empirical models. In this respect, response surface methodology (RSM) is a practical method of analysing, improving, and optimizing the structures over the feasible domain of parameter settings. This method is a collection of statistical and mathematical techniques in which a response of interest is influenced by several variables. RSM reduces the number of experimental trials needed to evaluate multiple parameters and their interactions [
12]. Thus, it is less substantial without consuming time, material, and labour efforts [
11,
13]. Rajakumar and Balasubramanian [
14] employed RSM to develop empirical relationships relating the FSW input parameters such as rotational speed, traverse speed, axial force, shoulder diameter, pin diameter, and tool hardness for three outputs; tensile strength, hardness, and corrosion rate of the FSW joints of the AA1100 alloy. Periyasamy et al. [
15] used RSM to establish the relationship between the FSW process parameters (tool rotational speed, traverse speed, and axial force) and the responses (ultimate tensile strength (
UTS), notch tensile strength, and weld nugget hardness) of FSW of cast AA6061 with 20%
. Ashok Kumar and Murugan [
16] developed two regression models using RSM in order to predict the UTS and
E% of the friction stir welded AA6061/
composite by correlating the process parameters including the tool rotational speed, traverse speed, axial force, and percentage of reinforcement. Rambabu et al. [
17] employed RSM to develop a mathematical model to predict the corrosion resistance of the FSW AA2219 aluminum alloy by incorporating FSW process parameters. Kadaganchi et al. [
18] utilized the response surface method to develop a regression model to predict the responses of mechanical properties of friction stir welds of the AA 2014-T6 Al alloy such as ultimate tensile strength, yield strength, and percentage elongation (
E%). Venkateswarlu et al. [
19] developed a mathematical model using RSM regression analysis to predict the effects of tool geometry and process variables (i.e., rotational speed, axial force, and traverse speed) on the dissimilar FSW of the AA2219 and AA7039 alloys joint.
It is obvious that welding processes have multiple responses. In order to optimize a process with multiple objectives, various multi-objective optimization approaches such as statistical techniques and evolutionary algorithms provide good results. In the case of statistical techniques, Kasman [
20] combined Taguchi with grey relational analysis to optimize a multi-response FSW of AA6082 and AA5754 Al alloys. Rajakumar and Balasubramanian [
14] employed the desirability approach to find the optimal conditions in order to maximize UST and minimize the corrosion rate for FSW AA1100 Al alloys. In the case of metaheuristic algorithms, Teimouri and Baseri [
13] developed a fuzzy network with an artificial bee colony and imperialist competitive algorithm for both forward and backward mapping of friction stir welded aluminum joints in order to maximize tensile strength, elongation, and hardness. Roshan et al. [
21] employed adaptive neuro-fuzzy inference systems to determine the relationship between the main factors of the process such as tool pin profile, tool rotary speed, welding speed, and axial force, and the main responses including tensile strength, yield strength, and hardness of FSW aluminum 7075 plates. Then, the developed models were applied as an objective function to find the optimal process parameters by using a simulated annealing algorithm. Shojaeefard et al. [
10] performed a study to model and Pareto optimize the mechanical properties of friction stir welded AA7075/AA5083. To this aim, they developed an artificial neural network model to simulate the relationship between the UTS and hardness of butt joints of AA7075-AA5083 as a function of rotational and welding speeds. Moreover, a multi-objective particle swarm optimization was employed to obtain the Pareto optimal solutions. Finally, to determine the best compromise solution, the TOPSIS approach was applied. Furthermore, Naghibi et al. [
22] carried out an experimental investigation for modelling and parametric optimization of the FSW process to maximize UST and elongation for dissimilar FSW joints of AA5052 and AISI 304. In order to determine the correlation between process parameters such as tool rotational speed, welding speed, tool offset, and the mentioned responses, a back-propagation neural network was designed and developed. The developed model was then associated with the genetic algorithm to find the optimal process parameters.
One of the main contributions of this study is to solve the addressed problem by applying an efficient metaheuristic algorithm. In 2008, a new population-based evolutionary algorithm based on the geographic distribution of biological organisms was firstly introduced by Simon [
23], titled biogeography based optimization (BBO). He noted that this is a novel method of solving the NP hard problems. While BBO is a naturally inspired algorithm, it has some fundamental distinctions from common natural algorithms such as genetic algorithm (GA), particle swarm optimization (PSO), or ant colony optimization (ACO). In BBO, the initial population is not discarded among different generations. Instead, the migration concept is used to modify the population. As another distinction, in each generation, the fitness function is not used directly to modify the population, in which BBO uses fitness to determine the immigration and emigration rates. BBO has revealed a good performance on real-world optimization problems such as machining parameters selection [
24,
25], various power system applications such as economic dispatch [
26], optimal power flow [
27], and the design placement of phasor measurement units (PMU) [
28]. It should be noted that there are no previous studies in the literature which consider using the BBO algorithm to solve the process parameters’ optimization problem for fabricating FSW aluminum joints.
The objective of this research is to model the relationship between the FSW process parameters (tool rotational speed, tool traverse speed, tool tilt angle, tool offset) and the mechanical properties of interest (i.e., tensile strength, minimum hardness in the HAZ zone, and elongation), while a solution algorithm, the multi-objective biogeography based optimization algorithm (MOBBO), is employed to compute the Pareto optimal frontier in objective space. Consequently, the ultimate objective of this study is to obtain the combination of process factors for which the mechanical properties are optimal. The best optimal value of the Pareto frontier for three and two objective functions is selected through two different decision making techniques, TOPSIS and Shannon’s entropy.
2. Experimental Works
In this study, dissimilar aluminum alloys (namely AA6061 and AA7075 in T6 temper conditions) were selected to be butt welded by the FSW process. Both plates were of 6 mm thickness and they were cut before welding to a dimension of 100 mm long and 50 mm wide. The weld direction of the FSW is vertical to the rolling direction of the plates. The mechanical properties of the base aluminum alloys, AA6061 and AA7075, are measured before running the experiments. The ultimate tensile strength of AA6061 and AA7075 are 310 MPa and 524 MPa, respectively, and the elongation of AA6061 and AA7075 are 12% and 11%, respectively.
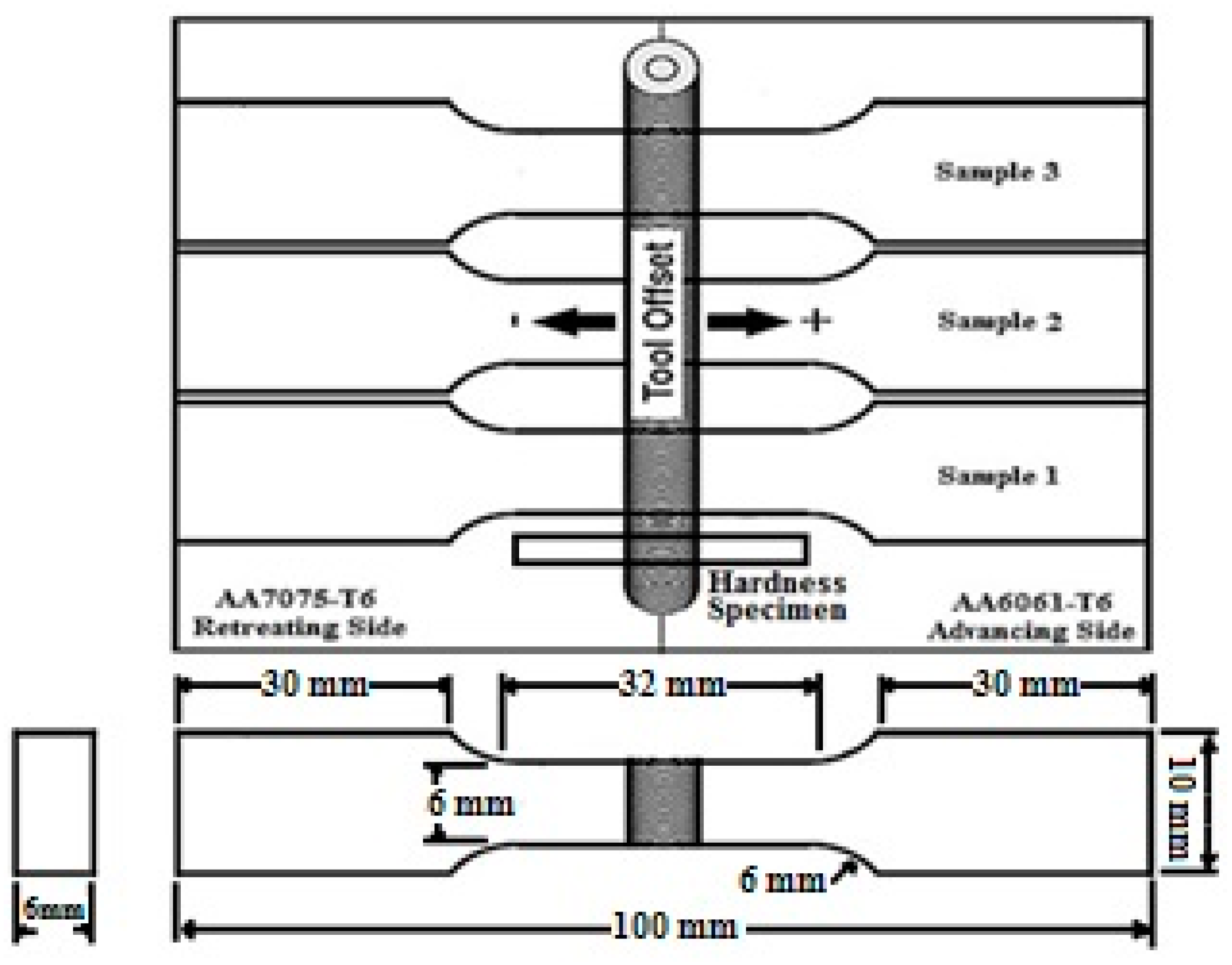
A tool made of AISI H13 hot work steel with a square pin profile that was heat treated to a hardness of 52 HRC after machining to increase its wear resistance is used for the experiments (see
Figure 1).
The side where the spindle rotation direction is in the same direction with the tool traversing is called the advancing side and the opposite side is called the retreating side. AA6061 was placed in the advancing side and AA7075 was placed in the retreating side in order to improve the mechanical properties of the joint [
6,
8,
29,
30].
Based on the literature and previous studies, the parameters with greater influence on the mechanical properties of dissimilar FSW were selected, with their notations and units described in
Table 1 [
6,
31].
Experiments were conducted based on the plan of the surface response, in a central composite design matrix, in which the four factors in five levels were chosen, consisting of 30 sets of coded conditions, which are presented in
Table 2. The first 16 experimental runs are derived from the full experimental design matrix of corner points at the
level (
). The next eight experimental runs comprise a combination of each process parameter at either the highest (+2) or lowest (−2) level with the other three variables at the middle level (0). The remaining six experimental runs included the variables at the intermediate (0) level constituting the six center points.
Three tensile testing specimens were extracted from the welds. The configuration and dimension of each transverse tensile specimen, tool offset position, and hardness specimen are shown in
Figure 2.
Each specimen was conducted according to the ASTM E8M standard at a test speed of 1 mm/min. Care was taken during this stage to align the center of the weld with the center of the tensile specimen. At least three specimens were extracted from each FSWed joint. The tensile testing of the FS welded joints was conducted in a precise Universal Testing Machine Instron 3382, and their UTS and E were measured. To measure the minimum hardness which is located on the AA6061 side in the HAZ regions very close to the thermo-mechanically affected zone (TMAZ) in tensile testing [
8], microhardness measurements using a load of 200 g for 20 s were conducted to determine the average minimum hardness of each joint in this region. The average results of the above mentioned tests are presented in
Table 2.
Thus the 30 experimental conditions allowed the prediction of the linear, quadratic, and two-way interactive effects of the variables on the ultimate tensile strength (UTS), elongation (E), and minimum hardness (H) of the FS welded joints.
4. Multi Objective Optimization
Over the past few years, a number of multi objective evolutionary algorithms have been proposed. The main reason is for the capability to generate multiple Pareto optimal solutions in only one run. The non-dominated sorting genetic algorithm (NSGA) is a widely used non-domination based genetic algorithm used to solve multi-objective optimization problems [
32]. The population based search capability in the evolutionary algorithms has made them very suitable for solving multi-objective optimization problems. Thus, employing these algorithms can eliminate the difficulties of classical solution approaches. In the present work, a multi objective biogeography based optimization (MOBBO) algorithm is proposed to deal with the addressed multi-objective process parameter optimization problem. The proposed method consists of two phases: generation of a Pareto frontier by MOBBO, and employing the decision making method to achieve the best compromised optimal solution from the Pareto frontier.
Multi-objective optimization has been defined as an approach to find a vector for all objective functions. Mathematically, the multi-objective optimization process uses a vector of that should be found so as to optimize , subject to inequality constraints, and equality constraints, where is the vector of the decision, and is the vector of objective functions, both of which must be minimized.
In several multi-objective optimizations, the objectives are normally in conflict. Hence, it is impossible to find a solution that satisfies a number of different objectives simultaneously. One of the possible answers for these kinds of problems is a set of solutions, called the Pareto optimal frontier. However, before defining the Pareto optimal frontier, the concept of dominance must be clearly specified. Assume that
and
are vectors in
n-dimensional space and
is a function.
dominates
if the following conditions are satisfied:
The Pareto optimal frontier defines a solution that is not dominated by any other points in the solution area. The Pareto optimal solution cannot yield better results regarding an objective unless at least one other objective is worsened. A set of all these non-dominated solutions is called the Pareto optimal frontier. The main goal in multi objective optimization problems is to obtain the Pareto front, which is comprised of Pareto optimum solutions [
10].
4.1. Biogeography Based Optimization
The BBO is a new evolutionary algorithm among the popular metaheuristic approaches which have arisen as attractive optimization algorithms due to their competitive results [
23]. This population-based algorithm is a naturally inspired algorithm which mimics the migration process of species for solving engineering problems [
33]. This algorithm has revealed notable performance in many well-known case studies [
34]. The BBO algorithm starts the optimization process with a number of candidate solutions, called habitats or islands. Each island feature is considered by a suitability index variable (
SIV). Each habitat is characterized by a quantitative performance index, named the habitat suitability index (
HSI). This algorithm starts the optimization process with a number of candidate solutions, named habitats. Each feature of this habitat is considered as a suitability index variable (
SIV). The performance of each habitat is characterized by an index, called the habitat suitability index (
HSI), to measure how good the solution is [
35].
The main principle of BBO is based on the immigration and emigration of species in a habitat, known as migration. With probabilistic migration, BBO is able to share more information from good solutions to the poor solutions. In other words, this algorithm prevents good solutions from being demolished during its evolution. Thus, it can efficiently utilize the characteristics and information of the population per iteration. This feature leads to finding better solutions in a short time as opposed to other metaheuristics [
36]. In evolutionary strategies, the recombination approach is employed to generate a new solution, while in BBO the migration operator is executed to make changes within existing solutions. Recombination in evolutionary algorithms is a reproductive process, whereas the migration operator in BBO is an adaptive process, which is employed to alter an existing population [
37].
Additionally, the mutation operator increases the diversity among the population. Without the mutation operator that can increase diversity among the population, the solutions with high HSI have a tendency to be more dominant in the population. The mutation approach makes both solutions with low or high HSI likely to mutate and gives a chance of improvement to both types of solutions in comparison with their earlier values [
38].
4.1.1. Initialize the Habitats
Defining an appropriate habitat representation plays a key role in designing and implementing an optimization algorithm. Each habitat is a potential solution to the problem. The habitat length depends on the number of decision variables. To solve the addressed optimization problem, a real-valued habitat representation is employed in which the variables, the process parameters, are randomly generated within its minimum and maximum bounds. The individual habitat is represented as in which denotes the number of variables. The objective function or HIS of the habitats can be computed.
4.1.2. Migration
In biogeography, migration is the adaptive process which is used to move the species between different habitats. The migration process occurs based on a probabilistic operator. In BBO, the probability of selecting the solution
as the immigrating habitat is related to its immigration rate
and the solution
is related to its emigration rate
. Migration can be express as Equation (8).
The immigration and emigration rates are functions of the solutions’ fitness. They can be evaluated by Equations (9) and (10), respectively.
In Equations (9) and (10),
and
represent the maximum possible immigration and emigration rate, respectively;
is the rank of habitat
after sorting all habitats according to their
; and
is the number of solutions in the population. It is clear that the better solution has a higher emigration and a lower immigration rate, while the opposite is true for a poor solution. Often,
and
set equal to one or slightly less than one [
39].
After determining the immigrating and emigrating habitats, the migration process can be performed like a crossover in evolutionary algorithms. In this study, the migration process for each habitat vector is implemented separately.
To perform the migration, an arithmetic crossover operator that defines a linear combination of two chromosomes is used. The selected immigrating and emigrating habitats may produce two new habitats, called modified habitats, by taking the linear combination of the habitats’ SIVs as follows:
where
is the weight which governs the dominant individual in reproduction and it is between 0 and 1.
4.1.3. Mutation
In BBO, the mutation rate is inversely related to the solution probability and can be calculated by Equation (11).
In Equation (11),
is a user-defined maximum probability,
(
is the population size), and
. is the solution probability. In the mathematics of biogeography, the solution probability depends on the immigration and emigration rate of the habitat and can be calculated by Equation (12).
The species count in the habitat changes from time to time.
and
are the immigration rates of the habitat having
and
species, respectively.
and
are the emigration rates of the habitat having
and
species, respectively.
,
, and
are the species count probabilities of the habitat with
,
, and
species, respectively.
is the maximum species count in the habitat [
23].
Based on the mutation probability, the mutation operators can be implemented to make a random change in the mth SIV selected randomly for the habitat by generating a random real value within its minimum and maximum limits.
4.1.4. Evaluating the HSI
In BBO, each habitat is evaluated based on its corresponding HSI. Generally, the fitness value is measured according to the objective function.
4.1.5. Update Habitat
To update the population for the next generation in single objective optimization, three steps (merging, sorting, and truncating) have been implemented. This scheme is used to preserve elite habitats for the next generation. Merging is related to the combination of habitats, before and after applying BBO operators which makes the habitat population size double at a time. Then, the combined habitats must be sorted based on their HSI in ascending order (in the minimization problem). Finally, the best habitats are selected from the combined and sorted habitat with the amount of the original habitat size for the next generation.
In multi-objective biogeography based optimization, the habitats are updated based on the non-dominated sorting and ranking (NDSR) scheme proposed by [
32]. This scheme is employed to determine the Pareto optimal frontier. The newly generated habitats are combined with the habitats before and after executing the BBO operators, which makes the original habitat size double at a time. Then, the NDSR procedure is performed on the updated and combined habitats. A diversity rank is allocated to the solution vectors which are in the same non-dominated front, using the crowding distance metric.
This metric is an indication of the density of the solution vectors neighbouring a particular solution vector. The crowding distance can be measured for the
kth objective of the
jth solution as follows.
An infinite distance index is assigned to the solutions having the smallest and largest values. The overall crowding distance is measured by using the sum of the individual distance values of each objective.
where
gives the number of objectives and
is the individual index. Finally, the best habitat is selected from the combined habitat in the order of their ranking for the next iteration.
4.1.6. Stopping Criterion
The optimization algorithm with various operators such as migration and mutation is performed repeatedly until a stopping criterion is met. In this study, the BBO algorithm is stopped when the number of generations has been met.
4.1.7. Implementation
Based on aforementioned BBO operators, the BBO algorithm used to solve the scheduling problem in FMS is described as follows.
| Generate a set of habitats for a problem |
| Evaluate the fitness value or HSI for each habitat |
| while stopping criterion is not met |
| Determine immigrating rate and emigrating rate for each habitat |
| Modify the habitats based on and |
| for: N (population size) do |
| Use to probabilistically decide whether to modify to emigration |
| if rand (0, 1) < |
| Select Habitat through roulette wheel method to emigration |
| Perform migration on and |
| Evaluate the fitness value or his |
| Replace the new solution with |
| end if |
| if rand (0, 1) < |
| Apply mutation on |
| Evaluate the fitness value or HSI for the newly generated solution |
| end if |
| end for |
| Update habitats’ population |
| end while |
4.2. Objective Function, Decision Variables, and Constraints
This study has been carried out using the ultimate tensile strength, yield strength, elongation, and hardness function as the four objective functions, as given in Equations (4)–(6) with the tool rotational speed (RS), tool traverse speed (TS), tilt angle (TA), and tool offset (TO) as the four decision variables. The objective function and constraints for carrying out the multi objective optimization are expressed as follows.
Subject to:
4.3. Decision Making Methods in Multi-Objective Optimization
The Pareto set has numerous optimal solutions which are preferred based on the decision making requirements. Hence, the decision making methods are important to pick the best solution from the Pareto frontier. Several multi criteria decision making (MCDM) methods are proposed in the literature [
40,
41]. This study considers two decision making approaches, TOPSIS and Shannon’s entropy. Few decision makers evaluate a concrete solution on the basis of how far the solution is from nadir, while others use the proximity index with the ideal solution. The decision making methods used in this study are described in the following section.
4.3.1. Shannon Entropy Method
Shannon’s entropy approach is a useful technique to determine the hold weights of alternatives [
42]. This approach gives a matrix
with a decision matrix
considering
different alternatives with
objectives in the system. For the
jth objective, arrays of the
matrix can be computed for the formulae:
Shannon’s entropy is presented as:
The deviation (
) degree is defined as:
The following equation calculates the
jth objective weights as:
To end with
, Shannon’s entropy method finds the point on the Pareto optimal frontier where the maximum
is the final desired optimal result. Therefore,
4.3.2. TOPSIS Decision Making Method
TOPSIS is an MCDM approach which is used to rank the alternatives of the obtained Pareto solutions. The basic concept of TOPSIS is to obtain the best compromise solution according to the objective weights. It is clear that in the multi-objective optimization problem it is impossible to find the optimal condition of each objective achieved by a single objective optimization. Thus, the ideal solution and non-ideal solution are not located on the Pareto frontier. The ideal (non-ideal) point is the coordination in the objective’s solution area in which each objective has its best (worst) value. In order to select the best compromise solution, an evaluation matrix
should be created (
m alternatives and
n criteria).
is also the
jth objective value of the
ith alternative. The computed matrix should then be non-dimensionalized through the Euclidian approach using Equation (20):
The weighted non-dimensionalized decision matrix is computed as follows:
where
is the weight calculated by Shannon’s entropy method. The solution distance on the Pareto optimal frontier from the ideal point denoted by
is measured as follows:
where
denotes the number of objectives while
represents each solution on the Pareto frontier (
. In Equation (22),
is the ideal value for the
jth objective. In addition to the distance of each solution from the ideal point
, the solution distance from the non-ideal point denoted by
should be calculated. Therefore,
In computing the TOPSIS method, the
parameter is defined as follows:
In the TOPSIS approach, a solution with a maximum
is chosen as a desired ultimate solution, therefore,
is the index for the final selected solution, which is:
5. Results and Discussion
The optimal value of the ultimate tensile strength, elongation, and hardness function is obtained by implementing the evolutionary algorithm based on the multi objective BBO algorithm. The optimization problem is implemented by the proposed MOBBO algorithm coded using Matlab R2013a and run on an Intel® core™ CPU i7-4500U at 1.8 GHZ, 8 GB RAM computer with Windows 8.1. The MOBBO parameters are set in this study after a number of careful runs as follows; the habitat size (N) = 70, maximum migration and immigration rate of each habitat = 1, mutation probability = 0.05, and maximum iteration = 300.
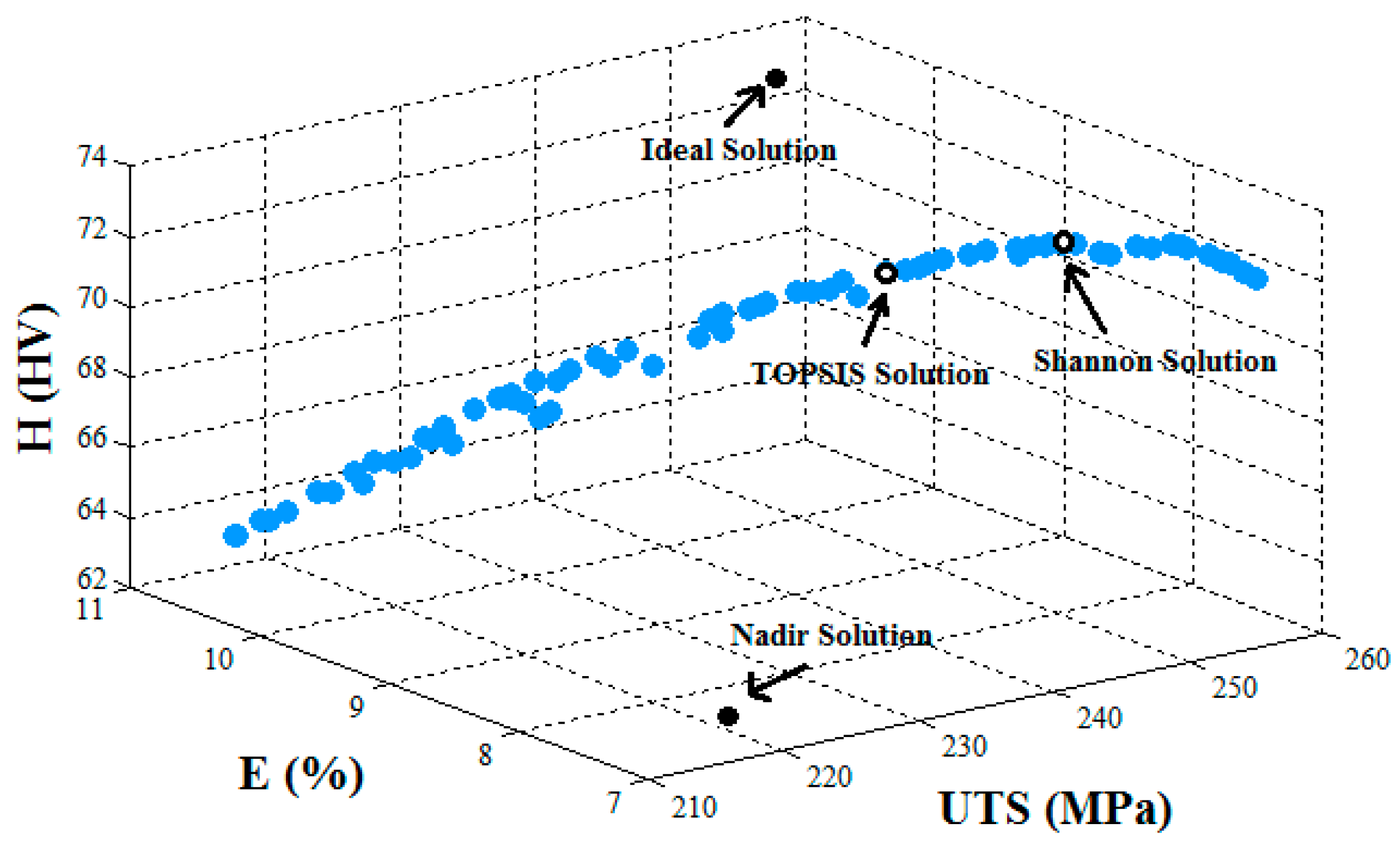
The final optimal solution selected by the TOPSIS and Shannon’s entropy decision making approaches for the triple objective and the results of two and single objective were computed. As can be seen in
Table 5, the ideal and nadir solution for the three objectives’ (
UTS-E-H) optimization are 256.28 MPa, 10.92%, 72.62 HV, and 216.93 MPa, 7.13%, 63.02 HV, respectively. Therefore, the optimal solution for the triple objective optimization lies in
,
, and
. It is clearly seen that the optimal solution selected by the decision making methods for the triple objective optimization is inclined towards a rotational speed from 967.41 to 1002.41 rpm, traversing speed from 164.40 to 149.73 mm/min, tilt angle from 1.92° to 1.97°, and tool offset from −0.74 to −1.05 mm.
Figure 4 shows the Pareto frontier for the triple objective (
UTS-E-H) with the best optimal solutions selected through the TOPSIS and Shannon’s entropy decision making approaches, as well as the ideal and nadir solutions.
In order to measure the distinction between the results obtained, the deviation index of the results obtained by two different decision making approaches from the ideal value is computed as follows:
The deviation index of the optimal solution obtained by TOPSIS and Shannon’s entropy for the triple and dual optimization approaches are illustrated in bold in the last column of
Table 5. Shannon’s entropy decision making method yields a lower value of the deviation index as 0.12 with the triple objective optimization.
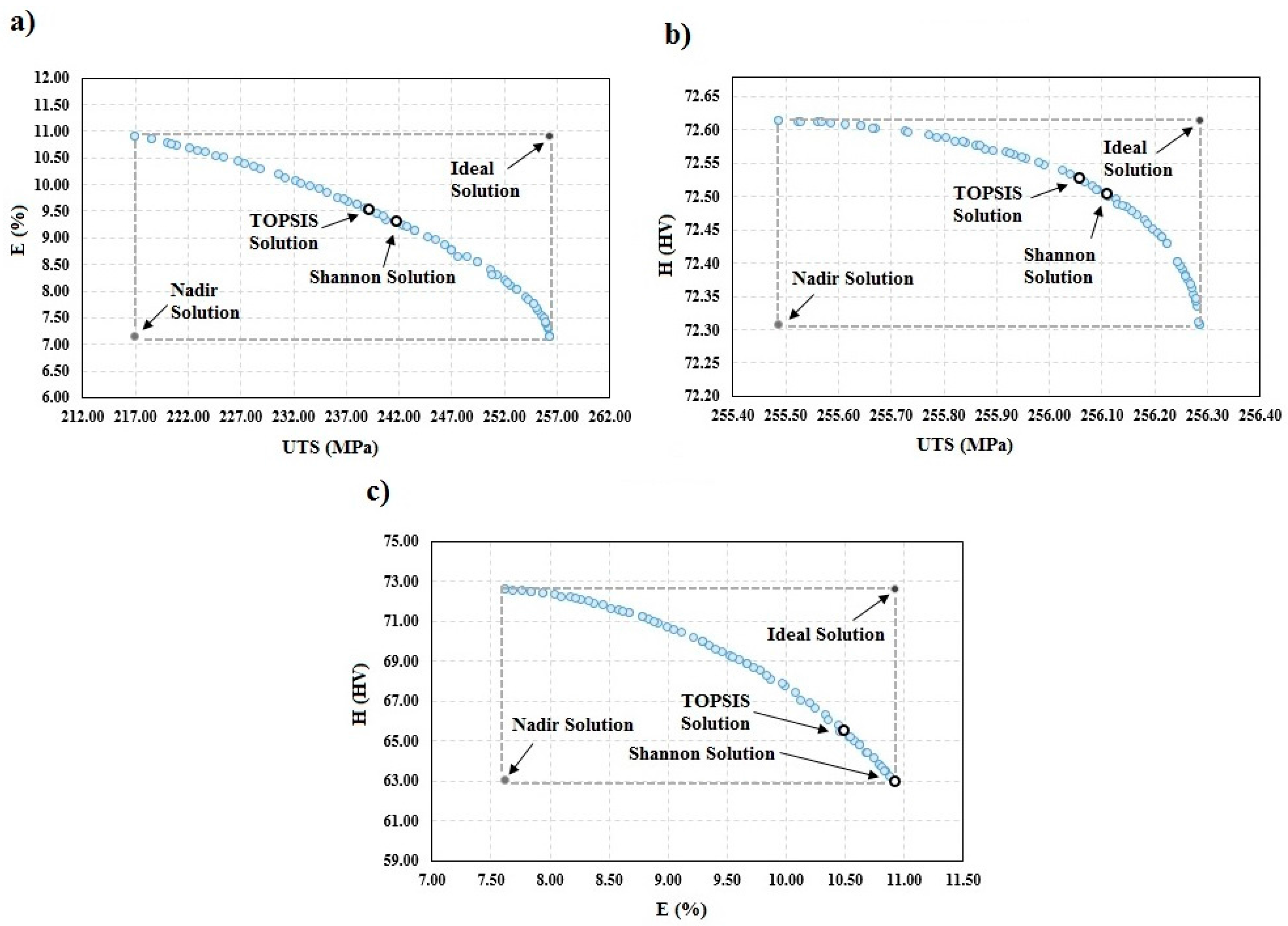
Figure 5a shows the optimal results for the dual objective (
UTS-E) optimization. The optimal results based on the two decision making methods and the ideal and non-ideal solutions are indicated in this figure. The optimal solution’s population in
and
can be seen in this figure. Therefore, the optimal answers are probably in this region and as it is mentioned, the results of TOPSIS and Shannon’s entropy are in this region. As shown in
Table 5, the chosen responses through Shannon’s entropy method are the closest to the ideal solution with a deviation index of 0.37. Similarly, the optimal results for the other dual objective optimization (
UTS-H and
E-H) are illustrated in
Figure 5b,c, respectively, and the obtained solutions through the decision making methods are displayed.
The final optimal solution of the dual objective optimization picked from the Pareto frontier by the decision making methods with the lowest value of the deviation index are shown in bold font in the last column of
Table 5.
It is observed from
Figure 5a,c that the elongation percentage function dramatically decreases with the increase in the ultimate tensile strength and minimum hardness in the HAZ area. Hence, with the use of the obtained Pareto frontier, one has to determine the point of maximum overall elongation without considerable compromise in the ultimate tensile strength and minimum hardness. The final optimal solution for the single optimization is illustrated in
Table 5 for comparison purposes.
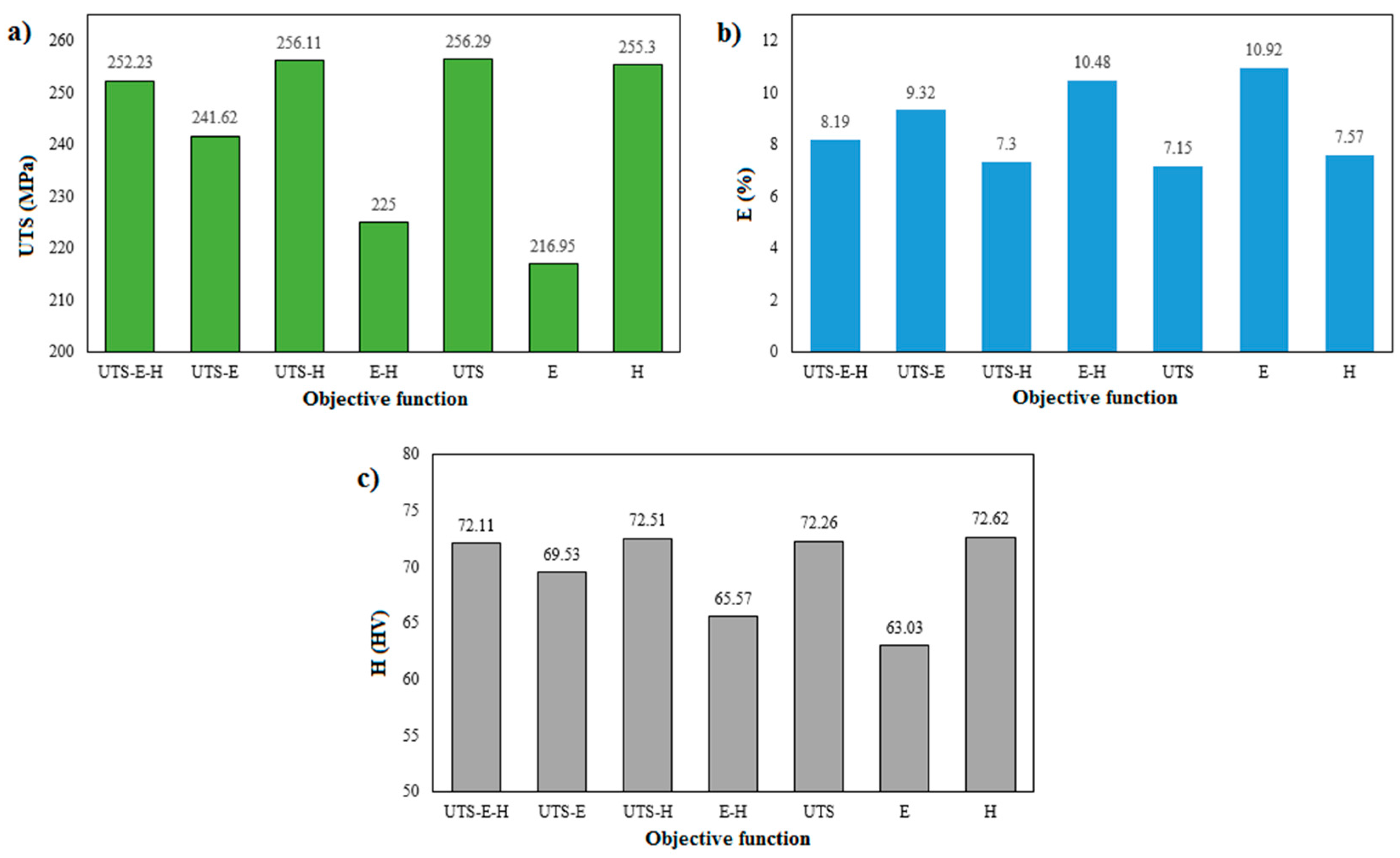
Figure 6 shows comparative studies of the ultimate tensile strength, elongation, and minimum hardness in the HAZ zone function obtained through various optimization schemes. Therefore, it is concluded that three objective optimization can lead to more desired results as compared to dual and single objective optimization.
It is evident that considering all of the competing criteria such as UTS, E, and H in optimizing the process parameters of dissimilar FSW welded AA6061-T6 and AA7075-T6 joints is impossible without solving a multi-objective optimization procedure. However, it should be noted that there are no stringent protocols for the application of decision making methods, as other techniques might produce superior results for the same problem.
In order to carry out error analysis of the implemented decision making methods used in this study, mean absolute percentage error (MAPE) is applied. To achieve this, 30 different runs for the computer code were performed and a final solution for each run was obtained using the Shannon’s entropy and TOPSIS decision making methods. Then, the magnitudes of each objective (ultimate tensile strength, elongation, and minimum hardness in the HAZ zone) were compared with the best solutions gained after 30 runs by each method. The first three columns of
Table 6 demonstrate the average percentage error and second three columns display the maximum percentage error of the decision making methods for each objective.
The MAPE technique has been executed for the error analysis which shows that the average error and maximum error of the solutions attained from the two decision making methods are 0.41%, 2.22%, 0.24% and 0.85%, 4.13%, 0.59% for the ultimate tensile strength, elongation, and minimum hardness in the HAZ zone, respectively. According to the results, the Shannon approach has a better solution for UTS, E, and H in contrast with other decision making methods.
6. Conclusions
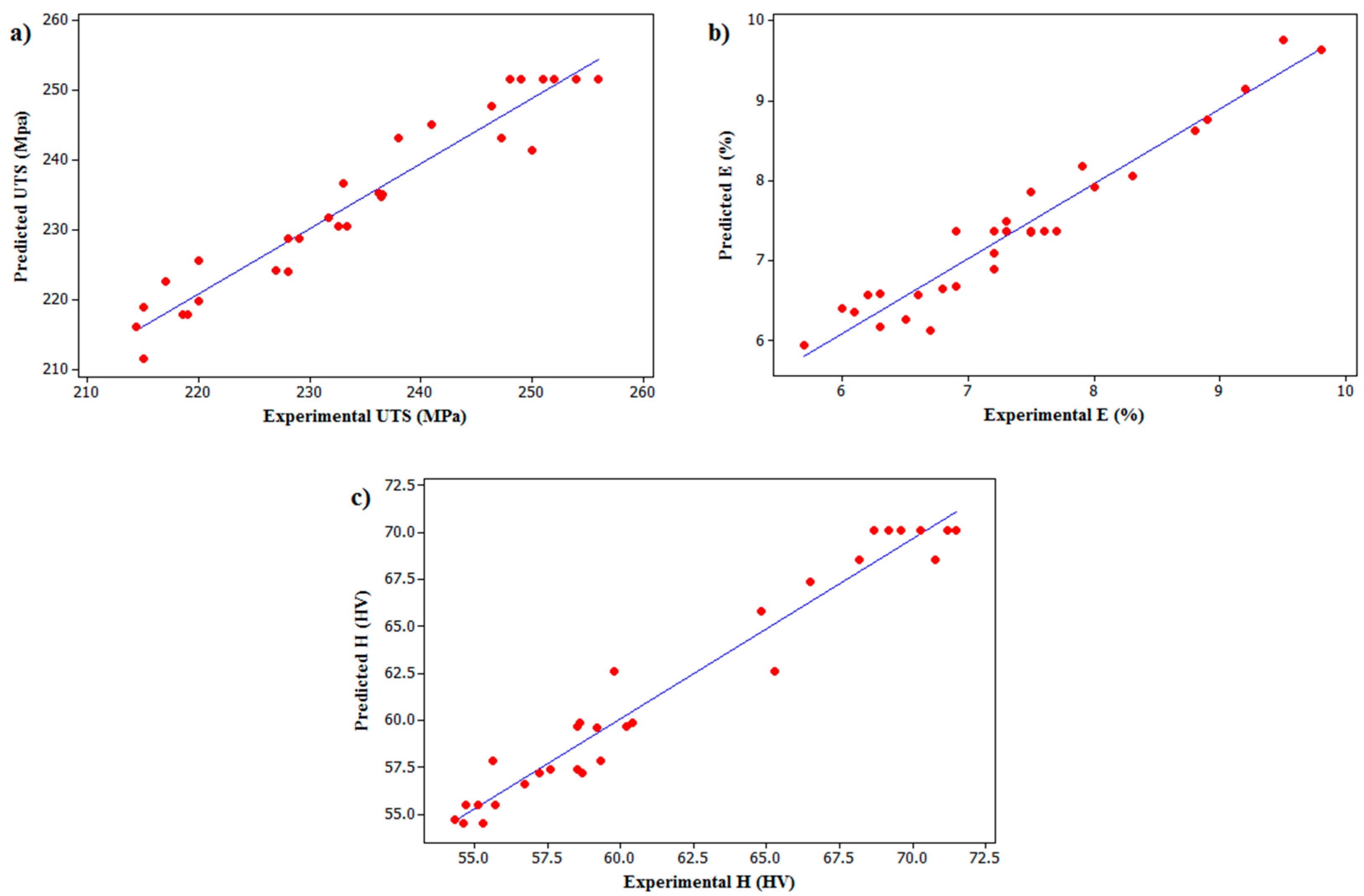
Friction stir welding with different process parameters was developed successfully by using a conventional milling machine for dissimilar aluminum alloys AA6061-T6 and AA7075-T6. The mathematical regression model was developed based on an experimental study on ultimate tensile strength, elongation, and minimum hardness of the dissimilar FS welded joints, and was validated. Analysis of the experimental data by the developed model revealed that the mathematical regression model can be employed to predict the aforementioned mechanical properties of the dissimilar friction stir welded joints of AA6061 and AA7075 Al alloys within of their experimental values at a 95% confidence level.
In order to deal with this multi response optimization problem, a multi objective optimization algorithm was proposed. This proposed solution algorithm is comprised of two phases: generation of a Pareto set by MOBBO, and the use of two different decision making methods (Shannon’s entropy and TOPSIS) to achieve the best compromise solution from the Pareto set.
The results indicated that the multi-objective BBO algorithm in combination with the mathematical regression model is a useful technique to optimize the FSW process parameters to obtain the maximum mechanical properties of the FSW joints. The best theoretical compromise solution chosen by Shannon’s entropy for the three-objective optimization has the optimal values for the tool rotational speed of 1002.14 rpm, tool traversing speed of 149.73 mm/min, tilt angle of 1.92°, and tool offset of −0.74 mm at which the ultimate tensile strength, elongation, and hardness are 252.23 MPa, 8.19%, and 72.11 HV, respectively. By setting those parameters as close as possible to the theoretical values in the vertical milling machine, the multi-objective optimum experimental values of UTS, E, and H are 253 MPa, 8.2%, and 71.4 HV, respectively. Further research can be carried out by combining multi-objective biogeography based optimization with other decision making methods such as fuzzy bellman Zadeh or linear programming technique for multidimensional analysis of preference (LINMAP) to obtain the best compromise solution from the Pareto set.