1. Introduction
The presence of a boundary is inevitable for any solid. The material in the vicinity of the boundary often has different material properties to that lying further from the boundary due to various effects. In concrete, one of the main effects is that the boundary layer typically contains a lower amount of larger mineral aggregates and more small aggregates and mortar compared to the interior material [
1]. The boundary layer thickness is determined by the sieve curve of the material and is independent of the size of the specimen/member. The presence of the boundary layer may affect the elastic and inelastic mechanical behavior of concrete members.
In the numerical analysis of concrete members using continuous homogeneous models, the boundary layer is typically not represented. However, some approaches lead to the creation of a boundary layer that is different from the interior (nonlocal models [
2], for example) or a boundary layer is directly created on purpose [
3]. In the case of mesoscale models, the different distribution of mineral aggregates in the boundary layer can be directly imposed when creating the model.
The paper focuses on a specific type of discrete mesoscale model with random geometry where every model node represents one larger aggregate and its surroundings. This type of model is often called a particle model [
4,
5]. Its advantage, compared to the classical lattice models of concrete [
6,
7,
8] with material structure projected onto the independent lattice structure, is the great reduction in computational time that it provides. Specifically, the focus in this paper is placed on models with geometry generated via Voronoi or similar tessellation [
9,
10,
11].
It will be demonstrated that the boundary layer is inevitable in this type of model, and affects its mechanical behavior. For a positive Poisson’s ratio, the boundary layer becomes more compliant than the bulk material, while, for a negative Poisson’s ratio, it becomes stiffer. In the nonlinear regime, the boundary layer is weaker and less ductile than the interior material. All of these phenomena are consequences of geometrical bias in the boundary layer. While the elements inside the specimen are oriented with the same probability in any direction, the boundary layer has more elements oriented along the boundary.
When the discrete model is understood to be only some kind of discretization technique, the presence of a boundary layer with a thickness that is related to the discretization density is inconvenient. Recently, an iterative technique capable of removing both elastic stress fluctuations and the elastic effects of the boundary layer with no limits in Poisson’s ratio has been developed [
12,
13]. The disadvantage of this approach is the loss of splitting forces under compression. However, the boundary layer might still have an effect in the nonlinear regime, depending on the applied constitutive law. Another approach with similar consequences uses a constitutive law based on the volumetric-deviatoric split of a strain tensor [
14].
Viewing the discrete particle model not as a discretization technique but as a meso-level model mimicking real material structure, the aforementioned boundary layer might also be viewed as realistic. However, the underlying origin of the boundary layer in the numerical model is completely different from a real heterogeneous solid. Because there are no experiments known to the author that evaluate the boundary layer effect, it is not possible to determine its appropriateness in the model.
The author was confronted with boundary layer effects for the first time in [
15], where the elastic tensorial stress in the boundary layer layer clearly deviated from the theoretical behavior and exhibited strong dependence on Poisson’s ratio. Another influence of the boundary layer in the elastic regime was noted in [
16]. The macroscopic elastic modulus and Poisson’s ratio deviated for decreasing discretization density. This was caused by the increasing fraction of the boundary layer in the specimen volume. Finally, in the nonlinear regime, the adaptive technique [
16] showed sensitivity to the construction of the model geometry in the boundary region. All of these effects are explained by the findings presented in this paper.
2. Model
The studied model is a discrete system of rigid bodies connected at common facets by linear or nonlinear contacts. The constitutive equations are taken from [
17,
18] and simplified. A full description of both linear and nonlinear constitutive equations, model kinematics and the creation of the model geometry is provided in [
16]. The interested reader is kindly asked to find all additional model-related information there, as, for sake of simplicity, only the most necessary information is included in this paper.
The kinematics of the bodies is dictated by rigid body motion assuming small rotations, and is thus often called a rigid-body–spring network [
19,
20]. Each body has three degrees of freedom (DOFs) in two dimensions (2 × translation
u, 1 × rotation
φ), and six in three dimensions (3 × translation
u, 3 × rotation
φ). Both the 2D and 3D versions of the model are used in this paper.
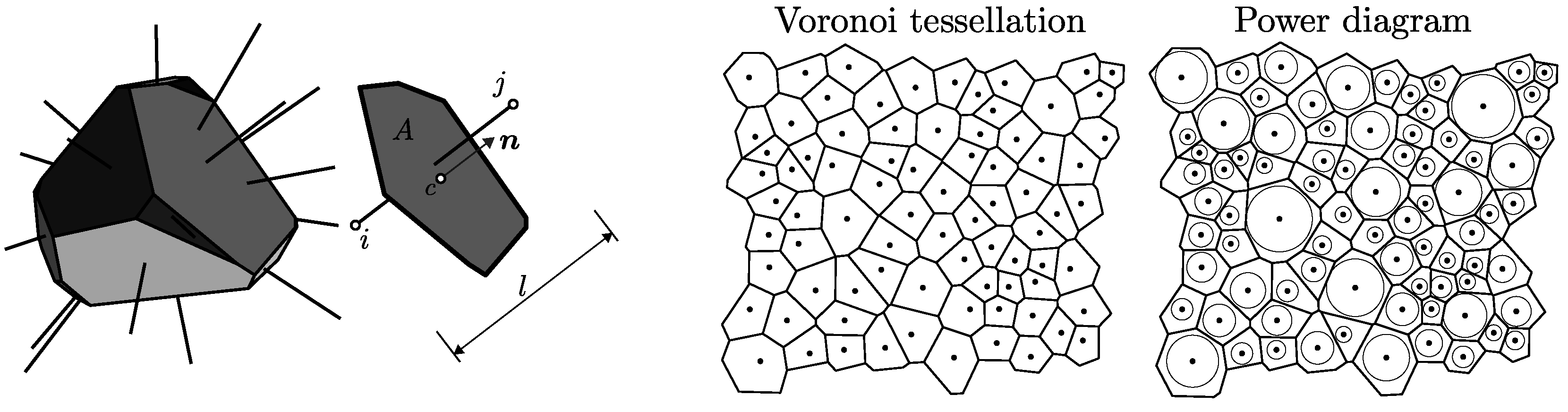
One rigid body and one facet are shown in
Figure 1. The orientation of the facet is described by its
normal direction,
; the length of the contact is denoted
, its area is
A and centroid is
.
Three algorithms are used for geometry construction. The first two types are controlled by the parameter
, while the third type needs a sieve curve of the mineral aggregates on input. The differences between the tessellation types are schematically demonstrated in 2D in
Figure 2 left.
In the first type (denoted A), the specimen domain is randomly filled with nuclei that are not closer to each other than
. The filling is carried out sequentially, one nucleus at a time, and stops after a large number of trial nuclei have been rejected due to violation of the minimum distance. Then, Voronoi tessellation is performed to divide the domain into bodies. The rigid body associated with nucleus
i encompasses all the points
that are closer to
i than to any other nucleus. Voronoi faces, here referred to as facets, represents the bonds between two bodies. The boundary region requires special treatment. According to Bolander et al. [
20], the nuclei are mirrored across the boundary before performing the Voronoi tessellation. The tessellation then creates the boundaries of the rigid bodies exactly at the boundaries of the specimen.
The second tessellation type (denoted B) differs only slightly from the first. The nuclei are randomly placed into a larger volume than needed. After the random placing is complete, nuclei outside the true specimen domain are removed. The tessellation and the treatment of the boundary region both proceed exactly as in case A. The only difference between the A and B tessellation is in the random placing of the nuclei in the boundary region. In case A, the presence of the boundary already affects the placing process; while, in case B, the boundary is effective only during the tessellation.
Finally, tessellation type C accounts for different aggregate sizes. Spherical aggregates of different radii,
r, are generated based on the sieve curve. The Fuller curve with 75% of aggregate volume with radii within the range
is used. The aggregates are sequentially randomly placed into the domain, starting with the largest ones. No overlapping of the boundary is allowed, and the minimal mutual distance between two spherical centers is 1.1 × the sum of their radii. The power diagram [
21] is used instead of the Voronoi tessellation. The power diagram, which is a weighted version of Voronoi tessellation, is based on the power of the point to the sphere defined as
, where
d is the distance of the point from the spherical center and
r is the sphere radius. The body of the power diagram associated with sphere
i is a set of all points with lower power to sphere
i than to any other sphere. The power diagram is computed with the help of [
22].
The last modification of the tessellation procedure is periodic repetition of the model structure. The periodicity allows for complete removal of the boundary. Though it can be generally used with tessellation types A or C, it is employed here only in connection with A. During random placement of nuclei, every nucleus is periodically repeated twice in the
y- and
z-directions. The tessellation is then performed on a periodic structure that is 3 × larger in both the
y- and
z-directions. When solution of the mechanical system is carried out, periodic images of nuclei have dependent DOFs and only one periodic image of each contact contributes to the strain energy and is therefore included in the stiffness matrix. This approach completely removes boundaries and creates ideal directionally unbiased geometry. When boundaries are present in the periodic structure, the nuclei in the central part of the prismatic specimen are mirrored across the
and
plane. After tessellation, the planes
and
behave in the same way as a specimen boundary with directionally biased geometry in its vicinity. An example of the periodic boundary
free and periodic
bounded structures in 2D is shown in
Figure 2.
All of the three tessellation types have two fundamental features used later in the theoretical derivations: (i) the facets on the contacts of the rigid bodies are perpendicular to the vector connecting corresponding nuclei,
; (ii) the volume is filled by bodies with no space left. Based on these two properties, the volume of the whole discretized specimen can be computed via summation over all contacts
eAs the system deforms, a displacement jump,
Δ, occurs between bodies. The displacement jump is measured at the centroid of the contact facets,
. The contact strain in the normal direction,
, and tangential direction,
, are defined based on the projection of the displacement jump into the normal direction. The normal strain is represented by a real number and its direction is always
. In contrast, the tangential strain is represented by a vector perpendicular to
Contact stresses are evaluated from contact strains
where
and
α are elastic parameters of the model dictating its elastic behavior. In the elastic regime, damage parameter
D is null but may grow up to 1 in the inelastic regime. The evolution of the damage parameter is governed by two additional model parameters, meso-level tensile strength,
, and fracture energy in tension,
, and the straining direction
ωAn element strained in direction
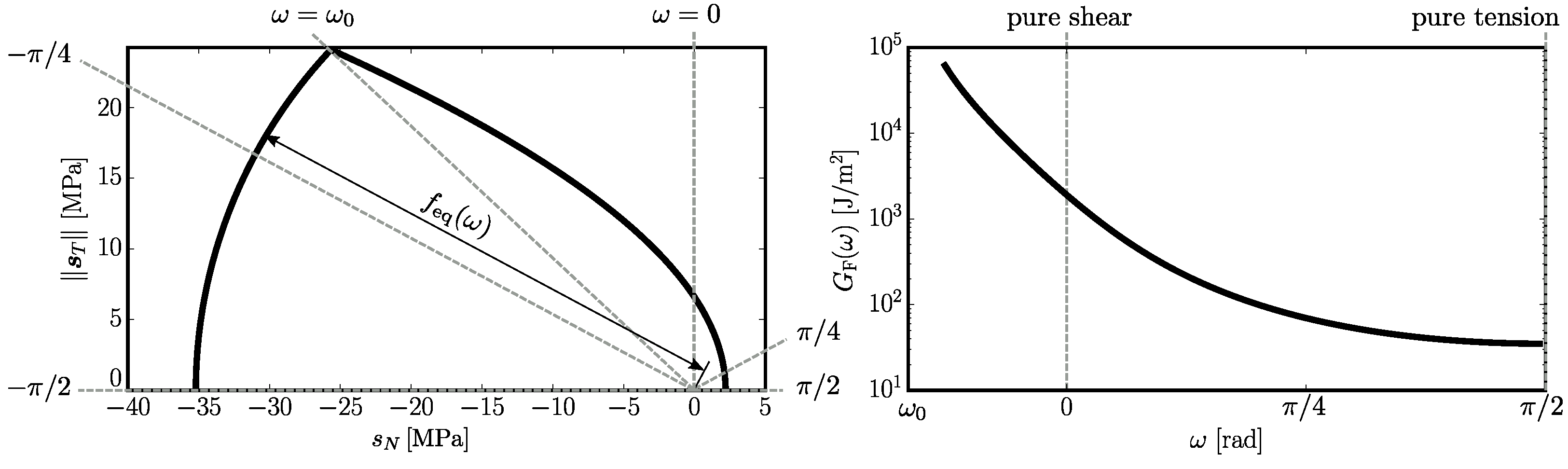
ω behaves linearly until an equivalent stress
reaches elastic limit
. The limit is dependent on
ω and has two branches that intersects at
(see
Figure 3 left). The tensile part active in examples from
Section 7 reads
After reaching the strength, an exponential softening follows with total energy dissipation
. In pure tension (
), the strength and fracture energy equal the model parameters
and
. The more shear involved, the higher the strength and fracture energy. The fracture energy dependent on straining direction is plotted in
Figure 3 on the right-hand side.
As stated previously, a complete description of the model’s kinematics (the relation between
,
and
Δ) and nonlinear constitutive equations can be found in [
16]. The original, more complex and robust version of the nonlinear constitutive law is published in [
18]. The simplification used here is obtained from the full model using the recommended values of the remaining model parameters. The nonlinear solution is found in incremental steps via an arc-length iterative solver; the model is static.
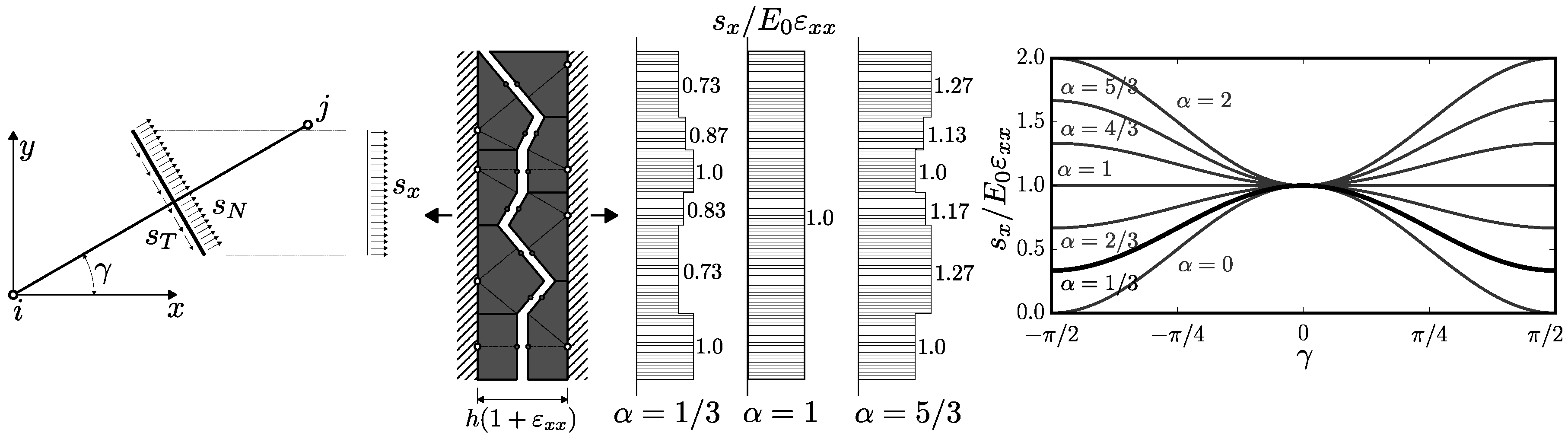
3. Simple Example
Imagine a simple 2D setup of width
h sketched in
Figure 4. Eight bodies are strained in the
x-direction by
with restricted rotations and deformation in the
y-direction. The displacement jump at all the contacts is clearly
. Denoting
is the angular deviation from the
x-axis, the normal is
and length
. The elastic normal and tangential stresses are (from Equations (
2) and (
3))
and the stress acting in the
x-direction on the projection of the facet to the
y-direction is
The stress
transferred by the facet projections is shown in
Figure 4 for three values of
α. It increases with angular deviation
γ for
but decreases with
γ for
. Therefore, the elements that are more inclined away from the straining direction behave in a stiffer or more compliant manner when
α is larger or lower than 1, respectively. The inclined elements also have lower normal stress; shear stress becomes maximal when
.
This is the simple idea which lies behind this paper. In reality, there are also rotations and translations perpendicular to the stress direction. However, when the element is parallel to the straining direction, the active stress component is mainly normal stress. When inclined, shear stress is activated. Because the elements in the boundary layer are aligned with the boundary, the properties of the boundary layer differ. The same effect was recently used for generating anisotropic discrete model via introducing systematic bias into the angular distribution of the elements [
23].
4. Macroscopic Elastic Behavior of a Discrete System
It is convenient to derive general elastic properties of a discrete system with unbiased geometry. This derivation has already been performed in 3D in Kuhl et al. [
24]. The reader may wish to skip the following details regarding such derivation, moving straight to Equation (
25), which summarizes the results of this section.
The analytical equations in the paper are hereinafter based on a simple assumption about the displacements and rotations of the bodies in the system when subjected to macroscopic uniform strain. It is assumed that all the rotations are null (
), and the difference in displacements between any two nodes is
The second order tensor is the applied uniform strain. This assumption is clearly not satisfied exactly, except in one special case when . However, it will be shown that the real system elastic behavior is not very far from this assumption.
Using assumption (
8) and perpendicularity of the facet area to the element, the displacement jump is determined by the strain tensor
The facet strains in the normal and tangential direction are (from Equations (
2) and (
9))
According to Kuhl et al. [
24], one can define the second order tensor
, the fourth order tensor
with
being the Kronecker delta, and the third order tensor
. Then, Equation (
10) can be rewritten as
The constitutive law in the elastic regime yields
The virtual work done by one element on virtual strain
is
To derive macroscopic elastic parameters, one starts with the equivalence of virtual work done by a mesoscopic discrete system and by macroscopic homogenized elastic continua [
24]
The virtual work of elastic continua in volume
V, using
, is simply
while the work done by the discrete system is a summation of all contributions from individual contacts
The fourth order tensor of elastic constants follows on from Equations (
15) and (
16)
In the model used here, the normal stiffness,
, is identical for all the elements and can thus be moved outside the summation. Further simplification of this equation is possible, providing the model geometry is properly constructed. When there is no directional bias, the tensors
and
do not have any statistical dependence on elemental area,
A, and length,
l. Therefore, the summation can be rewritten using the mean value (
) of terms with
and
Both
and
are functions of normal
only; the normal should have the same probability of occurrence for any possible orientation. Using two independent random angles,
ξ and
ζ, with the following probability distribution function (pdf)
the normal is
in 2D and
in 3D. The mean values are calculated by analytical integration. Having arbitrary function
dependent on two (or one in 2D) statistically independent random variables
ξ and
ζ with the probability distribution function
(or
in 2D), the mean value of
G is
Evaluating Equation (
20) for
and
yields
where
in 3D and
in 2D;
is the second order unit tensor.
Combining Equations (
1), (
18), (
21) and (22), one obtains analytical formulas for the tensor of elastic constants
For an isotropic elastic continuum, strain tensor
has the following form
where
E and
α are Young’s modulus and Poisson’s ratio. Solving system of Equations (
23) and (
24), a set of equations relating elastic constants of homogenized continua,
E and
ν, and the discrete system,
and
α, are derived.
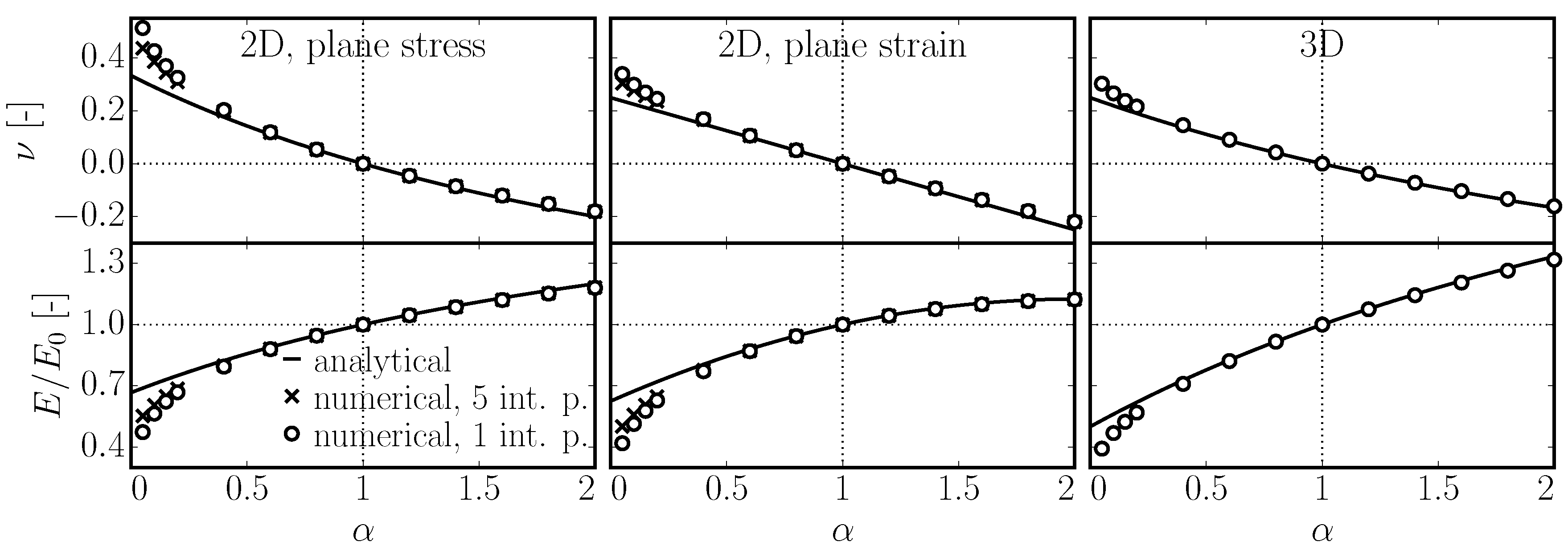
Numerical Verification
The set of Equation (
25) is numerically verified here. A large prism is loaded by stress
. The elastic parameters
E and
ν are found by fitting the displacements of the rigid bodies; see e.g. [
16,
25].
Figure 5 shows a comparison of the analytical formulas from Equation (
25) and numerical results. An exact match only happens in case of
. Increasing or decreasing
α, the discrete system yields a lower elastic modulus and higher Poisson’s ratio than values derived analytically. When
α is close to zero, the system becomes unstable. Some improvement can be gained by calculating the elemental response not only at one point (centroid) but along the whole facet area, where the stresses generally differ due to the rotations of rigid bodies. The results with an improved 2D model that uses five points to integrate the stress on the facet are shown in
Figure 5 as well. Since this improvement basically adds additional rotational stiffness to the elements, rigid body rotations are reduced and the system is stabilized. It shows slightly better agreement with analytical formulas.
5. Angular Bias in the Boundary Layer
The boundary layer shows strong bias in elemental orientation. In the ideal case when all the directions have the same probability, the angular deviation from the
x-direction should have the following pdf
The mean value (already defined in Equation (
20)) and standard deviation of any function
G dependent on
γ are from the definition
To calculate the mean and standard deviation of
γ, Equation (
27) is used with
.
These numbers are compared to the analysis of the actual discrete system in 2D (
Figure 6) and 3D (
Figure 7). In 2D, the discrete system was generated 500 times in a rectangular domain of size
, with a different seed of random generator each time. The weighted average and standard deviation of elemental inclination
γ were calculated for different
y locations; the weights were facet areas.
Figure 6 shows one symmetrical half of the cross section in the range
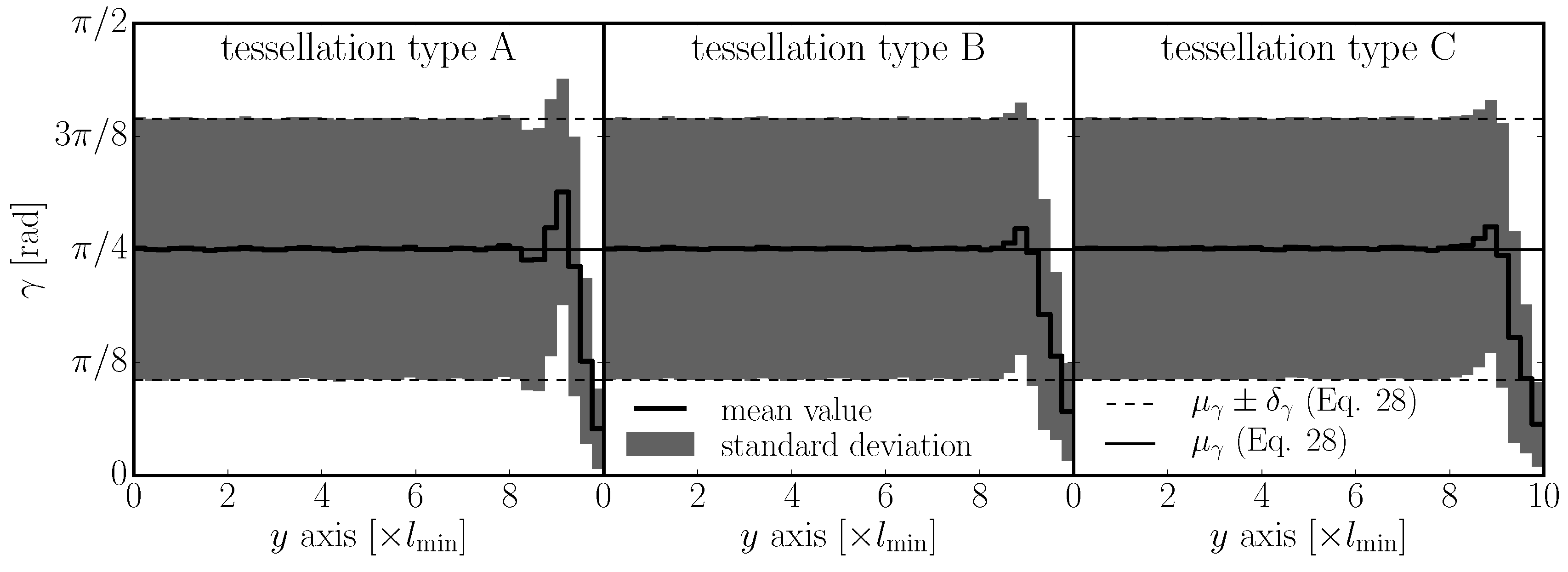
(center of the cross section) up to
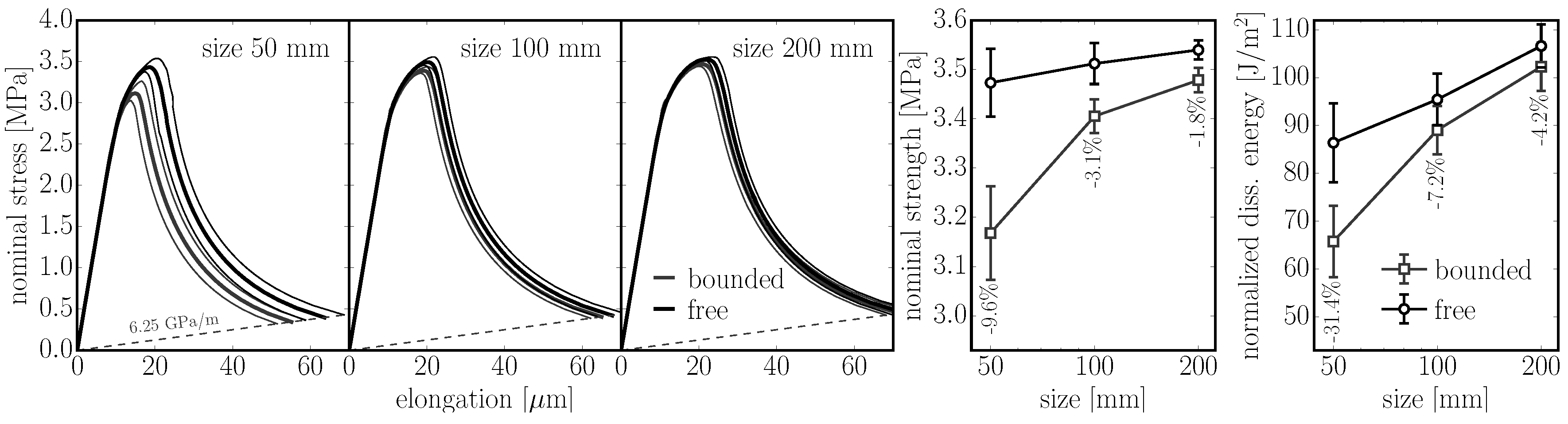
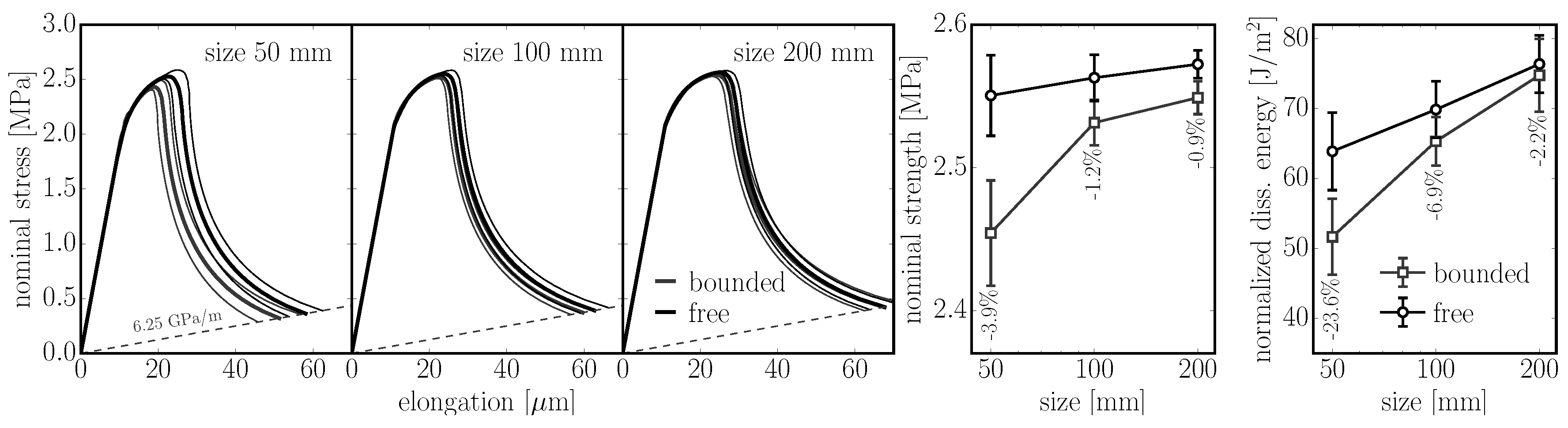
(boundary). The interior part is unbiased, while the boundary layer shows a strong decrease in the mean, indicating that the elements are more aligned with the boundary. Between the interior and the boundary, there is also a layer that exhibits a lower amount of aligned elements. All three tessellation types are investigated, and similar trends are observed.
In 3D, only tessellation type A is used. The discrete system was generated 3000 times in a prismatic domain
. The average and standard deviation of
γ (weighted by facet area) are calculated for different locations in the cross section.
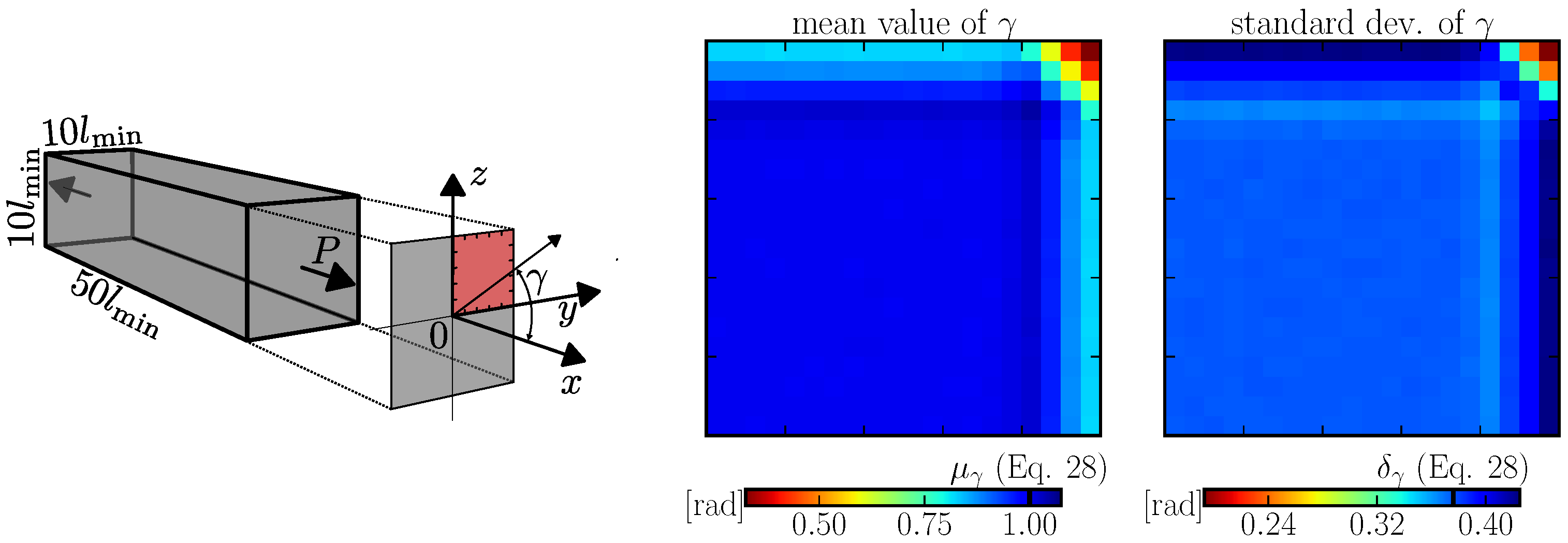
Figure 7 shows a symmetrical quarter of the cross section ranging from
(center of the cross section) up to
(boundary). The bias in the boundary layer is similar to what was seen in 2D; it gets strongly emphasized in corners.
6. Effects on Elastic Behavior
The rectangle and prism from the previous section were loaded by straining in the
x-direction (
), while deformations in the
y- and
z-direction were unconstrained. Such loading results in a single stress component
and the following relations (these can be derived from Equation (
24))
Since all the shear strains are zero and
, one can assume convenient rotation of the 3D coordinate system around the
x-axis in such a manner that the elements are always parallel to plane
and the normal
is the same for 2D and 3D models. The normal and tangential strain can be evaluated from Equation (
11)
and the magnitude of the shear strain is
Finally, strains
and
are substituted by Equation (
29) and elastic constants
E and
ν by Equation (
25). The stresses
and
are obtained by multiplying strains with
and
α according to Equation (
12). All the three cases—3D, 2D plain strain and 2D plane stress—collapse into one
Assuming no directional bias, the mean value and standard deviations are calculated (Equation (
27),
or
)
These characteristics are based on (i) an ideal unbiased directional distribution of elements, therefore only the interior parts will behave accordingly; (ii) assumption (
8), therefore these will be exactly satisfied only for
. For
, the translations do not obey Equation (
8) exactly and rotations are nonzero.
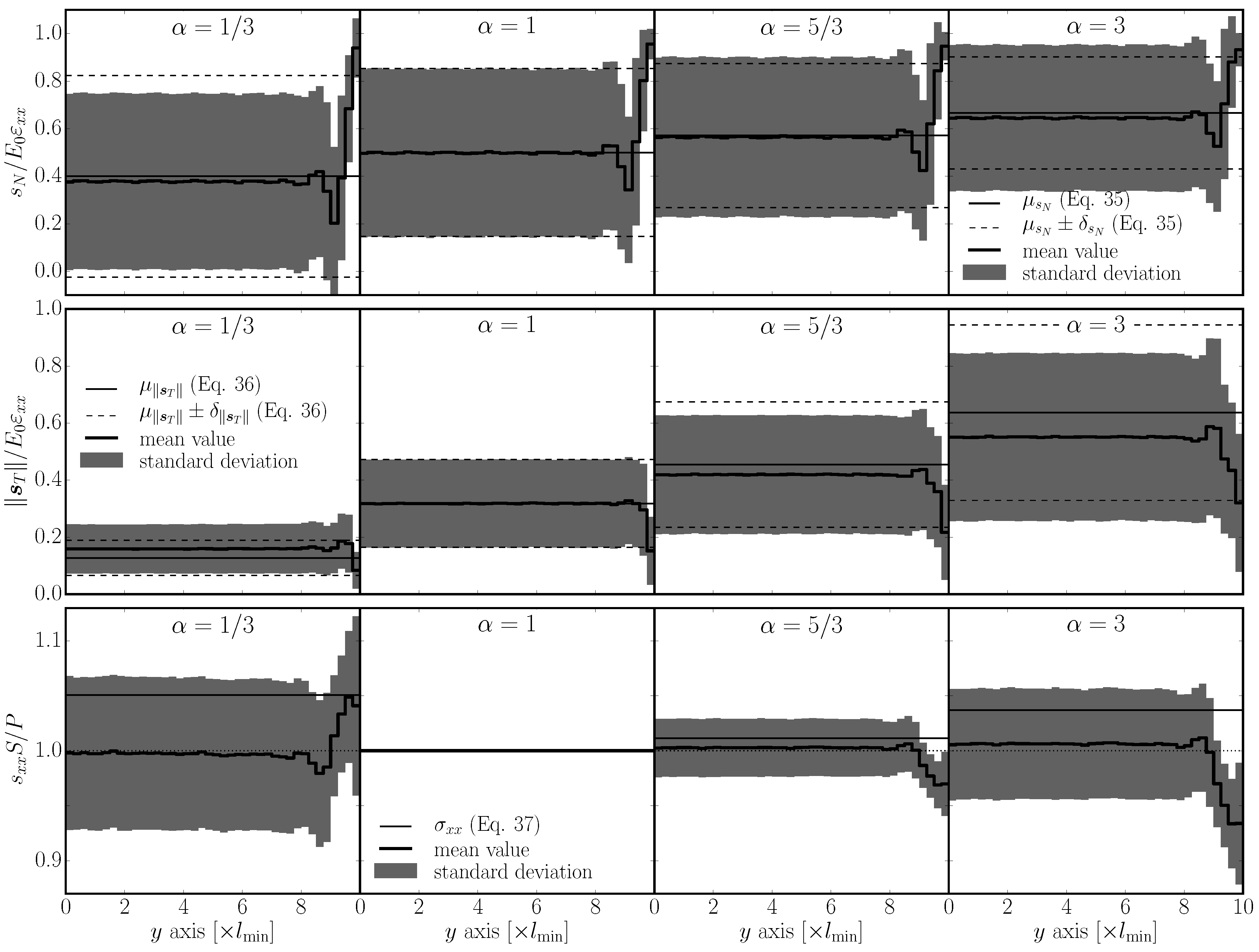
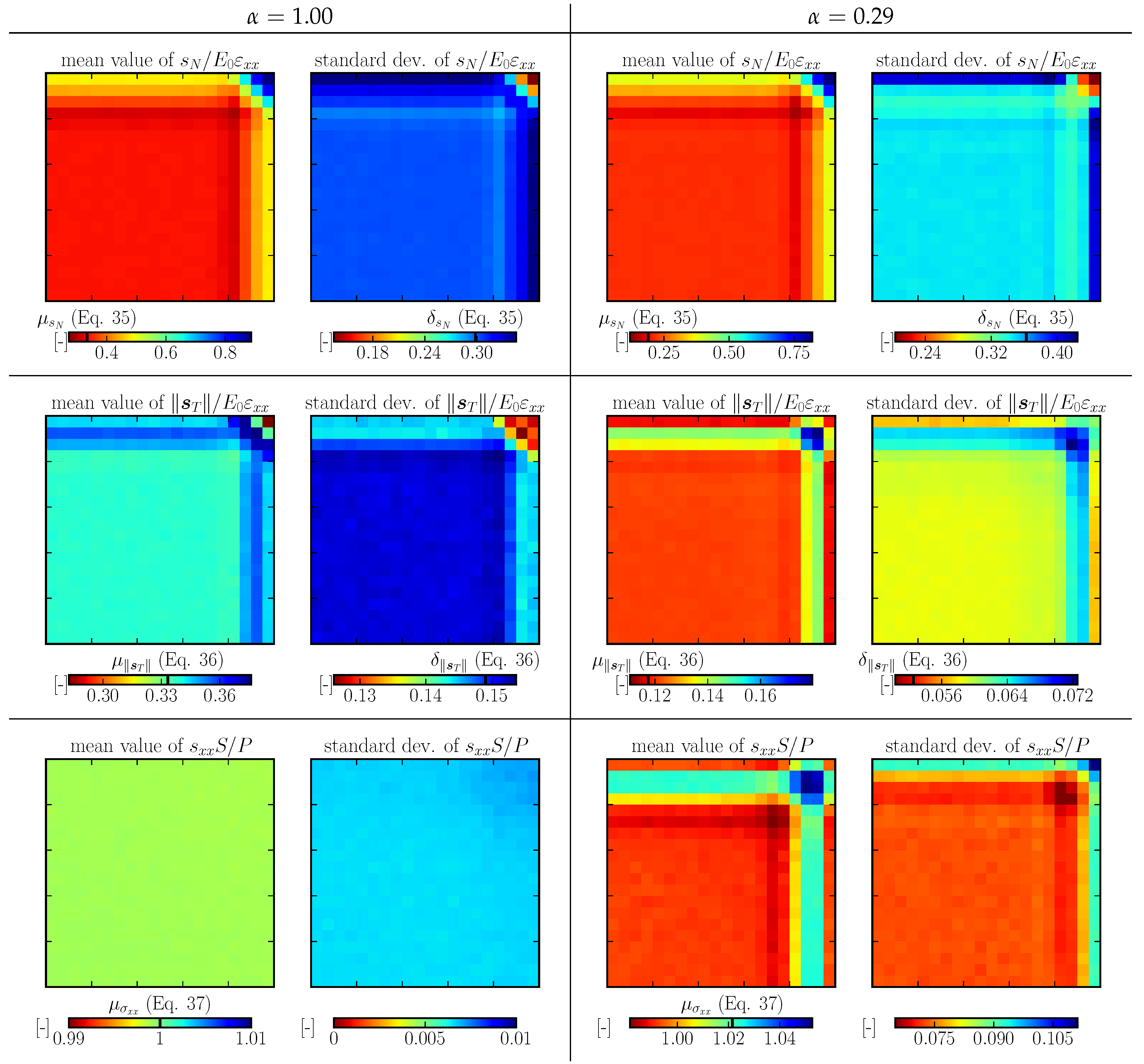
A comparison with real discrete system behavior is shown for 2D and 3D in
Figure 8 and
Figure 9 in the first two rows for selected
α parameters. The value
has been chosen for the 3D model because it is typical for concrete. The normal and shear stresses are normalized by
; the calculation of the mean and standard deviation was weighted by facet area. Only tessellation type A is shown, as the other two types perform very similarly. One can see reasonable approximation of the stresses by analytical Equations (
35) and (36) in the interior. Close to the boundary, the normal stress increases while the shear stress decreases. Moving further from the boundary, there is an opposite stress deviation as the amount of elements parallel with the boundary decreases.
Besides the stress at the contacts, one can also look at the average stress in the bodies. The tensorial stress,
, can be computed in three ways:
The average and standard deviation (weighted by
) of tensorial stresses
are plotted in
Figure 8 and
Figure 9 in the third row. The stress is normalized by
and also compared to theoretical
. The boundary layer with a higher fraction of elements aligned with the straining direction is stiffer for
and more compliant for
.
It is worth exploring whether
is a sufficient condition to obtain elastically uniform structure. The contact force is
but reduces to
for
. If facets are perpendicular to elements and Equation (
9) holds, then
. Starting with Equation (
38) and assuming the same
for all the elements, one arrives at
where the second and third expressions are just expanded multiplication and reordered summation. Finally, when all the facets of the rigid body forms an enclosed object, the last summation can be greatly simplified. Expression
is either 0 for
or
for
. Thanks to the symmetry of the strain tensor, one can write
Three conditions were used to obtain the elastically uniform structure: (i)
; (ii) facets are perpendicular to elements; and (iii) the rigid bodies are enclosed. All three tessellation types from
Section 2 meet these conditions.