Material State Awareness for Composites Part I: Precursor Damage Analysis Using Ultrasonic Guided Coda Wave Interferometry (CWI)
Abstract
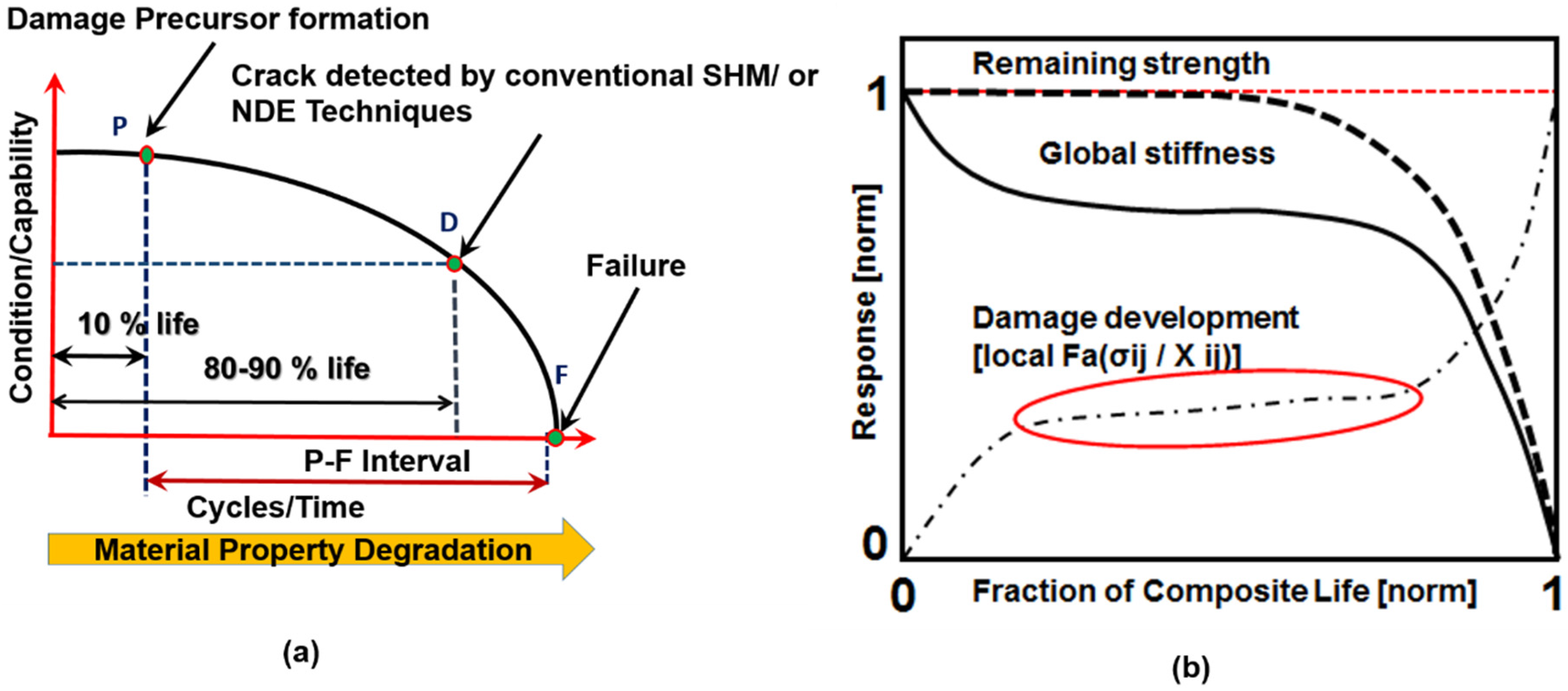
:1. Introduction
2. Materials and Methods
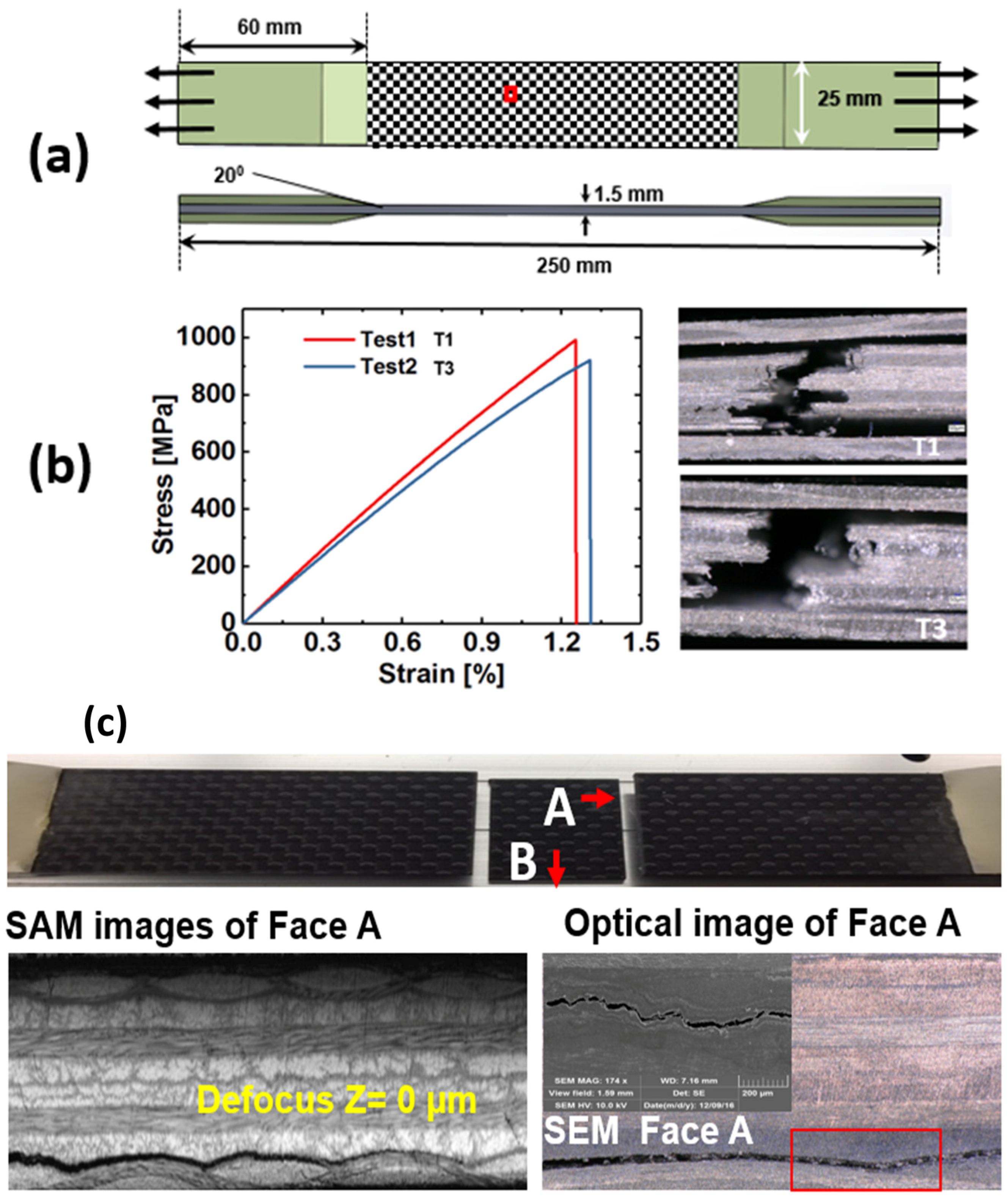
2.1. Materials and Specimen Preparation
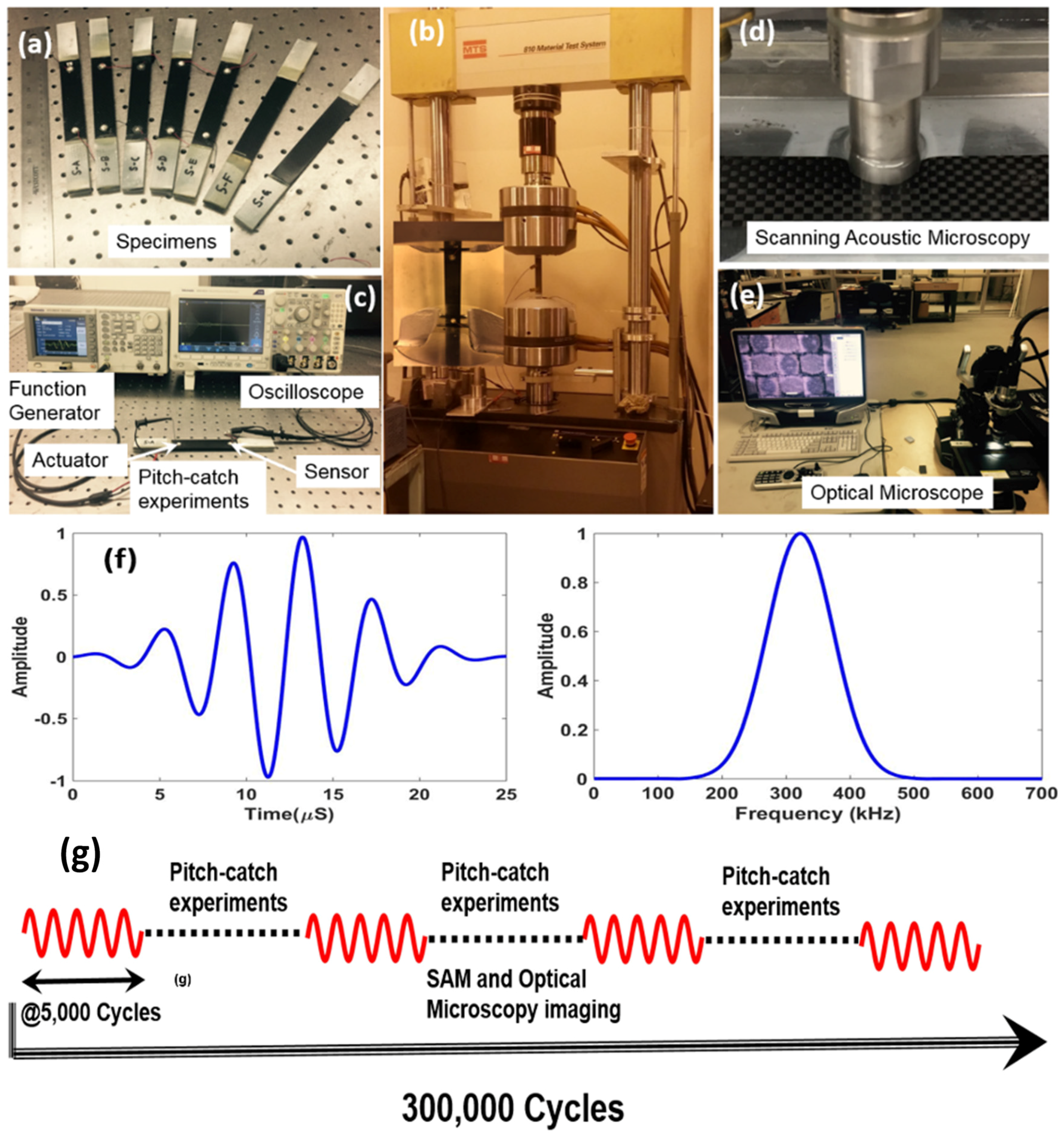
2.2. Tensile Tests and Non-Accelerated Fatigue Testing
2.3. Pitch-Catch Ultrasonic Lamb Wave Experiments
2.4. Stretching Technique with Cross-Correlation
2.5. Taylor Series Expansion
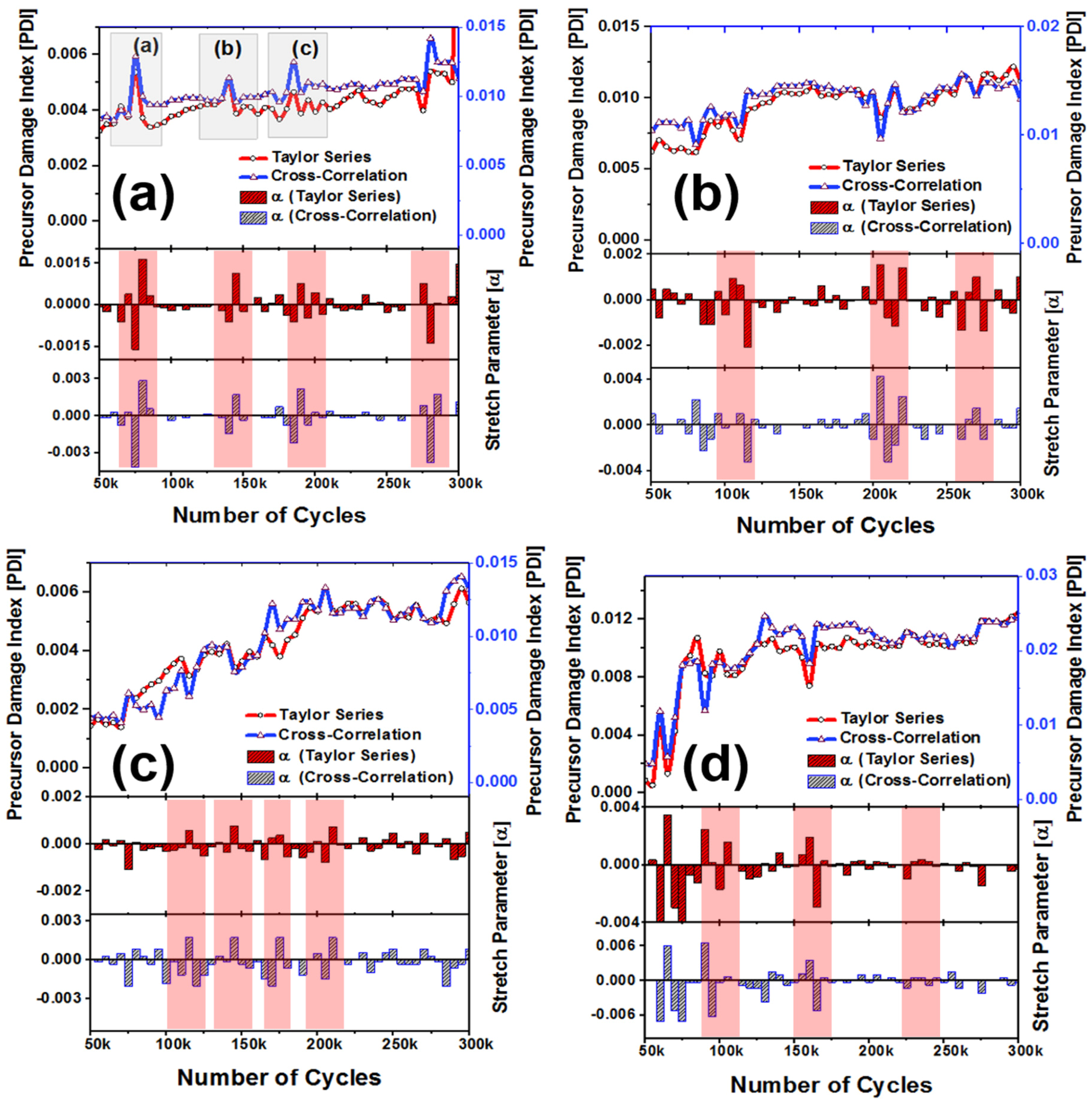
2.6. Precursor Damage Growth Parameter
3. Results
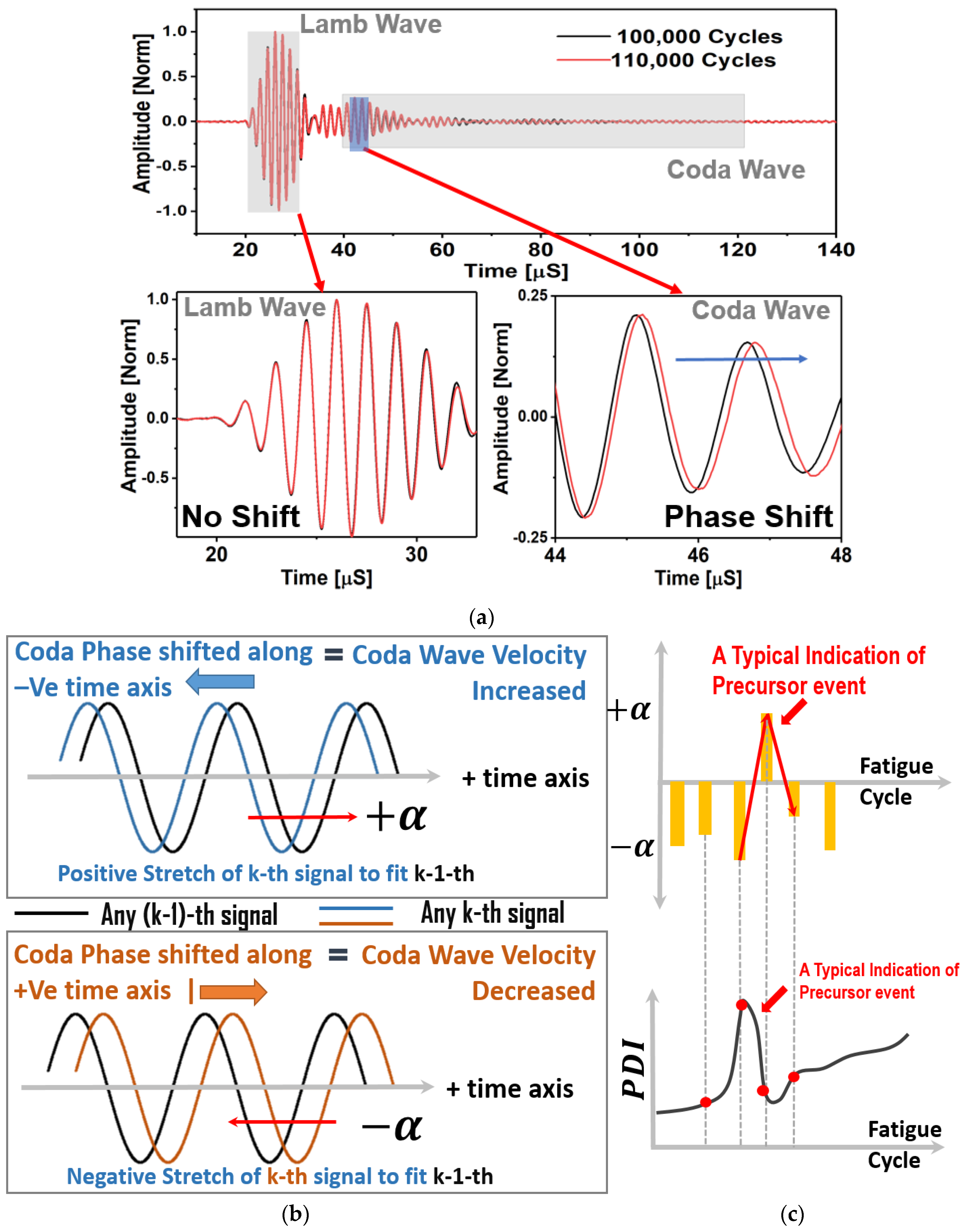
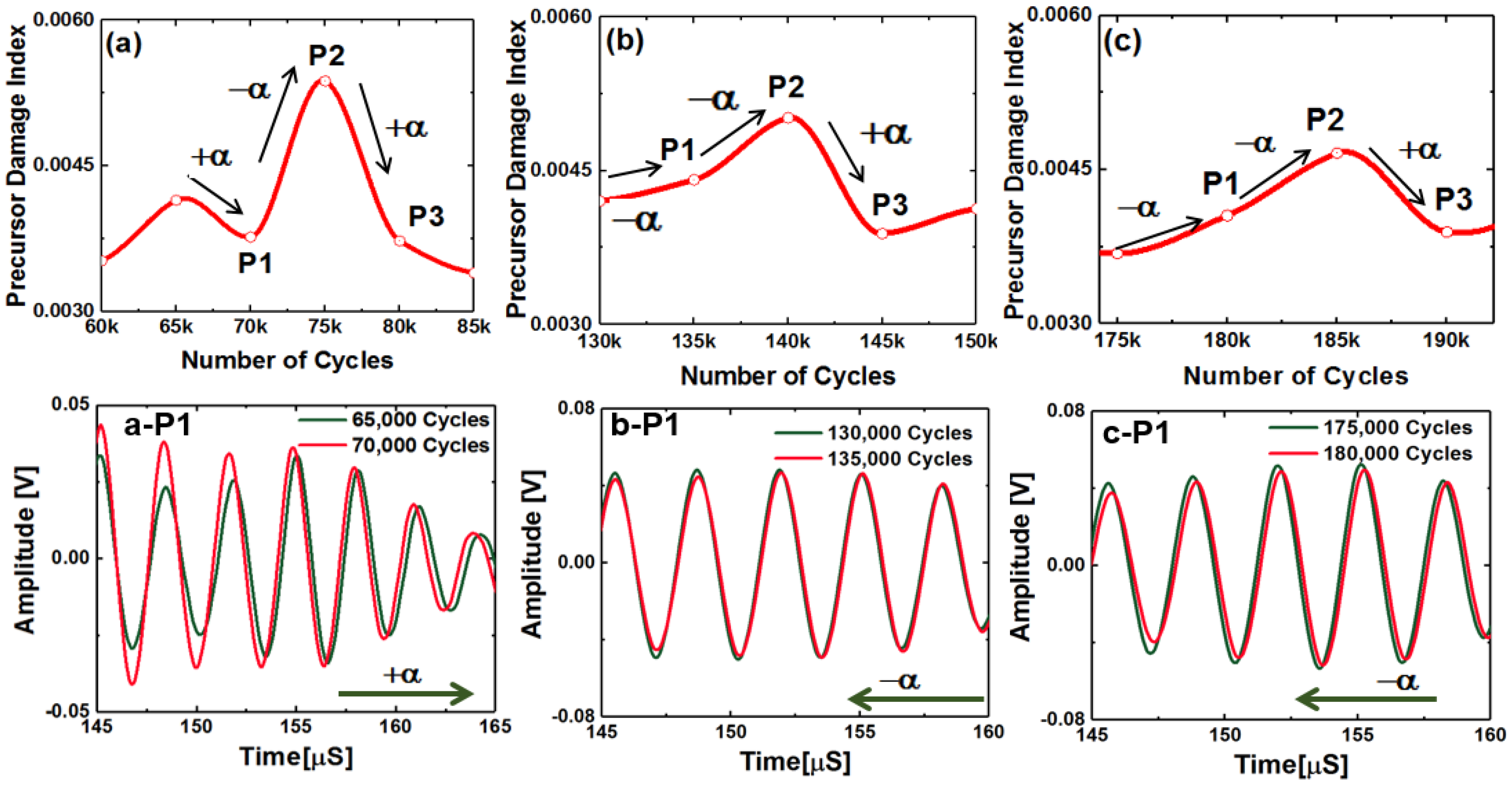
3.1. Understanding the Stretch Parameter
- A positive (+) stretch parameter is defined, when it is required to pull the coda signal from the () state towards the positive time axis to match the previous signal from the previous fatigue interval (). This means that the is to compensate the increased coda wave velocity.
- A negative (−) stretch parameter is defined, when it is required to push or squeeze the coda signal from the () state towards the negative time axis to match the previous signal from the previous fatigue interval (). This means that the is to compensate the decreased coda wave velocity.
- Next, using the definition of PDI in Equation (9), it is observed that when the stretch parameter flips its sign from negative to positive or positive to negative, the PDI decreases or increases, respectively.
- It was found from the fatigue experiments that the stretch parameter is usually negative for the decreasing wave velocity, which should give rise to the PDI. However, after a sudden peak in the negative stretch parameter, the stretch parameter switches its sign to the positive, whenever the negative stretch is maximum. This makes the PDI decrease due to the increase in the coda wave velocity. Again, this is specific to the coda wave velocity only.
- Almost every time when the stretch parameter switches to positive at the end of any material state k, it is observed that at the end of the following state, k + 1 resulted inevitable negative stretch parameter. The reason for this phenomenon is explained in the Discussion section.
- The above is not applicable for the Lamb wave modes that arrive first. In case of macro-scale damage, the resulted slowness in fundamental Lamb wave modes result monotonically increasing damage index, but this is not the case reported in this article.
- It is emphasized again that the decrease in the PDI happens only and only due to the coda wave characteristics during the precursor events. A decrease in PDI is an indication of accumulated damage due to precursor in the composite which cannot be ignored and must be reported.
- It is reported herein that these unique features are found to be the pivotal in studying the precursor damage in composites using the guided coda wave.
3.2. Damage Growth Quantification Using PDI
4. Discussion
4.1. Explanation of PDI Data
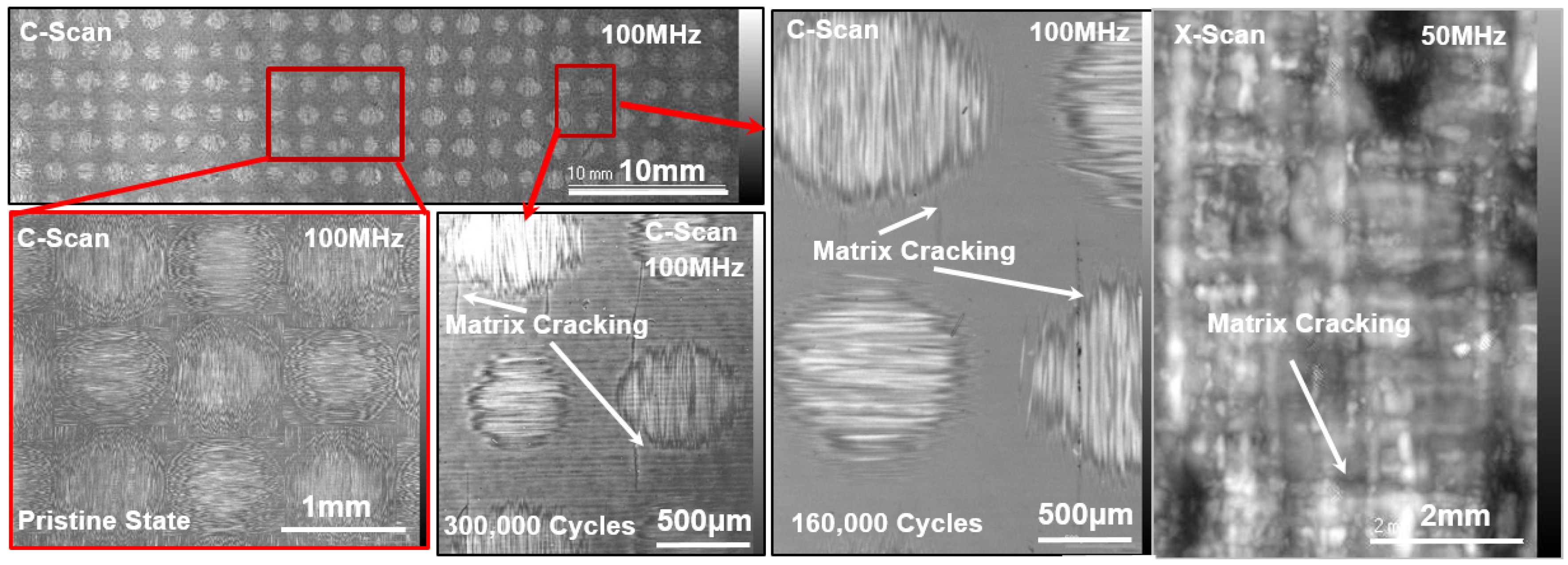
4.2. Proof of Damage Development Using Optical Microscopy
4.3. Damage Characterization Using SAM
4.3.1. SAM Method Showing Damage Growth in the Specimen S-E
4.3.2. SAM on the Decommissioned Specimen S-A
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Talreja, R.; Varna, J. Modeling Damage, Fatigue and Failure of Composite Materials; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Reifsnider, K.L.; Case, S.W. Damage Tolerance and Durability of Material Systems; Reifsnider, K.L., Case, S.W., Eds.; Wiley-VCH: Weinheim, Germany, 2002; p. 435. ISBN 0-471-15299-4. [Google Scholar]
- Bathias, C.; Cagnasso, A. Application of X-ray tomography to the nondestructive testing of high-performance polymer composites. In Damage Detection in Composite Materials; ASTM International: West Conshohocken, PA, USA, 1992. [Google Scholar]
- Banerjee, S.; Ahmed, R. Precursor/incubation of multi-scale damage state quantification in composite materials: Using hybrid microcontinuum field theory and high-frequency ultrasonics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
- Aymerich, F.; Meili, S. Ultrasonic evaluation of matrix damage in impacted composite laminates. Compos. Part B Eng. 2000, 31, 1–6. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M.; Soutis, C. Damage detection in composite materials using Lamb wave methods. Smart Mater. Struct. 2002, 11, 269. [Google Scholar] [CrossRef]
- Diamanti, K.; Soutis, C. Structural health monitoring techniques for aircraft composite structures. Prog. Aerosp. Sci. 2010, 46, 342–352. [Google Scholar] [CrossRef]
- Banerjee, S. Estimation of intrinsic damage state in materials using non-local perturbation: Application to active health monitoring. J. Intell. Mater. Syst. Struct. 2009, 20, 1221–1232. [Google Scholar] [CrossRef]
- Bell, J. Condition Based Maintenance Plus DoD Guidebook; Department of Defense: Washington, DC, USA, 2008. [Google Scholar]
- Hall, A.J.; Brennan, I.; Raymond, E.; Ghoshal, A.; Liu, K.C.; Coatney, M.; Haynes, R.; Bradley, N.; Weiss, V.; Tzeng, J. Damage Precursor Investigation of Fiber-Reinforced Composite Materials under Fatigue Loads; US Army Research Laboratory: Aberdeen, MD, USA, 2013. [Google Scholar]
- Thostenson, E.T.; Chou, T.W. Carbon nanotube networks: Sensing of distributed strain and damage for life prediction and self healing. Adv. Mater. 2006, 18, 2837–2841. [Google Scholar] [CrossRef]
- Haile, M.A.; Hall, A.J.; Yoo, J.H.; Coatney, M.D.; Myers, O.J. Detection of damage precursors with embedded magnetostrictive particles. J. Intell. Mater. Syst. Struct. 2016, 27, 1567–1576. [Google Scholar] [CrossRef]
- Martini, F.; Bean, C.J.; Saccorotti, G.; Viveiros, F.; Wallenstein, N. Seasonal cycles of seismic velocity variations detected using coda wave interferometry at Fogo volcano, São Miguel, Azores, during 2003–2004. J. Volcanol. Geotherm. Res. 2009, 181, 231–246. [Google Scholar] [CrossRef]
- Snieder, R.; Grêt, A.; Douma, H.; Scales, J. Coda wave interferometry for estimating nonlinear behavior in seismic velocity. Science 2002, 295, 2253–2255. [Google Scholar] [CrossRef] [PubMed]
- Larose, E.; Hall, S. Monitoring stress related velocity variation in concrete with a 2 × 10−5 relative resolution using diffuse ultrasound. J. Acoust. Soc. Am. 2009, 125, 1853–1856. [Google Scholar] [CrossRef] [PubMed]
- Planès, T.; Larose, E. A review of ultrasonic Coda Wave Interferometry in concrete. Cem. Concr. Res. 2013, 53, 248–255. [Google Scholar] [CrossRef]
- Zhang, Y.; Abraham, O.; Grondin, F.; Loukili, A.; Tournat, V.; Le Duff, A.; Lascoup, B.; Durand, O. Study of stress-induced velocity variation in concrete under direct tensile force and monitoring of the damage level by using thermally-compensated coda wave interferometry. Ultrasonics 2012, 52, 1038–1045. [Google Scholar] [CrossRef] [PubMed]
- Schurr, D.P.; Kim, J.-Y.; Sabra, K.G.; Jacobs, L.J. Damage detection in concrete using coda wave interferometry. NDT E Int. 2011, 44, 728–735. [Google Scholar] [CrossRef]
- Zhang, Y.; Planès, T.; Larose, E.; Obermann, A.; Rospars, C.; Moreau, G. Diffuse ultrasound monitoring of stress and damage development on a 15-ton concrete beam. J. Volcanol. Geotherm. Res. 2016, 139, 1691–1701. [Google Scholar] [CrossRef] [PubMed]
- Snieder, R. The theory of coda wave interferometry. Pure Appl. Geophys. 2006, 163, 455–473. [Google Scholar] [CrossRef]
- Abraham, O.; Zhang, Y.; Chapeleau, X.; Durand, O.; Tournat, V. EWSHM-7th European Workshop on Structural Health Monitoring. In Proceedings of the Monitoring of a Large Cracked Concrete Sample with Non-Linear Mixing of Ultrasonic Coda Waves, Nantes, France, 8–11 July 2014. [Google Scholar]
- Astm, D. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; 3039/D 3039M; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- Liu, S.; Wu, Z.; Zhu, J.; Yang, H. A Novel Coda Wave Interferometry Calculation Approach Using Taylor Series Expansion. Struct. Health Monit. 2015. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patra, S.; Banerjee, S. Material State Awareness for Composites Part I: Precursor Damage Analysis Using Ultrasonic Guided Coda Wave Interferometry (CWI). Materials 2017, 10, 1436. https://doi.org/10.3390/ma10121436
Patra S, Banerjee S. Material State Awareness for Composites Part I: Precursor Damage Analysis Using Ultrasonic Guided Coda Wave Interferometry (CWI). Materials. 2017; 10(12):1436. https://doi.org/10.3390/ma10121436
Chicago/Turabian StylePatra, Subir, and Sourav Banerjee. 2017. "Material State Awareness for Composites Part I: Precursor Damage Analysis Using Ultrasonic Guided Coda Wave Interferometry (CWI)" Materials 10, no. 12: 1436. https://doi.org/10.3390/ma10121436
APA StylePatra, S., & Banerjee, S. (2017). Material State Awareness for Composites Part I: Precursor Damage Analysis Using Ultrasonic Guided Coda Wave Interferometry (CWI). Materials, 10(12), 1436. https://doi.org/10.3390/ma10121436





