Modeling and Optimization of the Thermal Performance of a Wood-Cement Block in a Low-Energy House Construction
Abstract
:1. Introduction
2. Methods
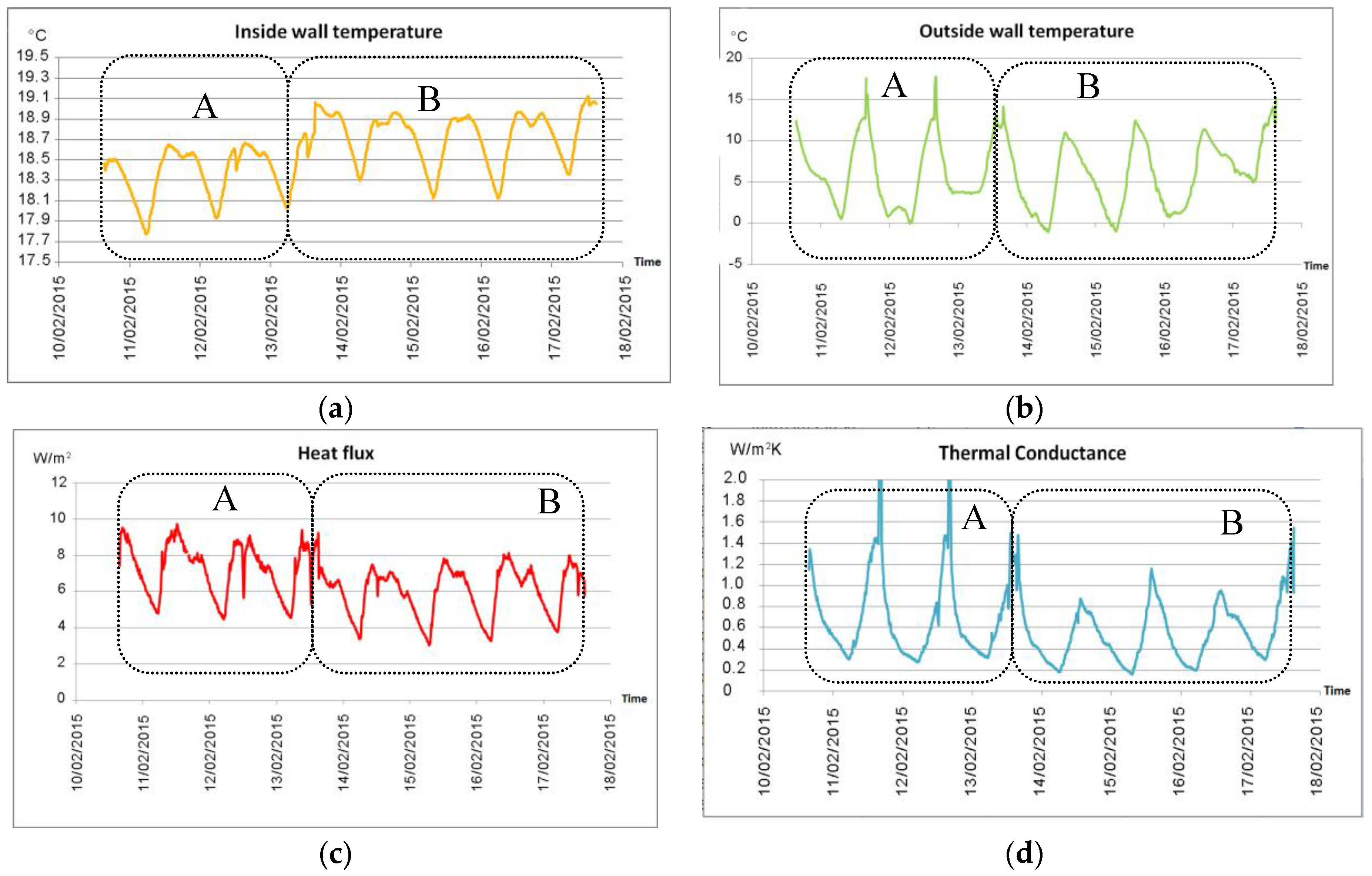
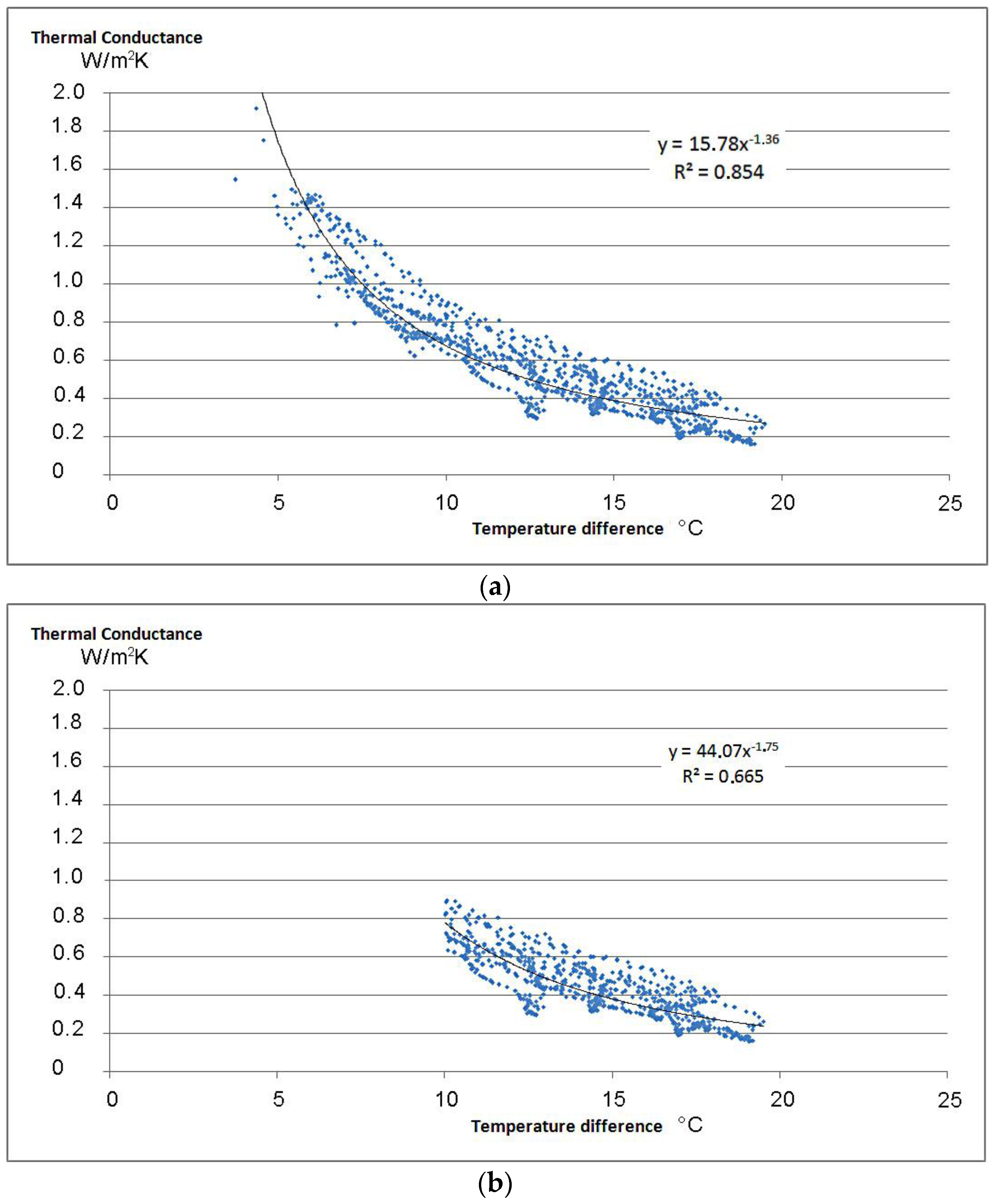
2.1. Heat Flow Meter
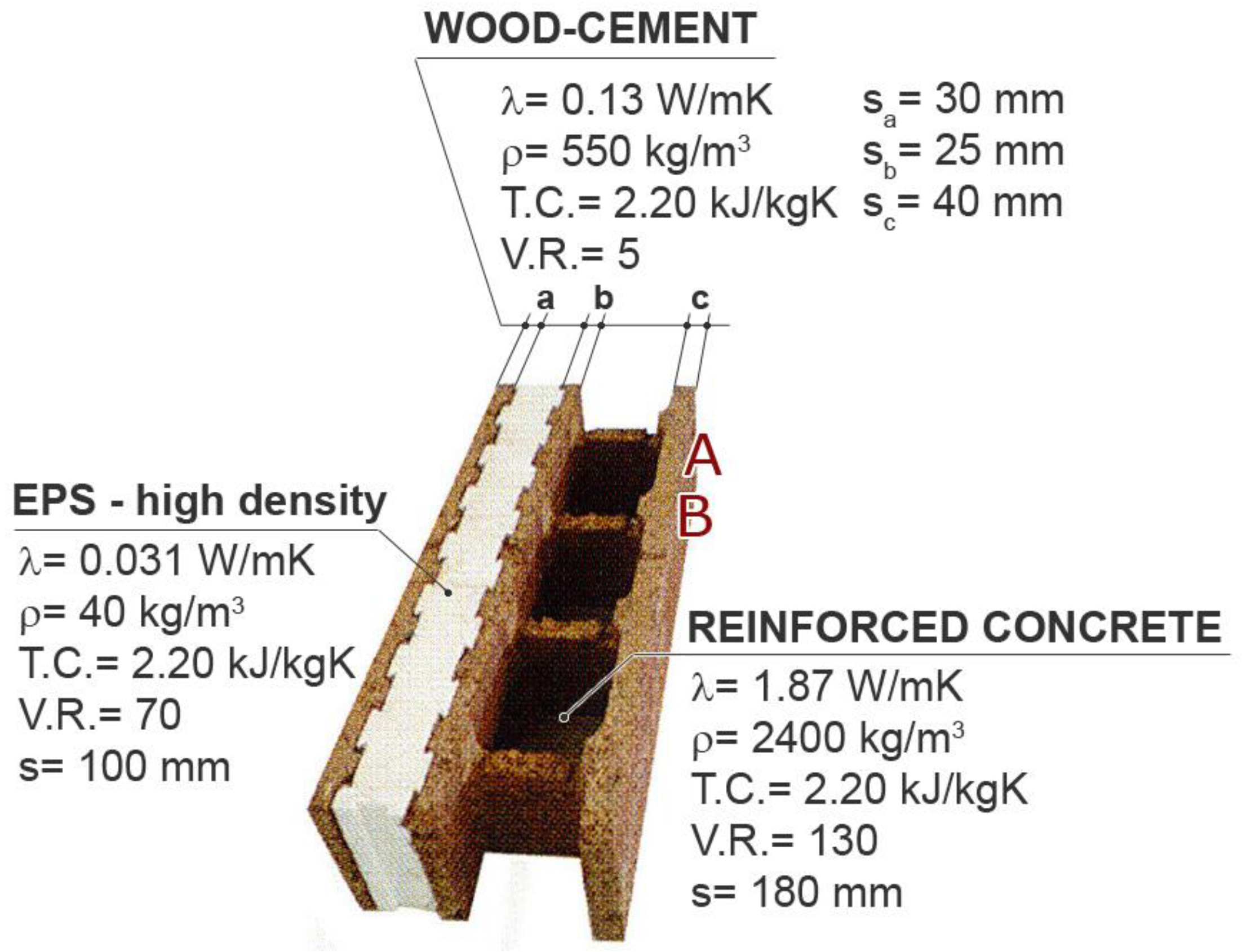
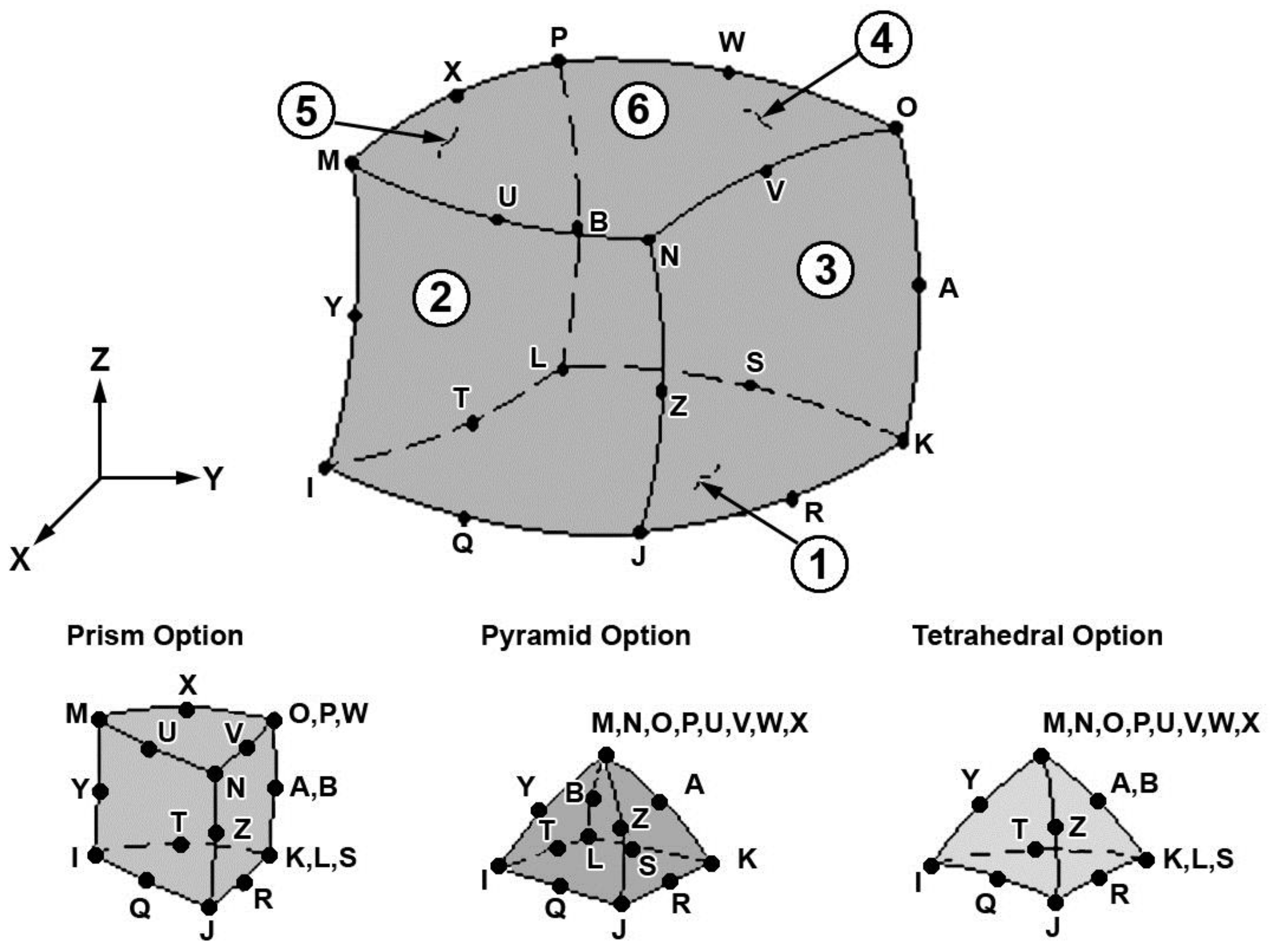
2.2. FEM Simulations
- System geometry;
- Layer configuration;
- Chemical/physical material properties;
- Thermal conductivity and global transmittance for comparing the obtained results.
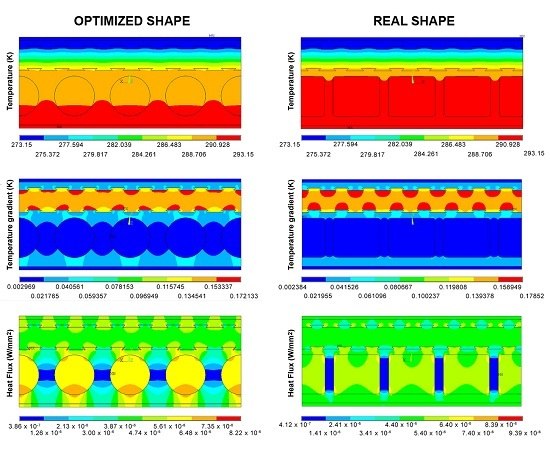
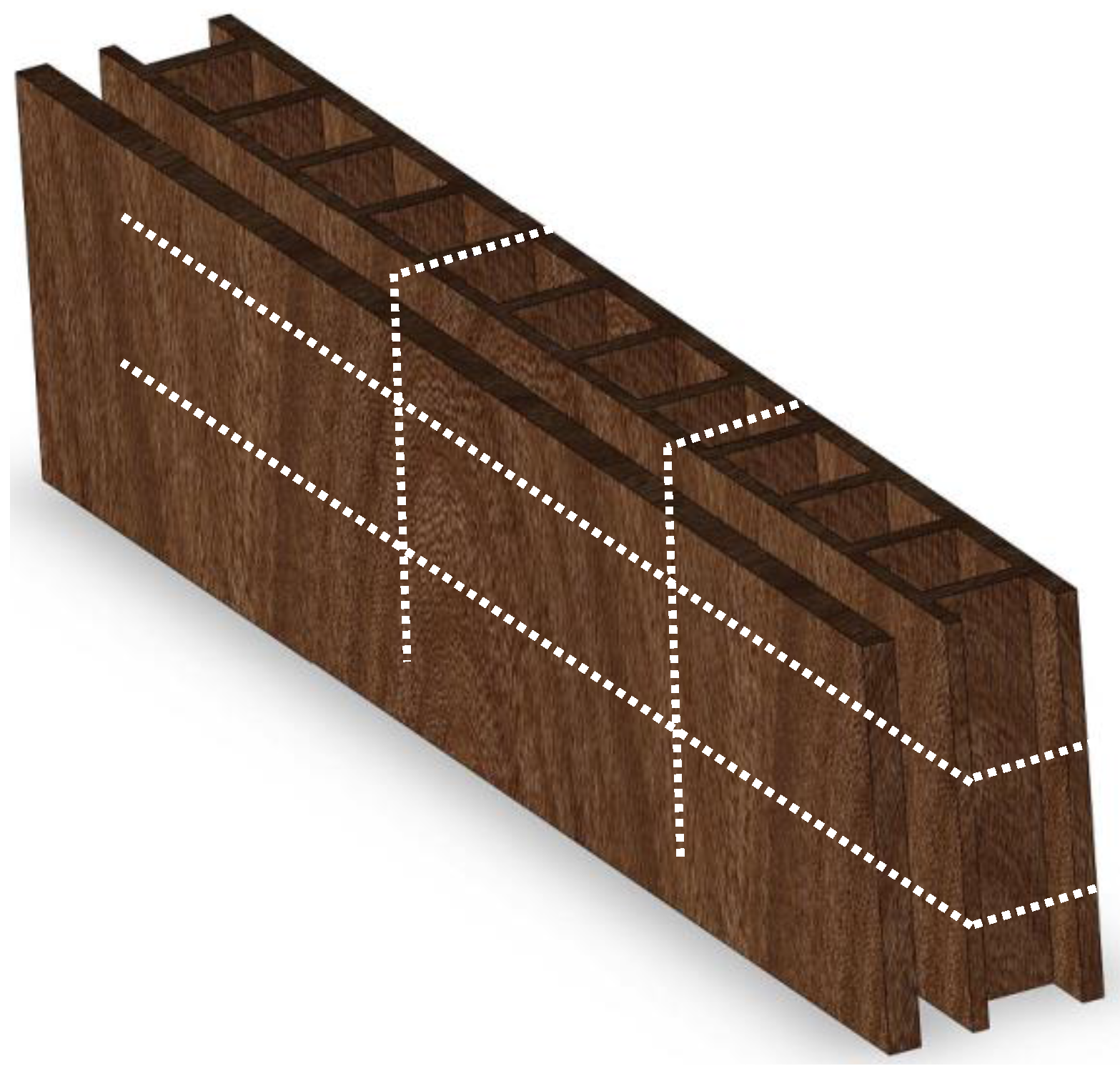
- A geometry simplification for the reinforced concrete seats: the rounded shape of the corner has been replaced by an angular one;
- A simplification of the EPS seat: a straight line has been used, running in the middle of the original swallow-tail shape.
3. Results
3.1. Heat Flow Meter Measurements
3.2. FEM Simulations
- Case 1: outside wall temperature Tout = 0 °C, inside wall temperature Tin = 20 °C;
- Case 2: outside wall temperature Tout = −5 °C, inside wall Tin = 20 °C;
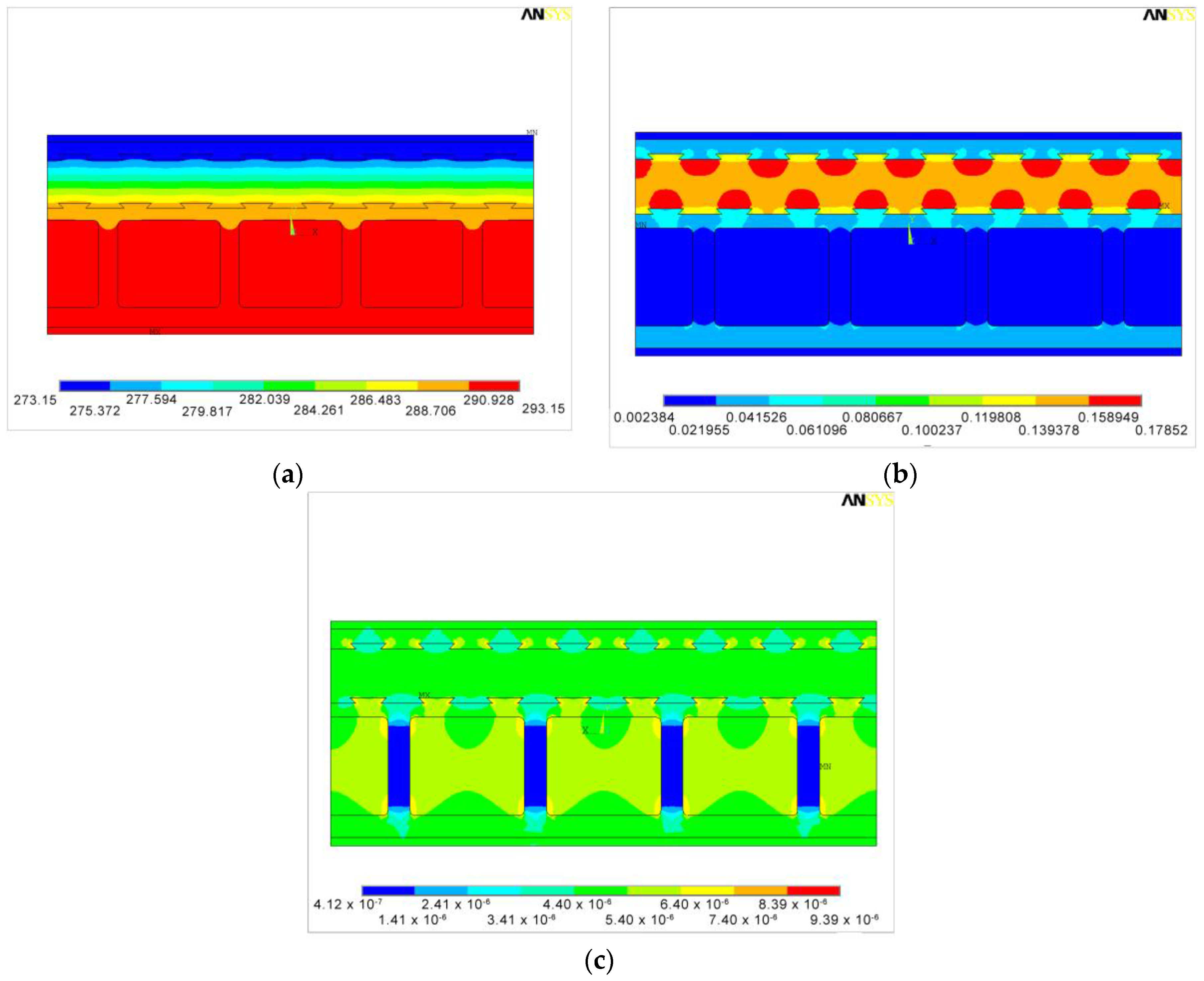
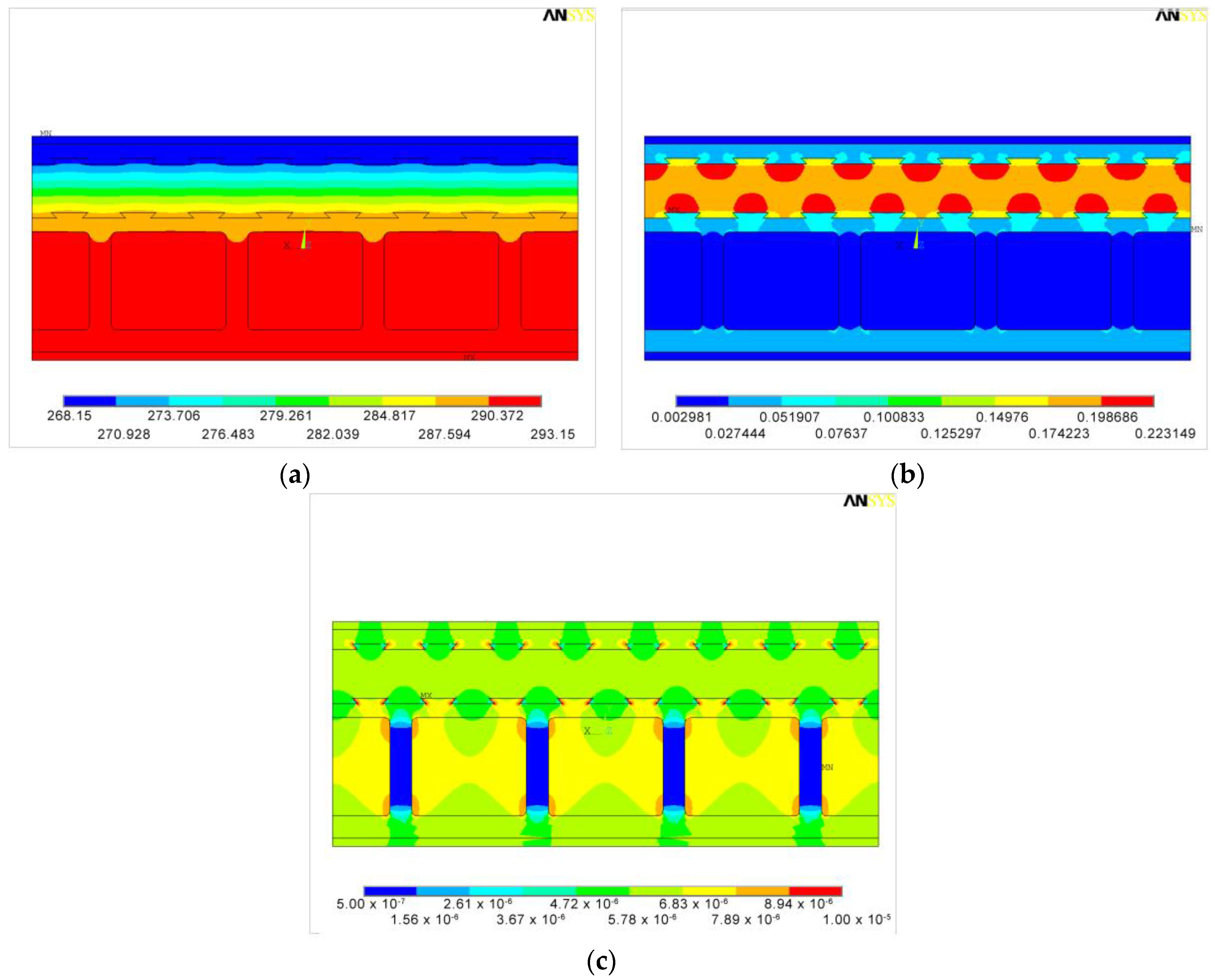
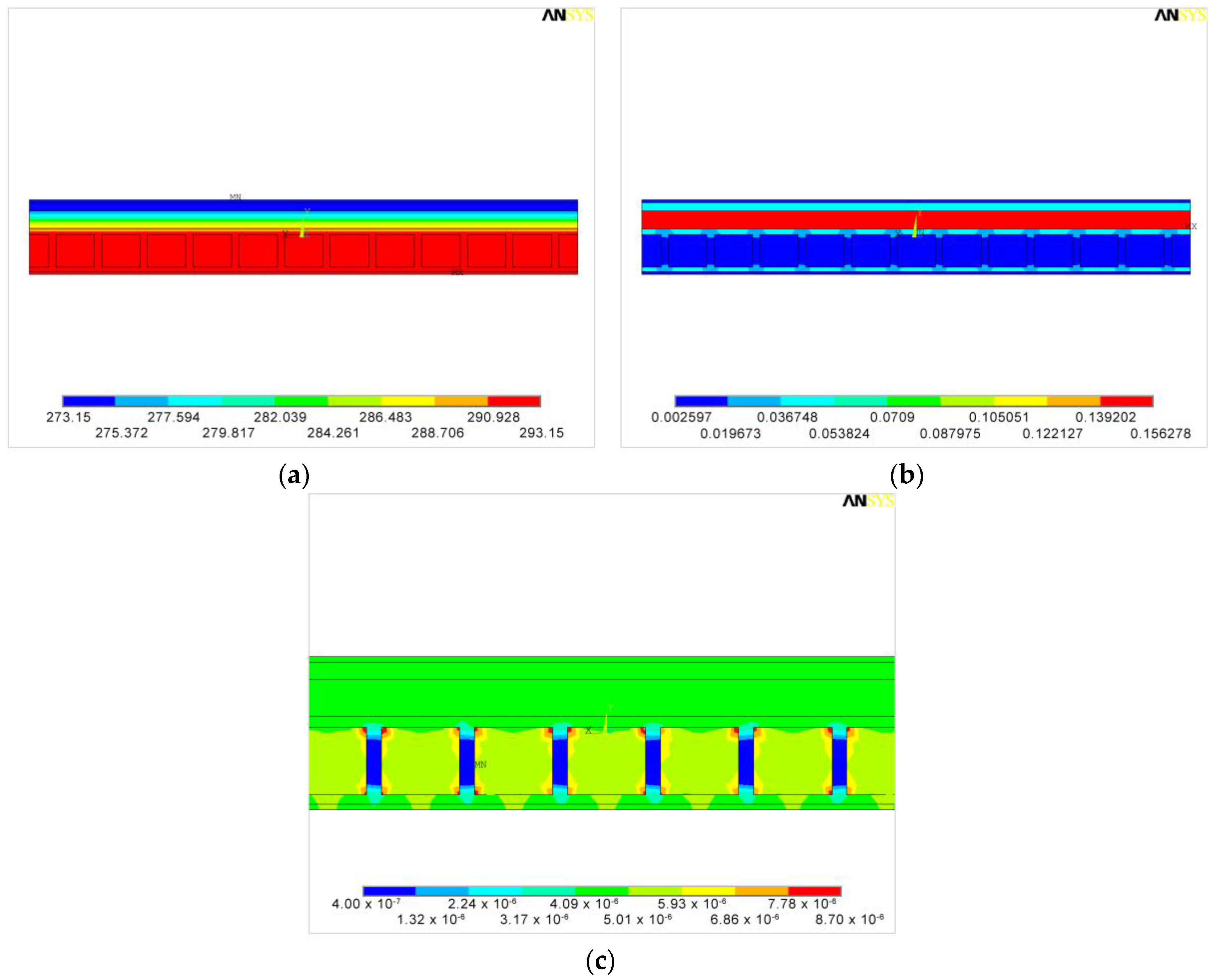
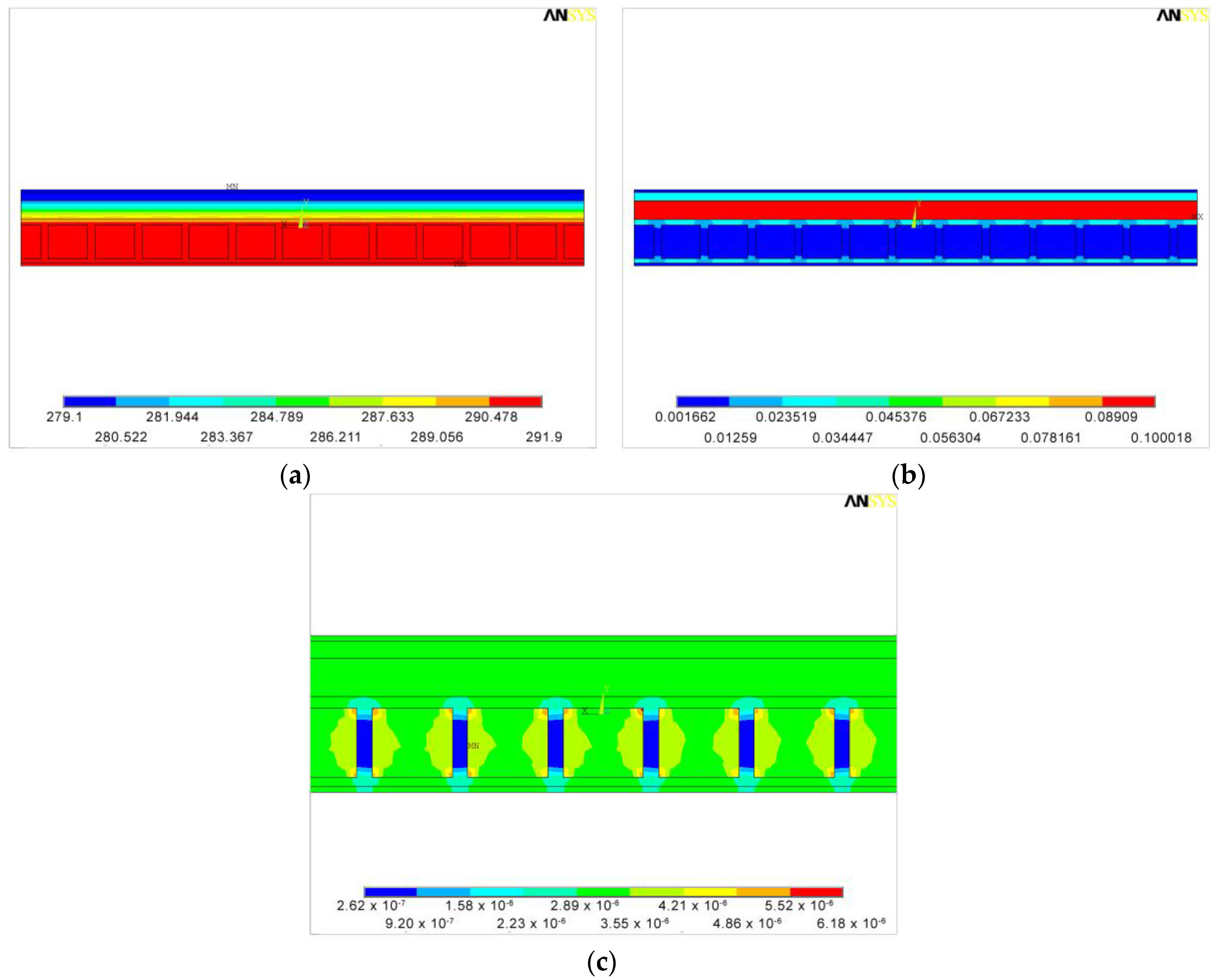
3.2.1. FEM Simulation of a Single Block (SBC)
Case 1
Case 2
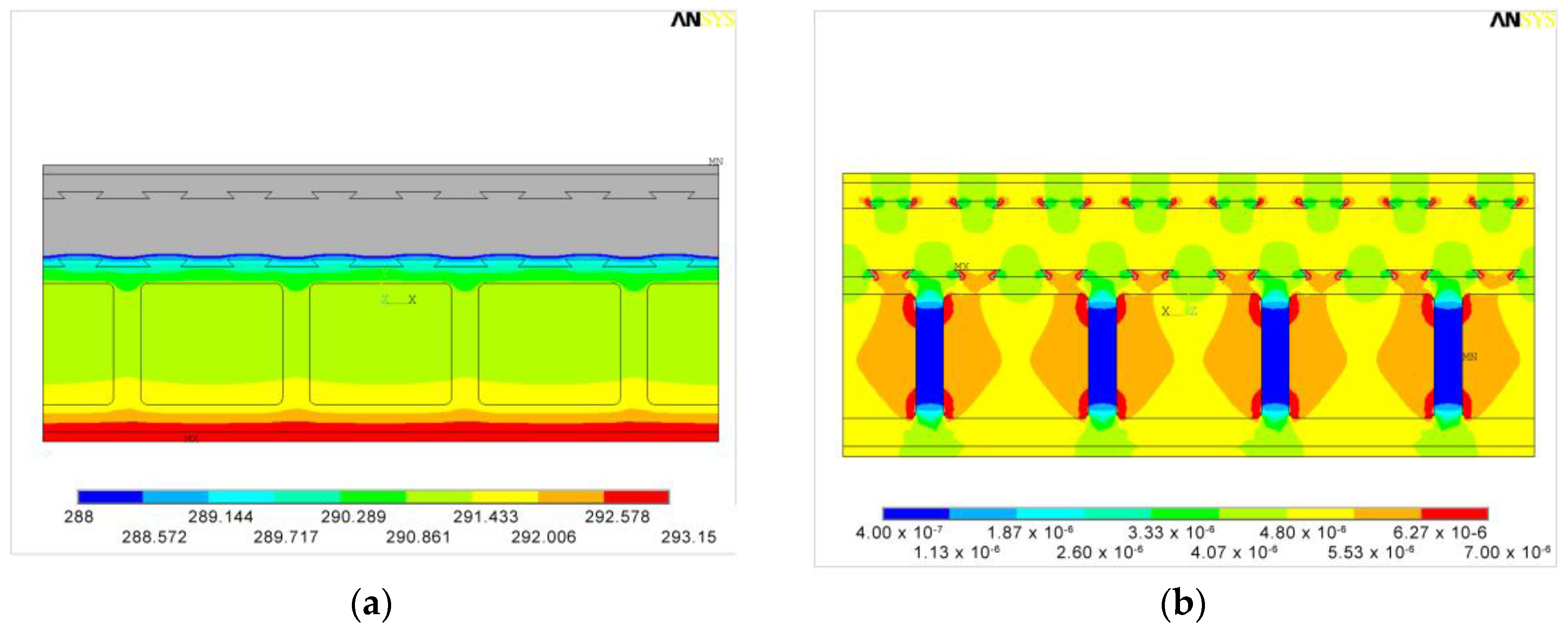
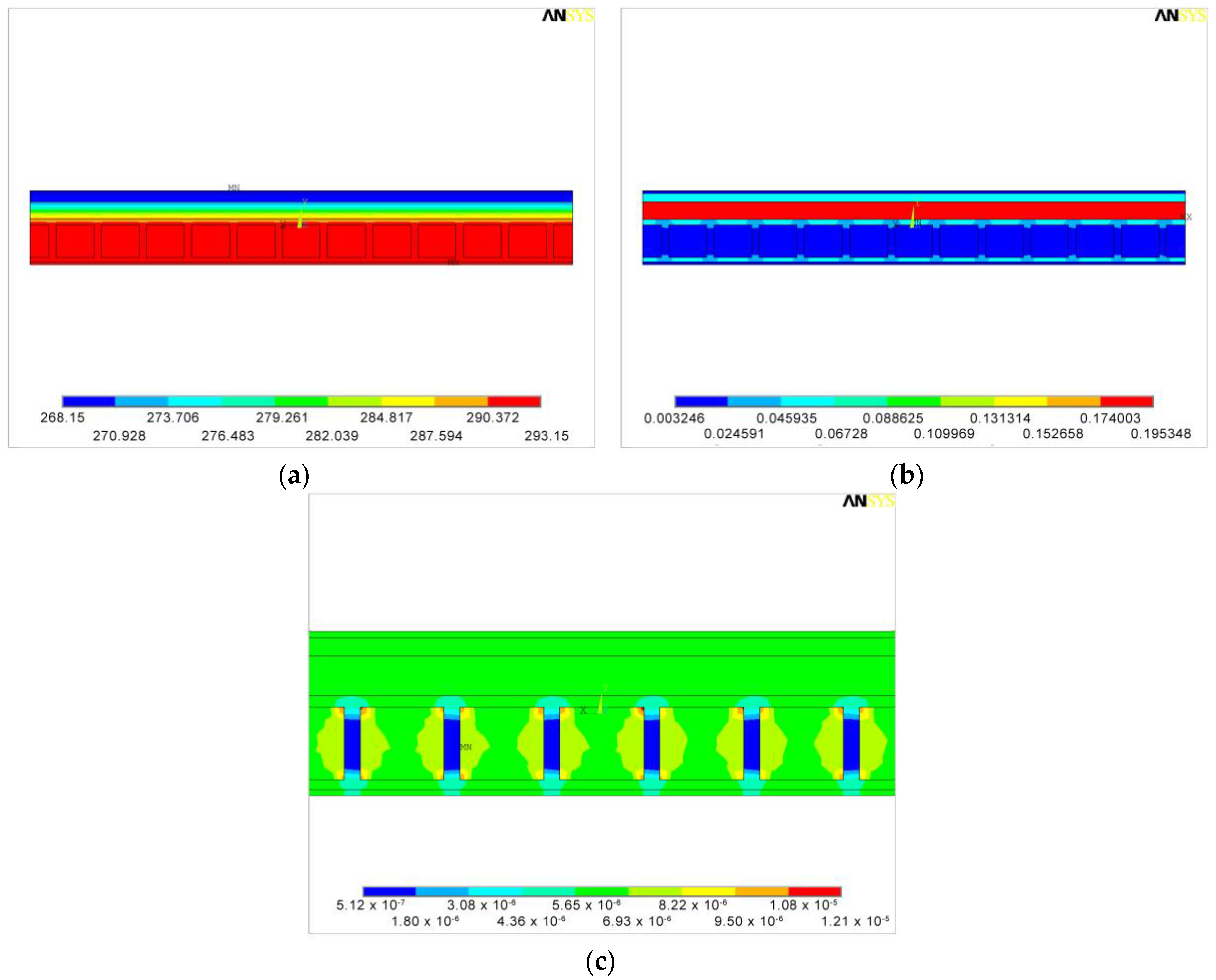
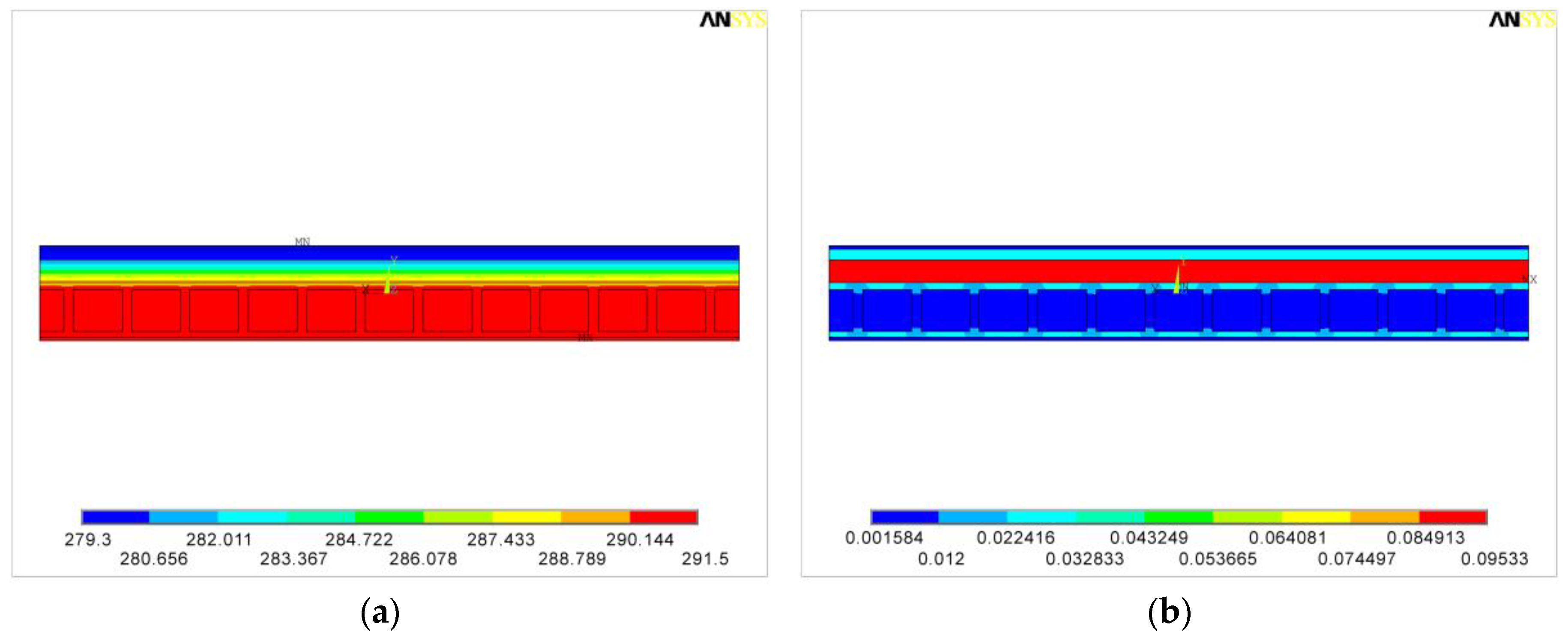
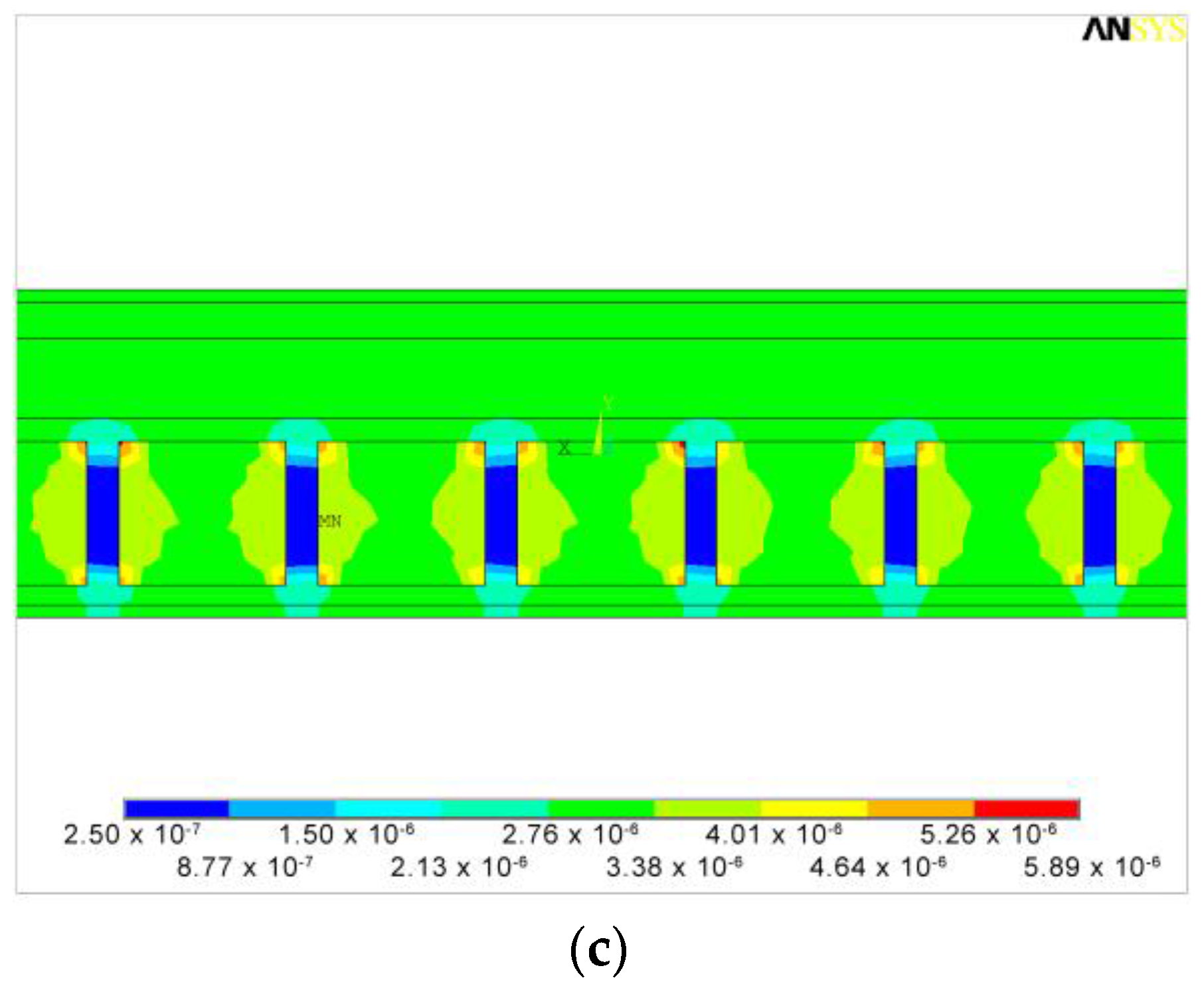
3.2.2. FEM Simulation of Nine Adjacent Blocks (9BC)
- Case 3: outside wall temperature Tout = 6.2 °C, inside wall temperature Tin = 18.4 °C;
- Case 4: outside wall temperature Tout = 6 °C, inside wall temperature Tin = 18.7 °C.
Case 1
Case 2
Case 3
Case 4
- (1)
- Results did not vary with different wall temperatures, therefore they are not influenced by the imposed boundary conditions;
- (2)
- Results did not vary with different block configurations. This means that relevant mutual exchanges between adjacent blocks do not occur, and that the study of this kind of material can be focused even on a single block;
- (3)
- Results are coherent with the value provided by the manufacturer, this means that the fem simulations (in terms of modeled block and boundary conditions) well represent the conditions of the theoretical calculus;
- (4)
- The models and geometries employed for the SBC ensure the numerical stability of the simulation;
- (5)
- The geometrical simplifications adopted for the study of configuration 9BC, needed to reduce the computational effort of the simulations, guarantee a proper modeling of the wall behavior;
- (6)
- Results obtained via fem simulation differ from the ones obtained via in field measurements, since the latter are affected by the dynamic thermal behavior of the wall;
- (7)
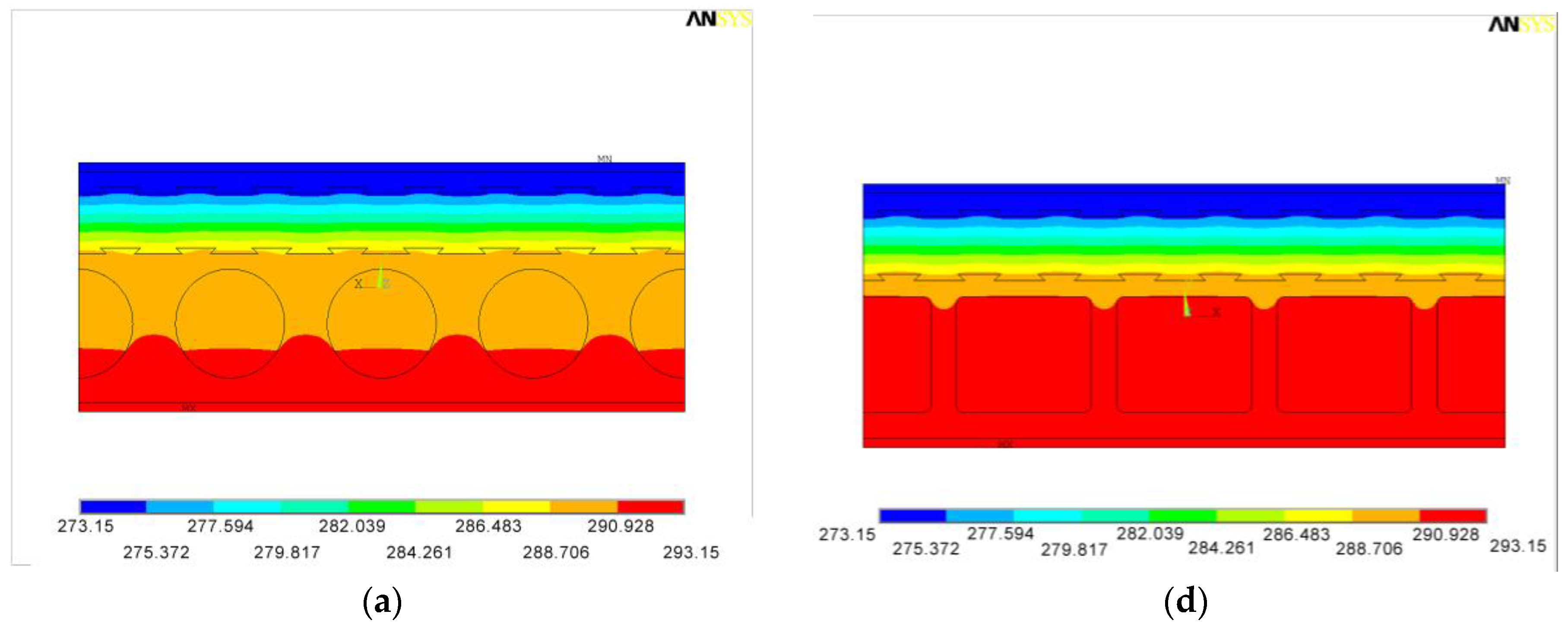
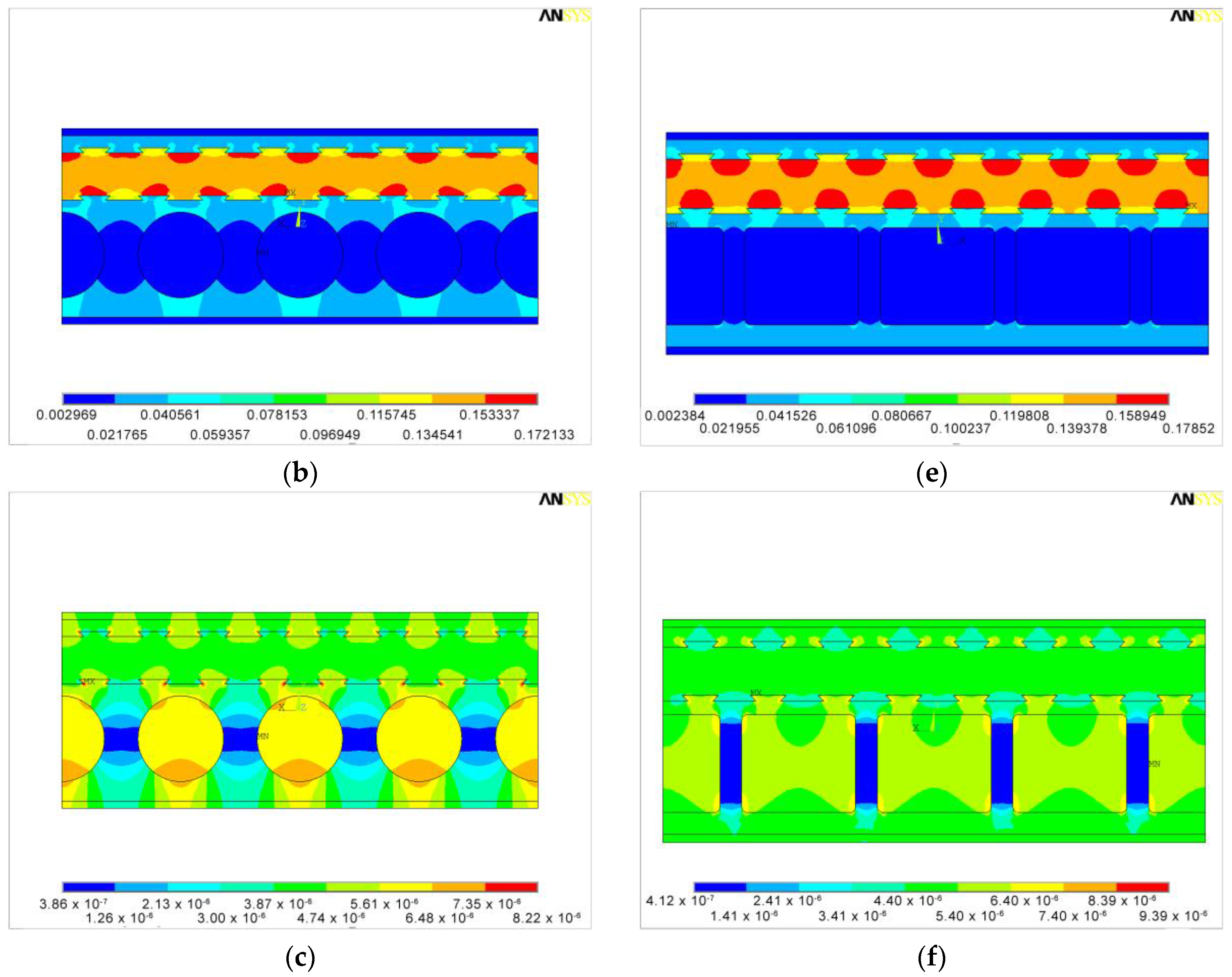
4. Shape Optimization
5. Conclusions
- -
- the manufacturer,
- -
- on-site HFM measurement on a real building made of this kind of material, and
- -
- FEM simulations.
- -
- homogeneous, continuous and isotropic materials,
- -
- steady-state condition,
- -
- one-dimensional heat flow and absence of material discontinuities.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baetens, R.; Jelle, B.P.; Gustavsen, A. Aerogel insulation for building applications: A state-of-the-art review. Energy Build. 2011, 43, 761–769. [Google Scholar] [CrossRef]
- Stahl, T.; Brunner, S.; Zimmermann, M.; Ghazi Wakili, K. Thermo-hygric properties of a newly developed aerogel based insulation rendering for both exterior and interior applications. Energy Build. 2012, 44, 114–117. [Google Scholar] [CrossRef]
- Serina, N.G.S.; Jelle, B.P.; Sandberg, L.I.C.; Gao, T.; Wallevik, O. Experimental investigations of aerogel-incorporated ultra-high performance concrete. Constr. Build. Mater. 2015, 77, 307–316. [Google Scholar]
- Ibrahim, M.; Wurtz, E.; Biwole, P.H.; Achard, P.; Salle, H. Hygrothermal performance of exterior walls covered with aerogel-based insulating rendering. Energy Build. 2014, 84, 241–251. [Google Scholar] [CrossRef]
- Soares, N.; Costa, J.J.; Gaspar, A.R.; Santos, P. Review of passive PCM latent heat thermal energy storage systems towards buildings’ energy efficiency. Energy Build. 2013, 59, 82–103. [Google Scholar] [CrossRef]
- Lee, K.O.; Medina, M.A.; Raith, E.; Sun, X. Assessing the integration of a thin phase change material (PCM) layer in a residential building wall for heat transfer reduction and management. Appl. Energy 2015, 137, 699–706. [Google Scholar] [CrossRef]
- Lee, K.O.; Medina, M.A.; Sun, X. On the use of plug-and-play walls (PPW) for evaluating thermal enhancement technologies for building enclosures: Evaluation of a thin phase change material (PCM) layer. Energy Build. 2015, 86, 86–92. [Google Scholar] [CrossRef]
- Serrano, S.; Barreneche, C.; Fernández, A.I.; Farid, M.M.; Cabeza, L.F. Composite gypsum containing fatty-ester PCM to be used as constructive system: Thermophysical characterization of two shape-stabilized formulations. Energy Build. 2015, 86, 190–193. [Google Scholar] [CrossRef]
- Fricke, J.; Heinemann, U.; Ebert, H.P. Vacuum insulation panels—From research to market. Vacuum 2008, 82, 680–690. [Google Scholar] [CrossRef]
- Kwon, J.S.; Choong, H.J.; Jung, H.; Song, T.H. Effective thermal conductivity of various filling materials for vacuum insulation panels. Int. J. Heat Mass Transf. 2009, 52, 5525–5532. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.P.; Thue, J.V.; Tenpierik, M.J.; Grynning, S.; Uvsløkk, S.; Gustavsen, A. Vacuum insulation panels for building applications: A review and beyond. Energy Build. 2010, 42, 147–172. [Google Scholar] [CrossRef]
- Alam, M.; Singh, H.; Limbachiya, M.C. Vacuum Insulation Panels (VIPs) for building construction industry—A review of the contemporary developments and future directions. Appl. Energy 2011, 88, 3592–3602. [Google Scholar] [CrossRef]
- Schiavoni, S.; D’Alessandro, F.; Bianchi, F.; Asdrubali, F. Insulation materials for the building sector: A review and comparative analysis. Renew. Sustain. Energy Rev. 2016, 62, 988–1011. [Google Scholar] [CrossRef]
- Asdrubali, F.; D’Alessandro, F.; Schiavoni, S. A review of unconventional sustainable building insulation materials. Sustain. Mater. Technol. 2015, 4, 1–17. [Google Scholar] [CrossRef]
- Jelle, B.P. Traditional, state-of-the-art and future thermal building insulation materials and solutions—Properties, requirements and possibilities. Energy Build. 2011, 43, 2549–2563. [Google Scholar] [CrossRef]
- Korjenic, A.; Petránek, V.; Zach, J.; Hroudová, J. Development and performance evaluation of natural thermal-insulation materials composed of renewable resources. Energy Build. 2011, 43, 2518–2523. [Google Scholar] [CrossRef]
- Madurwar, M.V.; Ralegaonkar, R.V.; Mandavgane, S.A. Application of agro-waste for sustainable construction materials: A review. Constr. Build. Mater. 2013, 38, 872–878. [Google Scholar] [CrossRef]
- Aigbomian, E.P.; Fan, M. Development of wood-crete from treated sawdust. Constr. Build. Mater. 2014, 52, 353–360. [Google Scholar] [CrossRef]
- Ledhem, A.; Dheilly, R.M.; Benmalek, M.L.; Quéneudec, M. Properties of wood-based composites formulated with aggregate industry waste. Constr. Build. Mater. 2000, 14, 341–350. [Google Scholar] [CrossRef]
- Adamopoulos, S.; Foti, D.; Voulgaridis, E.; Passialis, C. Manufacturing and properties of gypsum-based products with recovered wood and rubber materials. BioResources 2015, 10, 5573–5585. [Google Scholar] [CrossRef]
- Krüger, E.L.; Adriazola, M.; Matoski, A.; Iwakiri, S. Thermal analysis of wood-cement panels: Heat flux and indoor temperature measurements in test cells. Constr. Build. Mater. 2009, 23, 2299–2305. [Google Scholar] [CrossRef]
- Krüger, E.L.; Adriazola, M. Thermal analysis of wood-based test cells. Constr. Build. Mater. 2010, 24, 999–1007. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). ISO 8301: 1991. Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Heat Flow Meter Apparatus; ISO: Geneva, Switzerland, 1991. [Google Scholar]
- Binici, H.; Aksogan, O. Eco-friendly insulation material production with waste olive seeds, ground PVC and wood chips. J. Build. Eng. 2016, 5, 260–266. [Google Scholar] [CrossRef]
- Becchio, C.; Corgnati, S.P.; Kindinis, A.; Pagliolico, S. Improving environmental sustainability of concrete products: Investigation on MWC thermal and mechanical properties. Energy Build. 2009, 41, 1127–1134. [Google Scholar] [CrossRef]
- Raut, S.P.; Ralegaonkar, R.V.; Mandavgane, S.A. Development of sustainable construction material using industrial and agricultural solid waste: A review of waste-create bricks. Constr. Build. Mater. 2011, 25, 4037–4042. [Google Scholar] [CrossRef]
- Al Rim, K.; Ledhem, A.; Douzane, O.; Dheilly, R.M.; Quéneudec, M. Influence of the proportion of wood on the thermal and mechanical performances of clay-cement-wood composites. Cem. Concr. Compos. 1999, 21, 269–276. [Google Scholar] [CrossRef]
- European Standard. UNI EN 15498: 2008. Prodotti Prefabbricati di Calcestruzzo—Blocchi Cassero di Calcestruzzo con Trucioli di Legno—Proprietà e Prestazioni dei Prodotti; CEN European Committee for Standardization: Brussels, Belgium, 2008. (In Italian) [Google Scholar]
- Product Datasheet. Available online: http://www.gruppolegnobloc.it/prodotti/blocchi-cassero (accessed on 9 February 2016).
- International Organization for Standardization (ISO). ISO 9869: 1994. Thermal Insulation. Building Elements. In-Situ Measurement of Thermal Resistance and Thermal Transmittance; ISO: Geneva, Switzerland, 1994. [Google Scholar]
- Ansys® Online Manual. Available online: http://www.ansys.stuba.sk/html/elem_55/chapter4/ES4-90.htm (accessed on 6 January 2016).
- Del Coz Diaz, J.J.; Garcia-Nieto, P.J.; Alvarez-Rabanal, F.P.; Alonso-Martìnez, M.; Dominguez-Hernandez, J.; Perez-Bella, J.M. The use of response surface methodology to improve the thermal transmittance of lightweight concrete hollow bricks by FEM. Constr. Build. Mater. 2014, 52, 331–344. [Google Scholar] [CrossRef]
- Arendt, K.; Krzaczek, M.; Florczuk, J. Numerical analysis by FEM and analytical study of the dynamic thermal behavior of hollow bricks with different cavity concentration. Int. J. Therm. Sci. 2011, 50, 1543–1553. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nardi, I.; De Rubeis, T.; Buzzi, E.; Sfarra, S.; Ambrosini, D.; Paoletti, D. Modeling and Optimization of the Thermal Performance of a Wood-Cement Block in a Low-Energy House Construction. Energies 2016, 9, 677. https://doi.org/10.3390/en9090677
Nardi I, De Rubeis T, Buzzi E, Sfarra S, Ambrosini D, Paoletti D. Modeling and Optimization of the Thermal Performance of a Wood-Cement Block in a Low-Energy House Construction. Energies. 2016; 9(9):677. https://doi.org/10.3390/en9090677
Chicago/Turabian StyleNardi, Iole, Tullio De Rubeis, Edoardo Buzzi, Stefano Sfarra, Dario Ambrosini, and Domenica Paoletti. 2016. "Modeling and Optimization of the Thermal Performance of a Wood-Cement Block in a Low-Energy House Construction" Energies 9, no. 9: 677. https://doi.org/10.3390/en9090677