Real Time Hybrid Model Predictive Control for the Current Profile of the Tokamak à Configuration Variable (TCV)

Abstract

Plasma stability is one of the obstacles in the path to the successful operation of fusion devices. Numerical control-oriented codes as it is the case of the widely accepted RZIp may be used within Tokamak simulations. The novelty of this article relies in the hierarchical development of a dynamic control loop. It is based on a current profile Model Predictive Control (MPC) algorithm within a multiloop structure, where a MPC is developed at each step so as to improve the Proportional Integral Derivative (PID) global scheme. The inner control loop is composed of a PID-based controller that acts over the Multiple Input Multiple Output (MIMO) system resulting from the RZIp plasma model of the Tokamak à Configuration Variable (TCV). The coefficients of this PID controller are initially tuned using an eigenmode reduction over the passive structure model. The control action corresponding to the state of interest is then optimized in the outer MPC loop. For the sake of comparison, both the traditionally used PID global controller as well as the multiloop enhanced MPC are applied to the same TCV shot. The results show that the proposed control algorithm presents a superior performance over the conventional PID algorithm in terms of convergence. Furthermore, this enhanced MPC algorithm contributes to extend the discharge length and to overcome the limited power availability restrictions that hinder the performance of advanced tokamaks.

1. Introduction

Nuclear fusion has the potential capability to satisfy the world population’s increasing demand for energy. As is known, fusion is the process by which the nuclei of two light atoms are fused together to form a heavier nucleus, with energy produced as a by-product. In this sense, there exists a sufficient fuel supply for several thousand years since the necessary hydrogen isotopes can be generated from water, and lithium is available during the reaction cycle. Moreover, fusion would produce no air pollution or greenhouse gases during normal operation since the fusion reaction product is helium, and it constitutes an intrinsically safe process since a nuclear meltdown with a large, uncontrolled release of energy cannot occur. In spite of significant advances over the last twenty years, nuclear fusion suffers from plasma instabilities that provoke reaction decay. Therefore, the social and economic benefits of being able to achieve controlled fusion are invaluable.

A consortium of governments that includes the European Union, China, Japan, South Korea, Russia, and the United States has promoted the construction of the ITER tokamak (originally an acronym for International Thermonuclear Experimental Reactor), which will generate five to ten times as much energy as it consumes.

Tokamaks are toroidal fusion reactors that confine the hot plasma using a helical magnetic field. They are inherently pulsed devices because a limited power-supply induces a current that heats the plasma up to its operational temperature. Therefore, the aim is to maintain the reaction by self-heating from internal fusion reactions and minimal non-inductive current drive. Since tokamak plasmas are high-order, nonlinear distributed systems with a large number of instabilities, there are many challenging control problems whose solutions are required for ITER. In this sense, plasma control is one of the most basic problems in tokamaks for improving the plasma performance and the pulse duration by avoiding the premature reaction decay. Once the plasma has been created using the primary, electromagnetic fields generated by a set of poloidal field (PF) coils distributed around the vacuum vessel are used to control the plasma current, position and shape.

TCV is one of the existing tokamaks around the world that is being used as a test bench for developing control techniques in order to address the control problems that must be solved before fusion power production becomes viable. A model for plasma current, position and shape based on the RZIp model, and PID control schemes are used in the TCV tokamak. However, the control capabilities on some crucial parameters of the system, as is the case of the plasma current, could be improved. This set up provides the basis for implementing an additional control over the plasma current that, on the one hand should be fast enough to perform real time control of plasma instabilities which require a time response of milliseconds, and on the other hand minimizes the control action in order to adequately deal with the limited power available from actuators. Thus, a natural improvement of the existing magnetic control systems is to optimize these current drive actuators. Moreover, predicting the state changes that will be caused by the control actions, will allow for a smooth shape transition minimizing plasma instabilities. These are the reasons why Model Predictive Control (MPC) has been considered as an excellent control scheme candidate for tokamak operation due to its ability to optimize the future behavior while intrinsically minimizing the control action [1,2,3,4,5].

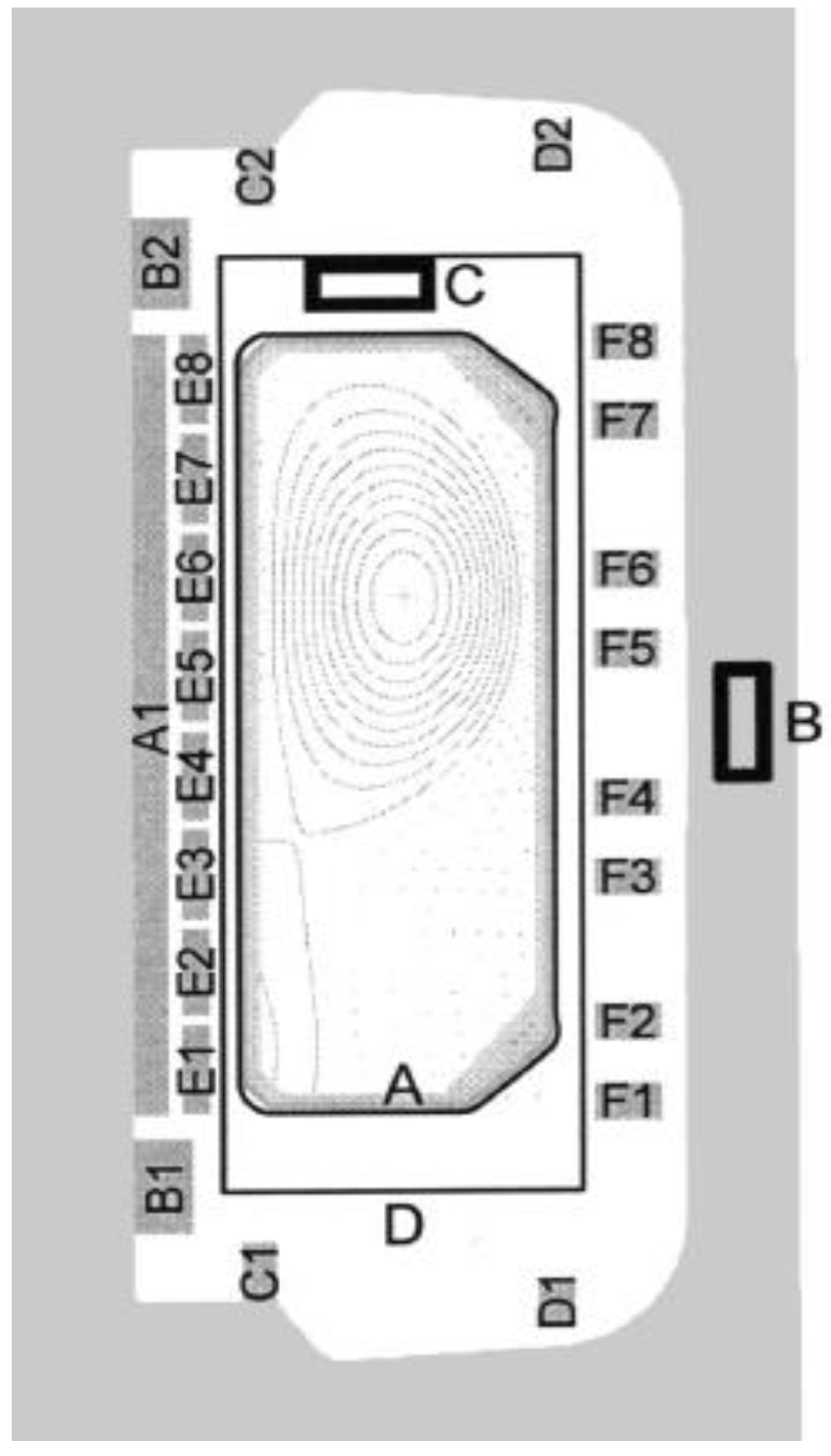
TCV is a tokamak that operates with a modular and scalable distributed digital control system able to study the hot-ion, high-β ITER-like plasmas (see Figure 1). Even when TCV plasmas would have Te/Ti in the range of 2–5, a new Neutral Beam Injection heating system (NBI 1 MW) [6], combined with an increment in the electron cyclotron plasma heating power at the third harmonic (2 MW) [7] will bring this ratio close to ITER and reactor relevant domain, Te/Ti~1. Therefore, TCV will bring the plasma at the β limit in H-mode (βN~2.8), which is of great interest for ITER and DEMO (Demonstration Power Station that is intended to build upon the ITER) [8], will provide variations in the momentum input to the plasma, and will generate fast ions that can be used to study wave-particle interaction phenomena of interest for burning plasmas [9]. The main parameters, are major radius 0.88 m, horizontal minor radius 0.25 m, toroidal field at major radius 1.5 T, and plasma current 1MA with elongation up to 2.8 and high triangularity from −0.7 to 1. This uniquely expansive shaping capability extends to limited and diverted plasmas, the latter featuring open divertor geometry and including single- and double-null as well as snowflake topologies [10]. Due to the flexible configuration and control, TCV is a tokamak that is especially active in control research, and all of this invaluable experience is expected to provide important input for safe and effective operation of ITER [11,12,13,14,15,16].

TCV has achieved stable plasma current and position control. In a typical plasma discharge, the plasma is feedback controlled using a sequence of PIDs with a multiloop structure [17,18]. PIDs are partly designed using decoupled models of the system to be controlled, and later, fine-tuned during plant operation. Decoupling of the controllers has often meant that the effect on a particular plasma parameter from coils other than the actuator has been neglected, (see Figure 2). Recent efforts seek to design more complex and robust controllers focusing the attention on these effects [19,20,21,22]. In this sense, MPC has been favored in this article as the controller choice due to the well-known advantages that this kind of controllers present and in particular because it is able to deal in an optimal sense with opposite behaviors in strongly coupled variables.

Common problems within real time optimization for distributed model predictive control when executing a control action with objectives are stability, constraint satisfaction, performance guarantee and real time execution guarantee. The key challenge is to obtain a fast, fixed time optimization. Interior point methods resolve within milliseconds, fast gradient methods in microseconds, while explicit methods solve in nanoseconds. Nowadays, CPLEX [23,24], is among the most popular optimization engines, although there are other very popular ones such as SeDuMi [25] or Multi-Parametric Toolbox [26].

The current interior point methods for solving real time MPC consider a warm start, exploiting the internal structure in MPC problems and terminating the online optimization early. Therefore, the solution obtained during online optimization steps is suboptimal, so that it may be infeasible, it can destabilize the system and it may cause steady-state offset. This is to say, the requirements to solve the system within a time window restricts the algorithm to maximum on-line optimization steps which, in turn, may destroy the stability properties of optimal MPC. Wang et al. developed a custom solver that yields a fast solution of the tracking problem with guaranteed stability for all suboptimal iterates for all time constraints [27]. They modified the matrix structure in the Newton step computation using the tracking formulation and Lyapunov constraint.

Fast gradient methods will require a number of iterations that are strongly dependent on the choice of initial iterate. Therefore, a warm starting is favored [28].

Explicit model predictive control uses offline computations to determine all operating regions in which the optimal control moves are determined by evaluating a linear function. Thus, these controllers require a maximum computational time per control interval equal to that needed to test each region, computing the violation term in each case, and then calculating the suboptimal control adjustment and are therefore useful for applications that require small sample times. However, explicit MPC may not satisfy given real time constraints and it is exponentially sensitive to model dimension and changes in system dynamics.

In the centralized MPC a single controller decides all actions to take. On the other hand, a distributed MPC approach facilitates the coordination of highly complex or independent system plants (see [5]). Reviews such as [29,30] present different compatible ways to label distributed control architectures. In this context, the main novelty of the paper relies on the application of the hybrid MPC control scheme to the particular case of the TCV.

The control method presented in this article is based on a multiloop concept where the traditional PID is combined with a fast MPC that only acts over a reduced system. The intrinsic minimization of the MPC further reduces the current drive source requirements [31]. Therefore, MPC composes an excellent control option since it not only considers the information related to the system at an operation instant as in other advanced controllers [32,33], but also takes into account the predicted future information so as to obtain an optimal control action. Furthermore, the Ohmic Heating (OH) coil may reduce the power requirements of the non-inductive current drive sources required for current profile control due to its ability to transiently manipulate the low order moments of the current profile. Until recently, this line of research [31,32,33] had been carried out with plant models of the type described in [34], which are two orders of magnitude smaller than the RZIp model. These models are excellent for real time control algorithms although the underlying plasma physics are reflected in a limited manner. The current choice of a more complex model such us RZIP is motivated from the need to faithfully represent the plasma dynamics. However, model size is paramount in real-time control on these systems, since it implies that there is a time window to gather data, process that data, and update the system. This is quite a strong limitation since the stability of the system degrades when the time window is missed. To achieve this restriction, all the MPC developments within this article will attempt to reduce the computational time as much as possible. Thus, only strictly needed computations will be performed and analytical expressions will be prioritized over numerical solvers. The main novelty of the paper relies on the application of novel hybrid MPC control scheme to the particular case of the TCV so that the performance improvements that this controller affords are of special relevance to ITER and DEMO, since these Advanced Tokamaks have to rely on having large bootstrap current fractions and/or a pulsed operation [35,36,37] with limited power available for non-inductive current drive actuators.

This article is organized as follows: The RZIp model for TCV plasma control is presented in Section 2. The plasma enhanced MPC for the TCV model and its block diagram are discussed in Section 3. Next, in Section 4 experimental results for the implementation of the novel enhanced controller that was developed in the previous section, are presented and compared with those obtained from a traditional PID control scheme. Comparisons of experimental data with simulations generated using different algorithms are also shown. Finally, Section 5 will present some concluding remarks to end the article.

2. RZIP Model for the TCV Tokamak

RZIp considers a rigid plasma displacement model, where the plasma is assumed to be a unit that is allowed to move either vertically or radially, and the vessel eddy currents will use an eigenmode representation. The model is derived from the plasma and circuit equations, perturbing the vertical and radial force balance equations. It was first developed by Lister and Sharma [27,28,38] with the aim of extending the stability region of the resulting closed-loop plasma dynamical system via the implementation of adequate control techniques.

2.1. RZIp System Formulation

The model is represented in state space form where state variables are the plasma current, the structure currents and the position variation of the plasma current:

$$\dot{q}=\left[\begin{array}{c}{{\rm I}}_e\\ {{\rm I}}_s\\ \dot{r}\end{array}\right], \text{where} r=\left[\begin{array}{c}R\\ z\end{array}\right]$$

(1)

The entries of the input vector are the effective voltages applied to each element and a vector of externally applied poloidal field coil voltages:

$$U=\left[\begin{array}{c}{V}_e\\ V_s\\ 0\end{array}\right]$$

(2)

The model addresses flux and energy conservation issues that may be extended into four vector equations, the Kirchoff voltage law for the plasma elements, the Kirchoff voltage law for the structural and poloidal circuits and the force balance in the R and z directions, respectively

$$\frac{d\left(L_e{I}_e+M_{es}{I}_s+RE{I}_e\right)}{dt}+{\Omega }_e{I}_e=V_e$$

(3)

$$\frac{d\left(L_s{I}_s+M_{se}{I}_e\right)}{dt}+{\Omega }_s{I}_s=V_s$$

(4)

$$\frac{d\left(m_e\dot{R}\right)}{dt}=\frac{1}{2}{I^{\prime }}_e\frac{\partial L_e}{\partial R}{I}_e+{I^{\prime }}_s\frac{\partial M_{se}}{\partial R}{I}_e+\frac{E{I}_e^2}{2}$$

(5)

$$\frac{d\left(m_e\dot{z}\right)}{dt}=\frac{1}{2}{I^{\prime }}_e\frac{\partial L_e}{\partial z}{I}_e+{I^{\prime }}_s\frac{\partial M_{se}}{\partial z}{I}_e$$

(6)

2.2. Lumping, Linearization and Eigenmode Reduction

A lumped model may be derived from Equations (3)–(6) by defining averaged plasma quantities. The total plasma current will be denoted by I_p, while the density distribution j(R,z) is calculated from the Grad-Shafranov equation by an inverse equilibrium reconstruction code. The Grad-Shafranov equilibrium equation describes the shape and current profile of a toroidally symmetric plasma in an externally applied magnetic field. The equilibrium equations are found by considering the plasma almost charge neutral so that the condition for balance is that the thermodynamic pressure and magnetic force satisfy:

$$j\times B=\nabla p$$

(7)

subject to toroidal symmetry, where j is the current density, B is the magnetic field and p is the pressure. Thus, the magnetic surfaces are surfaces of constant pressure, and the lines of current lie on the magnetic surfaces. For computational simplicity the variables (R,z) are replaced with $\left(R{I}_p^0,z{I}_p^0\right)$, where $I_p^0$ denotes the constant equilibrium plasma current. The system is solved in incremental form, so that the state vector is rewritten as:

$$x=\left[\begin{array}{c}{I}_s-I_s^0\\ \left(z-z^0\right)I_p^0\\ \left(R-R^0\right)I_p^0\\ I_p-I_p^0\end{array}\right]=\left[\begin{array}{c}\delta I_s\\ \delta z{I}_p^0\\ \delta R{I}_p^0\\ \delta I_p\end{array}\right]$$

(8)

The resulting equations may be linearized around the chosen operation point. The plasma circuit equation, structure circuit equation, and both vertical and radial force balance equations yield a state space model whose values may be found in Supplementary Materials:

$$\begin{array}{l}\dot{x}=Ax+Bu\\ y=Cx+Du\end{array}$$

(9)

where A = M^–1·R, M being the mutual inductance matrix and R a diagonal matrix of structure resistances. However, since the passive structure model is very large, an eigenmode reduction is performed by considering only those associated with the largest eigenvalues. In particular, the passive structure will be expressed in terms of the current eigenvalues instead of the passive structure currents themselves. A very positive side effect of this procedure is the increment of the stability of the system by removing modes closer to the imaginary axis.

Some relevant values of the RZIp-based TCV plant model that have been used are shown in

Table 1. TCV relevant values.

Inner PF Coils (V)		Outer PF Coils (V)		Plasma Current & OH Current (A)
E2	−715	F2c	−4914	OH	1.7 × 104
E4	−3817	F3c	−1930	DOH	87 (max. 150)
E5	−1443	F5c	−1662	IP	2.5 × 105
E7	−204	F6c	−316	ZIPp	0.17 × 104
E8	−1571	F8c	−578	ZIPslow	4.5 × 104

. In particular, values for the actuators Poloidal Field coils may be found, where the inner ones are responsible for the fastest control action. The control action of these coils is explicitly stated in the model through Equations (3) and (4). Besides, an Ohmic Heating current peak value and its variation are also given since these both are relevant actuators for the case of the plasma current. Their effect is reflected in the internal energy and inductances of Equations (5) and (6). Finally, the plasma current average values are given since this is the output variable which value has been improved with the MPC controller.

3. Enhanced MPC

The proposed hybrid control scheme uses combined proportional integral derivative (PID) control of the full state space system coupled with a predictive control model for the plasma current. The excellent performance of the scheme relies on the matrices that decouple the PID control scheme. Decoupling of the control involves a process of modifying the dynamic system matrix of the system so as to reduce some of the off-diagonal elements to zero. For the axisymmetric system (9) characterized by the state vector (8) decoupling can also be regarded as a process of equalizing the eigenmodes of inductances and Green functions (between the structure and the plasma). The corresponding plasma current decoupling matrix can be viewed as the best fit port voltages under the condition that produces a zero field when a specific mode is excited. Thus, PIDs are partly designed using decoupled models of the system to be controlled, and later, fine-tuned during plant operation. The PID scheme gain values are provided jointly with the data of the TCV pulse 49,626 in Supplementary Materials. Decoupling of the controllers means that the effect on a particular plasma parameter from coils other than the actuator has been neglected. The aim is now to combine these system couplings by adding an MPC over a reduced system in a multiloop structure.

Advanced Tokamak control suffers from high power requirements, and, most importantly, in future tokamaks both the total and peak actuator power is strongly limited. In this context, MPC provides a systematic method of dealing with constraints on inputs and states. In MPC these limitations are explicitly accounted for by solving a constrained optimization problem in real-time to determine the optimal predicted control. In addition to this, nonlinear plant dynamics can be similarly incorporated in the prediction mode.

3.1. Model Predictive Plasma Current Control

This section is concerned mainly with the case of plasma current model predictive control for the discrete-time linear system. The real system has a time constant in the order of milliseconds so that the discretization time step has to be of that order of magnitude to obtain an acceptable difference between the continuous and the discretized optimal control profiles. However, such a small discretization time step creates a need to significantly reduce the computational time at each optimization step. The formulations discussed in this paper adopt a discretization time step of 50 msec, which is found to be sufficiently small to approximate the continuous optimal control profile. For this purpose, the plant dynamics are linearized at each time step with the last computed state space variable values other than plasma current. The resulting optimization problem is solved with an analytical solution equation approach using an exact Hessian approximation. Thus, the future response of the controlled tokamak plasma current is predicted using a reduced dynamic model:

$$\begin{array}{c}{\mathrm{x}}_{\mathrm{d}}\left(\mathrm{k}+1\right)={\mathrm{A}}_{\mathrm{d}}{\mathrm{x}}_{\mathrm{d}}\left(\mathrm{k}\right)+{\mathrm{B}}_{\mathrm{d}}{\mathrm{u}}_{\mathrm{d}}\left(\mathrm{k}\right)\\ \mathrm{y}\left(\mathrm{k}\right)={\mathrm{C}}_{\mathrm{d}}{\mathrm{x}}_{\mathrm{d}}\left(\mathrm{k}\right)\end{array}$$

(10)

where $\mathrm{y}\left(\mathrm{k}\right)$ is the plasma current, while ${\mathrm{x}}_{\mathrm{d}}\left(\mathrm{k}\right)$ and ${\mathrm{u}}_{\mathrm{d}}\left(\mathrm{k}\right)$ are the states and input vectors at the kth sampling instant. In particular, the discrete matrix ${\mathrm{C}}_{\mathrm{d}}$ is a reduced matrix from the original system output matrix that corresponds to the row vector for the plasma current.

There is a tradeoff between the plant model size and the accuracy of the solution. In this sense, on the one side, most of the transport models are not useful for real-time control due to the fact that they are computationally expensive. On the other side, the reduced state-space models do not fully reflect the plant behavior. In the particular case of the RZIp model considered it would not be feasible to implement a real-time MPC involving the complete set of variables, so that it is necessary to adequately choose the variables to be considered.

Given a predicted input sequence, the corresponding sequence of plasma current prediction values is generated by simulating the model forward over the prediction horizon. For notational convenience, these predicted sequences are often stacked into vectors that may be denoted by:

$$\mathrm{x}\left(\mathrm{k}\right)=\left[\begin{array}{c}\mathrm{x}\left(\mathrm{k}+1|\mathrm{k}\right)\\ \mathrm{x}\left(\mathrm{k}+2|\mathrm{k}\right)\\ \begin{array}{c}⋮\\ \mathrm{x}\left(\mathrm{k}+{\mathrm{N}}_{\mathrm{p}}|\mathrm{k}\right)\end{array}\end{array}\right],\text{ u}\left(\mathrm{k}\right)=\left[\begin{array}{c}\mathrm{u}\left(\mathrm{k}|\mathrm{k}\right)\\ \mathrm{u}\left(\mathrm{k}+1|\mathrm{k}\right)\\ \begin{array}{c}⋮\\ \mathrm{u}\left(\mathrm{k}+{\mathrm{N}}_{\mathrm{c}}-1|\mathrm{k}\right)\end{array}\end{array}\right]$$

(11)

where $\mathrm{x}\left(\mathrm{k}+\mathrm{i}|\mathrm{k}\right)$ and $\mathrm{u}\left(\mathrm{k}+\mathrm{i}|\mathrm{k}\right)$ denote plasma current value and ohmic heating voltage input at time $\mathrm{k}+\mathrm{i}$ that are predicted at time $\mathrm{k}$. Therefore, ${\mathrm{x}}_{\mathrm{d}}\left(\mathrm{k}+\mathrm{i}|\mathrm{k}\right)$ evolves according to the prediction model:

$${\mathrm{x}}_{\mathrm{d}}\left(\mathrm{k}+\mathrm{i}+1|\mathrm{k}\right)={\mathrm{A}}_{\mathrm{d}}{\mathrm{x}}_{\mathrm{d}}\left(\mathrm{k}+\mathrm{i}|\mathrm{k}\right)+{\mathrm{B}}_{\mathrm{d}}{\mathrm{u}}_{\mathrm{d}}\left(\mathrm{k}+\mathrm{i}|\mathrm{k}\right)$$

(12)

with an initial condition at the beginning of the prediction horizon defined $x_d\left(k|k\right)=x_d\left(k\right)$$k=0,1,\dots$ and a control horizon, $N_c,$ whose value is smaller than or equal to that of the prediction horizon, $N_p$.

The predictive control feedback law is computed by minimizing a predicted performance cost, which is defined in terms of the predicted sequences $\mathrm{x}\left(\mathrm{k}\right)$ and $\mathrm{u}\left(\mathrm{k}\right)$. In particular, rewriting the output current in compact form as:

$$\widehat{\mathrm{y}}=\text{Fx}\left(\mathrm{k}\right)+\mathrm{G}\widehat{\mathrm{u}}\left(\mathrm{k}\right)$$

(13)

$\widehat{u}\left(k\right)$ denotes the ohmic heating voltage for a given reference signal $r\left(k\right)$ at a given time. Within a prediction horizon the control system aims to bring the plasma current as close as possible to the reference:

$$\widehat{\mathrm{r}}={\left[\begin{array}{ccc}\mathrm{r}\left(\mathrm{k}\right)& \cdots & \mathrm{r}\left(\mathrm{k}+{\mathrm{N}}_{\mathrm{p}}-1\right)\end{array}\right]}^{\mathrm{T}}$$

(14)

The corresponding quadratic cost function:

$$\mathrm{J}={\left(\widehat{\mathrm{r}}-\widehat{\mathrm{y}}\right)}^{\mathrm{T}}\left(\widehat{\mathrm{r}}-\widehat{\mathrm{y}}\right)+{\widehat{\mathrm{u}}}^{\mathrm{T}}\mathrm{R}\widehat{\mathrm{u}}$$

(15)

is clearly a function of the predicted OH voltages and a positive definite weighing matrix $R$. The optimal voltage sequence for the problem of minimizing this cost function takes into account the input restrictions as equivalent constraints on $\widehat{\mathrm{u}}$ in the optimization.

Only the first element of the $N_c$ optimal predicted voltage sequence is input back into the plant. This procedure, known as the receding horizon strategy, provides a degree of robustness to modeling errors and uncertainty since the input at each step takes into account the current state values to compute future events. Additionally, by continually shifting the horizon to where future inputs are optimized, it attempts to compensate for the fact that this horizon is finite. Therefore, a receding horizon strategy aims to ensure that the performance of the closed-loop system is at least as good as that of the optimal prediction.

3.2. Control System Multiloop Structure

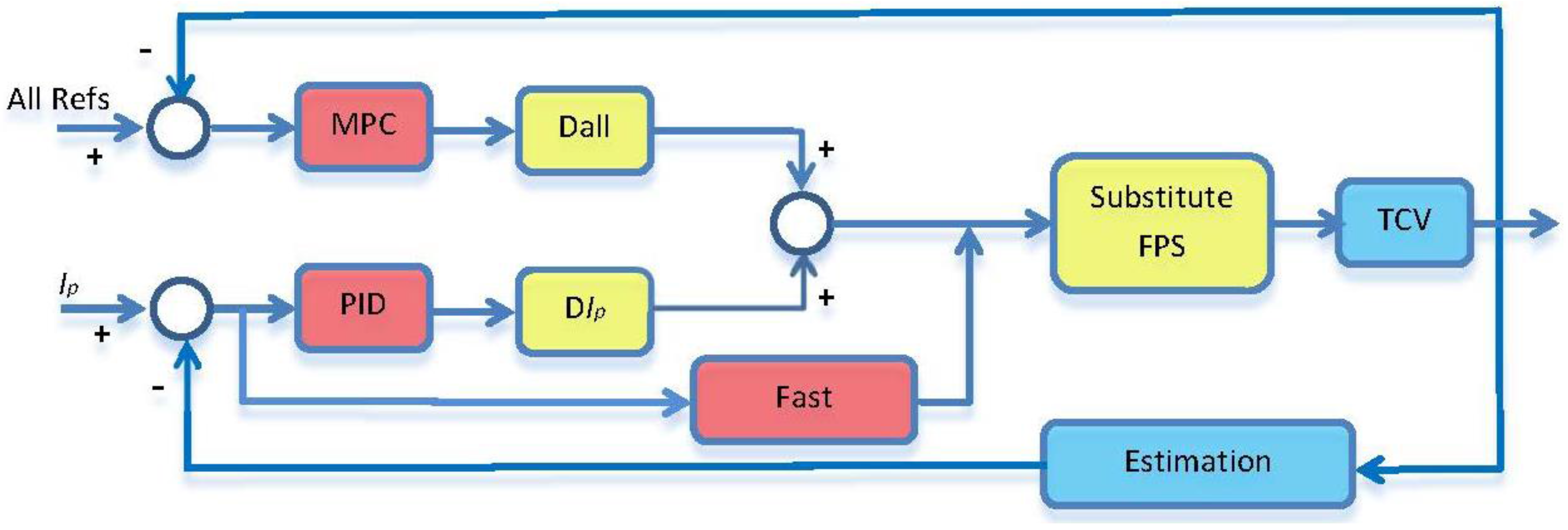
This novel hybrid control system for the TCV has been developed with the aim of achieving closed-loop performance objectives that cannot be accomplished using a PID or a MPC on its own.

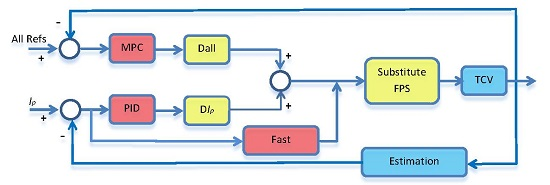
A block diagram with a brief summary of the proposed scheme may be seen in Figure 3. The error between all the references and the estimated values serves as an input to the block that contains the PID control. The output is composed by a set of commands for different coils that are given in Dall. In parallel, the reference error for the plasma current is the input to the MPC. This block performs the MPC of the plant computed as shown in Equation (10). The computational load within this block is reduced as much as possible, since the controller involves the analytical solution of the minimization for the functional given in Equation (15). The corresponding control command output is provided in DIp. The block denoted by “Fast Control” is a third block that commands an independent set of coils located inside the vessel to perform vertical stabilization, which requires a very fast control response of about 5 μs. These three blocks determine a control action over the different coils. Moreover, the block “Substitute FPS” represents the data transmission from the Fast Power Supply (FPS) channels to the internal coil system. Finally, the estimated values obtained from the diagnostics close the control loop.

Considering different time–scales, makes it possible to compete with homogeneous control schemes. On the other hand, the benefits derived from the model predictive control horizon, such as stability and robustness, do automatically apply. Additionally, the hybrid scheme allows for computational cost efficiency by restricting the MPC usual overhead to the plasma current computation.

The PID and receding horizon control algorithms are implemented in two separate loops which run in parallel. The MPC is implemented over a reduced plant model and the overall execution time remains unchanged with respect to the implementation of the PID without MPC. Assuming that both loops start at time t_k, the Pseudo code is as follows:

• PID loop

  1:

  Solve PID for j = k and obtain v_k, where two of the entries will be corrected with u_k.

  2:

  Wait until u_k.

  3:

  Update the entries of v_k.

  4:

  Apply inputs to the model.

  5:

  k = k + 1.

  6:

  post process.

  7:

  Jump to 1.

• MPC loop

  1:

  Wait until k + 1.

  2:

  Reduce the plant model to compute Ip.

  3:

  Solve (15) for j = k; … ; k + N_p and obtain uk; … ; u_k+Nc.

  4:

  Apply u_k to the inputs.

  5:

  Jump to 1.

4. Numerical vs. Experimental Results

A study of the MPC control action on a real shot for the already described TCV is performed. As previously mentioned, a correct modeling of the tokamak has a large influence over the control cost-effectiveness because the minimization of the cost function is based on the system state space matrices. Therefore, it can be emphasized that obtaining an accurate and computationally efficient system model is one of the main challenges in order to successfully implement a MPC. In this article the control oriented RZIp model has been considered, because it is widely recognized as a good control oriented model by the fusion research community.

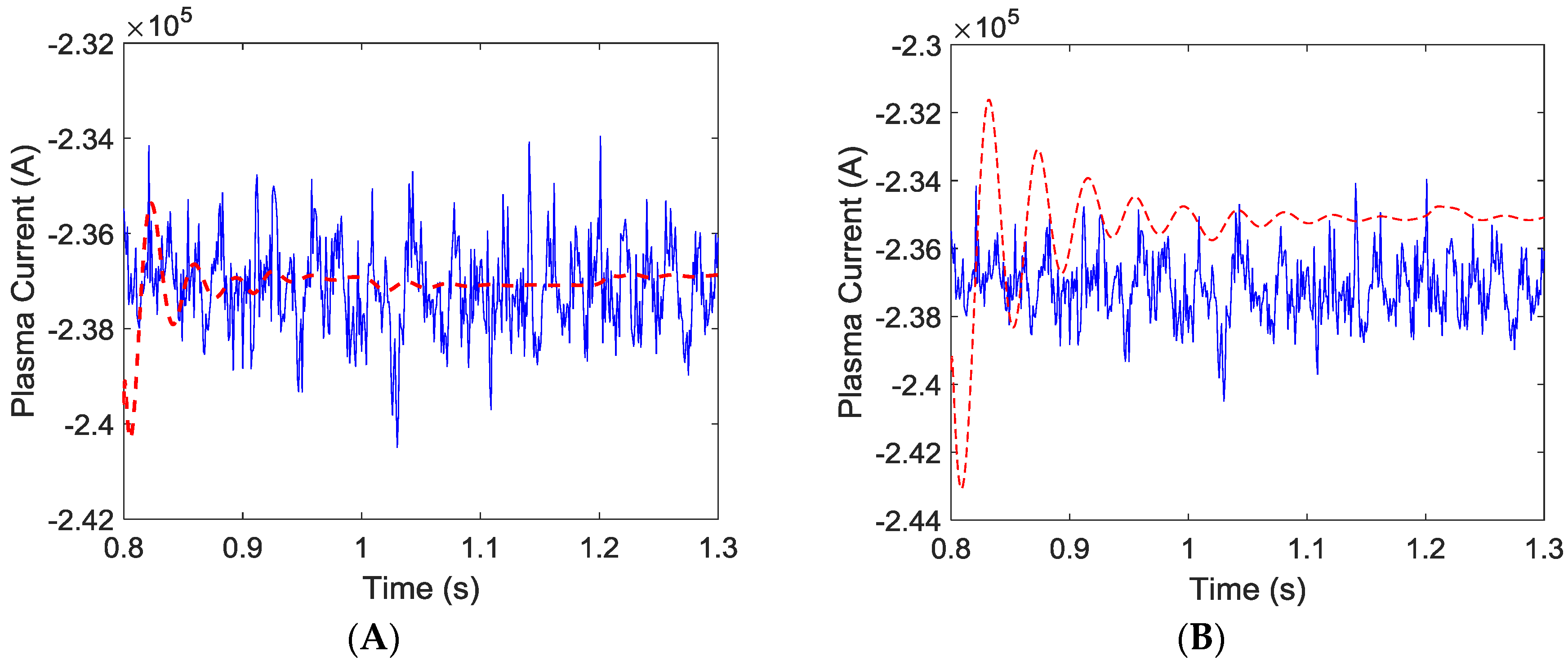
Once the prediction and control horizons have been defined in the algorithm with $N_p=5$ and $N_c=3$, the TCV system response is obtained, (see left hand side of Figure 4). It can be seen how the plasma current follows the given reference. The values of the parameters of the MPC have been set in order to get an adequate adjustment with the set point. The results for the TCV pulse 49,626 are shown in the right hand side of Figure 4, where a fine-tuned PID controller was used, instead of the hybrid MPC.

It can be clearly seen from these two figures that using an enhanced MPC (red line in the left hand side figure), it gives a better fit than the PID without the enhancement (red line in the right hand side figure) to the real measure (blue line). This effect is associated with the fact that the MPC has the plant model embedded, which enables the controlled TCV to yield a better fit of the tracking variable. Other plant model outputs are not shown because there are no significant differences between them when using either a PID or the PID enhanced with the MPC, as should be expected since the plasma current was the variable to improve.

Prediction Horizon and Control Horizon

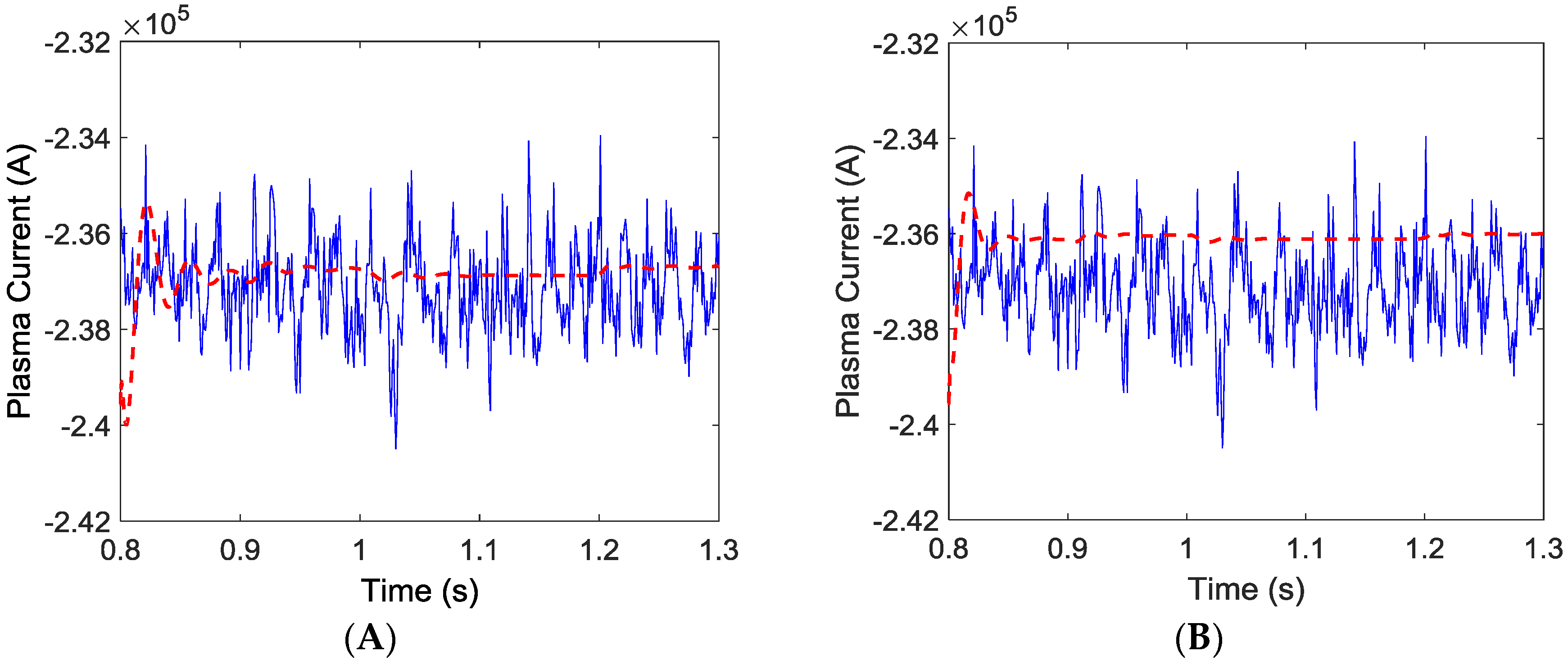
In this section the effect of different horizons on the TCV pulse 49626 will be studied. There are two kinds of horizons: the prediction horizon ${\mathrm{N}}_{\mathrm{p}}$, and the control horizon, ${\mathrm{N}}_{\mathrm{c}}$. The value ${\mathrm{N}}_{\mathrm{p}}$ denotes the number of time-steps ahead in the horizon where the expanded system solution will predict the change in the plasma current that will be caused by changes in the independent variables. These chosen dependent variables are determined by the value of ${\mathrm{N}}_{\mathrm{c}}$, that denotes when the control law stops trying, and which might be smaller than the prediction horizon. High values of horizons are supposed to provide a better system response while small ones may present difficulties for achieving the control objectives; also, both horizon values have to be balanced. Furthermore, there is a tradeoff between the computational effort and the desired accuracy.

To analyze the effect of different horizons on the controlled horizon, let us recall the satisfactory results achieved for the TCV system by an enhanced MPC with ${\mathrm{N}}_{\mathrm{p}}=5$ and ${\mathrm{N}}_{\mathrm{c}}=3$ (see Figure 4).

First at all, the horizon values will be increased up to ${\mathrm{N}}_{\mathrm{p}}=9$ and ${\mathrm{N}}_{\mathrm{c}}=5$. It may be seen that even when the left of Figure 5 shows an improvement of the plasma current response with respect to that displayed in the left of Figure 4, the added control complexity might not fully justify the improved accuracy in the controlled plasma current.

A very small number for both the control horizon and the predictive horizon has also been considered, with only two steps. The result corresponds to a system that has not been adequately controlled. As might be expected, the response of the system when using a short prediction horizon and a short control horizon is not stable. The plasma current does not even reach the set point. The control is unable to anticipate its response quickly enough so that the plasma current slides out of bounds while the TCV system clearly moves out of its stability region. In the other cases, the system stays within the stable region.

Finally, a long predictive horizon together with a small control horizon, shown in the right hand side of Figure 5, provides a poor response. This is due to the propagation of the last calculated manipulated variable value over the rest of the prediction horizon, which becomes too long. It is important to maintain an adequate relation between the two horizons.

5. Conclusions

An enhanced MPC control system has been designed for the TCV that takes advantage of a global PID control algorithm. The RZIp has been chosen to implement the control because it is widely accepted within the fusion research community as a reputed control oriented modeling tool. RZIp considers both active coils and the passive structure, which are strongly coupled in the physical system, so that it requires an eigenmode reduction in the passive structure. This procedure not only reduces the system size but also contributes to system stabilization by removing those modes corresponding to eigenvalues close to the imaginary axis. Although the PID scheme has been designed to work over the whole system, the system reduction gives the opportunity to implement a multiloop control system, such as is the case of the one presented in this article considering an MPC on the plasma current.

This novel enhanced MPC system meets the plasma current control target. Experimental evidence has also been provided, showing that the closed loop system yields improved results with respect to the global PID control. Furthermore, these satisfactory results are obtained for relatively short horizons. It is, therefore, concluded that the enhanced MPC implementation in RZIp for the TCV tokamak provides an excellent complementarity with respect to a more traditional PID control system. The benefits are twofold because it not only provides a smoother fit to the state of interest but also minimizes the control action, saving much needed energy from the non-inductive limited resources.

There are two distinct future lines of research. The obvious way forward is to extend the MPC to other variables, by considering different time control actions. Also, it would be desirable to validate other models based on RZIp simplifications, with the aim to reduce the computational load while still representing the particular plasma dynamics at hand. Finally, it would also be interesting to consider parareal type algorithm solvers to deal with the optimization problem. These kinds of time domain predictor-corrector solvers allow high performance computations so that the prediction part of the MPC algorithm could be implicitly treated within the solver itself, allowing the solution of more complex models.