Abstract
This paper presents an application and extension of multiple-criteria decision-making (MCDM) methods to account for stochastic input variables. More in particular, a comparative study is carried out among well-known and widely-applied methods in MCDM, when applied to the reference problem of the selection of wind turbine support structures for a given deployment location. Along with data from industrial experts, six deterministic MCDM methods are studied, so as to determine the best alternative among the available options, assessed against selected criteria with a view toward assigning confidence levels to each option. Following an overview of the literature around MCDM problems, the best practice implementation of each method is presented aiming to assist stakeholders and decision-makers to support decisions in real-world applications, where many and often conflicting criteria are present within uncertain environments. The outcomes of this research highlight that more sophisticated methods, such as technique for the order of preference by similarity to the ideal solution (TOPSIS) and Preference Ranking Organization method for enrichment evaluation (PROMETHEE), better predict the optimum design alternative.
Keywords:
multi-criteria decision methods; wind turbine; support structures; weighted sum method (WSM); weighted product method (WPM); technique for the order of preference by similarity to the ideal solution (TOPSIS); analytical hierarchy process (AHP); preference ranking organization method for enrichment evaluation (PROMETHEE); elimination et choix traduisant la realité (ELECTRE); stochastic inputs 1. Introduction
Multiple-criteria decision-making (MCDM) is a procedure that combines the performance of decision alternatives across several, contradicting, qualitative and/or quantitative criteria and results in a compromise solution [1]. Relevant methods are frequently applicable, implicitly or explicitly, in numerous real-life problems and can be encountered in industrial activities where sets of decision alternatives are evaluated against conflicting criteria [2]. MCDM methods are widely used in problems within the renewable energy (RE) industry. Indicatively, methods employed include the weighted sum and weighted product methods (WSM/WPM), the analytical hierarchy process (AHP), the technique for the order of preference by similarity to the ideal solution (TOPSIS), elimination et choix traduisant la realité (ELECTRE) and the preference ranking organization method for enrichment evaluation (PROMETHEE), among others. These methods have been successfully applied in a wide range of applications related to energy and sustainability problems [3,4]. Reference to the generic methodology behind MCDM can be found in [3,5], where one can find the most popular approaches to the most widely-applied multi-criteria methods in order to evaluate alternative solutions for real-world applications. MCDM was introduced by Saaty [6,7,8] and was initially developed to evaluate priorities. MCDM is very useful for policy making, new technologies and energy sources’ evaluation, being capable of incorporating both technical and non-technical attributes, i.e., economic, influencing factors [9], in the decision-making process.
Successful selection of the most appropriate multi-criteria methodology should consider a range of different perspectives in order to comprehend all sides of the problem and, when necessary, consider inter-connections among the criteria. MCDM methods need to structure the decision procedure, to demonstrate the trade-off among the criteria, to assist decision-makers to reflect upon, articulate and apply worthy judgments related to satisfactory trade-offs, resulting in suggestions when considering alternatives, to estimate risk and uncertainty more consistently and reasonably, to simplify negotiation and to keep a record of how decisions are made [10]. Real-world applications are often considered as MCDM problems; however, complications can be encountered when, for example, outlining the nature of the problem before defining the necessary alternatives, quantifying data and, finally, finding the optimum solution. Even in the seemingly simpler cases of qualitative attributes, the quality of data can be a significant source of statistical uncertainty. Further, the alternatives are derived from a wide range of choices, which are aimed at being prioritised and finally ranked or arranged in a hierarchical manner. An important issue that should be carefully considered is the fact that different attributes/criteria can cause conflicts due to their degree of completeness, redundancy, mutuality and independence, which can further complicate the decision-making process [5].
This paper aims to provide a comparative study of widely-applied MCDM methods in a real-world application and to introduce a methodology for their extension to account for stochastic inputs. An overview of selected multi-criteria methods is presented, together with a detailed analysis of the process of each method, for the easy implementation and discussion of their generic advantages and disadvantages. A case study of the selection of the optimum configuration of a support structure for a wind farm in a given location is then presented, where the criteria and alternatives of the problem are defined. Next, the data obtained through expert elicitation are presented together with the results from the implementation of each of the methods, deterministically and stochastically. A review of the results is carried out to highlight the differences and discrepancies in order to draw useful conclusions.
2. Literature Review
2.1. Review of Multiple-Criteria Decision-Making (MCDM) Methods
A focused study of MCDM over the last 12 years illustrated the effectiveness of applying these methods in the areas of sustainable and renewable energy applications [11]. The development of MCDM methods has been widely reported in the literature throughout the years, for example by Peng et al. [12], where different methods and their extensions, among others, were employed to solve a problem. Kolios et al. [13] have performed a Political, Economic, Social, Technological, Legal and Environmental (PESTLE) study, employing two different MCDM approaches for multi-criteria risk prioritisation. Kabak and Dağdeviren [9] have used a hybrid MCDM method when studying the energy sector and prioritising the alternative renewable energy sources (RESs) in developing countries. Shafiee and Kolios [14] have applied an MCDM method in order to minimise the operational risks of wind energy assets, while Govindan et al. [15] conducted research on hybrid MCDM methods, including AHP for green supplier selection using a range of conflicting environmental criteria. Localised renewable energy planning has been studied for the island of Thassos in Greece by Mourmouris [16], who implemented an MCDM methodology, defining several criteria for the exploitation of RESs, the local optimum energy mix and electricity production. MCDM methods have also been applied in various engineering problems due to their clarity and robustness after years of study [17,18].
For the purpose of this paper, several methods have been reviewed, and eventually, the following ones have been selected, as they are the most widely applied in multi-criteria analysis problems for energy applications: WSM, WPM, TOPSIS, AHP, ELECTRE and PROMETHEE. In the next paragraphs, a brief review is given with indicative applications of each of them in the literature.
Despite the disadvantages of WSM and WPM, i.e., sensitivity to units’ ranges and exaggeration of specific scores, there are numerous applications in the literature that employ either of them primarily due to their straightforward implementation. Pilavachi et al. [19] have used an MCDM method according to a statistical estimation of weighted factors, while technical, social and economic features have also been considered. The method has been employed on the problem of risk identification and assessment within the tidal energy sector, as can be seen in [13,20], also introducing a comparison between the TOPSIS and WSM methods and showing results with good agreement.
Among many methods, TOPSIS is used extensively in different areas of research. Lozano-Minguez et al. [18] employed this deterministic methodology on the selection of the most desirable support structure of an offshore wind turbine, among three design options, under the consideration of a combination of multiple qualitative and quantitative criteria. The same concept was extended by Kolios et al. [17], where an extended version of TOPSIS is introduced, which takes into consideration the stochasticity of inputs, which is a common issue towards the successful implementation of MCDMs. With the same aim, Martin et al. [21] presented a methodology to evaluate a number of floating support structure configurations, for offshore wind turbines deployed in deep waters. Doukas et al. [22] used TOPSIS on energy policy objectives for sustainable development and renewable energy preferences, while Datta et al. [23] identified the best islanding detection method for a solar photovoltaic system by using TOPSIS along with other MCDM methods. Saelee et al. [24] employed TOPSIS as the best tool for the selection of the best among three biomass types of boiler. Finally, TOPSIS has been applied to a wide range of applications, as described in [25], where it was suggested to further investigate how to calculate the distance among positive and negative solutions.
Considering relevant applications implementing the AHP method, Kahraman and Kaya [10] implemented a fuzzy MCDM method, based on the AHP method, so as to find the optimum amongst energy policies in Turkey. Cobuloglu and Büyüktahtakιn [26] developed a new AHP-based methodology applicable to problems where uncertain data were available, and the criteria weights are identified from the MCDM case. Other applications of AHP in renewable energy-related problems can be found in [27,28], which deal with the evaluation of solar water heating systems and assessment of the local viability of renewable energy sources. AHP and the analytical network process (ANP) have been presented in [29], by using a commercial software package, so as to demonstrate the diversity of applications to which it could be employed.
Applications can certainly be found in the literature, as the use of ELECTRE is widespread. Indicatively in [30], the goal was to select the optimum site location to install an offshore wind farm among four different choices/alternatives through an innovative method based on many MCDM methods, including ELECTRE. In [31], the ELECTRE method was applied to the optimisation of decentralised energy systems. A comprehensive review of the applications of ELECTRE can be found in [32], which supports the argument that it is still an active field of research.
Outranking methods in general, such as PROMETHEE, after several applications have demonstrated their suitability in energy-related problems. PROMETHEE has been used in a wide range of renewable-related applications, such as in [33], where the authors developed and tested a decision support system using the PROMETHEE II method in RES exploitation, and [34] implemented both PROMETHEE and AHP methods in order to choose the most appropriate desalination system in RES plants. In [35], the PROMETHEE method was applied in order to choose the best among four alternative energy exploitation projects in an MCDM problem. More applications and a comprehensive literature review can be found in [36,37,38], where different renewable energy scenarios were explored for energy planning.
Continuing from the above, multi-objective optimisation (MOO) is another important MCDM method and is one of the most commonly-encountered types of optimisation problems. If there are a number of different and conflicting objectives, then the problem will fall into the category of MOO. Naturally, as a process, MOO reveals a number of non-dominated solutions [39]. A significant renewable energy-related problem is described, modelled and solved in [40], where the optimum design of switching converters was searched, in order to be integrated into related renewable technologies. The conflicting objectives were efficiency and reliability, where the optimum solution is obtained from solutions in the Pareto front. In a study on photovoltaic systems and electro-thermal methods, MOO was suggested and applied to two conflicting objectives: the maximisation of the efficiency of the solutions from Europe and their cost minimisation [41]. A lot-sizing mixed integer linear optimisation model was proposed in order to find the optimum ethanol production from several biomass sources, so as to minimise the cost and the environmentally-related issues in [42]. The trade-offs between two types of crop, i.e., food and biofuel crops, was optimised using multi-objective mixed integer programming. A model was proposed and the optimum solution obtained according to economic advantages and environmental impacts in [43]. More studies of MOO can be found in [40,44,45]. The methodology suggested by the authors in the present paper can be further applied to MOO under uncertain inputs.
2.2. Review of the Stochastic Expansion of Deterministic MCDM
A study that focused on earlier applications of MCDM methods demonstrated that developing fuzzy MCDM methods is the upcoming trend [46]. Many instances of the applications of fuzzy MCDM methods can be found in [47,48], where it was highlighted that most of the applications had selected to implement variants based on AHP. In [49], a novel fuzzy multi-actor MCDM method was used in an application of hydrogen technology, where 15 criteria were used for the sustainability assessment. In [17], during deterministic TOPSIS, the weights for each criterion were considered fixed, but under stochastic modelling, statistical distributions were employed to best fit the acquired data of the experts’ opinions. In [50,51], fuzzy VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) and AHP methods were applied using nine evaluation criteria for the assessment of renewable energy technologies in Turkey. The performance of several types of wind turbines was assessed in a case study in Taiwan, where the fuzzy ANP method was implemented [52]. The fuzzy ANP method was also implemented in [53], so as to mitigate the risks related to offshore wind farms, and finally, a comparison between these outcomes with the ANP and AHP methods was provided. Perera [54] has presented a study that combines MCDM and MOO in the designing process of Hybrid Energy Systems (HESs), using the fuzzy TOPSIS extension along with level diagrams. In [55], MCDM under uncertainty is discussed in an application where the alternatives’ weights are partially known. An extended and modified stochastic TOPSIS approach was implemented using interval estimations. In [56], a new stochastic-fuzzy MCDM method, called Fuzzy Stochastic Ordered Weighted Averaging (FSOWA), is presented so as to rank the alternatives and acquire the optimum alternative. The Monte Carlo method is applied to a decision-making, multi-stakeholder and hydro-environmental management case study in order to solve the uncertainty problem in [57]. A fuzzy MCDM method was also applied among energy technology alternatives so as to treat uncertainty. The AHP method under fuzziness is implemented while evaluating scores from experts [10].
3. Methodology
3.1. An Overview of Selected MCDM Methods
3.1.1. Weighted Sum Method (WSM) and Weighted Product Method (WPM)
The WSM is the simplest available method, applicable to single-dimensional problems, due to the fact that it follows an intuitive process. In the background of this method, the additive utility hypothesis is applied, which implies that the overall value of every alternative is equivalent to the products’ total sum. In problems with the same units’ ranges across criteria, WSM is easily applicable; however, when the units’ ranges vary, for example when qualitative and quantitative attributes are employed, the problem becomes difficult to handle, as the aforementioned hypothesis is violated, and hence, normalisation schemes should be employed. It is common practice to use WSM along with other methods, for instance AHP, because of the method’s plain nature.
For the case of criteria and alternatives, the optimum solution to the problem is obtained by the following equation:
where represents the weighted sum score, is the score of the -th alternative with respect to the -th criterion and is the weight of the -th criterion.
An alternative to the WSM is the WPM. WPM is closely related to the WSM with the main difference being a product instead of a sum in the method. Each alternative is compared to the rest through a multiplication of ratios that are related to every criterion. Finally, WPM is considered suitable for both single and multi-dimensional cases.
This method compares alternatives and in the equation below. The optimum solution in a pairwise comparison is the one that is at least equal to the rest of the alternatives, and more specifically, the best solution is when (when considering a maximisation problem).
where, as previously, is the score of the -th alternative with respect to the -th criterion and is the weight of the -th criterion.
3.1.2. TOPSIS
TOPSIS, depicted in Figure 1, was initially proposed by Hwang et al. [58], and the idea behind it lies in the optimal alternative being as close in distance as possible from an ideal solution and at the same time as far away as possible from a corresponding negative ideal solution. Both solutions are hypothetical and are derived within the method. The concept of closeness was later established and led to the actual growth of the TOPSIS theory [59,60].
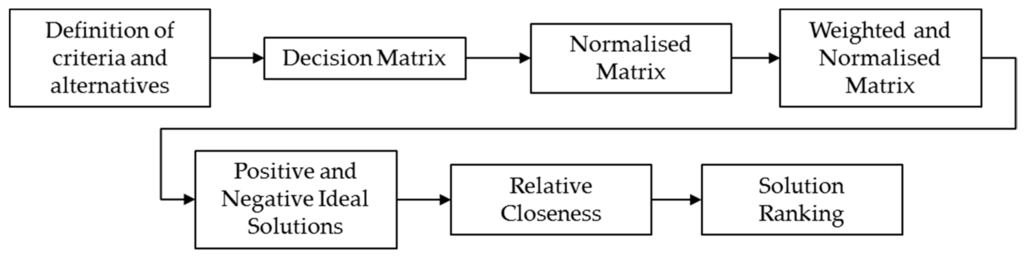
Figure 1.
TOPSIS methodology.
After defining criteria and alternatives, the normalised decision matrix is established. The normalised value is calculated from Equation (3), where is the -th criterion value for alternative ( and ).
The normalised weighted values in the decision matrix are calculated as follows:
The positive ideal and negative ideal solution are derived as shown below, where and are related to the benefit and cost criteria (positive and negative variables).
From the -dimensional Euclidean distance, is calculated in (7) as the separation of every alternative from the ideal solution. The separation from the negative ideal solution follows in (8).
The relative closeness to the ideal solution of each alternative is calculated from:
After sorting the values, the maximum value corresponds to the best solution to the problem.
3.1.3. AHP
AHP was developed by Saaty [7], in 1980, and it is extensively applied in problems involving multiple, often conflicting, criteria [34]. The aim of AHP is to define the optimum alternative and to categorise the others considering the criteria that describe them. In order to apply the original AHP method, four steps should be followed, as shown in Figure 2.

Figure 2.
AHP methodology.
The first phase involves the structuring of the decision problem into a hierarchical structure. The aim is at the top of the hierarchy; the next level includes the criteria affecting the decision; and finally, the alternatives are placed at the bottom of the hierarchy. In the second phase, the weights for each criterion should be obtained. A pairwise comparison matrix (), or judgmental matrix, should be compiled. The entry in row and column of () represents how much more important criterion is than with respect to the alternative. Saaty [7] suggested, for the quantification of qualitative data, a scale of relative importance, i.e., the values used for any given pair vary from 1 (where and have equal importance) to 9 (where is absolutely more important than ). If criterion . has one of the previous non-zero numbers assigned to it when compared to , then has the reciprocal value when compared to . reflects the importance of the -th criterion and is estimated as the average of the entries in row of the matrix normalised. Equations (10) and (11) are used to check the consistency of the pairwise comparisons.
where is the maximum Eigen value, is the pairwise comparison matrix and is the weight vector.
The Consistency Index () is defined as:
where is the maximum Eigen value from the previous equation.
The CI is then compared to the Random Index (RI) for the appropriate value of (Table 1).

Table 1.
Random Index (RI) for different values of n [3].
If > 0.10, serious inconsistencies may exist, while if < 0.10, the degree of consistency is considered satisfactory.
The third step refers to finding the score of each alternative for each criterion. A pairwise comparison matrix for each aim must be constructed. In the end, the best alternative (in the maximisation case) is the one that has the greatest value in the following expression:
where is the score of the i-th alternative, is the number of alternatives, is the number of the criteria, represents the actual value of the i-th alternative in terms of the j-th criterion and is the weight of importance of the j-th criterion.
The AHP is particularly relevant when qualitative criteria, such as environmental or political impacts, are considered. It is widely employed for energy planning problems because of its plainness and its ability to check consistency. Furthermore, throughout this method, the hierarchy is revealed after the breakdown of the problem, which enables understanding and defining the process itself. It is also suitable for dealing with technological characteristics and future aspects that are not well known [3,34]. It should be noted that AHP cannot directly consider potential associations amongst many components, as it performs poorly when different levels are independent, which implies that the method is unsuccessful in representing the complicated connections among the components. A few extensions of the AHP method have been proposed that are able to deal with these problems [61], such as the ANP method [14].
3.1.4. Elimination Et Choix Traduisant la Realité (ELECTRE)
The ELECTRE method was conceived of by Bernard Roy [62]. ELECTRE is not just a method, but a different decision support philosophy. Until recently, it has been successfully applied in many diverse fields. ELECTRE appears in the following variations: ELECTRE I, II, III, IV, IS and TRI [12]. Each extension is based on the same background, but they operate in different ways [63]. Through a selection procedure, when employing ELECTRE I and IS, a single option or group of options is selected and assigned to a kernel of preferred alternatives. A ranking of all options considered in pairs is achieved by employing ELECTRE II, III and IV, which serve as classification procedures. Finally, all options to predefined categories are assigned by ELECTRE TRI [4,64]. The method is characterised by thresholds and the outranking notion. ELECTRE presents the indifference threshold idea, and the preferences are defined again [63]. The decision-makers are the ones to define the indifference threshold. Theoretically, there is a good reason to insert a middle area in between the indifference and the strict preference. Such a hesitation zone is regarded as a weak preference [63].
ELECTRE generates a whole system of binary outranking relations among the alternatives. Since the system may be incomplete, the preferred alternative occasionally cannot be identified. A core of leading alternatives is produced. According to this method, there is a better view of the alternatives when the least favourable choices are removed, which is particularly suitable when there are only a few criteria and many alternatives in the case [5].
As mentioned earlier, there are many variations of ELECTRE. In this study, ELECTRE I is selected, as described in [4,65], and as based on the scope and relevant literature, seems the most appropriate variation. In general two new matrices have to be created: the concordance matrix and dis-concordance matrix, as shown below:
where denotes the whole set of criteria and ′ corresponds to the set of criteria that belong to the concordant coalition, by following ELECTRE’s outranking framework.
where represents the performance of the i-th alternative against the j-th criterion and denotes the maximal difference between the performance of alternatives.
3.1.5. Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE)
PROMETHEE is an MCDM method that was developed in 1985 [66]. Six different extensions based on the ranking were developed and used by decision-makers. First, PROMETHEE I uses partial ranking; PROMETHEE II uses complete ranking; PROMETHEE III ranks based on intervals; PROMETHEE IV is the continuous instance of the previous; PROMETHEE V includes integer linear programming and net flows; and PROMETHEE VI represents the human brain. PROMETHEE ranks the alternatives using the outranking procedure.
PROMETHEE is applied in five steps as shown in Figure 3. First, the decision-maker’s preference between two actions is presented by a preference function independently. Second, the proposed set alternatives are compared between each other with respect to the preference function, and third, the comparisons’ results and the criterion’s value of each alternative are illustrated in a matrix. At the fourth step, PROMETHEE I’s approach is used so as to sort out the partial ranking, and finally, the fifth action contains the PROMETHEE II process in order to finish the alternative rankings [3].

Figure 3.
PROMETHEE methodology.
The formulae used in this implementation of PROMETHEE I are listed below, as described in [3,67]. An important feature of PROMETHEE I is that the sum of the scores equals zero, which informs the reader how far an alternative is from the average performance of the whole set. The decision-makers may select different types of criteria, which are associated with different graphical representations of the preference function. The Type I (usual) and Type IV (level from) preference functions are the best options for qualitative criteria, while the Type III (V-shaped) and Type V (linear) preference functions are the best options for quantitative criteria [68]. The choice between them (Type I or IV; and Type III or V) will depend on whether the decision-maker wants to introduce an indifference threshold or not. The Type II (U-shaped) and Type VI (Gaussian) preference functions are used less often. The preference functions of both Types I and V are defined below, since in the case study to follow, qualitative criteria are included.
The preference function for Type I is:
where denotes the numerical difference in the evaluation of two alternatives for a certain criterion.
The preference function for Type V is:
where and denote the indifference and preference for each evaluation . The multi-criteria preference degree is calculated from:
where w represents the weight of each criterion.
Outgoing flow is represented as:
Incoming flow is defined as:
Net flow is derived from:
3.2. Stochastic Expansion of Deterministic MCDM
In a real-life scenario, there are always unknown facts, which are often practically impossible to identify. For this reason, vague simplifications are often necessary in order to represent a realistic condition. The earlier researchers and practitioners used to address uncertainty by assigning numerical values to each factor and logically combining them together [69], i.e., through employing most likely values or corresponding quantiles. The term “deterministic” is related to a certain entity. Deterministic models are used to describe one out of many possible results in a reference problem. On the other hand, “stochastic” comes from the Greek “to aim” and refers to a “random” outcome. A number of potential outcomes, which are characterised by their probabilities or likelihood, is best represented through stochastic modelling. Consequently, stochastic processes denote the set of random variables that are related to a varying factor. Such processes consist of a state space, which represents the potential values, where the random variables may be related to each other [57].
Real-life problems and human judgment are, in most cases, unclear and vague and cannot be represented as fixed values. For that reason, the fuzzy set logic is often implemented in MCDM problems. Fuzzy logic allows capturing the concept of the fuzziness of a system as measurable values. Fuzzy logic and probabilities show a different view and expression for uncertainty. The former theory implements the concept of fuzzy set membership, whereas the latter implements the concept of subjective probability [70]. A wider review of the fuzzy modelling and renewable energy systems is provided in [70].
A stochastic method can be more informative than a deterministic method because the former accounts for the uncertainty due to the varying behavioural characteristics of the target system. Deterministic methods are mainly used to describe simple, natural phenomena on the basis of physical laws and are not fit-for-purpose for large and complicated applications. Consequently, real-world behaviour is better reflected by employing methods relevant to stochastic simulations. The latter can include the uncertainty of real-world applications, where system modelling is not trivial. Stochastic methods can increase the confidence of the decision-maker in the final results and analysis and can be more appropriate for cases where the heterogeneity of important factors is critical as the uncertainty of the considered system increases. In general, it is not feasible to obtain an analytical expression for stochastic problems, which would require more computational time and resources to deliver a satisfactory solution [57].
The Monte Carlo simulation method is a particularly useful approach in stochastic modelling, as it can mitigate the problems of deterministic analysis. Such an expansion of deterministic methods is developed in this paper. Principally, the Monte Carlo simulation method is an approach to represent the random nature of stochastic processes. The most fundamental part of such a method is the generation of random numbers as input sets, which are drawn randomly. Algorithms that implement the Monte Carlo simulation method consist of a sequence of finite states, a mapping function for the finite states, the probability distribution of finite states, the output space and a mapping function between the finite states and the output space [71].
The approach proposed in this paper for the stochastic expansion of deterministic methods, follows the approach proposed in [17], expanded for different methods, and is based on the fact that input variables are considered stochastically as statistical distributions that are derived by best fitting of the data collected for each value in the decision matrix and weight vector. Stochastic input data will allow Monte Carlo simulations to perform numerous iterations of analysis in order to quantify results and identify the number of cases where the optimum solution will prevail, i.e., there is a Pi probability that option Xi will rank first. Figure 4. Stochastic expansion algorithm of deterministic MCDM methods illustrates the sequence of steps followed.
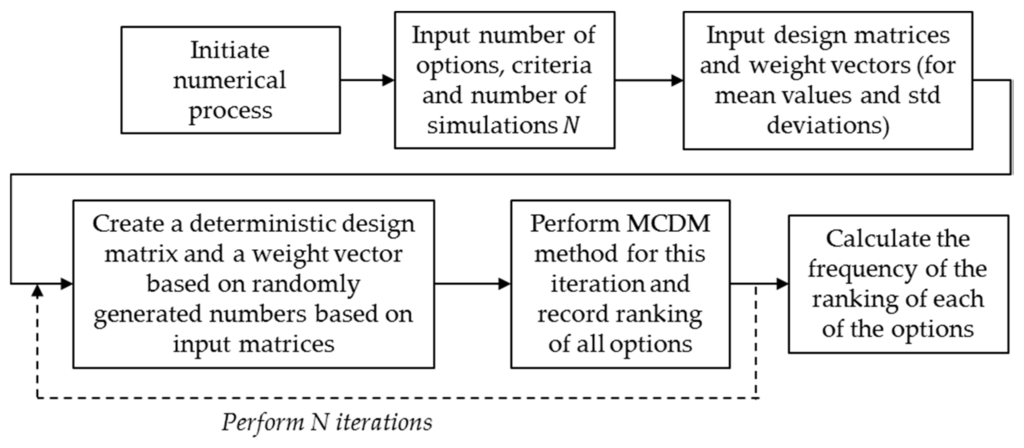
Figure 4.
Stochastic expansion algorithm of deterministic MCDM methods.
4. Case Study
Among most of the operating offshore wind turbines installed in the Round 1 and 2 regions in the U.K., monopile foundations have been constructed in water depths of no more than 35 m [72] while the average water depth in an offshore wind farm in Europe was 27 m and distance from shore 43 km, as recorded by 2016 [73,74]. Due to risk and cost limitations related to fabrication, transportation and installation, these foundation options are not considered viable solutions in depths that exceed 30–35 m [72], although extensive research is currently taking place to push this boundary further. Moving further away from the shore, towards deeper waters, can lead to higher electricity production primarily due to the higher wind shear, more available space and lower social impact; however, deep water installations demand considerably higher volumes of materials and installation effort, resulting in higher costs.
The advantage of fixed structures is that the designs have already been deployed in many wind farms for years and similar concepts have been deployed for decades in the oil and gas industry. However, fixed structures are not compatible in deeper waters because the designs became impractical, more complicated and unsuitable for mass production. For sites that exceed the limit of 60–70 m, the bottom-fixed foundations encounter both technical and economic restrictions, and it is expected that the floating wind turbine support structure concepts will become more applicable solutions [75,76]. Currently, several floating concepts are being developed and tested in order to qualify for scaling and further production. Floating structures still have high costs, face issues with the footprint of the moorings, limitations for the minimum water depth in which to operate and finally design constraints regarding the complications of volume construction.
In this case study, data were collected considering both fixed and floating structures from structured questionnaires from 20 experts in the wind energy field, with at least seven years’ experience in the design and implementation of RE projects. The data received were statistically processed accordingly in a preliminary study of the authors, as presented extensively in [17]. This present study aims to highlight the suitability of different MCDM methods for this problem with a view toward illustrating how well each method performs following a qualitative validation of the outcomes.
Decision Criteria and Alternatives
For this analysis, 10 design alternatives for offshore support structures are chosen, each evaluated based on 10 different criteria, listed in Table 2 and Table 3 (where TLP stands for Tensioned Leg Platform). These were selected so as to extend previous work and for comparison purposes [18,21,75,77,78]. The 10 selected criteria have been qualified through a comprehensive list of 36 criteria for practicality purposes, based on semi-structured experts’ interviews and have been evaluated using qualitative variables.
- The compliance/maximum displacement of the rotor is considered to be a negative variable, and it represents the maximum displacement likely to be expected at the hub of the rotor that is affected by the support structure. It is treated in a different way for the floating and fixed structures; however, it does affect the rotor similarly for both structures.
- Dynamic performance is a positive variable, and it defines qualitatively the performance of a support structure in combination with the environmental effects and the operating loads. It is treated in a different way for the floating and fixed structures; the former has to combine the coupled effect of waves and turbine loads.
- Design redundancy is a positive variable, and it defines the capability to redistribute the load when a local failure is encountered.
- The cost of maintenance is a negative variable, and it reflects the qualitative assessment of the possible maintenance costs when, for example, any necessary equipment is involved or weather issues occur.
- The cost of installation is a negative variable, and it represents the qualitative assessment of the possible installation costs along with procedures, such as piling, etc.
- Environmental impact is a negative variable regarding the installation, operation and decommissioning impact of the foundation. Impacts on the natural environment can be considered as noise, visual, shadowing effects, disruption of the fish population’s routes, etc.
- Carbon footprint is a negative variable that takes into account the CO2 emissions that were produced during all of the procedures needed for the support structure, such as the fabrication and installation processes.
- Certification is a positive variable and reflects the confidence level against a range of engineering uncertainties. This covers a number of cases from existing installations related to the current application, to different applications or no applications at all.
- The likely cost is a negative variable. It represents the relative qualitative assessment of each of the concept’s costs, which, to some extent, could be quantified through the Net Present Value (NPV).
- Depth compatibility is a positive variable and represents the confidence levels when deploying a concept, which considers current installations for any applications with respect to a reference depth.

Table 2.
List of criteria.

Table 3.
List of alternatives.
A Likert scale has been employed in the questionnaires in order to provide uniform input data. The experts were asked to identify their level of agreement or disagreement using a number from within the 1–9 scores, as the Likert scale suggests. The scale usually states nine as the most critical response. The same 1–9 scales was used to rank the different alternatives that correspond to the design criteria. According to the positive or negative nature of the criteria, nine and one are the optima, respectively. Although usually in practice, the Likert scale is defined through a 1–5 scale, due to the fact that statistical processing has followed the collection of the data, a broader range of values was deemed more appropriate.
In order to define the problem, a relatively large-scale wind turbine (such as 5.5 MW) was considered to be installed in a 40-m water depth, and 10 design configurations were proposed for the support structure against the 10 selected criteria. The depth is considered to be a key parameter of the problem, as it is expected that it will influence the final outcome based on the experts’ responses. The designs included five fixed and five floating support options.
All design alternatives have both advantages and disadvantages, and that is the reason behind the proposed criteria and how their aggregation can qualify as the best performance. Several more support structures can be found in the literature, including some concepts that combine different types’ features in a single design. These types usually have some advantages, overcoming some of the problems, and are suitable for a wide range of water depths. These hybrid structures are outside the scope of this paper, but could be investigated further in the future; however, the approach suggested in this paper is applicable for their assessment.
In Table 4, the mean evaluation values of the processed questionnaires are presented.

Table 4.
Mean evaluation values (design matrix) and normalised mean values of the weights.
5. Results and Discussion
5.1. Deterministic Results
The results of the deterministic application of the MCDM methods are presented in this section. In the context of this application, certain criteria had to be maximised, and others had to be minimised. Here, only maximisation is considered, and any criteria for minimisation are multiplied by −1, where relevant. Most of the methods provide absolute scores, which are used for ordering the solutions at the end. Since maximisation is considered, the score should be as high as possible. When a method generates a pairwise solution, the solution that outperforms most of the other alternatives is considered to be the optimum.
As can be seen from Figure 5, in most cases, the methods derive close optimum solutions. Table 5 summarises the WSM, WPM, TOPSIS, AHP, PROMETHEE I and ELECTRE I results and ranking.
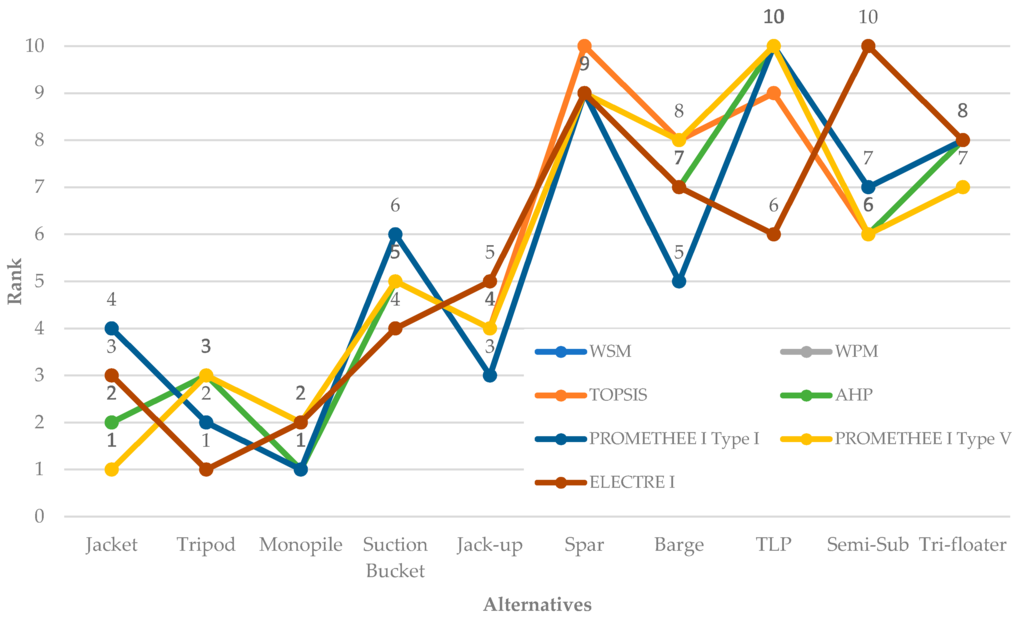
Figure 5.
Ranks comparison for the WSM, WPM, TOPSIS, AHP, PROMETHEE I and ELECTRE I methods.

Table 5.
WSM, TOPSIS, AHP, PROMETHEE I and ELECTRE I results and rank.
In more detail:
- WSM: This has been the simplest method applied, and the result for the optimal solution is Alternative A3, the monopile design, followed by A1 (jacket) as the second option.
- WPM: WPM generates a matrix with pairwise comparison performance, as shown in Table 6. Hence, in this case, A1 (jacket) is superior to all of the other alternatives, because the ratio is higher than one in all cases. Following this, the monopile stands as the second best option.
 Table 6. WPM pairwise comparison matrix.
Table 6. WPM pairwise comparison matrix. - TOPSIS: According to this method, again, the jacket (A1) design achieves the highest score followed by the monopile concept.
- AHP: This method ranks the monopile (A3) design highest, followed by the jacket. The final ranking seems to be closer to the rest of the methods, and this can be explained due to the similarity of this method to the WSM.
- PROMETHEE I: Two different types of criteria were employed for the PROMETHEE I method. First, the Type I preference function was applied, and the monopile (A3) was found to be the best alternative in this case. Second, the results from the Type V preference function indicate that the jacket design achieves the highest score (A1).
- ELECTRE I: As a result, this method generates two matrices, which cumulatively qualify the tripod (A2) as the best option followed by the monopile and jacket.
Jacket qualifies as the best alternative for WPM, TOPSIS and PROMETHEE I Type V, while monopile is the best alternative for WSM, AHP and PROMETHEE I Type I. From experience, it would be expected that these two concepts would score higher, as their implementation would introduce lower risk, as they are the most widely-used concepts to date [74]. Although the applicability boundaries of monopiles are pushed to account for deeper waters in order to take advantage of their ease in fabrication and installation, the threshold of 35 m would still face challenges to be achieved due to practical, technical difficulties [79,80,81]. Hence, the jacket would be expected to be the prevailing concept for this problem.
It is not surprising that WSM, AHP and PROMETHEE I Type I methods consider the monopile as the best alternative, since they are the least sophisticated methods among those evaluated. The maintenance and likely costs, which have a negative nature, are the criteria that obtained the highest values for the vector weight, and for both of them, the monopile has a much lower score than the jacket; hence, it can be concluded that the effect of these extreme scores has been underestimated by using these less sophisticated methods. Results obtained from the deterministic application of the different methods employed in this paper can be supported by the findings of other studies for similar problems comparing different MCDM methods, i.e., [82,83,84].
5.2. Stochastic Results
For all deterministic MCDM methods, stochastic expansion through Monte Carlo simulations was performed through appropriately-developed stochastic algorithms, following the process presented in Section 3. Input variables were modelled through truncated normal distributions. Each Monte Carlo iteration produced random inputs for each of the stochastic variables, which were fed into an iterative generation of deterministic decision matrices. The output from each case was recorded, and the best solution for each iteration was stored, so as to aggregate how frequently each alternative outperformed the others. Due to the relatively high probabilities of failure to be captured, the rule of thumb of two orders of magnitude more simulations than the expected measured probability was followed (resolution of 1%), consisting of 100,000 iterations for each simulation. A convergence study highlighted that this resolution of analysis was sufficient for this problem. Figure 6 presents the probability of an alternative to score first, while Table 7 lists the results for 100,000 iterations with the probability of each design alternative scoring in each rank.
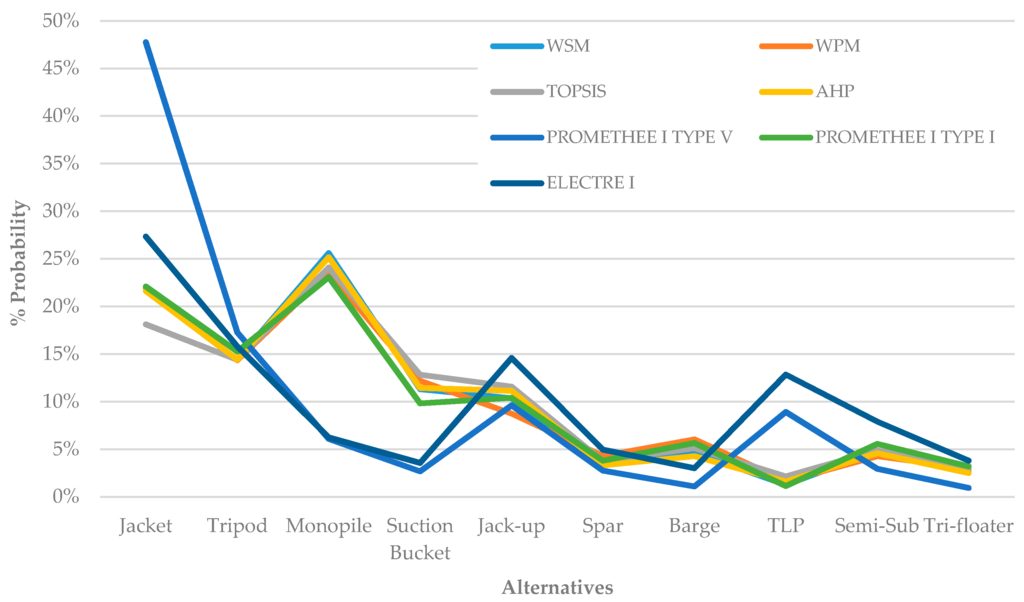
Figure 6.
Comparative stochastic MCDM results: probability of an alternative to score first.

Table 7.
Stochastic WSM, TOPSIS, AHP, PROMETHEE I and ELECTRE I results.
From the results of the stochastic analysis, it can be observed that Alternatives A1, A2 and A3 (jacket, tripod and monopile) consistently perform better than the rest with probabilities of ranking first between 49.4% (ELECTRE I) and 71.1% (PROMETHEE I TYPE V). Comparing fixed with floating options, the former rank higher with probabilities between 67.5% (ELECTRE I) and 83.7% (AHP). It should be noted that the PROMETHEE I TYPE V exaggerates in the prediction of the optimum alternative and presents some relative inconsistency with respect to the others, while ELECTRE I also seems to be mis-ranking the least optimum options; hence, these methods seem to be less suitable for the reference application.
The results above are countersigned by current practice as fixed support structures, and particularly, monopiles and jackets have reached far higher Technology Readiness Level (TRL) than floating concepts, which are still to achieve full commercialisation due to the various risks associated with their wider implementation (i.e., design for volume production, cost of moorings, dynamic performance, etc.). It should also be observed that the definition of the problem, referring to a 40-m depth deployment, consists of a determining factor of this conclusion, as it is expected that for the case of a deeper installation (i.e., 70 m), fixed concepts would have scored much lower in the criteria of cost of maintenance, cost of installation, certification, likely cost and depth compatibility.
Based on the results obtained, two separate studies were also evaluated, considering separately the fixed and floating concepts. The outcomes have shown again that the three fixed concepts (jacket, monopole and tripod) have significantly higher scores than the suction bucket and jack-up, while for the floating concepts, spar, barge and TLP outperform the tri-floater and semi-sub. These findings illustrate that the stochastic approach proposed in this paper is able to evaluate the relative risks encountered with the selection of each of the chosen options.
6. Conclusions
The application of MCDM methods in engineering problems and particularly those related to renewable energy applications, can provide useful insight for decision-makers towards more qualified decisions. The present study demonstrated the application of six MCDM methods that are frequently used on numerous renewable energy applications, namely WSM, WPM, TOPSIS, AHP, PROMETHEE I and ELECTRE I, and their extension to consider stochastic inputs and assign confidence levels in the resulting outputs.
For the reference case study, 10 significant technical and non-technical criteria were employed to assess the optimal solution among 10 different alternatives of support structures for offshore wind turbines. After applying the MCDM methods on the case deterministically, it can be concluded that most methods agree on identifying the set with the highest score, with the most sophisticated methods, i.e., TOPSIS and PROMETHEE, more accurately predicting the jacket type configuration as the prevailing one, followed by the monopile. The expansion of the methods to account for uncertain inputs has shown similar results, qualifying the fixed concepts and, in particular, the jacket, tripod and monopile, as the prevailing options. A reasonable agreement can be observed among the methods, with the exceptions of PROMETHEE I TYPE V and ELECTRE I, which seem less suitable for this purpose, as they misjudge the ranking of the less optimal options. It should be noted here that a conclusion cannot be generalised, i.e., that one method outperforms the rest, as accuracy in prediction depends on the nature of the problem, as well as the data collection and processing in a way that best fits each individual method and application.
Acknowledgments
This work was supported by Grant EP/L016303/1 for Cranfield University, Centre for Doctoral Training in Renewable Energy Marine Structures (REMS) (http://www.rems-cdt.ac.uk/) from the U.K. Engineering and Physical Sciences Research Council (EPSRC).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dadda, A.; Ouhbi, I. A decision support system for renewable energy plant projects. In Proceedings of the 2014 Fifth International Conference on Next Generation Networks and Services (NGNS), Casabalanca, Morocco, 28–30 May 2014.
- Triantaphyllou, E.; Mann, S.H. Using the analytic hierarchy process for decision making in engineering applications: Some challenges. Int. J. Ind. Eng. Appl. Pract. 1995, 2, 35–44. [Google Scholar]
- Mateo, J.R.S.C. Multi-Criteria Analysis in the Renewable Energy Industry; Springer-Verlag: London, UK, 2012. [Google Scholar]
- Rogers, M.; Bruen, M.; Maystre, L.-Y. ELECTRE and Decision Support, Methods and Applications in Engineering and Infrastructure Investment; Springer Science+Business Media, LLC: New York, NY, USA, 2000. [Google Scholar]
- Triantaphyllou, E.; Shu, S.; Sanchez, S.N.; Ray, T. Multi-criteria decision making: An operations research approach. Encycl. Electr. Electron. Eng. 1998, 15, 175–186. [Google Scholar]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 1996; Volume 4922. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resources Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. What is the analytic hierarchy process? In Mathematical Models for Decision Support; Mitra, G., Greenberg, H.J., Lootsma, F.A., Rijkaert, M.J., Zimmermann, H.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 109–121. [Google Scholar]
- Kabak, M.; Dağdeviren, M. Prioritization of renewable energy sources for Turkey by using a hybrid MCDM methodolog. Energy Convers. Manag. 2014, 79, 25–33. [Google Scholar] [CrossRef]
- Kahraman, C.; Kaya, İ. A fuzzy multicriteria methodology for selection among energy alternatives. Exp. Syst. Appl. 2010, 37, 6270–6281. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K.; Cavallaro, F.; Khalifah, Z. Sustainable and renewable energy: An overview of the application of multiple criteria decision making techniques and approaches. Sustainability 2015, 7, 13947–13984. [Google Scholar] [CrossRef]
- Peng, J.-J.; Wang, J.Q.; Wang, J.; Yang, L.J.; Chen, X.H. An extension of ELECTRE to multi-criteria decision-making problems with multi-hesitant fuzzy sets. Inf. Sci. 2015, 307, 113–126. [Google Scholar] [CrossRef]
- Kolios, A.; Read, G.; Ioannou, A. Application of multi-criteria decision-making to risk prioritisation in tidal energy developments. Int. J. Sustain. Energy 2016, 35, 59–74. [Google Scholar] [CrossRef]
- Shafiee, M.; Kolios, A.J. A multi-criteria decision model to mitigate the operational risks of offshore wind infrastructures. In Proceedings of the European Safety and Reliability Conference, ESREL 2014, Wroclaw, Poland, 14–18 September 2014; CRC Press/Balkema: Wroclaw, Poland, 2015. [Google Scholar]
- Govindan, K.; Rajendran, S.; Sarkis, J.; Murugesan, P. Multi criteria decision making approaches for green supplier evaluation and selection: A literature review. J. Clean. Prod. 2013, 98, 66–83. [Google Scholar] [CrossRef]
- Mourmouris, J.C.; Potolias, C. A multi-criteria methodology for energy planning and developing renewable energy sources at a regional level: A case study thassos, greece. Energy Policy 2013, 52, 522–530. [Google Scholar] [CrossRef]
- Kolios, A.J.; Rodriguez-Tsouroukdissian, A.; Salonitis, K. Multi-criteria decision analysis of offshore wind turbines support structures under stochastic inputs. Ships Offshore Struct. 2016, 11, 38–49. [Google Scholar]
- Lozano-Minguez, E.; Kolios, A.J.; Brennan, F.P. Multi-criteria assessment of offshore wind turbine support structures. Renew. Energy 2011, 36, 2831–2837. [Google Scholar] [CrossRef]
- Pilavachi, P.; Roumpeas, C.P.; Minett, S.; Afgan, N.H. Multi-criteria evaluation for CHP system options. Energy Convers. Manag. 2006, 47, 3519–3529. [Google Scholar] [CrossRef]
- Kolios, A.; Read, G. A political, economic, social, technology, legal and environmental (PESTLE) Approach for risk identification of the tidal industry in the United Kingdom. Energies 2013, 6, 5023–5045. [Google Scholar] [CrossRef]
- Martin, H.; Spano, G.; Küster, J.F.; Collu, M.; Kollios, A.J. Application and extension of the TOPSIS method for the assessment of floating offshore wind turbine support structures. Ships Offshore Struct. 2013, 8, 477–487. [Google Scholar] [CrossRef]
- Doukas, H.; Karakosta, C.; Psarras, J. Computing with words to assess the sustainability of renewable energy options. Exp. Syst. Appl. 2010, 37, 5491–5497. [Google Scholar] [CrossRef]
- Datta, A.; Saha, D.; Ray, A.; Das, P. Anti-islanding selection for grid-connected solar photovoltaic system applications: A MCDM based distance approach. Solar Energy 2014, 110, 519–532. [Google Scholar] [CrossRef]
- Saelee, S.; Paweewan, B.; Tongpool, R.; Witoon, T.; Takada, J.; Manusboonpurmpool, K. Biomass type selection for boilers using TOPSIS multi-criteria model. Int. J. Environ. Sci. Dev. 2014, 5, 181–186. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Exp. Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Cobuloglu, H.I.; Büyüktahtakın, İ.E. A stochastic multi-criteria decision analysis for sustainable biomass crop selection. Exp. Syst. Appl. 2015, 42, 6065–6074. [Google Scholar] [CrossRef]
- Mohsen, M.S.; Akash, B.A. Evaluation of domestic solar water heating system in jordan using analytic hierarchy process. Energy Convers. Manag. 1997, 38, 1815–1822. [Google Scholar] [CrossRef]
- Nigim, K.; Munier, N.; Green, J. Pre-feasibility MCDM Tools to aid communities in prioritizing local viable renewable energy sources. Renew. Energy 2004, 29, 1775–1791. [Google Scholar] [CrossRef]
- Saaty, R.W. Decision Making in Complex Environments: The Analytic Hierarchy Process (AHP) for Decision Making and the Analytic Network Process (ANP) for Decision Making with Dependence and Feedback; Super Decisions: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Fetanat, A.; Khorasaninejad, E. A novel hybrid MCDM approach for offshore wind farm site selection: A case study of Iran. Ocean Coast. Manag. 2015, 109, 17–28. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Karagiannidis, A. Application of the multi-criteria analysis method electre III for the optimisation of decentralised energy systems. Omega 2008, 36, 766–776. [Google Scholar] [CrossRef]
- Govindan, K.; Jepsen, M.B. ELECTRE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2016, 250, 1–29. [Google Scholar] [CrossRef]
- Georgopoulou, E.; Sarafidis, Y.; Diakoulaki, D. Design and implementation of a group dss for sustaining renewable energies exploitation. Eur. J. Oper. Res. 1998, 109, 483–500. [Google Scholar] [CrossRef]
- Georgiou, D.; Mohammed, E.S.; Rozakis, S. Multi-criteria decision making on the energy supply configuration of autonomous desalination units. Renew. Energy 2015, 75, 459–467. [Google Scholar] [CrossRef]
- Goumas, M.; Lygerou, V. An extension of the PROMETHEE method for decision making in fuzzy environment: Ranking of alternative energy exploitation projects. Eur. J. Oper. Res. 2000, 123, 606–613. [Google Scholar] [CrossRef]
- Madlener, R.; Kowalski, K.; Stagl, S. New ways for the integrated appraisal of national energy scenarios: the case of renewable energy use in Austria. Energy Policy 2007, 35, 6060–6074. [Google Scholar] [CrossRef]
- Tsoutsos, T.; Drandaki, M.; Frantzeskaki, N.; Iosifidis, E.; Kiosses, I. Sustainable energy planning by using multi-criteria analysis application in the island of crete. Energy Policy 2009, 37, 1587–1600. [Google Scholar] [CrossRef]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. PROMETHEE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Branke, J.; Deb, K.; Miettinen, K.; Slowiński, R. Multiobjective Optimization: Interactive and Evolutionary Approaches; Springer-Verlag: Heidelberg, Germany, 2008; Volume 5252. [Google Scholar]
- Adinolfi, G.; Graditi, G.; Siano, P.; Piccolo, A. Multiobjective optimal design of photovoltaic synchronous boost converters assessing efficiency, reliability, and cost savings. IEEE Trans. Ind. Inform. 2015, 11, 1038–1048. [Google Scholar] [CrossRef]
- Graditi, G.; Adinolfi, G.; Tina, G.M. Photovoltaic optimizer boost converters: Temperature influence and electro-thermal design. Appl. Energy 2014, 115, 140–150. [Google Scholar] [CrossRef]
- Kantas, A.B.; Cobuloglu, H.I.; Büyüktahtakιn, İ.E. Multi-source capacitated lot-sizing for economically viable and clean biofuel production. J. Clean. Prod. 2015, 94, 116–129. [Google Scholar] [CrossRef]
- Cobuloglu, H.I.; Büyüktahtakın, İ.E. Food vs. biofuel: An optimization approach to the spatio-temporal analysis of land-use competition and environmental impacts. Appl. Energy 2015, 140, 418–434. [Google Scholar] [CrossRef]
- Ippolito, M.G.; Di Silvestre, M.L.; Sanseverino, E.R.; Zizzo, G. Multi-objective optimized management of electrical energy storage systems in an islanded network with renewable energy sources under different design scenarios. Energy 2014, 64, 648–662. [Google Scholar] [CrossRef]
- Mirjafari, M.; Balog, R.S. Multi-objective optimization of the energy capture and boost inductor mass in a module-integrated converter (mic) photovoltaic energy system. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012.
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Exp. Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Nor, K.M.D.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications—A review of the literature from 2000 to 2014. Econ. Res.-Ekon. Istraž. 2015, 28, 516–571. [Google Scholar]
- Ren, J.; Fedele, A.; Mason, M.; Manzardo, A.; Scipioni, A. Fuzzy multi-actor multi-criteria decision making for sustainability assessment of biomass-based technologies for hydrogen production. Int. J. Hydrogen Energy 2013, 38, 9111–9120. [Google Scholar] [CrossRef]
- Kaya, T.; Kahraman, C. Multicriteria renewable energy planning using an integrated fuzzy VIKOR & AHP methodology: The case of istanbul. Energy 2010, 35, 2517–2527. [Google Scholar]
- Şengül, Ü.; Eren, M.; Shiraz, S.E.; Gezder, V.; Şengül, A.B. Fuzzy TOPSIS method for ranking renewable energy supply systems in Turkey. Renew. Energy 2015, 75, 617–625. [Google Scholar] [CrossRef]
- Lee, A.H.I.; Hung, M.-C.; Kang, H.-Y.; Pearn, W.L. A wind turbine evaluation model under a multi-criteria decision making environment. Energy Convers. Manag. 2012, 64, 289–300. [Google Scholar] [CrossRef]
- Shafiee, M. A fuzzy analytic network process model to mitigate the risks associated with offshore wind farms. Exp. Syst. Appl. 2015, 42, 2143–2152. [Google Scholar] [CrossRef]
- Perera, A.T.D.; Attalage, R.A.; Perera, K.K.C.K.; Dassanayake, V.P.C. A hybrid tool to combine multi-objective optimization and multi-criterion decision making in designing standalone hybrid energy systems. Appl. Energy 2013, 107, 412–425. [Google Scholar] [CrossRef]
- Xiong, W.; Qi, H. A extended TOPSIS method for the stochastic multi-criteria decision making problem through interval estimation. In Proceedings of the 2010 2nd International Workshop on Intelligent Systems and Applications (ISA), Wuhan, China, 22–23 May 2010.
- Zarghami, M.; Szidarovszky, F.; Ardakanian, R. A fuzzy-stochastic OWA model for robust multi-criteria decision making. Fuzzy Optim. Decis. Mak. 2008, 7, 1–15. [Google Scholar] [CrossRef]
- Taylor, H.M.; Karlin, S. An Introduction to Stochastic Modeling, 3rd ed.; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Hwang, C.-L.; Yoon, K.P. Multiple Attribute Decision Making, 1981; Lecture Notes in Economics and Mathematical Systems; SAGE Publications: Thousand Oaks, CA, USA, 1981. [Google Scholar]
- Yoon, K.P.; Hwang, C.-L. Multiple Attribute Decision Making: An Introduction; SAGE Publications: Thousand Oaks, CA, USA, 1995; Volume 104. [Google Scholar]
- Zeleny, M. Multiple Criteria Decision Making; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- Deng, X.; Hu, Y.; Deng, Y. Supplier selection using AHP methodology extended by D numbers. Exp. Syst. Appl. 2014, 41, 156–167. [Google Scholar] [CrossRef]
- Roy, B. The outranking approach and the foundations of ELECTRE methods. Theroy Decis. 1991, 31, 49–73. [Google Scholar] [CrossRef]
- Buchanan, J.; Sheppard, P.; Vanderpoorten, D. Ranking projects using the ELECTRE method. In Proceedings of the 33rd Annual Conference Operational Research Society of New Zealand, Auckland, New Zealand, 30 August–1 September 1998.
- Milani, A.S.; Shanian, A.; El-Lahham, C. Using different ELECTRE methods in strategic planning in the presence of human behavioral resistance. Adv. Decis. Sci. 2006, 2006. [Google Scholar] [CrossRef]
- Botti, L.; Peypoch, N. Multi-criteria ELECTRE method and destination competitiveness. Tour. Manag. Perspect. 2013, 6, 108–113. [Google Scholar] [CrossRef]
- Brans, J.; Vincke, P. A preference ranking organization method: The PROMETHEE method for multiple criteria decision-making. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; CRC Press: New York, NY, USA, 2011. [Google Scholar]
- Mareschal, B. The PROMETHEE-GAIA FAQ. 2013. Available online: http://www.promethee-gaia.net/faq-pro/index.php?action=article&cat_id=003002&id=4 (accessed on 7 July 2016).
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Fransisco, CA, USA, 2014. [Google Scholar]
- Suganthi, L.; Iniyan, S.; Samuel, A.A. Applications of fuzzy logic in renewable energy systems—A review. Renew. Sustain. Energy Rev. 2015, 48, 585–607. [Google Scholar] [CrossRef]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bhattacharya, S.; Nikitas, N.; Garnsey, J.; Alexander, N.A.; Cox, J.; Lombardi, D.; Wood, D.M.; Nash, D.F.T. Observed dynamic soil–structure interaction in scale testing of offshore wind turbine foundations. Soil Dyn. Earthq. Eng. 2013, 54, 47–60. [Google Scholar] [CrossRef]
- Arapogianni, A.; Genachte, A.-B. The members of the European Wind Energy Association’s (EWEA) Offshore Wind Industry Group (OWIG). In Deep Water, The Next Step for Offshore Wind Energy; EWEA: Brussels, Belgium, 2013. [Google Scholar]
- European Wind Energy Association. Offshore Statistics. 2016. Available online: http://www.ewea.org/statistics/offshore-statistics/ (accessed on 7 July 2016).
- Collu, M.; Kolios, A.J.; Chahardehi, A.; Brennan, F. A Comparison Between the Preliminary Design Studies of a Fixed and a Floating Support Structure for a 5 MW Offshore Wind Turbine in the North Sea; Marine Renewable and Offshore Wind Energy–Papers 2010; RINA, Royal Institution of Naval Architects: London, UK, 2010; pp. 63–74. [Google Scholar]
- Borg, M.; Collu, M.; Kolios, A. Offshore floating vertical axis wind turbines, dynamics modelling state of the art. part ii: mooring line and structural dynamics. Renew. Sustain. Energy Rev. 2014, 39, 1226–1234. [Google Scholar] [CrossRef]
- Kolios, A.; Collu, M.; Chahardehi, A.; Brennan, F.; Patel, M.H. A multi-criteria decision making method to compare support structures for offshore wind turbines. In Proceedings of the European Wind Energy Conference, Warsaw, Poland, 20–23 April 2010.
- DNV-OS-J101, Offshore Standard. Design of offshore wind turbine structures. DET NORSKE VERITAS AS, May 2014. Available online: http://www.germanlloyd.org/pdf/DNV-OS-J101_2014-05.pdf (accessed on 7 July 2016).
- Yi, J.H.; Kim, S.-B.; Yoon, G.-L.; Andersen, L.V. Natural frequency of bottom-fixed offshore wind turbines considering pile-soil-interaction with material uncertainties and scouring depth. Wind Struct. Int. J. 2015, 21, 625–639. [Google Scholar] [CrossRef]
- Natarajan, A. An overview of the state of the art technologies for Multi-MW scale offshore wind turbines and beyond. Wiley Interdiscip. Rev. Energy Environ. 2014, 3, 111–121. [Google Scholar] [CrossRef]
- Arany, L.; Bhattacharya, S.; Macdonald, J.H.G.; Hogan, J. Closed form solution of eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and SSI. Soil Dyn. Earthq. Eng. 2016, 83, 18–32. [Google Scholar] [CrossRef]
- Kittur, J.; Vijaykumar, S.; Bellubbi, V.P.; Vishal, P. Comparison of different MCDM techniques used to evaluate optimal generation. In Proceedings of the 2015 International Conference on Applied and Theoretical Computing and Communication Technology, iCATccT 2015, Davangere, India, 29–31 October 2015.
- Mobinizadeh, M.; Raeissi, P.; Nasiripour, A.A.; Olyaeemanesh, A.; Tabibi, S.J. A model for priority setting of health technology assessment: The experience of ahp-topsis combination approach. DARU J. Pharmaceutical Sci. 2016, 24. [Google Scholar] [CrossRef] [PubMed]
- Mulliner, E.; Malys, N.; Maliene, V. Comparative analysis of MCDM methods for the assessment of sustainable housing affordability. Omega (UK) 2016, 59, 146–156. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).