Mitigation Emission Strategy Based on Resonances from a Power Inverter System in Electric Vehicles
Abstract
:1. Introduction
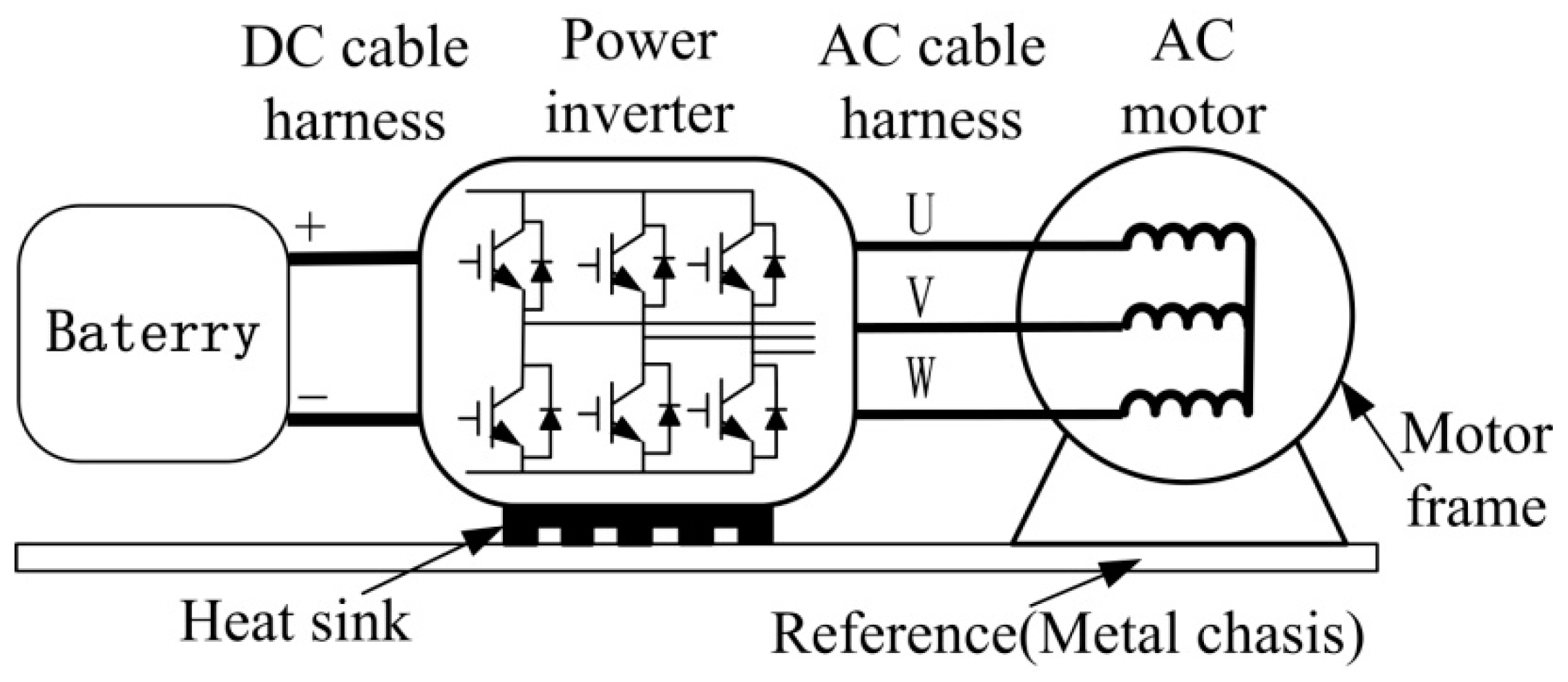
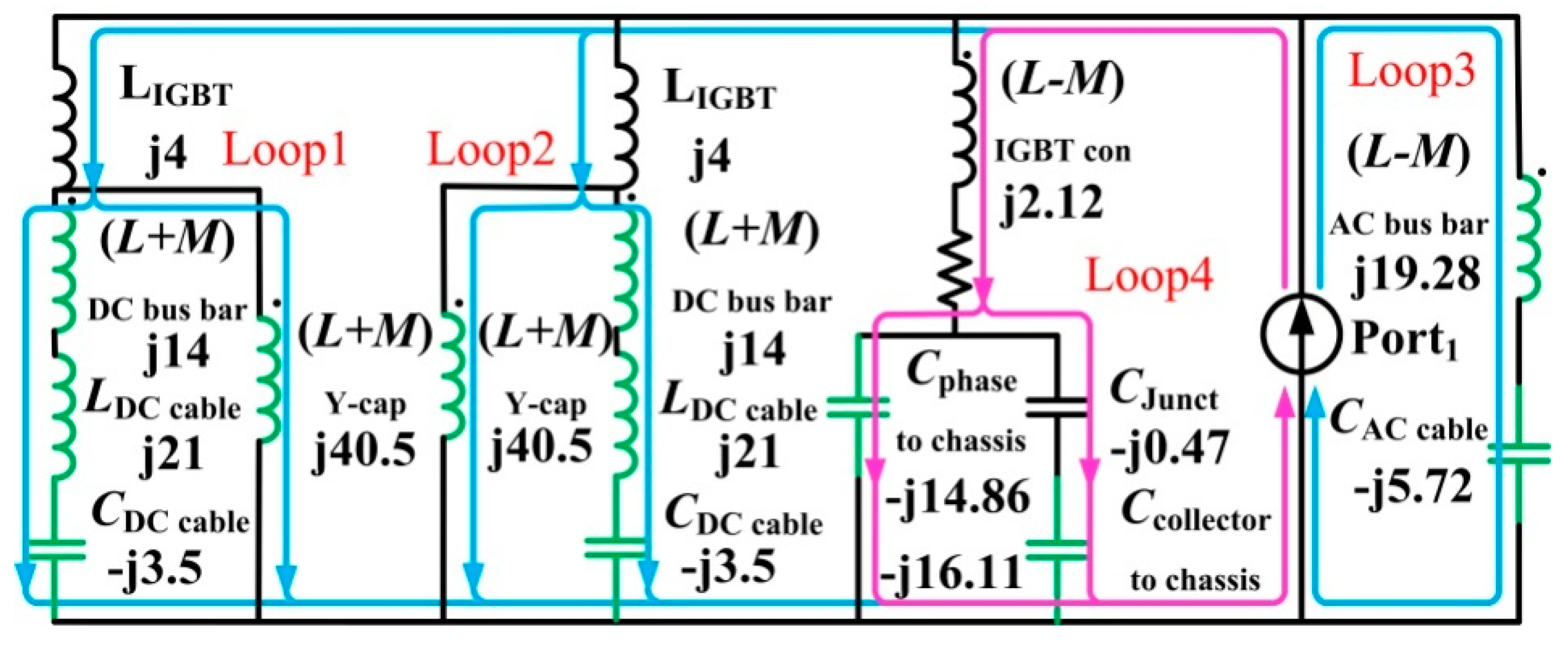
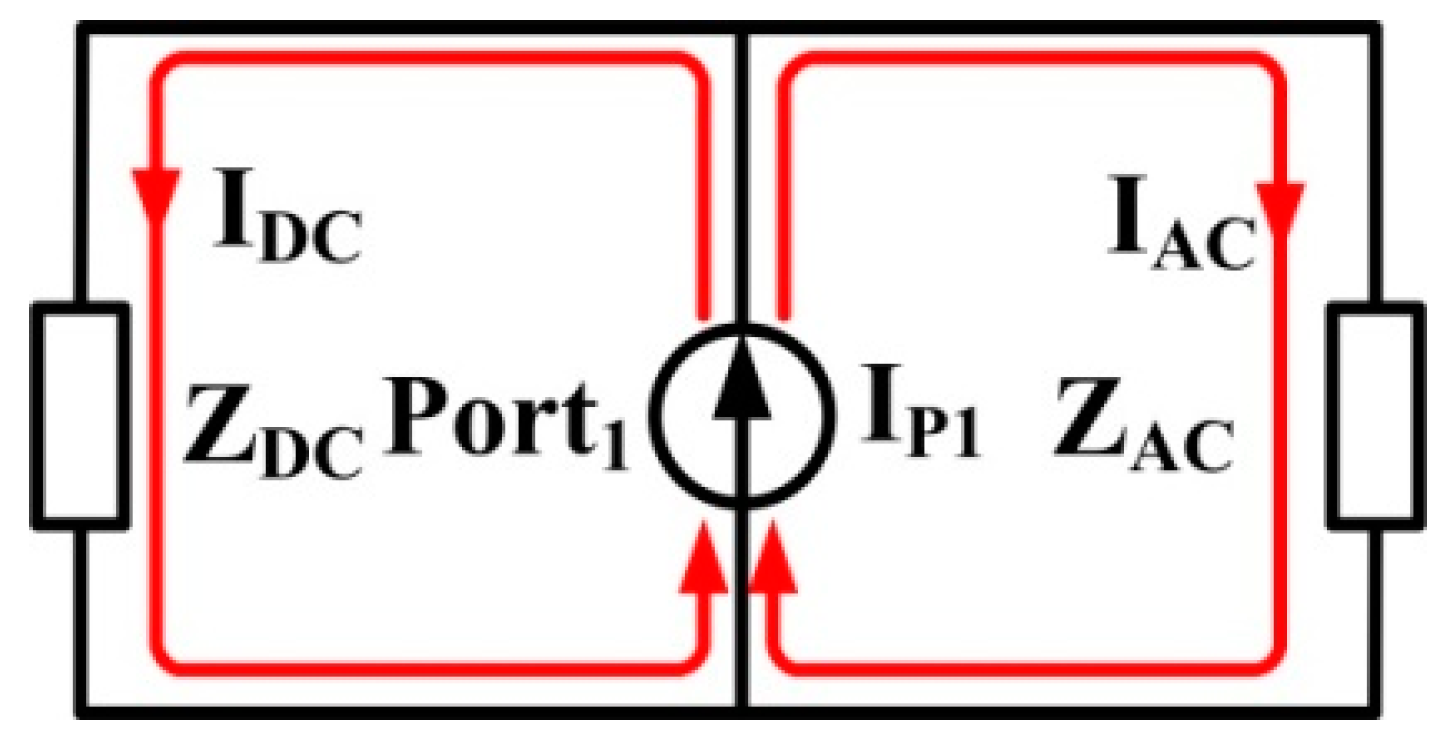
2. Construction of the Power Inverter System
3. System Modeling and Analysis
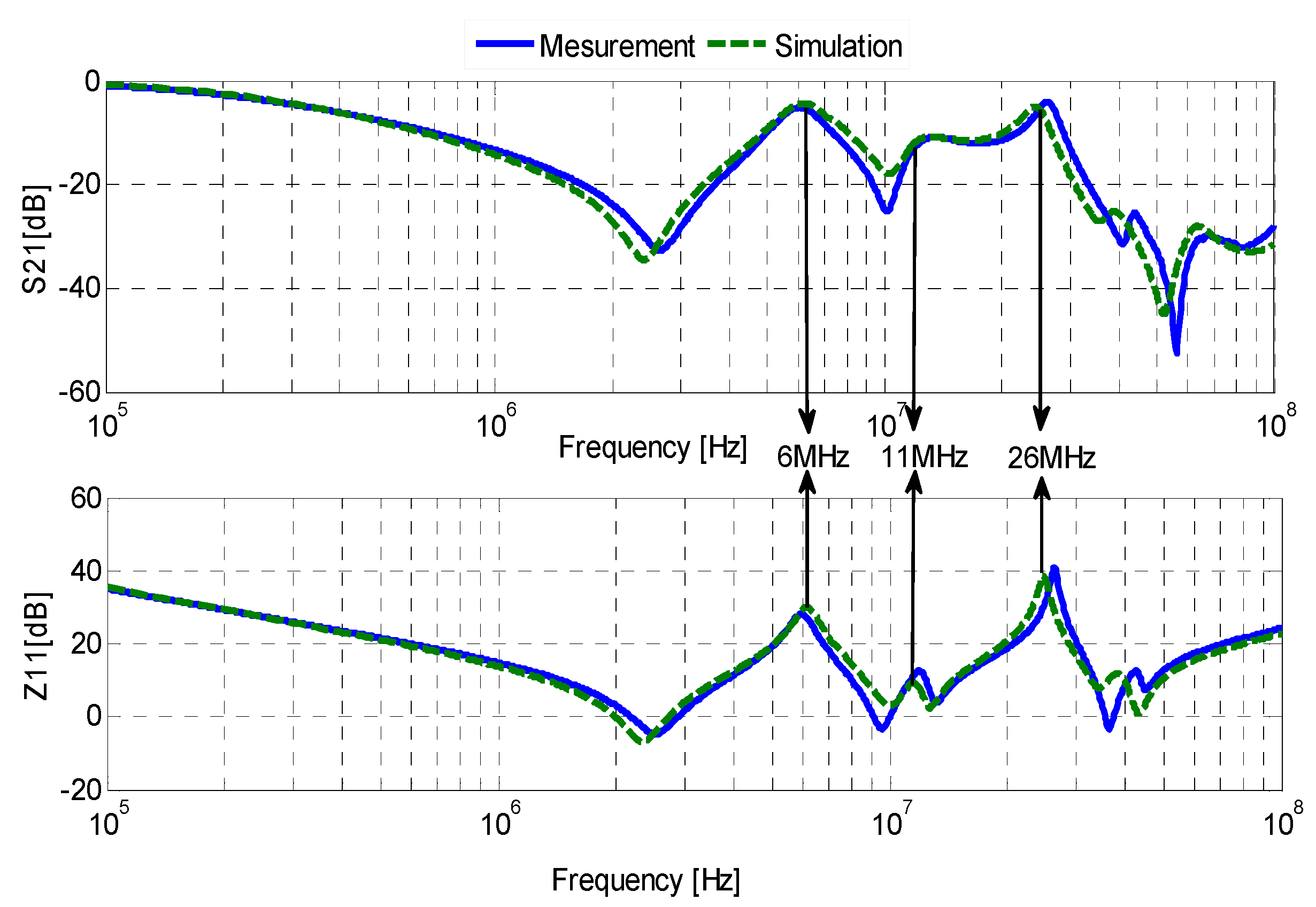
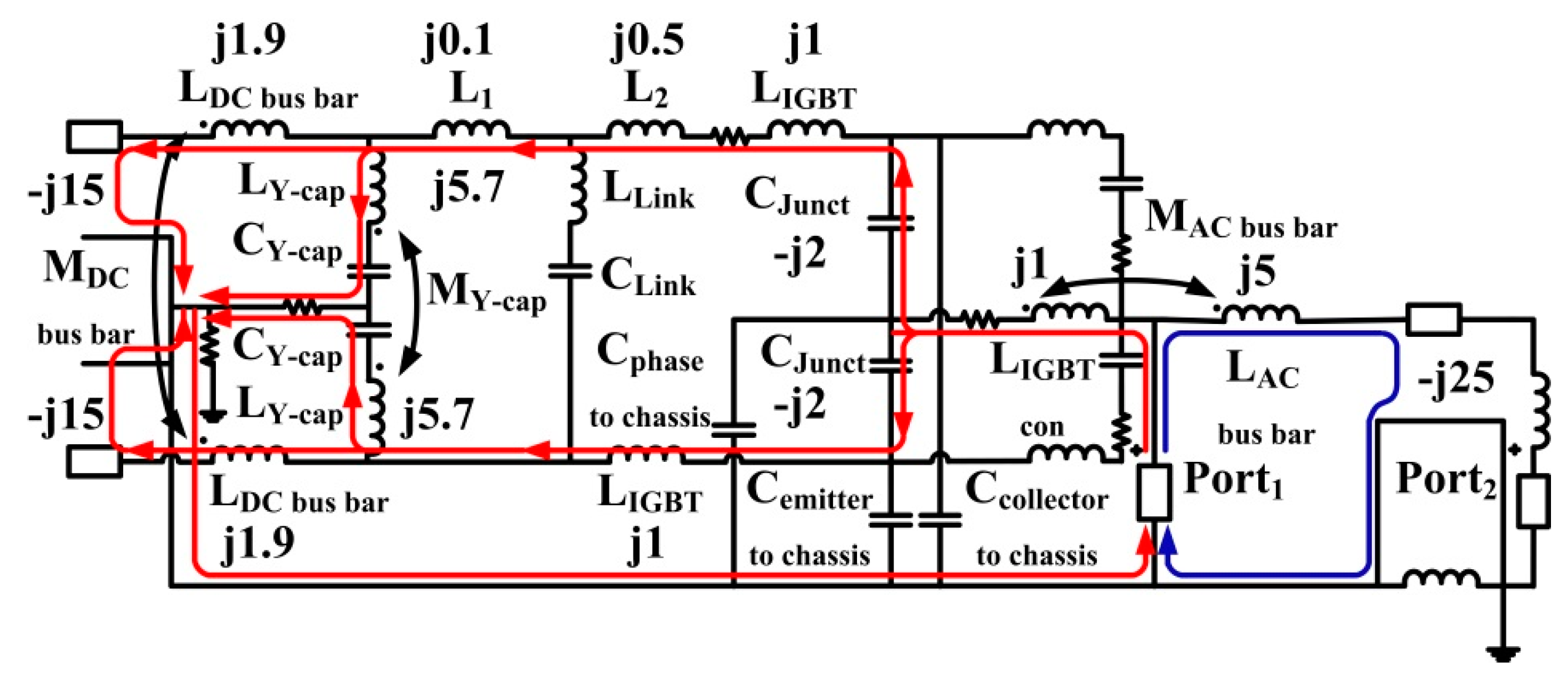
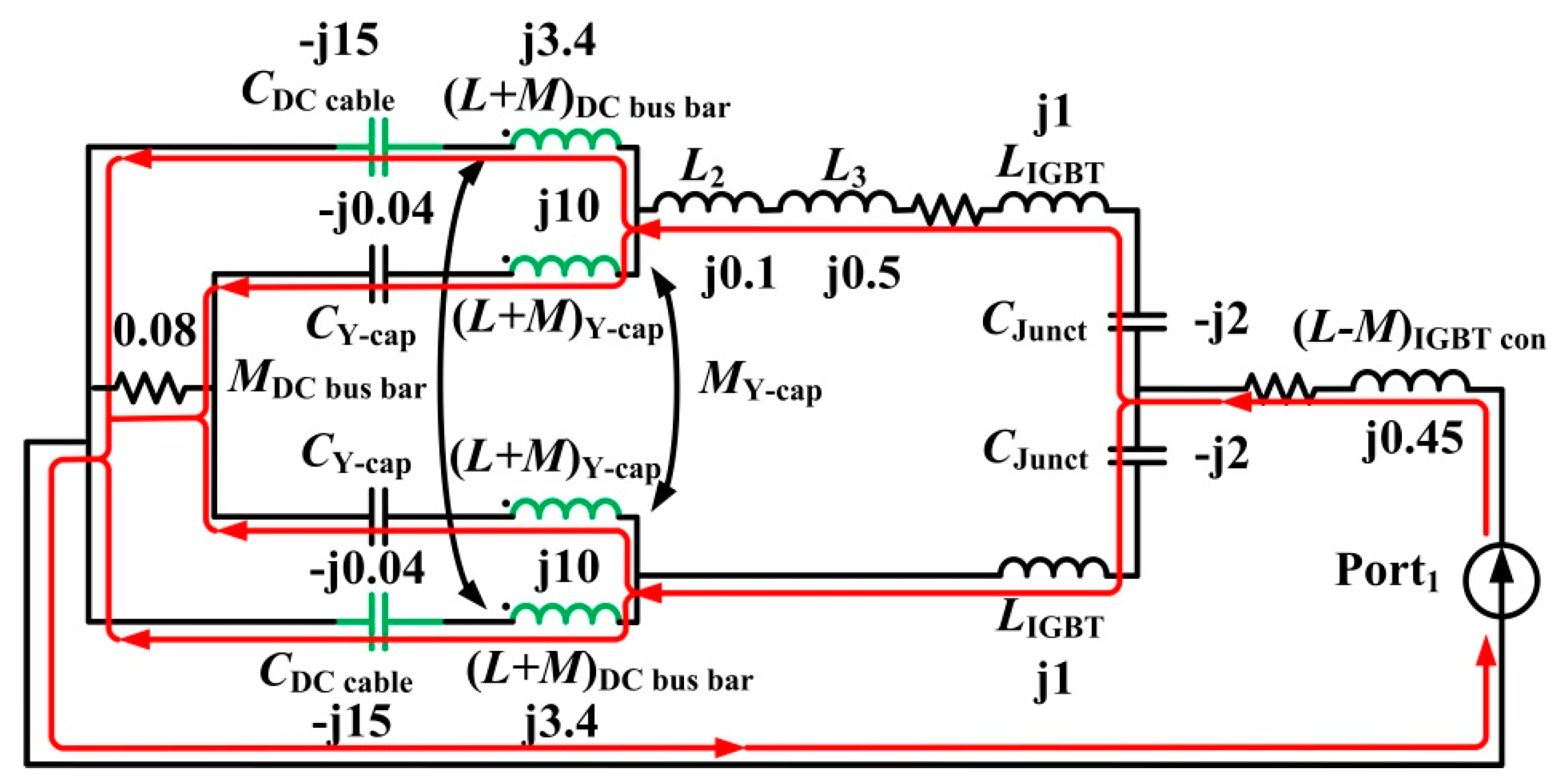
3.1. Analysis of Current Path for 6 MHz
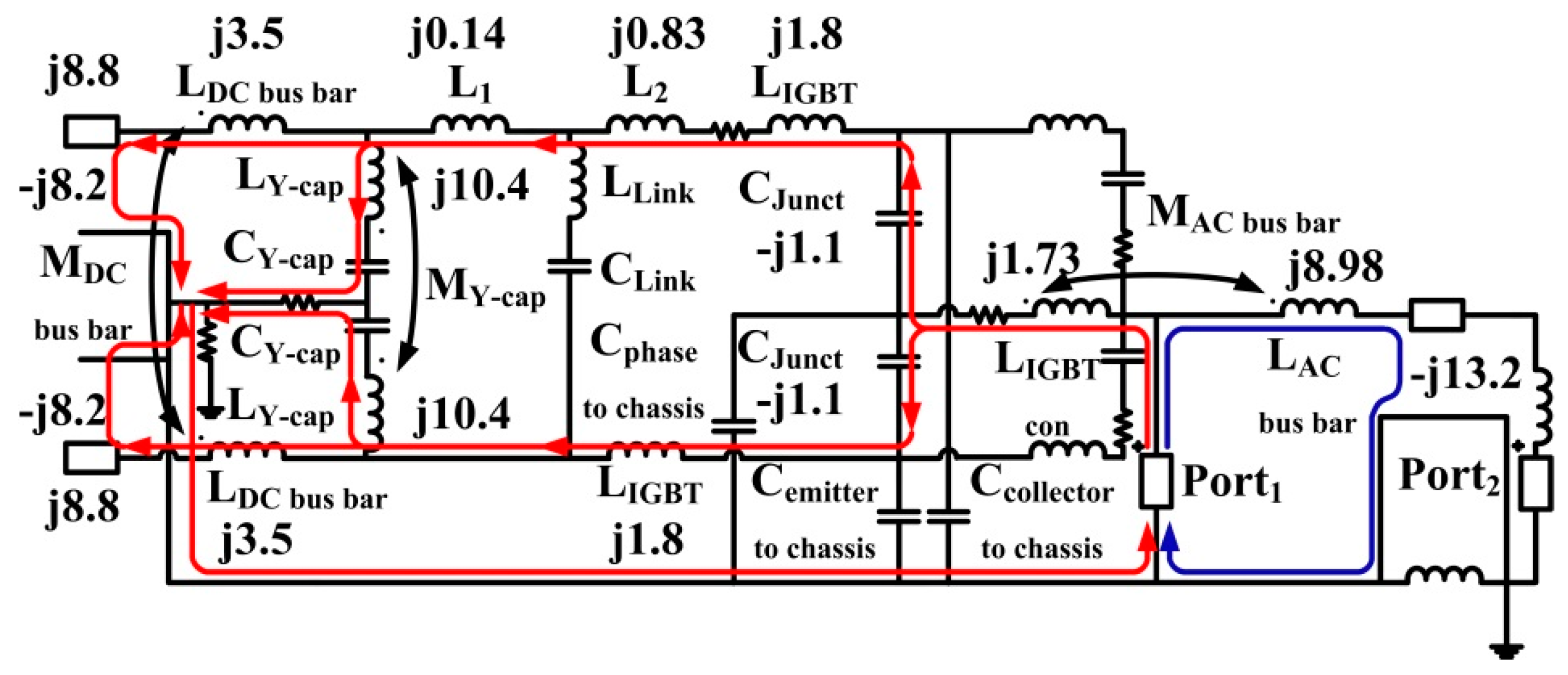
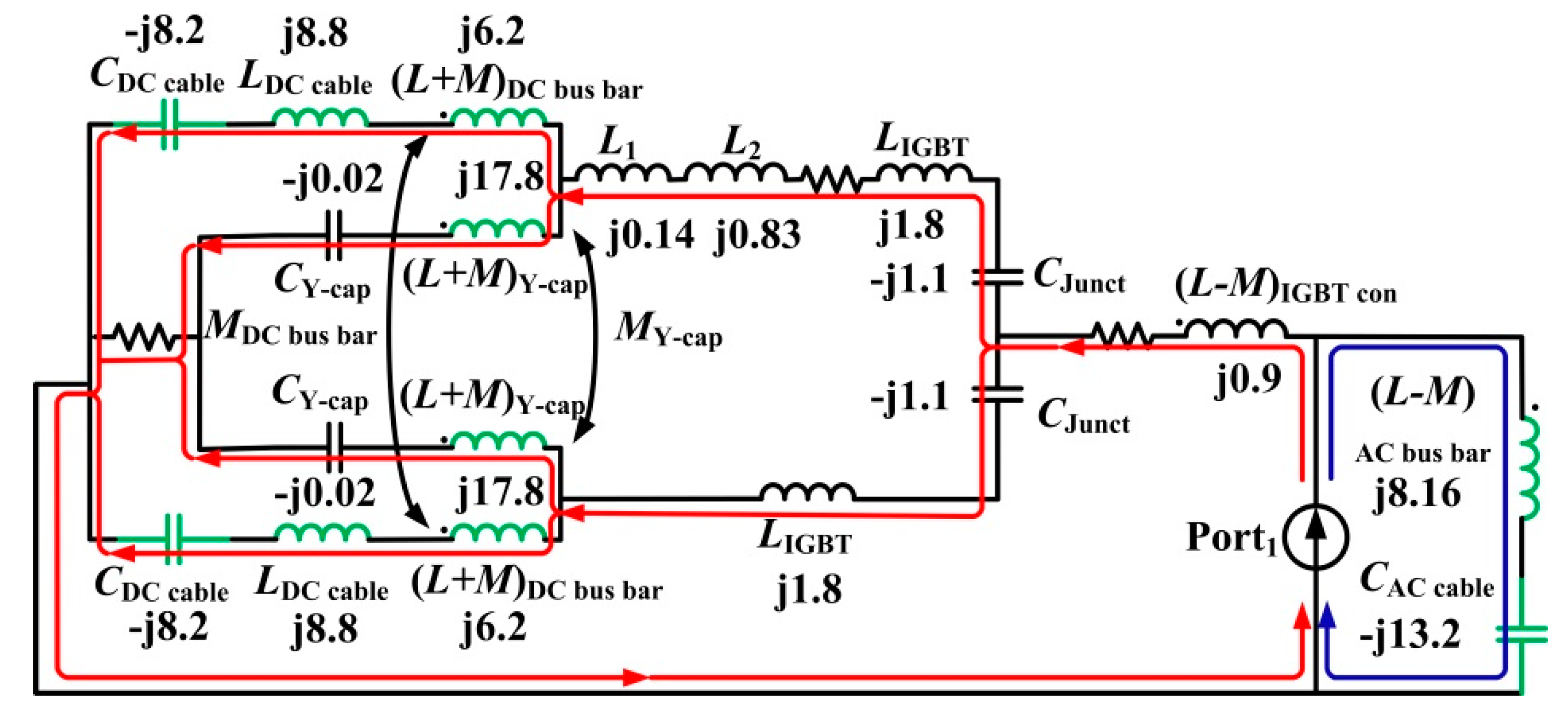
3.2. Analysis of Current Path for 11 MHz
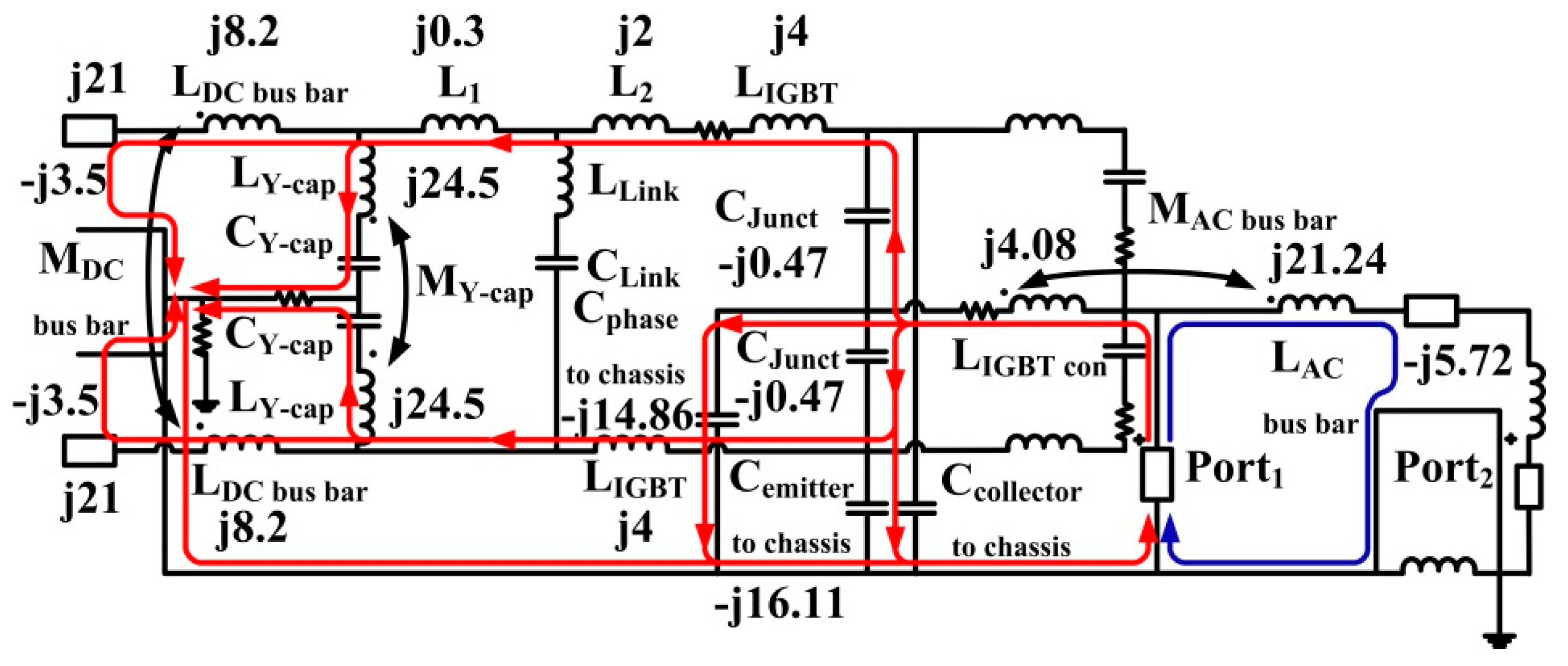
3.3. Analysis of Current Path for 26 MHz
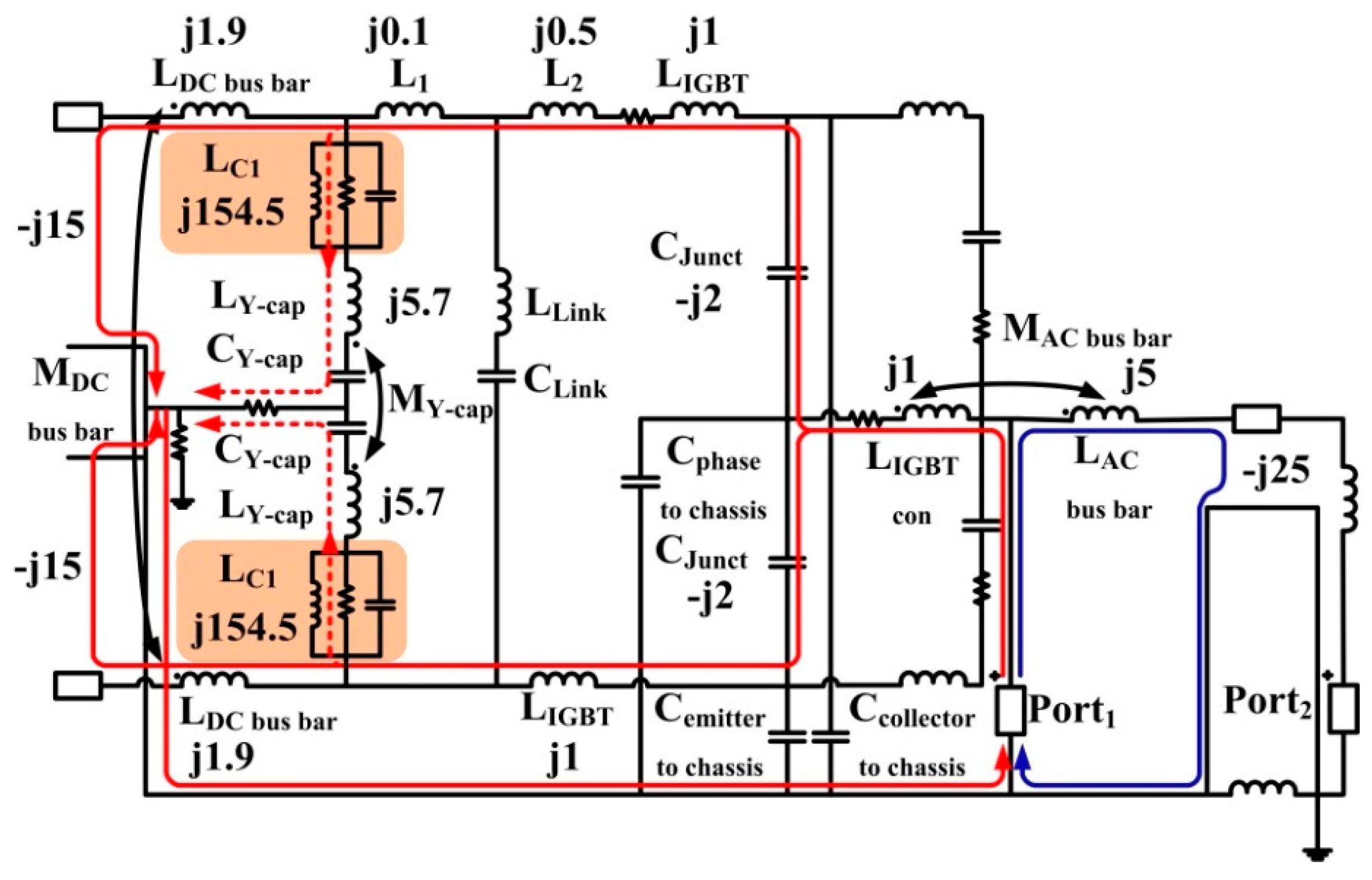
4. Mitigation of System Resonances
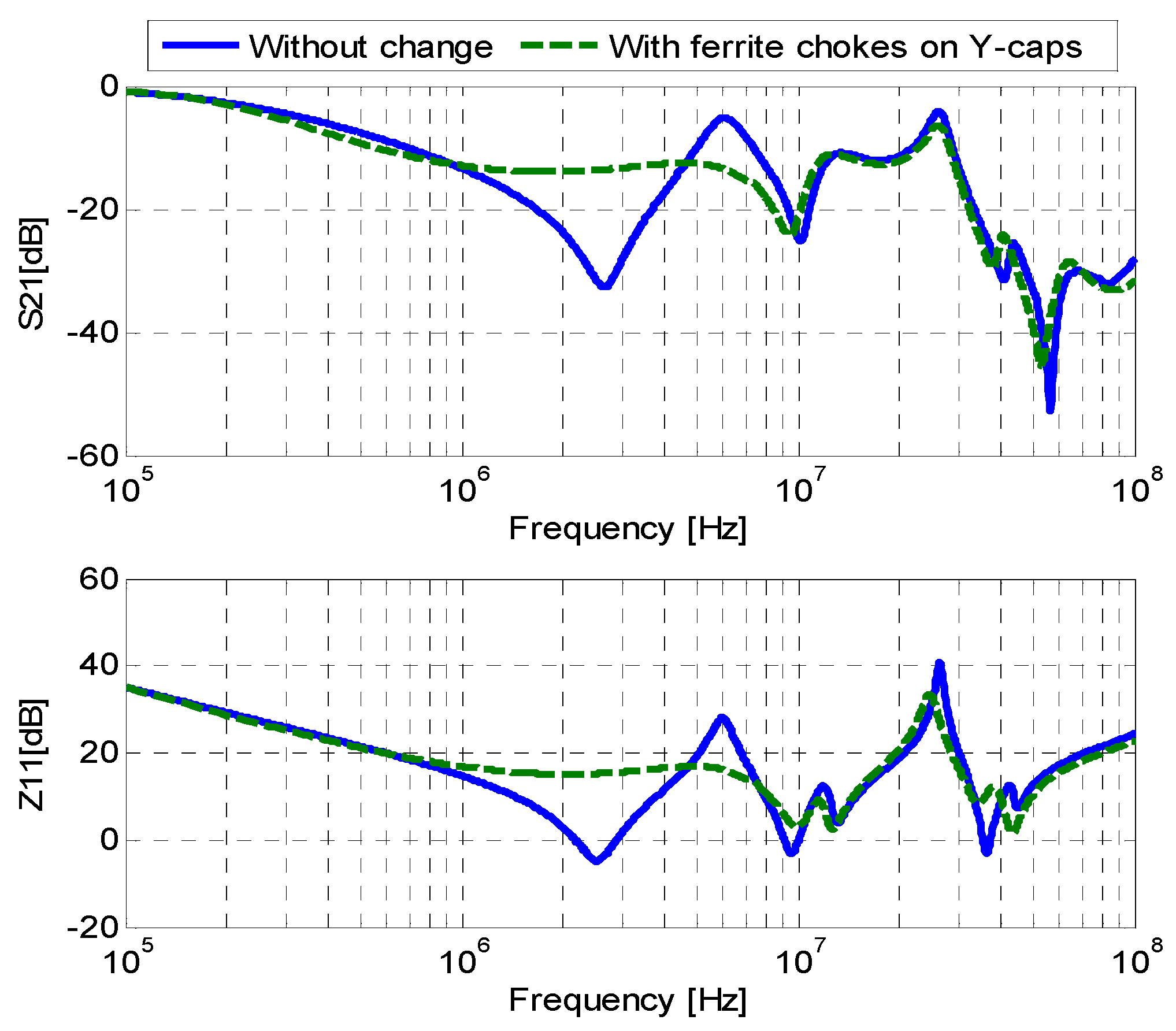
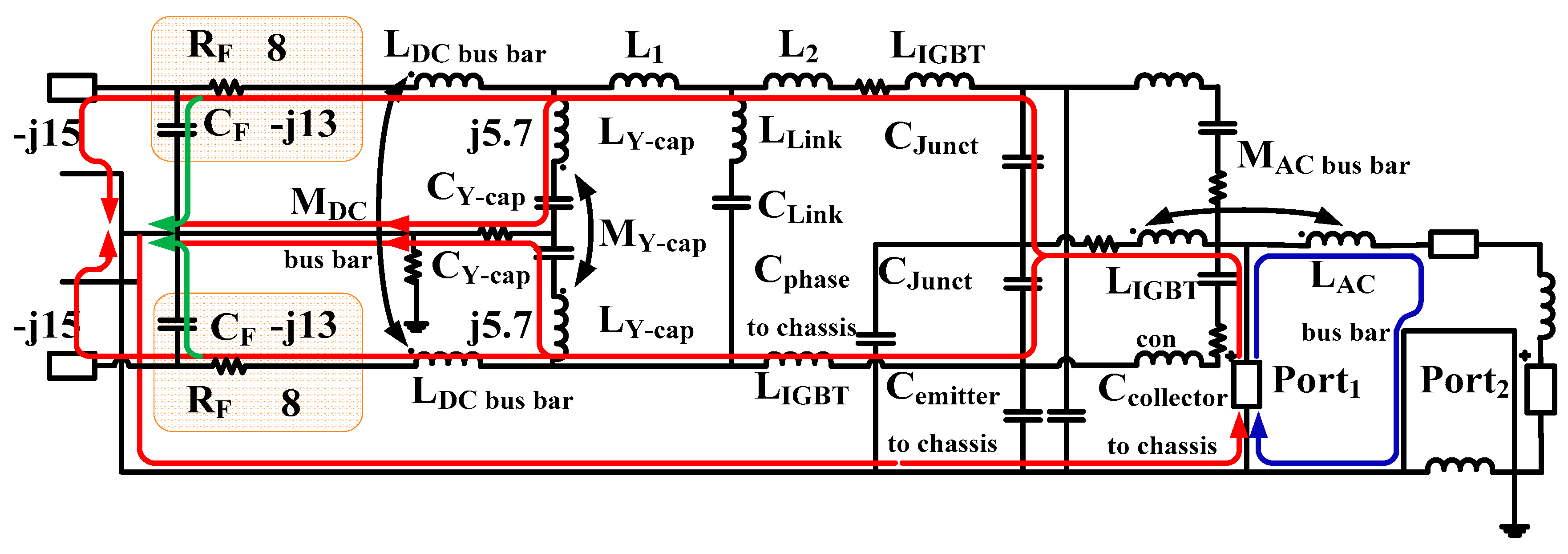
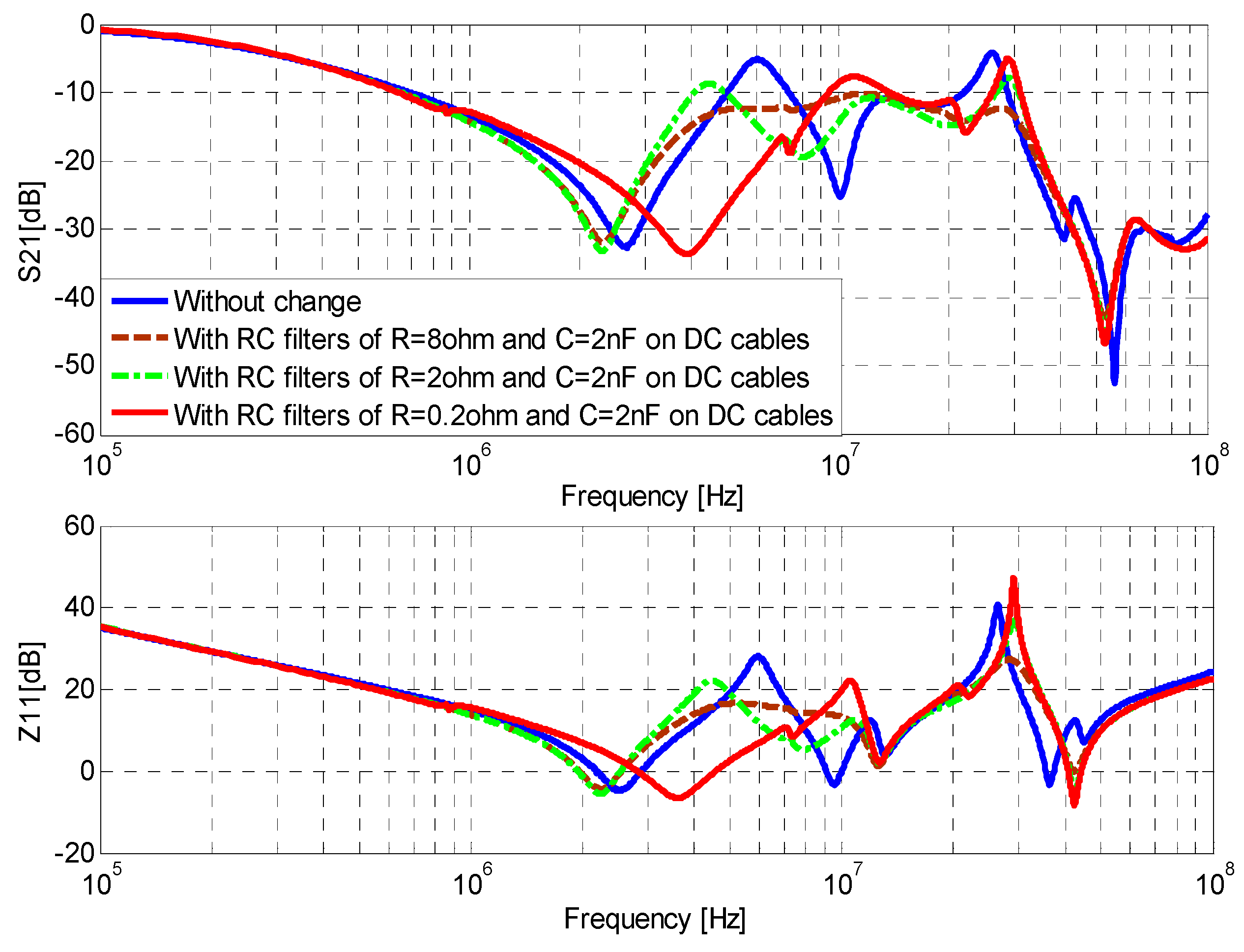
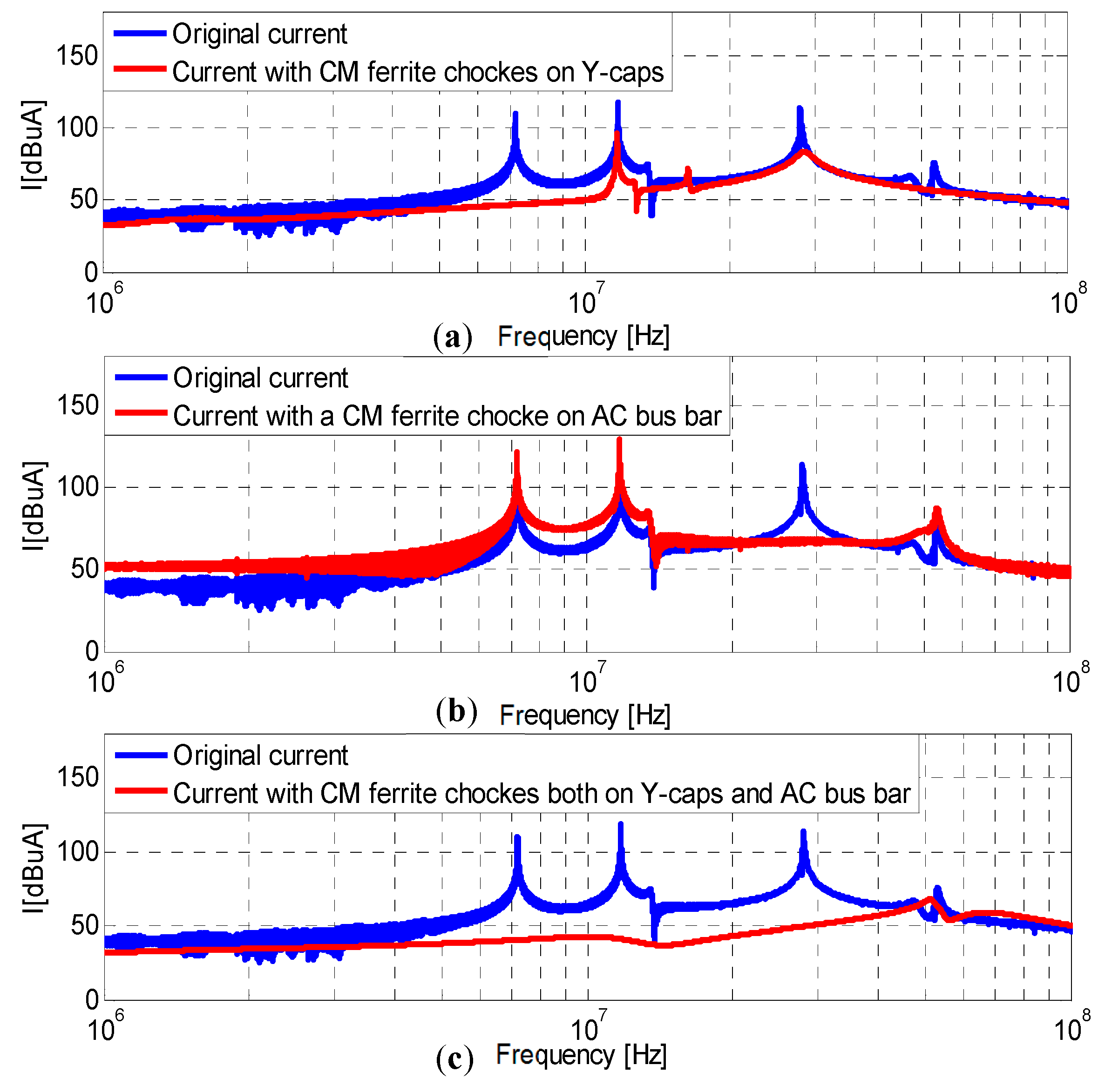
4.1. Mitigation Circuit Design at 6 MHz
4.1.1. Design of CM Ferrite Choke
4.1.2. Design of RC Filter
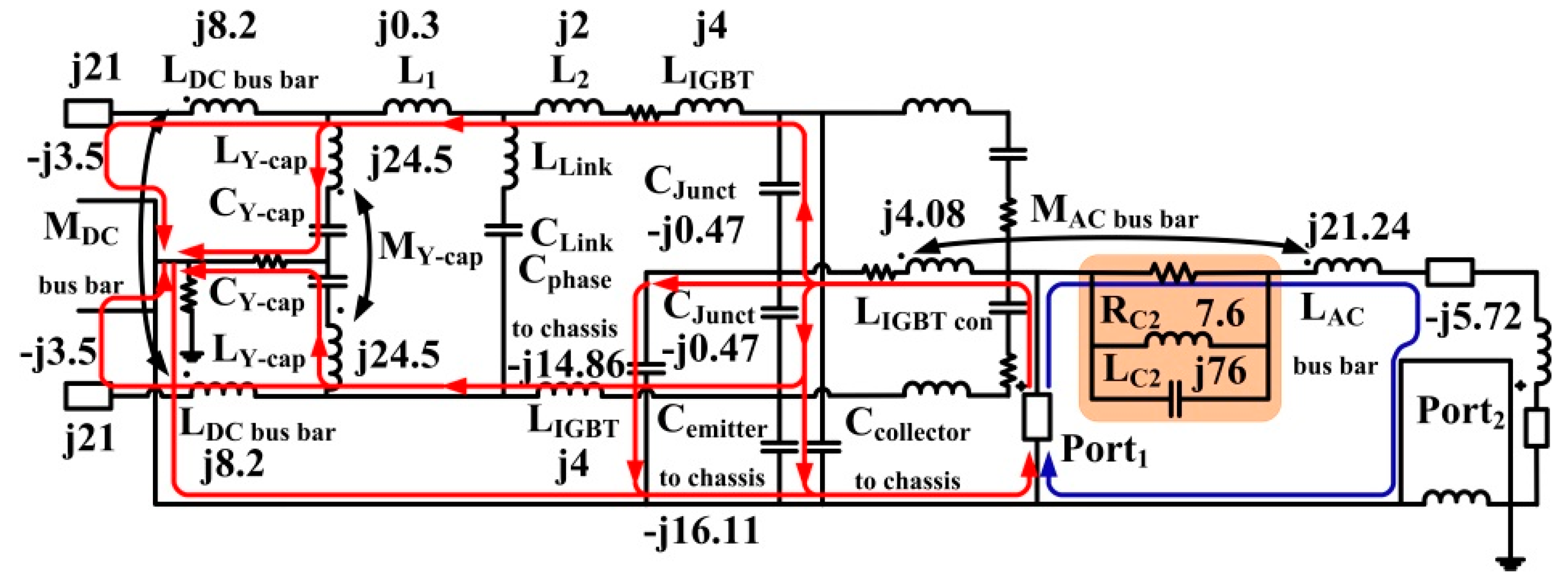
4.2. Mitigation Circuit Design at 26 MHz
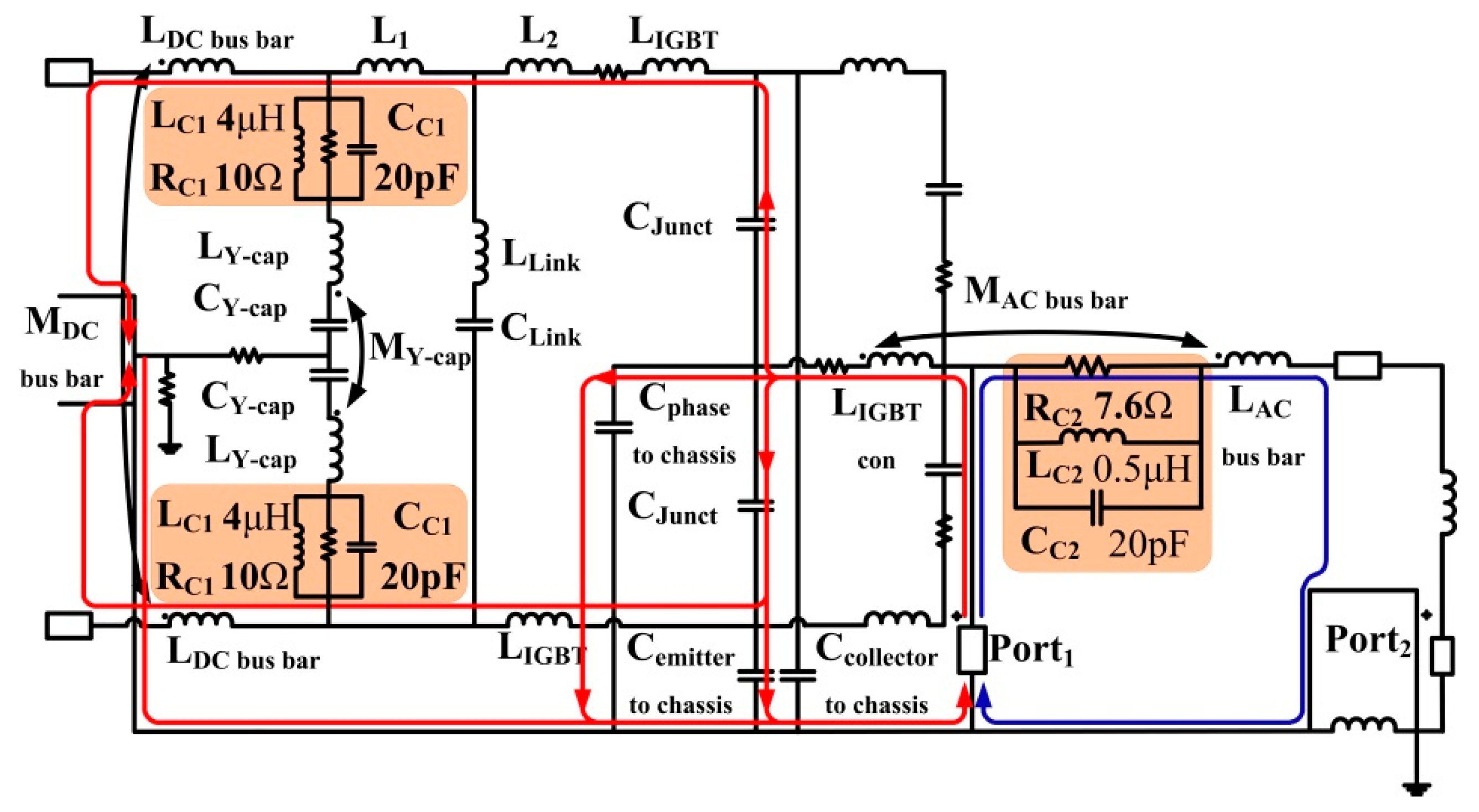
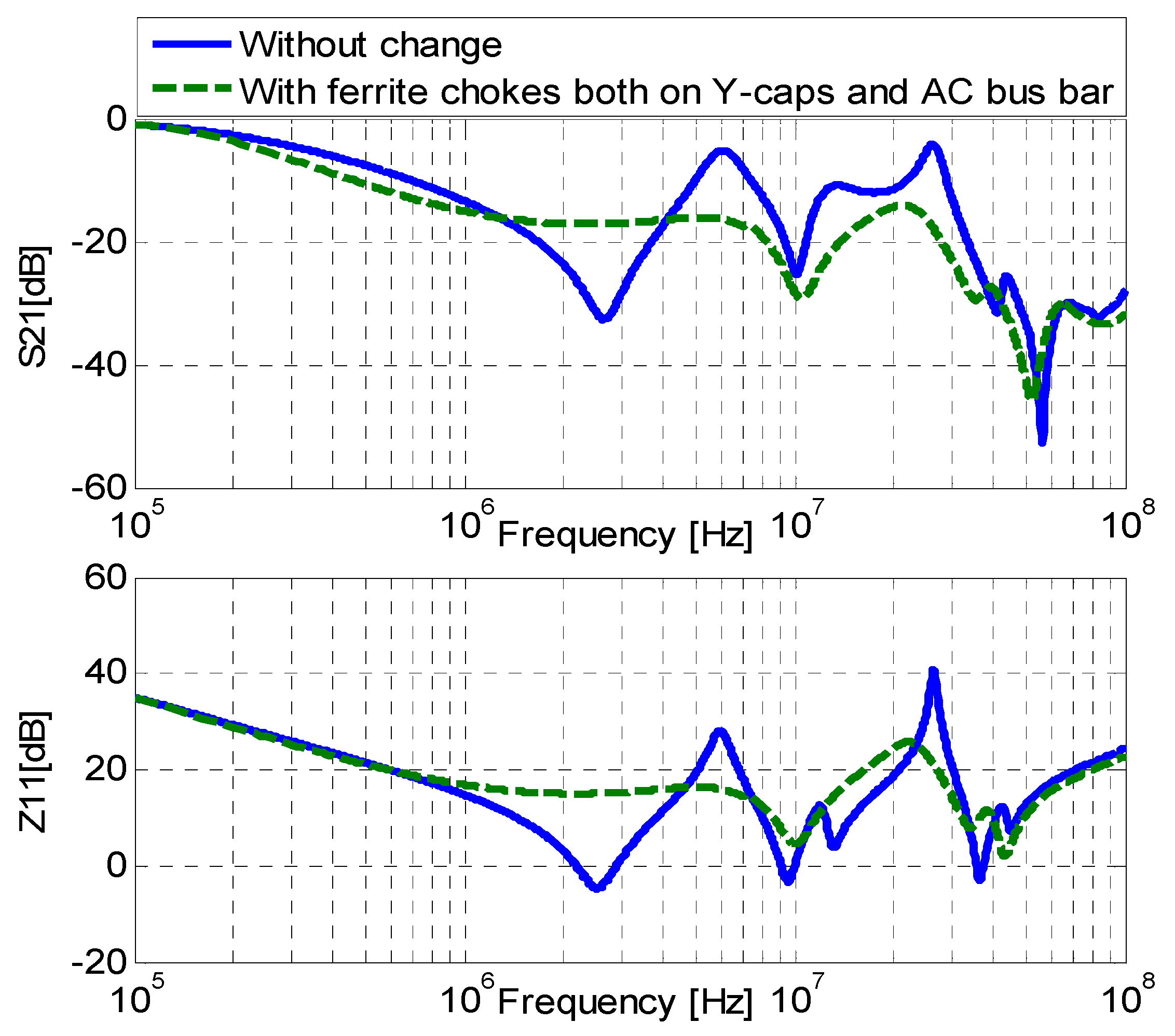
4.3. Combined Mitigation Circuit Design
5. Verification of Mitigation Method with Time Domain Simulation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ehsani, M.; Gao, Y.; Gay, S.E.; Emadi, A. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles: Fundamentals, Theory, and Design; Chemical Rubber Company (CRC) Press: New York, NY, USA, 2005. [Google Scholar]
- Zhu, H.; Lai, J.S.; Hefner, A.R., Jr.; Tang, Y.; Chen, C. Modeling-based examination of conducted EMI emissions from hard-and soft-switching PWM inverters. IEEE Trans. Ind. Appl. 2001, 37, 1383–1393. [Google Scholar]
- Chen, S.; Neh, T.W.; Lai, J.S.; Huang, X.; Pepa, E.; Doncker, R.D.; Voss, I. Towards EMI prediction of a PM motor drive for automotive applications. IEEE Appl. Power Electron. Conf. Expo. 2003, 1, 14–22. [Google Scholar]
- Ran, L.; Gokani, S.; Keith, J.C.; Bradley, J. Conducted electromagnetic emissions in induction motor drive systems Part I: Time domain analysis and identification of dominant modes. IEEE Trans. Power Electron. 1998, 13, 757–767. [Google Scholar] [CrossRef]
- Reuter, M.; Friedl, T.; Tenbohlen, S.; Köhler, W. Emulation of conducted emissions of an automotive inverter for filter development in HV networks. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility (EMC), Denver, CO, USA, 5–9 August 2013; pp. 236–241.
- Piazza, D.; Carmela, M.; Antonella, R.; Giovanni, T.; Gianpaolo, V. A model of electromagnetic radiated emissions for dual Voltage automotive electrical systems. IEEE Int. Symp. Ind. Electron. 2004, 1, 317–322. [Google Scholar]
- Nobuyoshi, M.; Mitsukatsu, O.; Kayhan, G.; Fumio, H. New methods to suppress EMI noises in motor drive systems. IEEE Trans. Ind. Electron. 2002, 49, 474–485. [Google Scholar]
- Mutoh, N.; Ogata, M. New methods to control EMI noises generated in motor drive systems. IEEE Trans. Ind. Appl. 2004, 40, 143–152. [Google Scholar] [CrossRef]
- Akagi, H.; Tamura, S. A passive EMI filter for eliminating both bearing current and ground leakage current from an inverter-driven motor. IEEE Trans. Power Electron. 2006, 21, 1459–1469. [Google Scholar] [CrossRef]
- Akagi, H.; Doumoto, T. A passive EMI filter for preventing high-frequency leakage current from flowing through the grounded inverter heat sink of an adjustable-speed motor drive system. IEEE Trans. Ind. Appl. 2005, 41, 1215–1223. [Google Scholar] [CrossRef]
- Akagi, H.; Shimizu, T. Attenuation of conducted EMI emissions from an inverter-driven motor. IEEE Trans. Power Electron. 2008, 23, 282–290. [Google Scholar]
- Wang, S.; Maillet, Y.Y.; Wang, F.; Lai, R.; Luo, F.; Boroyevich, D. Parasitic effects of grounding paths on common-mode EMI filter’s performance in power electronics systems. IEEE Trans. Ind. Electron. 2010, 57, 3050–3059. [Google Scholar] [CrossRef]
- Bishnoi, H.; Baisden, A.C.; Mattavelli, P.; Boroyevich, D. Analysis of EMI terminal modeling of switched power converters. IEEE Trans. Power Electron. 2012, 27, 3924–3933. [Google Scholar] [CrossRef]
- Gong, X.; Josifovic, I.; Ferreira, J.A. Comprehensive CM filter design to suppress conducted EMI for SiC-JFET motor drives. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 720–727.
- Lai, J.; Huang, X.; Chen, S.; Nehl, T.W. EMI characterization and simulation with parasitic models for a low-Voltage high-current AC motor drive. IEEE Trans. Ind. Appl. 2004, 40, 178–185. [Google Scholar] [CrossRef]
- Jettanasen, C.; Ngaopitakkul, A. Minimization of common-mode conducted noise in PWM inverter-fed AC motor drive systems using optimized passive EMI filter. Lect. Notes Eng. Comput. Sci. 2010, 2181, 1249–1252. [Google Scholar]
- ReVol, B.; Roudet, J.; Schanen, J.; Loizelet, P. EMI study of three-phase inverter-fed motor drives. IEEE Trans. Ind. Appl. 2011, 47, 223–231. [Google Scholar] [CrossRef]
- Espina, J.; Balcells, J.; Arias, A.; Ortega, C. Common mode EMI model for a direct matrix converter. IEEE Trans. Ind. Electron. 2011, 58, 5049–5056. [Google Scholar] [CrossRef]
- Lai, J.-S.; Huang, X.; Pepa, E.; Chen, S.; Nehl, T.W. Inverter EMI modeling and simulation methodologies. IEEE Trans. Ind. Electron. 2006, 53, 736–744. [Google Scholar]
- Toure, B.; Schanen, J.; Gerbaud, L.; Meynard, T.; Carayon, J. EMC modeling of drives for aircraft applications: Modeling process, EMI filter optimization and technological choice. IEEE Trans. Power Electron. 2013, 28, 1145–1156. [Google Scholar] [CrossRef]
- Ardon, V.; Aime, J.; Chadebec, O.; Clavel, E.; Guichon, J.; Vialardi, E. EMC modeling of an industrial variable speed drive with an adapted PEEC method. IEEE Trans. Magn. 2010, 46, 2892–2898. [Google Scholar] [CrossRef]
- Jettanasen, C.; Costa, F.; Vollaire, C. Common-mode emissions measurements and simulation in variable-speed drive systems. IEEE Trans. Power Electron. 2009, 24, 2456–2464. [Google Scholar] [CrossRef]
- Bondarenko, N.; Zhai, L.; Xu, B.; Li, G.; Makharashvili, T.; Loken, D.; Berger, P.; Doren, T.P.V.; Beetner, D.G. A measurement-based model of the electromagnetic emissions from a power inverter. IEEE Trans. Power Electron. 2015, 30, 5522–5531. [Google Scholar] [CrossRef]
- Abdolreza, E.; Fazel, T. Suppressing of common-mode voltage, shaft voltage, leakage current and EMI generated by voltage source PWM inverter. Int. Electr. Eng. J. (IEEJ) 2011, 1, 529–535. [Google Scholar]
- Mo, Y. EMC Characteristics and Model of Power Battery in Electric Vehicle. Master’s Thesis, Chongqing University, Chongqing, China, 2014. [Google Scholar]
- Stevanovic, I.; Skibin, S.; Masti, M.; Laitinen, M. Behavioral Modeling of Chokes for EMI Simulations in Power Electronics r. IEEE Trans. Power Electron. 2013, 28, 695–705. [Google Scholar] [CrossRef]

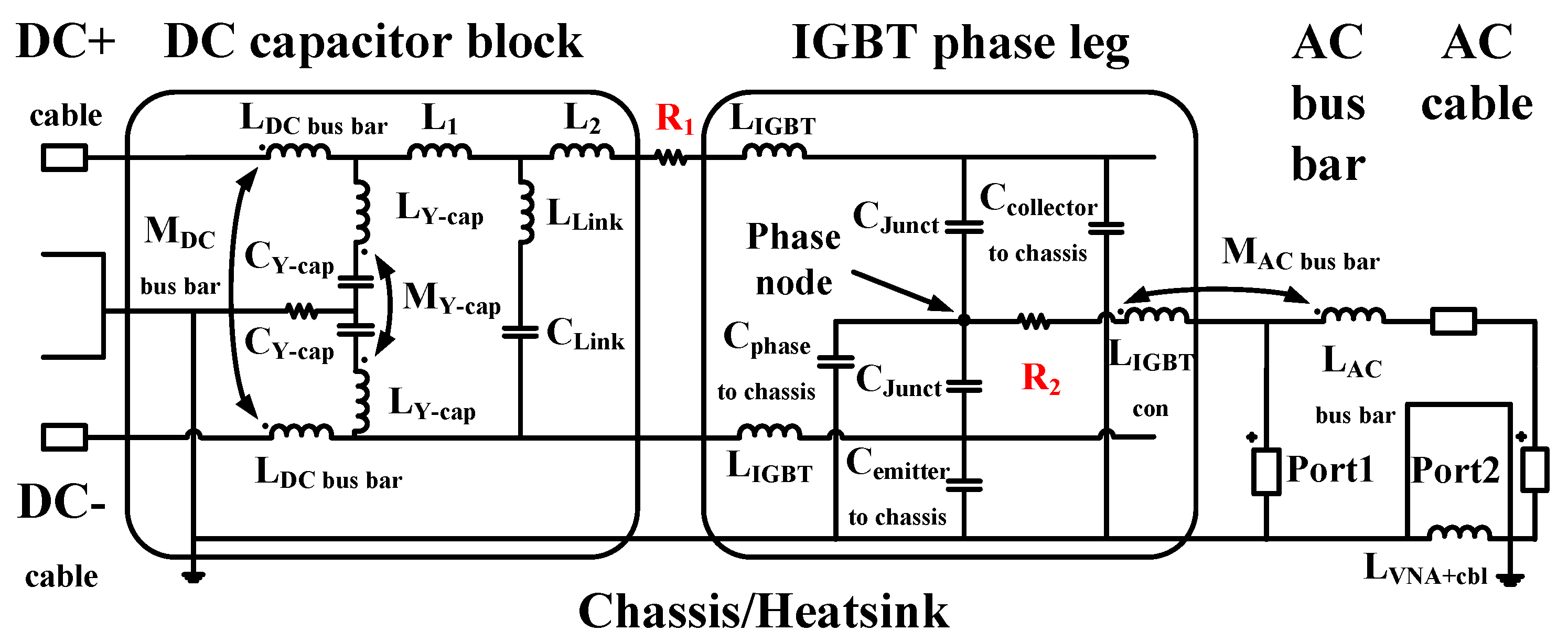

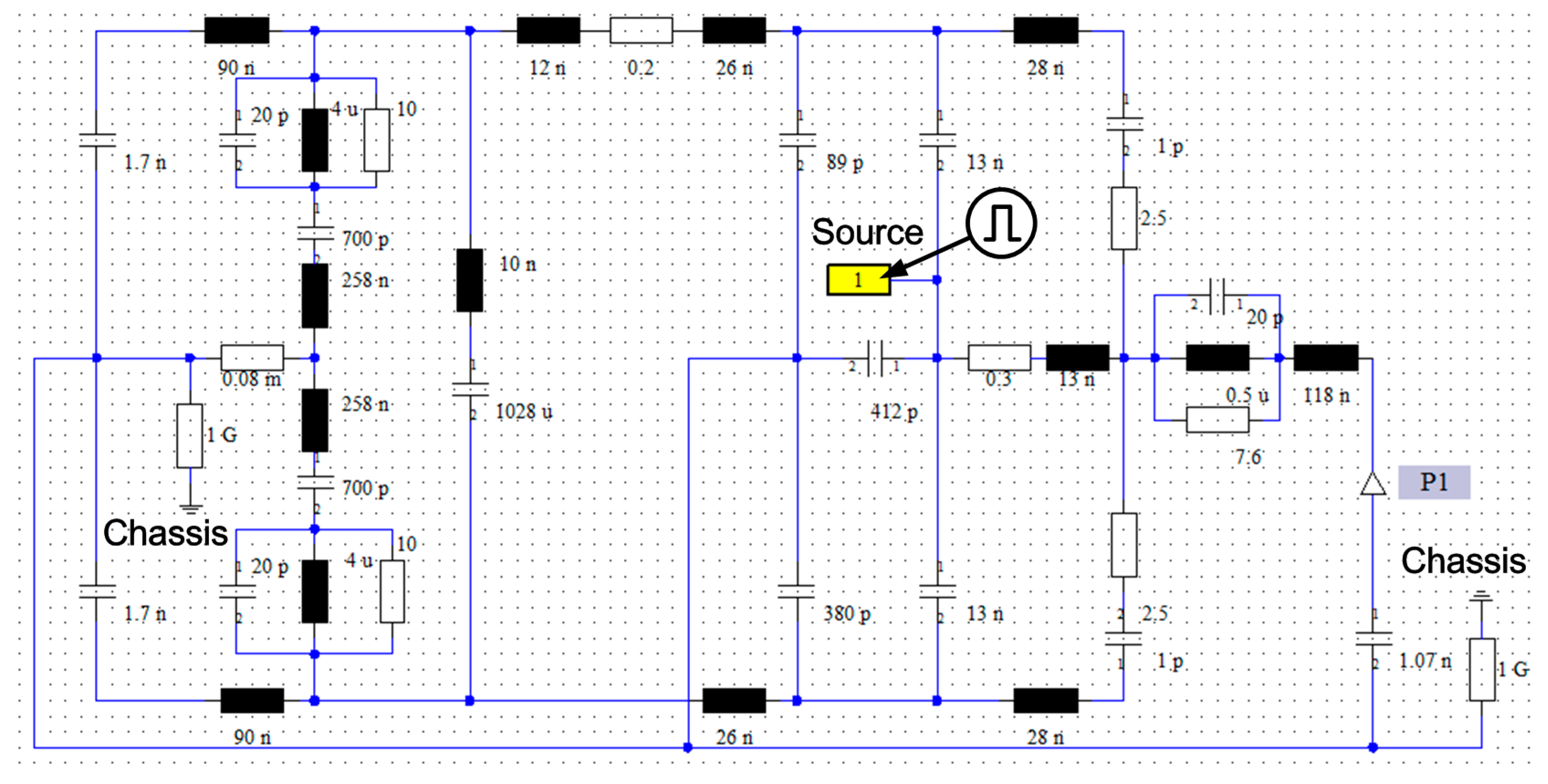
| Elements | Meaning | Value |
|---|---|---|
| Inductance of the DC bus bar | 50 nH | |
| Mutual inductance between the two DC bus bars | 40 nH | |
| Capacitance of the Y capacitor (Y-cap) | 700 nF | |
| Parasitic inductance of the Y-cap | 150 nH | |
| Mutual inductance between the two Y-caps | 108 nH | |
| Inductance between the Y-cap and the DC link capacitor | 12 nH | |
| Inductance between the DC link capacitor and the IGBT | 2 nH | |
| R1 | Conductive resistance of the IGBT | 0.2 Ω |
| Capacitance of the DC link capacitor | 1028 μF | |
| Parasitic inductance of the DC link capacitor | 10 nH | |
| Lead inductance of the IGBT | 26 nH | |
| Capacitance between the IGBT phase node and the chassis | 412 pF | |
| Capacitance between the emitter and the collector of the IGBT | 13 nF | |
| Capacitance between the collector of the IGBT and the chassis | 89 pF | |
| Capacitance between the emitter of the IGBT and the chassis | 280 pF | |
| R2 | Resistance between the IGBT phase node and the AC bus bar | 0.3 Ω |
| Inductance between the IGBT phase node and the AC bus bar | 25 nH | |
| Inductance of AC bus bar | 130 nH | |
| Mutual inductance between the two AC bus bars | 12 nH |
| Frequency | Responsible Elements |
|---|---|
| 6 MHz resonance | Capacitances of the DC cables, inductances of the two DC bus bars and inductances of the two Y-caps |
| 11 MHz resonance | Capacitances of the DC cables, inductances of the DC bus bar, inductances of the two Y-caps, inductances of the AC bus bar and capacitances of the AC cable |
| 26 MHz resonance | Capacitances of the DC cables, inductances of the two DC bus bar, inductances of the two Y-caps, capacitance between the IGBT phase node and the chassis, capacitance between the emitter of the IGBT and the chassis, capacitances of the AC cable and inductances of the AC bus bar |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, L.; Zhang, X.; Bondarenko, N.; Loken, D.; Van Doren, T.P.; Beetner, D.G. Mitigation Emission Strategy Based on Resonances from a Power Inverter System in Electric Vehicles. Energies 2016, 9, 419. https://doi.org/10.3390/en9060419
Zhai L, Zhang X, Bondarenko N, Loken D, Van Doren TP, Beetner DG. Mitigation Emission Strategy Based on Resonances from a Power Inverter System in Electric Vehicles. Energies. 2016; 9(6):419. https://doi.org/10.3390/en9060419
Chicago/Turabian StyleZhai, Li, Xinyu Zhang, Natalia Bondarenko, David Loken, Thomas P. Van Doren, and Daryl G. Beetner. 2016. "Mitigation Emission Strategy Based on Resonances from a Power Inverter System in Electric Vehicles" Energies 9, no. 6: 419. https://doi.org/10.3390/en9060419
APA StyleZhai, L., Zhang, X., Bondarenko, N., Loken, D., Van Doren, T. P., & Beetner, D. G. (2016). Mitigation Emission Strategy Based on Resonances from a Power Inverter System in Electric Vehicles. Energies, 9(6), 419. https://doi.org/10.3390/en9060419






