1. Introduction
Academic research and applications of lithium-ion batteries have seen a growth in interest during the past decade [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. This is mainly due to the increased use of applications ranging from small to high energy and power demanding systems [
4], stationary applications encompassing grid energy storage, uninterruptible power supply and renewable power management systems [
20]. The automotive industry is investing in the research and development of electric vehicles (EV) based on new batteries and driveline technologies to transition their market from fully internal combustion engine (ICE) to a more environmental and efficient fleet of hybrid electric vehicles (HEVs), plug-in electric vehicles (PEVs) which encompass extended range electric vehicles (EREV), plug-in hybrid electric vehicles (PHEVs) and battery electric vehicles (BEVs) [
1,
2,
3,
21,
22,
23]. The development of EREV and PHEV electric applications has led to vastly different required battery properties regrading both the power and energy needed in these type of vehicles, compared to conventional HEVs and pure BEVs. The development of lithium-ion batteries to fulfil these demanding properties and in this way enable these type of vehicles has been a great achievement.
Thus, to understand and to control the behavior of the battery in terms of its chemical, electrical and thermal aspects during the different operational conditions is of high importance. Moreover equivalent circuit model (ECM) models not only are needed to manage the cells inside a battery pack with the battery management system (BMS), but also for the development and creation of efficient and proper battery packs [
24,
25,
26]. The jump from an individual cell to a battery pack needs proper development and correct power, energy and heat management design and operation [
24].
In this paper, an initial overview of the different lithium-ion battery models found in the literature is presented. The cell chemistry under investigation is a pouch nickel manganese cobalt (NMC) 20 Ah lithium ion with a nominal voltage 3.65 V as seen in
Table 1. The manufacturer of these cells is EIG (Cheonan, South Korea) and all the characteristics mentioned in
Table 1 are taken from the datasheet of the C020 model, available on the company website [
27].
The analysis starts by providing a concise state-of-the-art of lithium ion battery models. A categorization of these models is proposed and further information regarding electrical models is presented. The analysis continues with a summary of the different tasks and activities performed before the creation of electrical models. A review of the various parameters used for the creation of the ECM models is included continuing with the overview of the different electrical models based on ECM topologies of the NMC chemistry at different temperatures conditions and validation profiles. The models developed have been created with two types of state of charge (SoC) estimation techniques, Coulomb counting and extended Kalman filtering.
2. Overview of the State of the Art of Lithium Ion Models
Investigating the scientific literature regarding the modelling of lithium-ion batteries behavior, it is found that different models have been already created and used for the different interdisciplinary sciences based on battery system operation. The different types of existing models can be separated mainly by the different issues and phenomena the model should investigate. In
Table 2 the different model types have been separated into:
When modelling the behavior of a physical system, it is possible to identify three main general model categories. Depending on the method how the inputs are related to the outputs of the model they can be categorized in: empirical, physical and semi-empirical models [
29].
Empirical models are based on the “black-box” approach, where the inner physical behavior of the system is unknown and the relations between the inputs and outputs of the model are only based on experimental results and relations.
An example of the empirical models is the neural network model, which can capture the dynamic behavior of the battery and learn the relationship between the inputs to the outputs only through experimental data found prior to the creation of the model. Another example of empirical modelling of batteries is the analytical model called Peukert’s model which can simulate the time needed to discharge the battery and to investigate the discharge rate capability of a battery. The main constants of the mathematical equation governing the Peukert’s model have to be defined with the use of experimental activities [
30,
31].
Physical models are based solely on theoretical and physical knowledge of the system under investigation. No experimental activities regarding the relation between the inputs and outputs of the system have to be performed in order to determine the behavior of your system. Depending on the knowledge of the specific inner characteristics and physical process of the system a model can be created to simulate the performance of your system. An example of a physical model of a lithium-ion battery is the pure electrochemical model [
32,
33,
34]. Depending on the knowledge of the specific material composition and the properties of the chemical reactions, a set of physical equations were originally developed [
35,
36]. The fact that the model equations are based on physical relations, which describe real physical effects taking place in the battery, includes the pure electrochemical model in the category of physical modelling.
Finally, semi-empirical models lay between the physical and the empirical models. This category is a hybrid modelling category. The system under investigation is to a certain extent treated as a black-box where the relation of the inputs to your outputs and inner behavior of the system is investigated through experimental methods, as performed for empirical modelling. The difference being that, a link with some of the real physical effects inside the system can be implemented in the model. Examples of semi-empirical models are ECMs (e.g., dual polarization, partnership for a new generation of vehicles (PNGV)) that can be linked to in this case to the polarization effect and the different behavior during charging and discharging processes [
9,
14,
19,
28,
37,
38]. The models implemented to simulate the NMC cells for this publication belong to the semi-empirical model category. These kind of models are mainly created for the beginning of life (BoL) of cells were ageing phenomena have not yet affected the creation of the model parameters. When including in these type of models ageing phenomena to be echoed in the parameters created from the characterization tests the development of more advanced models is performed, thus diverging from the definition of semi-empirical models.
2.1. Battery Management System
Electric applications using a battery as their primary energy (
i.e., a BEV) and a power source (
i.e., HEV), will be typically accompanied by a BMS. This is mostly implemented in vehicle applications where the need to manage the battery performance, control internal parameters of the battery and inform the user of vital battery information is needed. The accurate prediction of SoC, state of heath and other characteristics (temperature, voltage, and current) are the main needed information to be calculated by a BMS. In addition, the proper management of the charging and discharging behavior of the battery by the BMS, will help to maintain for a longer period the rated capacity of the battery and increase its lifetime. This will keep the battery in good operating and stable conditions for a longer period. Thus, it is very important for the BMS software to be based on a battery model, which can calculate efficiently and accurate the battery states and characteristics and can run with low computational power and time [
39].
2.2. Electrical Models
Models that describe the electrical behavior of the battery have been extensively studied and developed in academia [
19,
40,
41,
42,
43,
44,
45]. There exist multiple models that can be used to describe the electrical response of the battery and in this study those have been categorized as follows:
Analytical models;
Electrical ECM models;
Frequency domain models.
Electrical models are mainly semi-empirical models where characterization techniques are performed to identify the different parameters of the battery. Those characterization techniques have been extensively described in different standardization documents [
44,
45,
46,
47,
48,
49] and they are generally composed of:
Capacity test: defining the discharge/charge capacity of the battery;
Open circuit voltage (OCV) versus SoC test: relating the SoC levels with the open circuit voltage of the battery;
Hybrid pulse power characterization (HPPC) test: to define the internal resistances and SoC of the battery;
Electrochemical impedance spectroscopy (EIS) test: define the internal resistance and impedance of the battery.
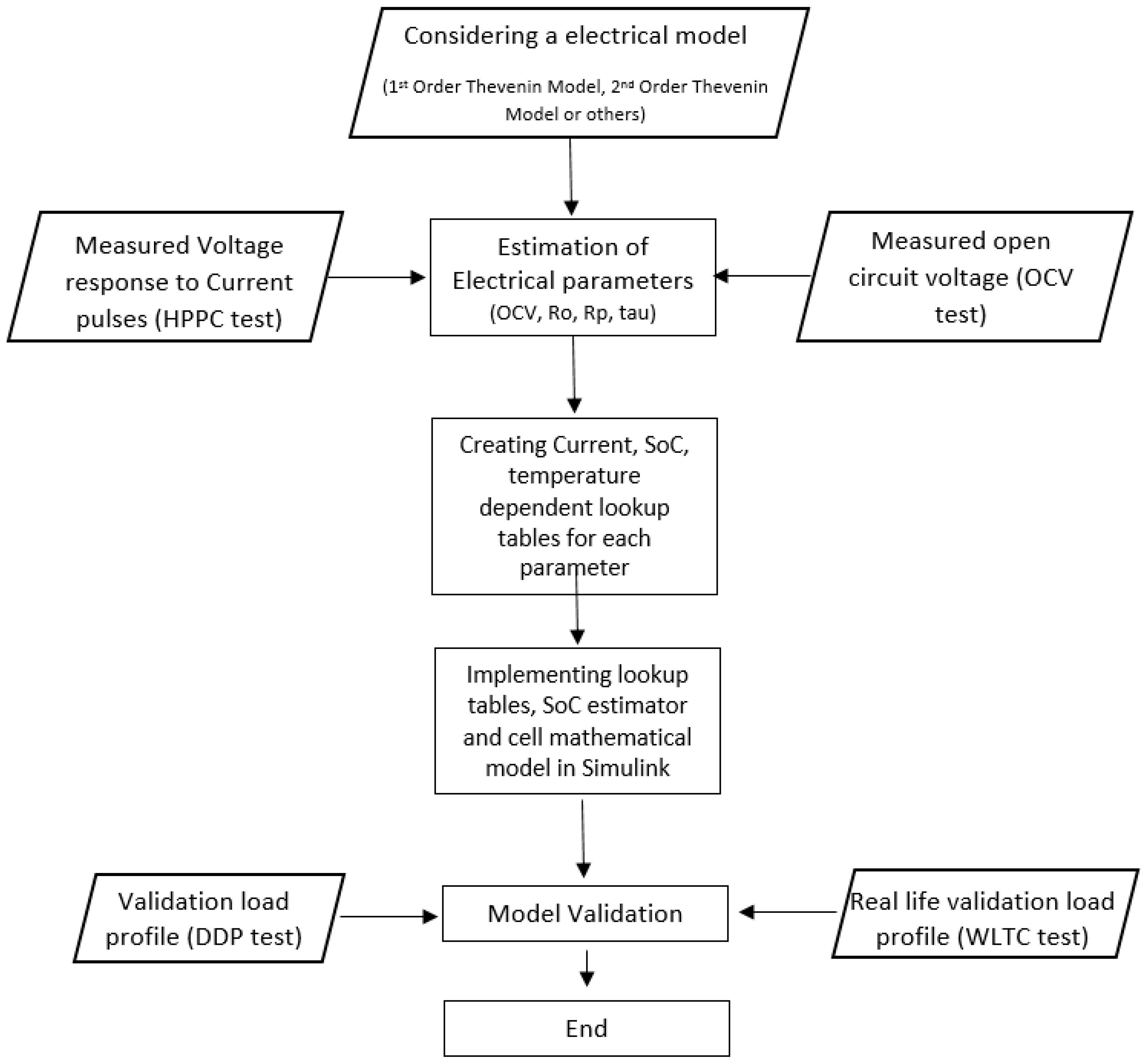
2.3. Creation of an Electrical Equivalent Circuit Model
In
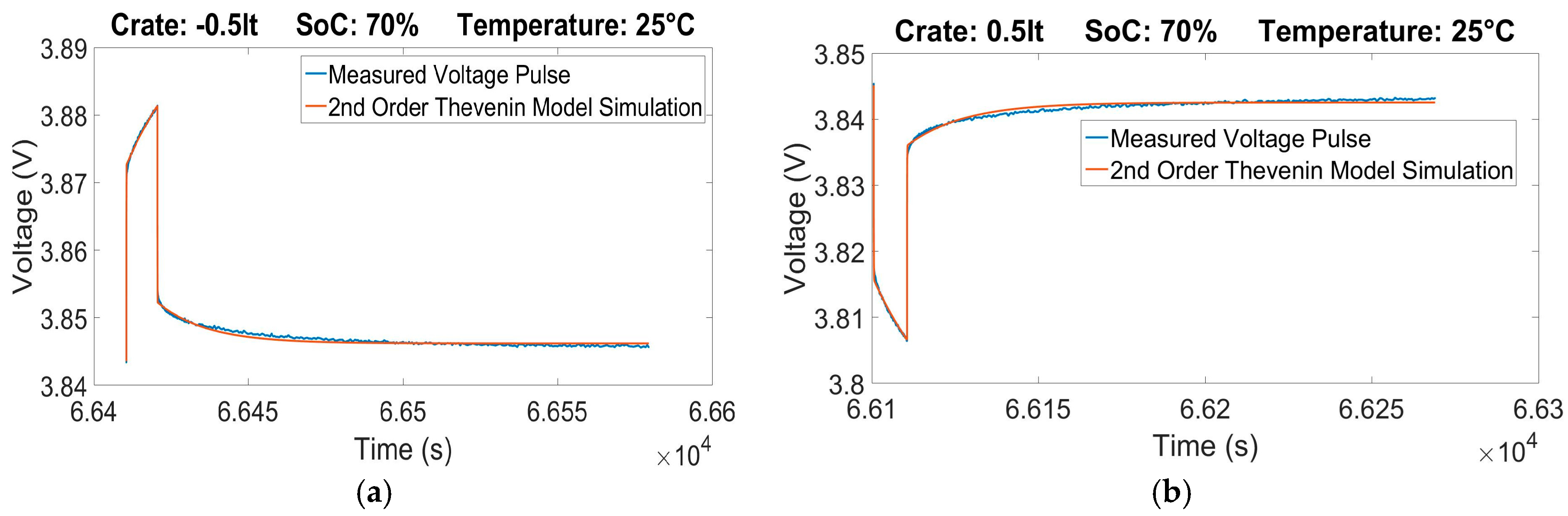
Figure 1, a schematic representation is presented showing the different theoretical steps that have to be taken to achieve a complete development of a model and validate it afterwards. Initially, the choice of the electrical model to use should be considered carefully. Depending on the model chosen, the creation of appropriate parameters have to be developed to represent the different components of the ECM model. These parameters would be collected and re-arranged in the appropriate format to create a lookup table, which would be in function of current, SoC, temperature and lifetime. Implementing correctly the variables inside the model would provide the required information to the model to simulate the behavior of the studied lithium ion cells. Based on these parameters a preliminary simulation can be performed taking as validation profile the different pulses performed during the HPPC test. This preliminary analysis can be observed for the 0.5 C pulse at the 70% SoC level in
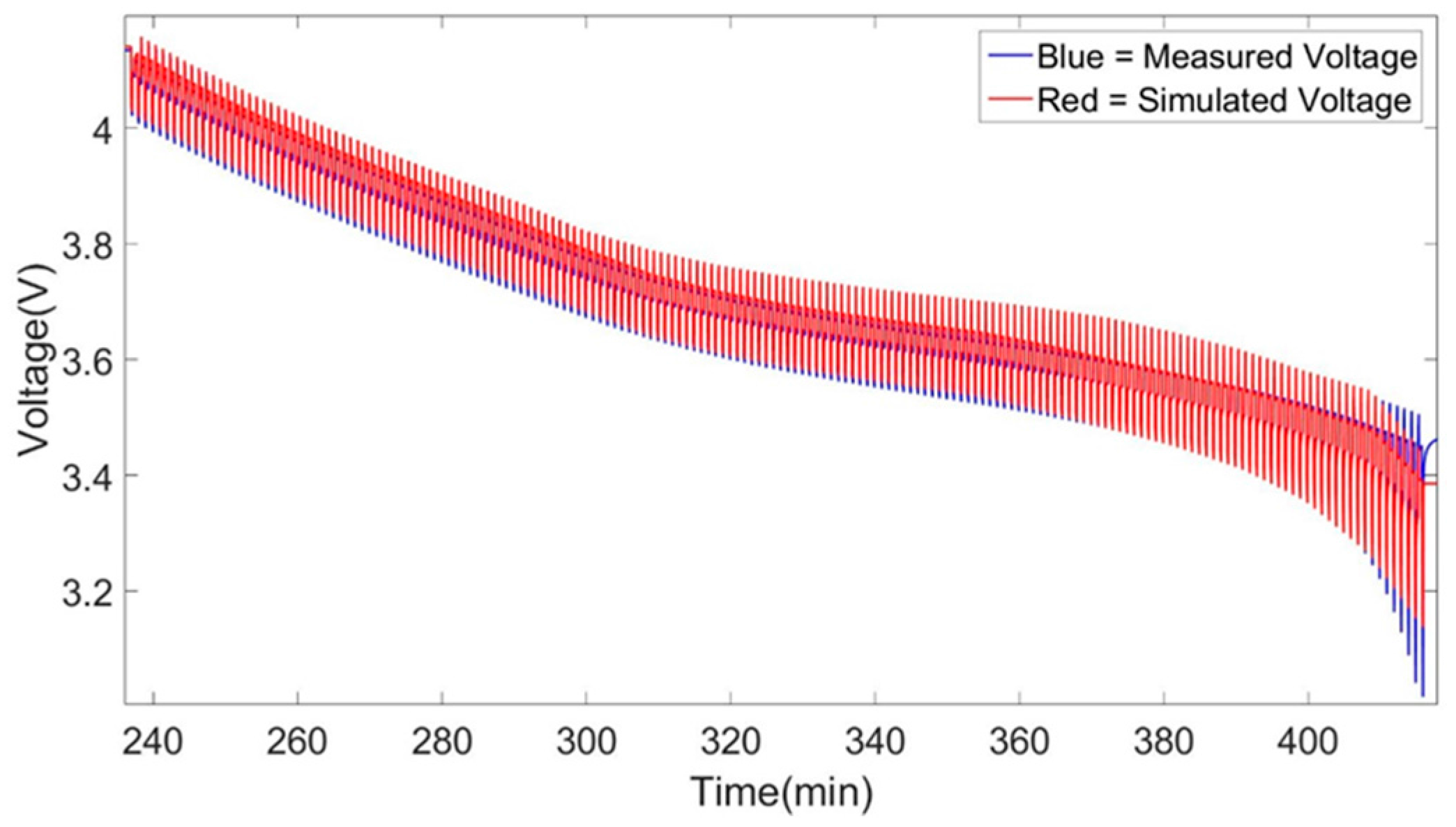
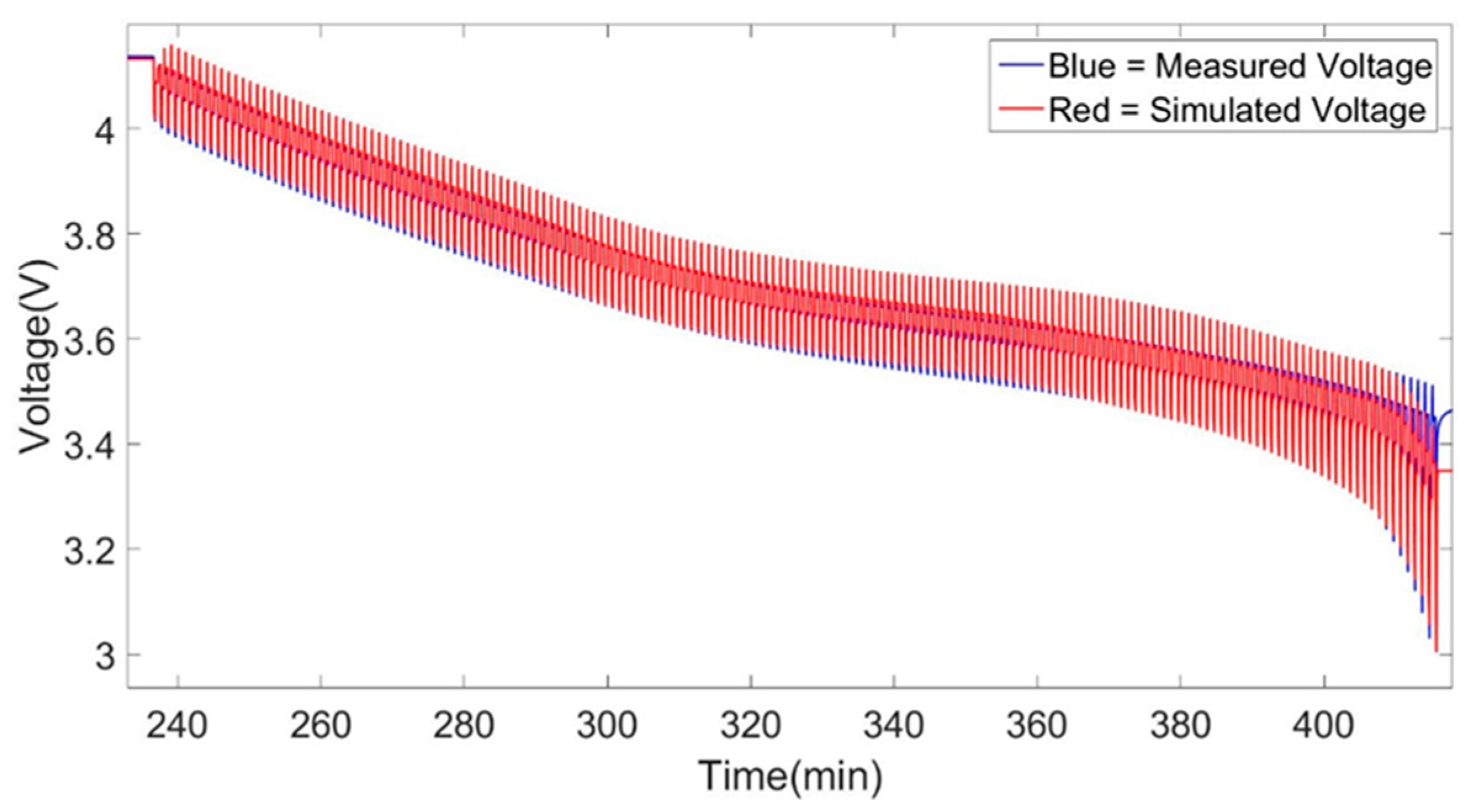
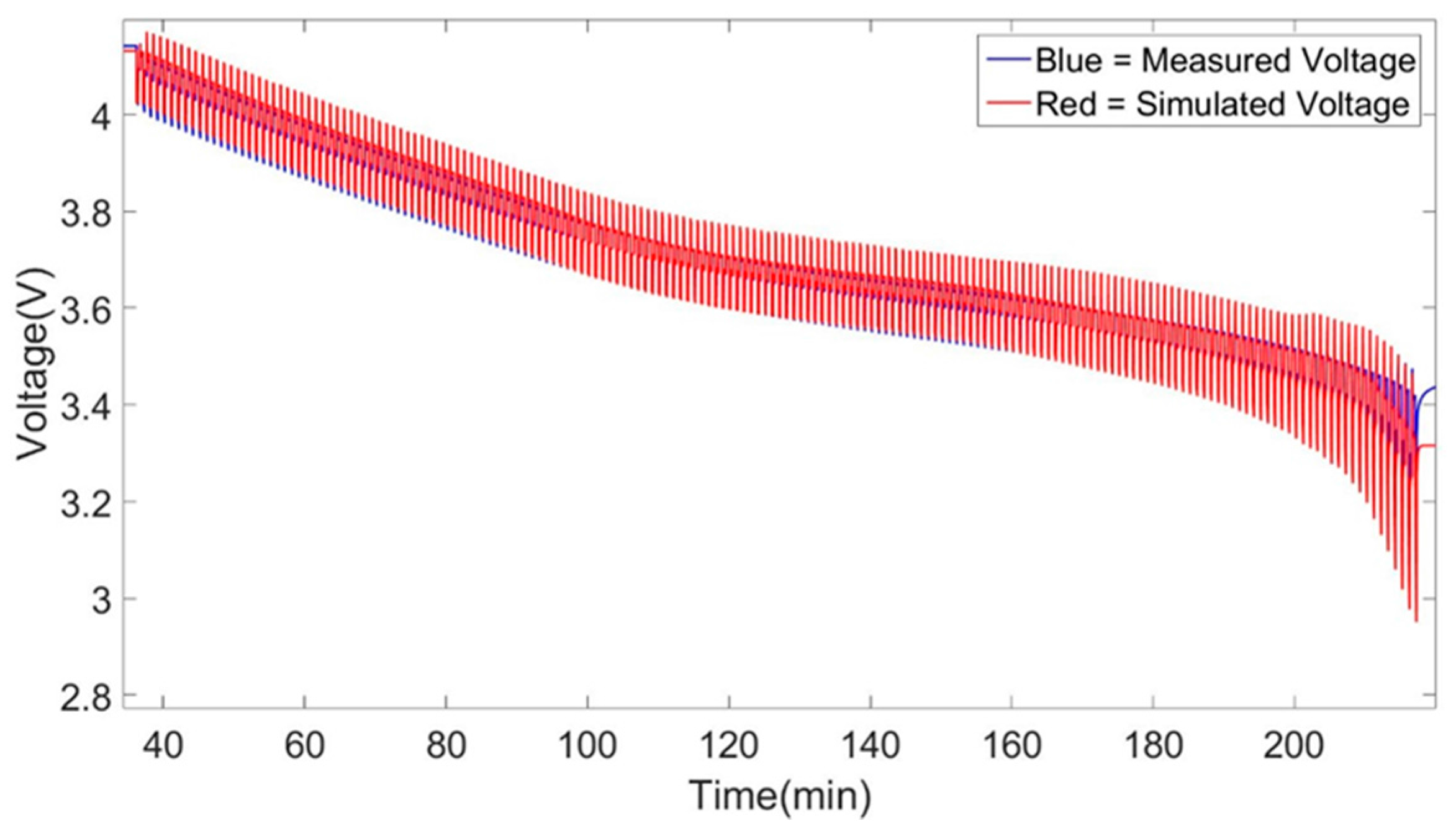
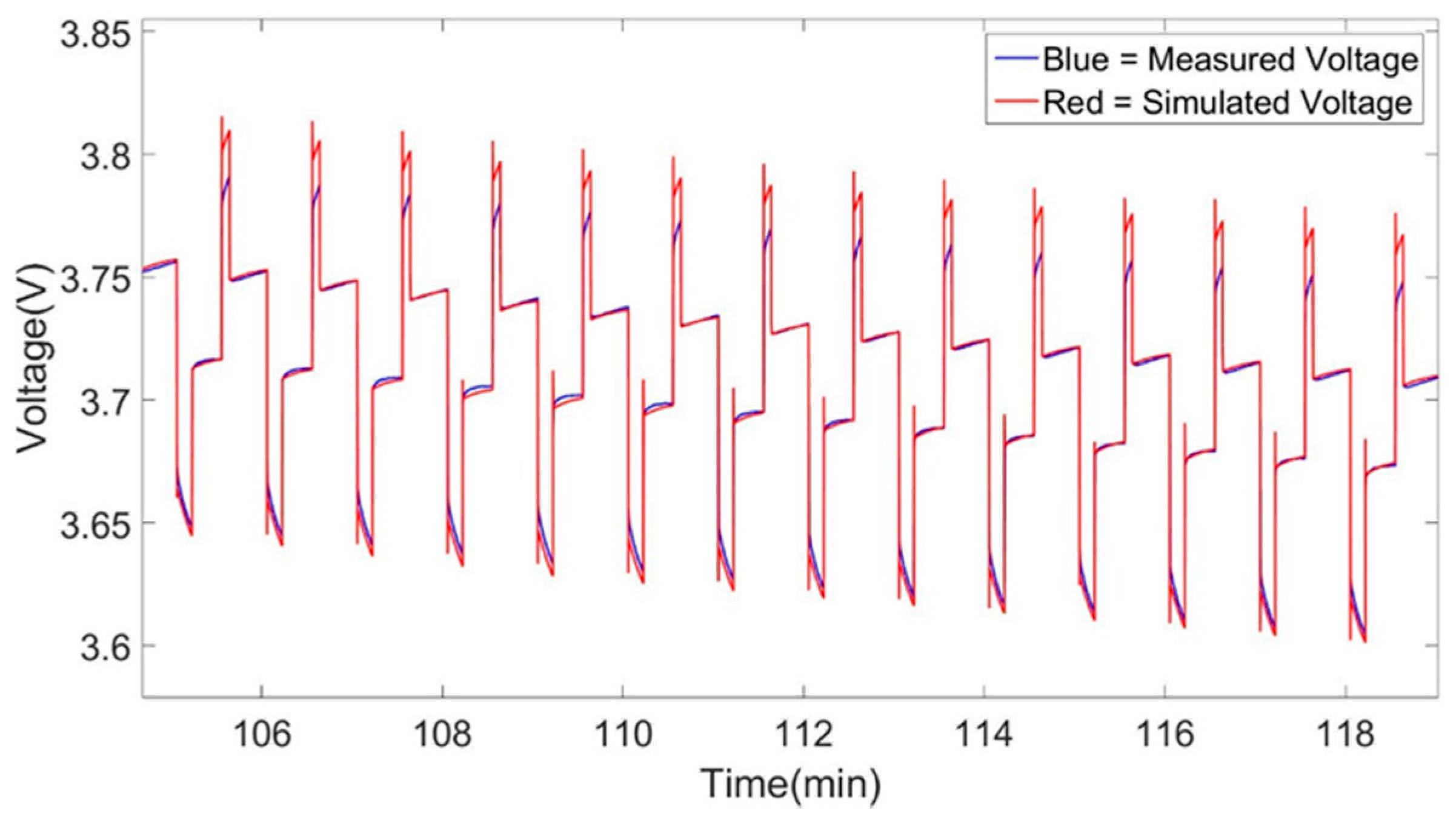
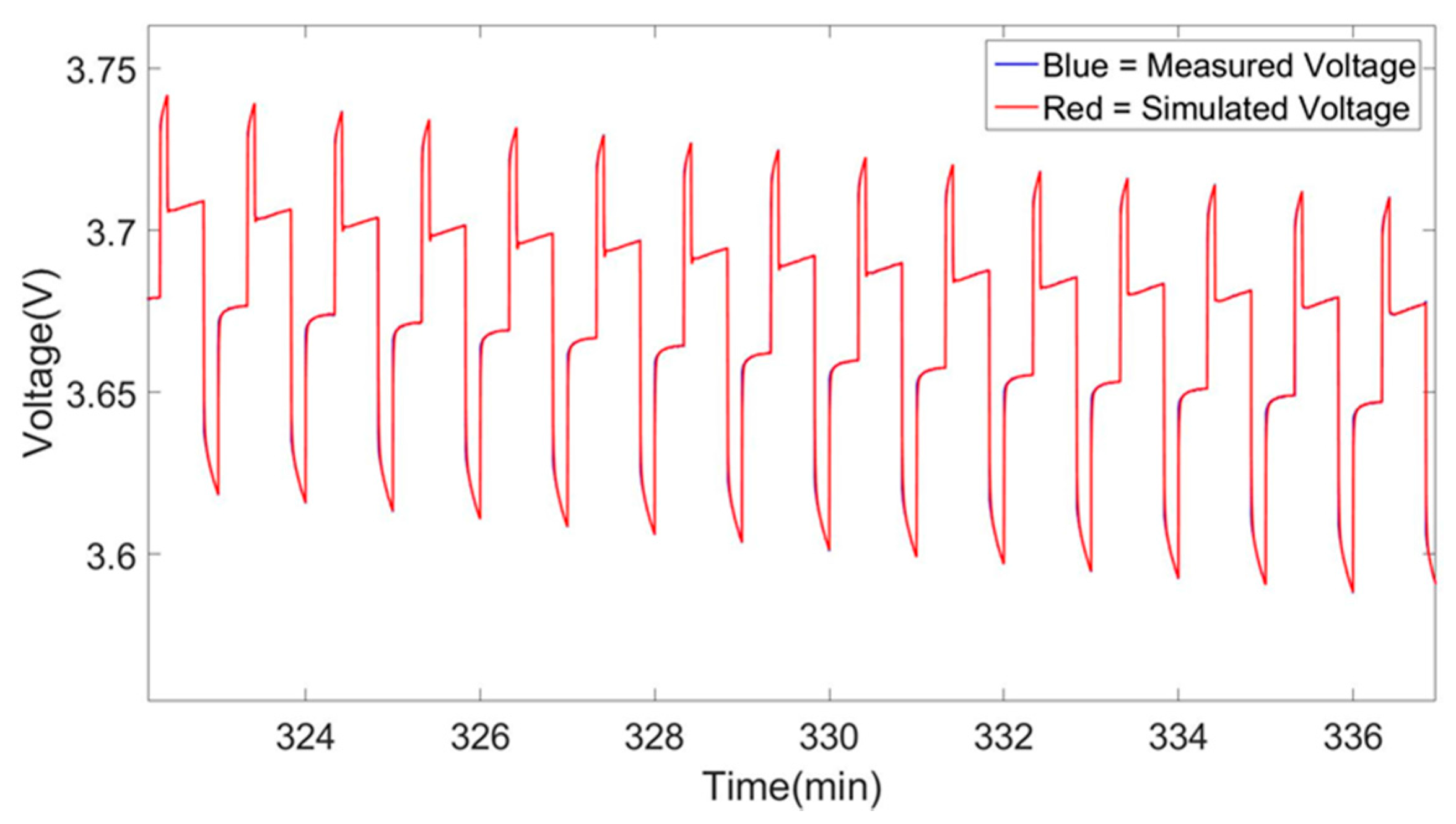
Figure 2. This comparison show us that the analysis of the characterization results can be correctly and easily performed while it gives the possibility to check the parameters created for each SoC level of the HPPC test.
In this paper the ECM topologies used during the simulations performed are the 1st order and 2nd order Thévenin battery models. The 1st order Thévenin battery model consists of a resistance (internal resistance (R
o)) connected to a branch in series, which consists of a second resistance (polarization resistance (R
p)) in parallel with a capacitor (polarization capacitor (C
p)). The 2nd order Thévenin model, which in theory should be more accurate than the 1st order Thévenin battery model consists of a resistance (internal resistance (R
o)) connected with two parallel branches in series. Each branch incorporates a resistance and a capacitor simulating the chemical behavior of the cell. The first branch is composed of an activation resistance and capacitor while the second one is composed of a concentration resistance and a capacitor. In
Table 3 a list of the different parameters needed for the parameterization of the ECM models is presented. From this table, we can observe the difference in required number of parameters between the 1st and 2nd order Thevenin model. In particular, the polarization resistance and time constants of the 1st order Thevenin model are separated in the activation and concentration chemical behavior of the cell in the case of the 2nd order Thevenin model.
2.4. State of Charge Estimation
The calculation of the correct SoC during simulation of any battery model is a key issue and is of great importance to determine the correct characteristics of the battery and to achieve good results [
50,
51,
52,
53,
54]. Specifically, battery models that are to be implemented in BMS systems for automotive and stationary applications need to estimate the SoC of the battery pack with high accuracy. In parallel, a proper BMS system implemented with a very accurate SoC estimator could be affected by the required high computational power and runtime.
There exist different types of techniques for determining the actual SoC [
55]. These different methods can be separated into experimental and adaptive techniques. This categorization is also utilized when describing the different techniques used in state-of-health (SoH) estimations [
54]. The experimental technique, which is a function of capacity, current and temperature called the Coulomb counting technique [
9]. The adaptive technique is called Kalman filtering and takes into consideration the output (simulated voltage) and input (load current and temperature) of the model to recalculate and update the SoC value in the model value back to the model [
56]. In this study a more advanced technique is used which is the extended Kalman filtering [
16,
53,
57].
The Coulomb counting SoC estimation technique has been used extensively in the literature [
50,
56,
58,
59,
60] and can be used to determine and update the battery cells SoC during simulations. It counts the charge transferred from or to the battery in order to calculate the remaining available capacity, expressed as the SoC [
54]. The proper implementation of the measured capacity values from the capacity test allows calculating the SoC through Coulomb counting technique in an accurate way. The Coulomb counting equation is described in Equation (1):
where:
z(t): The SoC at time t;
z(t0): Initial SoC (at time t = t0);
C: Estimated battery cell available capacity as function of temperature, current rate and charge/discharge state (Ah);
I(t): Battery current (A) assumed positive when discharging.
In general, the concept behind Kalman filtering is that, at each time step, an initial prediction of the state vector is made, which is used to predict the corresponding model output (
i.e., the terminal voltage) [
61,
62]. The true terminal voltage is then measured and compared to the battery model output. Based on the error and output noise covariance, the predicted state vector is optimally corrected via the Kalman gain to obtain the corrected or posterior state estimate [
16]. It is important to mention that, in contrast to the Coulomb counting-based SoC estimation, the Kalman filter-based SoC estimation, also requires a voltage measurement.
4. Discussion
Examining the 2nd order Thévenin parameters compared in
Section 3, a clear difference can be observed between the values corresponding to the fresh cell BoL and to the aged cell (90% SoH). The loss of total capacity throughout the lifetime of the NMC cells and the difference in the model parameters between a fresh BoL and aged (90% SoH) cell can be explained by different degradation mechanisms which are mainly due to structural changes in the cell, the chemical composition or dissolution reaction and surface film modifications [
59,
66,
67]. The degradation mechanisms can be separated into:
Loss of lithium inventory (LLI);
Loss of active material (LAM);
Increase of the solid electrolyte interphase (SEI) layer.
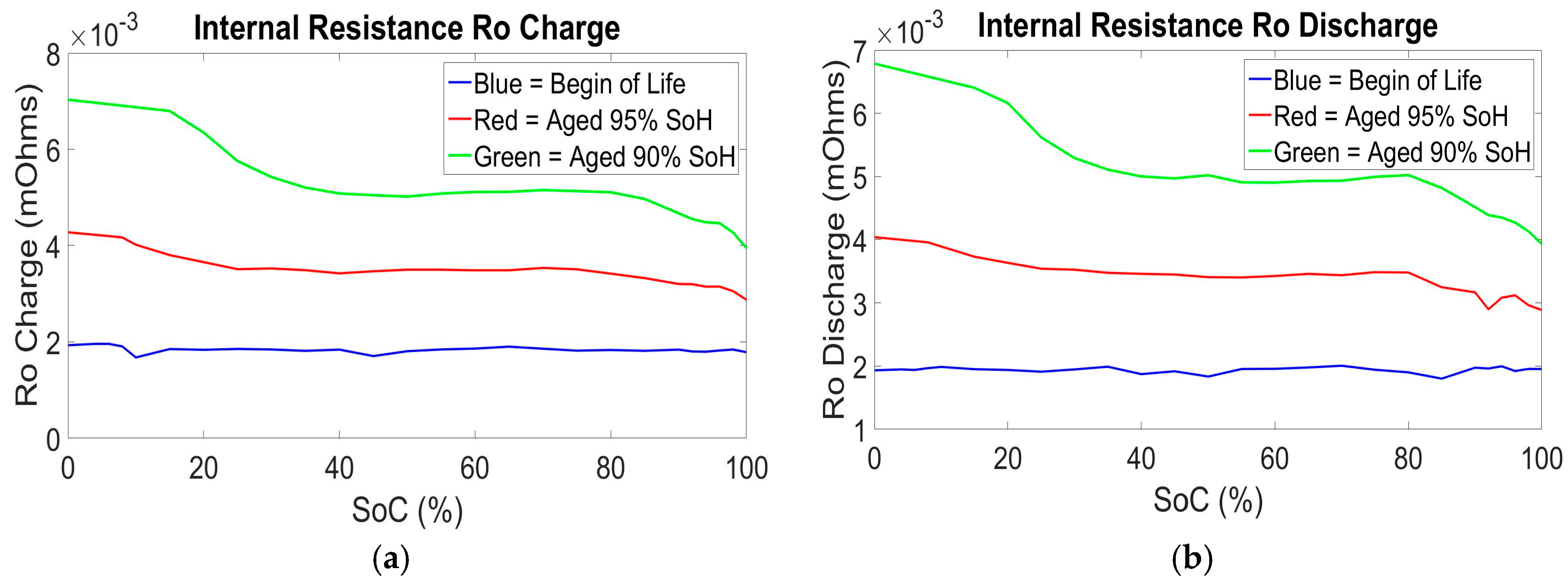
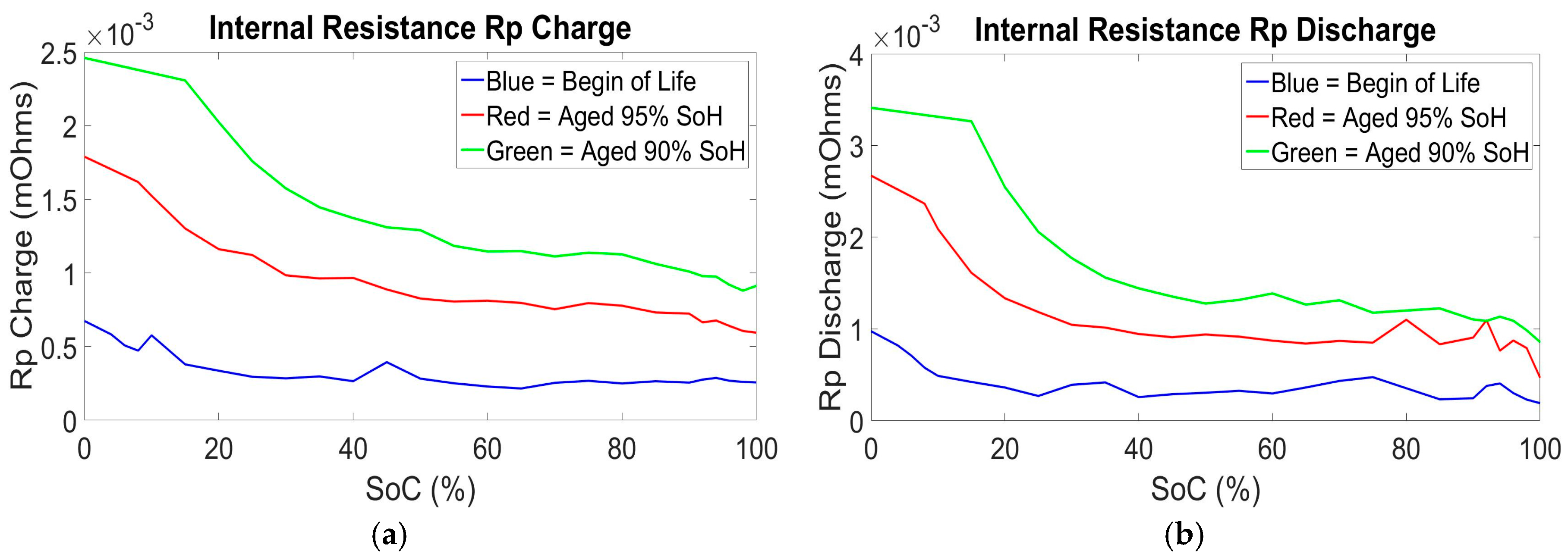
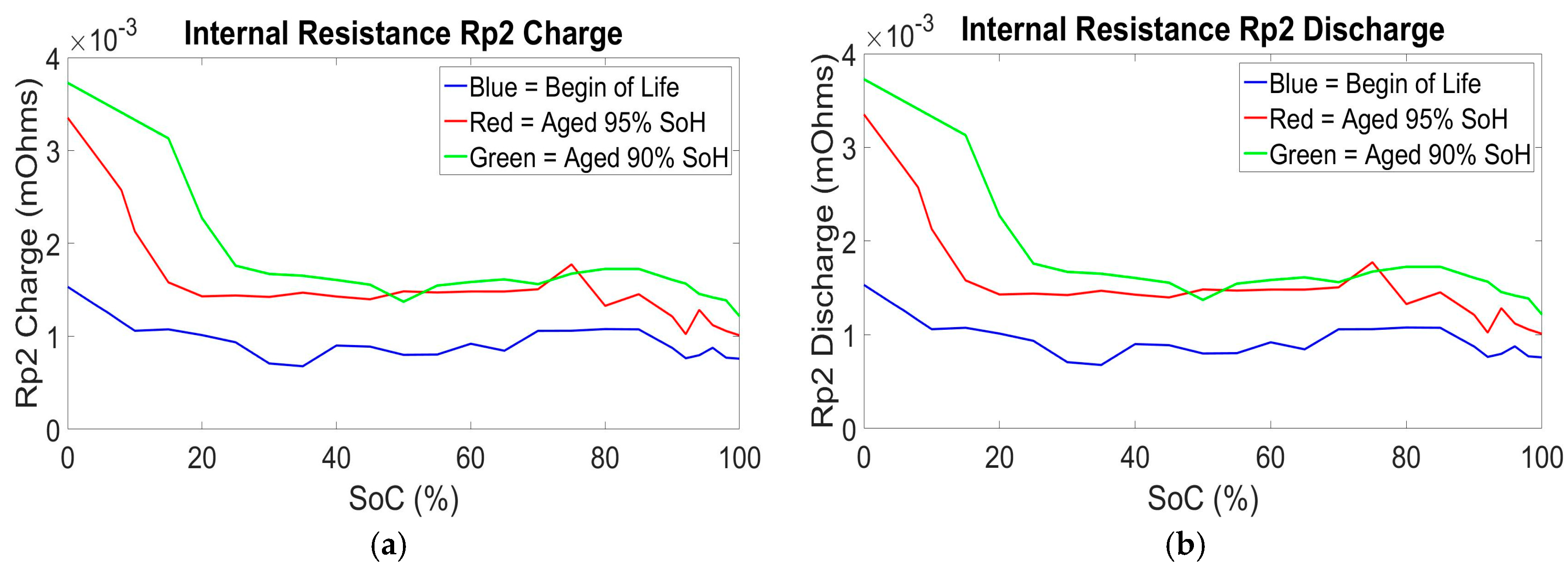
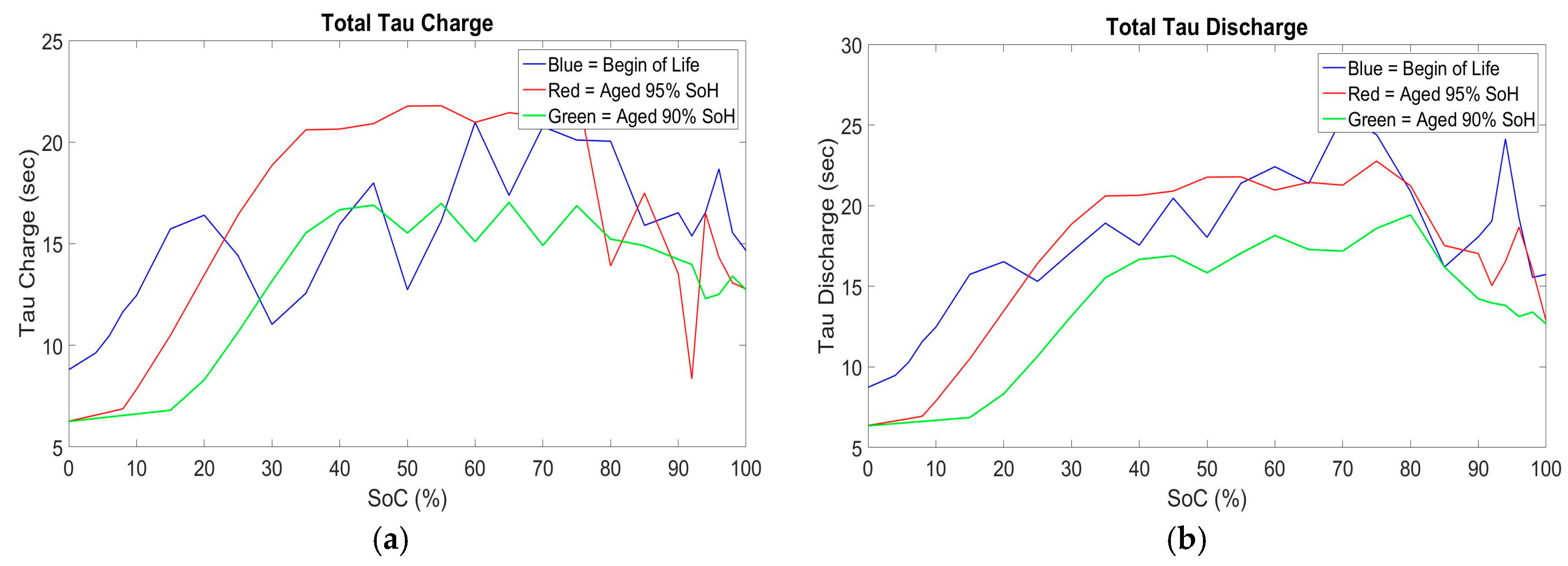
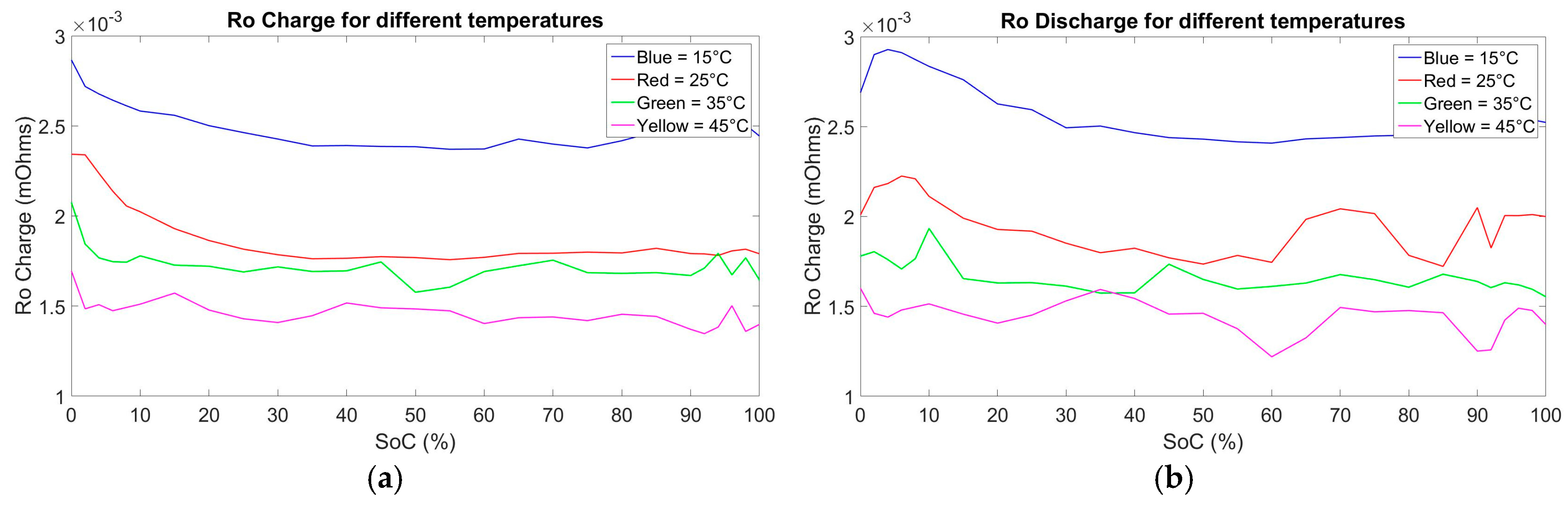
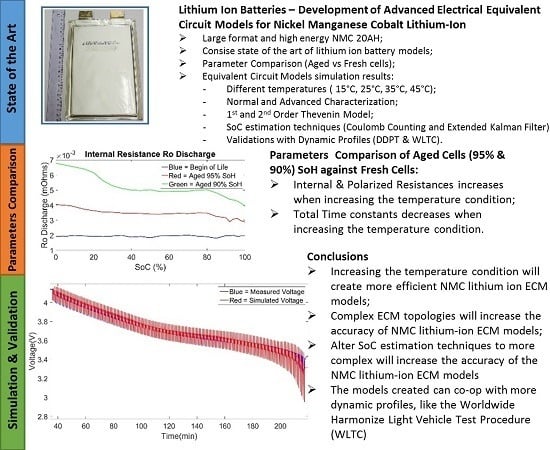
The values of Ro, Rp and Rp2 are higher for the aged cell (90% SoH) than the values corresponding to the fresh cell BoL in contrast to the time constant values τ, where the fresh cell BoL values are slightly higher than the aged cell (90% SoH) values. We observed a mean difference of 71.3% at the 100% SoC value and 61% of the 0% SoC value for the charge and discharge parameters of Ro and Rp, while 59.4% at the 100% SoC value and 43% at the 0% SoC value of the charge and discharge parameters of Rp2. For the total time constants, we observed a mean difference of 24.07% at the 100% SoC value and 13.33% at the 0% SoC value. The behavior of the internal resistance of the model and the time constant of the models RC’s branches was as expected. In this analysis we have considered the total time constant (τ
1 and τ
2) which are directly related with the total relaxation time of the cell. As a cell gets aged it is expected to see an increase in internal resistance due to the increased cycling numbers where lithium ions are intercalated between the anode and the cathode of the cell which increases the SEI layer, degrades the active materials (LLI and LAM) and decompose the electrolyte [
68]. Additionally, it is also expected that an aged cell has a smaller relaxation time than a new cell due to the formation of definite structure inside the cell including the anode, electrolyte and cathode, thus explaining the lower values for the total time constants (τ
1 and τ
2) parameter at 95% and 90% SoH when observing them in
Figure 8a,b [
66].
It can be concluded that even if the values of the total time constants are lower for an aged compared to a new cell, thus having a faster behavior during relaxation phases, it is compensated by the high increase of the internal resistance values R
o, R
p and R
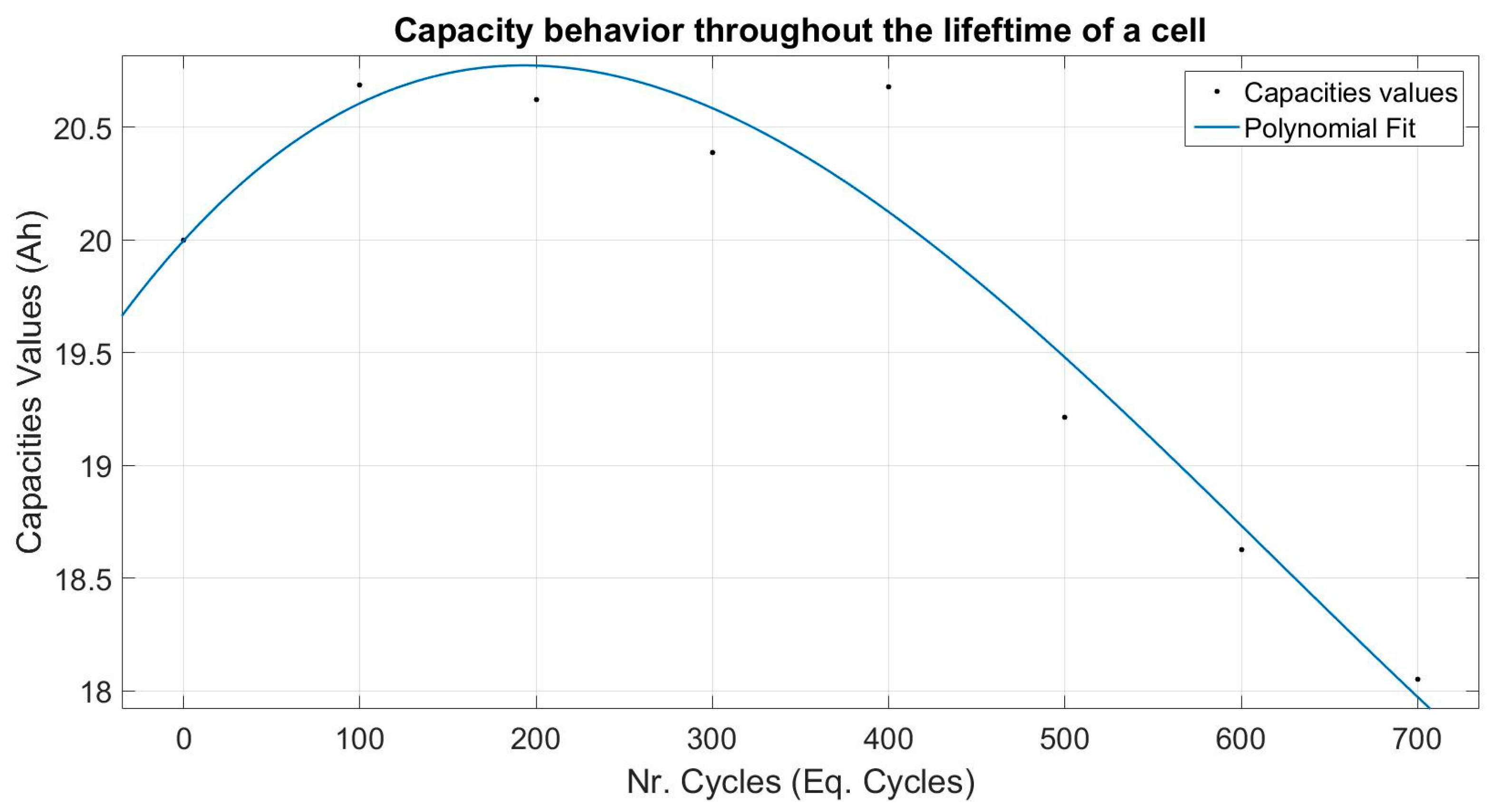
p2. This high increase of internal resistance is due to the different degradation mechanisms explained earlier. These effects can be also observed in the decreasing of the capacity value of the cell during its lifetime as seen in
Figure 3 [
69,
70].
Additionally, we observe the difference of the total time constant values (τ
1 and τ
2) at low SoC to respect the values at high SoC this can be explain as follow. When observing the relaxation phases after a specific current pulse at low SoC we see a faster saturation of the voltage measured to the rest Voltage value than what we observe in the middle or high SoC values. This can explain why we have lower Tau values at low SoC’s and higher at higher SoC’s. Meaning that we have a faster relaxation at low SoC’s than at high SoC’s. This is the opposite for the internal resistance as we can observe at
Figure 5 where we have higher internal resistance R
o at low SoC and lower R
o at high SoC’s.
Parameters like the ones described above were also calculated for other temperatures at BoL. Those parameters were used to create the models described in
Section 3.2 while additional parameters were created for the other temperatures under investigation. Observing the results of
Section 3.2 some general observations regarding the comparison of the simulated to the measured results of the models can be mentioned:
Increasing the temperature condition will create more efficient NMC lithium ion ECM models;
Complex ECM topologies will increase the accuracy of NMC lithium-ion ECM models;
Alter SoC estimation techniques to more complex will increase the accuracy of NMC lithium-ion ECM models;
The models created can co-op with more dynamic profiles, like the WLTC profile.
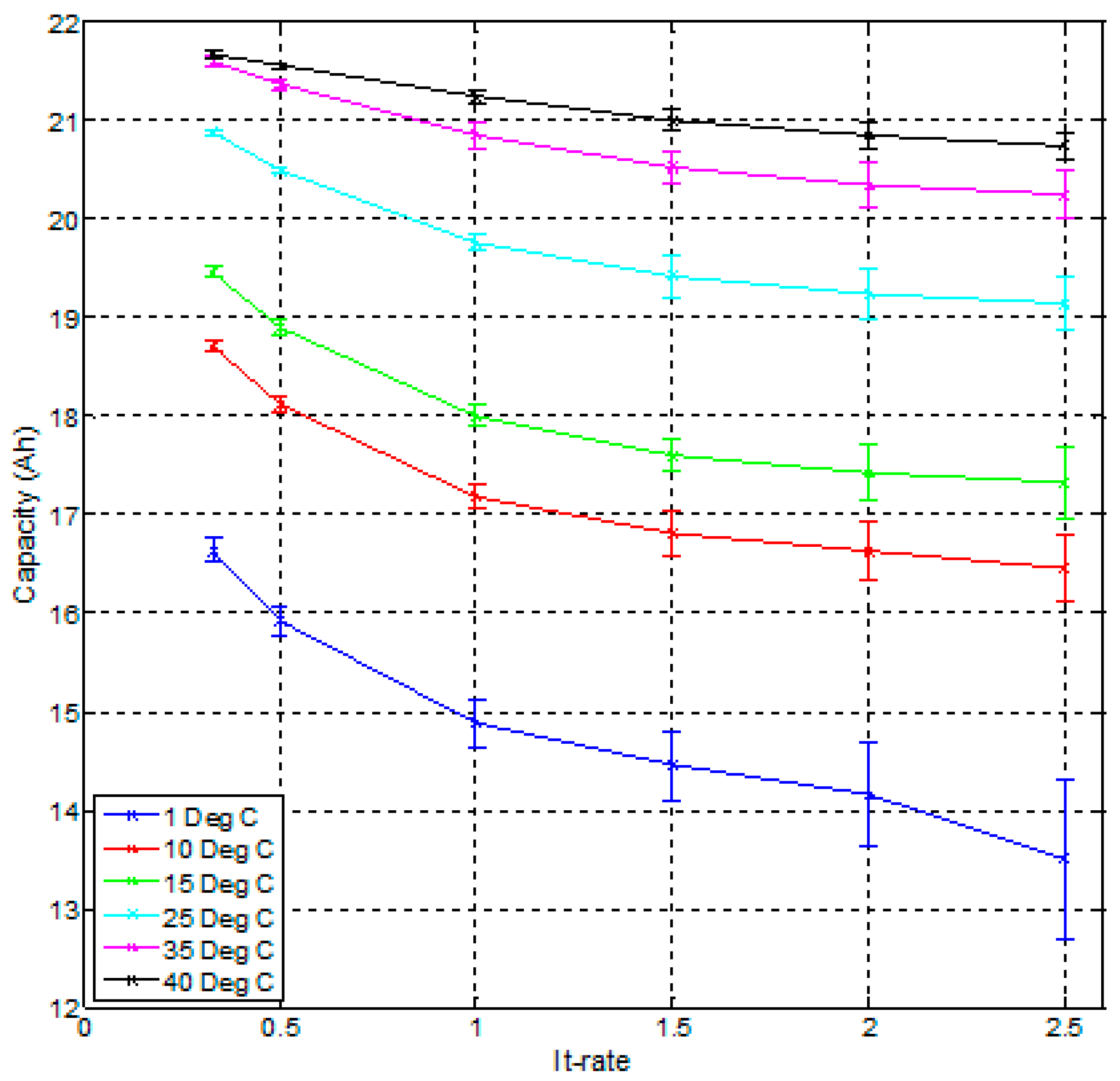
The main condition that is predominantly affecting the accuracy of the models is the temperature. This effect can be observed on all topologies, for both types of characterization results used and for both the Coulomb counting and the extended Kalman filtering SoC estimation technique. This phenomenon can be explained by the fact that when performing the characterization tests at a higher temperature value, the different parts of the cell becomes more homogeneous, making the behavior of the cell during this condition more pronounced compared to that at lower temperatures. Thus, when creating parameters from these tests, the models will have less non-linear errors during the simulation. Moreover, when increasing the temperature condition, an increase in available capacity of the cell is observed, as shown in
Figure 25.
Thus, when creating the parameters for these high temperatures, we have a better match between the energy used during our HPPC test (characterization test for the creation of Ro, Rp, Rp2 and τ parameters) and the energy used during our DDP validation test. The increasing mismatch occurring at lower temperatures between the energy used, together with increasing time step of the simulation have been identified as sources of increasing errors during the simulation.
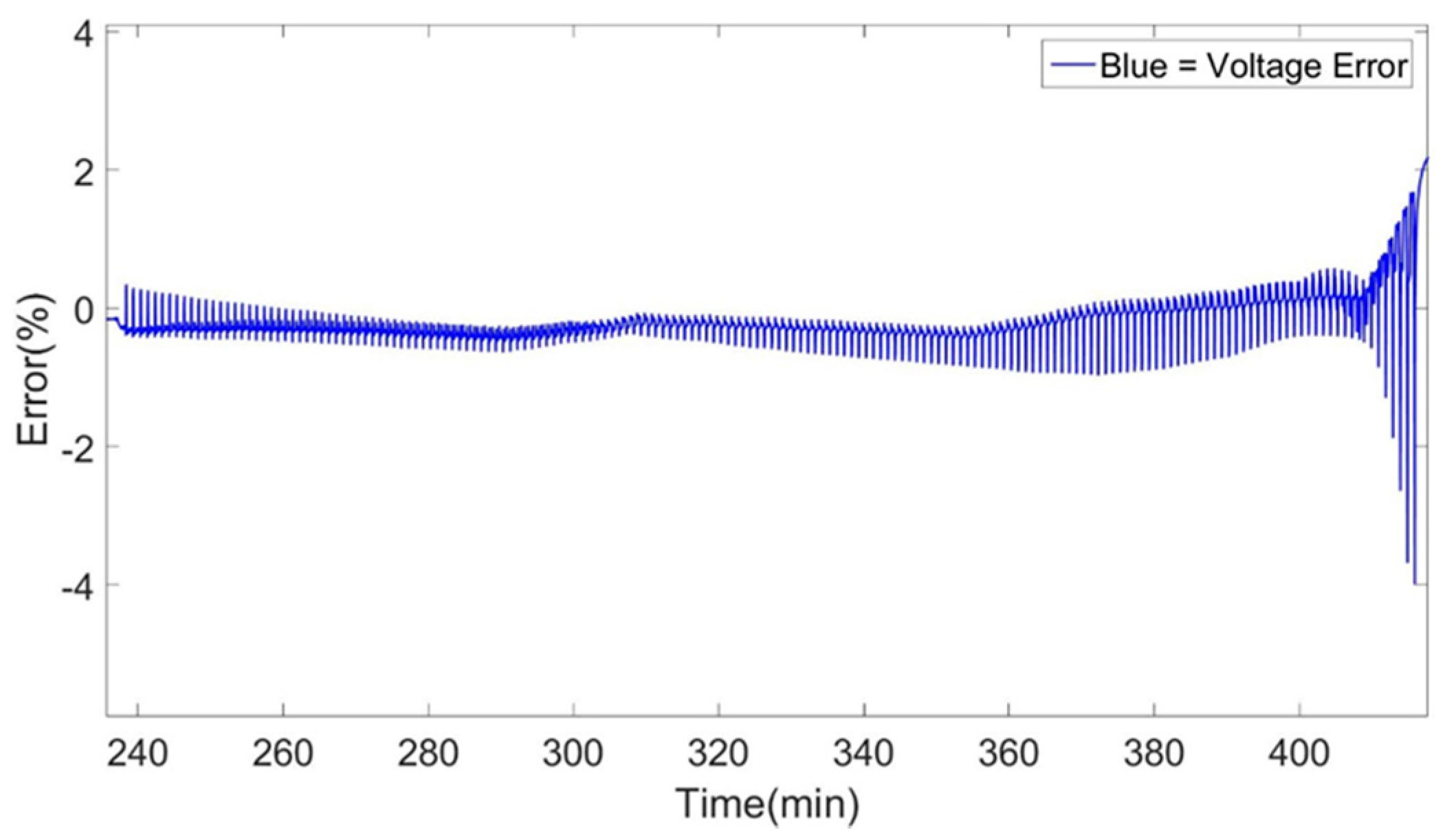
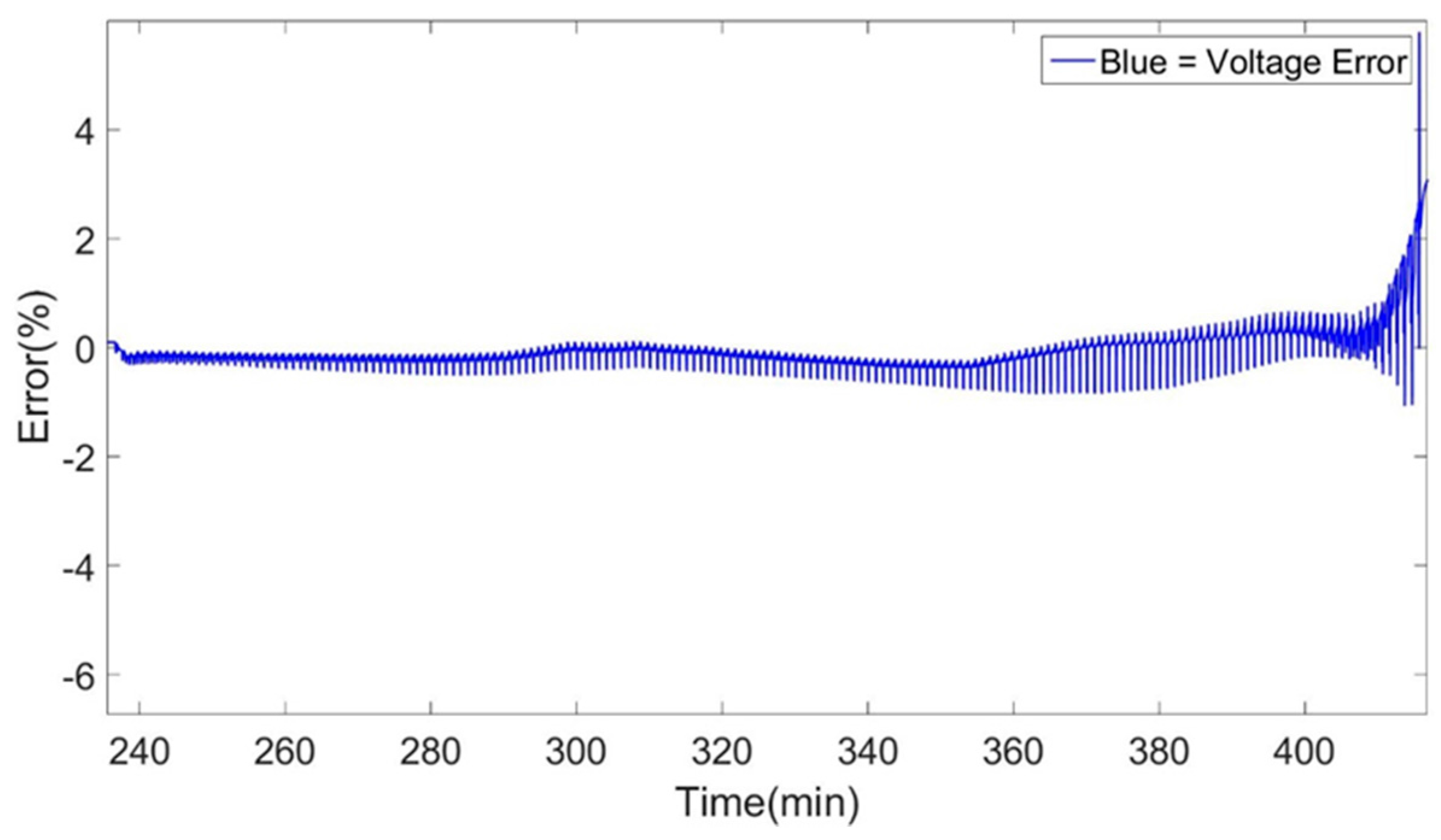
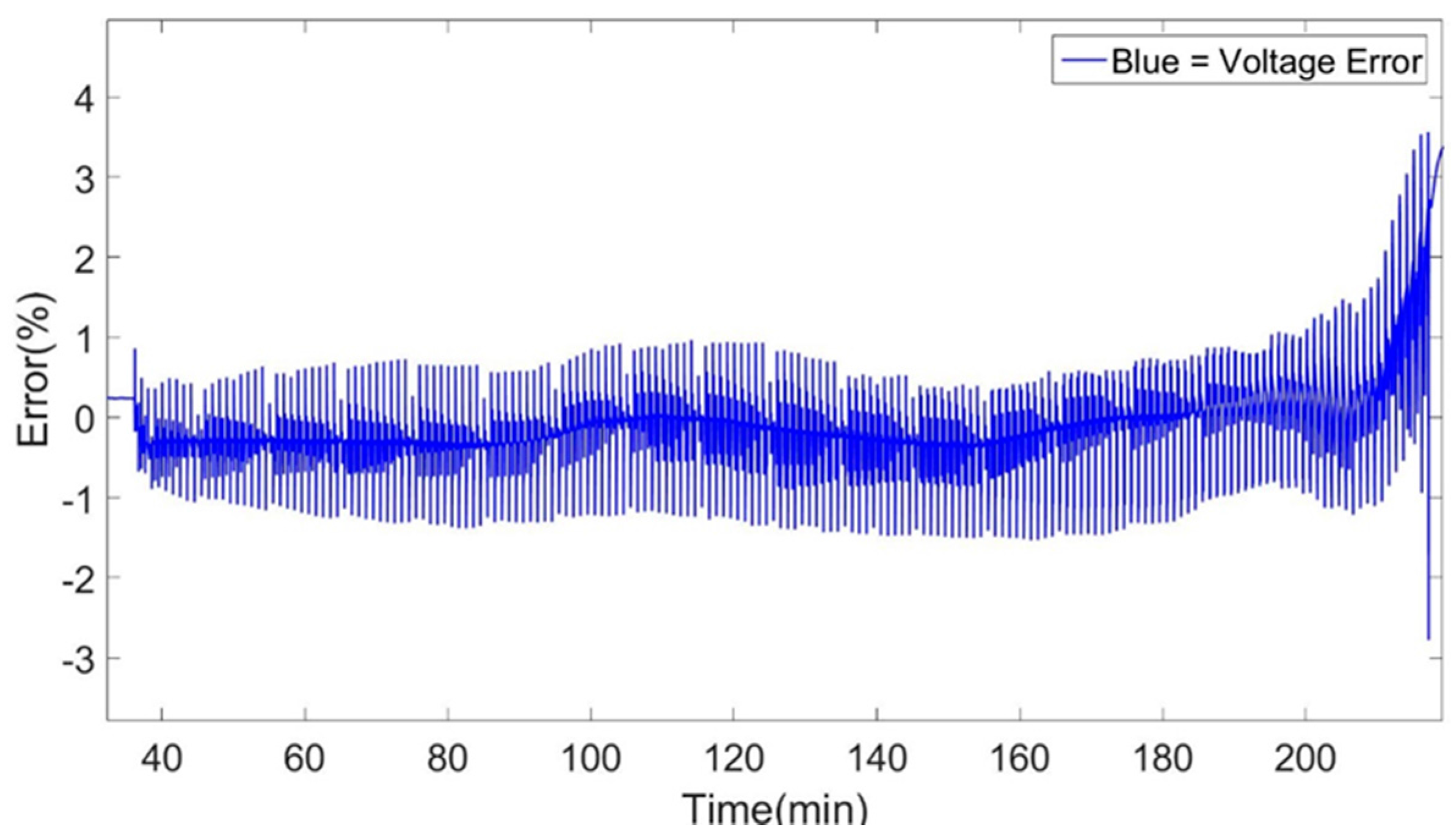
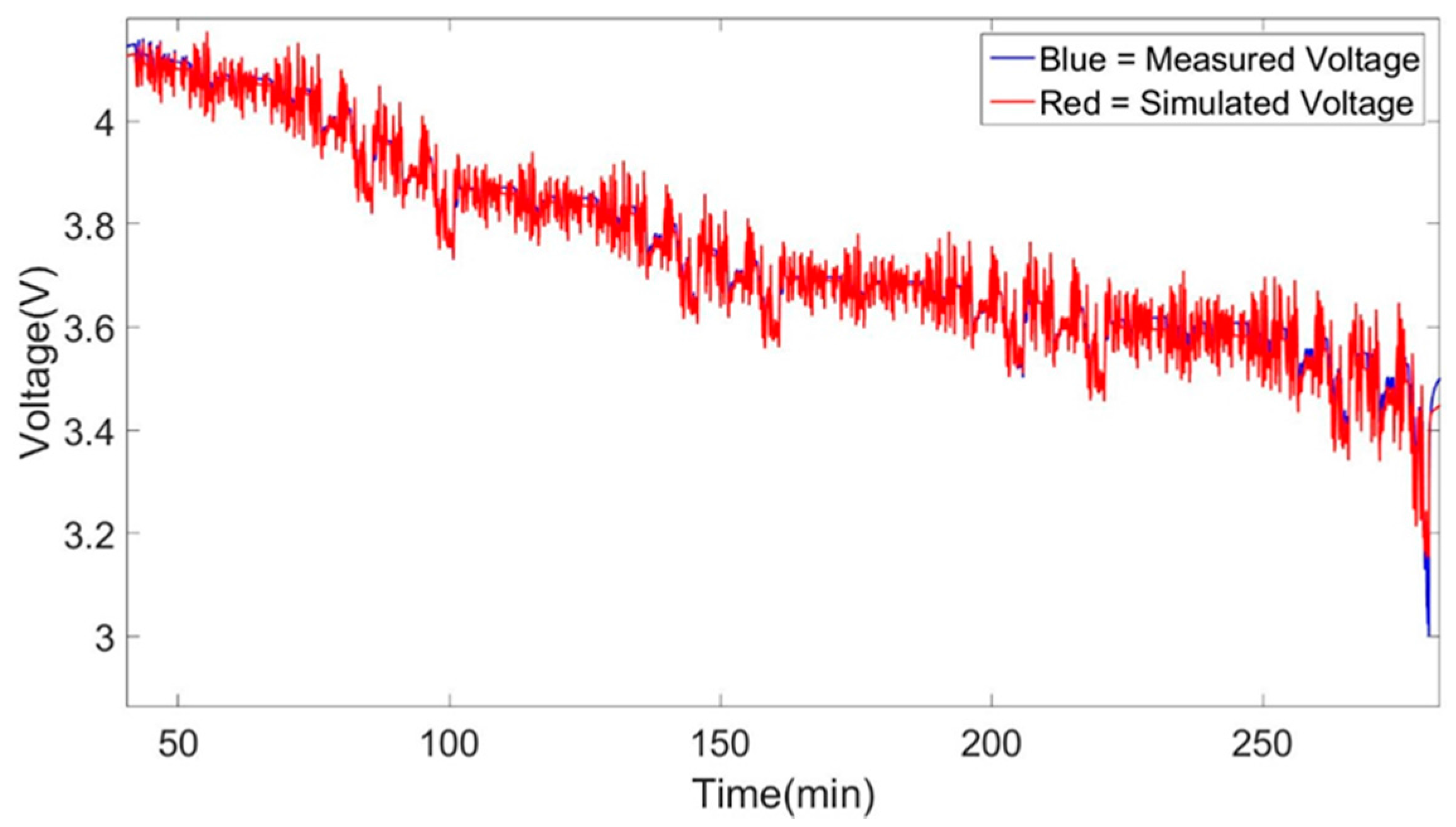
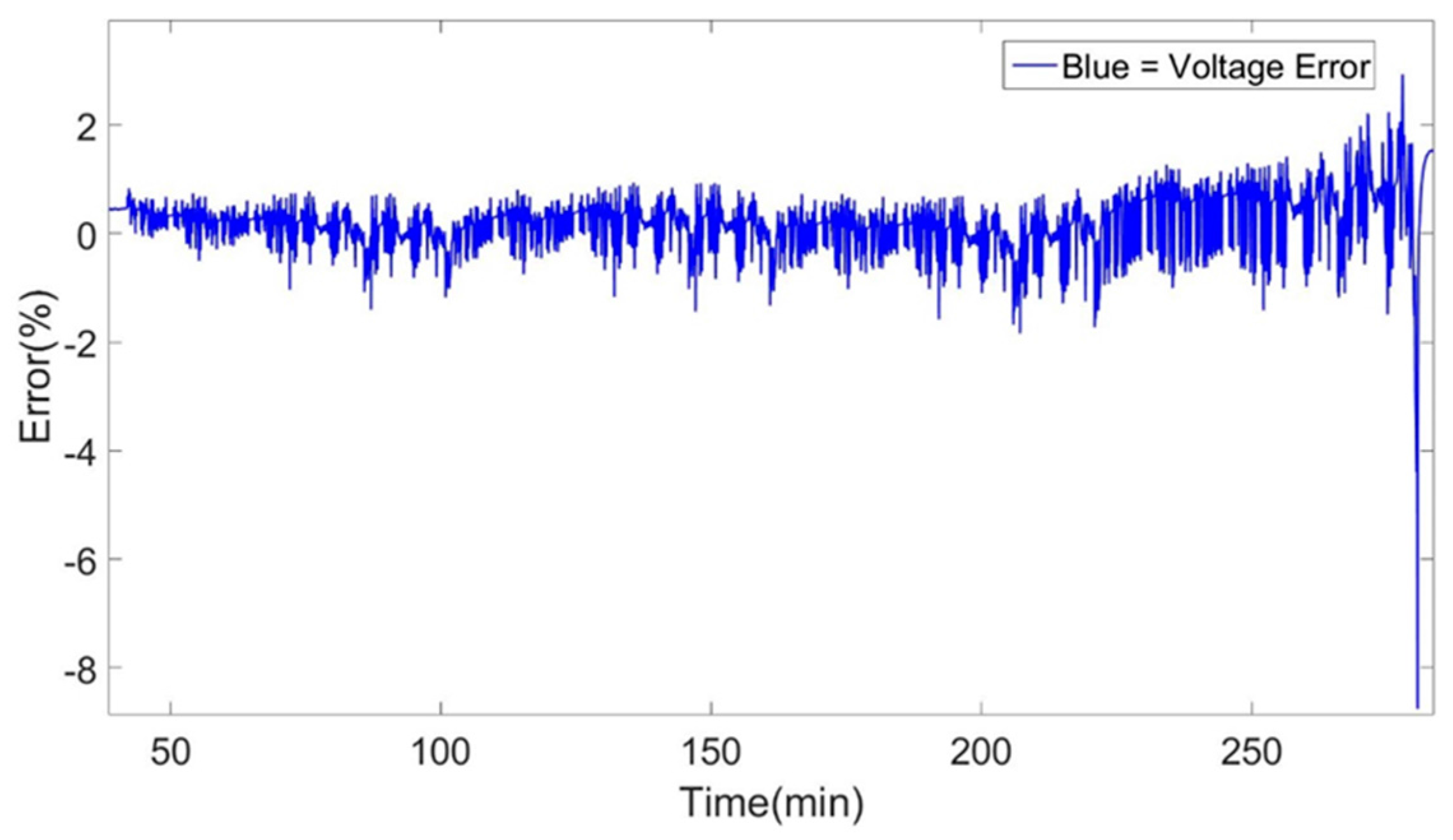
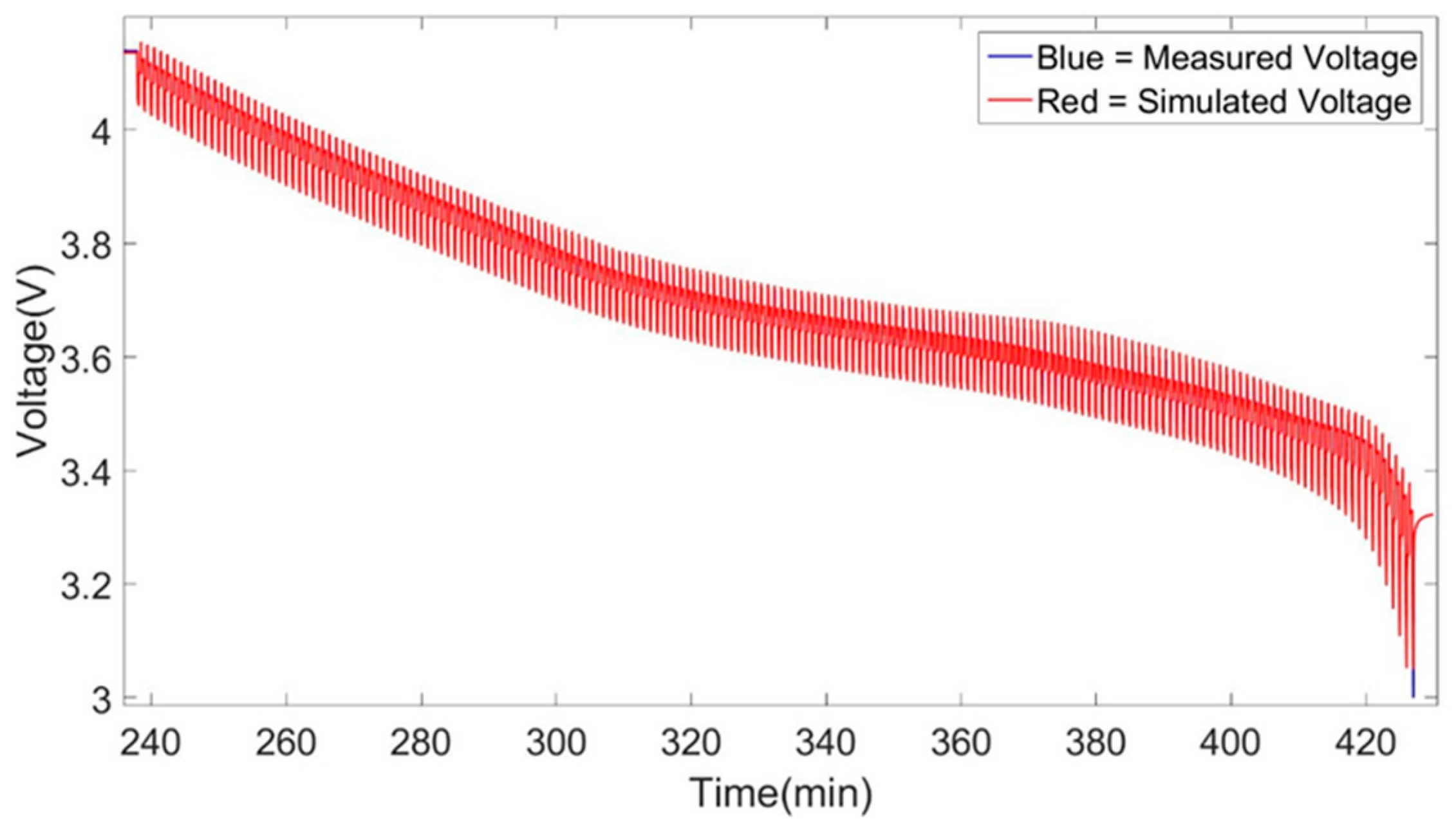
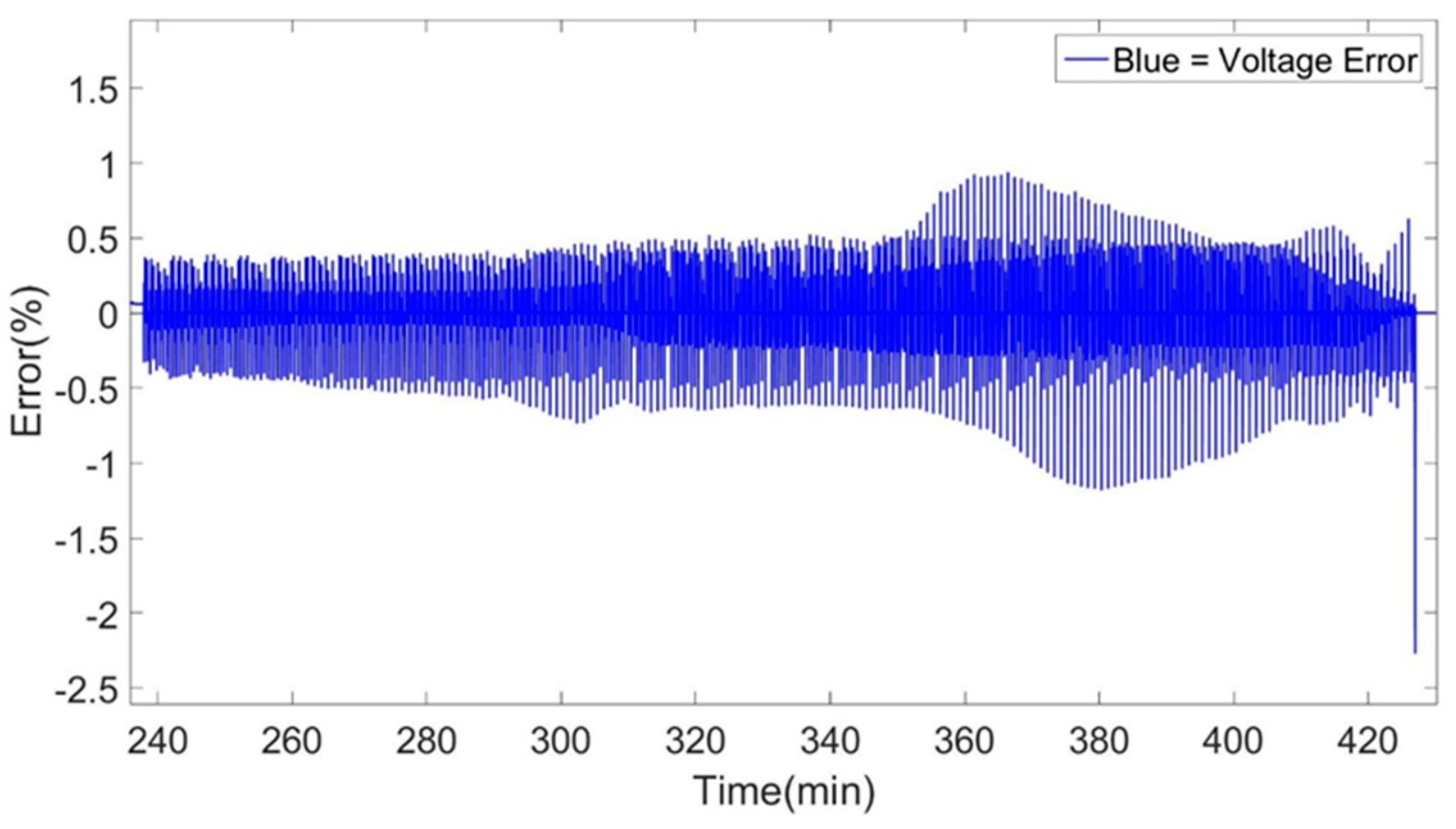
The main errors that have been encountered during the simulations can be identified at the high and low SoC window of the simulations. This effect as described above is minimized when increasing the temperature condition at which the models were created. Moreover, a clear improvement is observed in the models when changing the topology of the models from 1st to 2nd order Thévenin model. This effect can be observed between the 1st and 2nd order Thévenin model at 25 °C models while also at the others temperatures. The 1st order Thévenin model at 25 °C using advanced characterization datasets has identical accuracy as the 2nd order Thévenin model at 25 °C using advanced characterization datasets. But we see that the high and low SoC errors of the 2nd order Thévenin model is less pronounced specifically for the discharge behavior of the cell while there isn’t any increase in high errors (4%), as the 1st order Thevenin mdoel, at the very end of the simulation.
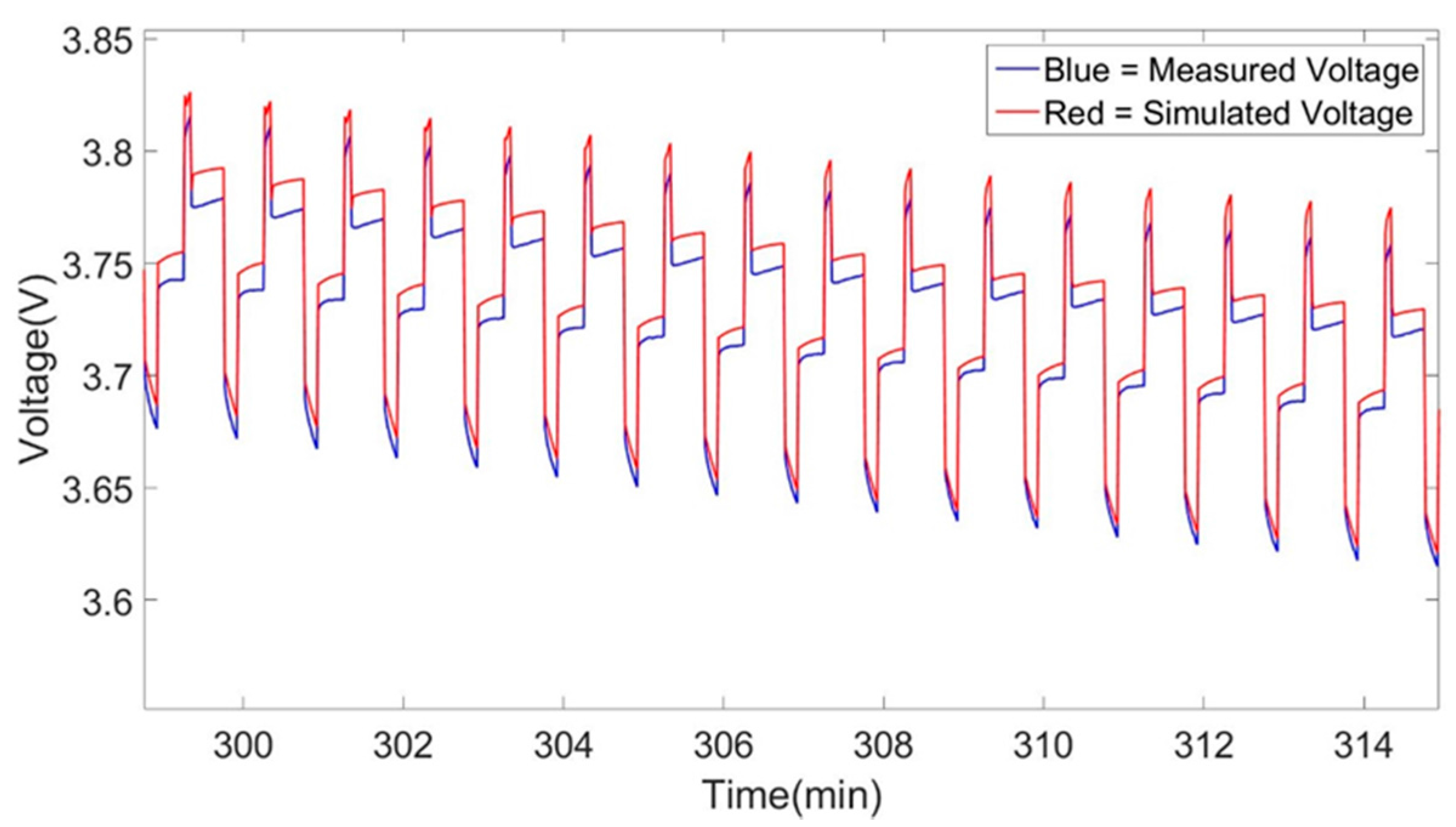
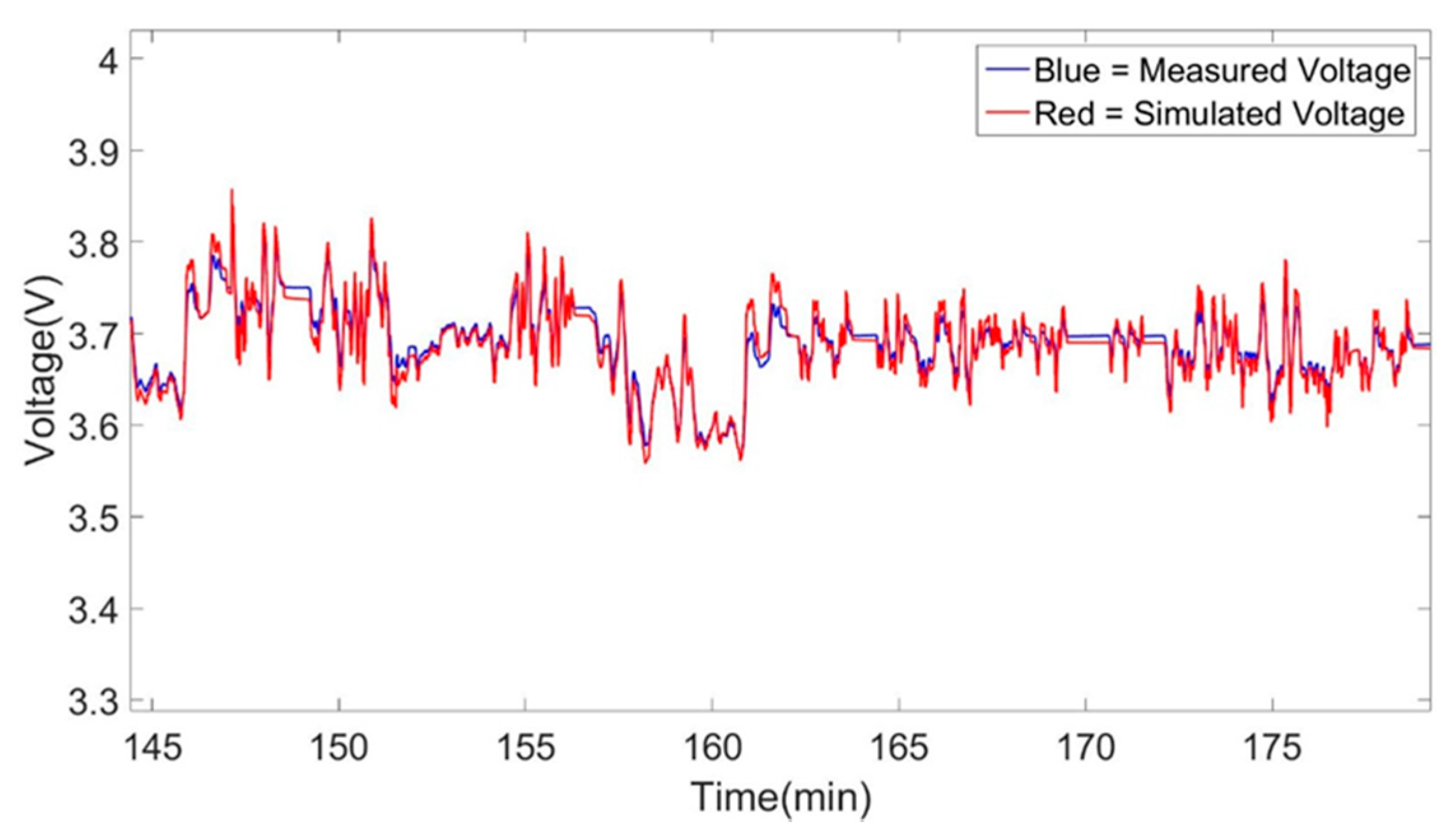
Inspecting the 2nd order Thévenin models with Coulomb counting and extended Kalman filtering SoC estimation technique we observe a clear improvement in the accuracy of the model. Due to the extended method used by Kalman filtering to re-calculate and actualize the SoC of the cell in the model, the accuracy of our models is increased while we observed a clear improvement in the dynamic representations of the models presented in
Figure 18. Comparing the 1st order models created with normal characterization and advance characterization datasets we observed that the accuracy of the models is increased but is not substantial as it is when changing temperature, topologies and SoC estimation techniques. Furthermore, the dynamic behavior has been affected more than the total accuracy of these models by the change of the characterization datasets from normal to advanced.
Collecting all these observations the model that should have created the best simulation accuracy and dynamic behaviors during the simulation should be models that are at high temperatures with complex topologies. In this regard, the most efficient model created for this study was the 2nd order Thévenin model with advanced characterization datasets and extended Kalman filtering SoC estimation technique at 45 °C. Future work will investigate more in depth the development of ECM models based on a high number of cells creating average parameters for a batch of cells and comparing them to average validations profiles provided by the combination of the validations results (average DDP and WLTC profiles for a batch of cells). This analysis will provide a better understanding of the behavior of a set of NMC cells which represents with higher fidelity the situation observed in an automotive battery pack combined with a BMS.
Additionally, in future publications, the incorporation of in-depth analysis of the simulation time needed to run such models in a specific CPU-based platform (i.e., automotive on-board computer) will be provided. Performing a preliminary investigation, it can be observed that the more complex the topology and extensive the parameters are, the longer it takes for a computer system to run the model. This time is in the order of 1 minute for the 1st and 2nd order Thevenin model combined with Coulomb counting SoC estimation technique. In contrast, with the use of the extended Kalman filtering where the computer system has to acquire and input the SoC values while he simulates the validation profile, we can observe a substantial increase in the simulation time needed to run the model. This time is in the order of 5 minutes. These simulations were performed by a computer with a Central Processing Unit (CPU) at 2.8 Ghz, with 16 GB Memory and a NVIDIA (Santa Clara, CA, USA) Quadro K2 100 M graphic card.
5. Conclusions
The proper simulation of lithium-ion batteries in today’s automotive and electric applications is of great important for an efficient use and correct understanding of the electrical, thermal, chemical behavior of the system under investigation. Different models exist in the industry and literature, each having their own advantages and disadvantages. ECMs are mainly used in electrical lithium ion battery models for the simulation of the electrical and thermal behavior of the cell. The 1st and 2nd order Thévenin model are used to simulate a large format and high energy NMC lithium-ion battery with a capacity of 20 Ah for different temperatures. The models are created by using the Coulomb counting and the extended Kalman Filter SoC estimations and different type of validation profiles like the dynamic discharge pulse (DDP) and world harmonized light duty profiles were taken into account. Moreover, a different set of parameters were created based on two types of characterization tests performed (normal and advanced characterization). The creation of aged parameters was also developed based on the same characterization tests procedures and they were compared to the BoL parameters used in the parameterization of the ECM models. The behavior of the aged parameters with respect to the BoL were as expected mainly observing higher internal resistances for a battery cell that has aged versus a fresh cell while an opposite relation was observed for the total time constant τ (τ1 and τ2), with higher values for a fresh cell than a cell that has aged.
The temperature condition, the models were created, has a great effect on the validation results. The higher the temperature at which the characterization tests were performed, the more accurate the parameters are, providing a better validation result of the model. The difference in the topology of the 1st and 2nd order Thévenin model while the difference between the normal and advanced characterization test methods will decrease the error of the validation results but mainly they will allow for better dynamic representations and less linear errors at high and low SoC levels of the cell. The 2nd order Thévenin model at 45 °C with advanced characterization and extended Kalman filtering is found to be the most accurate model.