Abstract
We present a thermo-economic analysis of an Organic Rankine Cycle (ORC) for waste heat recovery. A case study for a heat source temperature of 150 °C and a subcritical, saturated cycle is performed. As working fluids R245fa, isobutane, isopentane, and the mixture of isobutane and isopentane are considered. The minimal temperature difference in the evaporator and the condenser, as well as the mixture composition are chosen as variables in order to identify the most suitable working fluid in combination with optimal process parameters under thermo-economic criteria. In general, the results show that cost-effective systems have a high minimal temperature difference ΔTPP,C at the pinch-point of the condenser and a low minimal temperature difference ΔTPP,E at the pinch-point of the evaporator. Choosing isobutane as the working fluid leads to the lowest costs per unit exergy with 52.0 €/GJ (ΔTPP,E = 1.2 K; ΔTPP,C = 14 K). Considering the major components of the ORC, specific costs range between 1150 €/kW and 2250 €/kW. For the zeotropic mixture, a mole fraction of 90% isobutane leads to the lowest specific costs per unit exergy. A further analysis of the ORC system using isobutane shows high sensitivity of the costs per unit exergy for the selected cost estimation methods and for the isentropic efficiency of the turbine.
1. Introduction
Organic Rankine Cycle (ORC) systems for waste heat recovery have a high growth potential [1]. Numerous investigations are performed in order to maximize the efficiency of such power plants by working fluid selection with respect to the heat source temperature. Particularly, the use of zeotropic fluid mixtures is a promising optimization approach due to a good glide match of the temperature profiles at phase change. In this context, Angelino and Colonna di Paliano [2] show for a low-temperature application that mixtures of natural hydrocarbons (n-butane/n-hexane) lead to an efficiency increase of 6.8% compared to the pure working fluid n-pentane. Other case studies for geothermal heat sources prove the potential of zeotropic mixtures as working fluids in ORC systems [3,4]. For subcritical cycles an increase in efficiency by up to 16% is obtained compared to pure working fluids, like isobutane or isopentane. More recent investigations include sensitivity analyses for crucial parameters [5,6,7,8,9,10,11]. Heberle et al. [12] show high second law efficiencies for mixture compositions which lead to a good match of the temperature profiles at condensation. However, these concentrations show a significant increase in heat exchange capacity. Similar results are obtained by Andreasen et al. [13] considering pure components and their zeotropic mixtures as working fluids for subcritical and transcritical cycles in the case of a low-temperature heat source. For a heat source temperature of 120 °C, mixtures of propane and higher boiling natural hydrocarbons, as well as isobutane/isopentane show high first law efficiency for the subcritical cycle. At the same time, an increase of the heat exchange capacity for the condenser is presented. This is an indicator for the requirement of high heat transfer areas. Angelino and Colonna di Paliano [14] compare an equimolar mixture of n-butane/n-hexane and pure n-pentane as ORC working fluids in a case study for waste heat recovery. Fan power savings of the air-cooling system of 49% by using the zeotropic mixture are determined. However, an additional heat transfer area of 73% is required. Weith et al. [15] have recently shown for a waste heat recovery unit that the use of a siloxane mixture leads to an efficiency increase of 3% compared to the most efficient pure component. As a consequence, a 14% higher heat transfer area of the evaporator is obtained for the zeotropic mixture.
The described dependence suggests a thermo- or exergo-economic analysis of ORC systems in order to evaluate the increased power output and the additionally-required heat exchange area for fluid mixtures. Existing thermo-economic analyses of ORC systems are focused on pure working fluids [16,17,18,19,20]. Regarding small-scale waste heat recovery ORC units, Quoilin et al. [21] determined specific investment costs for eight working fluids in the range of 2136 €/kW and 4260 €/kW. For an electric capacity between 30 kW and 120 kW, Imran et al. [22] considered different plant schemes and working fluids. In this context, specific investment costs in the range of 3556 €/kW and 4960 €/kW are obtained. Quoilin et al. [23] indicate specific investment costs between 8000 €/kW and 1000 €/kW for an ORC waste heat recovery module in the range of 10 kW and 7500 kW electrical power output. In the case of a geothermal resource, Heberle et al. [24] identify isobutane as a cost-efficient working-fluid compared to isopentane. The lowest specific costs are obtained for a minimal temperature difference of 3 K in the evaporator and 7 K in the condenser. Current thermo-economic analyses consider also zeotropic mixtures as ORC working fluid. They show that cost efficiency of ORC systems using zeotropic mixtures is strongly dependent on the application. For a geothermal power generation at a heat source temperature of 160 °C, fluid mixtures lead to a reduction of electricity generation costs between 4.0% and 10.0% compared to the most cost-efficient pure component [25]. In contrast, case studies for waste heat recovery at a low-temperature level suggest that the choice of pure working fluids lead to slightly more profitable systems [26,27]. In this context, it should be noted that for waste heat recovery systems the selected working fluids and mixture components as well as the applied cost estimation methods have a far greater impact on cost efficiency due to significant lower costs for the exploitation of the heat source.
Under the consideration of zeotropic mixtures as potential ORC working fluids, we provide a thermo-economic analysis of waste heat recovery ORC, in order to clarify if an efficiency increase overcompensates the additional heat transfer requirements. A case study is performed for a heat source temperature of 150 °C. In this context, a second law analysis for the ORC working fluids R245fa, isobutane and isopentane, as well as for the zeotropic mixture isobutane/isopentane, is conducted. Based on the process parameters, the required heat exchange equipment is designed. Finally, the specific costs for the generated electricity are calculated. Depending on the working fluid composition and the minimal temperature difference in the condenser and evaporator, the most cost-efficient system is identified. Additionally, the dependence of specific costs per unit exergy on turbine efficiency, cost database, process integration costs, as well as cost estimation method, are examined based on selected operational parameters.
2. Methods
2.1. Exergy Analysis
For the exergy analysis, steady-state simulations are performed using the software Cycle Tempo [28]. Fluid properties are calculated by REFPROP Version 9.1 [29]. Additional citations to the specific models for each equation of state and the transport property models regarding each working fluid are provided in Appendix A. Process simulations are conducted for a subcritical and saturated cycle. The scheme of the module and the corresponding T,s-diagram in case of a pure working fluid is illustrated in Figure 1. Uncertainties of the simulation model and the reliability of the fluid properties regarding the selected working fluids are discussed in previous publications [25,30].
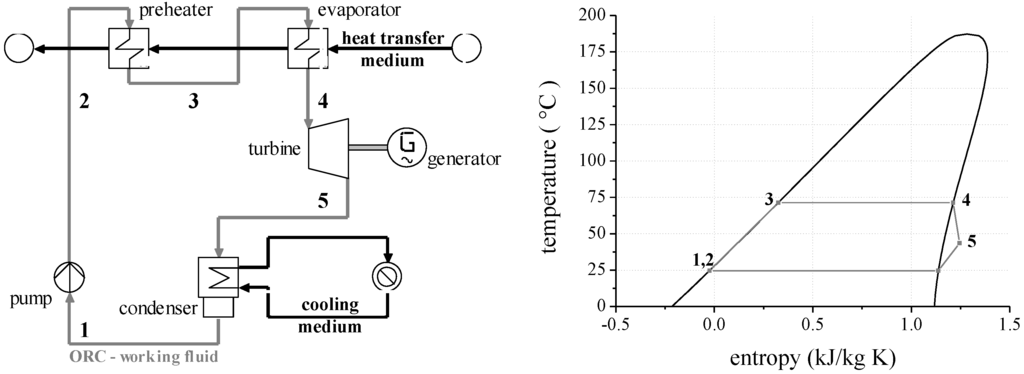
Figure 1.
Scheme of ORC system and corresponding T,s-diagram for the working fluid isopentane.
The present case study considers a low-temperature waste heat source of 150 °C. As a heat transfer medium, pressurized water is assumed (pHS = 6 bar). The mass flow and the outlet temperature of the heat source are chosen according to a thermal heat input of 3 MW. For the analysis, an air-cooled system is considered. R245fa, isobutane and isopentane, as well as the zeotropic mixture of isobutane/isopentane, are examined as ORC working fluids. Previous analysis show that isobutane and isobutane/isopentane lead to high second law efficiencies for the considered heat source temperature [25]. In order to evaluate the pure components of the fluid mixture, also isopentane is included to the analysis. In addition, R245fa is examined as benchmark, since this working fluid is commonly used in existing ORC power systems at the considered temperature level [30,31]. For the considered mixture, the composition is varied in discrete steps of 10 mol%. The temperature difference in the evaporator and condenser are chosen as independent design variables in order to identify the most cost-efficient process parameters. The analysis is conducted neglecting pressure and heat losses in the pipes and components. In Table 1 the boundary conditions for the cycle simulations are shown.

Table 1.
Boundary conditions assumed for the second law analysis.
To evaluate the cycle efficiency, the net second law efficiency ηII of the ORC is calculated by:
where PG and PPump correspond to the power of the generator and the pump. PFans is related to the power of the air cooler fans. The exergy flow of the heat source HS is obtained by multiplying the specific exergy eHS with the mass flow rate ṁHS. The specific exergy could be calculated by:
where the subscript 0 corresponds to the reference state (T0 = 15 °C and p0 = 1 bar). Corresponding to Bejan et al. [32], the exergy analysis is extended by an exergy balance for each system component k:
where F and P describe the exergy flow rate of the fuel and the product. The exergy flow rate L includes heat losses to the surrounding or exergy that leaves the system in a physical way, like exhaust gases. Here, L = 0, due to neglected heat losses. The exergy flow rate D represents the exergy destruction rate associated to irreversibilities. Exemplarily, the exergy destruction rate of the preheater can be calculated as:
where Tm,PH is the thermodynamic mean temperature of the heat source in the preheater.
2.2. Component Design and Economic Analysis
For the major components of the ORC module, the purchased equipment costs (PEC) are estimated based on cost data of Turton et al. [33]. In general, PEC are calculated for ambient operating conditions and a carbon steel construction C0 in US $ depending on the parameter Y:
where Y represents the capacity or size of a component. The parameters K1, K2, and K3 are listed in Table 2. Alternatively, bare module costs are estimated by data of Ulrich and Vasudevan [34]. A conversion ratio of 0.815 is considered to convert the PEC in Euro. Due to maximal ORC pressures below 35 bar, additional cost factors are only considered in Section 3.3.

Table 2.
Equipment cost data used for Equation (5) according to [33].
By setting the corresponding Chemical Engineering Plant Cost Index (CEPCI2001) of 397 into relation to the value of 2014 with 575, the inflation and the development of raw material prices are taken into account [33]. For the costs of the major components of the ORC power plant CORC,MC the PEC are summarized. In this study, the total investment costs of the power plant module CTM are calculated by multiplying CORC,MC by the factor Fcosts = 6.32. According to Bejan et al. [32] this parameter represents additional costs like installation, piping, controls, basic engineering, and others in the case of the construction of a new facility. In addition, the authors specify the factor Fcosts = 4.16 for the expansion of existing facilities. Alternatively, the total module costs are estimated according to Turton et al. [33]. Therefore, bare module equipment costs for a component at real operating conditions CBM is calculated by multiplying the obtained purchased equipment costs C0 by corrections factors depending on material Fm and pressure Fp.
For an addition to an existing facility, the total module costs CTM,Turton are defined by:
The described cost estimation methods are compared in the sensitivity analysis of Section 3.3.
For the shell and tube heat exchanger in counter flow, the heat exchange area A is determined according to Equation (10). Therefore, the overall heat transfer coefficient Utot of each heat exchanger is calculated by:
where αo represents the heat transfer coefficient at the outside of the tube, respectively, the shell side and αi corresponds to the heat transfer coefficient at the inside of the tube. The inner and outer radius of the tube are represented by ri and ro. The thermal conductivity of the tube corresponds to λt. The outer diameter of the tubes is 20 mm and the wall thickness of the tube is 2 mm. In order to calculate the required diameter of the shell and the number of tubes, the maximal flow velocities of 1.5 m/s for liquid flows and 20 m/s for gaseous flows are assumed according to chapter O1 of the VDI Heat Atlas [35]. In general, the ORC working fluid is led inside the tubes. Regarding the tube layout, a squared pitch and a pitch-to-diameter ratio of 1.22 are assumed. The considered heat transfer correlations for the calculation of αi, depending on phase state and flow configuration are listed in Table 3. A detailed overview of the correlations is provided in appendix B. In case of the preheater and the evaporator, the method of Kern [36] is applied for the shell side (αo). For the air-cooled condenser a tube bank staggered arrangement is applied. In this context, a cross-flow heat exchanger with finned tubes is considered and the following design parameters are assumed: fin height of 3 mm, a fin thickness of 0.3 mm, a fin spacing of 2 mm, and a transversal tube pitch of 60 mm. The air-side heat transfer coefficient is determined by the method of Shah and Sekulic [37]. For all considered heat exchangers, the heat transfer surface is finally calculated by:
where ΔTlog is the logarithmic mean temperature difference:

Table 3.
References for the considered heat transfer correlations (for details see Appendix B).
In general, the logarithmic mean temperature difference correction factor FLMTD is equal 1 for condensation and boiling heat transfer. In this study, the simplifying assumption of FLMTD = 1 is also met for single phase heat transfer.
2.3. Exergy Costing
The thermo-economic analysis combines thermodynamic and economic aspects. In this context, the product of the energy conversion as well as each component can be evaluated according to the cost formation process. For the presented analysis, the method by Tsatsaronis and Winhold [44], also known as exergo-economic method, is used. The exergy costing converts an exergy stream to a cost stream by multiplying the exergy with corresponding average costs per unit of exergy, respectively, specific costs c. In this context, a system of equations is set up consisting of the cost balance for each component k of system [24,32]:
The cost streams k describe the costs of the k-th component depending on operation and maintenance OM and capital investment CI. In order to calculate the described cost streams the economic boundary conditions listed in Table 4 are assumed.

Table 4.
Economic parameters for the calculation of the cost streams k.
The selected optimization criteria for the system is the minimization of the costs per unit exergy of the total system cP,tot. In this study, the generated electricity is considered as the product of the system and the P,tot correspond to the power output of the generator. In this context, the auxiliary power requirements are covered by electricity from the grid. Alternatively, the net power output of the system can be considered in the denominator of Equation (13). The exergy rate of the fuel F,tot represents the exergy rate of the waste heat source transferred to the ORC system.
In addition, the specific investment costs of the major components SICMC:
the specific investment costs of the total ORC module SICTM:
and the levelized costs of electricity LCOE are calculated:
here CCI are the yearly financial linked costs and Eannual is the annual amount of generated electricity.
3. Results and Discussion
3.1. Identification of Cost-Efficient Design Parameters
For each working fluid the minimal costs per unit exergy cp,tot are identified depending on the minimal temperature difference ΔTPP in the evaporator and condenser. In order to vary the minimal temperature difference, the corresponding upper and lower ORC pressure is adapted. In Figure 2, the specific costs of the product are shown exemplarily for R245fa. The most cost-efficient design parameters for this ORC working fluid are ΔTPP,E = 1 K and ΔTPP,C = 13 K. For these parameters, costs per unit exergy of 56.8 €/GJ are obtained. Considering a minimal temperature difference between 0.5 K and 6 K for the evaporator and 8 K and 14 K for the condenser, the maximum costs per unit exergy of 60.0 €/GJ are calculated (ΔTPP,E = 6 K; ΔTPP,C = 8 K). In general, the cost minimum is a compromise between rising power output and increasing costs with decreasing minimal temperature difference in the heat exchangers. The results show that the condenser is crucial for the total PEC. Due to the highest amount of transferred thermal energy combined with the lowest logarithmic mean temperature difference, the highest heat transfer areas and component costs are obtained for the condenser. In case of the most cost-efficient solution for R245fa, the PEC of the condenser are 47.6%, the PEC of the turbine are 36.8%, PEC of the preheater and the evaporator are 14.1% and PEC of the pump are 1.5% in relation to the total PEC of the major ORC components. To summarize: the most cost-effective parameters show a low ΔTPP for the evaporator and a high value in case of the condenser. This general result is also suitable for water-cooled systems. A previous thermo-economic study of geothermal, water-cooled ORC systems showed similar results [24].
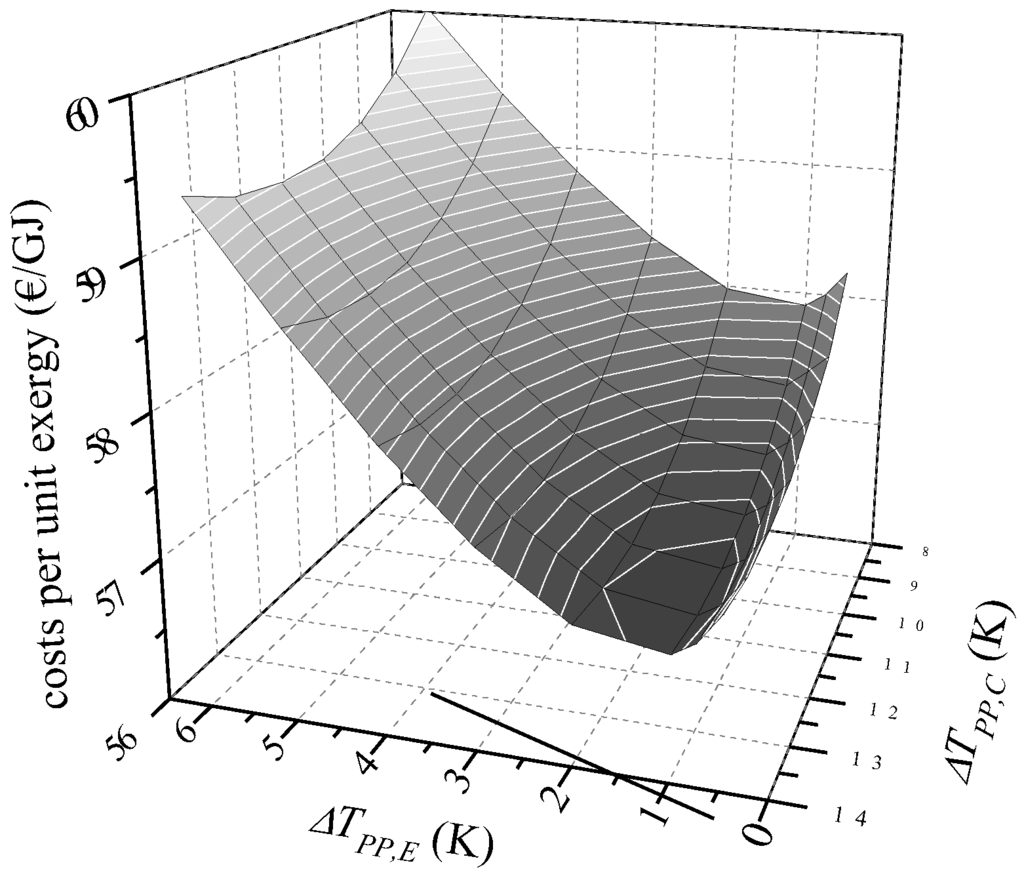
Figure 2.
Costs per unit exergy for R245fa as ORC working fluid depending on the minimum temperature difference in the evaporator and condenser.
3.2. Comparison of ORC Working Fluids
Power output, heat transfer area and, therefore, capital investment costs for the ORC modules may vary considerably due to the working fluid selection and the corresponding fluid properties. In this context, Figure 3a illustrates the costs per unit exergy for the pure ORC working fluids isopentane, isobutane, and R245fa as a function of the minimum temperature difference in the condenser. For ΔTPP,E, always the most cost-effective parameter is chosen. In Figure 3b specific costs of the product are shown for selected mole fractions of the zeotropic mixture isobutane/isopentane.
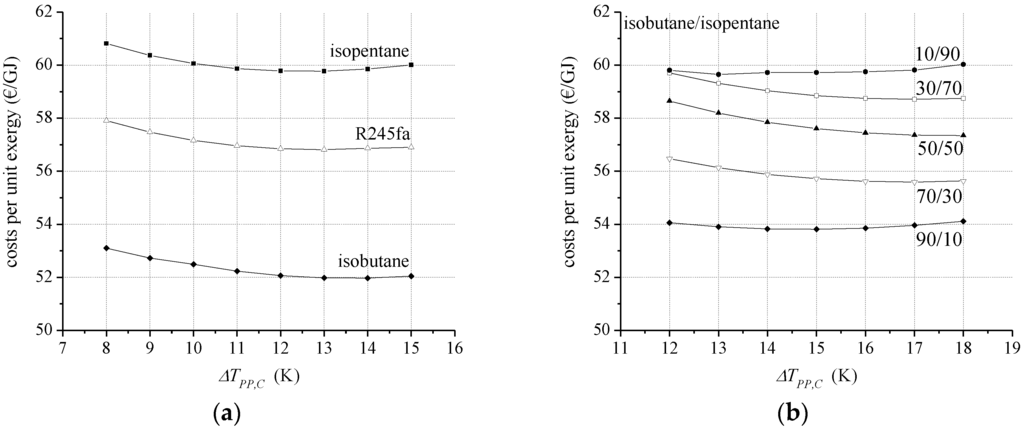
Figure 3.
Specific costs per unit exergy (a) for selected pure ORC working fluids and (b) for the zeotropic mixture isobutane/isopentane depending on the minimum temperature difference in the condenser.
Isobutane is identified as the most cost-effective working fluid for the considered case study with costs per unit exergy of 52.0 €/GJ. The corresponding design parameters are ΔTPP,E = 1.2 K and ΔTPP,C = 14 K. At these operational parameters the maximum ORC pressure is reached in case of isobutane. R245fa and isopentane lead to 9.2% and 15.0% higher costs per unit exergy (see Table 5). Although, these alternative pure working fluids show optimal design parameters with a lower minimum temperature difference, the gross power output is 10.8% and 14.6% lower. Due to the high power requirements of the ORC pump in case of isobutane, the net second law efficiency is only between 1.0% and 3.0% higher compared to R245fa and isopentane. The total heat exchange area differs only slightly for the considered working fluids. Compared to isobutane, the total heat exchange area is 0.3% lower for R245fa and 2.1% higher for isopentane.

Table 5.
Selected ORC parameters for the most-effective cycles depending on fluid selection.
For the working fluid isobutane, the distribution of the PEC for the major ORC components is analogous to R245fa. The condenser leads to the highest PEC (43%) followed by the turbine (38%), the heat exchangers for the heat input (16%), and the ORC feed pump (3%). Differences in the portion of costs compared to R245fa result mainly from the increased turbine capacity and the corresponding reduction of the amount of heat, released by the condenser. In spite of the highest CORC,MC (449,917 €), isobutane leads to the lowest SIC due the high power output. In comparison, R245fa leads to the lowest CORC,MC (439,336 €). Nevertheless the SIC are 9.3% higher compared to isobutane. The LCOE listed in Table 4 confirm the so-far described economic results for pure working fluids. In this context, the working fluid isobutane show the lowest LCOE with 106.5 €/MWh. R245fa and isopentane show 1.3% and 3.6% higher values.
Regarding the mixture isobutane/isopentane, a mole fraction of 90% isobutane leads to the lowest costs. In the case of ΔTPP,E = 2 K and ΔTPP,C = 15 K specific costs of 53.8 €/GJ are obtained. The costs per unit exergy are 3.5% higher compared to the most efficient component isobutane. The total heat exchange area is 3.6% lower for 90/10 compared to isobutane, which leads to 2.0% lower CORC,MC. At the same time the power output is 5.5% lower. It should be noted that, based on the LCOE, the zeotropic mixture leads to most cost-efficient solution. For the listed operational parameter in Table 4 the ORC with the working fluid isobutane shows a 0.5% higher LCOE. The differences between the discussed economic parameters result from a different cost balancing. For the calculation of LCOE, costs for capital investment and costs for operation and maintenance are considered. In contrast, the exergo-economic method also includes costs for unused exergy which is released to the environment (see Equation (12)). In the case of the zeotropic mixture, this portion of costs leads to higher specific costs per unit exergy compared to isobutane. The contrary results of the parameters LCOE and cp,tot suggest a nearly economic equivalence of the identified ORC system based on isobutane and the zeotropic mixture isobutane/isopentane as working fluid.
3.3. Sensitivity Analysis for Selected Boundary Conditions
In order to identify the most cost-important parameters of the estimated boundary conditions, Figure 4 illustrates the costs per unit exergy as function of interest rate, turbine efficiency, costs for process integration, costs for operation and maintenance, and F-factor. The sensitivity analysis is conducted for the working fluid isobutane at the operational parameters ΔTPP,E = 2 K and ΔTPP,C = 12 K.
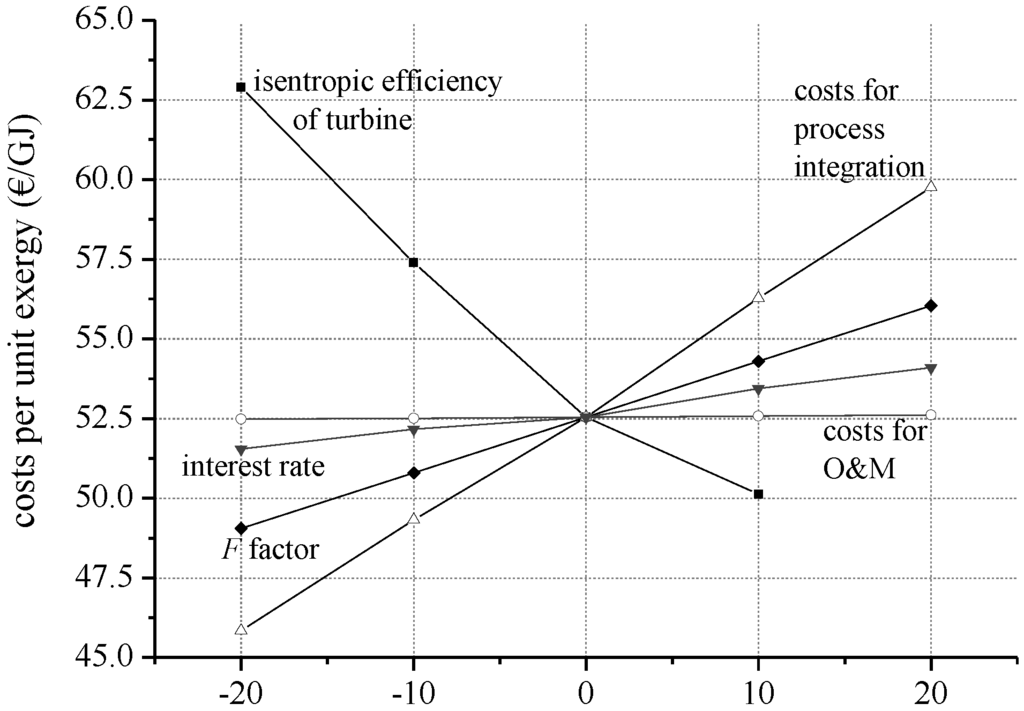
Figure 4.
Cost per unit exergy as a function of selected parameters for the working fluid isobutane (ΔTPP,E = 2 K; ΔTPP,C = 12 K).
The costs per unit exergy show the highest sensitivity for the isentropic efficiency of the turbine, the costs for process integration and the factor Fcosts. This general behavior can be adopted to other working fluids and operational parameters. The sensitivity analysis for the working fluids isobutane, isobutane/isopentane (90/10), and R245fa at the most cost-effective parameters show qualitatively equal results. Regarding the considered economic parameters, costs for process integration and the cost factor F are the most important input data. For systems with higher module costs the sensitivity is even more pronounced. In case of R245fa as working fluid, the specific costs increase by 0.19 €/GJ per % deviation from the standard costs for process integration. Compared to isobutane (according to Figure 4: 0.17 €/GJ per % deviation), this is an increase in sensitivity of 9.2%.
In order to quantify the uncertainties of the presented results due to the assumption of a constant isentropic efficiency and a specific cost estimation method, a detailed analysis for these main factors is conducted in the following. Since the process integration costs are mainly influenced by individual boundary conditions of the waste heat recovery application, a more detailed analysis of this proportion of costs is not in the scope of this study. In this context, the turbine efficiency and corresponding design parameters are calculated for the most cost-effective operational parameters of each working fluid (see Table 4). For the turbine, an axial and single-stage turbine is assumed. The corresponding design and loss correlations are applied according to Klonowicz et al. [45]. The results including the corresponding costs per unit exergy are listed in Table 6.

Table 6.
Turbine parameter and cost per unit exergy for a detailed design of an axial turbine.
The isentropic efficiency of the turbine differs between 78.5% and 80.6% for the considered working fluids and corresponding operational parameters. Isobutane shows a 1.9% lower efficiency compared to the assumption of a constant efficiency of 80% according to Table 1. For isopentane, the turbine efficiency is underestimated by 0.8%. With respect to the cost-efficiency, a more detailed estimation of turbine efficiency leads to a maximal deviation of 1.3% of the economic parameter cp,tot. In this context, the costs per unit exergy for the working fluid isopentane is decreased from 59.8 €/GJ to 59.1 €/GJ. Isobutane still leads to the most cost-effective ORC system. The specific costs are increased by 0.4% compared to the initial efficiency assumption. In case of R245fa or isopentane as workings fluid, the turbine design calculations show high values for the size parameter SP and the mean diameter Dm. Hence, high isentropic efficiencies are obtained in conjunction with a large turbine size. For further investigations, the design parameters could be used as input for more precise cost estimations. In this context, exemplarily the turbine cost correlation of Astolfi et al. [17] could be mentioned.
Finally, the relevant economic parameters are calculated for selected cost estimation methods and cost databases described in Chapter 2.2. For the working fluid isobutane at the operational parameters ΔTPP,E = 1.2 K and ΔTPP,C = 14 K the results are listed in Table 7.

Table 7.
Economic parameters for selected cost estimation methods and cost databases in case of isobutane at the operational parameters ΔTPP,E = 1.2 K and ΔTPP,C = 14 K.
In general, the considered cost estimation methods lead to high deviations for the economic parameters. The maximum deviation for cP,tot is 28.4 %, for LCOE 81.4% and for SIC 287.0%. The calculation of bare module costs in conjunction with cost correlation of Turton et al. [33] lead to the lowest economic parameters. For the alternative cost database of Ulrich and Vasudevan [34], which also provides bare module costs, the costs per unit exergy are 7.9% higher. A comparison of SIC for waste heat recovery units with literature data [22,23,26] or guide prices from manufactures indicate the generalization of the approach of Bejan et al. [32] by multiplying the total PEC by a certain factor Fcost. As a consequence, the resulting absolute costs should be interpreted with caution. Nevertheless, an evaluation of different technical solutions, working fluids, or operational parameters for constant boundary conditions seems justifiable.
4. Conclusions
A thermo-economic case study for waste heat recovery by ORC is conducted. Cost-efficient design parameters for the temperature difference at the pinch point are identified in the case of pure working fluids and mixtures. In general, low minimum temperature differences in the evaporator and high values in the condenser are suitable for a cost-efficient ORC system. Isobutane as a working fluid leads to the most cost-effective ORC (ΔTPP,E = 1.2 K; ΔTPP,C = 14 K). Regarding the considered mixture isobutane/isopentane, a mole fraction of 90% isobutane leads to the lowest costs per unit exergy. The economic parameters show a high sensitivity regarding the isentropic efficiency of the turbine and the selected cost estimation methods. First results are presented for an implementation of more detailed models concerning these impact factors. Based on this analysis, the presented thermo-economic model will be extended in further work.
Acknowledgments
The work was funded by the German Research Foundation (DFG) with project No. BR 1713/12. In particular, this publication was funded by the German Research Foundation (DFG) and the University of Bayreuth in the funding programme Open Access Publishing. The authors gratefully acknowledge this support.
Author Contributions
All authors contributed to this work. Florian Heberle is the main author of this work. The whole project was supervised by Dieter Brüggemann.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ORC | Organic Rankine Cycle |
Nomenclature
| A | heat transfer area | (m2) |
| c | costs per unit exergy | (€/GJ) |
| C | costs | (€) |
| cost rate | (€/h) | |
| D | diameter | (mm) |
| e | specific exergy | (kJ/kg) |
| exergy flow | (kW) | |
| F | correction factor | (-) |
| h | specific enthalpy | (kJ/kg) |
| K | constant | (-) |
| ṁ | mass flow | (kg/s) |
| Ns | specific speed | (-) |
| p | pressure | (bar) |
| P | power | (kW) |
| r | radius | (m) |
| rd | relative deviation | (%) |
| s | specific entropy | (kJ/(kgK)) |
| SIC | specific investment costs | (€/kW) |
| SP | size parameter | (-) |
| T | temperature | (°C) |
| U | overall heat transfer coefficient | (W/(m2K)) |
| Y | capacity/size parameter | (kW) or (m2) |
| cost rate | (€/h) | |
| α | heat transfer coefficient | (W/(m2K)) |
| ΔT | temperature difference | (K) |
| η | efficiency | (%) |
Subscript
| C | condenser |
| CI | capital investment |
| CM | cooling medium |
| D | destruction |
| E | evaporator |
| F | fuel |
| G | generator |
| HS | heat source |
| i | inner |
| in | inlet |
| is | isentropic |
| II | second law |
| k | k-th component |
| L | loss |
| LMTD | logarithmic mean temperature difference |
| log | logarithmic |
| m | mean |
| net | net |
| o | outer |
| out | outlet |
| O&M | operation and maintenance |
| P | product |
| PH | preheater |
| PP | pinch point |
| Pump | pump |
| s | specific |
| t | tube |
| tot | total |
| 0 | reference state |
Appendix A
In this section the references for each equation of state (EOS) and the transport models used in REFPROP are listed for the considered working fluids.
R245fa
EOS: Lemmon, E.W.; Span, R. Short fundamental equations of state for 20 industrial fluids. J. Chem. Eng. Data 2006, 51, 785–850. [Google Scholar] [CrossRef]
Viscosity: Huber, M.L.; Laesecke, A.; Perkins, R.A. Model for the Viscosity and Thermal Conductivity of Refrigerants, Including a New Correlation for the Viscosity of R134a. Ind. Eng. Chem. Res. 2003, 42, 3163–3178. [Google Scholar] [CrossRef]
Thermal conductivity: Marsh, K.N.; Perkins, R.A.; Ramires, M.L. Measurement and Correlation of the Thermal Conductivity of Propane from 86 to 600 K at Pressures to 70 MPa. J. Chem. Eng. Data 2002, 47, 932–940. [Google Scholar] [CrossRef]
Surface tension: Mulero, A.; Cachadina, I.; Parra, M. I. Recommended Correlations for the Surface Tension of Common Fluids. J. Phys. Chem. Ref. Data 2013, 41, 043105. [Google Scholar] [CrossRef]
Isobutane
EOS: Bücker, D.; Wagner, W. Reference Equations of State for the Thermodynamic Properties of Fluid Phase n-Butane and Isobutane. J. Phys. Chem. Ref. Data 2006, 35, 929–1019. [Google Scholar] [CrossRef]
Viscosity: Vogel, E.; Küchenmeister, C.; Bich, E. Viscosity Correlation for Isobutane over Wide Ranges of the Fluid Region. Int. J. Thermophys. 2000, 21, 343–356. [Google Scholar] [CrossRef]
Thermal conductivity: Perkins, R.A. Measurement and Correlation of the Thermal Conductivity of Isobutane from 114 K to 600 K at Pressures to 70 MPa. J. Chem. Eng. Data 2002, 47, 1272–1279. [Google Scholar] [CrossRef]
Surface tension: Mulero, A.; Cachadina, I.; Parra, M.I. Recommended Correlations for the Surface Tension of Common Fluids. J. Phys. Chem. Ref. Data 2013, 41, 043105. [Google Scholar] [CrossRef]
Isopentane
EOS: Lemmon, E.W.; Span, R. Short fundamental equations of state for 20 industrial fluids. J. Chem. Eng. Data 2006, 51, 785–850. [Google Scholar] [CrossRef]
Viscosity: Ely, J.F.; Huber, M.L. NIST Thermophysical Properties of Hydrocarbon Mixtures Database, NIST Standard Reference Database 14; Version 9.08; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1990. [Google Scholar]
Thermal conductivity: Ely, J.F.; Huber, M.L. NIST Thermophysical Properties of Hydrocarbon Mixtures Database, NIST Standard Reference Database 14; Version 9.08; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1990. [Google Scholar]
Surface tension: Mulero, A.; Cachadina, I.; Parra, M.I. Recommended Correlations for the Surface Tension of Common Fluids. J. Phys. Chem. Ref. Data 2013, 41, 043105. [Google Scholar] [CrossRef]
Isobutane/Isopentane
Mixing Rule: Kunz, O.; Klimeck, R.; Wagner, W.; Jaeschke, M. The GERG-2004 Wide-Range Equation of State for Natural Gases and Other Mixtures—GERG Technical Monograph; VDI-Fortschritts-Bericht: Düsseldorf, Germany, 2007. [Google Scholar]
Appendix B
Depending on phase state and flow configuration corresponding heat transfer correlations are applied. For the calculation of the heat transfer of turbulent, single phase flow in a plain tube, the model according to Sieder and Tate [38] is used for the working fluid in the preheater. The corresponding Nusselt number Nu depends on the Reynolds number Re and the Prandtl number Pr:
The single phase heat transfer on the shell side is predicted according to Kern [36]. The model is applied for the pressurized water in the preheater and evaporator:
In case of the evaporation of pure working fluids in a plain tube the correlation for flow boiling derived from Steiner [39] is applied:
Here the index l represents the liquid phase and g corresponds to the gaseous phase. The corresponding heat transfer coefficients αl and αg are calculated by Equation (B1). In Equation (B3) ρ correspond to density and x to vapor quality.
Considering the evaporation of fluid mixtures, a reduction of heat transfer has to be taken into account. In this context, the model of Schlünder [40] is applicable:
Here, β as well as B0 represent experimental fitted constants. The following assumptions are made: β = 2 × 10−4 m/s and B0 = 1. The mole fraction of liquid and gaseous phase of the component i corresponds to xi and yi. The temperatures Tsi describe the saturation temperature of the mixture component.
The condensation of a pure working fluid in plain tubes is calculated according to the correlation of Shah [41].
Here, x represents the vapor quality and p* corresponds to the reduced pressure. In analogy to the evaporation process, a reduction of heat transfer due to additional mass transfer has to be considered for zeotropic mixtures. Therefore, the method of Sliver, Bell, and Ghaly [42,43] is applied. In Equation (B6) αeff represents the heat transfer coefficient for the zeotropic mixture, while α(x) is calculated according to Equation (B5) using fluid properties of the fluid mixture. For the heat transfer coefficient in the gaseous phase αg Equation (B7) is applied:
The parameter Zg is the ratio between the sensible part of the condensation of the zeotropic mixture and the latent part. Here, cp,g represents the heat capacity of the gaseous phase, TG,Cond the temperature glide at condensation, and Δh the corresponding enthalpy difference.
References
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Low-grade heat conversion into power using organic Rankine cycles—A review of various applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979. [Google Scholar] [CrossRef]
- Angelino, G.; Di Paliano, P.C. Multicomponent Working Fluids for Organic Rankine Cycles (ORCs). Energy 1998, 23, 449–463. [Google Scholar] [CrossRef]
- Iqbal, K.Z.; Fish, L.W.; Starling, K.E. Advantages of using mixtures as working fluids in geothermal binary cycles. Proc. Okla. Acad. Sci. 1976, 56, 110–113. [Google Scholar]
- Demuth, O.J. Analyses of mixed hydrocarbon binary thermodynamic cycles for moderate temperature geothermal resources. In Proceedings of the Intersociety Energy Conversion Engineering Conference (IECEC), Atlanta, GA, USA, 9–14 August 1981.
- Borsukiewicz-Gozdur, A.; Nowak, W. Comparative analysis of natural and synthetic refrigerants in application to low temperature Clausius-Rankine cycle. Energy 2007, 32, 344–352. [Google Scholar] [CrossRef]
- Wang, X.D.; Zhao, L. Analysis of zeotropic mixtures used in low-temperature solar Rankine cycles for power generation. Sol. Energy 2009, 83, 605–613. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Rahman, M.M.; Stefanakos, E.K. A supercritical Rankine cycle using zeotropic mixture working fluids for the conversion of low-grade heat into power. Energy 2011, 36, 549–555. [Google Scholar] [CrossRef]
- Garg, P.; Kumar, P.; Srinivasan, K.; Dutta, P. Evaluation of isopentane, R-245fa and their mixtures as working fluids for organic Rankine cycles. Appl. Therm. Eng. 2013, 51, 292–300. [Google Scholar] [CrossRef]
- Dong, B.; Xu, G.; Cai, Y.; Li, H. Analysis of zeotropic mixtures used in high-temperature Organic Rankine cycle. Energy Convers. Manag. 2014, 84, 253–260. [Google Scholar] [CrossRef]
- Lecompte, S.; Ameel, B.; Ziviani, D.; Van Den Broek, M.; De Paepe, M. Exergy analysis of zeotropic mixtures as working fluids in Organic Rankine Cycles. Energy Convers. Manag. 2014, 85, 727–739. [Google Scholar] [CrossRef]
- Shu, G.; Gao, Y.; Tian, H.; Wei, H.; Liang, X. Study of mixtures based on hydrocarbons used in ORC (Organic Rankine Cycle) for engine waste heat recovery. Energy 2014, 74, 428–438. [Google Scholar] [CrossRef]
- Heberle, F.; Preißinger, M.; Brüggemann, D. Zeotropic mixtures as working fluids in Organic Rankine Cycles for low-enthalpy geothermal resources. Renew. Energy 2012, 37, 364–370. [Google Scholar] [CrossRef]
- Andreasen, J.G.; Larsen, U.; Knudsen, T.; Pierobon, L.; Haglind, F. Selection and optimization of pure and mixed working fluids for low grade heat utilization using organic rankine cycles. Energy 2014, 73, 204–213. [Google Scholar] [CrossRef]
- Angelino, G.; Colonna, P. Air cooled siloxane bottoming cycle for molten carbonate fuel cells. In Proceedings of the Fuel Cell Seminar, Portland, OR, USA, 30 October–02 November 2000; pp. 667–670.
- Weith, T.; Heberle, F.; Preißinger, M.; Brüggemann, D. Performance of Siloxane Mixtures in a High-Temperature Organic Rankine Cycle Considering the Heat Transfer Characteristics during Evaporation. Energies 2014, 7, 5548–5565. [Google Scholar] [CrossRef]
- Tempesti, D.; Fiaschi, D. Thermo-economic assessment of a micro CHP system fuelled by geothermal and solar energy. Energy 2013, 58, 45–51. [Google Scholar] [CrossRef]
- Astolfi, M.; Romano, M.C.; Bombarda, P.; Macchi, E. Binary ORC (Organic Rankine Cycles) power plants for the exploitation of medium–low temperature geothermal sources—Part B: Techno-economic optimization. Energy 2014, 66, 435–446. [Google Scholar] [CrossRef]
- Heberle, F.; Brüggemann, D. Thermoeconomic Analysis of Hybrid Power Plant Concepts for Geothermal Combined Heat and Power Generation. Energies 2014, 7, 4482–4497. [Google Scholar] [CrossRef]
- Calise, F.; Capuozzo, C.; Carotenuto, A.; Vanoli, L. Thermoeconomic analysis and off-design performance of an organic Rankine cycle powered by medium-temperature heat sources. Sol. Energy 2014, 103, 595–609. [Google Scholar] [CrossRef]
- Desai, N.B.; Bandyopadhyay, S. Thermo-economic analysis and selection of working fluid for solar organic Rankine cycle. Appl. Therm. Eng. 2016, 95, 471–481. [Google Scholar] [CrossRef]
- Quoilin, S.; Declaye, S.; Tchanche, B.F.; Lemort, V. Thermo-economic optimization of waste heat recovery Organic Rankine Cycles. Appl. Therm. Eng. 2011, 31, 2885–2893. [Google Scholar] [CrossRef]
- Imran, M.; Park, B.S.; Kim, H.J.; Lee, D.H.; Usman, M.; Heo, M. Thermo-economic optimization of Regenerative Organic Rankine Cycle for waste heat recovery applications. Energy Convers. Manag. 2014, 87, 107–118. [Google Scholar] [CrossRef]
- Quoilin, S.; Broek, M.V.D.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Heberle, F.; Bassermann, P.; Preissinger, M.; Brüggemann, D. Exergoeconomic optimization of an Organic Rankine Cycle for low-temperature geothermal heat sources. Int. J. Thermodyn. 2012, 15, 119–126. [Google Scholar] [CrossRef]
- Heberle, F.; Brüggemann, D. Thermo-Economic Evaluation of Organic Rankine Cycles for Geothermal Power Generation Using Zeotropic Mixtures. Energies 2015, 8, 2097–2124. [Google Scholar] [CrossRef]
- Le, V.L.; Kheiri, A.; Feidt, M.; Pelloux-Prayer, S. Thermodynamic and economic optimizations of a waste heat to power plant driven by a subcritical ORC (Organic Rankine Cycle) using pure or zeotropic working fluid. Energy 2014, 78, 622–638. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Sensitivity analysis and thermoeconomic comparison of ORCs (organic Rankine cycles) for low temperature waste heat recovery. Energy 2015, 82, 664–677. [Google Scholar] [CrossRef]
- Woudstra, N.; van der Stelt, T.P. Cycle-Tempo: A Program for the Thermodynamic Analysis and Optimization of Systems for the Production of Electricity, Heat and Refrigeration; Energy Technology Section, Delft University of Technology: Delft, The Netherlands, 2002. [Google Scholar]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. Physical and Chemical Properties Division. In NIST Standard Reference Database 23—Version 9.1; National Institute of Standards and Technology: Boulder, CO, USA, 2013. [Google Scholar]
- Heberle, F.; Jahrfeld, T.; Brüggemann, D. Thermodynamic Analysis of Double-Stage Organic Rankine Cycles for Low-Enthalpy Sources based on a Case Study for 5.5 MWe Power Plant Kirchstockach (Germany). In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015.
- ORC systems—Bosch KWK Systeme. Available online: http://www.bosch-kwk.de/en/solutions/bosch-kwk-systeme-orc-systems/ (accessed on 22 February 2016).
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Turton, R.; Bailie, R.C.; Whiting, W.B. Analysis, Synthesis and Design of Chemical Processes, 2nd ed.; Prentice Hall: Old Tappan, NJ, USA, 2003. [Google Scholar]
- Ulrich, G.D.; Vasudevan, P.T. Chemical Engineering—Process Design and Economics; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Stephan, P.; Kabelac, S.; Kind, M.; Martin, H.; Mewes, D.; Schaber, K. VDI Heat Atlas; Springer Verlag: Berlin, Germany, 2010. [Google Scholar]
- Kern, D.Q. Process Heat Transfer; McGraw-Hill: New York, NY, USA, 1950. [Google Scholar]
- Shah, M.M.; Sekulic, D.P. Heat Exchanger Design Procedures, in Fundamentals of Heat Exchanger Design; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Sieder, E.N.; Tate, G.E. Heat transfer and pressure drop of liquids in tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Steiner, D. Wärmeübertragung beim Sieden gesättigter Flüssigkeiten (Abschnitt Hbb). In VDI-Wärmeatlas; Springer Verlag: Berlin, Germany, 2006. [Google Scholar]
- Schlünder, E.U. Heat transfer in nucleate boiling of mixtures. Int. Chem. Eng. 1983, 23, 589–599. [Google Scholar]
- Shah, M.M. A general correlation for heat transfer during film condensation inside pipes. Int. J. Heat Mass Transf. 1979, 22, 547–556. [Google Scholar] [CrossRef]
- Silver, R.S. An approach to a general theory of surface condensers. Proc. Inst. Mech. Eng. Part 1 1964, 179, 339–376. [Google Scholar]
- Bell, J.; Ghaly, A. An approximate generalized design method for multicomponent/partial condensers. AIChe Symp. Ser. Heat Transf. 1973, 69, 72–79. [Google Scholar]
- Tsatsaronis, G.; Winhold, M. Exergoeconomic analysis and evaluation of energy-conversion plants—I. A new general methodology. Energy 1985, 10, 69–80. [Google Scholar] [CrossRef]
- Klonowicz, P.; Heberle, F.; Preißinger, M.; Brüggemann, D. Significance of loss correlations in performance prediction of small scale, highly loaded turbine stages working in Organic Rankine Cycles. Energy 2014, 72, 322–330. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).