Electric Load Forecasting Based on a Least Squares Support Vector Machine with Fuzzy Time Series and Global Harmony Search Algorithm
Abstract
:1. Introduction
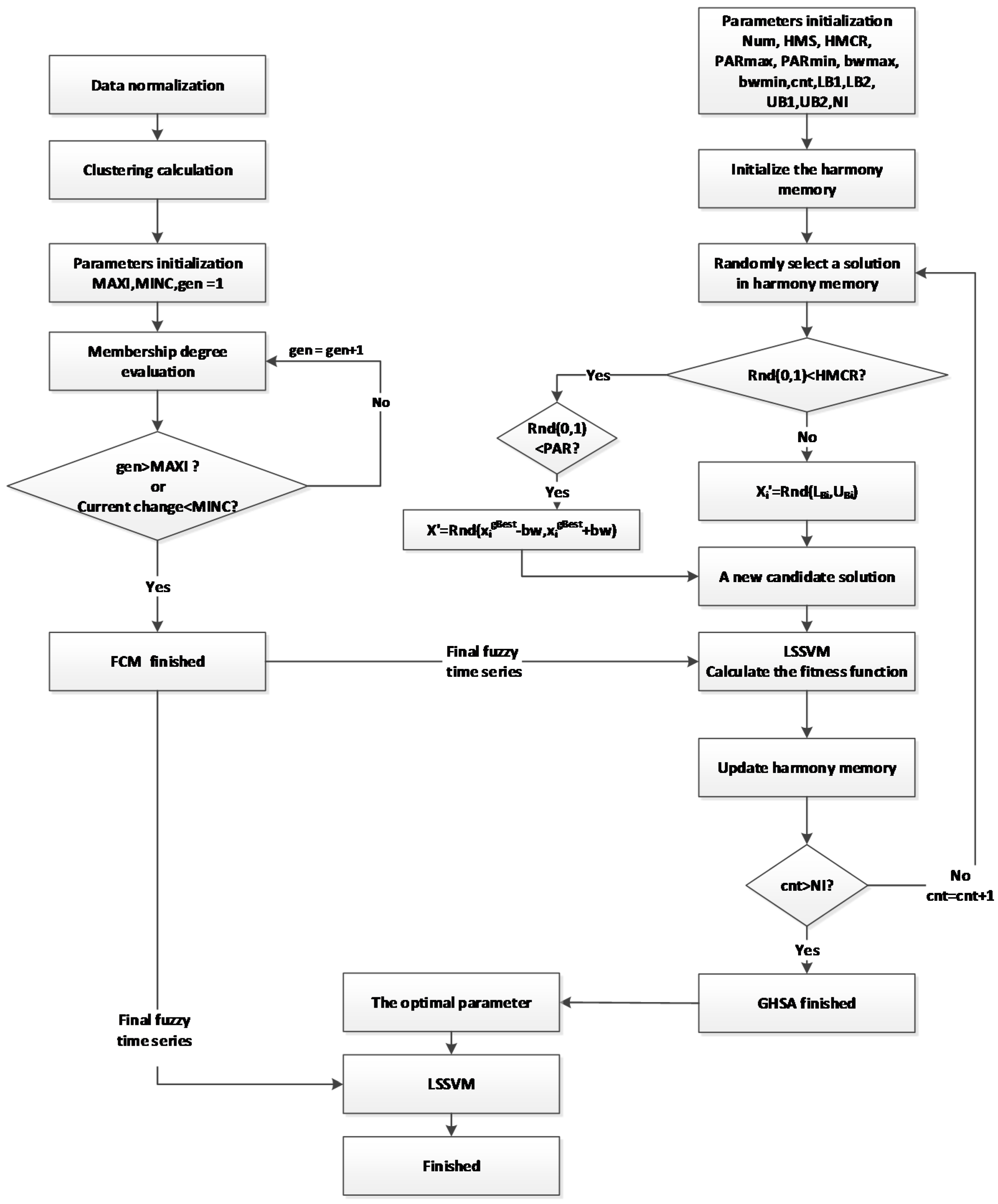
2. Methodology of Global Harmony Search Algorithm-Fuzzy Time Series-Least Squares Support Vector Machines Model
2.1. Least Squares Support Vector Machine Model
2.2. Global Harmony Search Algorithm in Parameters Determination of Least Squares Support Vector Machines Model
- Randomly generate a harmony memory in the size of from a uniform distribution in the range.
- Calculate the fitness of each candidate solution in the harmony memory and sort the results in ascending order.
- The harmony memory is generated by .
- If and , then . Palatino
- If and , then , where is an arbitrary distance bandwidth (BW) and is dimension of the best candidate solution.
- If , then .
2.3. Fuzzy Time Series Generation
2.3.1. Fuzzy Time Series Model
2.3.2. Fuzzy C-Means Clustering Algorithm
3. Numerical Example
3.1. Data Set
| Date | Load | Date | Load | Date | Load |
|---|---|---|---|---|---|
| January 2011 | 284.1 | May 2012 | 351.6 | September 2013 | 372.3 |
| February 2011 | 263.2 | June 2012 | 353.1 | October 2013 | 375.6 |
| March 2011 | 339.8 | July 2012 | 386.5 | November 2013 | 386.4 |
| April 2011 | 325.7 | August 2012 | 376.1 | December 2013 | 410.9 |
| May 2011 | 336.2 | September 2012 | 338 | January 2014 | 384.5 |
| June 2011 | 341 | October 2012 | 343 | February 2014 | 322.1 |
| July 2011 | 371.7 | November 2012 | 356.1 | March 2014 | 389.2 |
| August 2011 | 366.4 | December 2012 | 362.4 | April 2014 | 373.3 |
| September 2011 | 329.8 | January 2013 | 331 | May 2014 | 387.6 |
| October 2011 | 326.9 | February 2013 | 278.1 | June 2014 | 393.4 |
| November 2011 | 331.4 | March 2013 | 368.3 | July 2014 | 429.8 |
| December 2011 | 362.3 | April 2013 | 357.2 | August 2014 | 416.7 |
| January 2012 | 341.5 | May 2013 | 368.1 | September 2014 | 379.9 |
| February 2012 | 328.3 | June 2013 | 373.3 | October 2014 | 385.3 |
| March 2012 | 358.7 | July 2013 | 419.4 | November 2014 | 398.2 |
| April 2012 | 335.2 | August 2013 | 426.6 | December 2014 | 374.8 |
| Date | FTS | |||||||
|---|---|---|---|---|---|---|---|---|
| 11 January | 0.0104 | 0.0220 | 0.0338 | 0.0084 | 0.0036 | 0.9013 | 0.0063 | 0.0142 |
| 11 February | 0.0128 | 0.0227 | 0.0307 | 0.0108 | 0.0053 | 0.8928 | 0.0085 | 0.0163 |
| 11 March | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 11 April | 0.0064 | 0.0506 | 0.9181 | 0.0042 | 0.0011 | 0.0039 | 0.0026 | 0.0130 |
| 11 May | 0.0115 | 0.7581 | 0.1842 | 0.0066 | 0.0013 | 0.0026 | 0.0036 | 0.0322 |
| 11 June | 0.0026 | 0.9743 | 0.0106 | 0.0014 | 0.0002 | 0.0004 | 0.0007 | 0.0099 |
| 11 July | 0.1255 | 0.0054 | 0.0030 | 0.8256 | 0.0022 | 0.0006 | 0.0210 | 0.0165 |
| 11 August | 0.9547 | 0.0024 | 0.0012 | 0.0272 | 0.0006 | 0.0002 | 0.0037 | 0.0101 |
| 11 September | 0.0005 | 0.0064 | 0.9911 | 0.0003 | 0.0001 | 0.0002 | 0.0002 | 0.0011 |
| 11 October | 0.0029 | 0.0256 | 0.9604 | 0.0019 | 0.0005 | 0.0016 | 0.0011 | 0.0060 |
| 11 November | 0.0046 | 0.0747 | 0.9032 | 0.0028 | 0.0006 | 0.0017 | 0.0016 | 0.0107 |
| 11 December | 0.8419 | 0.0127 | 0.0058 | 0.0449 | 0.0019 | 0.0009 | 0.0098 | 0.0821 |
3.2. Global Harmony Search Algorithm-Least Squares Support Vector Machines Model
3.2.1. Parameters Selection by Global Harmony Search Algorithm
| Parameter | Value | Comment |
|---|---|---|
| num | Number of variables | |
| Range of each variable | ||
| Range of each variable | ||
| Harmony memory size | ||
| HMS considering rate | ||
| , | Pitch adjusting rate | |
| , | Bandwidth | |
| Number of iteration |
3.2.2. Fitness Function in Global Harmony Search Algorithm
3.2.3. Denormalization
3.2.4. Defuzzification Mechanism
| Month | Multiplier | Month | Multiplier |
|---|---|---|---|
| January | 1.00244 | July | 1.00612 |
| February | 0.98222 | August | 1.00567 |
| March | 0.99931 | September | 1.00069 |
| April | 0.99522 | October | 0.99932 |
| May | 0.99772 | November | 1.00937 |
| June | 1.00493 | December | 0.99996 |
3.3. Performance Evaluation
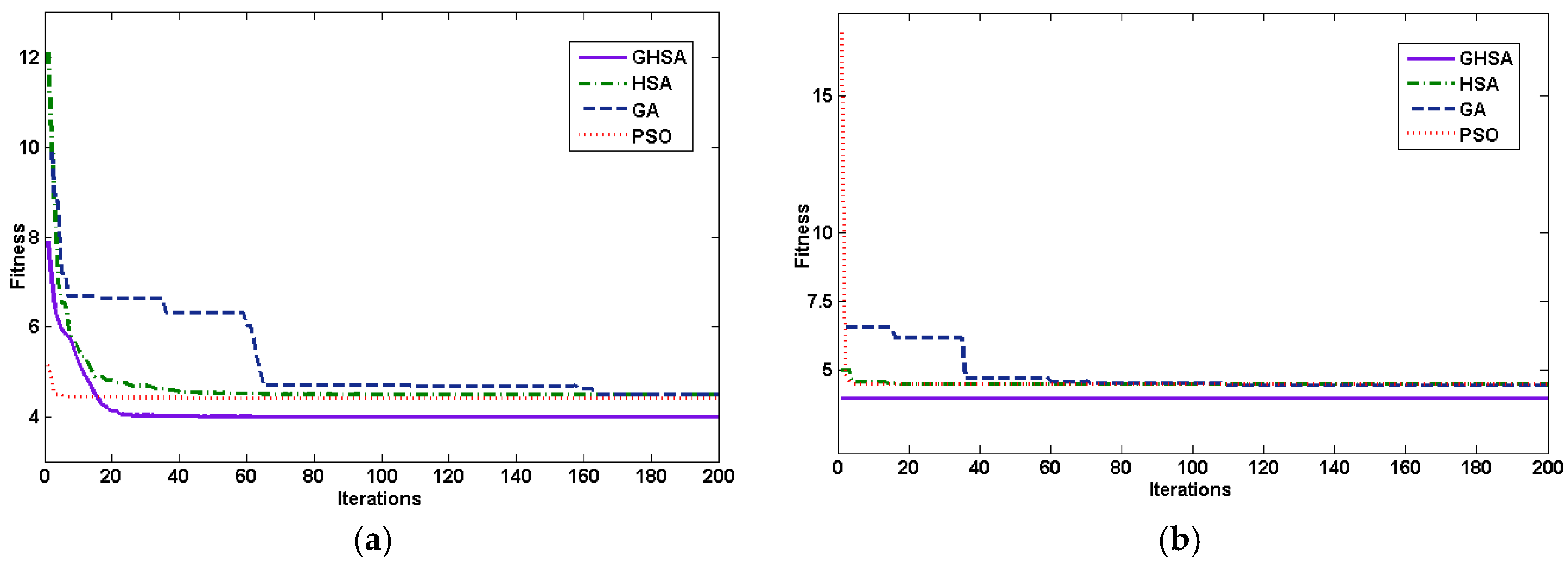
| Algorithm | Fitness | γ−1 | σ | Running Time/s |
|---|---|---|---|---|
| GHSA | 0.0397 | 0.00010 | 30.3977 | 9.2977 |
| HSA | 0.0489 | 0.00010 | 52.8422 | 8.2681 |
| GA | 0.0439 | 0.00010 | 52.8422 | 68.6248 |
| PSO | 0.0451 | 0.00011 | 22.3965 | 69.9352 |
| Time | Actual | GHSA-FTS-LSSVM | GHSA-LSSVM | GA-LSSVM [29] | PSO-LSSVM [30] | ARIMA |
|---|---|---|---|---|---|---|
| 15 January | 384.5 | 388.5989 | 387.094 | 387.066 | 393.205 | 399.142 |
| 15 February | 352.1 | 379.4326 | 372.661 | 372.65 | 373.62 | 381.038 |
| 15 March | 349.2 | 368.1298 | 355.006 | 355.01 | 352.864 | 359.864 |
| 15 April | 373.3 | 359.5839 | 353.429 | 353.434 | 351.189 | 377.003 |
| 15 May | 387.6 | 380.1802 | 366.55 | 366.545 | 366.026 | 362.173 |
| 15 June | 393.4 | 392.6603 | 374.353 | 374.341 | 375.799 | 361.905 |
| 15 July | 429.8 | 387.9569 | 377.522 | 377.506 | 379.962 | 399.488 |
| 15 August | 416.7 | 395.6517 | 397.452 | 397.409 | 408.614 | 432.612 |
| 15 September | 379.9 | 395.7048 | 390.271 | 390.239 | 397.814 | 423.027 |
| 15 October | 385.3 | 376.4279 | 370.15 | 370.142 | 370.449 | 404.338 |
| 15 November | 398.2 | 391.7981 | 373.098 | 373.086 | 374.179 | 390.129 |
| 15 December | 374.8 | 380.8968 | 380.146 | 380.127 | 383.494 | 385.307 |
| MAPE (%) | - | 3.709 | 4.579 | 4.579 | 4.654 | 5.219 |
| MAE | - | 14.358 | 18.035 | 18.035 | 18.215 | 20.153 |
| RMSE | - | 18.180 | 21.914 | 21.921 | 21.525 | 23.0717 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ghayekhloo, M.; Menhaj, M.B.; Ghofrani, M. A hybrid short-term load forecasting with a new data preprocessing framework. Electr. Power Syst. Res. 2015, 119, 138–148. [Google Scholar] [CrossRef]
- Kouhi, S.; Keynia, F. A new cascade NN based method to short-term load forecast in deregulated electricity market. Energy Convers. Manag. 2013, 71, 76–83. [Google Scholar] [CrossRef]
- Chen, J.F.; Wang, W.M.; Huang, C.M. Analysis of an adaptive time-series autoregressive moving-average (ARMA) model for short-term load forecasting. Electr. Power Syst. Res. 1995, 34, 187–196. [Google Scholar] [CrossRef]
- Nie, H.; Liu, G.; Liu, X.; Wang, Y. Hybrid of ARIMA and SVMs for short-term load forecasting. Energy Proced. 2012, 16, 1455–1460. [Google Scholar] [CrossRef]
- Nedellec, R.; Cugliari, J.; Goude, Y. GEFCom2012: Electric load forecasting and backcasting with semi-parametric models. Int. J. Forecast. 2014, 30, 375–381. [Google Scholar] [CrossRef]
- Kang, J.; Zhao, H. Application of improved grey model in long-term load forecasting of power engineering. Syst. Eng. Proced. 2012, 3, 85–91. [Google Scholar] [CrossRef]
- Bahrami, S.; Hooshmand, R.A.; Parastegari, M. Short term electric load forecasting by wavelet transform and grey model improved by PSO (particle swarm optimization) algorithm. Energy 2014, 72, 434–442. [Google Scholar] [CrossRef]
- Mandal, P.; Senjyu, T.; Urasaki, N.; Funabashi, T. A neural network based several-hour-ahead electric load forecasting using similar days approach. Int. J. Electr. Power Energy Syst. 2006, 28, 367–373. [Google Scholar] [CrossRef]
- Ko, C.N.; Lee, C.M. Short-term load forecasting using SVR (support vector regression)-based radial basis function neural network with dual extended Kalman filter. Energy 2013, 49, 413–422. [Google Scholar] [CrossRef]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Pai, P.F. Hybrid ellipsoidal fuzzy systems in forecasting regional electricity loads. Energy Convers. Manag. 2006, 47, 2283–2289. [Google Scholar] [CrossRef]
- Chandrashekara, A.S.; Ananthapadmanabha, T.; Kulkarni, A.D. A neuro-expert system for planning and load forecasting of distribution systems. Int. J. Electr. Power Energy Syst. 1999, 21, 309–314. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Y.; Liu, C.; Li, L. A hybrid application algorithm based on the support vector machine and artificial intelligence: An example of electric load forecasting. Appl. Math. Model. 2015, 39, 2617–2632. [Google Scholar] [CrossRef]
- Selakov, A.; Cvijetinović, D.; Milović, L.; Bekut, D. Hybrid PSO–SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank. Appl. Soft Comput. 2014, 16, 80–88. [Google Scholar] [CrossRef]
- Hong, W.C. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm. Energy 2011, 36, 5568–5578. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Proc. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Huang, S.C.; Wu, T.K. Integrating GA-based time-scale feature extractions with SVMs for stock index forecasting. Expert Syst. Appl. 2008, 35, 2080–2088. [Google Scholar] [CrossRef]
- Huang, S.C. Integrating nonlinear graph based dimensionality reduction schemes with SVMs for credit rating forecasting. Expert Syst. Appl. 2009, 36, 7515–7518. [Google Scholar] [CrossRef]
- Zhang, Y.; Lv, T. An empirical study on GPRS traffic forecasting based on chaos and SVM theory. J. China Univ. Post. Telecommun. 2010, 17, 41–44. [Google Scholar] [CrossRef]
- Li, X.L.; Yi, Q.Z.; Liu, X.Y. Tax forecasting theory and model based on SVM optimized by PSO. Expert Syst. Appl. 2011, 38, 116–120. [Google Scholar]
- Yang, Y.; Zhao, Y. Prevailing Wind Direction Forecasting for Natural Ventilation djustment in Greenhouses Based on LE-SVM. Energy Proced. 2012, 16, 252–258. [Google Scholar] [CrossRef]
- Lee, W.J.; Hong, J. A hybrid dynamic and fuzzy time series model for mid-term power load forecasting. Int. J. Electr. Power Energy Syst. 2015, 64, 1057–1062. [Google Scholar] [CrossRef]
- Efendi, R.; Ismail, Z.; Deris, M.M. A new linguistic out-sample approach of fuzzy time series for daily forecasting of Malaysian electricity load demand. Appl. Soft Comput. 2015, 28, 422–430. [Google Scholar] [CrossRef]
- Pereira, C.M.; De Almeida, N.N.; Velloso, M.L.F. Fuzzy Modeling to Forecast an Electric Load Time Series. Proced. Comput. Sci. 2015, 55, 395–404. [Google Scholar] [CrossRef]
- Sadaei, H.J.; Enayatifar, R.; Abdullah, A.H.; Gani, A. Short-term load forecasting using a hybrid model with a refined exponentially weighted fuzzy time series and an improved harmony search. Int. J. Electr. Power Energy Syst. 2014, 62, 118–129. [Google Scholar] [CrossRef]
- Day, P.; Fabian, M.; Noble, D.; Ruwisch, G.; Spencer, R.; Stevenson, J.; Thoppay, R. Residential power load forecasting. Proced. Comput. Sci. 2014, 28, 457–464. [Google Scholar] [CrossRef]
- Chen, S.M.; Kao, P.Y. TAIEX forecasting based on fuzzy time series, particle swarm optimization techniques and support vector machines. Inf. Sci. 2013, 247, 62–71. [Google Scholar] [CrossRef]
- Mahjoob, M.J.; Abdollahzade, M.; Zarringhalam, R. GA based optimized LS-SVM forecasting of short term electricity price in competitive power markets. In Proceeding of the IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 73–78.
- Xiang, Y.; Jang, L. Water quality prediction using LS-SVM and particle swarm optimization. In Proceeding of the IEEE Second International Workshop on Knowledge Discovery and Data Mining, Moscow, Russia, 23–25 January 2009; pp. 900–904.
- Mustaffa, Z.; Yusof, Y.; Kamaruddin, S.S. Gasoline Price Forecasting: An Application of LSSVM with Improved ABC. Proced. Soc. Behav. Sci. 2014, 129, 601–609. [Google Scholar] [CrossRef]
- Zhai, M.Y. A new method for short-term load forecasting based on fractal interpretation and wavelet analysis. Int. J. Electr. Power Energy Syst. 2015, 69, 241–245. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Hong, W.C.; Dong, Y.; Tsai, G.; Sung, J.T.; Fan, G.F. Application of SVR with chaotic GASA algorithm in cyclic electric load forecasting. Energy 2012, 45, 850–858. [Google Scholar] [CrossRef]
- Ghofrani, M.; Ghayekhloo, M.; Arabali, A.; Ghayekhloo, A. A hybrid short-term load forecasting with a new input selection framework. Energy 2015, 81, 777–786. [Google Scholar] [CrossRef]
- Enayatifar, R.; Sadaei, H.J.; Abdullah, A.H.; Gani, A. Imperialist competitive algorithm combined with refined high-order weighted fuzzy time series (RHWFTS–ICA) for short term load forecasting. Energy Convers. Manag. 2013, 76, 1104–1116. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Lin, J.; Li, X. Global harmony search optimization based ink preset for offset printing. Chin. J. Sci. Instrum. 2010, 10, 2248–2253. (In Chinese) [Google Scholar]
- Wang, C.M.; Huang, Y.F. Self-adaptive harmony search algorithm for optimization. Expert Syst. Appl. 2010, 37, 2826–2837. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Egrioglu, E.; Aladag, C.H.; Yolcu, U.; Uslu, V.R.; Erilli, N.A. Fuzzy time series forecasting method based on Gustafson–Kessel fuzzy clustering. Expert Syst. Appl. 2011, 38, 10355–10357. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Yang, Y.W.; Lin, Y.P. Multi-step forecasting of stock markets based on fuzzy time series model. Comput. Eng. Appl. 2014, 50, 252–256. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.H.; Hong, W.-C.; Shen, W.; Huang, N.N. Electric Load Forecasting Based on a Least Squares Support Vector Machine with Fuzzy Time Series and Global Harmony Search Algorithm. Energies 2016, 9, 70. https://doi.org/10.3390/en9020070
Chen YH, Hong W-C, Shen W, Huang NN. Electric Load Forecasting Based on a Least Squares Support Vector Machine with Fuzzy Time Series and Global Harmony Search Algorithm. Energies. 2016; 9(2):70. https://doi.org/10.3390/en9020070
Chicago/Turabian StyleChen, Yan Hong, Wei-Chiang Hong, Wen Shen, and Ning Ning Huang. 2016. "Electric Load Forecasting Based on a Least Squares Support Vector Machine with Fuzzy Time Series and Global Harmony Search Algorithm" Energies 9, no. 2: 70. https://doi.org/10.3390/en9020070
APA StyleChen, Y. H., Hong, W.-C., Shen, W., & Huang, N. N. (2016). Electric Load Forecasting Based on a Least Squares Support Vector Machine with Fuzzy Time Series and Global Harmony Search Algorithm. Energies, 9(2), 70. https://doi.org/10.3390/en9020070







