Augmented Nonlinear Controller for Maximum Power-Point Tracking with Artificial Neural Network in Grid-Connected Photovoltaic Systems

Abstract

Photovoltaic (PV) systems have non-linear characteristics that generate maximum power at one particular operating point. Environmental factors such as irradiance and temperature variations greatly affect the maximum power point (MPP). Diverse offline and online techniques have been introduced for tracking the MPP. Here, to track the MPP, an augmented-state feedback linearized (AFL) non-linear controller combined with an artificial neural network (ANN) is proposed. This approach linearizes the non-linear characteristics in PV systems and DC/DC converters, for tracking and optimizing the PV system operation. It also reduces the dependency of the designed controller on linearized models, to provide global stability. A complete model of the PV system is simulated. The existing maximum power-point tracking (MPPT) and DC/DC boost-converter controller techniques are compared with the proposed ANN method. Two case studies, which simulate realistic circumstances, are presented to demonstrate the effectiveness and superiority of the proposed method. The AFL with ANN controller can provide good dynamic operation, faster convergence speed, and fewer operating-point oscillations around the MPP. It also tracks the global maxima under different conditions, especially irradiance-mutating situations, more effectively than the conventional methods. Detailed mathematical models and a control approach for a three-phase grid-connected intelligent hybrid system are proposed using MATLAB/Simulink.

1. Introduction

Global energy consumption has increased noticeably because of the population explosion. The sustainable use of renewable energy solves one of the major concerns of the world community, since fossil energy sources will not last forever [1]. The energy generated using photovoltaic (PV) systems is inexhaustible; hence, the PV system is a suitable candidate for a long-term, reliable, and environmentally-friendly source of electricity [2]. This paper presents a study on intelligent PV systems used in the grid-connected mode.

The PV generator, also known as PV array, produces DC power that depends on the environmental conditions and the operating point imposed by the load. To provide a large amount of power, the PV system uses a DC/DC converter to isolate the operating point of the generator (voltage and current) from the load. Such a power converter is regulated by an algorithm that searches for the maximum power point (MPP, i.e., the optimal operation condition); this algorithm is known as the maximum power-point tracking (MPPT) algorithm. The classical structure of a grid-connected PV system is presented in Figure 1, in which the PV generator interacts with a DC/DC converter controlled by an MPPT algorithm [3,4]. Such a structure enables the PV system to modify the operation conditions according to the environmental circumstances (mainly dependent on the irradiance and temperature), so that maximum power is produced [5,6].

Figure 1 also illustrates the grid-interface of the PV system, which is composed of a DC-link capacitor C_dc and a DC/AC converter (inverter). The inverter is controlled to follow a required power factor, provide synchronization, and protect against islanding. Moreover, the inverter must regulate the DC-link voltage at the bulk capacitor C_dc, during which process, two scenarios can occur. In the first scenario, the inverter regulates the DC component of the C_dc voltage. However, due to the sinusoidal power injection into the grid, the C_dc voltage exhibits a sinusoidal perturbation at twice the grid frequency, with a magnitude inversely proportional to the capacitance [4]. In the second scenario, the DC component of the C_dc voltage is not properly regulated, which produces multiple harmonic components with amplitudes inversely proportional to the capacitance [4]. In both these cases, the DC/DC converter output terminals are exposed to voltage perturbations that can be transferred to the PV generator terminals, thereby degrading the MPPT process. The boost topology is the most widely used topology in the DC/DC power converter, because of the low voltage levels exhibited by commercial PV modules [7]. Figure 1 shows that the MPPT algorithm plays an important practical role in the utilization of the PV system. Each PV cell has a specific point named the maximum power point (MPP) on its operational curve (i.e., the power–voltage curve) at which it can generate maximum power [8]. Therefore, the non-linear characteristics of the MPP (depending on the environment) have led to the development of different MPPT techniques.

In the last decade, several researchers have focused on various MPPT methods to track the maximum power of PV modules/arrays [5,9,10]. The prevalent MPPT methods are the perturb-and-observe (P&O) method [11,12,13], incremental conductance (INC) method [14,15,16], fuzzy logic control (FLC) method [17,18,19], artificial neural network (ANN) method [20,21,22], sliding mode control (SMC) method [23,24,25], and the swarm-intelligence algorithm [26,27,28].

The P&O method is the most common MPPT method in industrial applications because of its proper balance between simplicity and operation. Albeit its simplicity, the main drawbacks of P&O are trapping in local minima, malfunctions in case of sudden changes in weather conditions, and incorrect recognition of MPP paths in different complex environments. Slow dynamic performance in the case of small step sizes, low efficiency, and permanent oscillations around the MPP are the other defects of the P&O algorithm.

The P&O method is a kind of hill-climbing methods. The INC method takes into account another hill-climbing method developed using the derivative of conductance (I_pv/V_pv). The INC method tracks the MPP based on whether the PV system operation proceeds to the right or to the left of the MPP. However, the INC method outputs are unsatisfactory at low irradiance levels as the differentiation process becomes more difficult.

The advantages of FLC are its robustness and non-linearity. FLC has a simple structure, as it does not require knowledge about the model; rather, it requires information regarding the operation of the model. On one hand, FLC can be effective if its parameters and membership functions are chosen through experiments along with an expert opinion. On the other hand, this is also a drawback. The other drawback of FLC is the high cost of implementation, which is due to the complexity of its algorithm.

ANNs feature several advantages such as robust operation, fast tracking, non-linear system tolerance, and offline training. Therefore, various ANN-based PV MPPT techniques have been developed recently.

SMC is applied in MPPT controllers, using the power-electronic-converter non-linearized model with high control precision. However, the chattering problem in the SMC systems and the requirement of model accuracy are major reasons that limit the development of SMC applications in PV systems.

With the development of heuristic algorithms and artificial intelligence, many optimization methods have been applied in various fields. One such example is the swarm-intelligence algorithm applied to MPPT, as proposed by some experts. The swarm-intelligence algorithm has strong global search capabilities to track the MPP under conditions of single irradiance or variable irradiance, without requiring a system model; however, it is likely to be premature at the initial stage.

It should be noted that the aforementioned papers lack proper evaluation of the system performance in intelligent systems, and no comparisons have been made between the hybrid ANN method and the conventional methods such as the P&O, IC, and FLC, in different complex environments. To the best of the authors’ knowledge, there is no published paper presenting a framework using an intelligent hybrid method for a PV system in the grid-connected mode. The results presented in this paper confirm the superiority and effectiveness of the proposed method. The major contributions of this paper are listed below:

• A grid-connected PV system including the topological structure, MPPT algorithm, DC/DC boost converter, and DC/AC inverter control strategy is proposed.
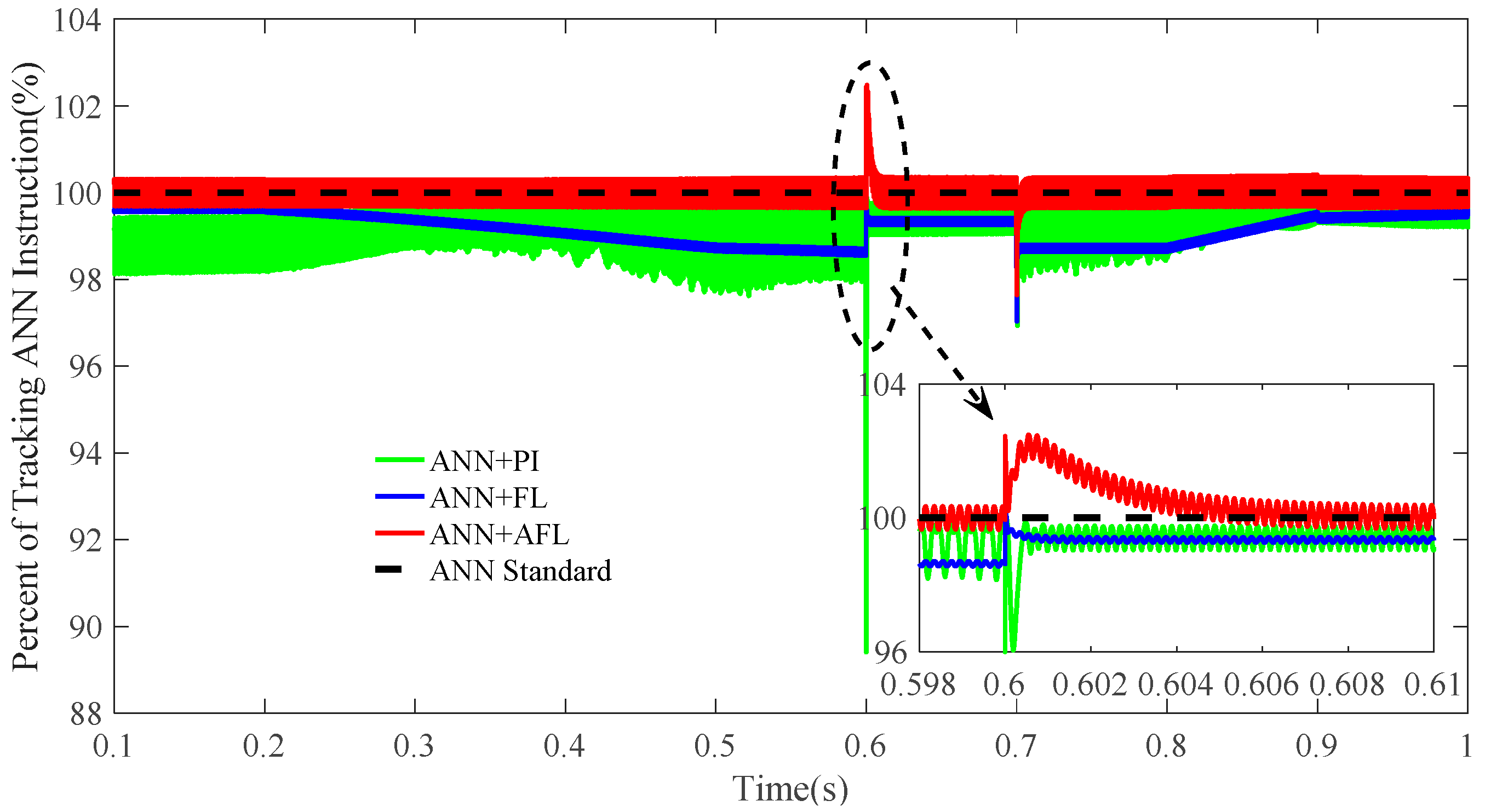
• The presented paper applies the ANN + AFL controller to extract maximum power from solar power. The control effect is compared with that of several algorithms (previously mentioned) under various conditions to prove its performance and superiority.
• The advantages and disadvantages of ANN + AFL are discussed based on the error analysis, in order to show the effectiveness and superiority of the presented controller over the conventional controllers.

The remainder of this paper is organized as follows: Section 2 presents the structure of the PV system proposed in this paper and a non-linear mathematical model of the solar cell. Section 3 introduces the training results of the proposed ANN structure for MPPT and analyzes the errors in the network. Section 4 presents the AFL non-linear control that tracks the output reference power of the ANN over a wide range based on the non-linear mathematical analysis of DC/DC convertors, and designs a DC/AC controller for connecting the PV system to the grid. Finally, Section 5 illustrates the performance of the proposed solution, using detailed simulations executed under various conditions, and compares it with the other MPPT technologies. The presentation of our conclusions ends the paper.

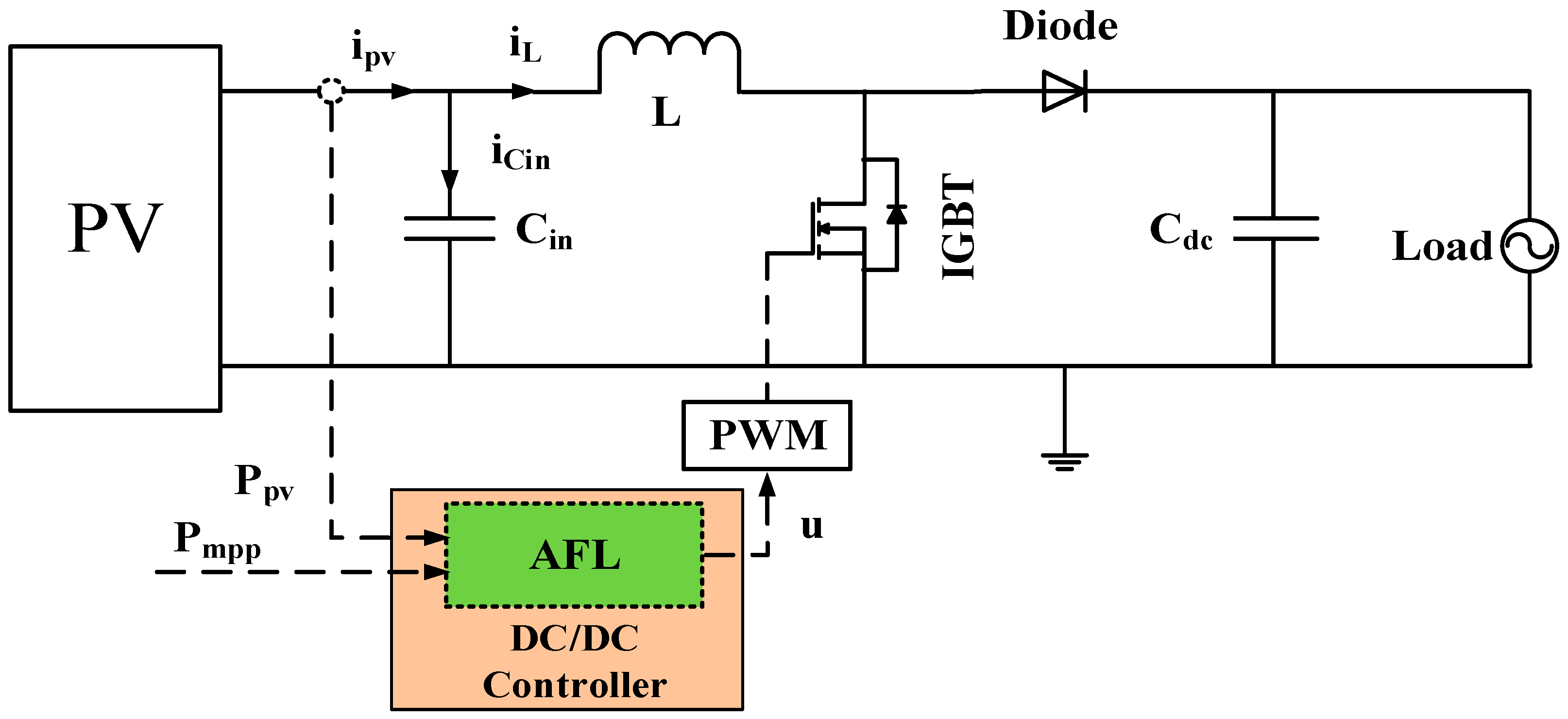
2. Grid-Connected Photovoltaic (PV) Generation System

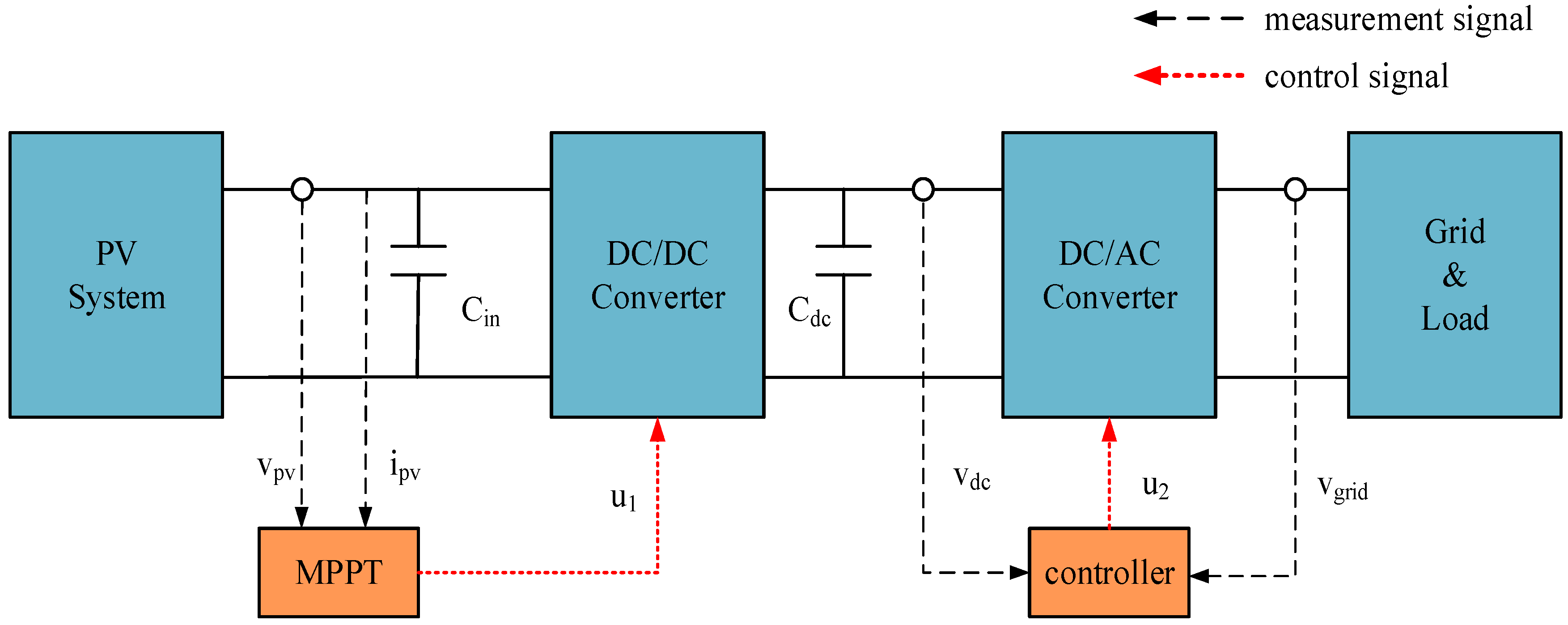
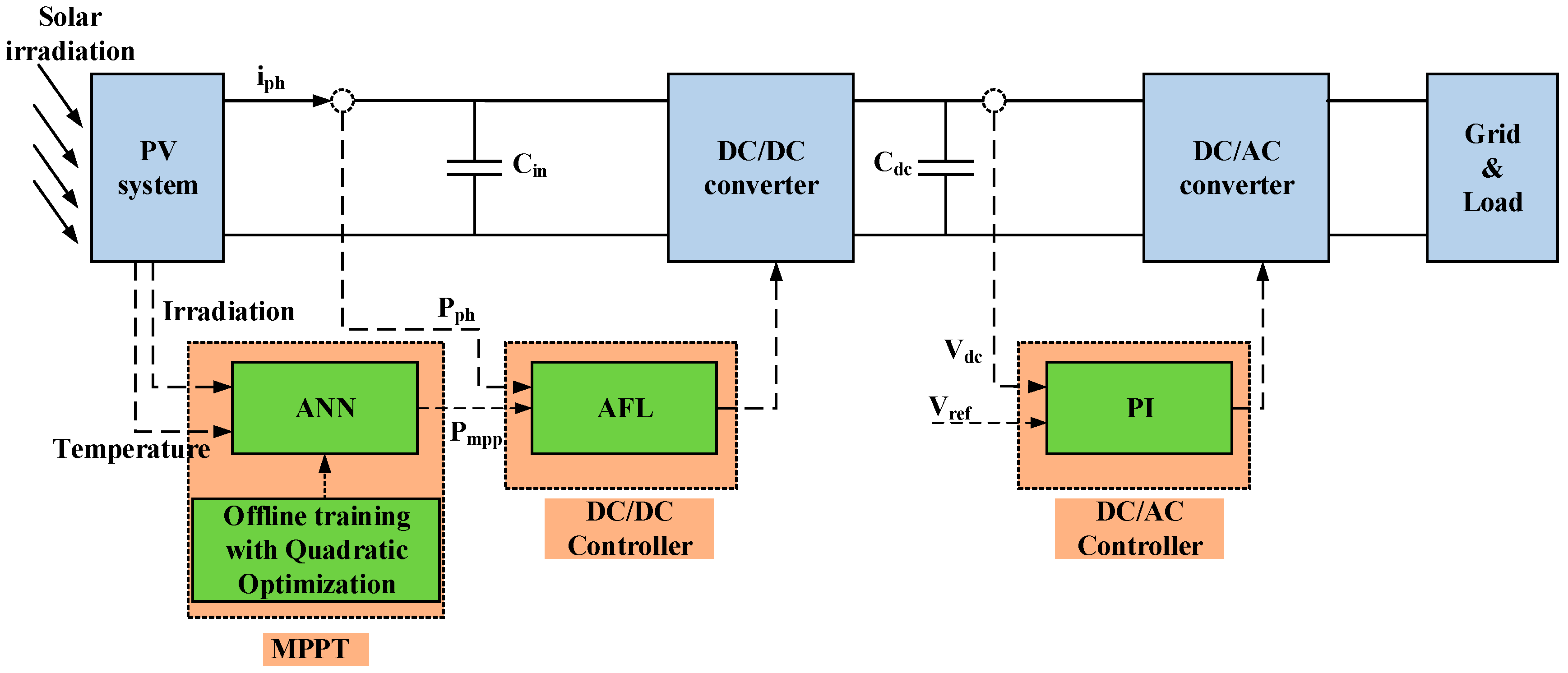
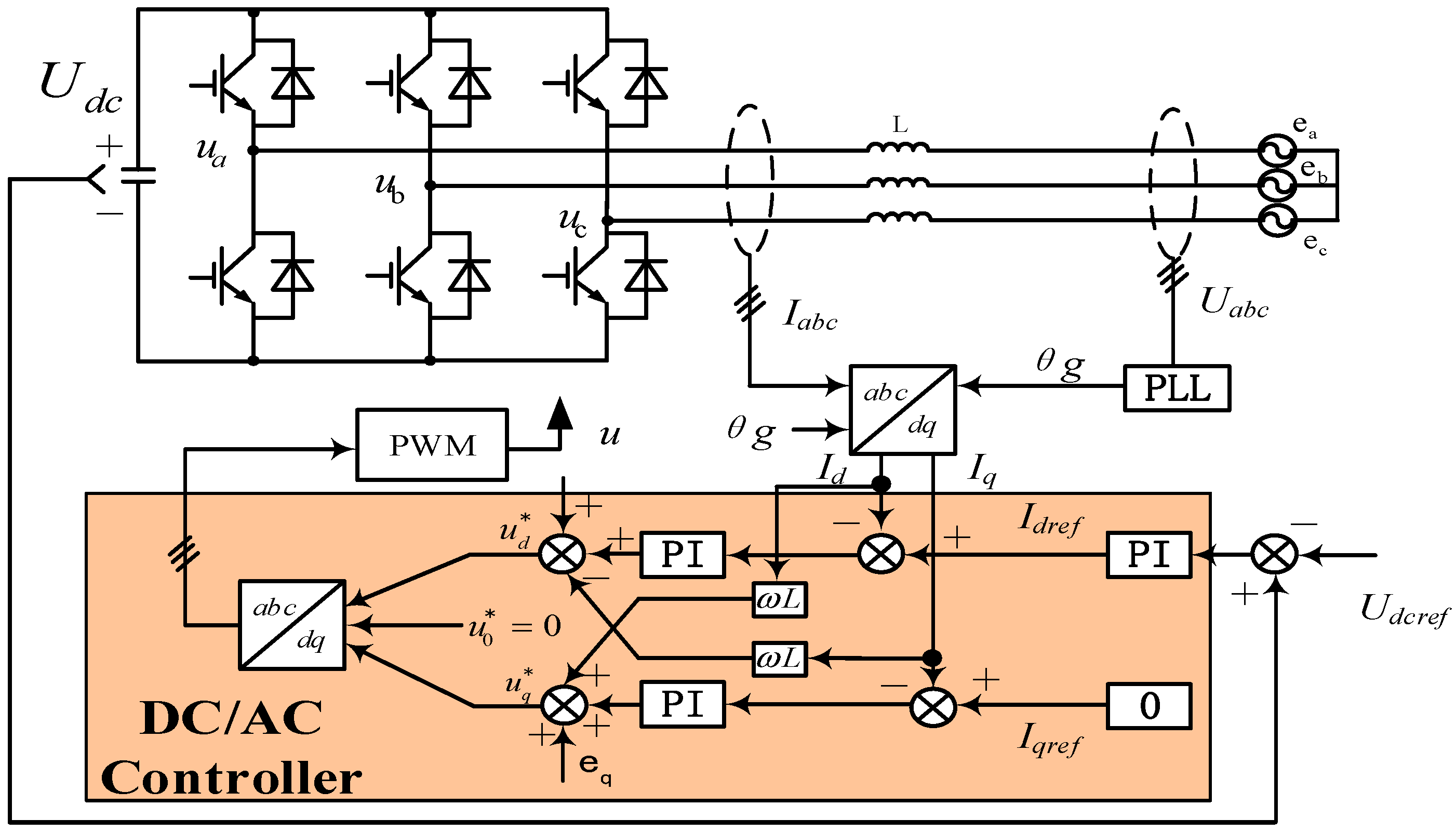
2.1. Structure of the Proposed System

As mentioned previously, irradiance and temperature create non-linear characteristics in the PV output power. Since the ANN can be used for non-linear tasks, its use in different areas has been increasing. An ANN does not require reprogramming because it is based on the learning process. Therefore, in this paper, irradiance and temperature are detected to train the ANN controller in order to obtain the MPP reference.

The power-electronic-converter model belongs to the class of the typical non-linear system models. Conventional controllers such as the proportional-integral (PI) controller based on small-signal modeling cannot track the reference rapidly or precisely under conditions where the converter quiescent operating point shifts within a wide dynamic range.

This paper proposes an AFL controller based on a DC/DC converter, which can solve the problems existing in conventional controllers.

Figure 2 shows the structure of the grid-connected PV system proposed in this paper, along with the whole PV scheme in which the PV generator interacts with a DC/DC converter controlled by an MPPT algorithm using an ANN. By detecting the irradiance and temperature information, the ANN produces the maximum power, with offline training. According to the theory of exact nonlinear-feedback linearization, the AFL controller is utilized to track the MPP reference given by the ANN. The DC/AC inverter control can maintain the DC-link voltage at a constant value, which is used as the reference in this paper.

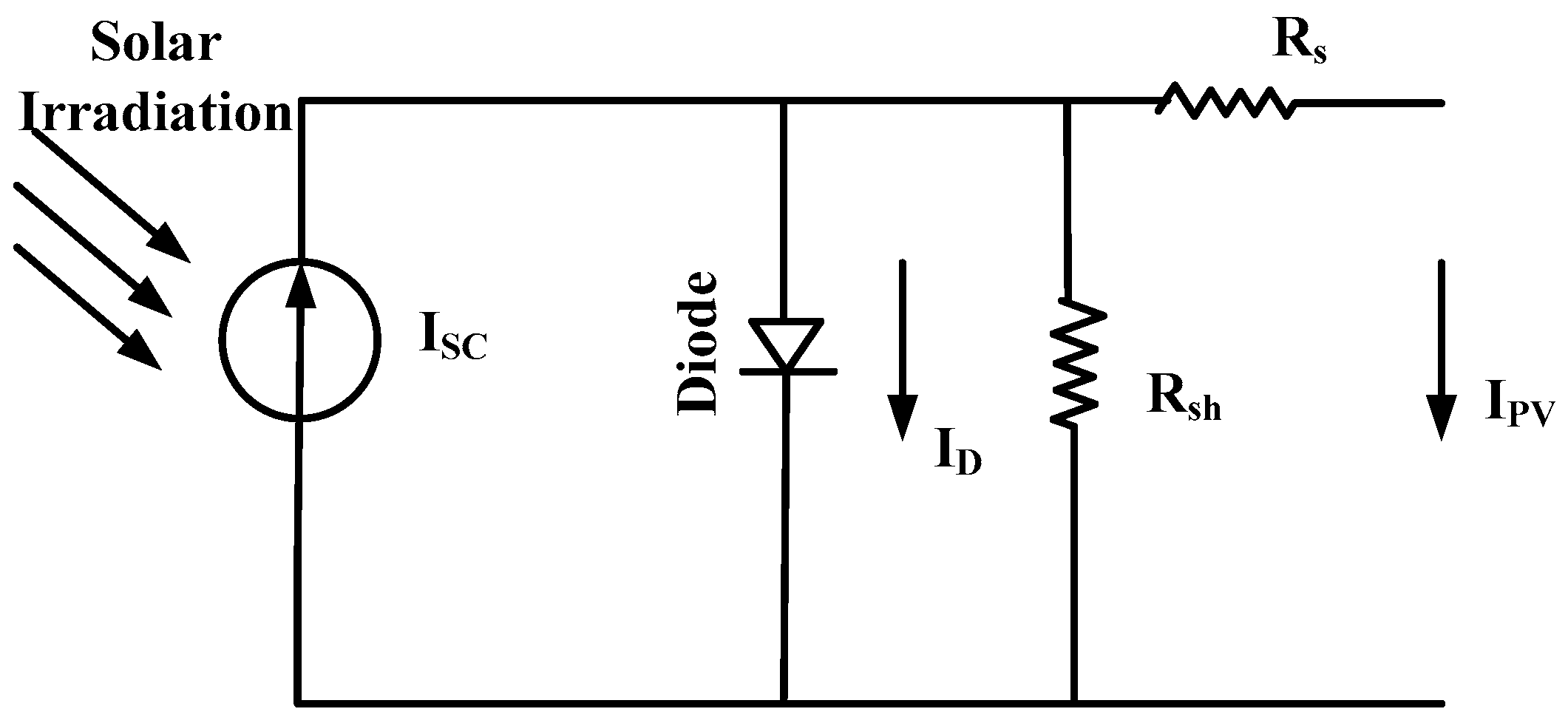
2.2. PV Cell Model

Several studies have presented the mathematical model for a PV cell. Ahmed and Salam studied a structure of the PV cell with a double diode [11], which consisted of a current source representing the light flux, which was connected parallel to two diodes. The diodes model the cell behavior in darkness. Two resistances—shunt and series—are used to represent the internal losses. Other models are proposed to simplify the model of the PV cell by using one diode. Similar to this last research, a single-model PV cell is utilized in this paper to formalize and simplify the PV cell as shown in Figure 3.

The basic equations representing the I–V characteristics of the PV-cell model are given below. By neglecting the series and parallel resistances of the PV array, i.e., by setting R_s = 0 and R_sh = ∞, the PV current can be approximated by the expression [23]:

$$i_{pv}=I_{sc}-B(e^{A{V}_{pv}}-1)$$

(1)

In such a model, I_sc represents the short-circuit current that is almost proportional to the irradiance [24], B is the diode saturation current, and A represents the inverse of the thermal voltage that depends on the temperature [29]. The model parameters are calculated as $A=I_{stc}{e}^{-B_{stc}{V}_{oc}}$, $B=\frac{B_{stc}}{1+{\alpha }_T(T_{pv}-T_{stc})}$, and $B_{stc}=\frac{\ln (1-i_{mpp}/i_{stc})}{V_{mpp}-V_{oc}}$, where i_stc and T_stc are the short-circuit current and temperature, respectively, of the module under standard test conditions (STC). V_oc represents the open-circuit voltage, while V_mpp and i_mpp correspond to the PV voltage and current, respectively, at the MPP for the given operating conditions. α_v is the voltage temperature coefficient. The nonlinear relation between the PV power and voltage, given in Equation (1), produces a nonlinear relation between the PV power and voltage, which exhibits a maximum as depicted in Figure 4. Meanwhile, Equation (1) establishes that the variable i_pv is nothing but a function of V_pv at a specific irradiance and temperature. Therefore, the output power of the PV, defined as P_pv, is a function of V_pv as shown in Equation (2):

$$P_{pv}=M(V_{pv})$$

(2)

A SunPower SPR-305NE-WHT-D 305W module is used as the reference module and attained under the STC with a solar irradiance of 1000 W/m² and a temperature of 25 °C. Simulations are performed using MATLAB/Simulink. The proposed MPPT method is developed for a 21.96 kW PV array consisting of 72 PV modules connected as 6 series modules and 12 parallel strings. The parameters of the solar module (SunPower SPR-305NE-WHT-D 305W) are presented in

Table 1. Parameters of the SunPower SPR-305NE-WHT-D 305W module under STC.

Parameter	Value
Voc (open-circuit voltage)	64.2 V
Isc (short-circuit current)	5.96 A
VMP (rated voltage)	54.7 V
IMP (rated current)	5.58 A
PMax (rated power)	305.2 W
NP (number of parallel cells)	1
NS (number of series cells)	96
αv (Temperature coefficient)	0.001 (%/°C)

.

Figure 4a,b present the power characteristics of the entire analyzed PV array, considering the solar irradiation and temperature changes. Figure 4a,b show the power characteristics of the entire analyzed PV array for the solar irradiation and temperature changes, respectively. The curves clearly show the nonlinear characteristics, and they are strongly influenced by climate changes.

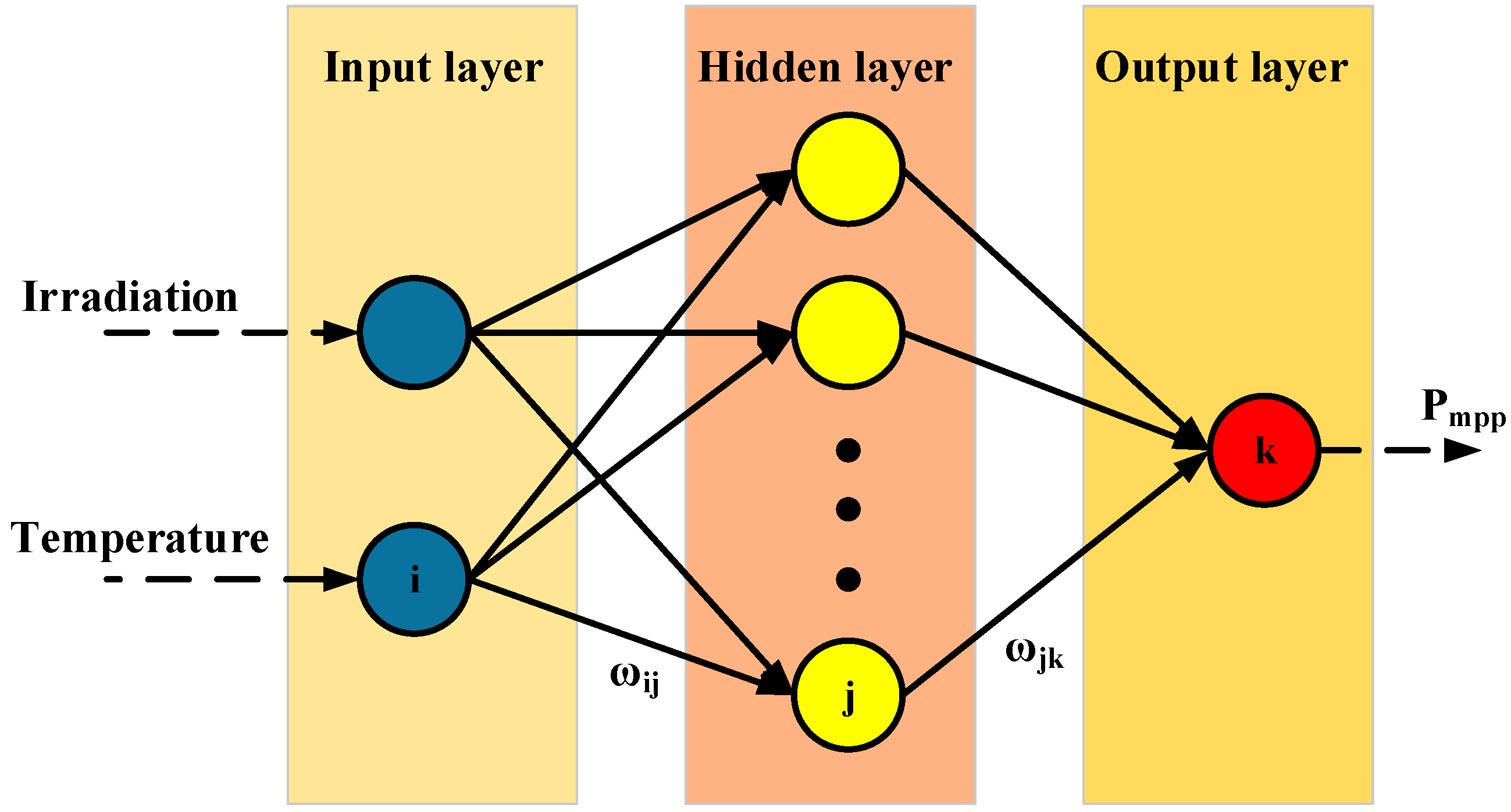
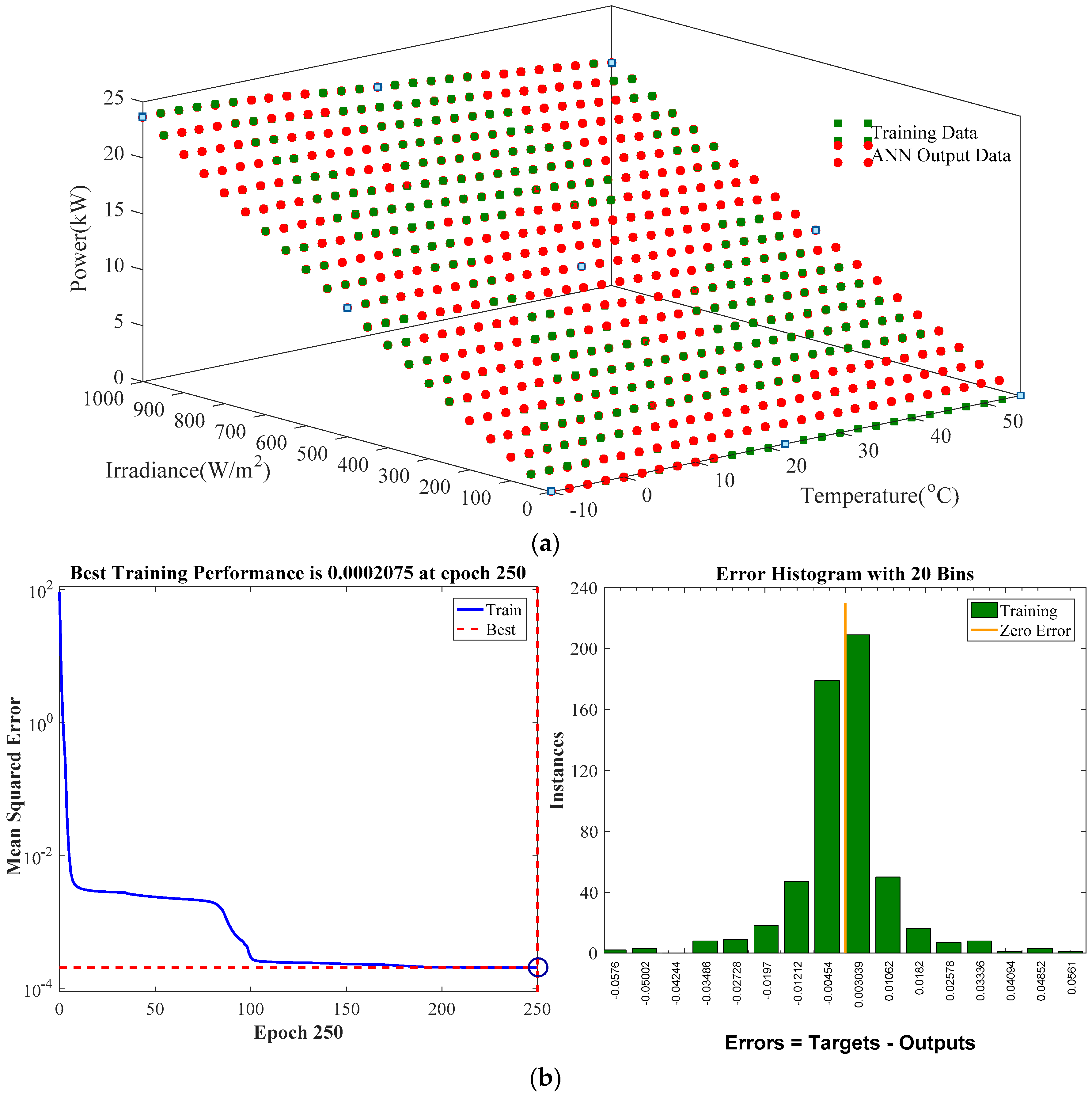
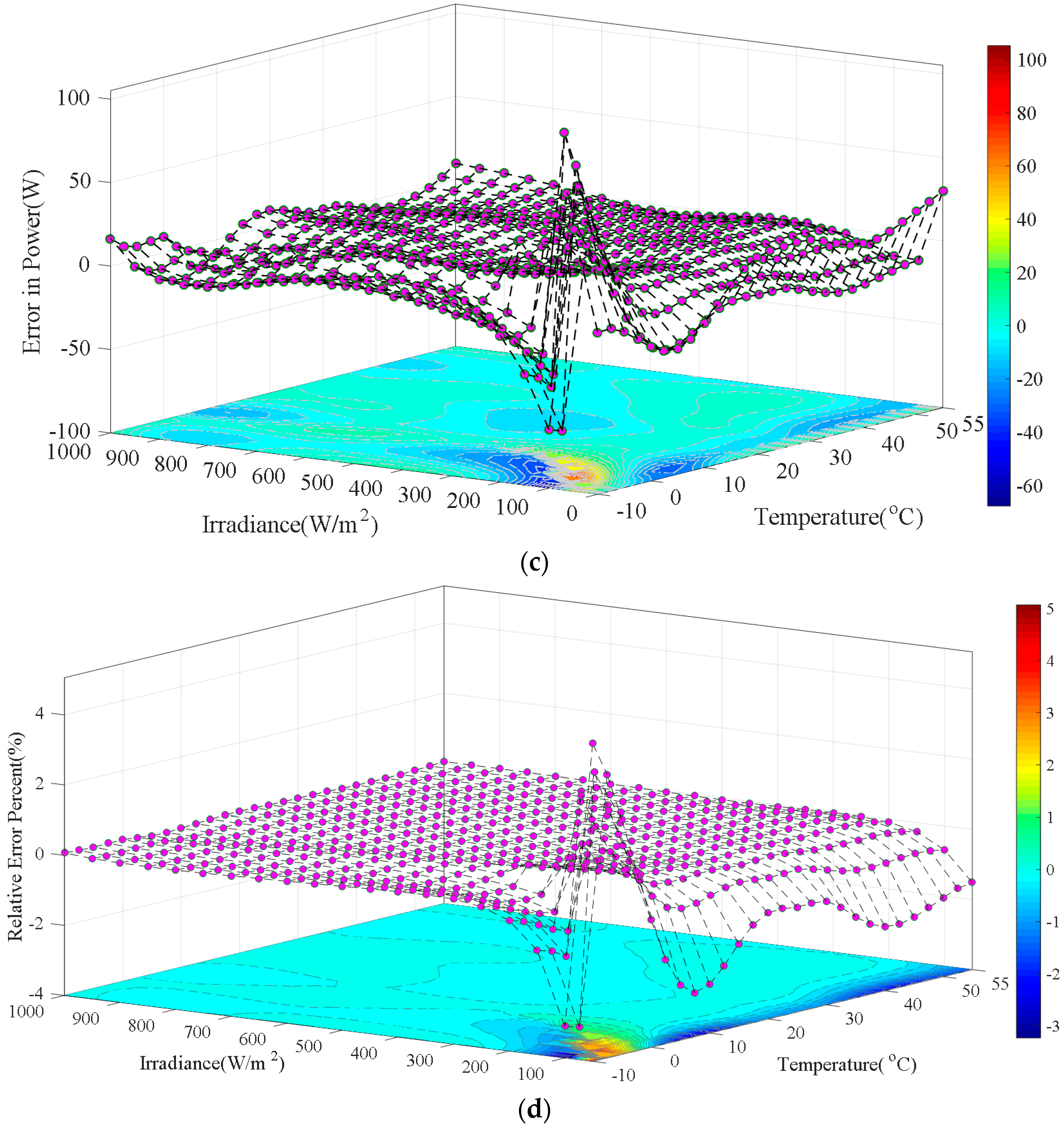
3. Artificial Neural Network (ANN) Method for Maximum Power-Point Tracking (MPPT)

3.1. Neural Network Construction for MPPT

ANNs have recently been developed further, not only in theory but also in practice [30,31,32,33,34,35]. A common ANN for MPPT, shown in Figure 5, has three layers: input, hidden, and output layers. Several studies that use ANNs to approximate nonlinear functions have been published. In this paper, the ANN input can be the PV-array environmental parameters such as irradiance or temperature and the output is the maximum power. The ANN output is used as the reference power for the DC/DC controller. The training data are determined by using MATLAB/Simulink to simulate the PV array based on parameters supplied by the manufacturer. For every case, the specific irradiance and temperature values are recorded as the input data to the ANN. The MPP corresponding to each input combination is also recorded as the output data of the ANN. The network is implemented for determining the maximum power of the PV array, when the PV array is subjected to various environmental parameter conditions. The network is obtained through training (supervised) using a training function—the Levenberg–Marquardt algorithm. However, the parameters of a specific PV array have changed over the years; hence, the data used to train the ANN may not be accurate. Therefore, the output reference power is not the exact optimal power Nevertheless, this reference operation point is close to the MPP.

The DC-DC boost-converter power reference given by the ANN, such a method proposed in this paper shows clear advantages over the conventional methods, especially under the condition of irradiance mutation.

3.2. Neural Network Analysis for MPPT

From Figure 4, it can be observed that the output of the PV system varies over time and with the environmental conditions; therefore, periodic training of the ANN is crucial. Five hundred and sixty-seven sample data (with irradiances between 0 W/m² and 1000 W/m² and temperatures between −10 °C and 55 °C) are generated to train the network. To create an ANN, the number of layers, number of neurons in each layer, transmission function of each layer, and type of training network, must be fixed. The proposed ANN has two layers in which the first layer has seven neurons and the second layer has one neuron. The first layer of the transfer function is “tansig” and the second layer is “purelin”. Moreover, the training function is “training”. The use of 250 training epochs and the application of “training” as a training function are sufficient to get good results as shown in Figure 6a. The training data are obtained by simulating the PV system in MATLAB/Simulink using the Levenberg–Marquardt algorithm. The error is computed by a mean-squared-error (MSE) algorithm during the training process. The admissible MSE for the ANN is approximately 10⁻⁴ in Figure 6b and the distribution of the error is around the center, at the zero point.

Figure 6c,d show the changing trend surfaces for the absolute and relative errors at different irradiances and temperatures. In most cases, the absolute error in the maximum ANN output power is less than 30 W and the relative error is under 0.5%. In addition, the errors in the ANN output maximum power are large at low irradiance conditions. The values of the errors are dozens of watts or below 4%. However, the PV system rarely works under these circumstances. Thus, the results of ANN training are satisfactory, and are regarded as the reference powers that are followed by the DC/DC converter controllers.

4. Topology and Control Strategy for Proposed Power Converter

4.1. Nonlinear Model of DC/DC Converter

A simplified circuit schematic of the PV system is presented in Figure 7. The circuit uses a boost converter because of the wide adoption of such a step-up DC/DC structure in PV systems; nevertheless, the analysis presented in this paper can be extended to other DC/DC topologies also. The scheme uses a voltage source as the system load, to model the DC links of double-stage structures in commercial PV inverters where the DC/AC stage regulates the DC-link voltage (C_dc capacitor voltage) [29]. This voltage-source model is widely used to represent the closed-loop grid-connected inverters owing to its satisfactory balance between accuracy and simplicity, which is confirmed in [36,37,38]. In the topological structure, P_mpp is the ANN output, namely, the reference power. The control goal of the boost converter is that the actual output power of the PV should be compatible with the P_mpp of the DC/DC controller.

The dynamic behavior of the DC/DC converter is modeled by the switched Equations (2) and (3) [39], where i_L represents the inductor current, V_pv is the PV voltage, i_pv represents the PV module current, V_b is the load voltage, and L and C_in represent the inductor and capacitor values:

$$\frac{\mathrm{d}{i}_L}{\mathrm{d}t}=\frac{V_{pv}-V_{dc}(1-u)}{L}$$

(3)

$$\frac{\mathrm{d}{V}_{pv}}{\mathrm{d}t}=\frac{i_{pv}-i_L}{C_{in}}$$

(4)

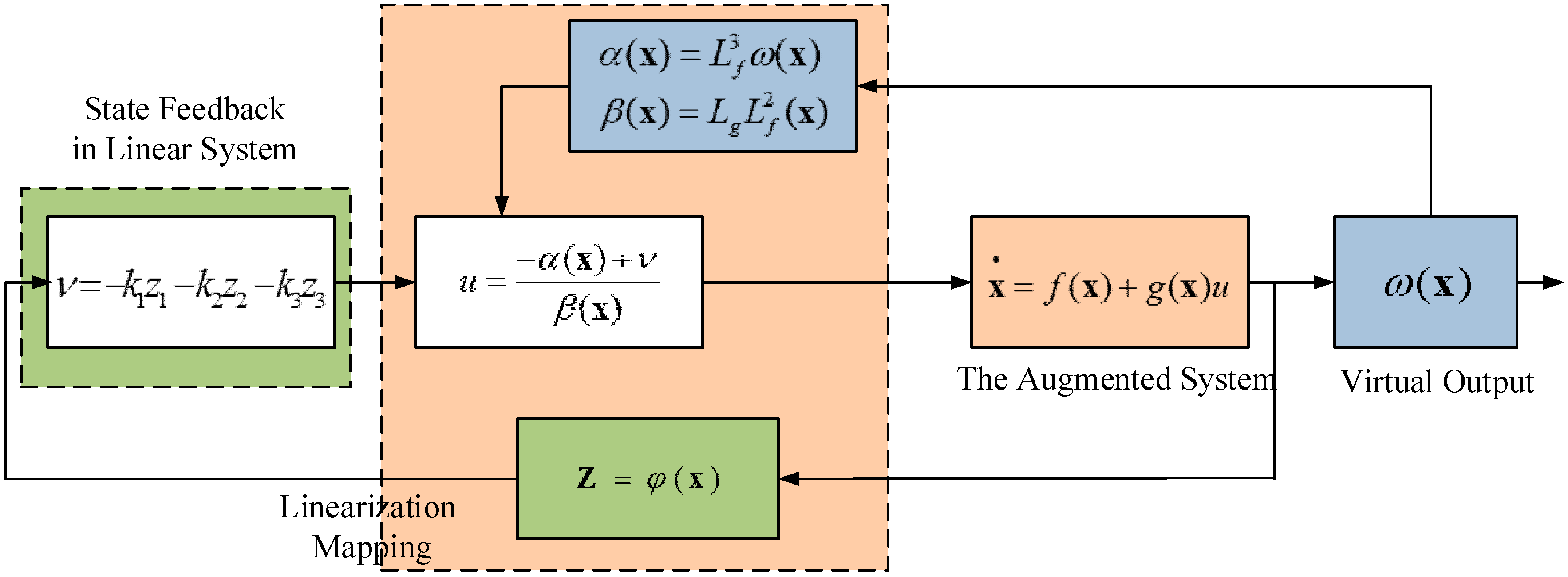
4.2. Augmented-State Feedback Linearization (AFL) Control for Nonlinear Systems

The nonlinear-equation system formed by Equations (1)–(4) describes the PV system dynamic behavior under all operating conditions. The traditional PI controller is designed as a linear system. In general, engineers linearize the nonlinear systems using small-signal modeling methods and adjust the parameters of PI in the linear systems. However, in this method, we need a steady-state point that is to be fixed as the converter working state. In other words, in the changing irradiance and temperature cases, a linear method such as small-signal modeling cannot satisfy the requirements.

Based on the nonlinear control theory presented in Appendix A, we can establish a transformational matrix that varies with time to linearize the nonlinear system under a particular condition [40,41,42]. Then, the state feedback controller is projected onto the linear system to accomplish dynamic tracking. However, the control effect of ordinary state feedback have steady-state errors.

In conclusion, this paper proposes an augmented control strategy based on the above-mentioned nonlinear control theory, which meets the goal of dynamic tracking to eliminate steady-state errors.

In order to eliminate the dynamic power-tracking error under the steady-state condition, a state variable x₃ is defined as x₃ = ∫(P_pv − P_mpp)dt. The augmented state-space description of the nonlinear system ∑ can be written as follows:

$$\{\begin{array}{l}\stackrel{•}{x_1}=\frac{x_2-V_{dc}}{L}+\frac{V_{dc}}{L}u\\ \stackrel{•}{x_2}=\frac{M(x_2)-x_1}{C_{in}}\\ \stackrel{•}{x_3}=x_{2}M(x_2)-P_{mpp}\end{array}$$

(5)

where the state variable x₁ is the inductor current and x₂ is the capacitor C_in voltage, which is the PV output voltage as well.

The description of ∑ can be written as:

$$\stackrel{•}{x}=f(x)+g(x)u$$

$$f(x)=\left[\begin{array}{l}\frac{x_2-V_{dc}}{L}\\ \frac{M(x_2)-x_1}{C_{in}}\\ x_{2}M(x_2)-P_{mpp}\end{array}\right],g(x)=\left[\begin{array}{c}\frac{V_{dc}}{L}\\ 0\\ 0\end{array}\right]$$

According to the nonlinear control theory and the definitions mentioned in Appendix A, the augmented system ∑ can be partially feedback-linearized by constructing the output function that will be mentioned below. Assuming the output function $y=\omega (\mathit{x})$, the criteria ${\mathrm{L}}_g\omega (\mathit{x})=0$, ${\mathrm{L}}_g{\mathrm{L}}_f\omega (\mathit{x})=0$, and ${\mathrm{L}}_g{{\mathrm{L}}^2}_f\omega (\mathit{x})\ne 0$ should be met.

By analyzing the characteristics of the control matrix $g(\mathit{x})$, the criteria can be met when the output function is considered to be $\omega (\mathit{x})=x_3$. A new state variable Z can be defined as $\mathit{Z}=\phi (\mathit{x})={[\omega (\mathit{x}),{\mathrm{L}}_f\omega (\mathit{x}),{{\mathrm{L}}^2}_f\omega (\mathit{x})]}^{\mathrm{T}}$ to construct the coordinate transformation.

The augmented system ∑ can be mapped to a third-order linear time-invariant system Π as presented in Equation (6):

$$\stackrel{•}{\mathit{Z}}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right]\mathit{Z}+\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\nu$$

(6)

where $\nu$ is the controlled variable in system Π.

The controlled variable u in system ∑ can be written as:

$$u=\frac{-{{\mathrm{L}}^3}_f\omega (\mathit{x})+\nu }{{\mathrm{L}}_g{{\mathrm{L}}^2}_f\omega (\mathit{x})}$$

(7)

From Equation (7), it can be seen that the controlled variables in system ∑ can be presented by the controlled variable $\nu$ in the third-order linear time-invariant system Π. The response curve of system ∑ is determined by the controlled variable $\nu$.

The control law $\nu =-\mathit{K}\mathit{Z}=-k_1{z}_1-k_2{z}_2-k_3{z}_3$ can be designed according to the theory of linear systems; then, substituting it into Equation (6), we obtain Equation (8):

$$\stackrel{••}{z_1}+k_3\stackrel{•}{z_1}+k_2{z}_1+k_1{\displaystyle \int z_1\mathrm{d}t}=0$$

(8)

where $z_1=\omega (\mathit{x})=x_3={\displaystyle \int (P_{pv}-P_{mpp})\mathrm{d}t}$.

The state variable $z_1$ is determined by the feedback-coefficient matrix $\mathit{K}=[k_1,k_2,k_3]$ in the third-order differential equation, and the effect of the PV output power $P_{pv}$ given by the ANN tracking reference $P_{mpp}$ is determined as well. The analysis of the feedback-coefficient matrix is presented in Appendix A.

A third-order system can be considered to be the product of a first-order system and a second-order system. The system can be reduced to a reasonable order according to the system distribution of the roots, i.e., by designing the dominant-pole placement. The system in this paper is designed as a second-order system, i.e., the distance between the roots and the imaginary axis in the first-order system is larger than 3 times the distance between the roots and the imaginary axis in the second-order system. The state variables $z_{1,1}$, $z_{1,2}$, and $z_{1,3}$ can be written as $z_{1,1}={\omega }_n$, $z_{1,2}=-\xi {\omega }_n+{\omega }_n\sqrt{{\xi }^2-1}$, and $z_{1,3}=-\xi {\omega }_n-{\omega }_n\sqrt{{\xi }^2-1}$, where $\xi$ is the second-order system damping ratio that affects the system’s dynamic performance. In order to be an overdamped system, $\xi$ should be greater than or equal to 3. ${\omega }_n$ is the system’s natural frequency, which affects the steady-state precision and the corresponding velocity, and ${\omega }_n$ is supposed to be k times LC_in , the circuit resonant frequency. The control parameters of the system are presented in Equation (9):

$$\{\begin{array}{c}{k}_1={\omega }_n^3=k{(1/\sqrt{L{C}_{in}})}^3\\ k_2=(2\xi +1){\omega }_n^2\\ k_3=(2\xi +1){\omega }_n\end{array}$$

(9)

The augmented state-space feedback linearization control strategy is presented in Figure 8.

4.3. DC/AC Inverter and Control

Figure 9 shows a typical topology of a two-stage grid-connected PV system, which includes a DC/DC boost converter and a DC/AC converter. The first-stage DC/DC boost converter connected to the PV panel steps up the output DC voltage of the DC bus to a proper level for the DC/AC inverter, based on the MPPT algorithm.

A three-phase voltage-source inverter is used as the interface between the DC-link voltage and the grid. The second-stage DC/AC inverter provides proper sinusoidal current to the grid with unity power factor and keeps the DC bus voltage at a stable operating point.

The control strategy of the DC/AC inverter involves two loops, which are an external DC bus voltage loop and an internal current loop. The external DC bus voltage loop is responsible for regulating the DC-link voltage to a stable value. The internal current loop should be controlled in terms of the unity power factor with the grid.

The DC/AC inverter control strategy is based on the instantaneous powers of the d–q frame references applied for pulse-width modulation (PWM) control. According to the instantaneous power theory, the active power p and reactive power q can be written as in Equation (10):

$$\{\begin{array}{l}p=\frac{3}{2}(e_d{i}_d+e_q{i}_q)\\ q=\frac{3}{2}(e_d{i}_q-e_q{i}_d)\end{array}$$

(10)

where $e_d$, $e_q$ and $i_d$, $i_q$ are the d–q components of the grid voltage and output current, respectively. $\left|E\right|$ is the amplitude of the grid voltage. At the d–q frame references under the voltage-oriented control (V_oc) method, $e_d=\left|E\right|$, $e_q=0$. Thus,

$$\{\begin{array}{l}p=\frac{3}{2}{e}_d{i}_d\\ q=\frac{3}{2}{e}_d{i}_q\end{array}$$

(11)

Ignoring the inverter attenuation losses, the instantaneous value of the DC-link power p_dc can be described as shown in Equation (12):

$$p_{dc}=i_{dc}{u}_{dc}$$

(12)

The active power p and p_dc can be represented as per the following equation

$$i_{dc}{u}_{dc}=p=\frac{3}{2}{e}_d{i}_d$$

(13)

It can be observed that the DC-link voltage is proportional to the d-axis current of the inverter output current, and the DC-link voltage control can be accomplished by controlling the d-axis current. The control scheme of the grid-side inverter is shown in Figure 9. The internal d–q current loop references can be calculated from the external loop, and the PI controller is used to regulate the d–q grid currents [43,44,45]. The outputs of the d–q current controllers, ΔV_gd and ΔV_gq, which denote a variation of the grid voltage, are added to the d–q grid voltages to obtain the dynamic response with the feedforward of the grid voltage [46]. In order to operate in terms of unity power factor with the grid, I_qref is set to 0.

5. Simulation Results and Discussion

There are two major operation criteria discussed in this paper for simulating the PV system operation under realistic conditions:

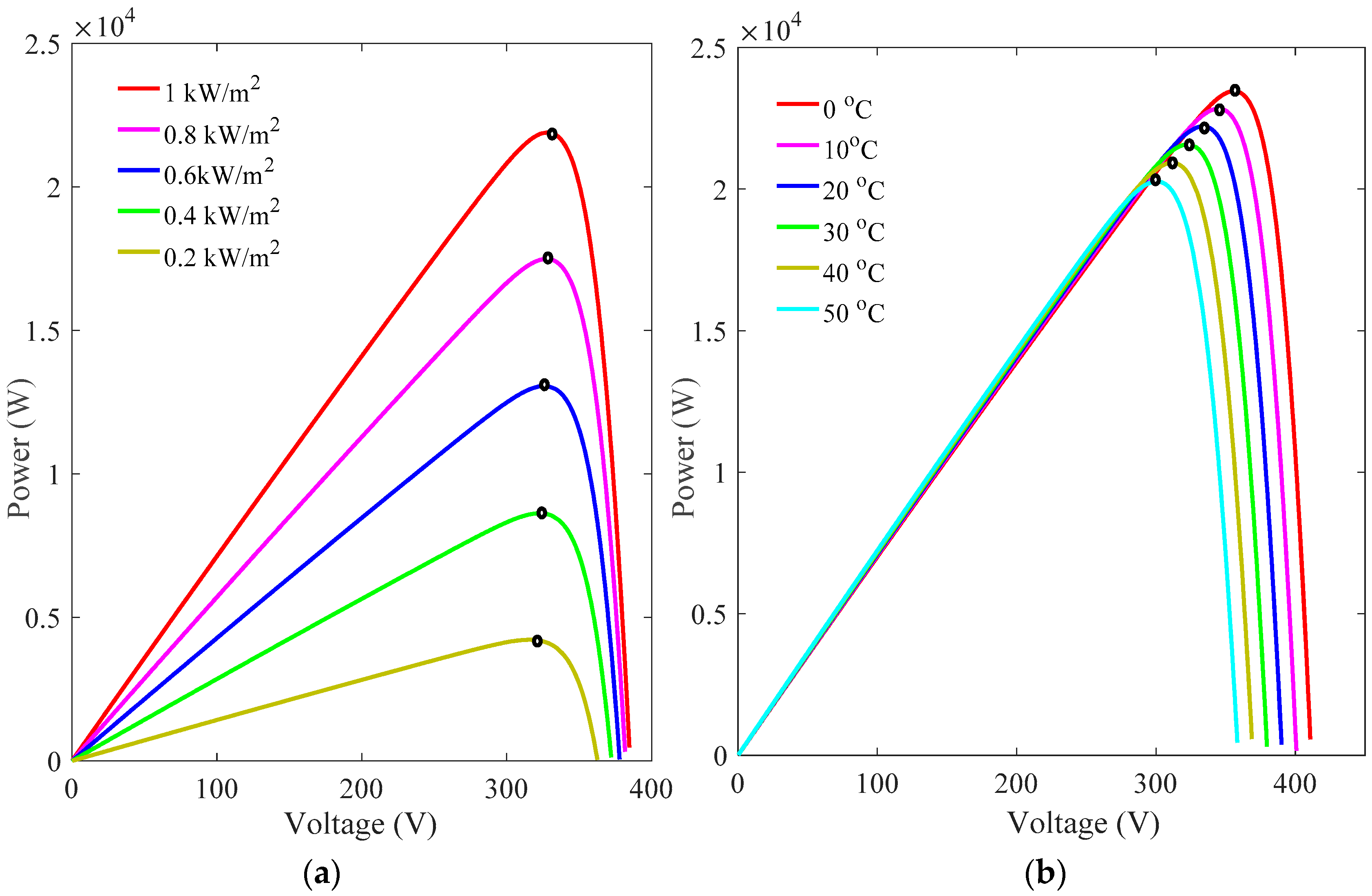
• The effect of fast irradiance variations must be investigated for the evolution of the operating point of the PV array for slow temperature variations.
• The operating point of the PV array must be analyzed under rapid irradiance changes at a fixed temperature of 25 °C.

Simulation parameters are presented in Appendix B.

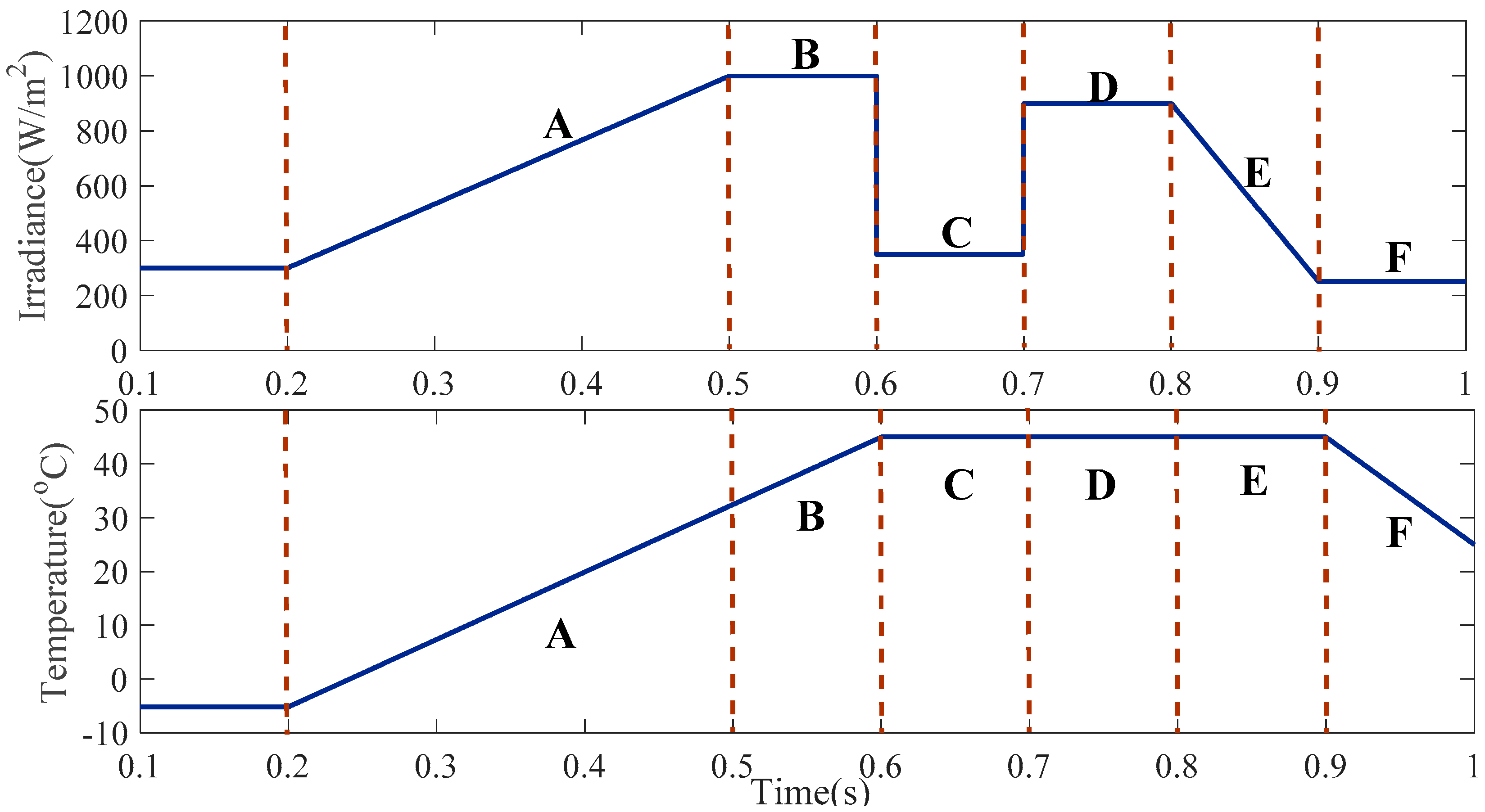
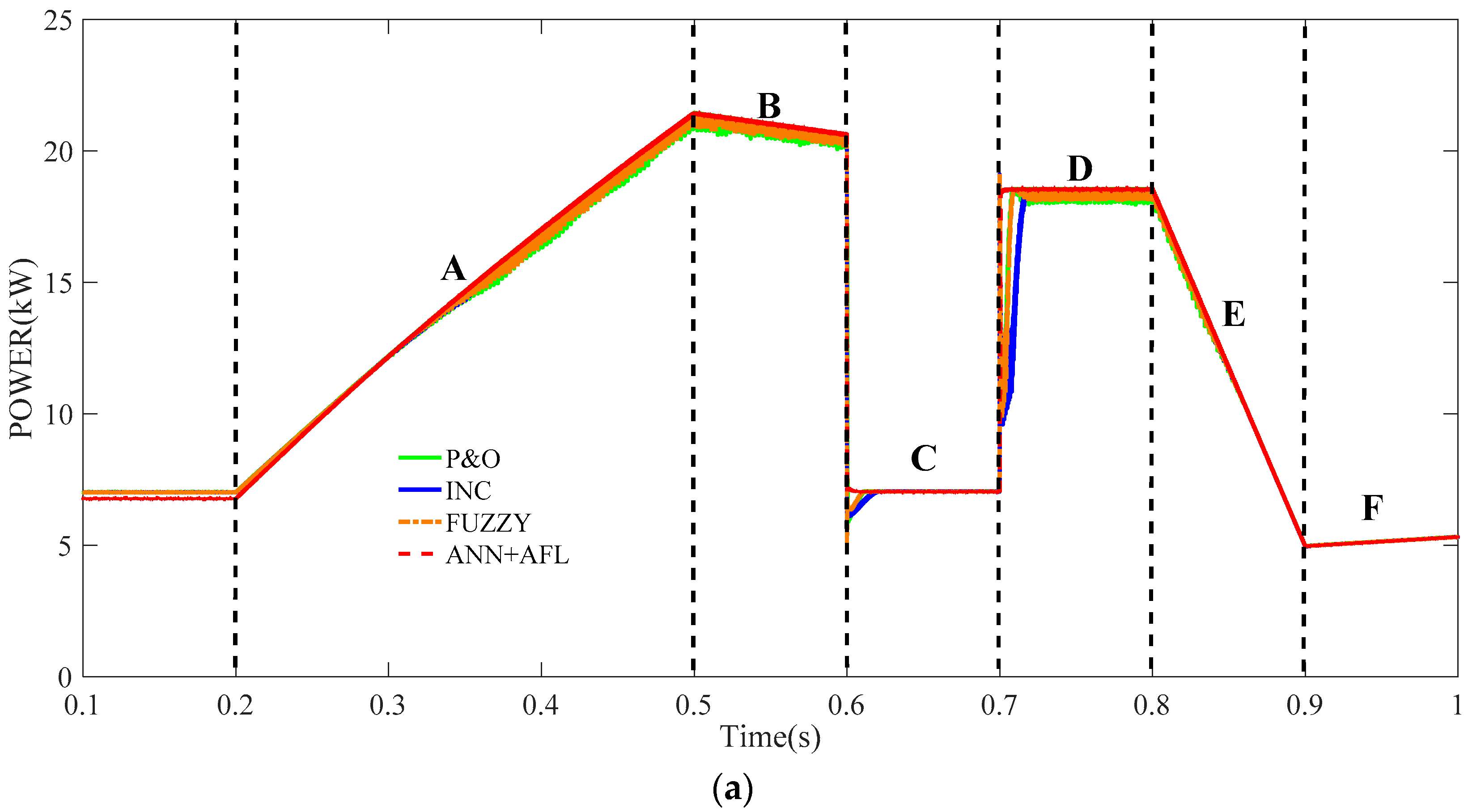
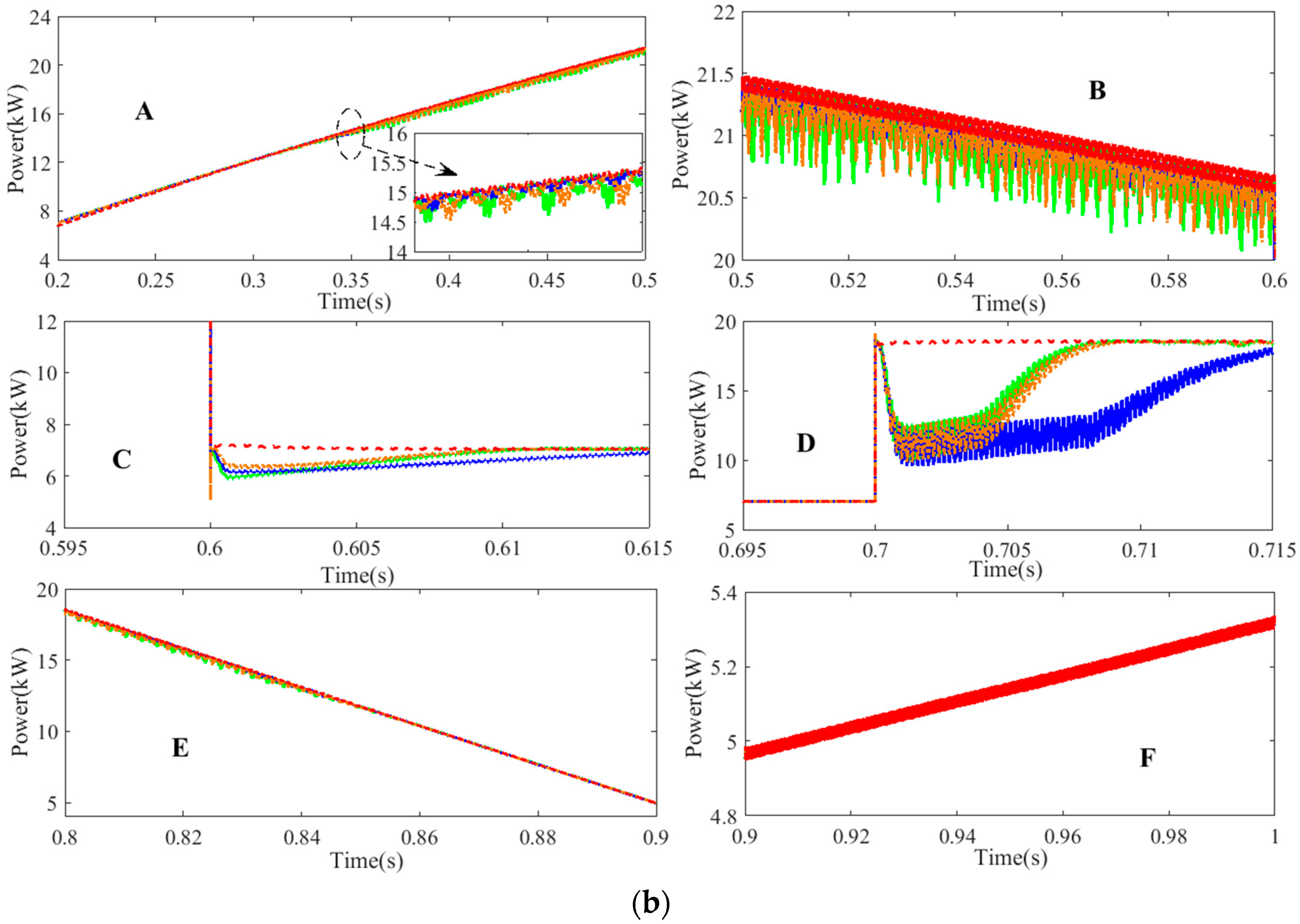
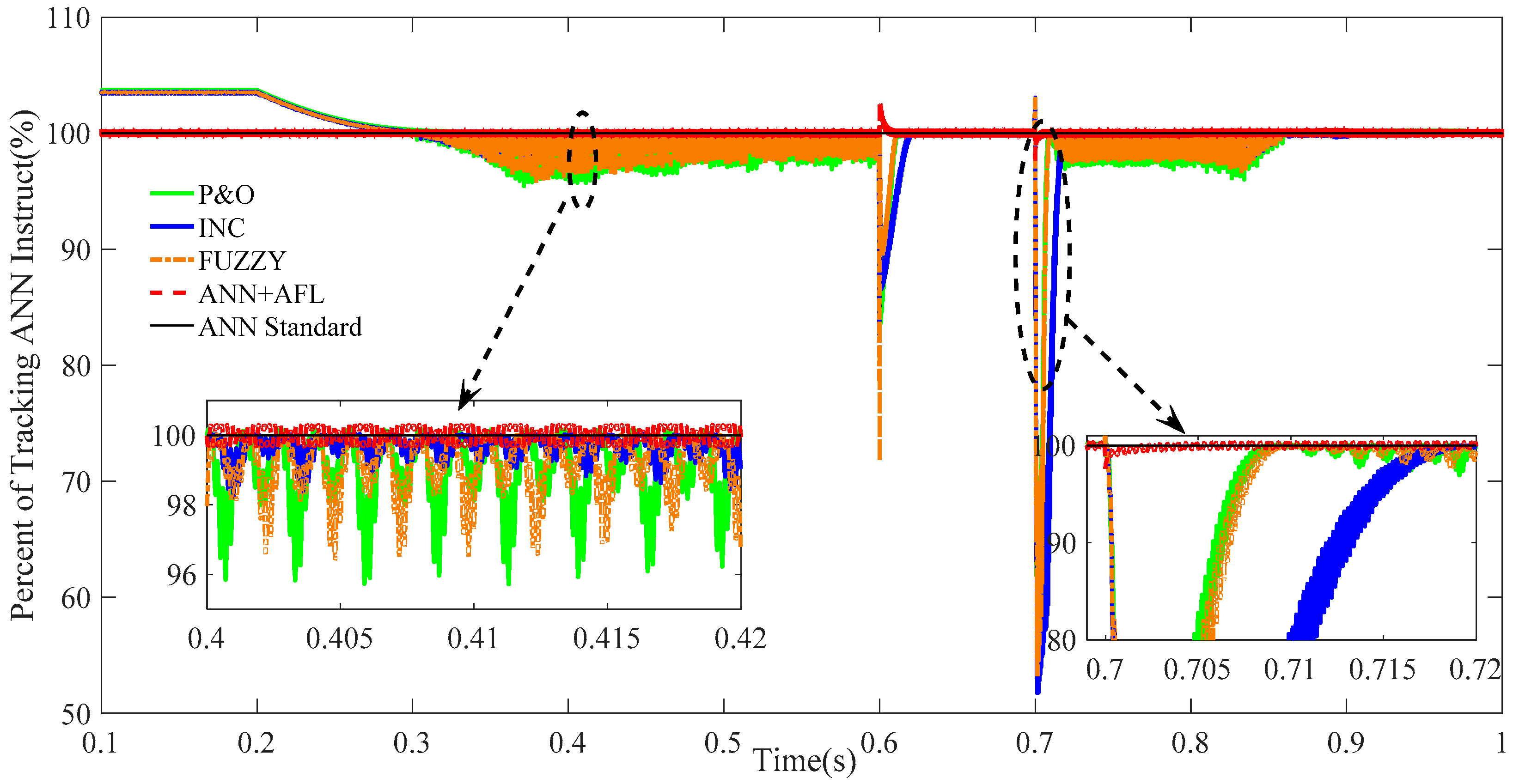
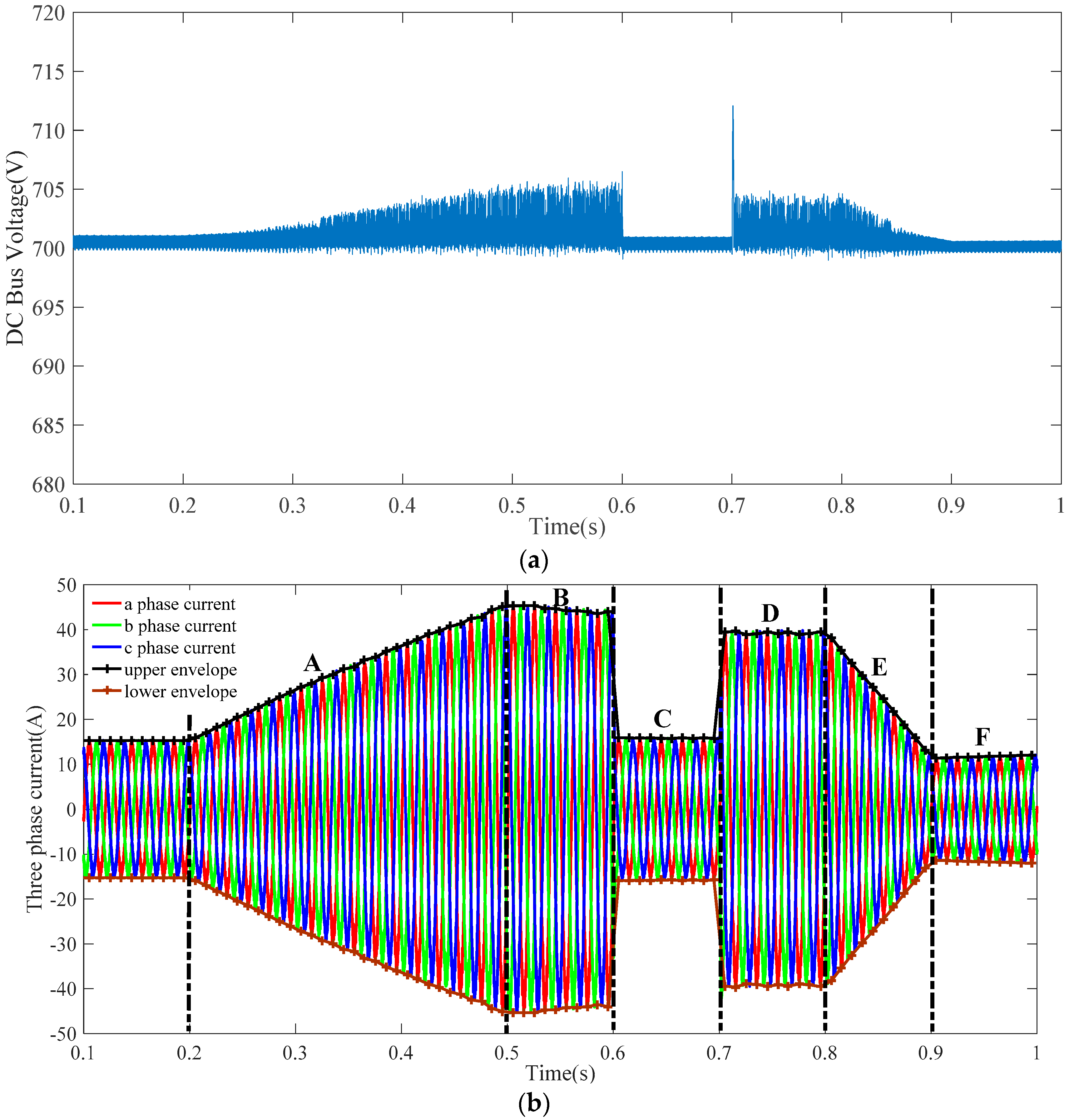
5.1. Simulation Case 1

In this case, the duration of simulation is 1 s which is separated into six parts as follows. The temperature and irradiance variations are illustrated in Figure 10.

Part A:

In order to assess the intelligence of the hybrid structure, the irradiance is increased to 1000 W/m² from 300 W/m² between 0.2 s and 0.5 s, at a uniform speed. The temperature is also increased from −5 °C between 0.2 s and 0.5 s at a uniform speed.

Part B:

The irradiance is maintained at a constant value of 1000 W/m², and the temperature is increased to 45 °C between 0.5 s and 0.6 s at a uniform speed.

Part C:

The irradiance is decreased to 350 W/m² from 1000 W/m² between 0.6 s and 0.7 s. The temperature is maintained at a constant value of 45 °C.

Part D:

The irradiance is increased to 900 W/m² from 350 W/m² between 0.7 s and 0.8 s. The temperature is maintained at a constant value of 45 °C.

Part E:

The irradiance is decreased to 250 W/m² from 900 W/m² between 0.8 s and 0.9 s at a uniform speed. The temperature is maintained at a constant value of 45 °C.

Part F:

The temperature is decreased from 45 °C at a uniform speed, between 0.9 s and 1.0 s, and the irradiance is maintained at a constant value of 250 W/m².

The control effects for the different DC/DC controllers under similar power references given by the ANN are shown in Figure 11 and Figure 12.

It can be observed that there is an obvious steady-state error in the feedback linearization method without augmentation (ANN + FL).The conventional PI controller (ANN + PI) tracks the ANN reference well under stable conditions or in the case of slow and uniform changes. However, a dynamic tracking overshoot exists under the condition of strong irradiance or when the irradiance changes rapidly. In other words, the ANN + FL and ANN + PI controllers cannot meet the demands of tracking the power reference under all conditions of the PV system.

In order to illustrate the comparisons between each method distinctly, the output of each method divided by the ANN reference, are shown in Figure 12. It can be clearly observed that ANN + AFL is better than ANN + PI, and ANN + PI is better than ANN + FL, especially when avoiding the steady-state error.

Under these operating conditions, Figure 13 and Figure 14 depict the performances of the various MPPT controllers including the INC, fuzzy, and P&O controllers. It can be observed that each algorithm can track the MPP effectively.

In terms of the power-tracking process, under the stable condition or with slow and uniform changes, each algorithm demonstrates acceptable effects.

The tracking operating point initially jumps, and then, it tracks the MPP slowly in the INC, fuzzy, and P&O methods, when the irradiation changes suddenly. This is because these three algorithms retain the duty cycles calculated at the last moment before the irradiation changed suddenly.

It can be observed that the method presented in this paper (ANN + AFL) provides good dynamic operation, faster convergence speed, less oscillations of operating point around MPP, and more effective tracking of global maxima under different conditions, than the INC, fuzzy, and P&O methods.

In order to illustrate the comparisons between each method distinctly, the output powers of each method divided by the ANN output power, are shown in Figure 14.

It is worth mentioning that, in Figure 14, the reason for the ratio being greater than 100% at the beginning, is an error existing between the output power reference given by the ANN and the PV output power at a low irradiance level. The error analysis remains consistent with that in Figure 6.

The DC-link voltage and the output current of the PV grid-connected inverter are depicted in Figure 15. It can be observed that the DC-link voltage is maintained at 700 V and the fluctuations are within an acceptable range about 10 V.

The effectiveness of the MPPT method presented in this paper is shown in Figure 15b. The output current is consistent with the PV output characteristic curve in Figure 4.

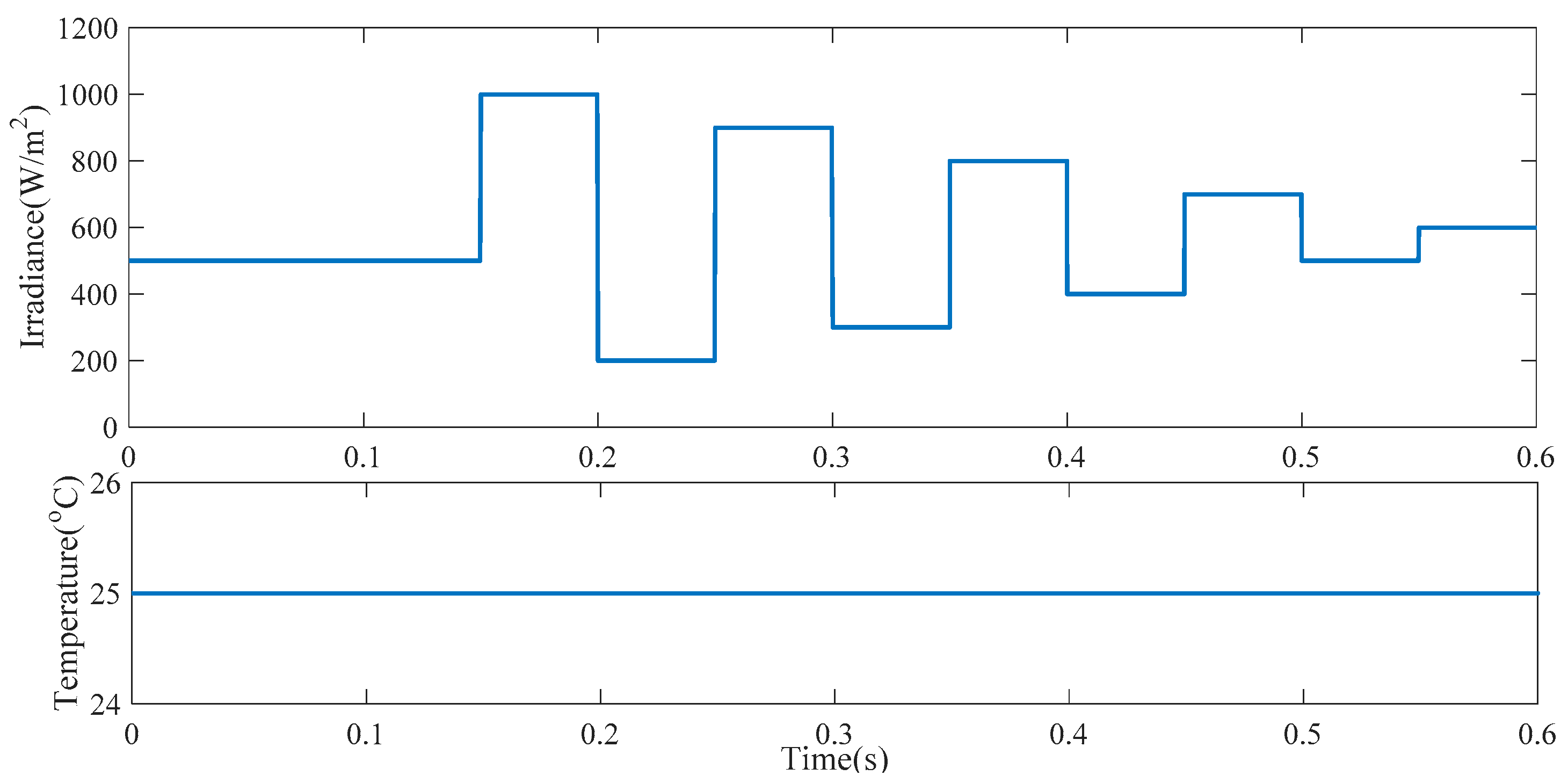
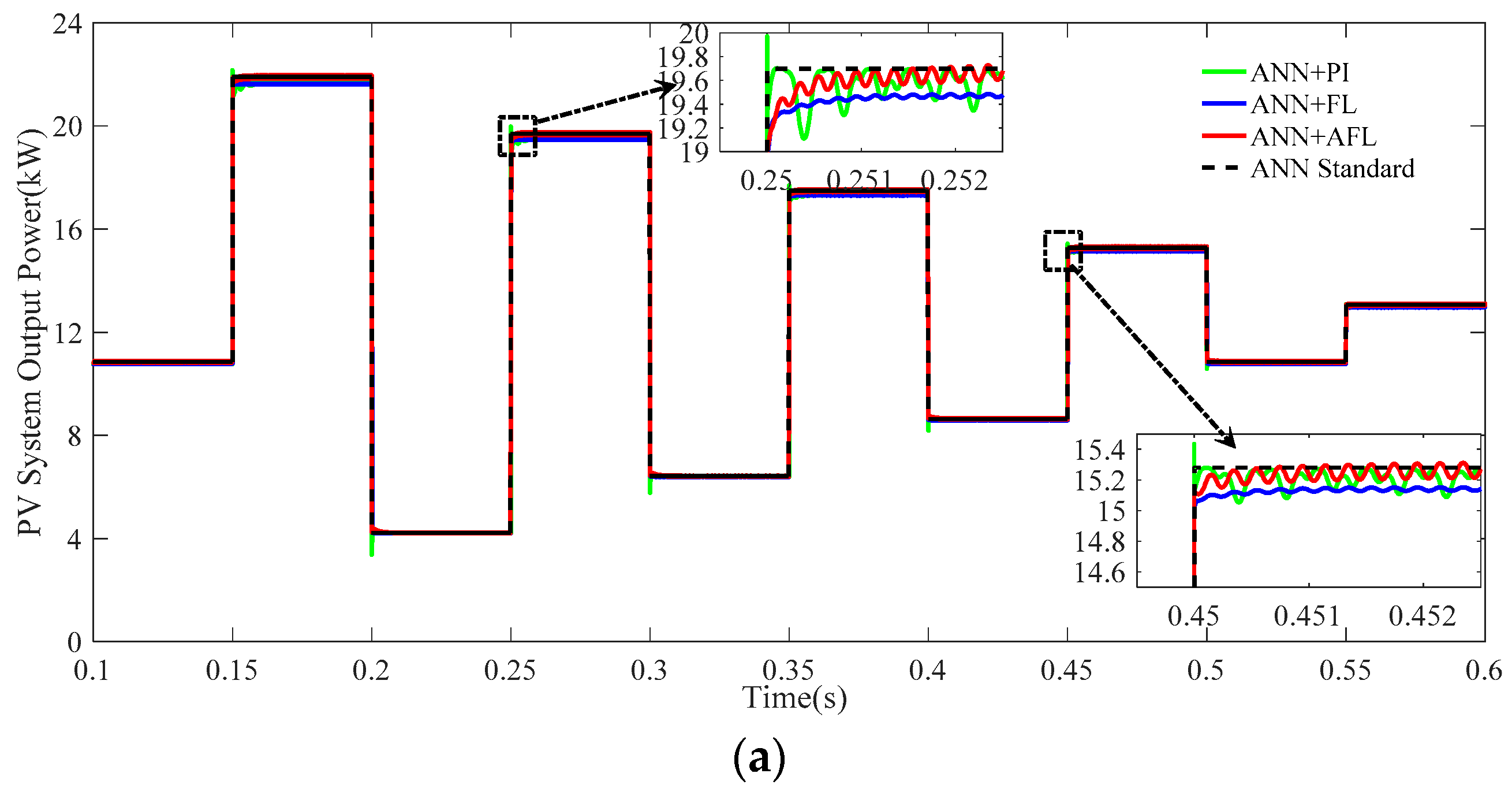
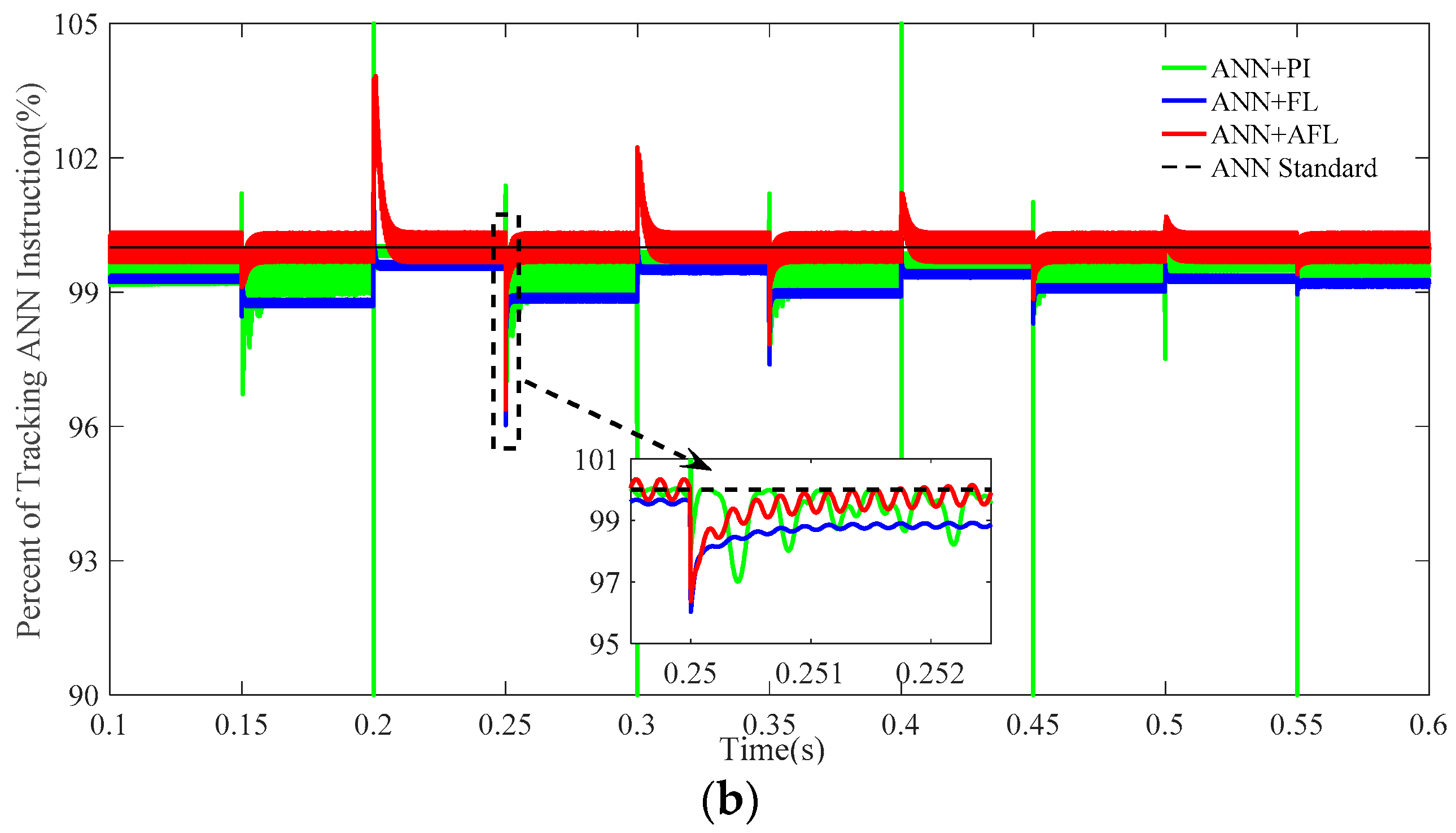
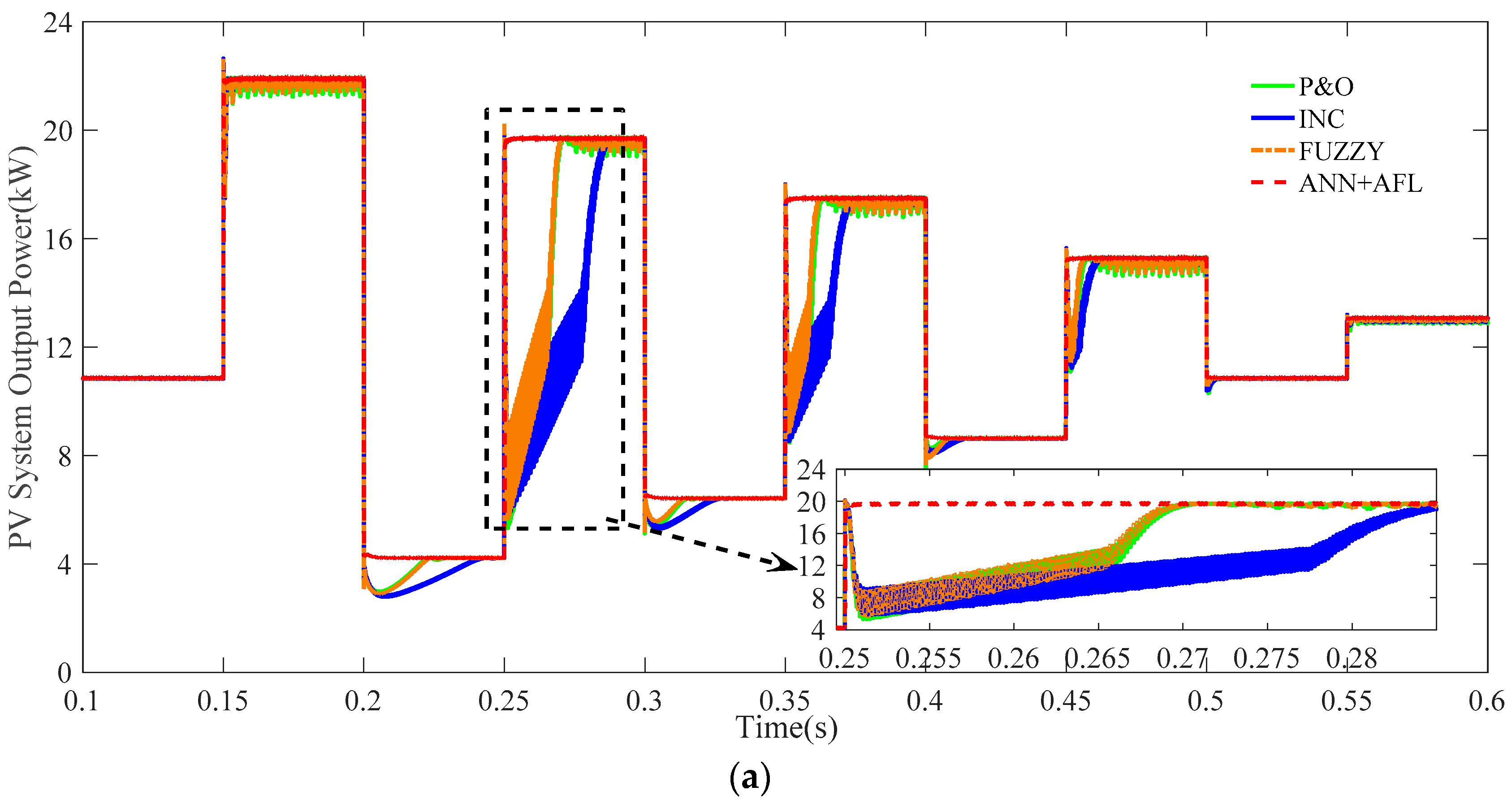
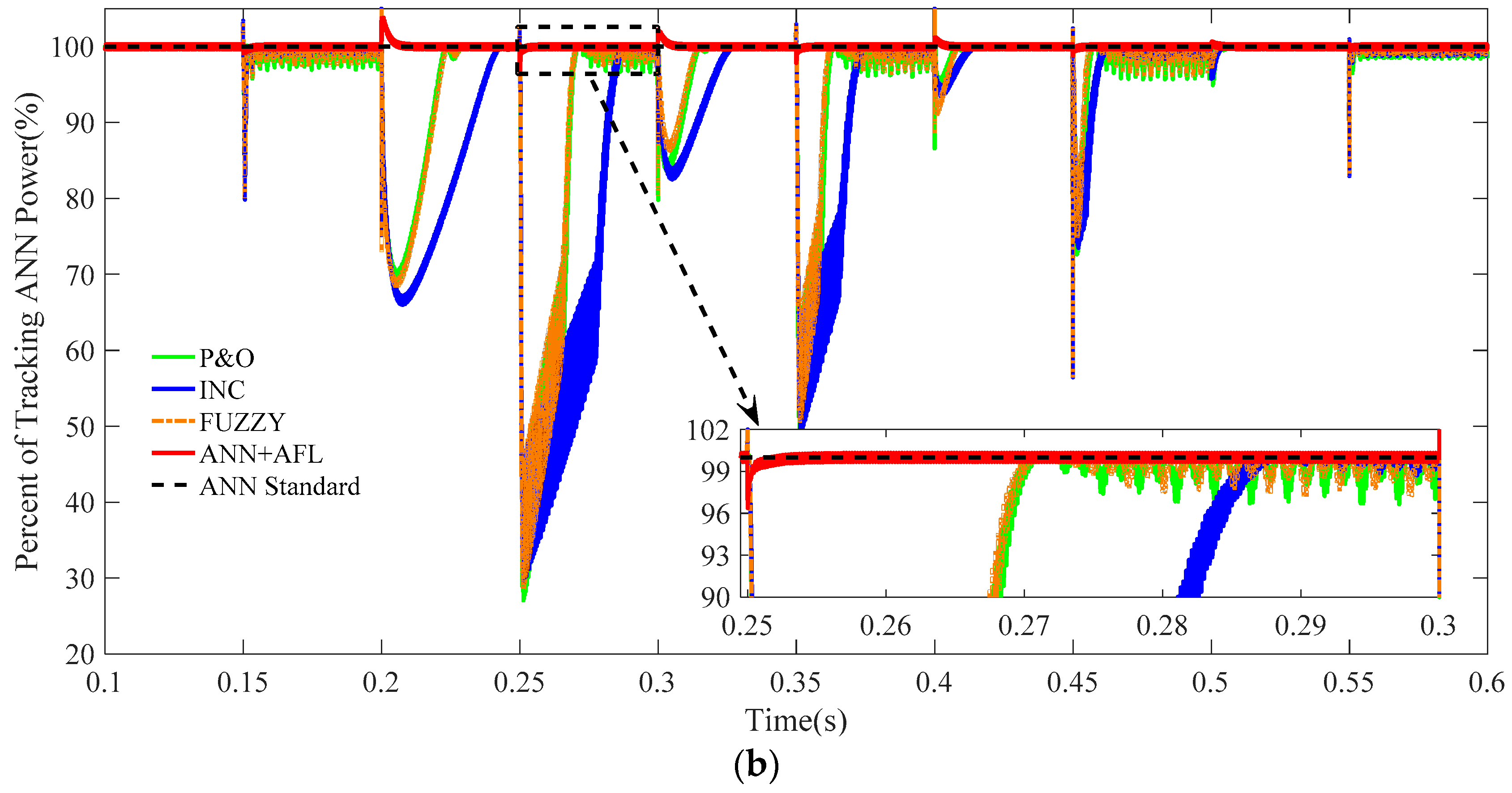
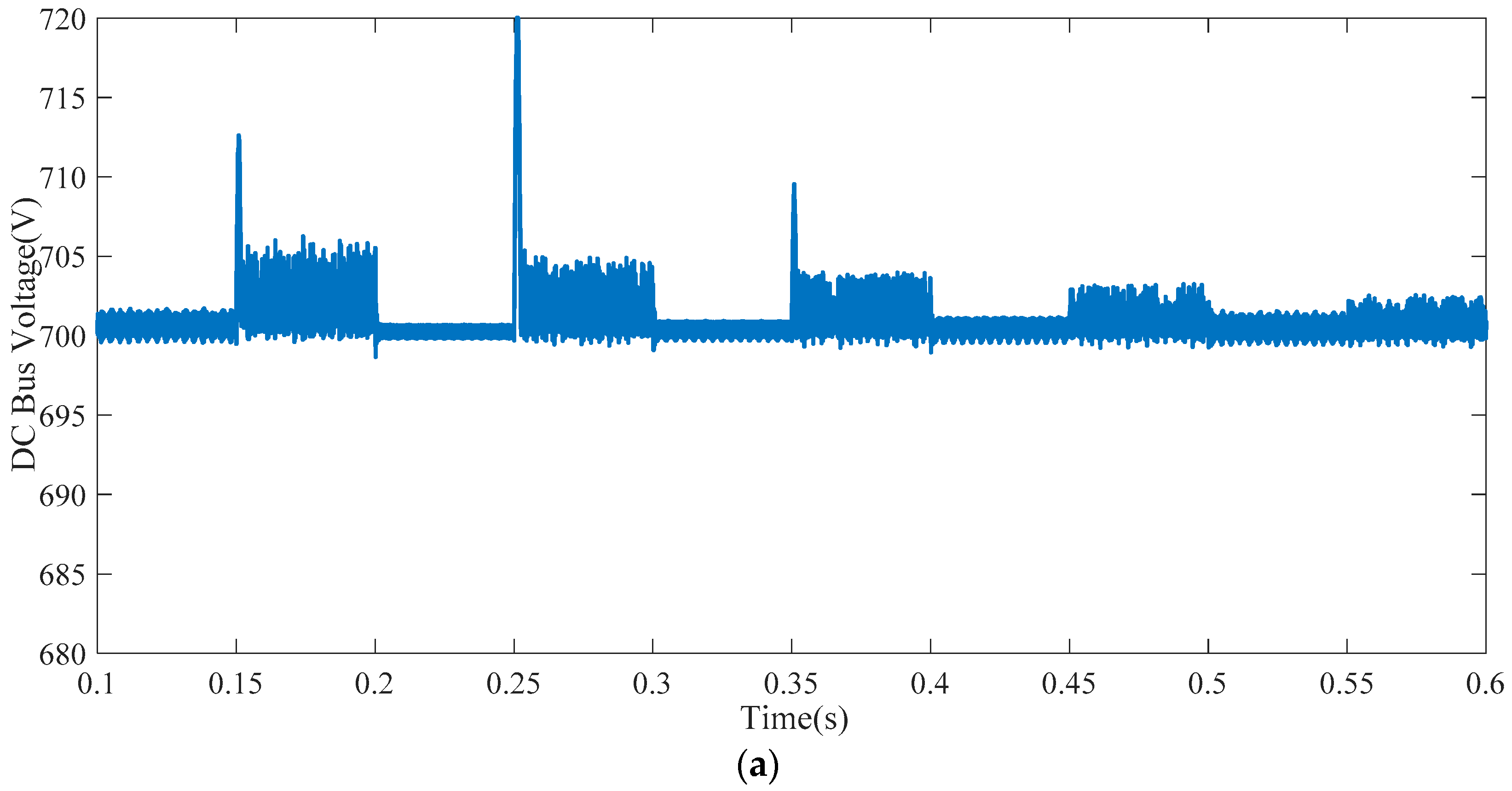
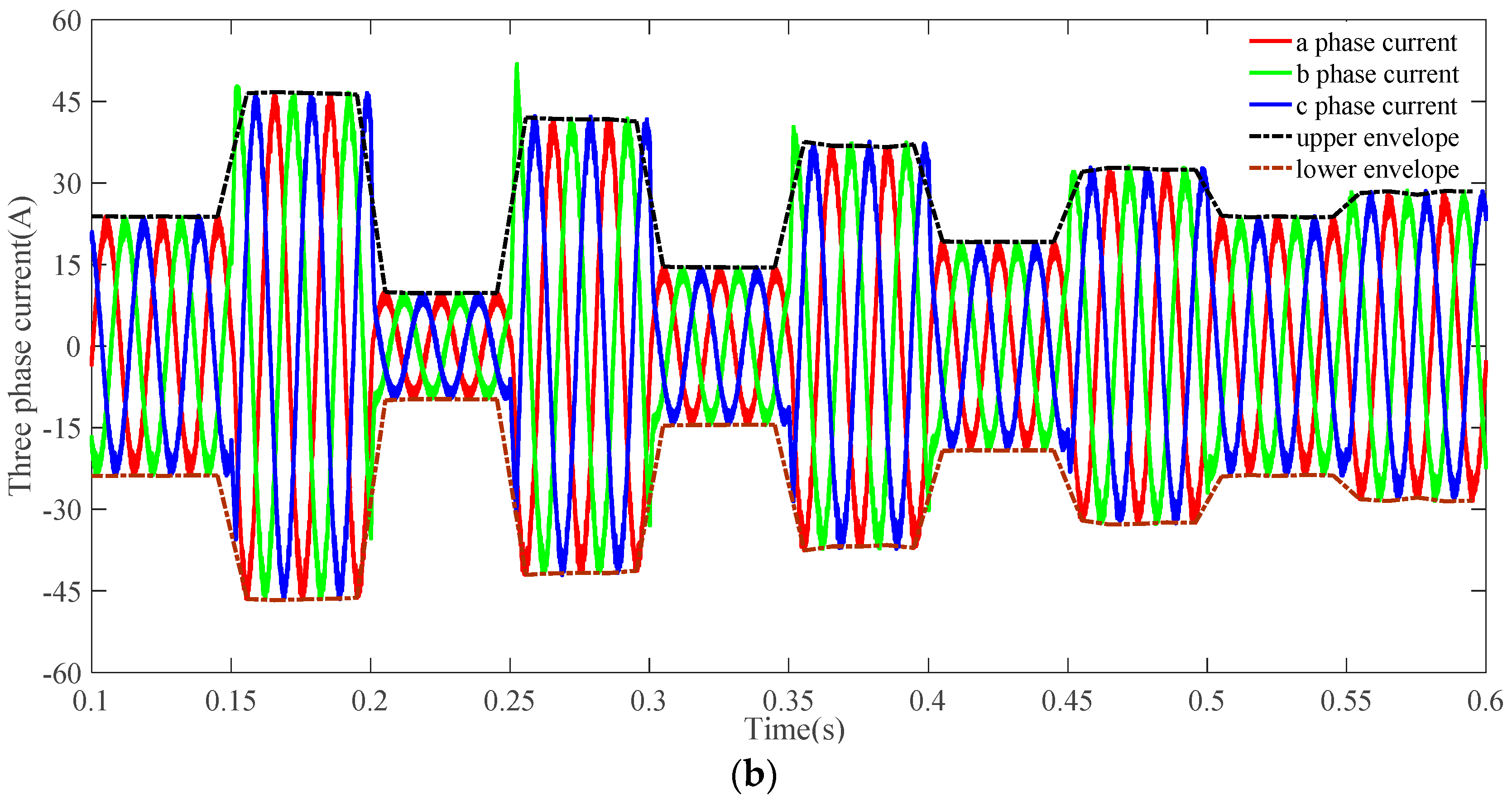
5.2. Simulation Case 2

In order to evaluate the performance of proposed method under extreme shading conditions, different control methods and algorithms which presented in simulation case 1 are tested under simulation case 2. In this case, the duration of simulation is 0.6 s. The temperature is maintained at a constant value of 25 °C in all sections. The temperature and irradiance variations are illustrated in Figure 16. The irradiance changes every 0.05 s from 0.15 s to 0.6 s as follows:

• 0 s~0.15 s: The irradiance is maintained at a constant value of 500 W/m².
• 0.15 s~0.2 s: The irradiance is increased to 1000 W/m² from 500 W/m².
• 0.2 s~0.25 s: The irradiance is decreased to 200 W/m² from 1000 W/m².
• 0.25 s~0.3 s: The irradiance is increased to 900 W/m² from 200 W/m².
• 0.3 s~0.35 s: The irradiance is decreased to 300 W/m² from 900 W/m².
• 0.35 s~0.4 s: The irradiance is increased to 800 W/m² from 300 W/m².
• 0.4 s~0.45 s: The irradiance is decreased to 400 W/m² from 800 W/m².
• 0.45 s~0.5 s: The irradiance is increased to 700 W/m² from 400 W/m².
• 0.5 s~0.55 s: The irradiance is decreased to 500 W/m² from 700 W/m².
• 0.55 s~0.6 s: The irradiance is increased to 600 W/m² from 500 W/m².

The analysis is similar to that of simulation case 1. The control effects with different DC/DC controllers are shown in Figure 17. Speed, accuracy, reliability, power loss, and oscillation during the tracking period are the main factors monitored in the evaluation and validation processes.

It can be observed from Figure 17 that the ANN + PI controller can track the MPP with a small steady-state error, but it cannot provide good dynamic operation when the irradiation changes suddenly. The ANN + FL controller can provide good dynamic operation; however, it demonstrates an obvious steady-state error. The MPP in this condition can be tracked by all methods proposed in Figure 17. The proposed ANN + AFL technique however tracked the MPP in a much shorter time and with fewer oscillations during the tracking period than other methods.

In order to illustrate the comparisons between each method distinctly, the output of each method divided by the ANN reference, are shown in Figure 17b. It can be clearly observed that the control effect of ANN + AFL is better than ANN + PI, and ANN + PI is better than ANN + FL, especially when avoiding the steady-state error.

Figure 18 depicts the performances of the MPPT controllers including the INC, fuzzy, and P&O controllers. It can be observed that each algorithm can track the MPP effectively. However, most of these methods suffer from slow convergence time or low efficiency.

As shown, the fuzzy and P&O method track the MPP within around half the tracking time of the INC algorithm. The proposed ANN + AFL algorithm tracks the MPP within a very short time and only little power loss. In order to illustrate the comparisons between each method distinctly, the output powers of each method divided by the ANN output power, are shown in Figure 18b.

It is worth mentioning that, in Figure 18b, the reason for the ratio being greater than 100% at the irradiance switching point, is an error existing between the output power reference given by the ANN and the PV output power at a low irradiance level. The error analysis remains consistent with that in Figure 6.

It can be observed that, even under conditions when the irradiation changes rapidly, the method presented in this paper (ANN + AFL) can provide good dynamic operation, faster convergence speed, less oscillations of operating point around MPP, and more effective tracking of global maxima under different conditions, than the INC, fuzzy, and P&O methods. An important outcome resulting from the application of the ANN + AFL technique for MPPT is the reduction in power loss during both the tracking and steady-state periods.

At the same time, the DC-link voltage is maintained at 700 V and the output current of the PV as shown in Figure 19, is consistent with the PV output characteristic curve in Figure 4.

6. Conclusions

A detailed analysis and design of an MPPT solution based on ANN and the nonlinear control theory was introduced in this paper. This solution aimed at performing fast MPPT in PV systems.

In terms of the nonlinear characteristics of PV systems, which were based on the temperature and irradiation, an ANN was utilized to deliver the reference power to the DC/DC boost converter. Under extremely low irradiance levels, the relative error percentage was lesser than 4%. Training data showed a trifling relative error percentage lesser than 0.5% in the normal irradiance range between 200 W/m² and 1000 W/m².

After the reference power was supplied by the ANN, an AFL control strategy was proposed for the DC/DC boost converter, according to the non-linear control theory.

The control effect of ANN + AFL was better than that of ANN + PI, which was better than that of ANN + FL, especially on avoiding steady-state errors. The proposed ANN + AFL control strategy showed a good dynamic performance with only a trifling steady-state error while tracking the MPP of the PV units even with rapid changes in irradiation. It demonstrated precise and fast tracking of the MPP, better than the ANN + PI and ANN + FL methods.

The control strategy of the inverter was designed with full consideration of the requirements of the PV system operating in the grid-connected mode. The results showed that, under the grid-connected mode, the DC-link voltage was maintained at 700 V and the output current of the PV system was consistent with the PV output characteristic curve.

The system was simulated using MATLAB/Simulink. From the simulation results, it could be observed that, an important outcome resulting from the application of the ANN + AFL technique for MPPT is the reduction in power loss during both the tracking and steady-state periods. With rapid changes in irradiation and temperature, the method presented in this paper (ANN + AFL) could provide good dynamic operation, faster convergence speed, trifling steady-state error, and fewer oscillations of the operating point around the MPP.