1. Introduction
Wireless sensor networks (WSNs) have become more and more widely used and important in recent years. The properties of WSNs—which contain hundreds or thousands of sensors—are limited by the energy, the bandwidth, the capability of computing, etc. Moreover, in most applications, the WSNs are arranged in the remote area where changing the sensor nodes always impossible or inconvenient, so how to save the node energy and prolong the network lifetime is important for WSN. There are many algorithms have been proposed to improve the network reliable and energy efficient for WSN. One remarkable approach is topology control. Topology control has been proposed to address many problems in WSNs by adding or deleting nodes/links according to certain algorithms. The aim of topology control is to reduce energy consumption and preserve other fundamental properties for the network at the same time [
1], such as network connectivity, reliability, fault-tolerant, coverage, etc.
In WSNs, topology control can be implemented in three approaches [
2]: (1) Power Adjustment Approach: minimizing the transmission power by adjusting the transmission range of node; in this approach, the long distance communication links will be eliminated while the short links will be chosen; (2) Power Model Management: controlling the feature of the operating mode to reduce energy consumption; there are four operating modes: sleep mode, idle mode, transmission mode, and receiving mode; since the energy consumption during the transmission mode and receiving mode is generally higher than that in the sleep mode [
3], so switching the redundant nodes into sleep mode can save energy obviously [
4]; (3) Clustering Approach [
5]: selecting a set of nodes in the network to construct an efficiently hierarchical topology; the clusterheads are restricted to certain tasks like collecting data, processing packets, or forwarding packets to non-clusterheads; the non-clusterheads nodes collect data and transmit the data packets to the clusterheads. In this paper, we mainly concentrate on the first one, i.e., the power adjustment approach.
To the power adjustment approach, on one hand, for reducing interference and energy consumption, each node transmits packets with relative low power [
6]. The algorithms are generally localized, i.e., each node uses only the information that is one or two hops away. The problem of minimizing the total energy consumption for the whole network is NP-hard in both two and three dimensional space [
7,
8]. In addition, if the WSN consists thousands of nodes, it is difficult to calculate the optimal transmission ranges for transmitting the packets to the concerned nodes [
3]. On the other hand, even reducing the transmission range of nodes is the most common and effective approach to control the network topology and reduce the energy consumption in WSN, but in this paper we will show that the long directly communication links can probabilistically spend less energy than the short indirectly communication links, i.e., it is probabilistic when reducing the energy consumption of network by reducing transmission range.
Motivated by these, in this paper, we explore the probability of reducing energy consumption by reducing the transmission range, and investigate the properties of this probability under different scenarios. Based on the conclusions, we propose an energy efficient and reliable topology control algorithm (ERTC) which meets the requirements of network connection and energy efficient at the same time. The contributions of this paper are as follows:
we propose a mathematic probability model for energy consumption analysis when applying the transmission power adjustment approach. To the best of our knowledge, this is the first probability analysis model for this kind of issue;
we analyze the probability model in detail and explore the features of this model under different network parameters;
we propose an ERTC based on these conclusions, which maintain the r-range of the node instead of the k-connection and can adapt the network dynamic.
The rest parts of the paper are organization as follows: in
Section 2, we will introduce the related works of the and topology control;
Section 3 will provide the network model and state the problems which will be investigated in this paper; we will introduce the probability model and analysis the properties of this model in
Section 4; in
Section 5, we will introduce the ERTC method in detail;
Section 6 explores the performance of ERTC based on simulation; in
Section 7, we conclude this paper.
2. Related Works
The latest surveys of network topology control algorithms can be found in [
2,
9,
10,
11]. The primary goals of topology control are to guarantee the network connection and reduce the energy consumption as far as possible. Many heuristic algorithms have been proposed, such as, Local Minimum Spanning Tree (LMST) [
12], Local Tree-based Reliable Topology (LTRT) [
6], A1 [
13], Poly [
14], Centralized Robust Topology Control Algorithm (CRTCA) [
15], Cooperative topology control scheme with Opportunistic Interference Cancelation (COIC) [
16], Local Mean Neighbor (LMN) [
17], Local Mean Algorithm (LMA) [
17], Smart Boundary Yao Gabriel Graph (SBYaoGG) [
18], BRASP [
19], etc. Almost all of these protocols regard topology control as a technique in which nodes dynamically change their transmission ranges to gain energy efficient and network connection. In [
12], each node builds its own LMST independently and only on-tree nodes that one-hop away are kept in the final topology. Considering the fact that the LMST always constructs one-connected network in the final topology, in [
6], the authors propose LTRT algorithm, which combines the idea of LMST and Tree-based Reliable Topology (TRT) together to guarantee
k-edge connectivity in the resulting topology. LTRT can maintain the network connection at low computational cost and energy consumption. In [
19], due to the lossy links in the real environment (which can provide only probabilistic connection), the authors propose a novel probabilistic network model, in which the network connectivity is metered by the network reachability. The authors explore the minimal transmission power for each node when the network reachability is above a given threshold. Based on the conclusion, the authors propose BRASP algorithm to improve the energy efficiency and reduce the average node degree. A1 assumes the network topology as a connected network and finds a set of active nodes to form connected dominating set (CDS) [
13]. This algorithm can form a reduced topology while keeping the network connection and coverage at the same time. In addition, A1 forms the CDS which comprising high energy nodes in a single phase construction process and a set of active nodes for energy efficiency and better sensing coverage, respectively. Similarly with A1, Poly [
14] is also the algorithm based on CDS. In Poly, the network is modeled as a connected graph. The protocol can turn off the unnecessary node and keep the network connection and coverage at the same time. LMN and LMA are the two typical power adjustment topology control algorithms [
17]. In LMA, all the nodes can get their node degree. The algorithm sets the minimum threshold and maximum threshold for this number; if the node degree is less than the minimum threshold, the transmission range will be increased; otherwise, transmission range will be reduced. The principle of LMN is similar with LMA, but LMN does not set the maximum and minimum thresholds for the node degree. In LMN, the nodes use the mean neighbors’ node degree as the threshold to adjust the transmission ranges.
3. Network Model and Problem Statement
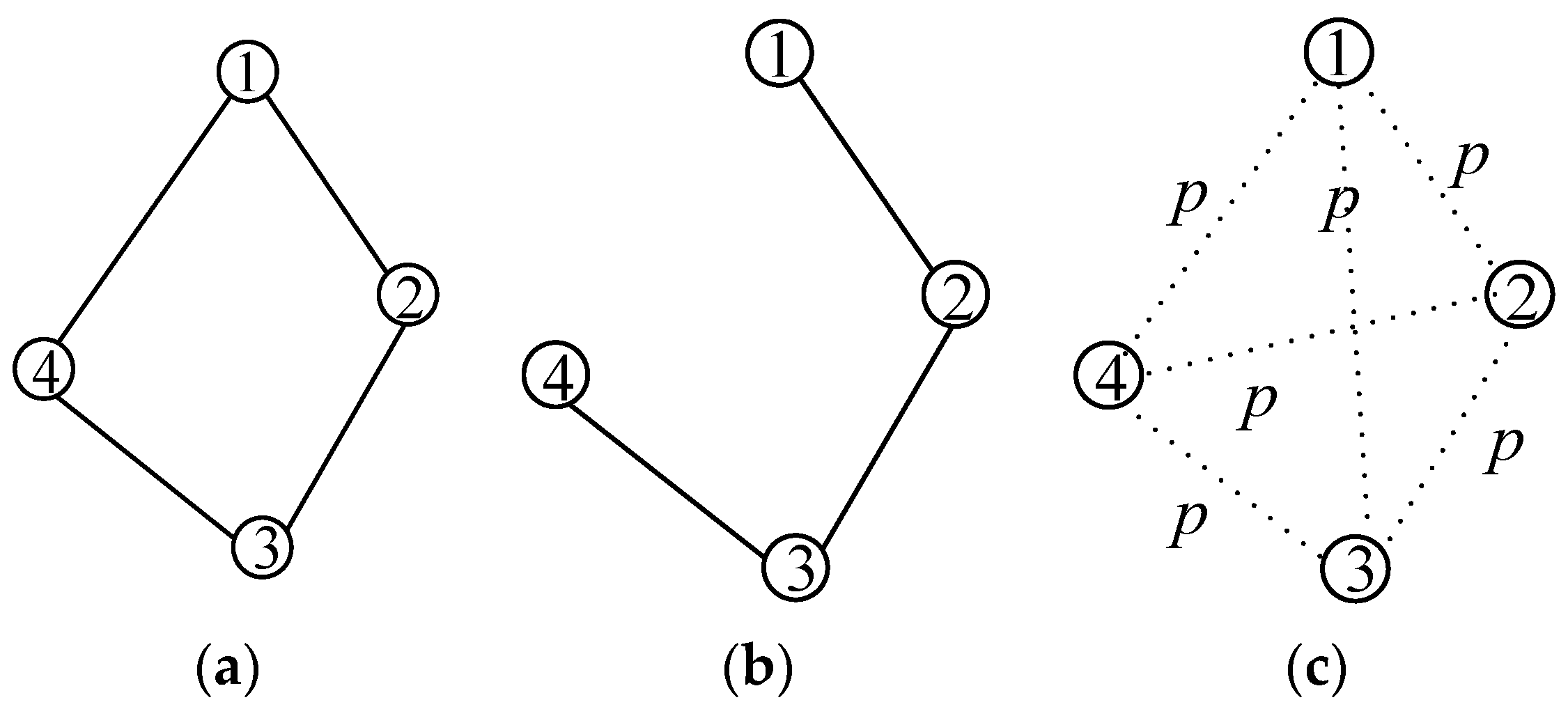
In general, there are three models can express the connection mode between nodes, which are shown in
Figure 1 [
20].
Figure 1a illustrates the
k nearest neighbor model; each node in this model has constant node degree and maintains the node degree by changing communication range dynamically.
Figure 1b illustrates the disc model; in this model, the transmission range is modeled as a disk with radius
r; the nodes connect with other nodes that fall into its communication range.
Figure 1c illustrates the Erdos-Renyi random graph that connects any two nodes by the same probability which is not appropriate in WSNs. Disc model is more plausible in WSN since obtaining
k neighbors is not always feasible due to the communication range limitation [
20]. Therefore, in this paper, we only interested in the Disc model. The nodes in this model are uniform distributed and fixed; moreover, the nodes have different initial transmission ranges and can change their transmission ranges from zero to the maximum.
The notations and network definitions used in this paper are as follows:
The node number of the whole network;
The Euclidean distance between two nodes u and v, in this paper, we also use r to represent the initial transmission range;
The distance-power gradient;
The energy required to transmit data from node u to node v;
The probability of energy efficient when applying the power adjustment topology control algorithm.
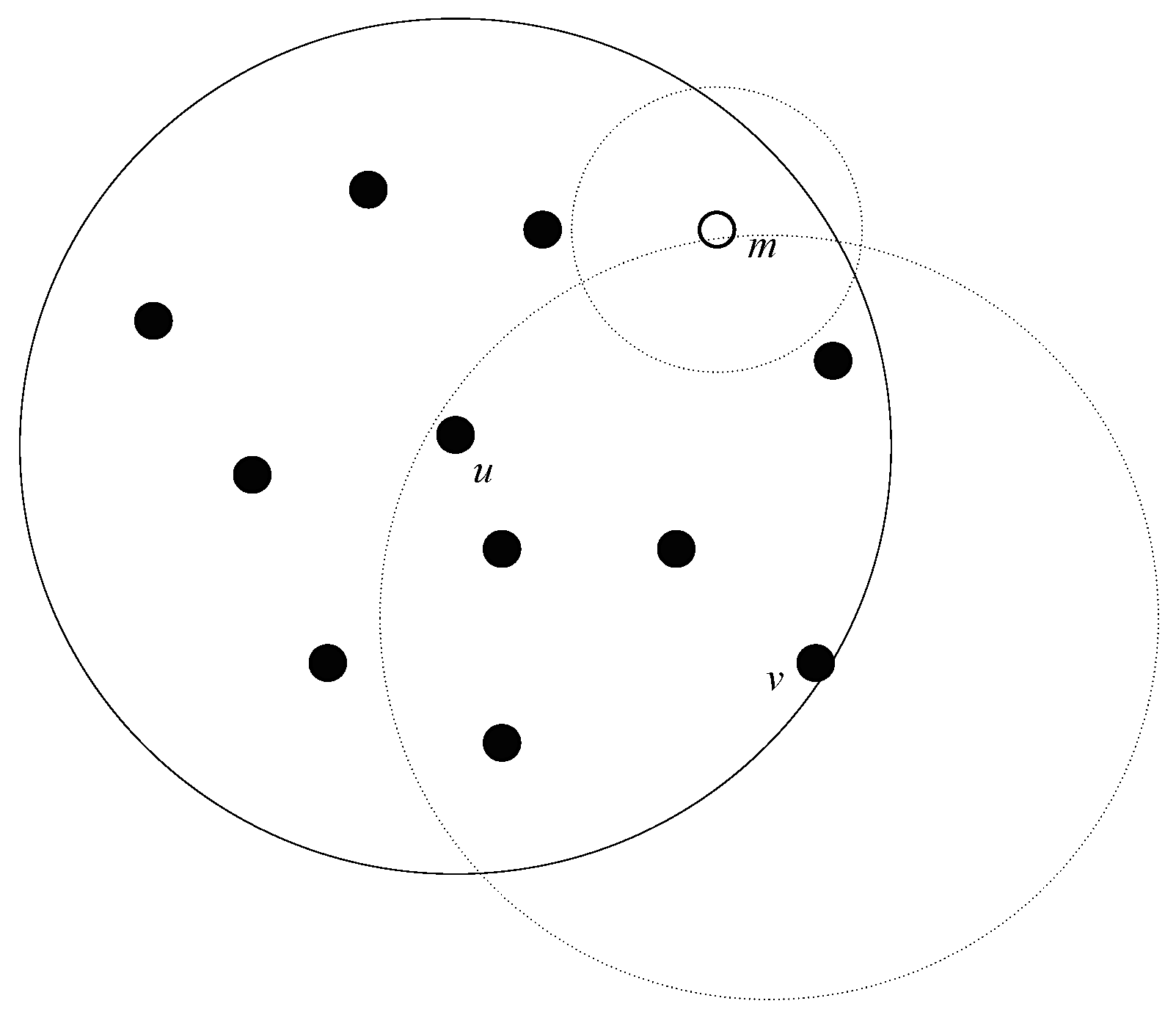
Definition 1. The communication range of node u is defined as the area where other nodes can receive u’s packet correctly.
In this paper, the communication ranges of nodes are circles, but may not be the same. Moreover, the transmission range can be changed from zero to maximum.
Definition 2. The energy required to transmit data packet from node u to node v is defined as , where r is the Euclidean distance between node u and node v, and γ
is a constant called the distance-power gradient whose typical value is between 2 and 4 [21,22,23]. Definition 3. The neighbors of node u are defined as the nodes which can receive the packet from node u and can reply message to node u.
Consequently, as shown in
Figure 2, according to the definition of the neighbors, if node
v is the neighbor of node
u, then the node
u is also the neighbor of node
v. In
Figure 2, even the node
m locates in the communication range of node
u, but it can not send packet to node
u due to the small transmission range, so node
m is not the neighbor of node
u. Node
v is the neighbor node of node
u, since node
u also locates in the transmission range of node
v.
Definition 4. r-range of the node is defined as the optimal transmission range which has high probability of energy efficient.
Like the definition of k-connection for the network reliability and considering the probability that reduce the energy consumption by reducing the transmission range, if the nodes can maintain the optimal transmission range, i.e., r-range, the probability of energy efficient will be high.
As discussed in
Section 2, many energy efficient topology control algorithms change the transmission range dynamically to gain energy efficient, but they fail to give the strict proof of whether this approach always effective or not; if not, what is the probability of this issue, and how to improve this probability? In this paper, we will analyze these issues in detail.
4. Probability Analysis
Theorem 1. After the transmission range adjustment, the probability that the energy consumption is less than the previous one is .
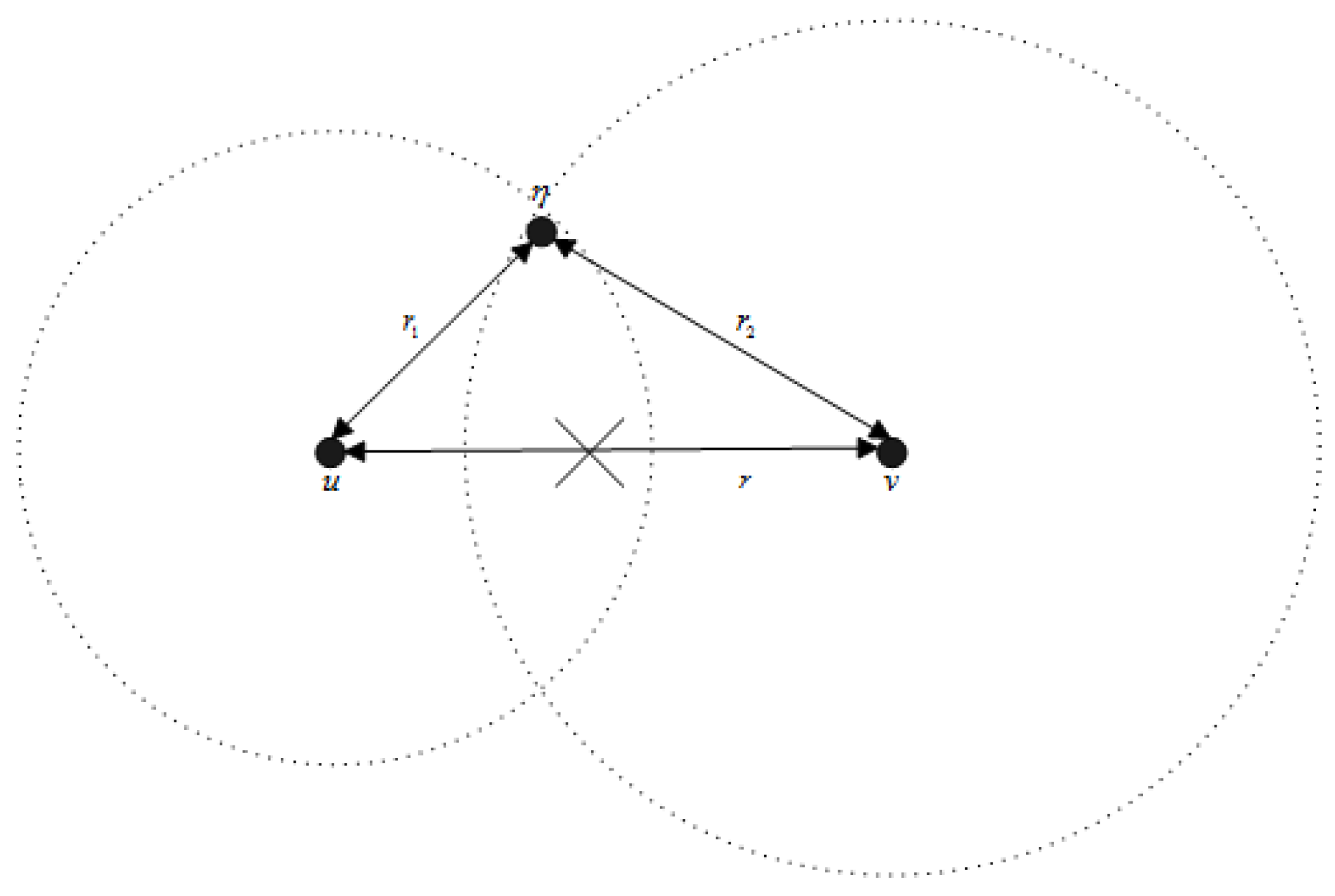
Proof. In WSN, supposing that node
v is the neighbor of node
u. when node
u transmits packet to node
v, the energy consumption is related to the distance between two nodes, which can be expressed as:
where
r is the Euclidean distance between node
u and node
v,
is the distance-power gradient that depending on the characteristics of the communication medium (
,
for outdoor propagation modes [
23]);
is the power needed for link between node
u and node
v.
If the transmission ranges of node
u and node
v are reduced based on the topology control algorithm, then node
u and node
v cannot communicate directly, which is shown in
Figure 3. As a result, node
n will be chosen as the relay node, where node
n is the neighbor of both node
u and node
v. Thus, the energy needed to transmit packets from node
u to node
v will be:
where
is the Euclidean distance between node
u and node
n,
is the Euclidean distance between node
n and node
v;
is the power needed for communicating between node
u and node
v by using relay node
n.
Therefore, the issues we need to solve are when
is smaller than
and what is the probability that
smaller than
. For exploring these issues, we define the Energy efficient Dominating Sets (EDS) as follows:
where the first constraint means the energy consumption after power adjustment is smaller than the previous one; the second constraint make sure node
u still can communication with node
v by using a relay node; the third and the fourth constraints guarantee the transmission ranges of each nodes are smaller than the previous. The EDS is shown in
Figure 4.
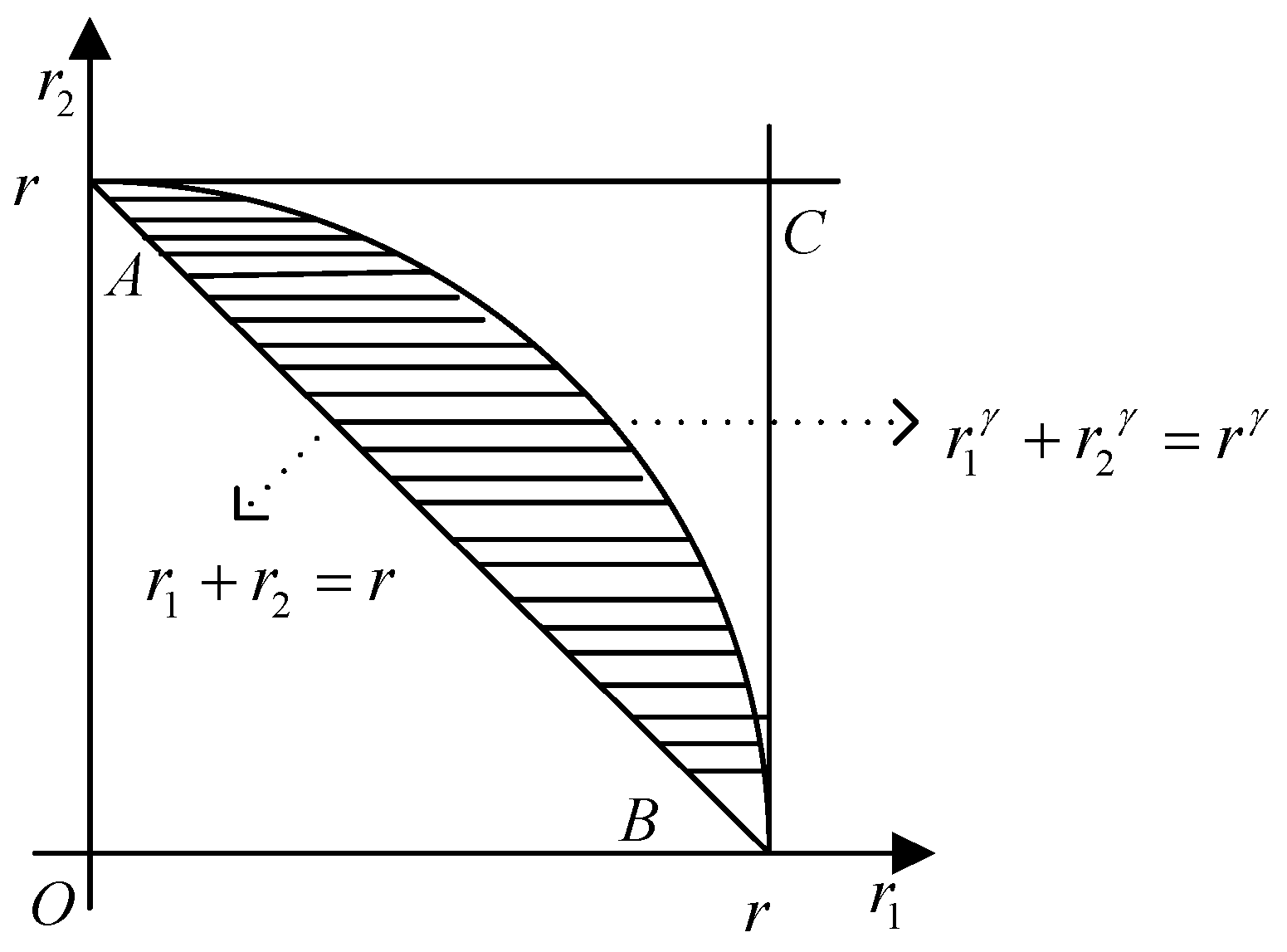
According the definition of EDS and the principle of linear programming, the EDS is the shadow area in
Figure 4. The area
ABC means the whole values which satisfy the second, third, and fourth constraints in Equation (3); the area
is the set that the energy consumption is smaller than the previous. Therefore, the probability that the energy consumption is less than the previous one is the proportion of area
in area
ABC, which can be calculated as:
where
x is the transmission range of nodes and
.
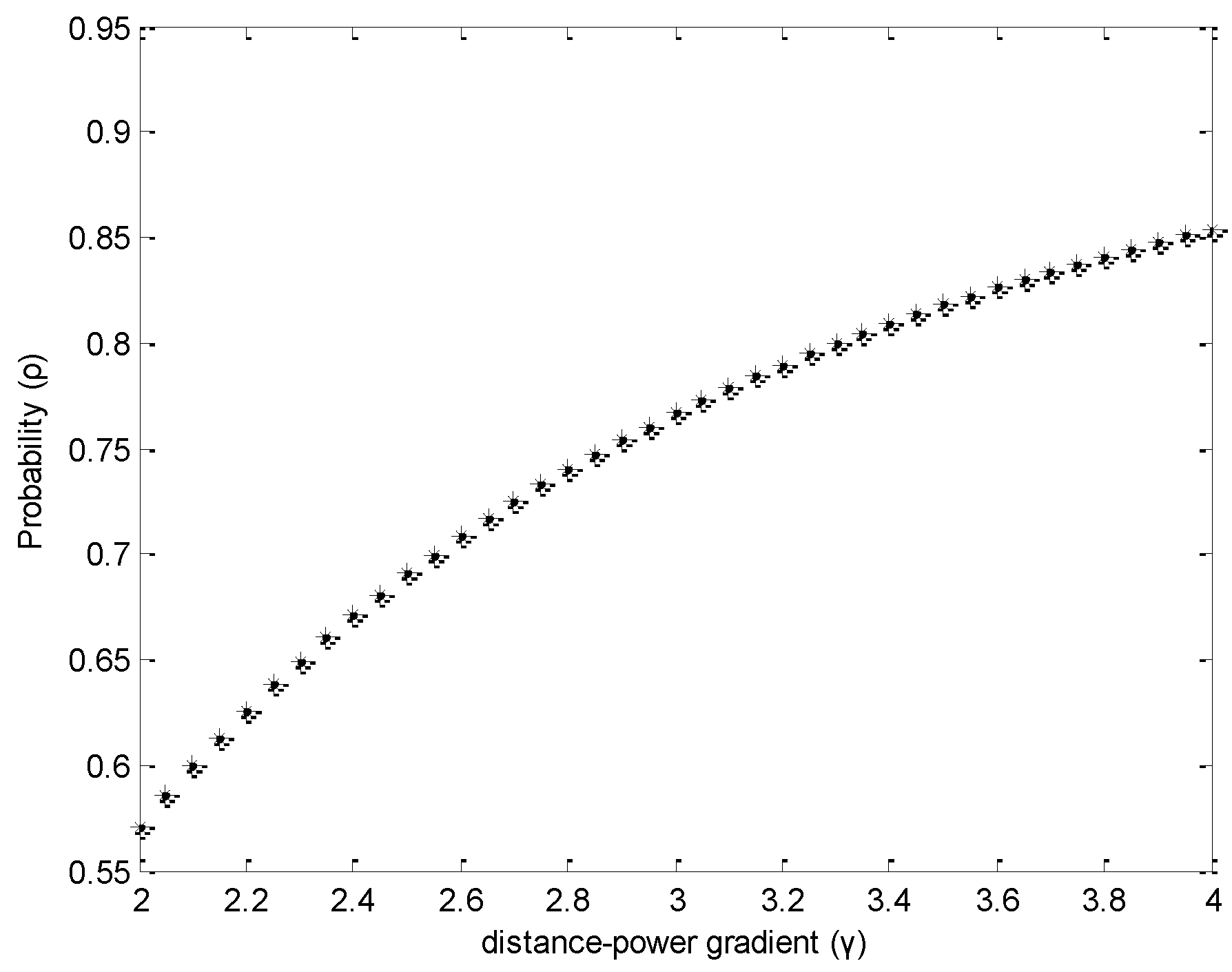
Lemma 1. With the increasing of (), the probability will increase from 0.5708 to 0.8541.
Proof. Considering the first derivative function of
on
:
In order to simplify the denotation, we define:
Therefore, Equation (5) can be rewritten as:
Since
, so if we can prove
is an increasing function, then we can conclude that
is also the increasing function with
. The first derivative function of
on
is:
As
, so
is an increasing function. Thus, the probability
will increase with the increasing of
. In addition, the maximum and minimum values of
are as follows:
As shown in
Figure 5, with the increasing of
, the probability
increases. The maximum value of
is 0.8741 and the minimum value is only 0.5708. This demonstrates that the algorithm which reduces the energy consumption by adjusting the transmission range is probabilistic, i.e., short transmission range does not mean small energy consumption. The reason why the probability increases with the increasing of
is that with the increasing of
, the energy consumption is more and more seriously effected by the distance between two nodes, which can be concluded from Equation (1); so if the transmission range changes, the energy consumption will be changed obviously.
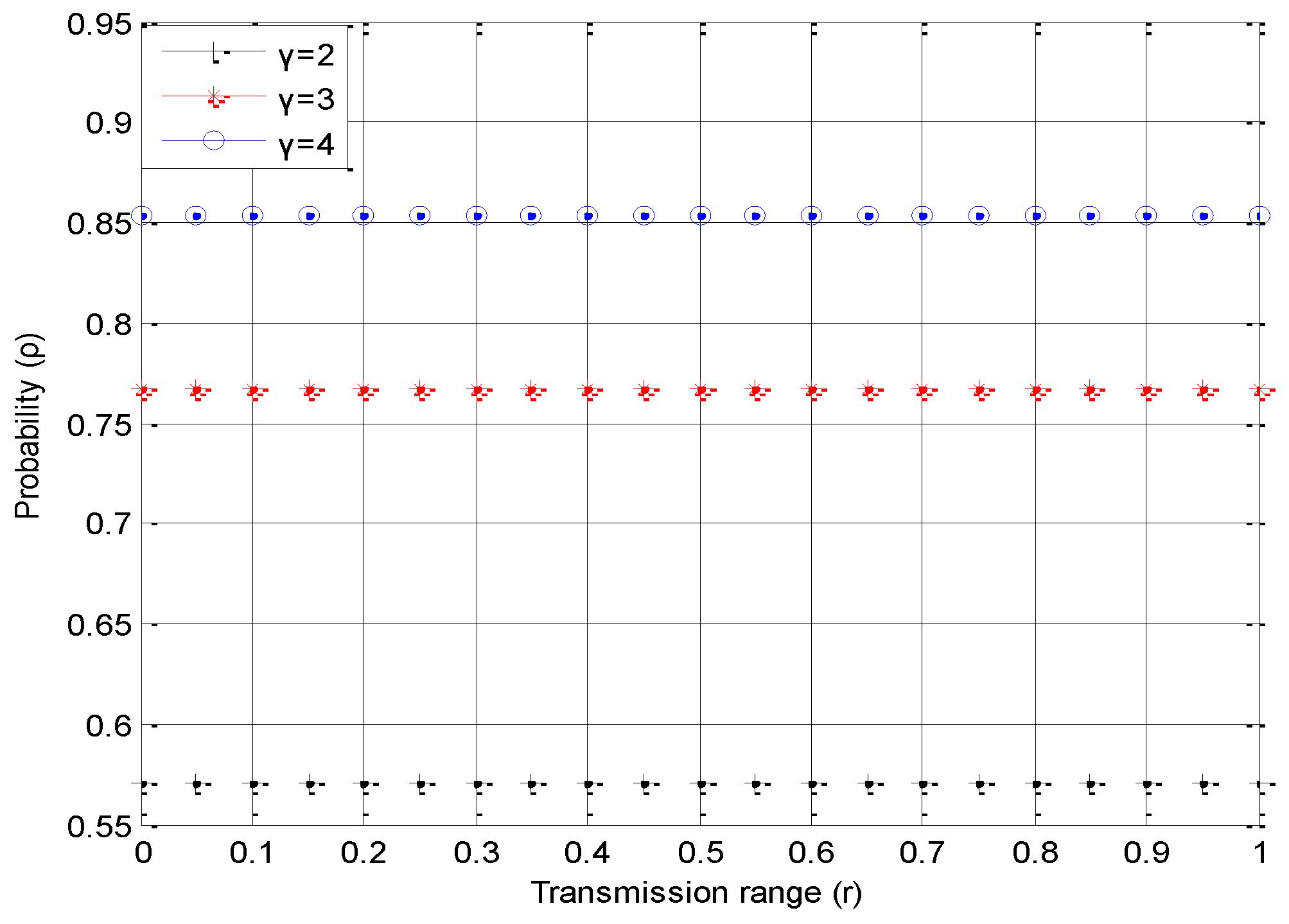
Lemma 2. With constant , the probability will keep constant with the variation of the initial transmission range r.
Proof. We can prove this conclusion by simulation. The result can be found in
Figure 6.
Figure 6 illustrates that with the increasing of
r, the probability
will keep constant. In addition, when
increases, the probability increases, too; and the bigger the
, the small increasing rate is, which is consistent with the conclusion of Lemma 1 (shown in
Figure 5).
The Lemma 2 indicates that the probability is nothing to do with the initial transmission range, i.e., no matter what r is, with constant , the probability will be the same.
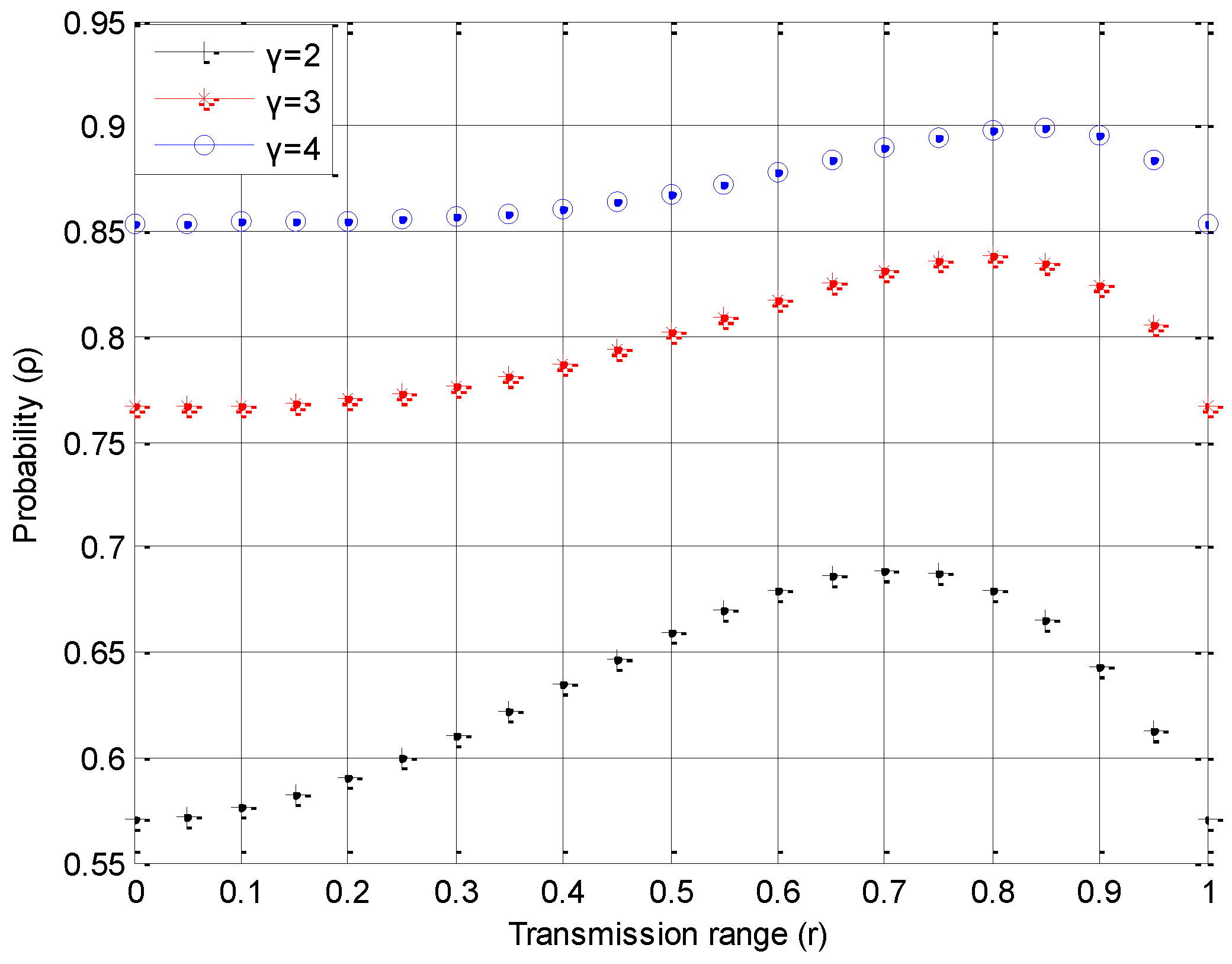
Lemma 3. With fixed value of , when the transmission range is , the probability can get the maximum value.
Proof. When applying the power adjustment topology control algorithm, the EDS of
and
are shown in Equation (3) and
Figure 4. Thus, similar with the definition of EDS, the Un-EDS of
and
can be shown as follows:
The meanings of each constraint are similar with Equation (3). The values which satisfy Un-EDS mean that the energy consumption of WSN does not decrease after reducing the transmission range. Therefore, how to reduce the size of Un-EDS is an effective method to increase the probability of energy efficient. A possible way is to eliminate some values of
and
from Un-EDS. Therefore, the new probability of energy efficient will be:
where
is the eliminated Un-EDS.
According the principle of linear programming, when
and
are in the boundary of Un-EDS, the eliminated Un-EDS
s can get the maximum value, i.e., the probability
can get the maximum value, which can be found in Equation (12). This means that
and
should satisfy the constraint as follows:
The first derivative function of
s and
on
can be expressed as:
Substitute Equation (15) into Equation (14), when
, the eliminated Un-EDS
s can get the extremum value when
. Furthermore, when
,
; when
,
; so
is the maximum value of
s. This conclusion also can be found in
Figure 7. In
Figure 7, we set the initial transmission range
r to 1, i.e.,
in this simulation.
When the probability
get the maximum value, the values of
are 0.7
r, 0.8
r, and 0.85
r where
,
, and
, respectively. The maximum value of
in
Figure 7 is consistent with the conclusion in
Table 1, which are got from Equations (4) and (12).
From
Table 1, we can find that after eliminating some values from the Un-EDS, the probabilities of energy efficient increase obviously: 11% when
, 7% when
, and 5% when
. Thus, in the power adjustment based topology control algorithm, we can use
as the optimal transmission range of nodes.
5. Energy Efficient and Reliable Topology Control Protocol
In
Section 4, we proved that the optimal transmission range for getting high probability of energy efficient is
. In this section, we propose an energy efficient and reliable topology control protocol based on this conclusion.
In
Section 4, we have explored the probability of energy efficient by reducing the transmission range in power adjustment based topology control algorithm. For guaranteeing the network connection, in this paper, we introduce the conclusions in [
24] into our algorithm as the constraints of network reliable. In [
24], the authors prove that when every node connects to its nearest
neighbors, the network is asymptotic connectivity (the asymptotic connectivity means that when the number of neighbor nodes is larger than
m, then the probability that the network is connected is asymptotic to 1); when each node connects to less than
nearest neighbors, the network is asymptotic disconnectivity (the asymptotic disconnectivity means that when the number of neighbor nodes is smaller than
k, then the probability that the network is disconnected is asymptotic to 1). The simulation result also shows that if the number of neighbors larger than
, the probability of connectedness increases rapidly to 1 for a modest number of nodes (e.g.,
). Therefore, in ERTC,
will be used as the lower limitation of the neighbors number, i.e., the node degree.
There are two stages in the ERTC: (1) neighbor information collection; (2) transmission range adjustment.
5.1. Neighbor Information Collection
In this section, node
i broadcast HELLO message
using initial transmission range
to calculate the node degree and the distances to the neighbor nodes. As shown in
Section 3, the transmission range is a circle, but may not same for each node. The HELLO message
includes the transmission power
, the source node ID
, and the version number
which is used to decide whether the received HELLO message is a new one or not. When the neighbor nodes receive this HELLO message, firstly, comparing the node ID
in the HELLO message
with the node IDs that in the neighbors-list; if the node ID already exist, then check the version number
to find out whether this HELLO message is a new one or not; if not, the HELLO message will be dropped immediately; otherwise, updating the neighbor-list; in case the node ID
does not exist in the neighbors-list, then adding the node ID to the neighbors-list. The distances
between two nodes are calculated when the node
i receives the HELLO message
from the neighbor nodes by using received signal strength indicator (RSSI) [
25,
26]. When the node
i receive the HELLO message
from other nodes, they will update the neighbors-list based on the same principle which described above and calculate the node degree
.
As shown in Lemma 4, the optimal transmission range for node i is , when the source node i receive the HELLO message from the neighbor nodes, it will compare the distance with ; the number of neighbor nodes whose distances to the source node i are smaller than will be the node degree of node i with transmission range , which is .
5.2. Transmission Range Adjustment
In this stage, the node
i adjusts their transmission range according the node degree
and
. As discussed in
Section 3, the optimal transmission range for energy efficient is
and for guaranteeing the network connection, the lower limitation of the neighbors number is
; therefore, for meeting the requirements of both the energy efficient and the network reliability, the node degree
and
should be compared with
for deciding the transmission range of node
i. There are three relationships between the node degree and the lower limitation of neighbor numbers in ERTC: (1)
; (2)
; and (3)
; different relationships will have different transmission range adjustment strategies:
- (i)
when , it means that when the transmission range of node i is , it has the highest probability to satisfy the requirements of both the energy efficient and network connection. Therefore, the transmission range of node i is reduced to , which is reasonable.
- (ii)
when
, this means that when the transmission range of node
i is
, the network connection can be satisfied; however, when the transmission range is
, it can not meet the requirement of network connection. As shown in
Figure 7, when the transmission range is close to
, the probability is close to the highest probability, too. In addition, considering the node in ERTC is uniform distributed, so the node degree
is proportional with the coverage area
; therefore, the transmission range in this situation can be set to
.
- (iii)
when , this means the initial transmission range of node i can not meet the requirement of network connection. Therefore, the transmission range should be increased. Similar with the reason in (ii), the transmission range closer to has higher probability of energy efficient than that far from and considering the node distribution in ERTC is uniform, so the transmission range in this range can be set to .
The process of the ERTC is:
| Energy Efficient and Reliable Topology Control Algorithm (ERTC) |
1. ERTC:
Input:
2. The length of the configuration area, Border_length;
3. The number of the nodes in the network, n;
4. The value of distance-power gradient, ;
Ensure:
5. Broadcast the HELLO message with initial transmission range ;
6. Receive the HELLO message ;
7. Update the neighbors-list;
8. Calculate the node degree ;
9. Compare the distance between node i and the neighbor nodes with ;
10. Calculate the node degree ;
11. if then
TR = ;
12. else if then
TR = ;
13. else
TR = ;
14. end if
15. = TR; |
As shown in the table above, the runtime complexity for ERTC is
O(
n), which is the same as the runtime complexity of LMA and LMN [
17]. Therefore, the ERTC can improve the network performance without increasing the algorithm complexity seriously.
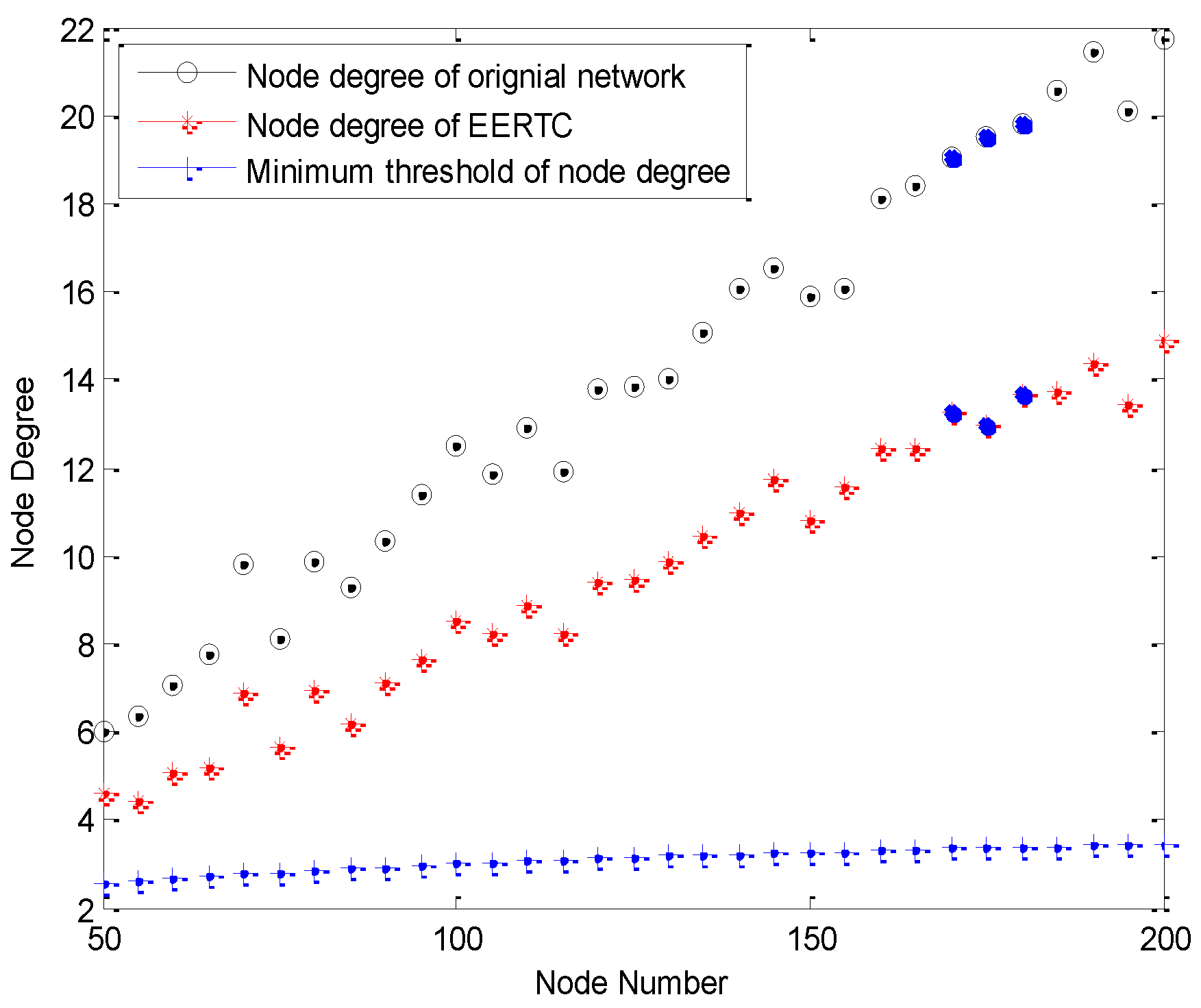
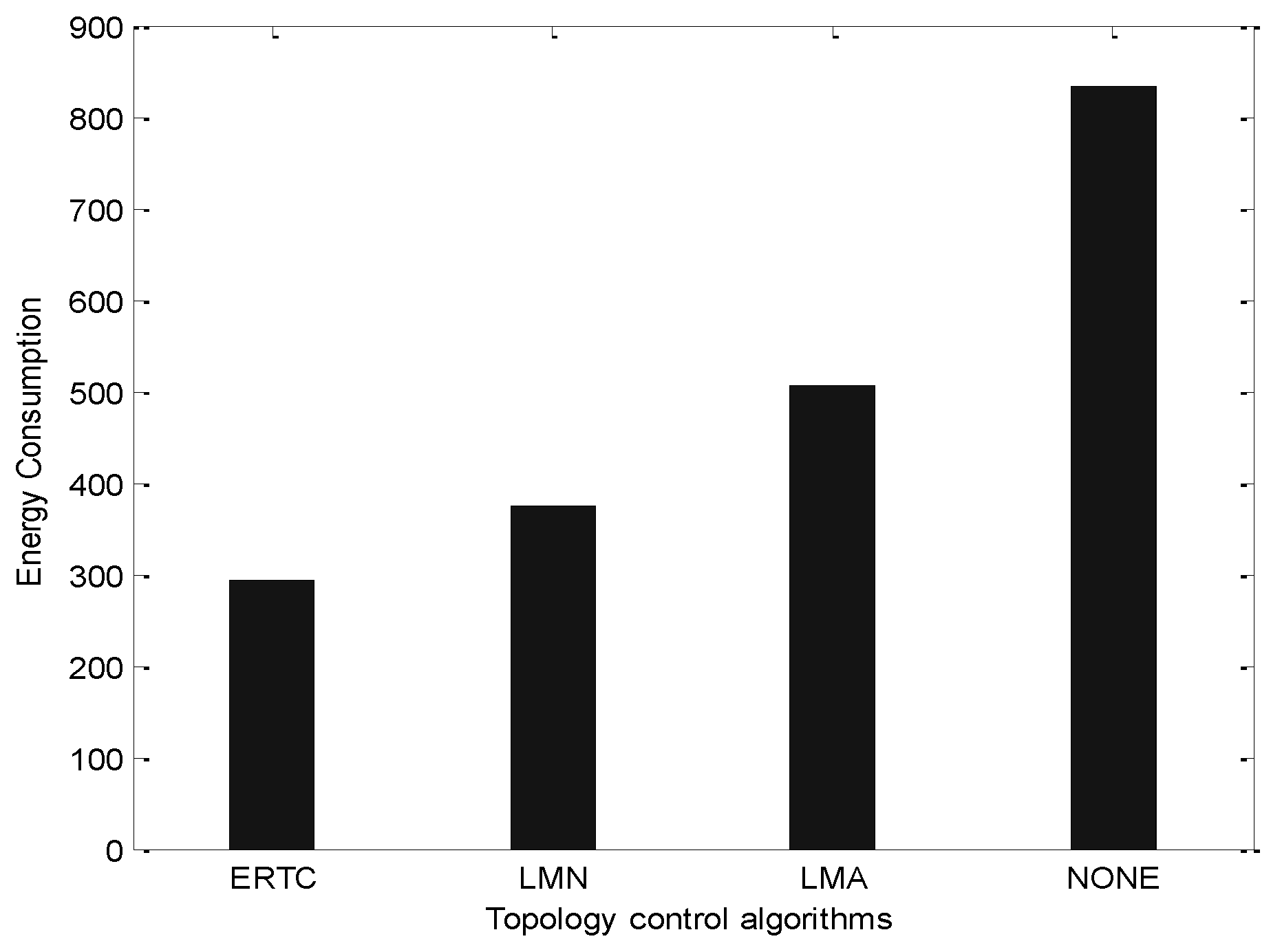
7. Conclusions
In this paper, for diminishing the energy consumption of WSN as far as possible, first, we propose a probability model for energy efficient in WSN; second, we analyze the properties of the probability model and find out the optimal transmission range; finally, we propose an ERTC based on the conclusions in
Section 4, which maintains
r-range for the nodes instead of
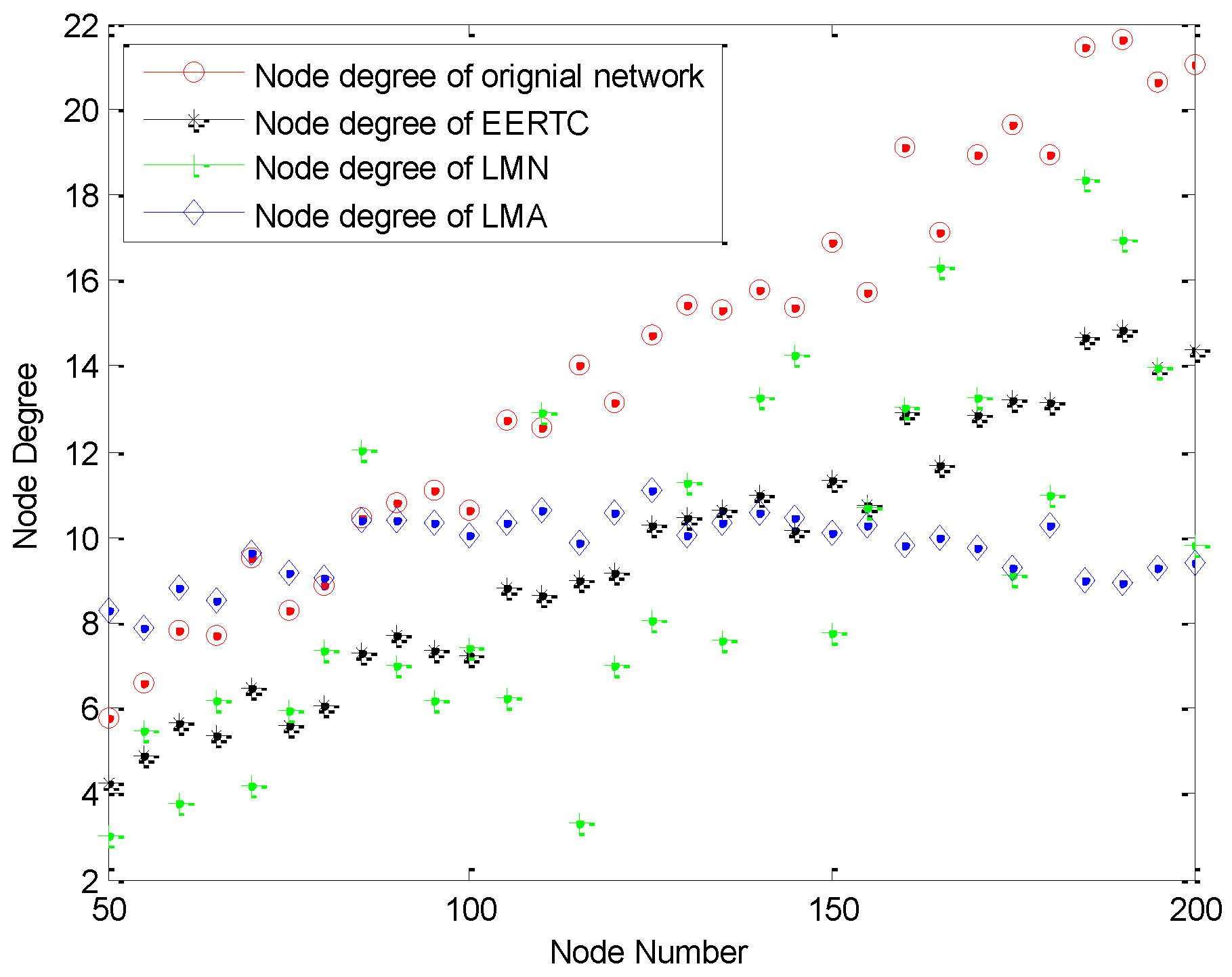
k-connection. To the best of our knowledge, this paper is the first one that provides the strict mathematic analysis model for these kinds of issues. In addition, in this paper, we also investigate the performance of ERTC and compare the performance with LMN and LMA, which are the typical power adjustment based topology control algorithms.
We have proved that when the transmission ranges are changed, the probability of energy efficient is , which varies with the distance-power gradient and keeps constant with different r, i.e., the probability is nothing to do with the initial transmission range. The probability varies from 0.5708 to 0.8541. We have also proved that when the transmission range is , the probability will get the maximum value. In this paper, we also propose an ERTC algotithm, which can guarantee both the energy efficient and network connection at the same time.