The Relationship between Residential Electricity Consumption and Income: A Piecewise Linear Model with Panel Data
Abstract
:1. Introduction
2. Methodology and Data
2.1. Methodology
2.2. Data
3. Empirical Results and Robustness Check
3.1. Empirical Results
3.2. Robustness Check
3.2.1. Estimate Methods
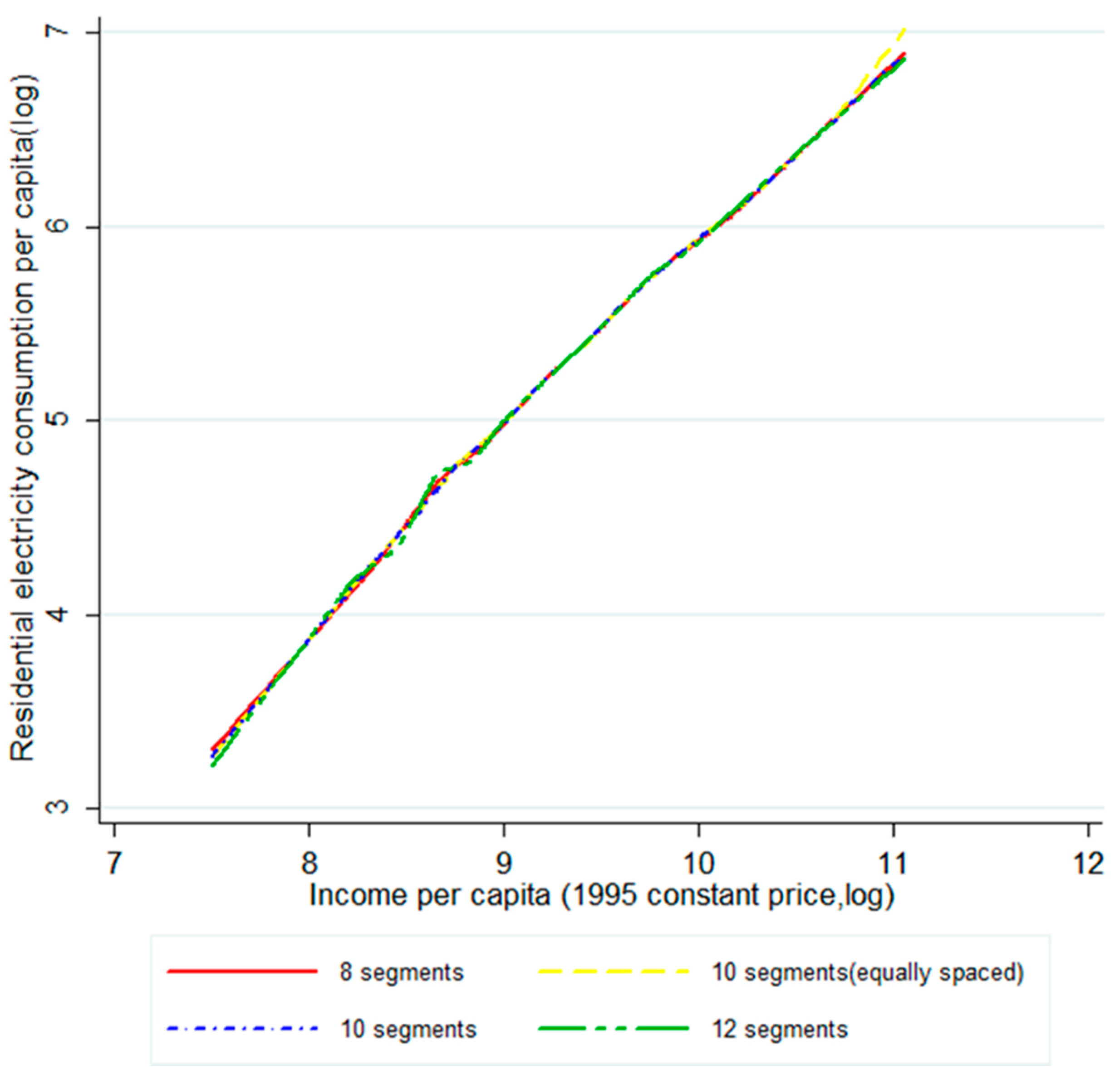
3.2.2. Segment Specifications
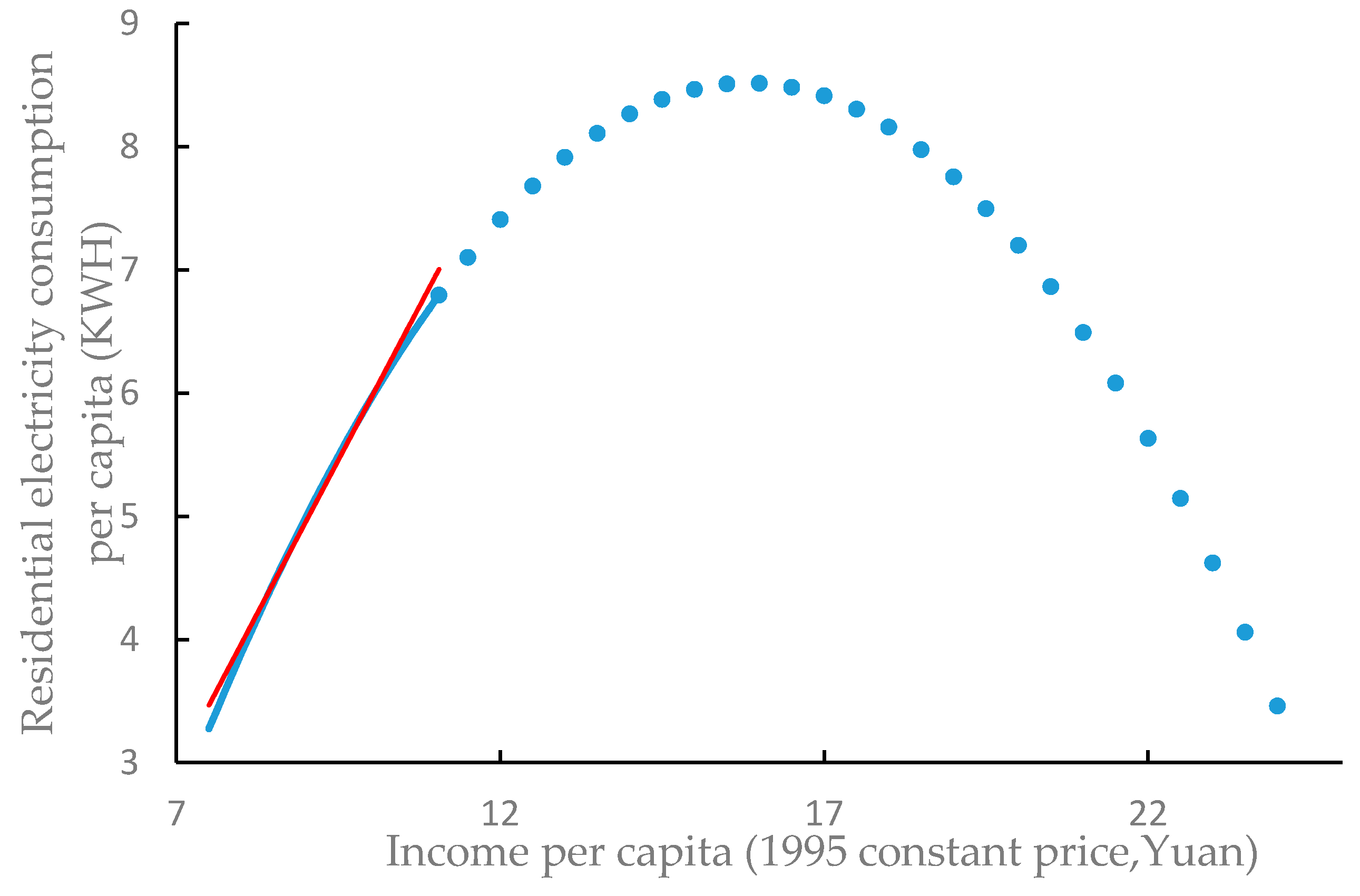
4. Comparisons and Discussion
5. Conclusions and Policy Implications
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kemmler, A. Factors influencing household access to electricity in India. Energy Sustain. Dev. 2007, 11, 13–20. [Google Scholar] [CrossRef]
- Musango, J.K. Household electricity access and consumption behaviour in an urban environment: The case of Gauteng in South Africa. Energy Sustain. Dev. 2014, 23, 305–316. [Google Scholar] [CrossRef]
- Auffhammer, M.; Wolfram, C.D. Powering up China: Income Distributions and Residential Electricity Consumption. Am. Econ. Rev. 2014, 104, 575–80. [Google Scholar] [CrossRef]
- National Bureau of Statistics of the People’s Republic of China. China Statistical Yearbook (1996–2013); China Statistics Press: Beijing, China, 1996–2013.
- Department of Energy Statistics of National Bureau of Statistics of the People’s Republic of China. China Energy Statistical Yearbook (1996–2013); China Statistics Press: Beijing, China, 1996–2013.
- Auffhammer, M.; Steinhauser, R. Forecasting the path of US CO2 emissions using state-level information. Rev. Econ. Stat. 2012, 94, 172–185. [Google Scholar] [CrossRef]
- Liao, H.; Cao, H.S. How does carbon dioxide emission change with the economic development? Statistical experiences from 132 countries. Glob. Environ. Chang. 2013, 23, 1073–1082. [Google Scholar] [CrossRef]
- Schmalensee, R.; Stoker, T.M.; Judson, R.A. World carbon dioxide emissions: 1950–2050. Rev. Econ. Stat. 1998, 80, 15–27. [Google Scholar] [CrossRef]
- Alberini, A.; Gans, W.; Velez-Lopez, D. Residential consumption of gas and electricity in the U.S.: The role of prices and income. Energy Econ. 2011, 33, 870–881. [Google Scholar] [CrossRef]
- Blázquez, L.; Boogen, N.; Filippini, M. Residential electricity demand in Spain: New empirical evidence using aggregate data. Energy Econ. 2013, 36, 648–657. [Google Scholar] [CrossRef]
- Dergiades, T.; Tsoulfidis, L. Estimating residential demand for electricity in the United States, 1965–2006. Energy Econ. 2008, 30, 2722–2730. [Google Scholar] [CrossRef]
- Silk, J.I.; Joutz, F.L. Short and long-run elasticities in US residential electricity demand: A co-integration approach. Energy Econ. 1997, 19, 493–513. [Google Scholar] [CrossRef]
- Ziramba, E. The demand for residential electricity in South Africa. Energy Policy 2008, 36, 3460–3466. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, H.; Guo, S.; Li, F.; Hu, Y. The Impact of Financial Crisis on Electricity Demand: A Case Study of North China. Energies 2016, 9, 250. [Google Scholar] [CrossRef]
- Rasheed, M.B.; Javaid, N.; Ahmad, A.; Jamil, M.; Khan, Z.A.; Qasim, U.; Alrajeh, N. Energy Optimization in Smart Homes Using Customer Preference and Dynamic Pricing. Energies 2016, 9, 593. [Google Scholar] [CrossRef]
- Tang, X.; Liao, H. Energy poverty and solid fuels use in rural China: Analysis based on national population census. Energy Sustain. Dev. 2014, 23, 122–129. [Google Scholar] [CrossRef]
- World Energy Outlook 2014; International Energy Agency (IEA): Paris, France, 2014.
- Bollen, K.A.; Brand, J.E. Fixed and Random Effects in Panel Data Using Structural Equations Models; California Center for Population Research: Los Angeles, CA, USA, 2008. [Google Scholar]
- Jamasb, T.; Meier, H. Household Energy Expenditure and Income Groups: Evidence from Great Britain; University of Cambridge: Cambridge, UK, 2010. [Google Scholar]
- Richmond, A.K.; Kaufmann, R.K. Is there a turning point in the relationship between income and energy use and/or carbon emissions? Ecol. Econ. 2006, 56, 176–189. [Google Scholar] [CrossRef]
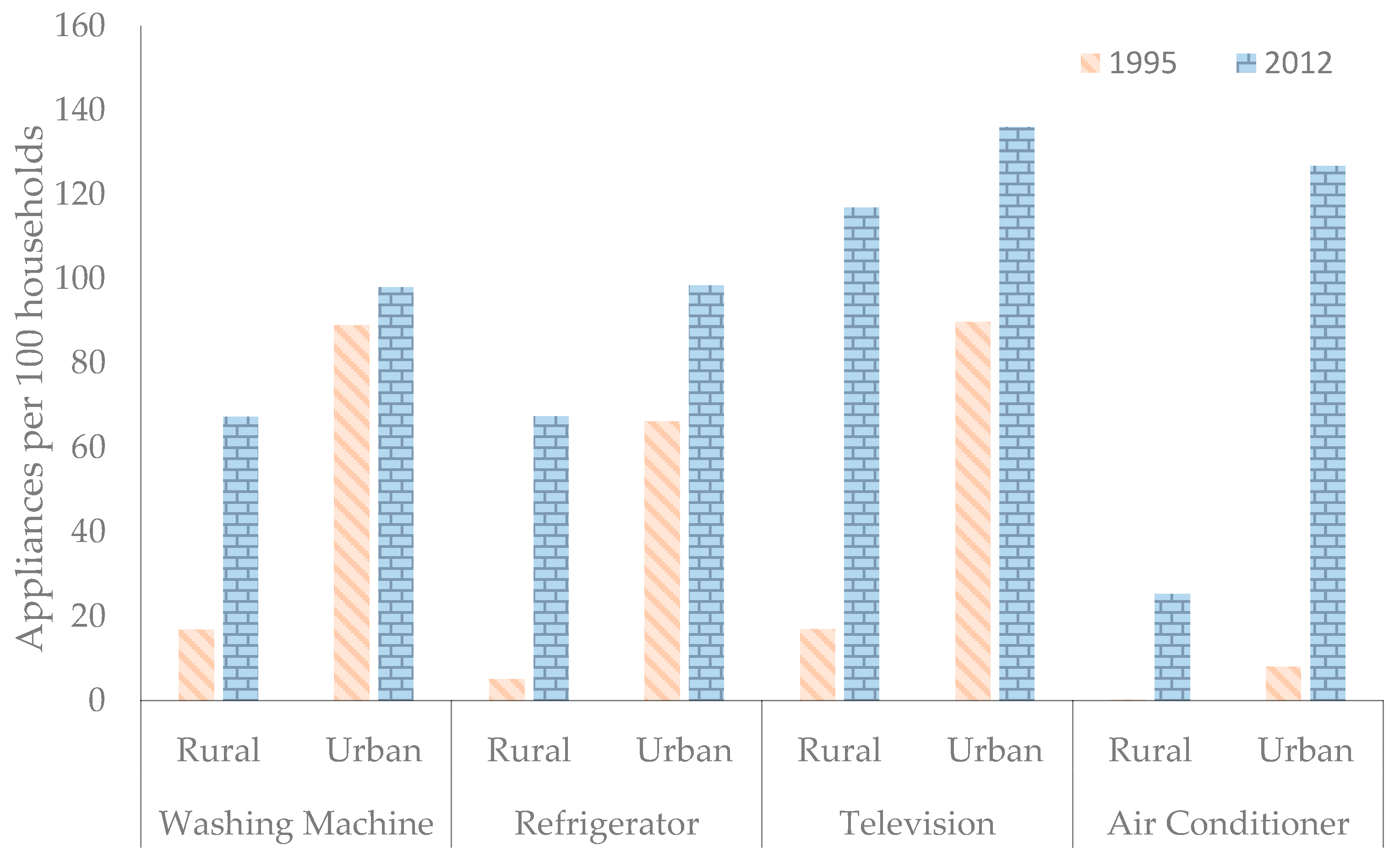
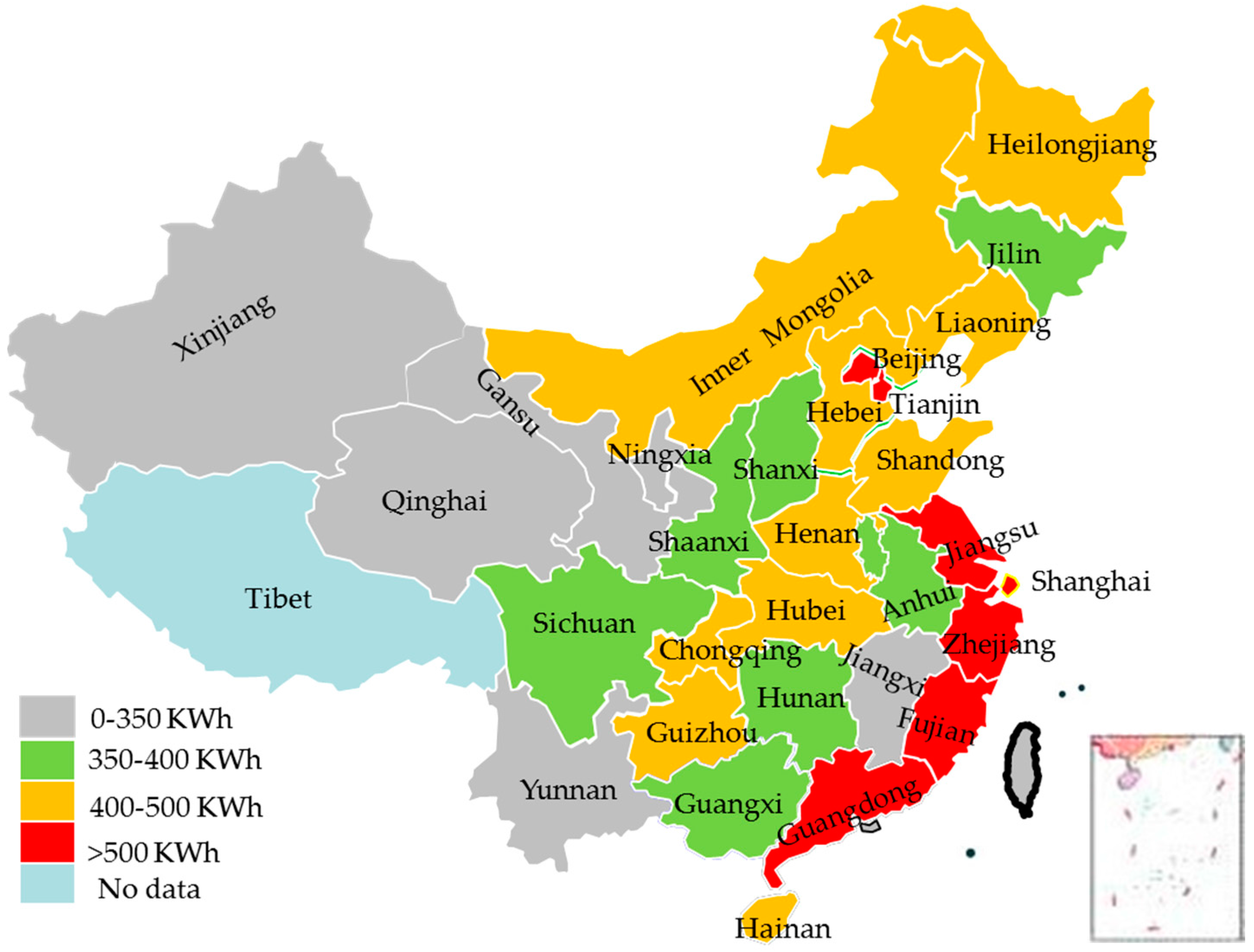
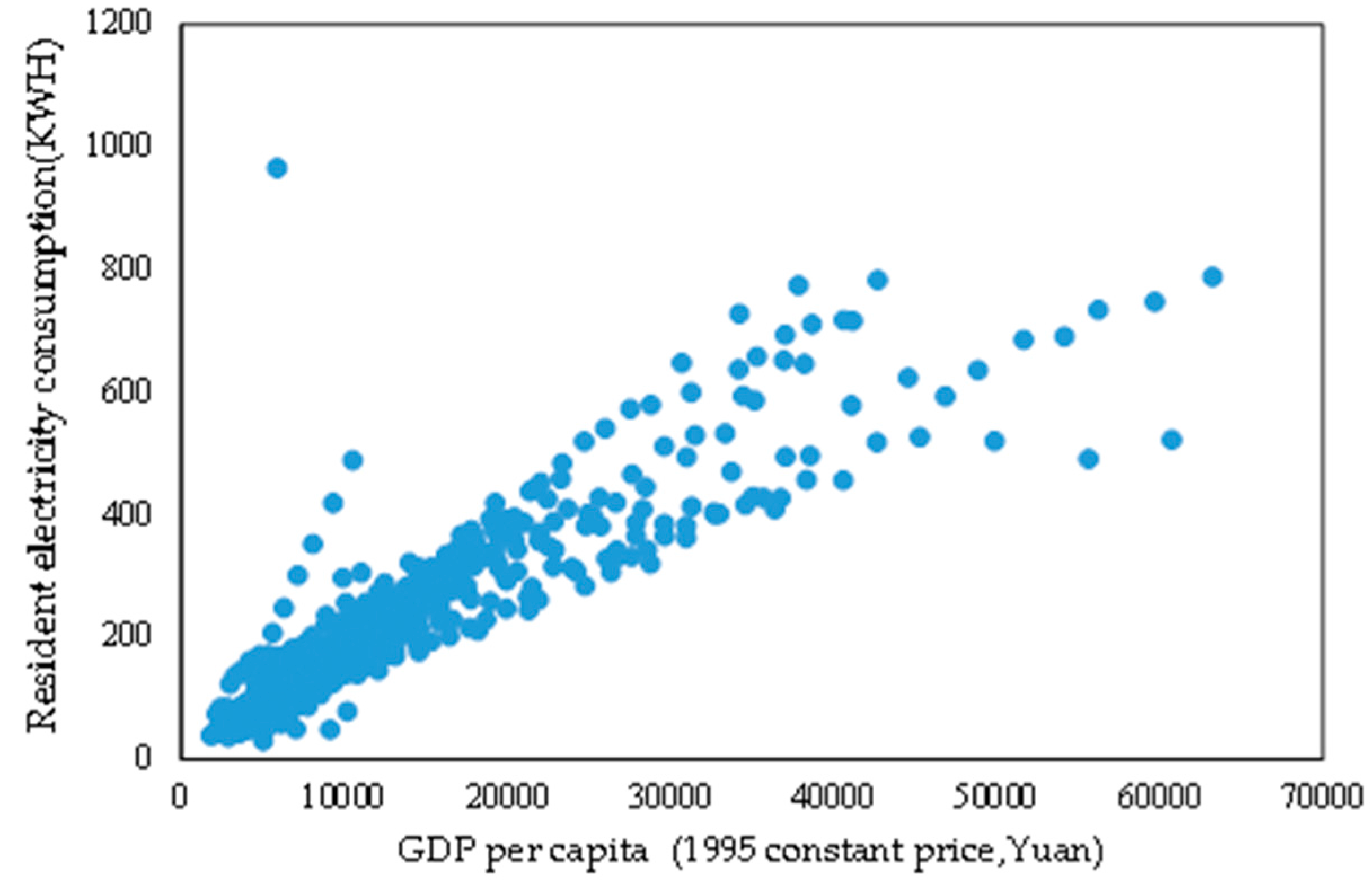
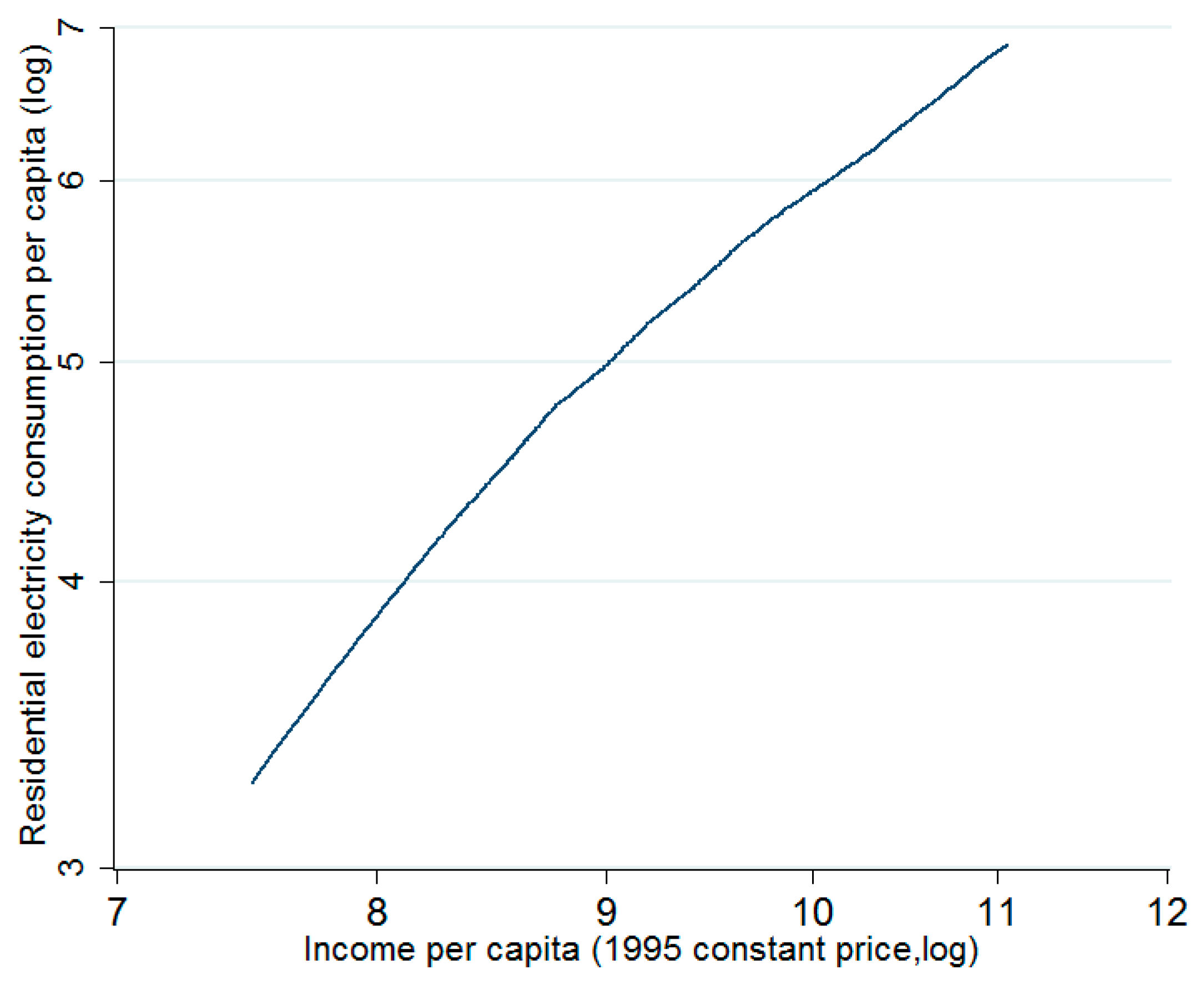
| Region | Electrification Rate (%) | Urban Electrification Rate (%) | Rural Electrification Rate (%) |
|---|---|---|---|
| Developing countries | 76.3 | 91.1 | 64.0 |
| Africa | 42.5 | 68.0 | 25.6 |
| Developing Asia | 83.0 | 95.2 | 74.4 |
| China | 99.8 | 100.0 | 99.6 |
| India | 75.4 | 93.9 | 66.9 |
| Latin America | 95.0 | 98.5 | 81.9 |
| Middle East | 91.7 | 98.3 | 78.0 |
| Transition economies & OECD | 99.9 | 100.0 | 99.7 |
| World | 81.7 | 94.1 | 68.0 |
| Variable | Definition | Observations | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|---|
| ln(E) | Residential electricity consumption per capita (kWh) | 538 | 5.4 | 0.7 | 3.4 | 6.9 |
| ln(Y) | GDP per capita (Yuan) | 538 | 9.5 | 0.6 | 7.5 | 11.1 |
| Modified Wald Test | |
|---|---|
| H0: sigma(i)^2 = sigma^2 for all i | Chi 2 (30) = 7442.88 |
| Prob > chi2 = 0.0000 | |
| Wooldridge Test | |
| H0: no first-order autocorrelation | F(1, 29) = 15.722 |
| Prob > F = 0.0004 | |
| Income | OLS | IV | FGLS |
|---|---|---|---|
| 0–3991 | 1.211 *** | 1.208 *** | 0.905 *** |
| (8.43) | (5.17) | (9.50) | |
| 3991–5130 | 1.120 *** | 1.337 ** | 1.061 *** |
| (4.98) | (2.73) | (9.72) | |
| 5130–6438 | 1.231 *** | 1.215 | 1.029 *** |
| (4.81) | (1.71) | (9.58) | |
| 6438–8002 | 0.850 ** | 0.499 | 1.040 *** |
| (3.12) | (0.60) | (10.02) | |
| 8002–9902 | 1.101 *** | 1.631 * | 0.990 *** |
| (3.98) | (2.02) | (9.77) | |
| 9902–12,365 | 0.888 *** | 0.458 | 1.019 *** |
| (3.33) | (0.66) | (10.39) | |
| 12,365–15,210 | 1.073 *** | 1.435 * | 1.052 *** |
| (3.70) | (2.27) | (10.35) | |
| 15,210–19,331 | 0.895 *** | 0.673 | 1.130 *** |
| (3.59) | (1.64) | (11.92) | |
| 19,331–28,541 | 0.783 *** | 0.877 *** | 0.707 *** |
| (5.16) | (4.68) | (8.08) | |
| >28,541 | 0.943 *** | 0.894 *** | 0.941 *** |
| (7.49) | (6.75) | (12.43) | |
| constant | −5.818 *** | −5.824 ** | −3.246 *** |
| (−4.98) | (−3.07) | (−4.17) | |
| N | 538 | 509 | 538 |
| Variables | Model (2) | Model (3) |
|---|---|---|
| ) | 0.996 *** | 2.396 *** |
| (58.08) | (7.83) | |
| - | −0.0757 *** | |
| - | (−4.58) | |
| constant | −4.006 *** | −10.44 *** |
| (−25.27) | (−7.39) | |
| N | 538 | 538 |
| Fixed Effects | YES | YES |
| Random Effects | NO | NO |
| 0.8694 | 0.8746 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gao, Y.; Hao, Y.; Liao, H. The Relationship between Residential Electricity Consumption and Income: A Piecewise Linear Model with Panel Data. Energies 2016, 9, 831. https://doi.org/10.3390/en9100831
Liu Y, Gao Y, Hao Y, Liao H. The Relationship between Residential Electricity Consumption and Income: A Piecewise Linear Model with Panel Data. Energies. 2016; 9(10):831. https://doi.org/10.3390/en9100831
Chicago/Turabian StyleLiu, Yanan, Yixuan Gao, Yu Hao, and Hua Liao. 2016. "The Relationship between Residential Electricity Consumption and Income: A Piecewise Linear Model with Panel Data" Energies 9, no. 10: 831. https://doi.org/10.3390/en9100831
APA StyleLiu, Y., Gao, Y., Hao, Y., & Liao, H. (2016). The Relationship between Residential Electricity Consumption and Income: A Piecewise Linear Model with Panel Data. Energies, 9(10), 831. https://doi.org/10.3390/en9100831






