A Permutation Importance-Based Feature Selection Method for Short-Term Electricity Load Forecasting Using Random Forest
Abstract
:1. Introduction
2. Mathematical Preliminaries
2.1. Decision Tree
2.2. Random Forest
- Assume S is the original sample set with n samples. When bagging is used to generate the training set for each CART, each of the samples in the original sample space has probability to be selected. Based on the characteristics of bagging, several samples may never be selected, whereas other samples may be selected more than once. All samples that have never been selected are the out-of-bag (OOB) dataset of this tree. Therefore, the training set of each CART is different, thus reducing the correlation between the trees in RF. The diversity of CART increases the capability of RF to resist noise and reduces its sensitivity to outliers. These are the main advantages that bagging brings to RF.
- RF differs from DT in terms of selecting a feature to split a non-leaf node. Specifically, instead of searching the entire original feature space M to select the best feature, RF randomly generates a candidate segmentation feature set m for each non-leaf node. The set m is a subset of the original feature set with features ( is no longer changed once determined). Thereafter, the optimal feature is selected from m to split this node.
3. Random Forest (RF) Learning Process and Feature Selection for Short-Term Load Forecast (STLF)
3.1. RF Learning Strategy
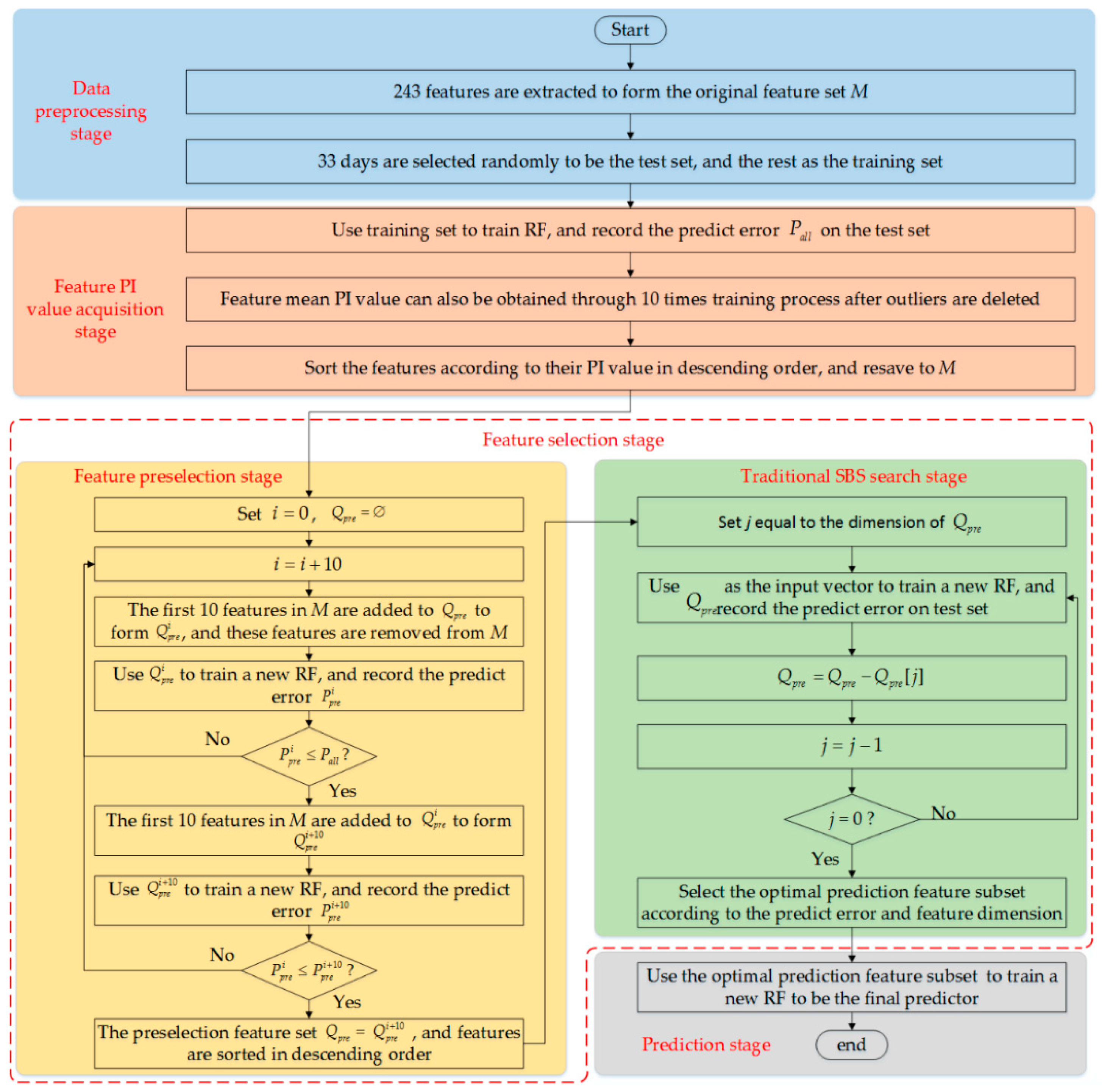
3.2. Feature Selection for Load Forecasting Based on Permutation Importance (PI) and Optimal SBS Method
3.2.1. Feature Importance Analysis Based on Permutation Importance (PI)
3.2.2. Optimal Sequential Backward Search (SBS) Method for Feature Selection of Short-Term Load Forecast (STLF)
- The original load feature set is used as the input to train an RF. After the training process is completed, the test set is used to evaluate the performance of this RF. Thereafter, the prediction error can be obtained and set as a threshold value. The PI value of each feature can also be obtained.
- According to the PI value, all features are rearranged in a descending order and are resaved to the original feature set M.
- The first 10 features with the highest PI value are added to the preselection feature set , which is an empty set at first. Subsequently, these features are removed from set M.
- Let set (superscript i represents the number of features in the set) be equal to set . Set is then used to retrain a new RF and the prediction error is recorded as .
- If , then the first 10 features of set M are added to set to form the set . The training and testing processes are repeated using set .
- If , then adding another feature to set is unnecessary. Otherwise, the first 10 features of set M must be added to set and must be removed from set M. This condition indicates that the stop conditions are and .
- The preceding steps are repeated until the stop condition is met or set M is empty.
- The preselection feature set is obtained and is equal to set , and the preselection stage ends.
4. Experimental Results and Analysis
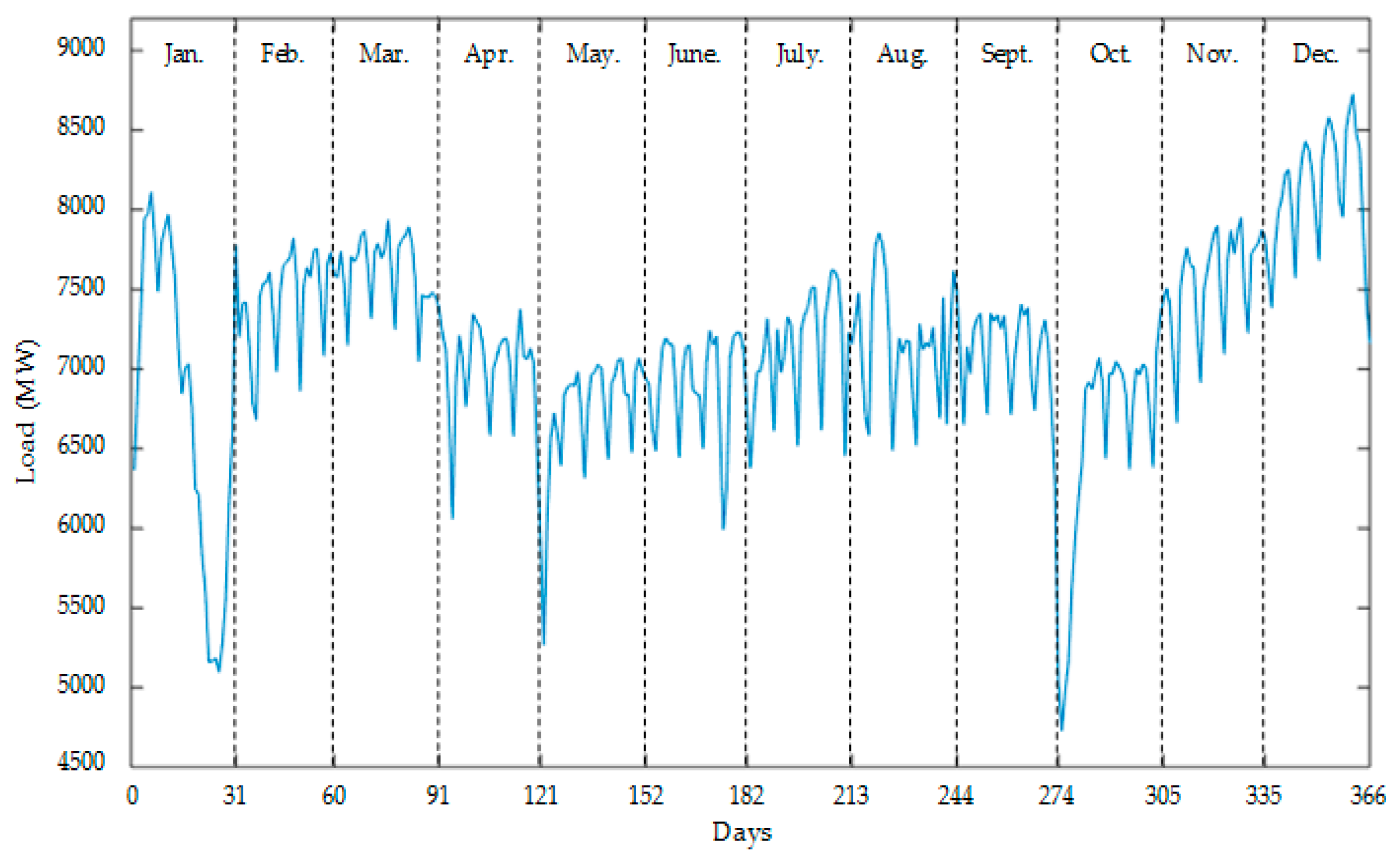
4.1. Dataset
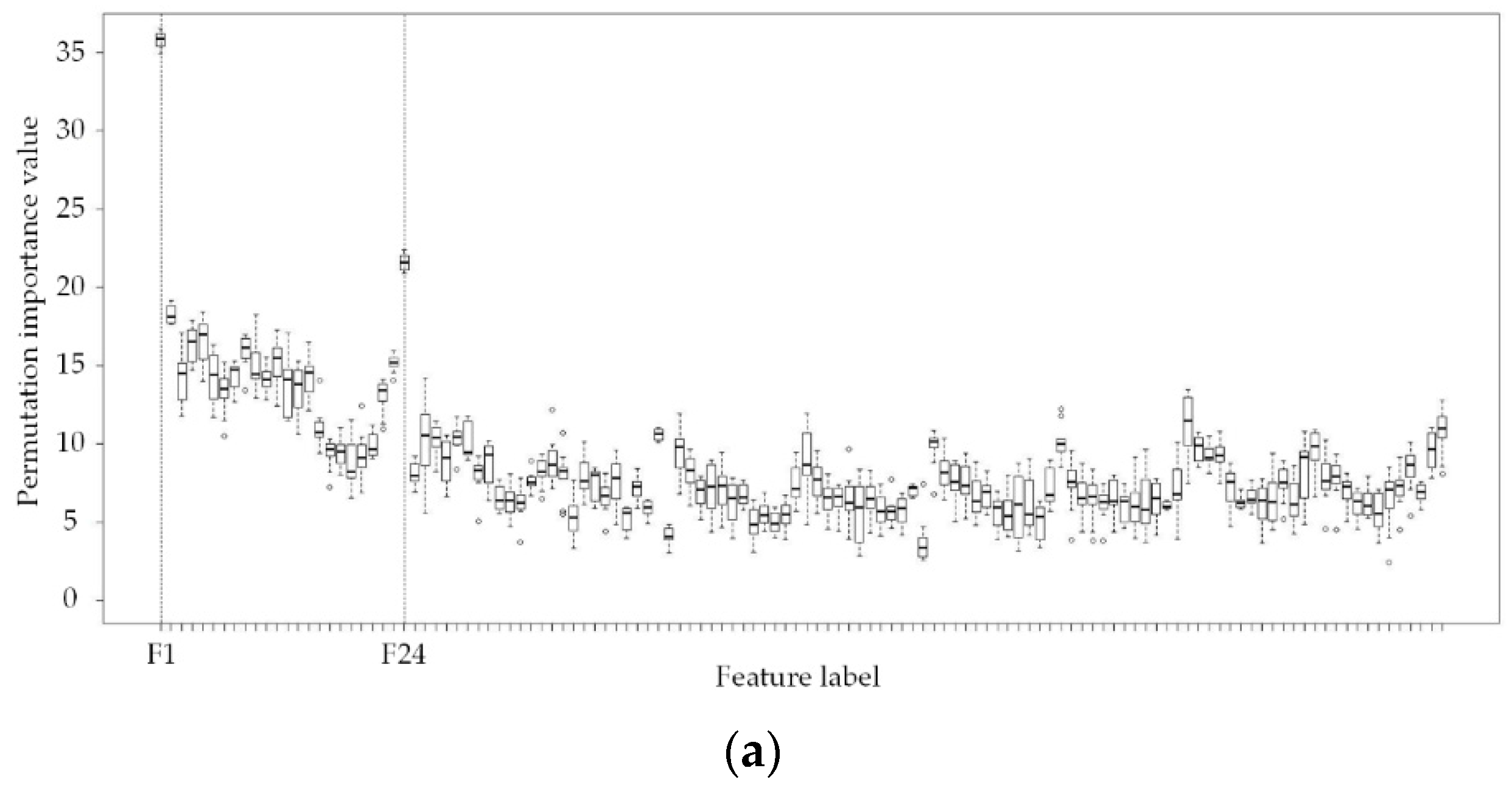
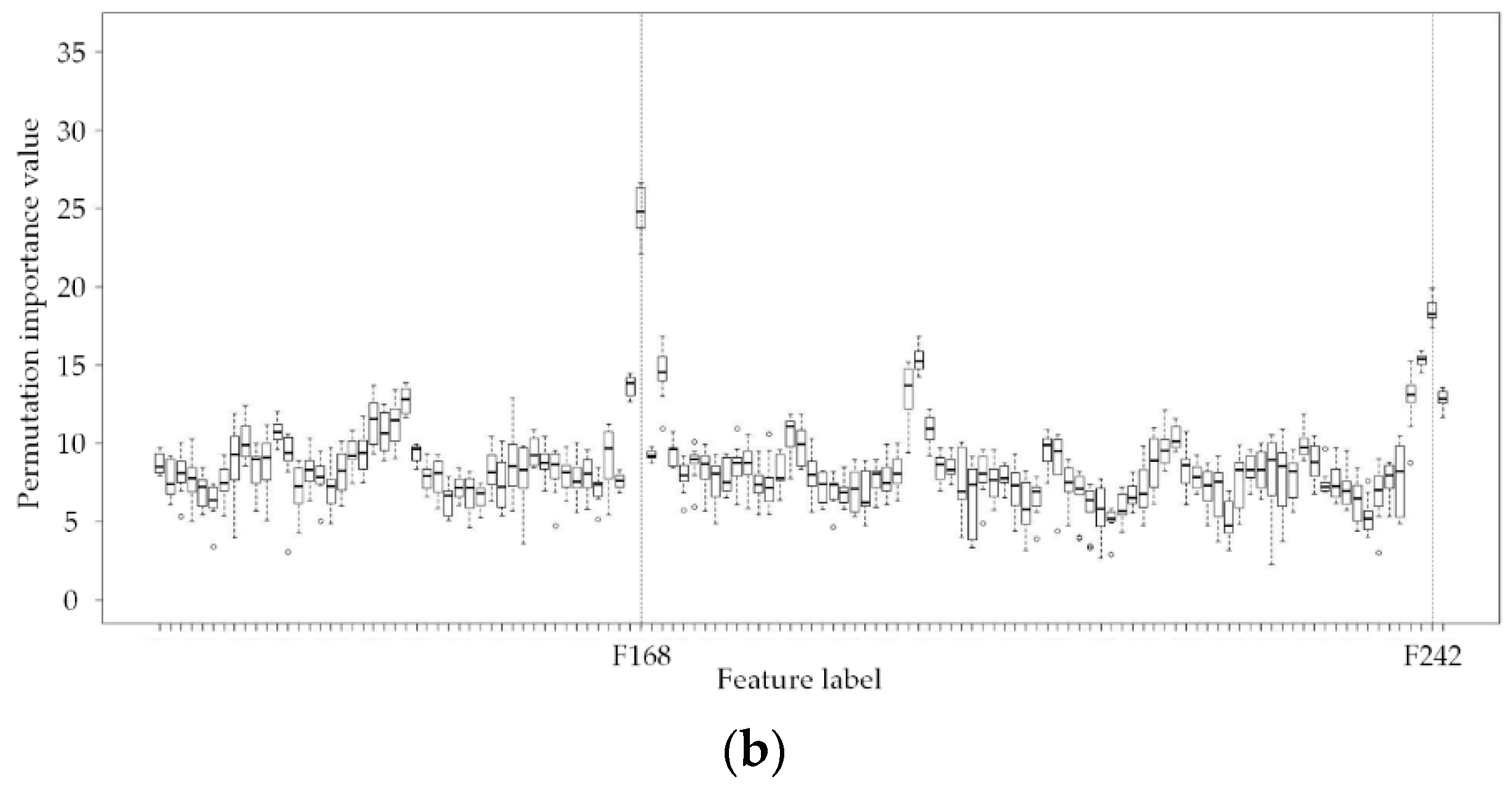
4.2. Load Feature Selection Based on Permutation Importance (PI) Value
- Persistent feature set 1: F1 (Lt-1, the load of the previous one hour), F241, and F242;
- Persistent feature set 2: F24 (Lt-24, the load of the same time of the previous day), F241, and F242;
- Persistent feature set 3: F168 (Lt-168, the load of the same time of the previous week), F241, and F242;
- Persistent feature set 4: F1, F24, F168, F241, and F242;
- Persistent feature set 5: from F1 to F24 (from Lt-24 to Lt-47, the load of the previous 24 h), F241, and F242;
- Persistent feature set 6: from F145 to F168 (from Lt-168 to Lt-191, the load of the past 24 h from the previous week), F241, and F242;
- Persistent feature set 7: from F1 to F24, from F145 to F168, F241, and F242;
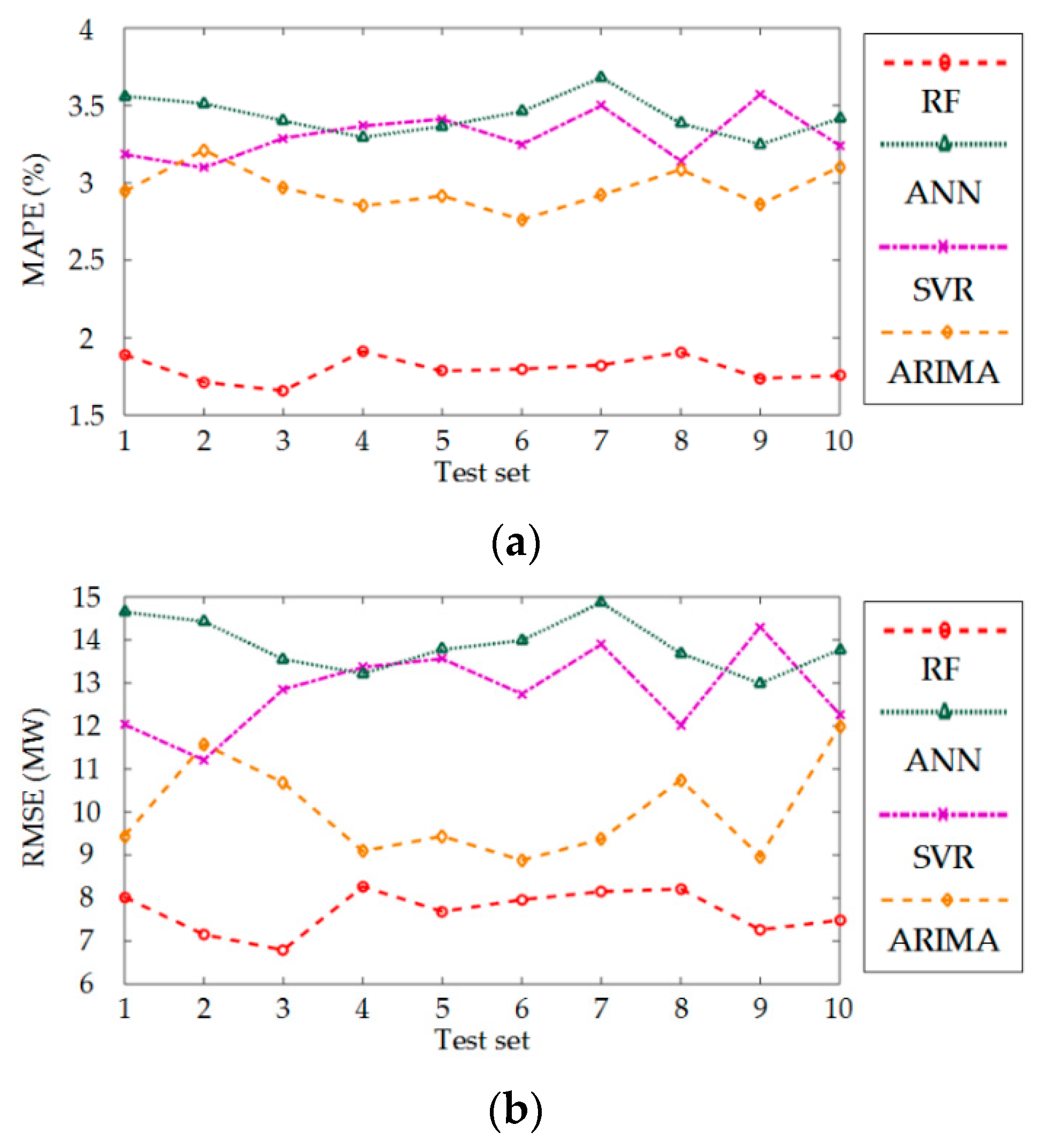
4.3. Load Forecasting Error of Different Models
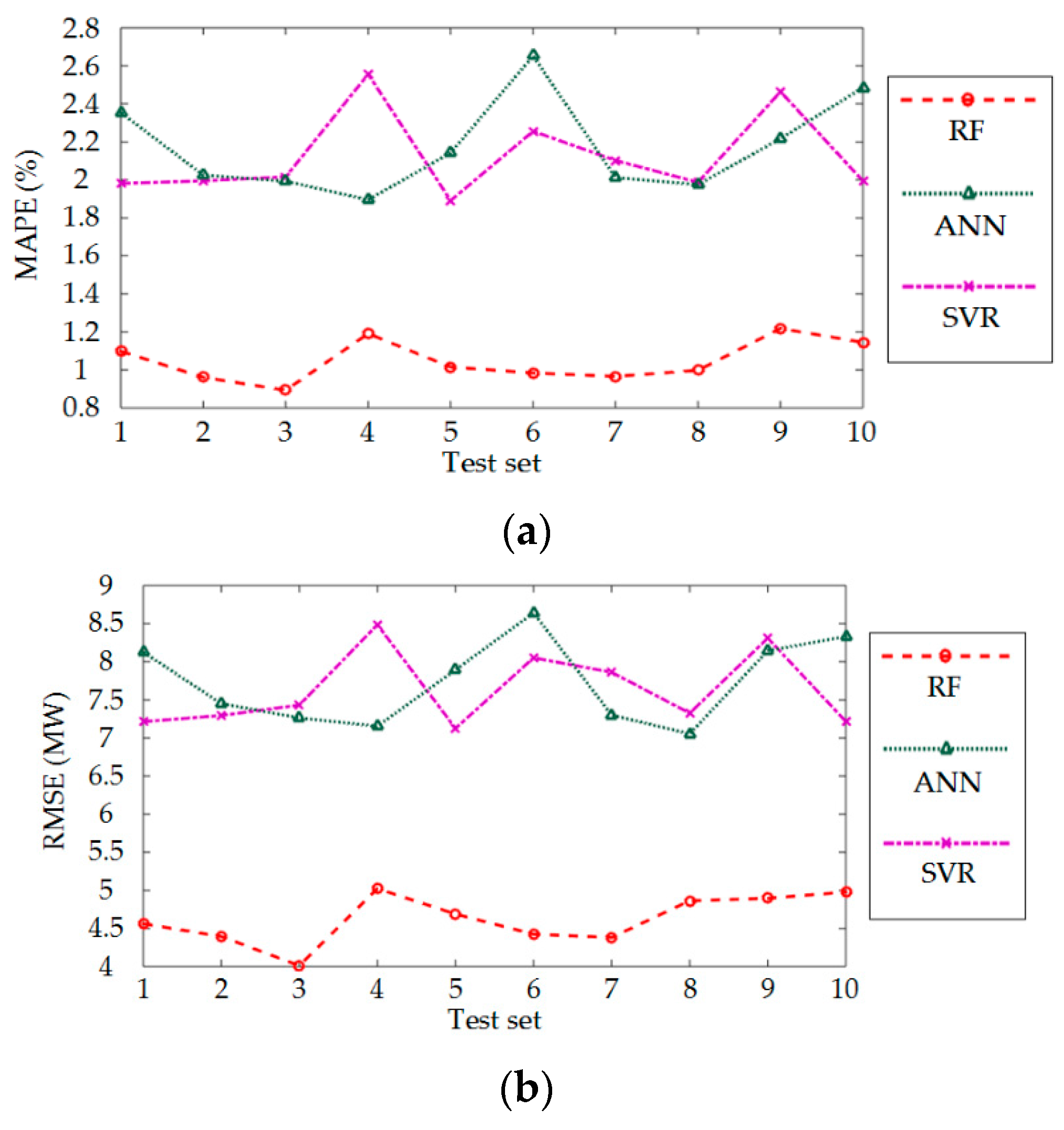
4.4. Further Validation of Effectiveness of the Proposed Method Based on 10-Fold Cross-Validation
5. Conclusions
- Compared with other STLF methods that use another feature selection method with high time complexity, the proposed approach designs a novel feature selection method based on PI value obtained in the training process of RF. The optimal forecasting feature subset is selected only by the improved SBS method with simple principle and high efficiency.
- In the process of feature selection, the prediction error of RF is used to determine the performance of each feature subset. Only two parameters of RF need to be adjusted, and the parameter selection method is clear. Considering this advantage, the proposed approach avoids the influence of unreasonable model parameters on the feature selection results.
- The traditional SBS method is optimized to reduce the number of iterations. Therefore, the efficiency of the search strategy is dramatically improved.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| STLF | Short-term load forecast |
| RF | Random forest |
| PI | Permutation importance |
| SBS | Sequential backward search |
| ARIMA | Autoregressive integrated moving average |
| FL | Fuzzy logic |
| ANN | Artificial neural network |
| SVR | Support vector machine |
| DT | Decision tree |
| CART | Classification and regression tree |
| OOB | Out-of-bag |
| MAPE | Mean absolute percentage error |
| RMSE | Root mean square error |
References
- Khan, A.R.; Mahmood, A.; Safdar, A.; Khan, Z.A.; Khan, N.A. Load forecasting, dynamic pricing and DSM in smart grid: A review. Renew. Sustain. Energy Rev. 2016, 54, 1311–1322. [Google Scholar] [CrossRef]
- Alvarez, F.; Troncoso, A.; Riquelme, J.C.; Ruiz, J.S. Energy time series forecasting based on pattern sequence similarity. IEEE Trans. Knowl. Data Eng. 2011, 23, 1230–1243. [Google Scholar] [CrossRef]
- Amjady, N. Short-term bus load forecasting of power systems by a new hybrid method. IEEE Trans. Power Syst. 2007, 22, 333–341. [Google Scholar] [CrossRef]
- Kulkarni, S.; Simon, S.P.; Sundareswaran, K. A spiking neural network (SNN) forecast engine for short-term electrical load forecasting. Appl. Soft Comput. 2013, 13, 3628–3635. [Google Scholar] [CrossRef]
- Al-Hamadi, H.M.; Soliman, S.A. Short-term electric load forecasting based on Kalman filtering algorithm with moving window weather and load model. Electr. Power Syst. Res. 2004, 68, 47–59. [Google Scholar] [CrossRef]
- Christiaanse, W.R. Short-term load forecasting using general exponential smoothing. IEEE Trans. Power Appar. Syst. 1971, 90, 900–911. [Google Scholar] [CrossRef]
- Wi, Y.M.; Joo, S.K.; Song, K.B. Holiday load forecasting using fuzzy polynomial regression with weather feature selection and adjustment. IEEE Trans. Power Syst. 2012, 27, 596–603. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Li, Y.; Zhu, S.; Zhao, J. Techniques of applying wavelet de-noising into a combined model for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2014, 62, 816–824. [Google Scholar] [CrossRef]
- Wang, B.; Tai, N.L.; Zhai, H.Q.; Ye, J.; Zhu, J.D.; Qi, L.B. A new ARMAX model based on evolutionary algorithm and particle swarm optimization for short-term load forecasting. Electr. Power Syst. Res. 2008, 78, 1679–1685. [Google Scholar] [CrossRef]
- Nie, H.; Liu, G.; Liu, X.; Wang, Y. Hybrid of ARIMA and SVMs for short-term load forecasting. Energy Procedia 2012, 16, 1455–1460. [Google Scholar] [CrossRef]
- Hinojosa, V.H.; Hoese, A. Short-term load forecasting using fuzzy inductive reasoning and evolutionary algorithms. IEEE Trans. Power Syst. 2010, 25, 565–574. [Google Scholar] [CrossRef]
- Mamlook, R.; Badran, O.; Abdulhadi, E. A fuzzy inference model for short-term load forecasting. Energy Policy 2009, 37, 1239–1248. [Google Scholar] [CrossRef]
- Feng, Y.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Carro, B.; Sánchez-Esguevillas, A.; Lloret, J. Artificial neural networks for short-term load forecasting in microgrids environment. Energy 2014, 75, 252–264. [Google Scholar] [CrossRef]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Pérez, F.; Fernández, Á.; Lloret, J. Artificial neural network for short-term load forecasting in distribution systems. Energies 2014, 7, 1576–1598. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid modified firefly algorithm and support vector regression model for accurate short term load forecasting. Expert Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Che, J.X.; Wang, J.Z. Short-term load forecasting using a kernel-based support vector regression combination model. Appl. Energy 2014, 132, 602–609. [Google Scholar] [CrossRef]
- Ceperic, E.; Ceperic, V.; Baric, A. A strategy for short-term load forecasting by support vector regression machines. IEEE Trans. Power Syst. 2013, 28, 4356–4364. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Jurado, S.; Nebot, À.; Mugica, F.; Avellana, N. Hybrid methodologies for electricity load forecasting: entropy-based feature selection with machine learning and soft computing techniques. Energy 2015, 86, 276–291. [Google Scholar] [CrossRef]
- Dudek, G. Short-Term Load Forecasting Using Random Forests. Intell. Systems'2014 2015, 323, 821–828. [Google Scholar]
- Wang, J.; Li, L.; Niu, D.; Tan, Z. An annual load forecasting model based on support vector regression with differential evolution algorithm. Appl. Energy 2012, 94, 65–70. [Google Scholar] [CrossRef]
- Breiman, L. Random forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Che, J.X.; Wang, J.Z.; Tang, Y.J. Optimal training subset in a support vector regression electric load forecasting model. Appl. Soft Comput. 2012, 12, 1523–1531. [Google Scholar] [CrossRef]
- Ghofrani, M.; Ghayekhloo, M.; Arabali, A.; Ghayekhloo, A. A hybrid short-term load forecasting with a new input selection framework. Energy 2015, 81, 777–786. [Google Scholar] [CrossRef]
- Kouhi, S.; Keynia, F. A new cascade NN based method to short-term load forecast in deregulated electricity market. Energy Convers. Manag. 2013, 71, 76–83. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman Hall: New York, NY, USA, 1984. [Google Scholar]
- Troncoso, A.; Salcedo-Sanz, S.; Casanova-Mateo, C.; Riquelme, J.C.; Prieto, L. Local models-based regression trees for very short-term wind speed prediction. Renew. Energy 2015, 81, 589–598. [Google Scholar] [CrossRef]
- Sirlantzis, K.; Hoque, S.; Fairhurst, M.C. Diversity in multiple classifier ensembles based on binary feature quantisation with application to face recognition. Appl. Soft Comput. 2008, 8, 437–445. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Goel, L. Short-term load forecasting by wavelet transform and evolutionary extreme learning machine. Electr. Power Syst. Res. 2015, 122, 96–103. [Google Scholar] [CrossRef]




| The First Quarter (1/1/2012 to 31/3/2012) | The Second Quarter (1/4/2012 to 30/6/2012) | The Third Quarter (1/7/2012 to 30/90/2012) | The Fourth Quarter (1/10/2012 to 31/12/2012) |
|---|---|---|---|
| 5 and 8/1/2012 (Thur., Sun.) 4, 9 and 24/2/2012 (Sat., Thur., Fri.) 3, 23 and 31/3/2012 (Sat., Fri., Sat.) | 1 and 20/4/2012 (Sun., Fri.) 10, 18, 25 and 31/5/2012 (Thur., Fri., Fri., Thur.) 18 and 27/6/2012 (Mon., Wed.) | 8 and 28/7/2012 (Sun., Sat.) 15, 23 and 31/8/2012 (Wed., Thur., Fri.) 17, 21, 25 and 27/9/2012 (Mon., Fri., Tues., Thur.) | 16, 21, 28 and 30/10/2012 (Tues., Sun., Sun., Tues.) 21 and 29/11/2012 (Wed., Thur.) 9 and 27/12/2012 (Sun., Thur.) |
| Names of the Features | Meanings of the Features |
|---|---|
| The historical load value of time | |
| Whether today is a working day? (1-Yes, 2-No) | |
| What day is today? (1-Mon., 2-Tues., 3-Wed., 4-Thur., 5-Fri., 6-Sat., 7-Sun.) | |
| The moment of t (from 0 to 23, corresponding to the 24 hours a day) |
| Names of the Features | Meanings of the Features |
|---|---|
| The historical load value of time | |
| Whether today is a working day? (1-Yes, 2-No) | |
| What day is today? (1-Mon., 2-Tues., 3-Wed., 4-Thur., 5-Fri., 6-Sat., 7-Sun.) | |
| The moment of t (from 0 to 23, corresponding to the 24 hours a day) |
| Feature Subset | Mean Absolute Percentage Error (MAPE) (%) | Root Mean Square Error (RMSE) (MW) |
|---|---|---|
| The original feature set | 1.016 | 4.434 |
| 1.068 | 4.696 | |
| 0.983 | 4.342 | |
| 0.987 | 4.393 |
| Feature Subset | Mean Absolute Percentage Error (MAPE) (%) | Root Mean Square Error (RMSE) (MW) |
|---|---|---|
| The original feature set | 1.773 | 7.212 |
| 1.835 | 7.689 | |
| 1.794 | 7.545 | |
| 1.767 | 7.194 | |
| 1.772 | 7.221 |
| Feature Selection Algorithm | Feature Subset Dimension | Prediction Error | |
|---|---|---|---|
| MAPE (%) | RMSE (MW) | ||
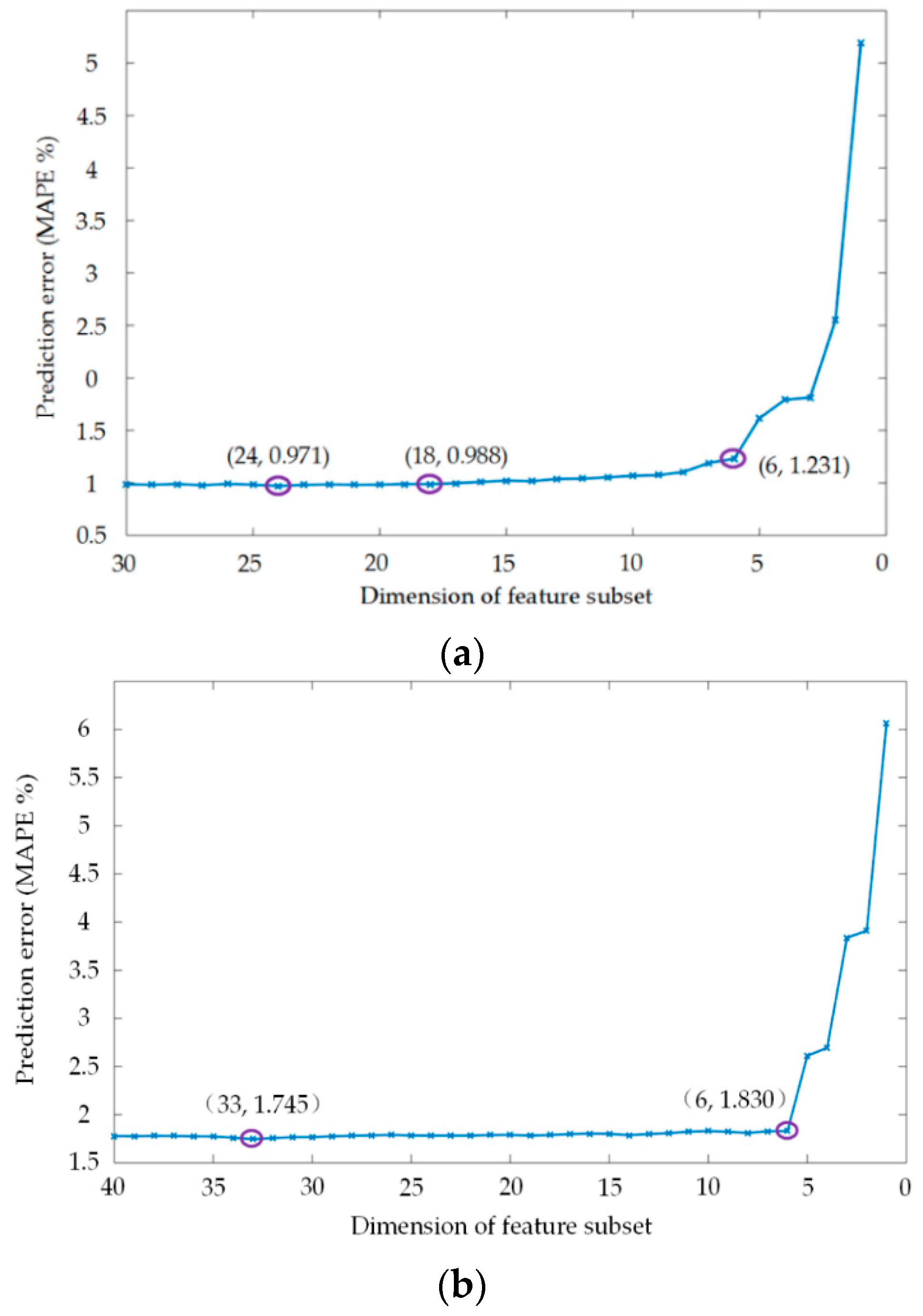
| PI | 24 | 0.971 | 4.372 |
| PCC | 29 | 1.491 | 6.155 |
| ReliefF | 19 | 1.201 | 5.128 |
| Feature Selection Algorithm | Feature Subset Dimension | Prediction Error | |
|---|---|---|---|
| MAPE (%) | RMSE (MW) | ||
| PI | 33 | 1.745 | 7.324 |
| PCC | 38 | 2.123 | 8.899 |
| ReliefF | 35 | 2.003 | 8.575 |
| Feature Selection Algorithm | Feature Subset Dimension | Prediction Error | |
|---|---|---|---|
| MAPE (%) | RMSE (MW) | ||
| PI | 24 | 0.971 | 4.372 |
| Persistent feature set 1 | 3 | 7.343 | 25.522 |
| Persistent feature set 2 | 3 | 6.311 | 22.834 |
| Persistent feature set 3 | 3 | 6.859 | 25.618 |
| Persistent feature set 4 | 5 | 2.825 | 11.233 |
| Feature Selection Algorithm | Feature Subset Dimension | Prediction Error | |
|---|---|---|---|
| MAPE (%) | RMSE (MW) | ||
| PI | 33 | 1.745 | 7.324 |
| Persistent feature set 5 | 26 | 1.792 | 7.877 |
| Persistent feature set 6 | 26 | 3.418 | 14.208 |
| Persistent feature set 7 | 50 | 1.891 | 9.028 |
| Time Period of Testing Set | Predict Error | Predictors/Dimension of Feature Subset | ||
|---|---|---|---|---|
| RF/24 | SVR/27 | ANN/22 | ||
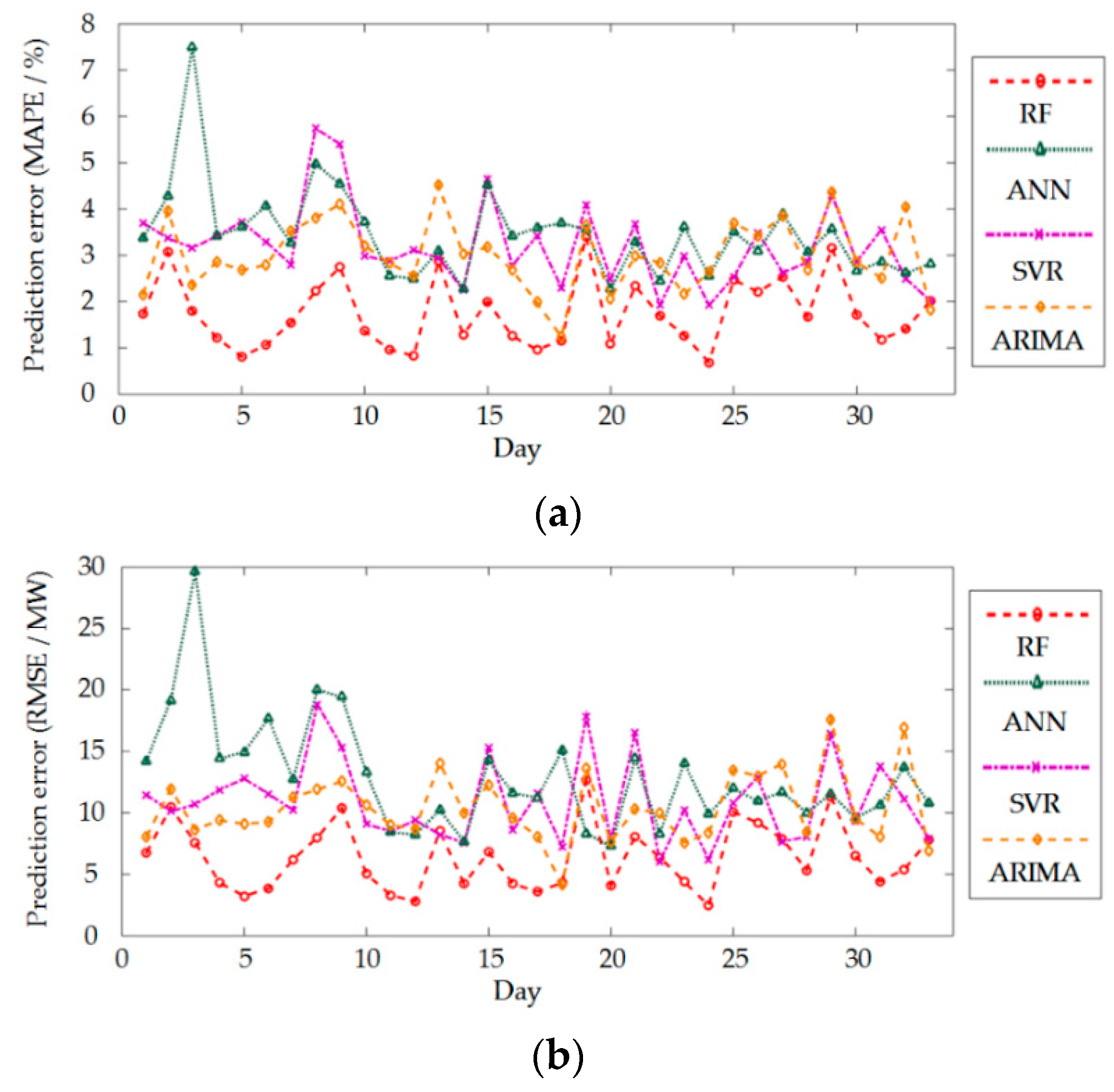
| The first quarter | MAPE (%) | 0.849 | 2.240 | 1.665 |
| RMSE (MW) | 3.924 | 7.396 | 6.723 | |
| The second quarter | MAPE (%) | 0.868 | 1.664 | 2.504 |
| RMSE (MW) | 3.281 | 6.741 | 8.467 | |
| The third quarter | MAPE (%) | 0.919 | 1.889 | 2.142 |
| RMSE (MW) | 3.985 | 7.381 | 7.315 | |
| The fourth quarter | MAPE (%) | 1.216 | 2.306 | 2.339 |
| RMSE (MW) | 5.901 | 8.894 | 9.057 | |
| Total | MAPE (%) | 0.971 | 2.021 | 2.165 |
| RMSE (MW) | 4.372 | 7.448 | 7.926 | |
| Time Period of Testing Set | Predict Error | Predictors/Dimension of Feature Subset | |||
|---|---|---|---|---|---|
| RF/33 | SVR/38 | ANN/36 | ARIMA/480 | ||
| The first quarter | MAPE (%) | 1.794 | 3.585 | 4.309 | 2.961 |
| RMSE (MW) | 7.659 | 12.884 | 18.546 | 9.586 | |
| The second quarter | MAPE (%) | 1.663 | 3.616 | 3.326 | 3.059 |
| RMSE (MW) | 6.187 | 12.652 | 12.211 | 9.833 | |
| The third quarter | MAPE (%) | 1.673 | 3.233 | 3.057 | 2.482 |
| RMSE (MW) | 7.057 | 12.279 | 11.506 | 8.179 | |
| The fourth quarter | MAPE (%) | 1.987 | 3.058 | 3.074 | 3.145 |
| RMSE (MW) | 7.874 | 11.754 | 11.971 | 9.996 | |
| Total | MAPE (%) | 1.745 | 3.273 | 3.430 | 2.957 |
| RMSE (MW) | 7.324 | 12.451 | 13.798 | 9.513 | |
| Data | Prediction Error | Predictors | ||
|---|---|---|---|---|
| RF | SVR | ANN | ||
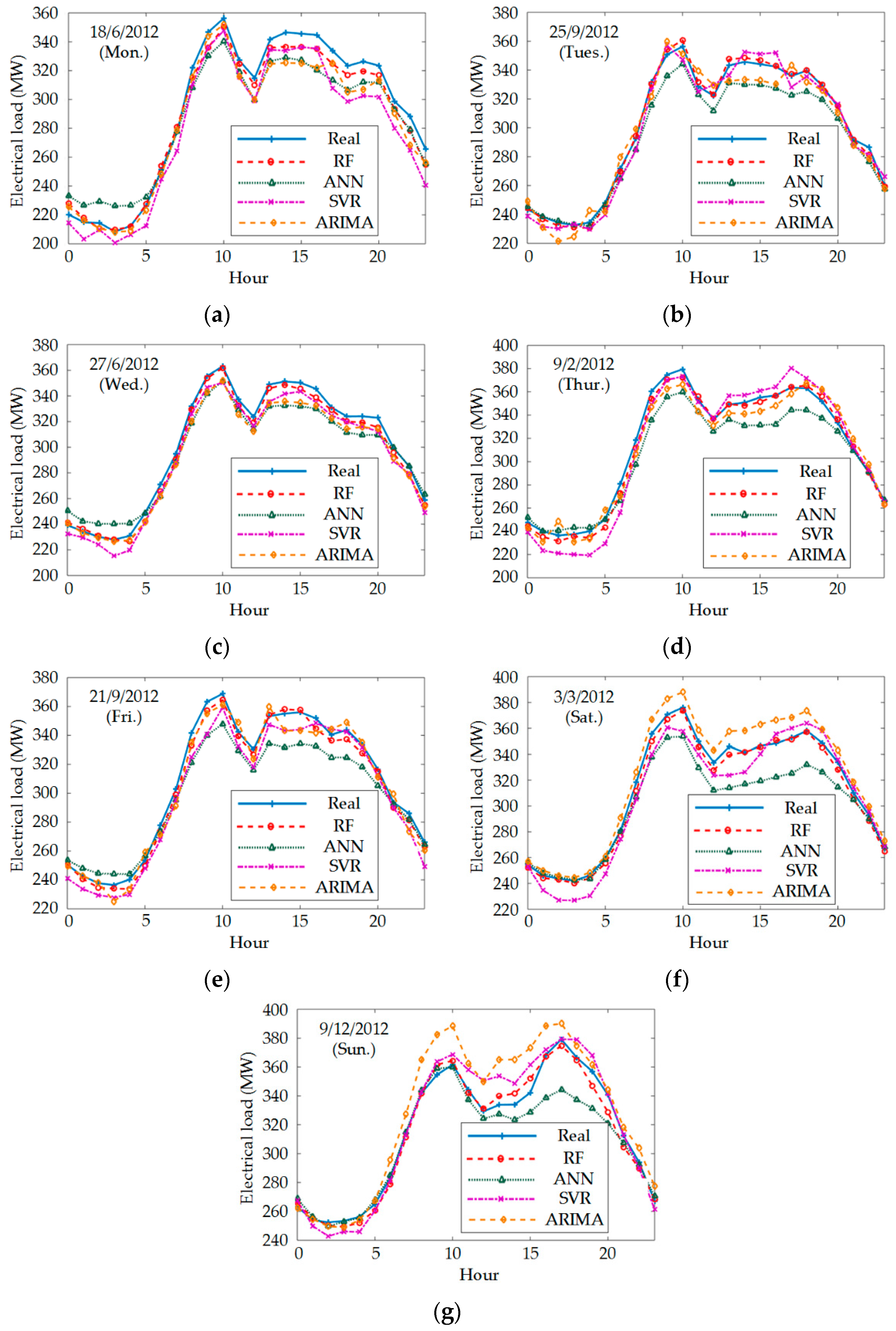
| June 18 (Mon.) | MAPE (%) | 0.870 | 2.027 | 3.198 |
| RMSE (MW) | 3.137 | 6.047 | 10.467 | |
| September 25 (Tues.) | MAPE (%) | 0.723 | 2.140 | 1.969 |
| RMSE (MW) | 2.813 | 8.879 | 6.711 | |
| June 27 (Wed.) | MAPE (%) | 0.633 | 1.414 | 1.791 |
| RMSE (MW) | 2.218 | 5.133 | 6.117 | |
| February 9 (Thur.) | MAPE (%) | 0.557 | 1.282 | 1.436 |
| RMSE (MW) | 2.049 | 5.618 | 5.614 | |
| September 21 (Fri.) | MAPE (%) | 0.554 | 1.132 | 1.524 |
| RMSE (MW) | 2.035 | 3.964 | 5.486 | |
| March 3 (Sat.) | MAPE (%) | 0.479 | 1.479 | 1.460 |
| RMSE (MW) | 2.103 | 5.638 | 5.351 | |
| December 9 (Sun.). | MAPE (%) | 0.910 | 1.346 | 1.716 |
| RMSE (MW) | 4.091 | 4.889 | 6.831 | |
| Data | Prediction Error | Predictors | |||
|---|---|---|---|---|---|
| RF | SVR | ANN | ARIMA | ||
| June 18 (Mon.) | MAPE (%) | 2.001 | 4.674 | 4.519 | 3.174 |
| RMSE (MW) | 6.817 | 15.332 | 14.235 | 12.279 | |
| September 25 (Tues.) | MAPE (%) | 0.688 | 1.929 | 2.552 | 2.638 |
| RMSE (MW) | 2.448 | 6.208 | 9.923 | 8.352 | |
| June 27 (Wed.) | MAPE (%) | 1.253 | 2.771 | 3.407 | 2.676 |
| RMSE (MW) | 4.224 | 8.594 | 11.591 | 9.570 | |
| February 9 (Thur.) | MAPE (%) | 1.215 | 3.423 | 3.419 | 2.854 |
| RMSE (MW) | 4.302 | 11.836 | 14.416 | 9.388 | |
| September 21 (Fri.) | MAPE (%) | 1.266 | 2.981 | 3.616 | 2.152 |
| RMSE (MW) | 4.399 | 10.195 | 14.055 | 7.587 | |
| March 3 (Sat.) | MAPE (%) | 1.066 | 3.285 | 4.072 | 2.792 |
| RMSE (MW) | 3.839 | 11.537 | 17.692 | 10.491 | |
| December 9 (Sun.). | MAPE (%) | 1.405 | 2.492 | 2.611 | 4.036 |
| RMSE (MW) | 5.399 | 10.053 | 13.683 | 16.960 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, N.; Lu, G.; Xu, D. A Permutation Importance-Based Feature Selection Method for Short-Term Electricity Load Forecasting Using Random Forest. Energies 2016, 9, 767. https://doi.org/10.3390/en9100767
Huang N, Lu G, Xu D. A Permutation Importance-Based Feature Selection Method for Short-Term Electricity Load Forecasting Using Random Forest. Energies. 2016; 9(10):767. https://doi.org/10.3390/en9100767
Chicago/Turabian StyleHuang, Nantian, Guobo Lu, and Dianguo Xu. 2016. "A Permutation Importance-Based Feature Selection Method for Short-Term Electricity Load Forecasting Using Random Forest" Energies 9, no. 10: 767. https://doi.org/10.3390/en9100767
APA StyleHuang, N., Lu, G., & Xu, D. (2016). A Permutation Importance-Based Feature Selection Method for Short-Term Electricity Load Forecasting Using Random Forest. Energies, 9(10), 767. https://doi.org/10.3390/en9100767







