1. Introduction
Modeling of fluid flow through fractured porous reservoirs is very complicated due to the extremely high heterogeneity in geometry scale and permeability between the matrix and fracture media. Accurate and efficient simulation of such systems remains a challenge. Recently many technical improvements are achieved to enable more reliable fracture predictions in the form of discrete fracture representations. These models, however, are generally too detailed for direct use in reservoir simulation, especially when many simulation runs are required to address the geological uncertainty. It is necessary to develop methods that can provide accurate and efficient flow models from high-resolution fracture characterizations.
The dual-porosity (DP) model was first proposed by Barenblatt and Zheltov [
1] and introduced to the petroleum industry by Warren and Root [
2]. In DP models, the fractured reservoir is represented by the matrix and fracture media, which are overlapping spatially. The matrix medium acts as a source of reserves while the fracture medium is assumed as the channel through which large-scale flow occurs. The fluid interaction between these two continua is represented by a transfer function called shape factor. Dual-porosity dual-permeability (DPDK) models, which consider matrix-matrix fluxes besides fracture-fracture fluxes, were introduced when flow through matrix medium is not negligible.
Although very efficient and to some extent capable for capturing the flow behavior of fractured reservoirs, the DP models suffer from some limitations due to its idealized representation of the actual geological description. For example, the complex flow behavior between fracture and matrix medium is represented by the shape factor as a function of fracture spacing only [
2,
3,
4]. Although a lot of research [
5,
6,
7,
8] aiming to obtain a more accurate shape factor under specific flow scenarios were carried out in those years, most of them were still based on idealized fracture distributions. Another drawback of DP models is they are not well suited for the modeling of a small number of large-scale fractures, which may dominate the flow. For these reasons, discrete-fracture models (DFMs), in which the fractures are represented explicitly, are beginning to find applications in reservoir simulation.
With a fully resolved fracture characterization, DFMs can naturally capture the complex flow phenomena that occur in fractured reservoirs. In order to accommodate the fracture geometry, unstructured grids are usually used in DFMs. Under the unstructured discretization scheme, Baca
et al. [
9] proposed a 2-D finite-element model for single-phase flow with heat and solute transport. Juanes
et al. [
10] presented a general finite-element formulation for 2-D and 3-D single-phase flow in fractured porous media. Kim and Deo [
11] and Karimi-Fard and Firoozabadi [
12] extended the work of Baca
et al. for two-phase flow. Karimi-Fard
et al. [
13] proposed a general and flexible control volume approach to construct connectivities of all control volumes in both 2-D and 3-D fractured models. In a series of works [
14,
15,
16], Hoteit and Firoozabadi proposed a numerical model combined mixed finite element (MFE) method and discontinuous Galerkin (DG) method to handle saturation discontinuity caused by capillary heterogeneity. In addition, by using a hybrid time scheme and without the use of the cross-flow equilibrium between the fractures and the adjacent matrix blocks, the MFE-DG method allows relatively large time steps and large matrix grid cells next to the fractures.
In recent years, DFM approaches have gained much wider applications due to the improvements in fracture prediction and computer technologies. However the field scale studies with DFMs are still not practical because geologically realistic DFMs remain prohibitively time-consuming, especially for probabilistic studies [
17]. In addition, the unstructured gridding could be a very tough issue when a large number of fractures in random distribution are present.
Upscaling techniques are developed to coarsen models that are difficult for direct simulation [
18,
19]. In terms of the target parameters to be upscaled, those techniques can be classified into single-phase upscaling and multi-phase upscaling. For single-phase upscaling, the only parameters to be upscaled are porosity and the transmissibility (or absolute permeability); while in multi-phase upscaling, multi-phase flow parameters like relative permeability and capillary pressure can be upscaled too. It is generally recognized that, in many cases, it is possible to develop reasonably accurate coarse-scale models for two-phase flow with only the absolute permeability or transmissibility upscaled, particularly when accurate upscaling is used in conjunction with flow-based grid generation. In this paper, we only focus on transmissibility upscaling. It is important to note that, however, multi-phase upscaling will be required when high degrees of coarsening are applied, especially when relative permeability and capillary pressure heterogeneity exist. Compared to the relative permeability upscaling, in addition, effective capillary pressure upscaling technique is paid much less attention on and there is still lack of a sound capillary pressure averaging technique [
20,
21,
22].
Among those upscaling methods, some techniques that entail combinations and variations of DFM and DPDK modeling ideas have been proposed to date. The research was first carried out by Dershowitz
et al. [
23] and Sarda
et al. [
24] and extended by others later [
25,
26]. Karimi-Fard
et al. [
27] and Gong
et al. [
28] developed a flow-based upscaling technique, which is referred to as the multiple subregion (MSR) method to construct dual-porosity models from detailed fracture characterizations. This method implements a flow-based division of subgrids and calculates the transmissibilities between each connected coarse blocks based on the discrete fracture network. The MSR method was later applied into multiple geologically realistic DFMs by Hui
et al. [
17]. The MSR method brings in the link between fine-scale fracture models and coarse dual-porosity/multi-porosity models. However, the determination of the flow scenarios and boundary condition remains an ambiguous issue. For example, in former works of Karimi-Fard
et al. [
27] and Gong
et al. [
28], the procedure was carried out in a local upscaling scheme that may result in a large deviation in heterogeneous media. Global upscaling scheme is more widely adopted in other upscaling procedures. However, the global upscaling scheme may be very computationally expensive for large models and therefore hardly be used in real field applications. For example, to solve a simple steady-state pressure field of 10 million grids in global fine-scale with algebraic multigrid (AMG) linear solver will cost at least 8 GB memories which are hardly affordable for most personal computers. In addition, there are always some negative transmissibilities that need special treatment.
Chen and Durlofsky [
29,
30,
31,
32] introduced an adaptive local-global (ALG) iterative upscaling technique to account for global flow effects without global fine-scale solutions. The main idea is to use a global coarse-scale pressure solution to determine boundary conditions of local fine-scale regions for computation of upscaled quantities. Using these quantities, another coarse-scale solution may be computed, and the process is repeated until the computed quantities are self-consistent. Near-well effects are incorporated directly into the coarse-scale description. Compared to existing pure local upscaling methods, the technique causes only a modest raise of computational cost but can significantly improve the accuracy of the coarse simulation results. However, the technique was only designed for Cartesian grids and applied in 2-D reservoirs without fractures.
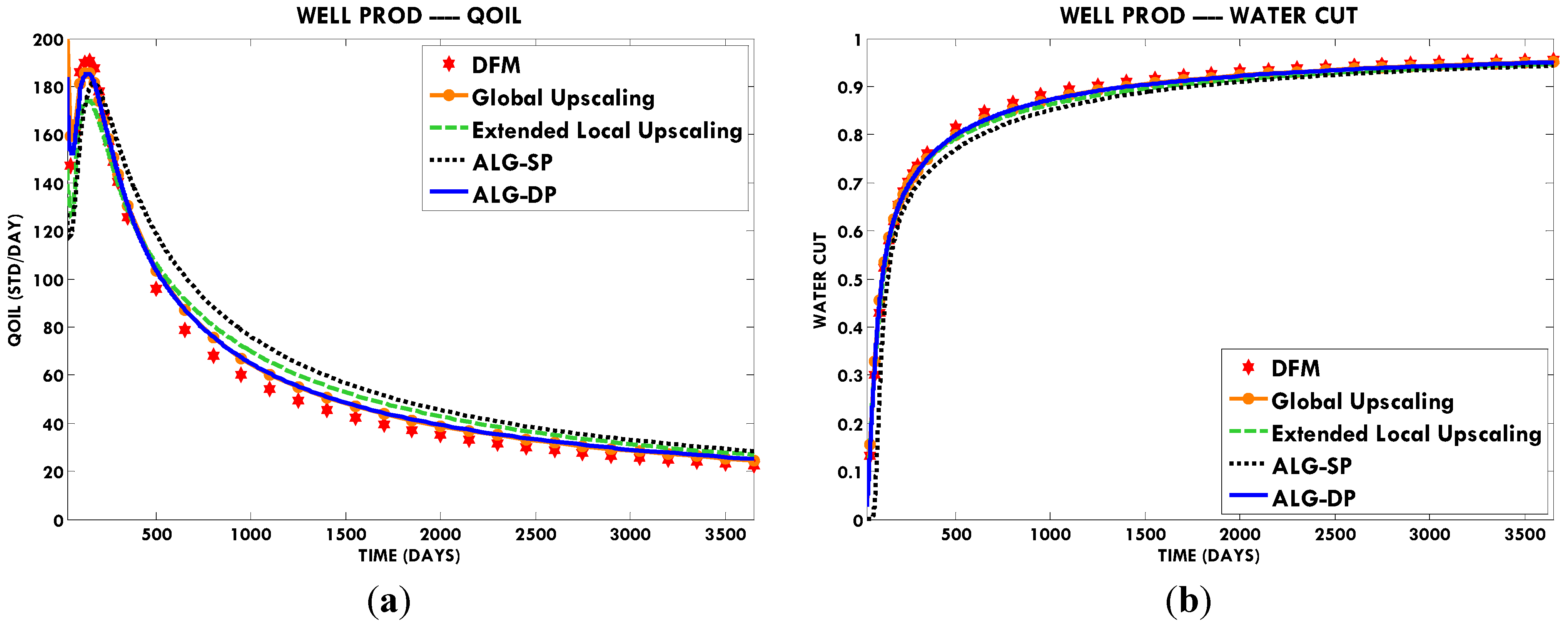
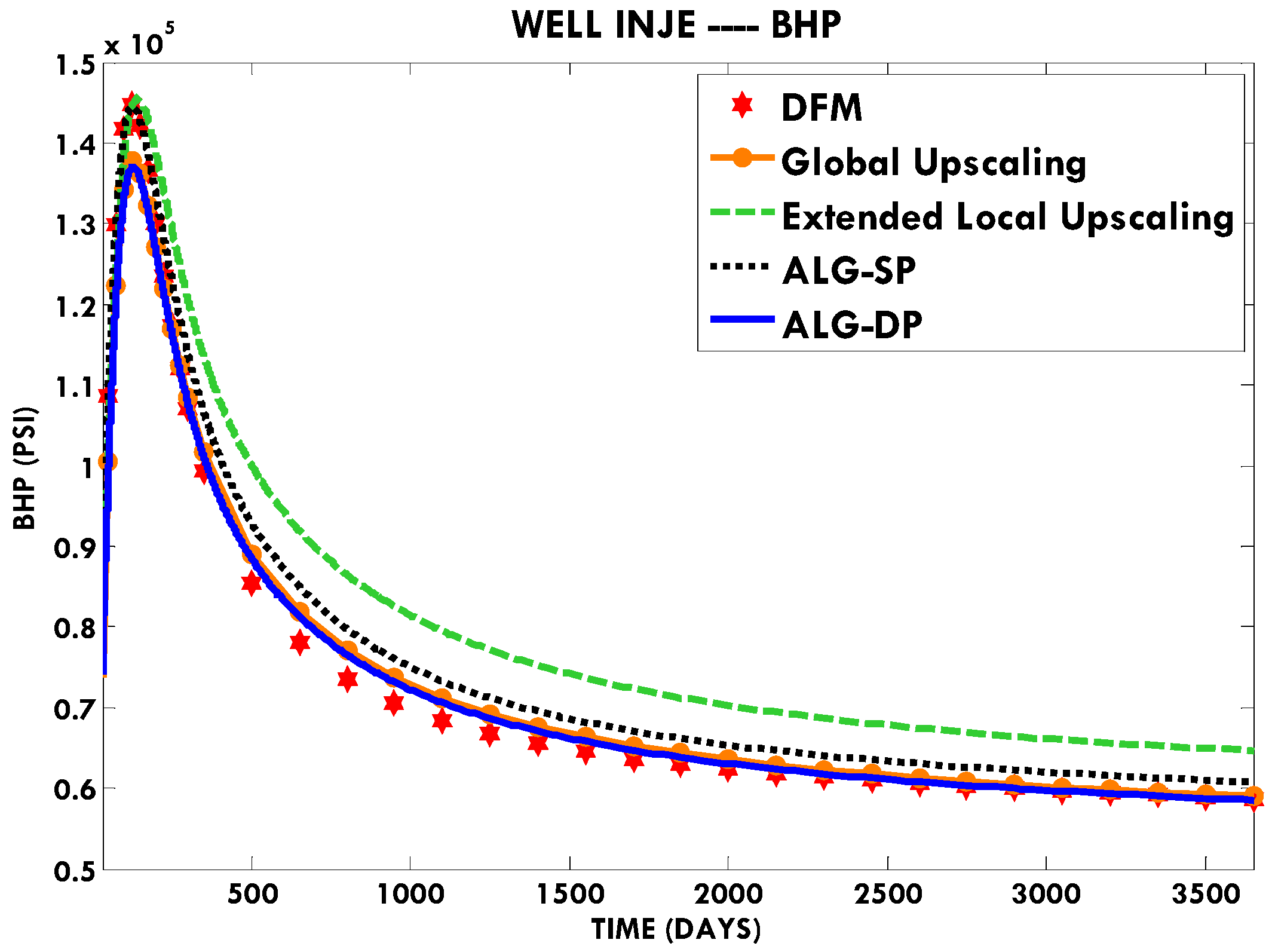
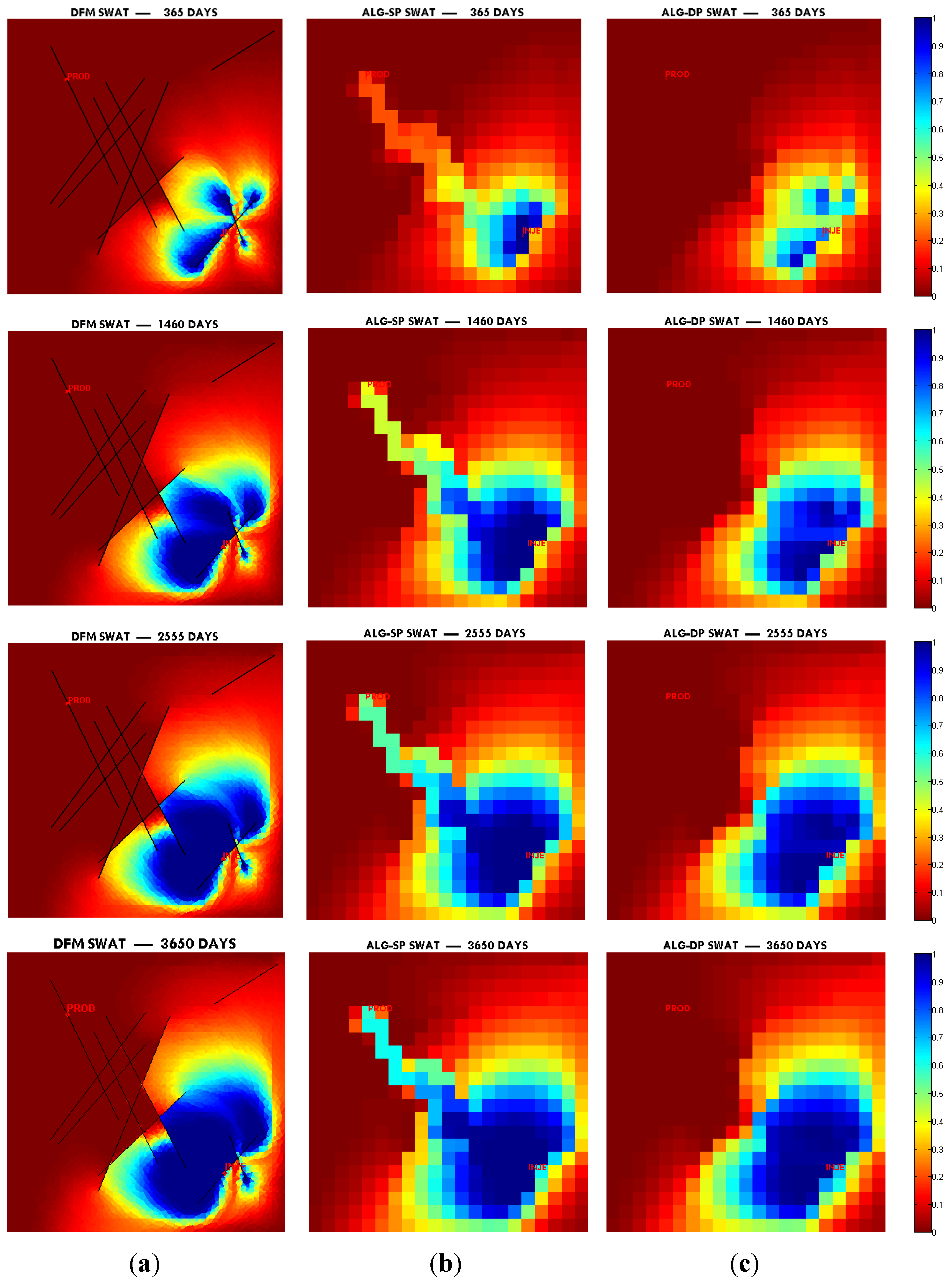
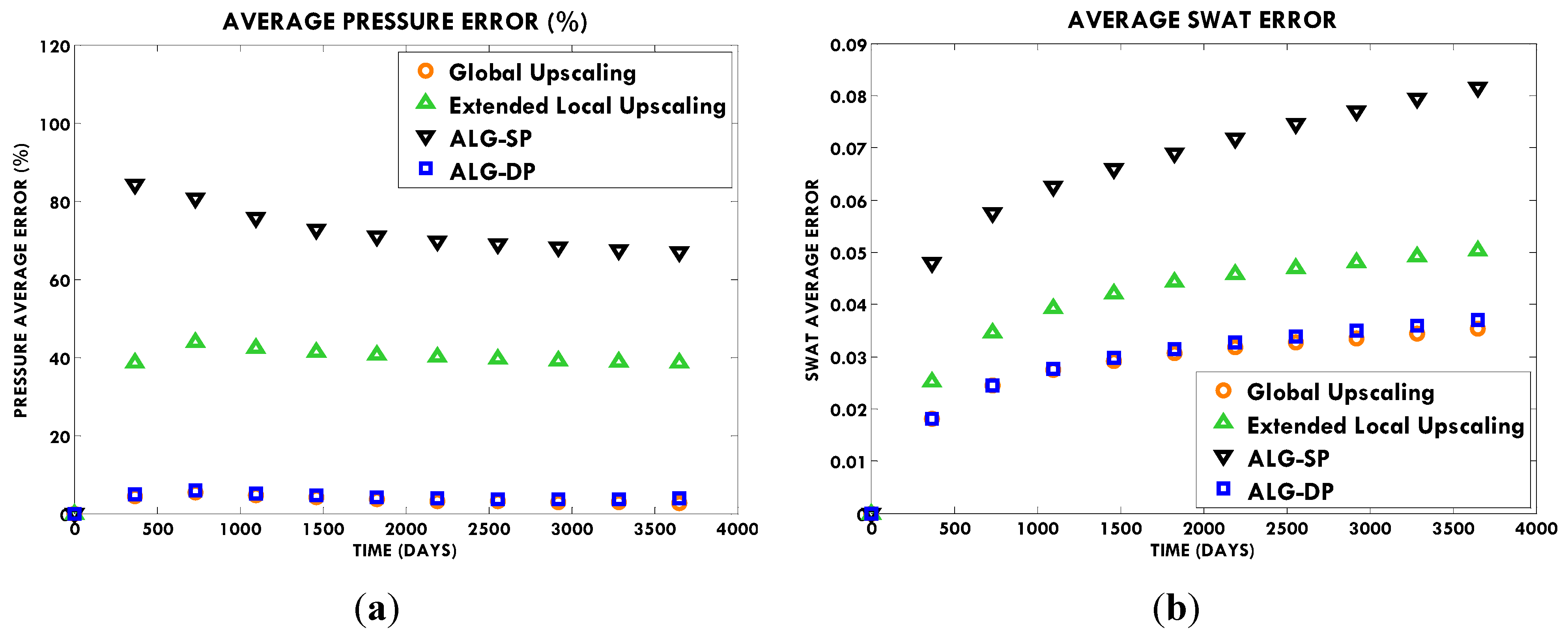
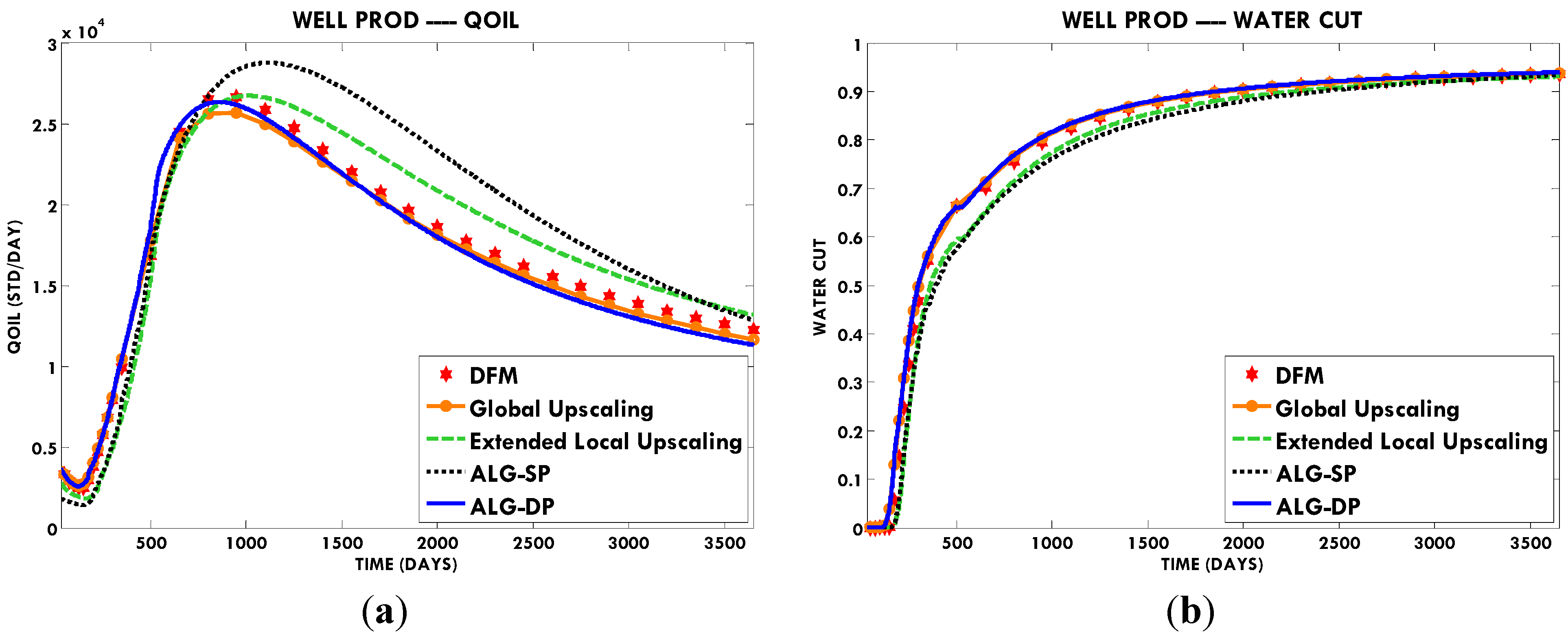
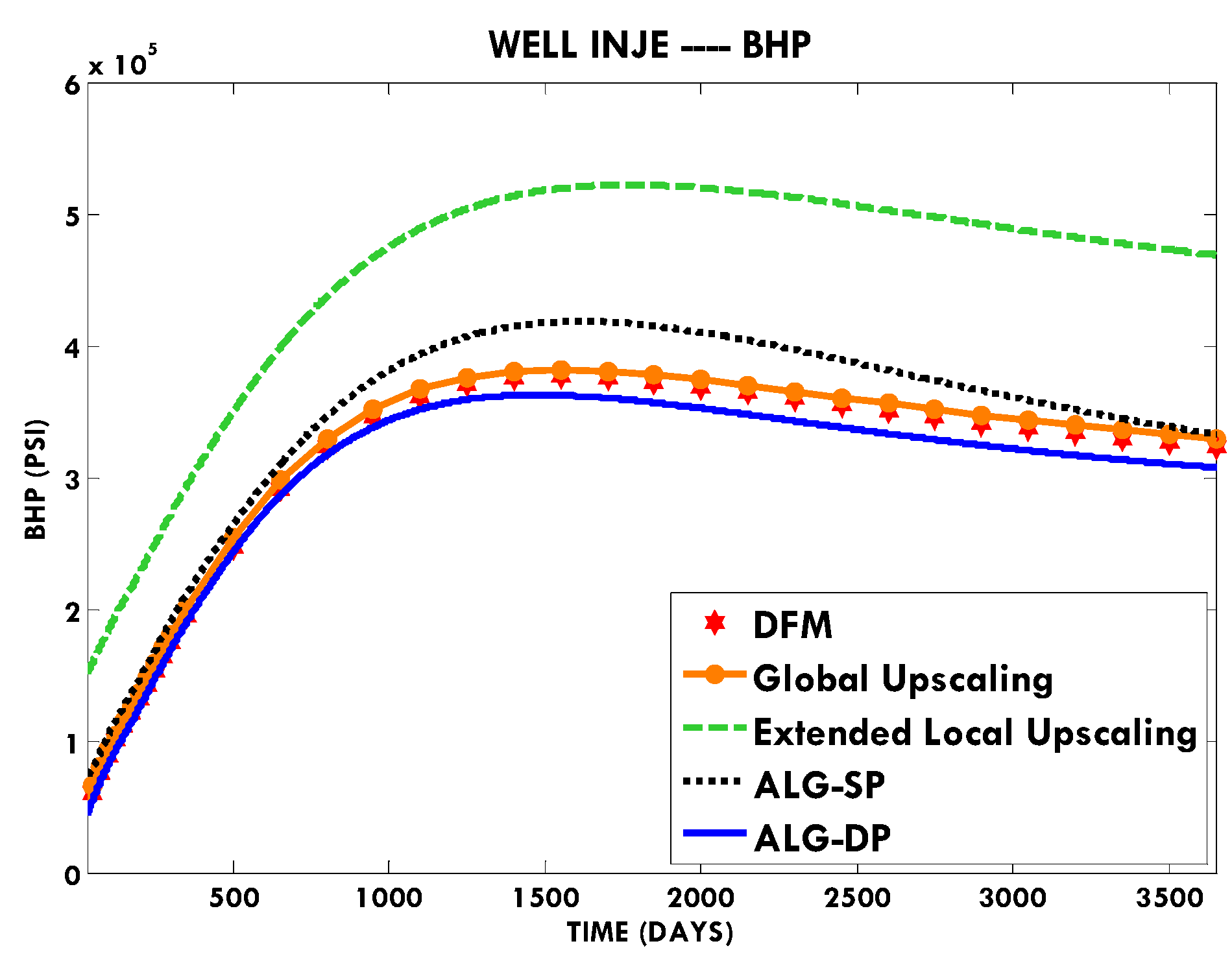
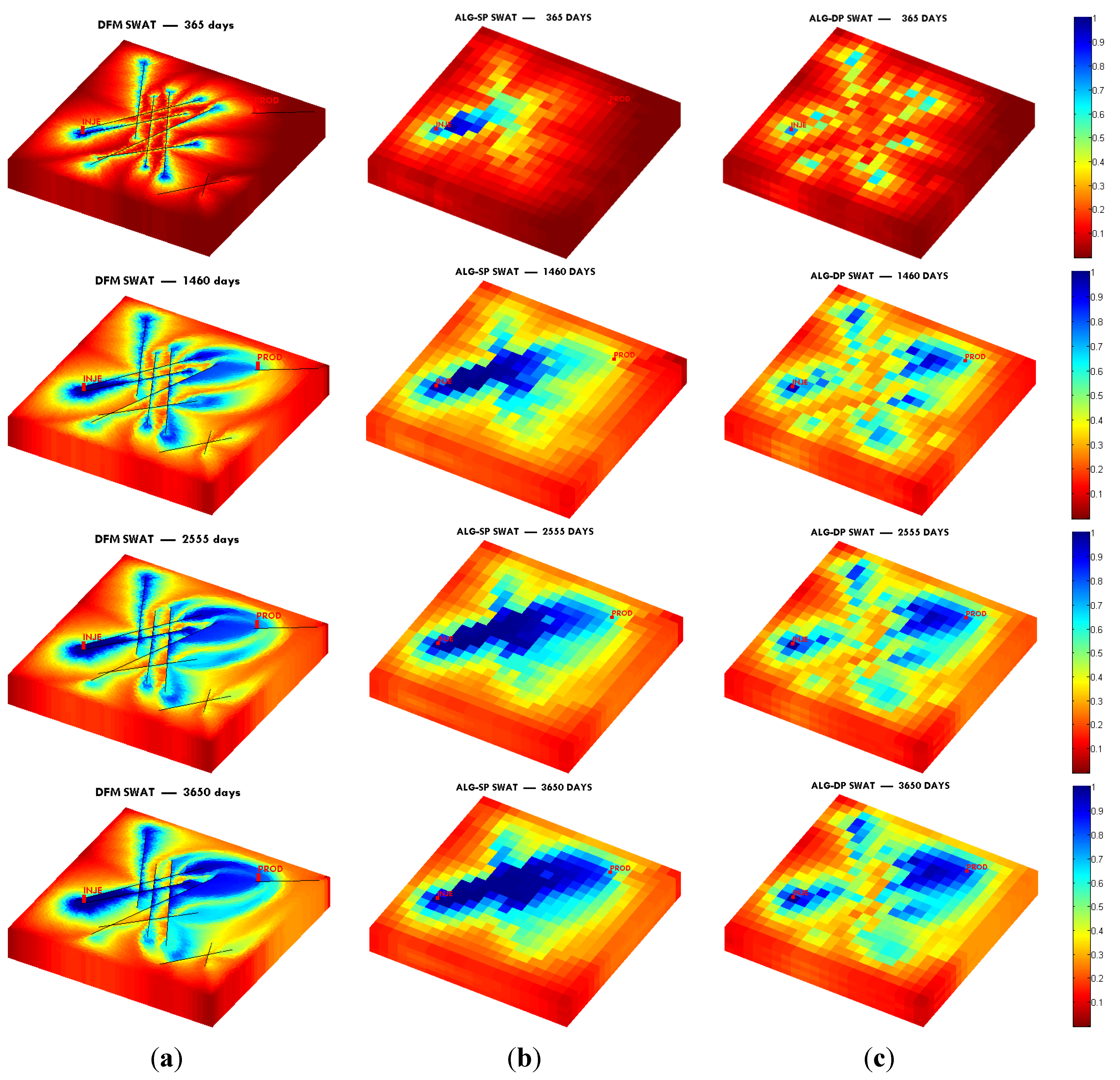
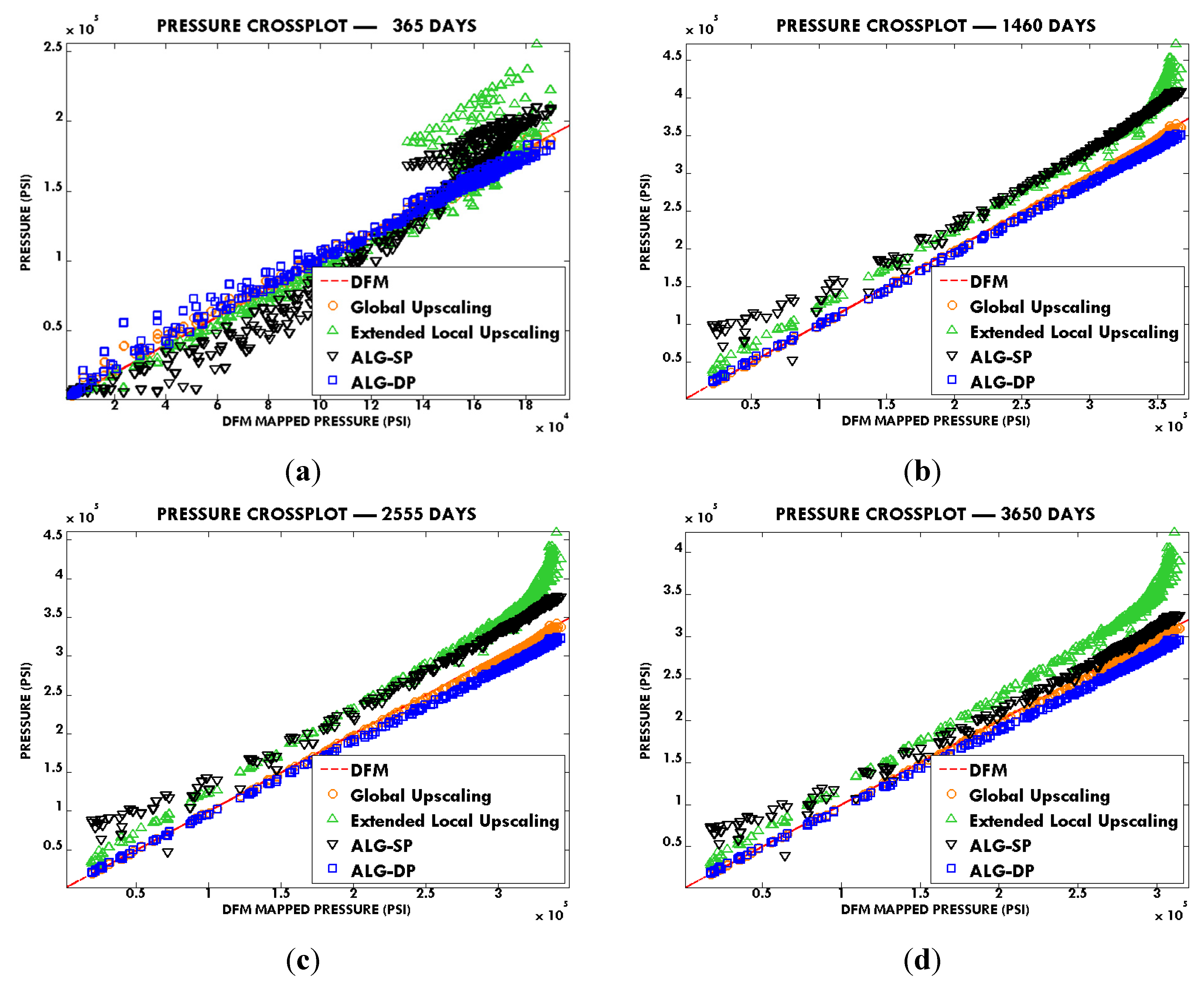
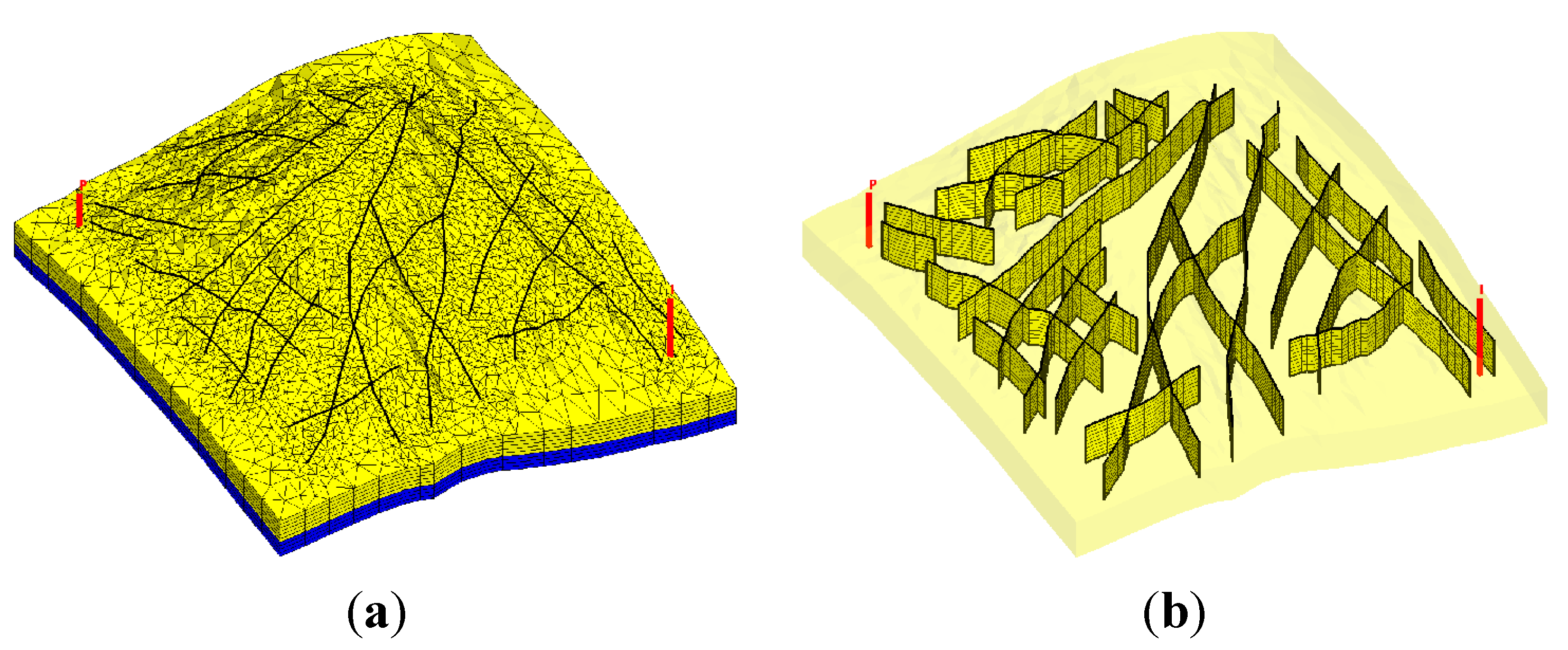
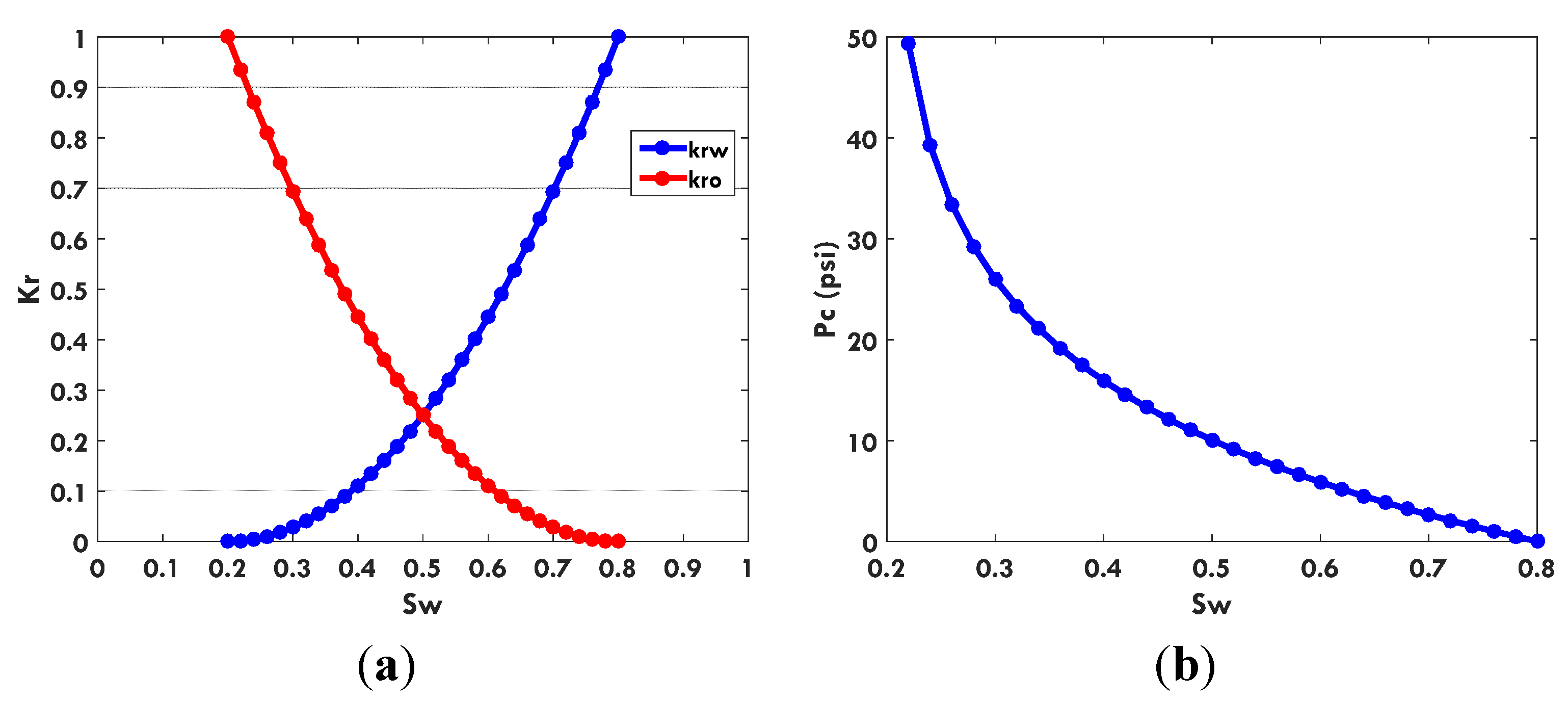
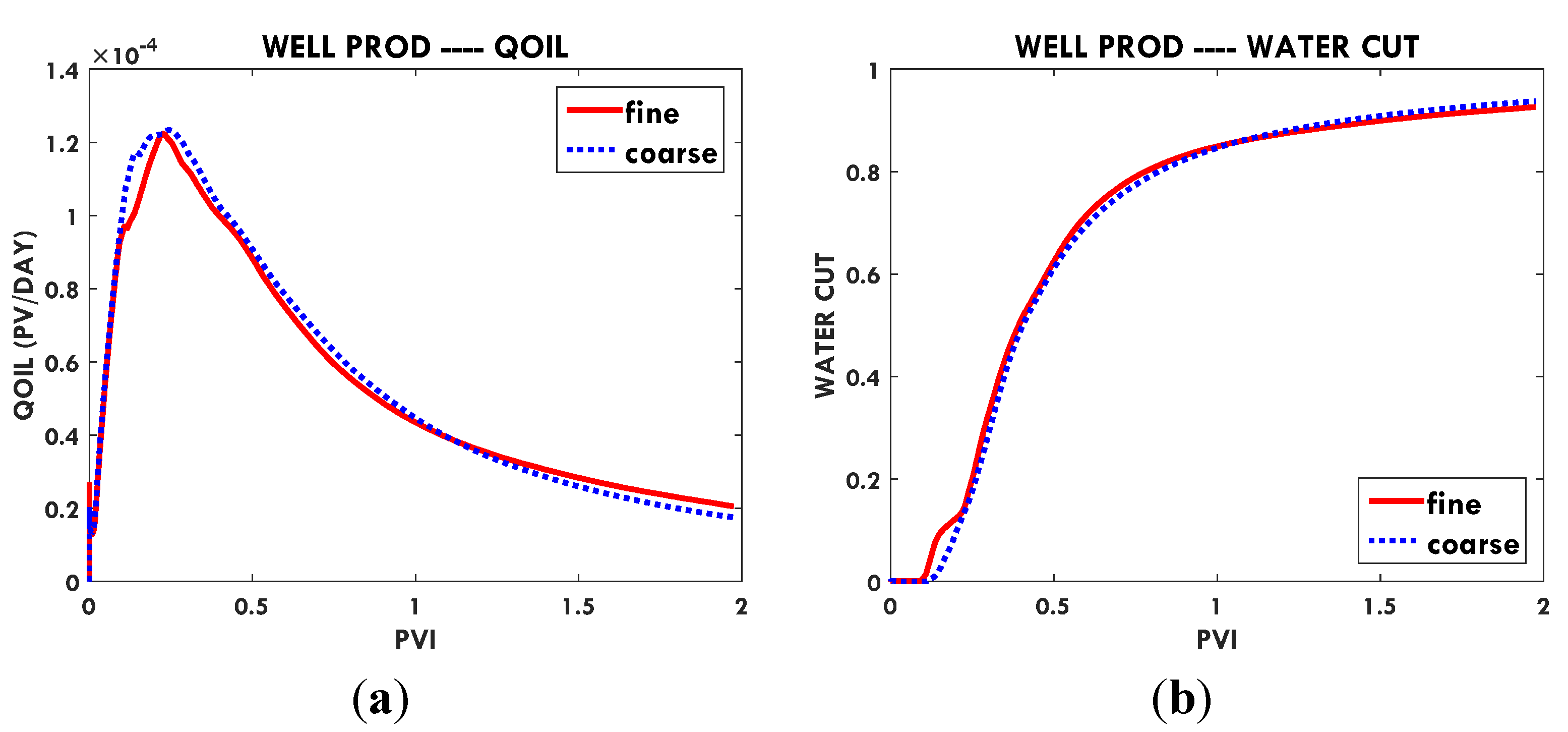
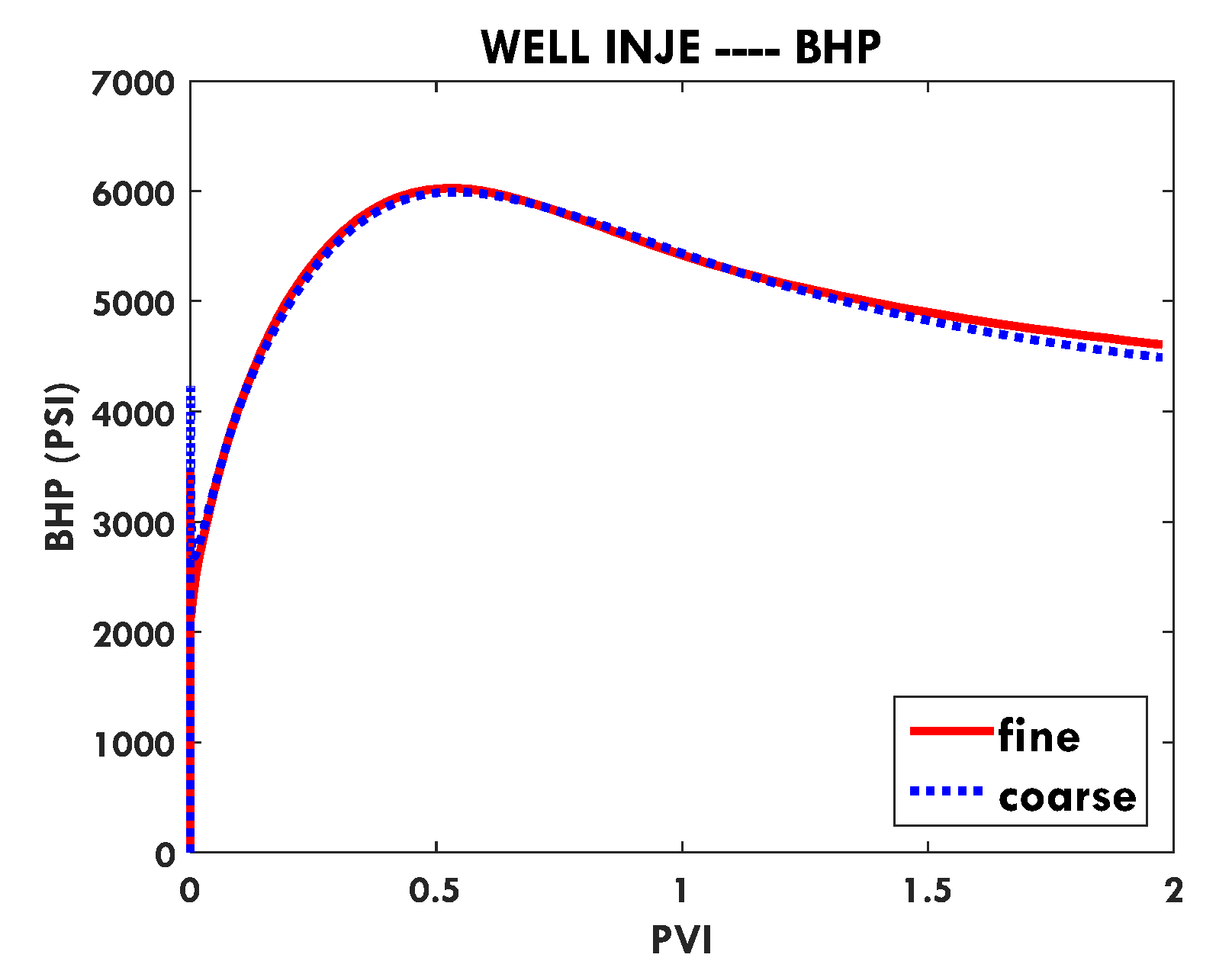
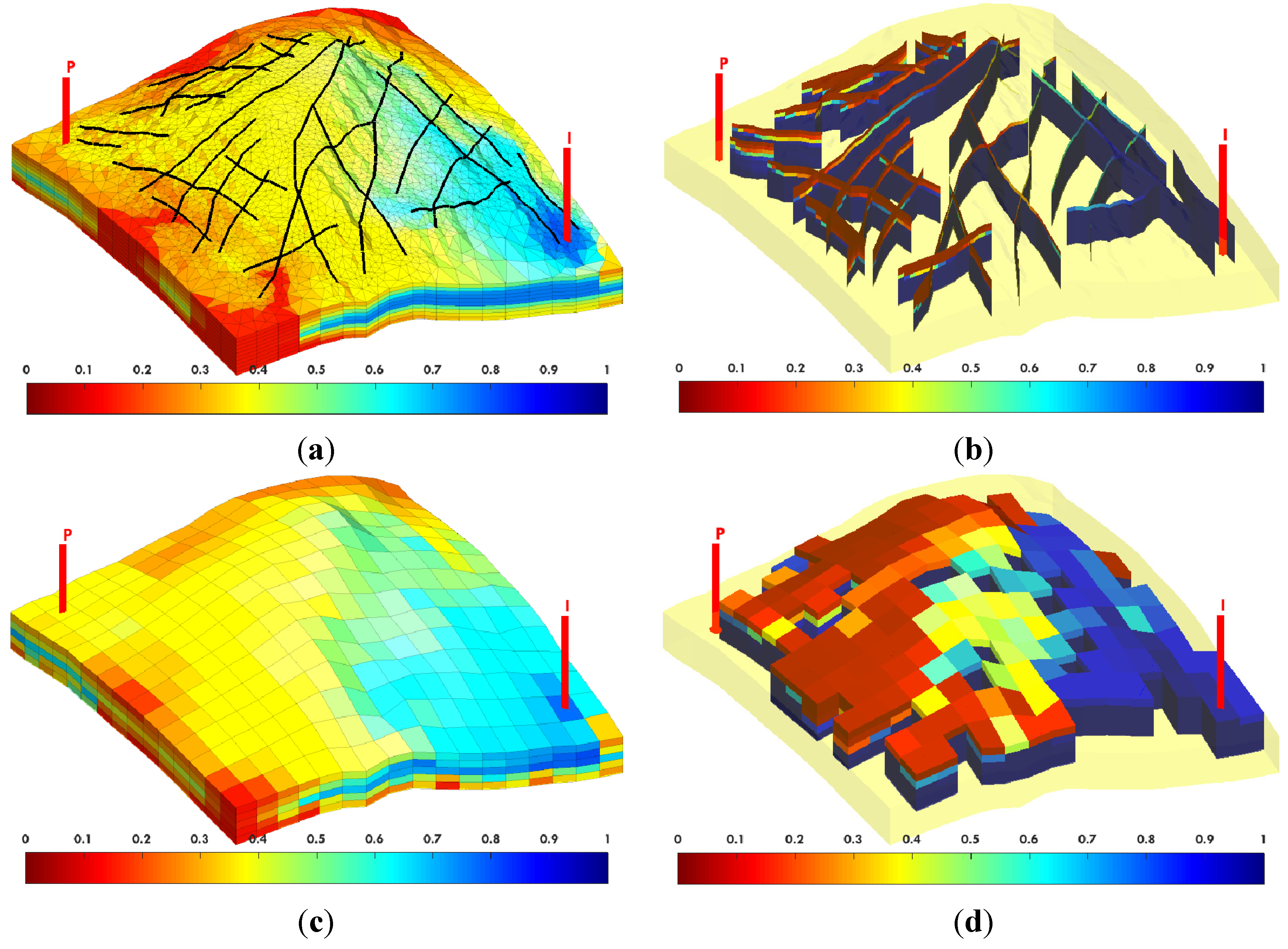
In this paper, we extend the single-phase local-global upscaling approach to handle discrete fractured models based on unstructured grids to construct coarse-scale DPDK models. The fine-scale discrete fractured models are performed under a finite volume scheme. The technique is designed to handle both 2-D and 3-D discrete fracture models based on unstructured grids. This method is applied in several fractured reservoir models. Results demonstrate that the technique is capable of generating highly accurate coarse models from fully-resolved DFMs.
2. Methodology
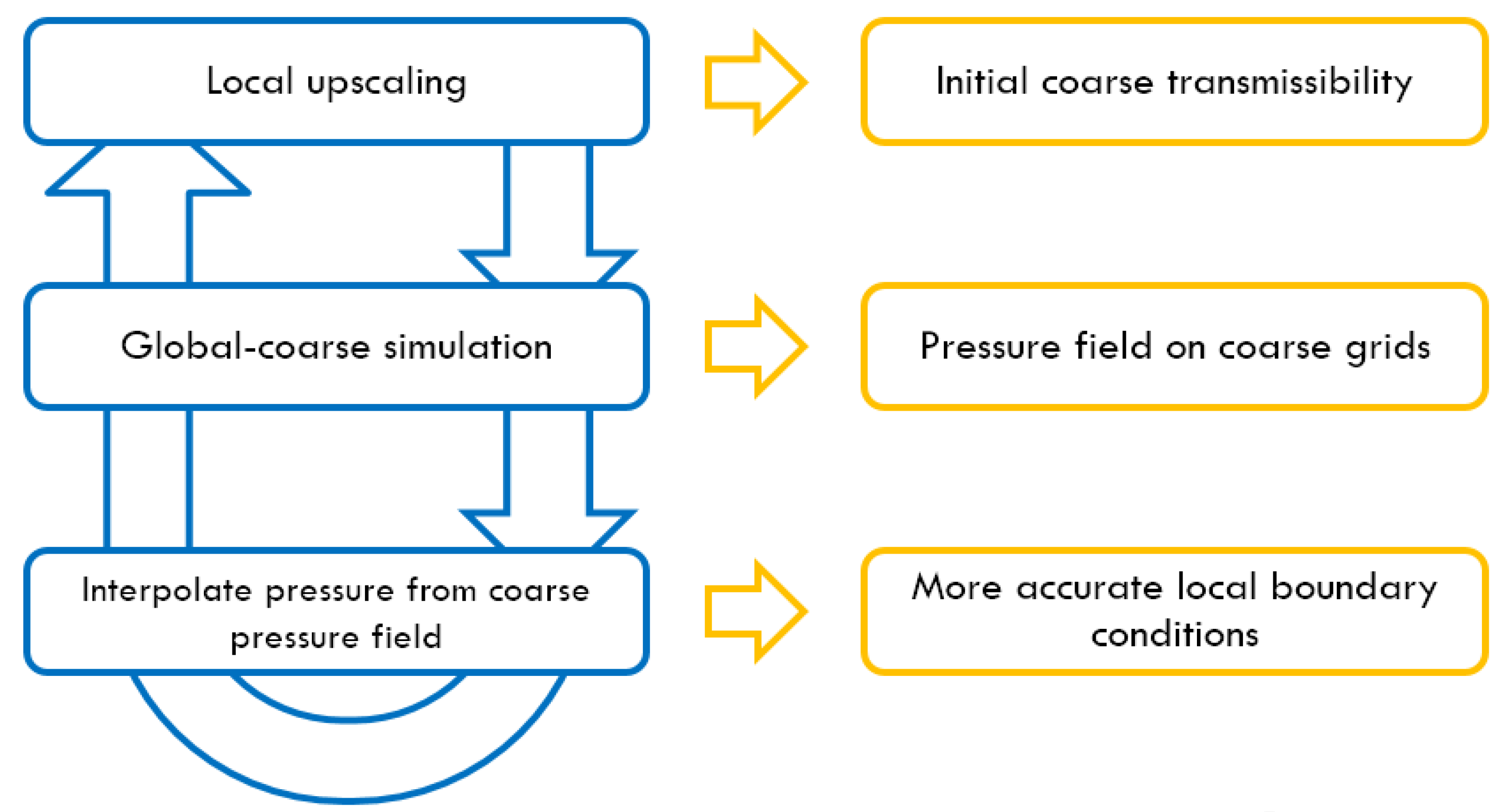
The workflow of the proposed method is shown in
Figure 1: (1) A standard extended local upscaling procedure is performed at first and the initial set of DPDK transmissibilities of coarse grids is obtained; (2) Using the initial transmissibilities, a single phase steady-state flow is simulated to generate a preliminary pressure field of the global coarse-scale model; (3) An interpolation technique is applied to construct a series of boundary conditions for each extended local region; (4) Extended local upscaling procedures are performed again with the boundary condition updated in previous step to gain a new set of coarse grid transmissibilities; (5) Repeat the procedures until differences of flow rates or pressures between two iterations get small enough, and a list of transmissibilities of the coarse-scale DPDK model is finally determined.
Figure 1.
Workflow of local-global upscaling technique.
Figure 1.
Workflow of local-global upscaling technique.
2.1. Fine-Coarse-Scale Grids Preparation
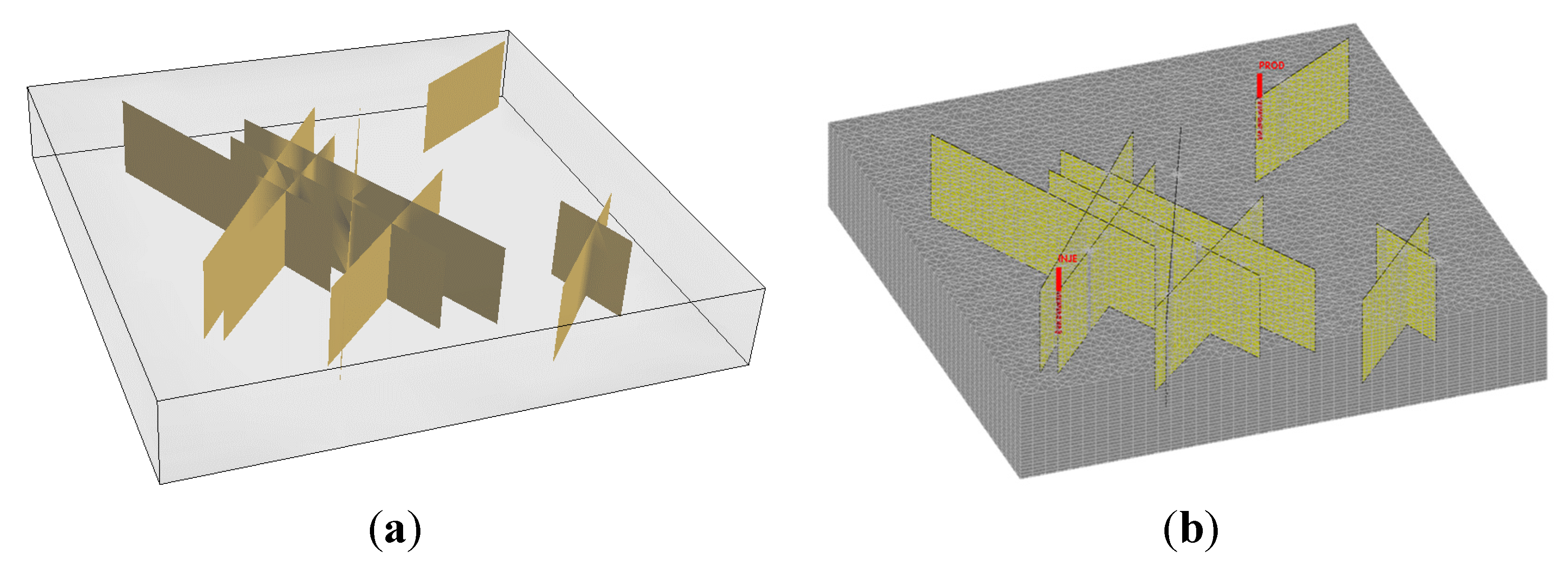
An unstructured grid fully conforming to the geometry constrains of the fracture networks is generated using Triangle [
33]/TetGen [
34] program. Based on this unstructured mesh, the fine-scale discrete fracture model is thus characterized through cell volume, porosity, permeability and depth information and a connection list of the control volumes. The corresponding transmissibility of each connected control volume pair is calculated following the technique by Karimi-Fard
et al. [
13]. For two-point flux approximations as applied in this study, the flow between two adjacent control volumes is proportional to the pressure difference between them and is written as Equation (1):
Here,
denotes the phase;
is the density of phase
;
and
are the pressures associated to cells
and
, and
is the transmissibility, which depends on the geometry of the control volumes and the permeability of the system.
The fine-scale DFM grids act as the geometry foundation of the entire upscaling workflow. The extensions and boundary grids of each local region are computed after the coarse model is determined. Then, the fine-scale connection list is applied in the upscaling computations in extended local regions to obtain transmissibilities of the coarse model. In addition, the fine-scale model provides the reference solutions used to validate the upscaled model.
Equations (2) and (3) are used to calculate volume and porosity for the coarse simulation block
respectively:
where
,
and
are the total volume, matrix volume and fracture volume of coarse block
, respectively;
and
are fine matrix grid number and fine fracture grid number in the block
;
and
are the fine grid volume and fine fracture grid volume which index is
;
denotes the matrix (
)/fracture medium (
);
is the porosity of coarse
-medium grid
and
is the porosity of fine
-medium grid
, respectively.
2.2. Adaptive Extended Local Upscaling for Coarse Block Transmissibility Calculation
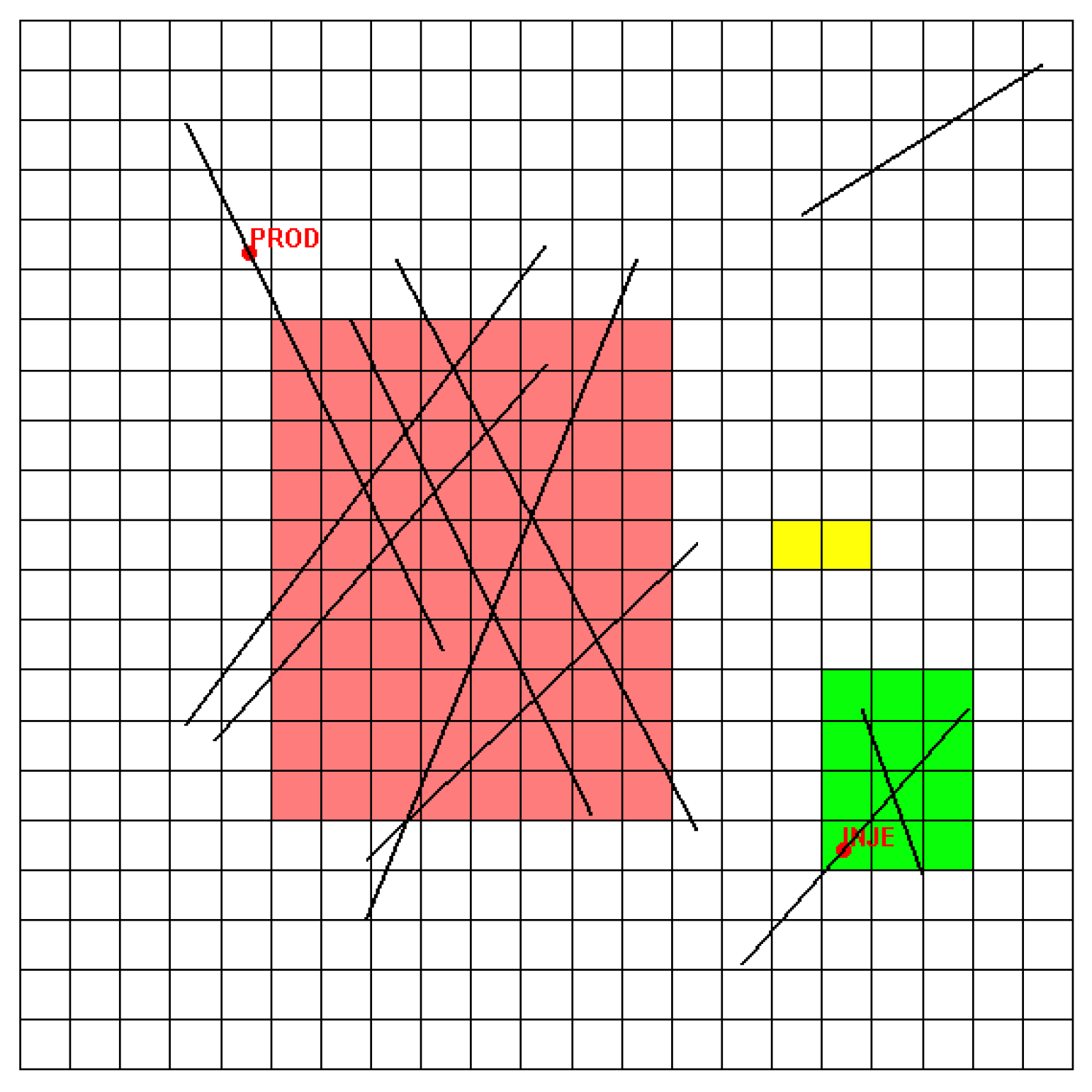
A given coarse block typically contains a network of fractures. The local boundary conditions have to be represented carefully in regions with high fracture density. In order to balance the computational accuracy and efficiency, the extended range of each local region is determined according to fracture density (P32). That is, the more fractures the coarse block contains, the larger local region will be used.
In addition to the fracture networks, well locations and conditions also have a strong impact on the flow. In former ALG works, a well region is considered separately to calculate well index. During local upscaling procedures, however, wells are excluded when determining transmissibilities. Besides, the radial distribution of pressure in near-well regions may also affect the boundary pressure interpolation, as will be discussed in
Section 2.4. For these reasons, we introduce a well priority strategy that appends well boundary conditions once any wells are located inside the local region (as the green region shows in
Figure 2). Note that, despite the fact that well conditions are included in a number of local regions during the entire workflow, the well properties,
i.e., well indices, are still computed and updated in the well regions.
Figure 2.
Adaptive extended local determination and near-well local region (region fracture density: red > green > yellow; the green local region has an injection well inside it).
Figure 2.
Adaptive extended local determination and near-well local region (region fracture density: red > green > yellow; the green local region has an injection well inside it).
Then, a single-phase incompressible solution of local pressure field is determined to count detailed matrix-matrix and fracture-fracture flow between adjacent coarse blocks and matrix-fracture flow exchange inside block. Balance equations of this type are written as Equation (4):
With impermeable (zero flux) boundaries at first step and specific constant pressure boundaries latter respectively, the mass balance equations are solved to obtain pressure fields of local regions. Equation (5) is then used to compute coarse-scale transmissibilities:
Here,
is the transmissibility between coarse block
and
;
is the total flow from coarse block
to
;
and
are the coarse block pressures, which can be calculated by Equations (6) and (7):
2.3. Global Solution under Coarse Grids
Using the connection list achieved above, it is easy to calculate the global single phase steady-state solution under coarse grids. For each local region, therefore, we can use the pressures of the coarse blocks to interpolate the pressures of the fine boundary blocks for the next iteration, which will be introduced below. This interpolation procedure updates the situation of extended local regions and is expected to improve the upscaled transmissibilities of the next extended local solution.
2.4. Pressure Interpolation Policy of Extended Local Boundary
Former ALG studies adopted a half grid extension for each local region. This treatment is quite convenient for Cartesian grids because the boundary fine cells are exactly on the lines connecting center points of coarse cells. In DFM upscaling procedures, however, it can hardly follow the strategy because the half range of a grid is difficult to determine and the relative position between fine and coarse grid centers is random due to the fine-scale grid is unstructured. In addition, former pressure interpolation uses a simple assumption of linear distribution of coarse pressure filed as shown in Equation (8):
Here,
means the distance with a positive direction from
to
.
Equation (8) implies a totally linear pressure field around target local region, which may result in a bias in some situations. In the case where high heterogeneity exists or in near-well regions with high-speed radial flow, the deviation may be quite large. Therefore, in fracture reservoirs, it is necessary to distinguish the matrix and fracture media when interpolating boundary pressures.
Since transmissibility is a measurement of connectivity, the adjacent cells with higher transmissibility tend to have a closer pressure with the pressure propagation. Therefore, we use a transmissibility and inverse-distance related weighted strategy to determine the local fine boundary pressures. For example, to determine the pressure of the target fine block
, the weight of a specific coarse block
must be positively-correlated to transmissibility between
and
, and be negatively-correlated to distance between
and
, as shown in Equations (9) and (10):
Here, the
is the set containing all fine-scale connection pairs from coarse cell
to
, is the distance from center of fine-scale cell
to center of coarse-scale cell
.
2.5. Iteration Procedures and Convergence Condition
The procedures described above are iterated until convergence is obtained. Convergence here represents self-consistency between the global coarse-scale solution and upscaled properties. The convergence criteria are based on the changes in pressure or flow rate from one iteration to the next. Specific values used here are as Equation (11):
Here,
is the coarse-scale flow difference between block
and
in the
-th iteration;
is a threshold value defined according to specific models. Smaller
is, stricter the iteration convergence condition will be.
We also set a maximum iteration number in case that sometimes it is not going to convergent to upscale a DFM model due to the high sensitivities of fracture conductivities. However, as we can find out in our cases, the simulation results after several iterations are going to convergent although the criteria above may not be reached.